High-frequency click-evoked otoacoustic emissions and behavioral thresholds in humans

Abstract

Relationships between click-evoked otoacoustic emissions (CEOAEs) and behavioral thresholds have not been explored above 5 kHz due to limitations in CEOAE measurement procedures. New techniques were used to measure behavioral thresholds and CEOAEs up to 16 kHz. A long cylindrical tube of 8 mm diameter, serving as a reflectionless termination, was used to calibrate audiometric stimuli and design a wideband CEOAE stimulus. A second click was presented 15 dB above a probe click level that varied over a 44 dB range, and a nonlinear residual procedure extracted a CEOAE from these click responses. In some subjects (age 14–29 years) with normal hearing up to 8 kHz, CEOAE spectral energy and latency were measured up to 16 kHz. Audiometric thresholds were measured using an adaptive yes-no procedure. Comparison of CEOAE and behavioral thresholds suggested a clinical potential of using CEOAEs to screen for high-frequency hearing loss. CEOAE latencies determined from the peak of averaged, filtered temporal envelopes decreased to 1 ms with increasing frequency up to 16 kHz. Individual CEOAE envelopes included both compressively growing longer-delay components consistent with a coherent-reflection source and linearly or expansively growing shorter-delay components consistent with a distortion source. Envelope delays of both components were approximately invariant with level.

INTRODUCTION

In response to a short-duration sound presented in the ear canal, a click-evoked otoacoustic emission (CEOAE) is generated within the cochlea and transmitted back through the middle ear into the ear canal, where it is detected using a miniature microphone (Kemp, 1978). The fact that a normal-functioning cochlea produces greater CEOAE signal energy than an impaired cochlea has led to the use of CEOAE testing to identify ears with a sensorineural hearing loss. Common techniques of measuring CEOAEs reviewed below share the property that the upper frequency of the CEOAE spectral response is limited to approximately 5 kHz. This also serves as the upper frequency of hearing for which a hearing loss can be identified using a CEOAE test. This report presents results showing a new form of CEOAE test, which can be used to measure CEOAE spectral energy and CEOAE latency up to 16 kHz in subjects with normal high-frequency hearing. The problem of measuring high-frequency CEOAEs is intimately related to the problem of assessing behavioral thresholds at high frequencies. A new incident-pressure technique to measure high-frequency audiometric thresholds is described that avoids effects of standing waves within the coupler used to calibrate the threshold sound pressure level (SPL).

This section reviews calibration issues related to the assessment of high-frequency hearing, followed by an overview of the procedure used to measure high-frequency CEOAEs. Methodological issues related to the measurement of behavioral thresholds and high-frequency calibration of the probe used to measure CEOAEs are next discussed. The experimental results of measurements of high-frequency CEOAEs are presented, which demonstrate the ability to measure level and latency responses in some ears up to 16 kHz. Potential applications of such a CEOAE test are described to highlight its possible utilization in audiological screening and diagnostic tests and as a probe of cochlear mechanics at high frequencies in human ears.

Assessment of high-frequency hearing

While normal-hearing humans can detect sound energy at frequencies up to 20 kHz, clinical hearing assessment, both behavioral and physiological, typically examines hearing only up to 8 kHz. One reason is that the majority of speech signals are present at frequencies of 8 kHz and below. Therefore, while the ability to hear at higher frequencies contributes to listening to music or other nonspeech auditory signals, sensitivity at the higher frequencies is usually of lesser concern. Another reason may be that responses at frequencies above 8 kHz are more difficult to measure accurately due to the short wavelengths involved and the increased difficulties of audiometry at high frequencies.

Nevertheless, there are situations where audiometric threshold measurements at frequencies above 8 kHz may be useful. Ototoxic damage to the cochlea typically occurs at the basal end of the cochlea and proceeds apically (Brummett, 1980; Konishi et al., 1983; Komune et al., 1981; Nakai et al., 1982; Schweitzer et al., 1984). Tests for detecting ototoxic hearing loss are therefore most sensitive at high frequencies, whether tested behaviorally (Dreschler et al., 1989; Fausti et al., 1999, 2003; Ress et al., 1999; Tange et al., 1985; van der Hulst et al. 1988) or using otoacoustic emissions (OAEs) (Mulheran and Degg, 1997; Ress et al., 1999; Stavroulaki et al., 2001; Stavroulaki et al., 2002). The measurement of behavioral thresholds and OAEs above 8 kHz may also be useful for detection of and∕or monitoring noise induced hearing loss (Kuronen et al., 2003), presbycusis (Lee et al., 2005; Matthews et al., 1997), high-frequency loss associated with otitis media (Margolis et al., 2000; Hunter et al., 1996), and possibly loss associated with other etiologies. The ability to noninvasively assess physiological correlates to hearing over the full bandwidth of hearing would also help improve our understanding of cochlear and middle-ear mechanics in human ears at high frequencies.

One of the main difficulties with high-frequency threshold testing is calibration error arising from acoustic standing waves. Measurements SPL, whether made in the ear canal or a mechanical coupler, have pressure minima at the microphone relative to the eardrum or terminating wall of the coupler. These minima are present near frequencies having quarter wavelengths equal to the distance between the microphone and the termination (to the extent that the acoustic volume velocity is approximately zero at the termination). At yet higher frequencies, alternating maxima and minima of SPL are present in the ear canal. The difference in SPL between the microphone and eardrum can be as large as 20 dB (Stinson et al., 1982; Siegel, 1994). Such differences may result in underestimation of the pressure at the eardrum, so that calibrated output levels are too high.

Various methods have been proposed to overcome these difficulties at high frequencies. Threshold-measurement systems have been calibrated up to 16–20 kHz based on measured responses in a flat-plate coupler (Fausti et al., 1979). High-frequency thresholds calibrated in this manner were elevated in subjects with a history of noise exposure compared to thresholds in young adults (Fausti et al., 1981). To estimate SPL at the eardrum in individual ears, Stevens et al. (1987) used a sound delivery system to the ear canal through a lossy cylindrical tube of 60 cm length between the sound source and ear canal. Their calibration involved fitting a model to the ear-canal spectrum to remove its zeros, indicative of standing-wave minima in the ear canal, and thus produce a spectrum that varied slowly with frequency. Because evanescent modes in the ear canal produce the largest effects at the frequencies at which the single propagating mode has a minimum, this calibration may have been influenced by evanescent modes. Stevens et al. (1987) also showed a frequency-response spectrum of the sound delivery system coupled to a long reflectionless cylindrical tube, and this spectrum was without of any standing-wave effects up to 20 kHz. This system was used to measure thresholds up to 20 kHz (Green et al., 1987) in terms of both the voltage level applied to the source transducer as well as an extrapolation of SPL to high frequencies based on the fitting model. Green et al. (1987) concluded that a substantial number of subjects would have thresholds determined at the higher frequencies that might be in error by 10 dB or more.

Stelmachowicz et al. (1988) reported measurements using the audiometer of Stevens et al. (1987) and found increased variability of thresholds using the extrapolated SPL approach than the input voltage-level approach. Thresholds measured using a system calibrated with supra-aural headphones on a flat-plate coupler were more reliable above 11 kHz than those calibrated with the audiometer of Stevens et al. (1987) (Stelmachowicz et al., 1989b). These studies indicate the complexity of estimating the SPL at the eardrum at high frequencies. With the simpler goal of calibrating in a flat-plate coupler and not attempting to estimate SPL at the eardrum, normative threshold data in the 8–20 kHz range were more elevated in older subjects relative to thresholds for the youngest age group (10–19 years) (Stelmachowicz et al., 1989a).

ANSI S3.6 (2004) (Specification for Audiometers) describes coupler calibration of headphones for testing up to 16 kHz. However, the standard describes only the use of circumaural headphones, which are not typically used in OAE testing; it contains no recommendation of a calibration technique to use with insert earphones, which are routinely used for audiometric and OAE measurements. One possible solution is to simply calibrate at frequencies below 2–3 kHz, determine the voltage level applied to the sound source that is required to generate a given SPL in an ear or coupler, and then use that same voltage to generate sound at higher frequencies. This constant-voltage method assumes that the acoustical output spectra of the transducers are relatively flat within the frequency range of interest. In practice, the output of many transducers rolls off at frequencies above 5–8 kHz.

High-frequency calibration errors may be reduced if an ear-canal simulator is used whose length matches the length of the ear canal of the subject being tested (Gilman and Dirks, 1986). Because of large variability in ear-canal lengths (Stinson and Lawton, 1989; Kruger and Rubin, 1987), subjects’ ear-canal lengths would need to be measured individually using, for instance, an operating microscope (Zemplenyi et al., 1985). A further problem is that the tympanic membrane lies at an oblique axis to that of the ear canal, so that the ear-canal length is not uniquely specified. Another calibration method is to attach a probe tube to the microphone and place it very close to the eardrum. The small radius and long length of such a probe tube attenuate high frequencies, which may limit its usefulness for recording low-level OAEs. Precise placement of the probe tube is required for this method. Chan and Geisler (1990) described an acoustic method, utilizing the presence of standing waves in the ear canal to locate the probe tip near the eardrum. Dreisbach and Siegel (2001) used an endoscope to aid in placing a probe tube very close to the eardrum. Depth of insertion was adjusted so that pressure minima in probe-tube responses were shifted above 20 kHz. While these methods have been successfully used in research settings, their practical use in the clinic may be limited because of increased test time.

Procedure to measure CEOAEs

CEOAEs are low-level sounds produced by the healthy cochlea in response to a brief acoustic stimulus (see Probst et al., 1991 for a review). CEOAEs are widely used in newborn screening protocols and are also used to test young children and difficult-to-test patients. By virtue of their short duration, CEOAE stimuli are broadband and therefore can be used to measure a response over a wide range of frequencies. In principle, a very broad range could be tested, from 0 Hz up to $\frac{1}{2}$ the sample rate of digitized signals, but measurement limitations have constrained CEOAE studies to frequencies up to approximately 4 kHz (Probst et al., 1991).

It should be noted that distortion-product OAEs have been measured in human ears up to 16 kHz (Dreisbach and Siegel, 2001; Dreisbach and Siegel, 2005) with adequate repeatability (Dreisbach et al., 2006). Stimulus-frequency OAEs (SFOAEs) have also been measured up to 14 kHz (Dreisbach et al., 1998). The ability to measure CEOAEs to high frequencies would complement the existing large literature relating to CEOAE measurements at lower frequencies, as well as studies based on measurements of high-frequency Distortion Product Otoacoustic Emissions (DPOAEs) and SFOAEs. CEOAEs have the advantage that a broad bandwidth of cochlear response is assessed in a single time-averaged response.

In practice, however, the CEOAE bandwidth may be limited by several factors. An electrical impulse is often used as the stimulus input to the sound source (earphone) producing the click used to evoke a CEOAE response. However, the earphones, which transduce the electrical signal into a sound wave, may not have a sufficiently flat magnitude transfer function extending into the high frequencies. As a result, the click energy at high frequencies may be less than that at lower frequencies, which contribute to the difficulty of detecting high-frequency CEOAEs.

Extraction of high-frequency CEOAEs from the stimulus and noise floor poses special challenges. CEOAEs recorded in human ears are typically on the order of 30 dB smaller than the stimuli that elicit them and may overlap the stimulus in both frequency and time. Low- and midfrequency (<5 kHz) CEOAEs can be extracted by taking advantage of the time it takes for the signal to travel from the eardrum to its characteristic places along the basilar membrane and for the emissions to travel back along the reverse pathway (Kalluri and Shera, 2007; Shera et al., 2007). Because of the tonotopic organization of the cochlea, low-frequency signals travel further along the cochlea and are delayed relative to higher-frequency signals. Based on an assumed source equivalence of CEOAEs and SFOAEs, the expected delays for the 1, 2, 4, 8, and 16 kHz components of CEOAEs are approximately 11, 7.1, 4.6, 3.0, and 1.9 ms (Shera et al., 2002). For one commonly used CEOAE system (Otodynamics ILO 88), the electrical pulse duration delivered to the loudspeaker is on the order of 80 μs, resulting in a biphasic response that decays over 2–3 ms due to the impulse response duration of the earphone and multiple internal reflections between probe and eardrum (Kemp et al., 1990; Glattke and Robinette, 2007). From these durations it can be seen that at frequencies ⩾8 kHz, the emission begins to overlap the acoustic stimulus in time. To avoid stimulus artifact in the CEOAE response, many analysis programs zero the first 2.5 ms of the response waveform and window the onset of the remaining response (Kemp et al., 1990). Based on the expected delay times described above, this process can be expected to eliminate the CEOAE response above 6–8 kHz.

When the stimulus and CEOAE overlap in both time and frequency, they may still be separated by exploiting the nonlinear (i.e., compressive) amplitude growth of the emission. This method has been used in several forms (Kemp and Chum, 1980, Zwicker and Schloth, 1984; Brass and Kemp, 1991; Keefe, 1998; Keefe and Ling, 1998). This technique consists of presenting the stimulus at a relatively low level and recording the resulting ear canal pressure. A second stimulus differing in level, frequency, or both is then presented one or more times, and the ear-canal pressure is again recorded. By appropriate scaling and vector subtraction techniques, the linear portions of the stimulus and emission are canceled. The remaining nonlinear component is thought to consist mostly of the emission. Section 4 describes the CEOAE extraction procedure, in which the initial part of the response was retained, thereby preserving the high-frequency content of the emission.

ADAPTIVE MAXIMUM-LIKELIHOOD PROCEDURE TO MEASURE THRESHOLD

An adaptive maximum-likelihood (ML) procedure that is based on a set of single-interval responses to a yes-no task was used to measure thresholds across the frequency range of hearing. Adaptive ML threshold estimation methods were developed by Green (1993) and generalized by Gu and Green (1994) to include catch trials to decrease the false-alarm rate. ML procedures provide a bias-free automatic technique to assess threshold that is more efficient than other commonly used bias-free threshold-measurement procedures.

The modified adaptive ML procedure used in the present research is described in more detail elsewhere (Keefe et al., 2009). The modification is that the stimulus level in each of the first four trials was selected by randomly choosing without replacement one of these subranges for the trial and then randomly choosing a stimulus level within the subrange. An initial threshold estimate was calculated using the ML estimate based on these initial four yes-no responses. In accord with the Green (1993) procedure, the stimulus level of the fifth and subsequent trials was chosen based on this current threshold estimate. This modified procedure substantially reduced the sensitivity of the usual ML procedure to errors when testing human subjects.

Preliminary data were acquired with a number of trials N as large as 30, and N=15 trials were selected as a sufficiently large number of trials. A false-alarm rate was also estimated. The 15 trials per run included three catch trials in which no stimulus was presented. The order of these three catch trials was uniformly randomized within the last 11 trials of a run. Once N was set at a total of 15 trials, preliminary data were acquired using a greater and lesser number of catch trials before settling on three trials as adequate, corresponding to a catch-trial rate of 20%. The responses to catch trials were included in the ML estimate of threshold and false-alarm rate by assuming that the stimulus level of the catch trial was the minimum stimulus level in the dynamic range.

Finally, if the subject answered No three times in succession, with the stimulus level set at its maximum value, the run was halted before N=15 trials were performed. This condition was not assessed until after the initial four trials. This condition gave sufficiently high confidence that the subject’s threshold was above the maximum stimulus level used by the system.

STIMULUS DESIGN AND CALIBRATION AT HIGH FREQUENCIES

The design of an electrical stimulus to serve as the input to an earphone producing a short-duration acoustic stimulus (a “click”) is complicated by the need for a wide stimulus bandwidth. Part of the complexity resides in the bandwidth limitations of existing earphones used in OAE probes, and another part has to do with how the sound output from the probe is calibrated at high frequencies.

Historically, insert earphones used in clinical hearing tests and hearing-research measurements in adult human subjects have been calibrated either in a 2 cm³ coupler or an artificial ear. The 2 cm³ coupler is a reference coupler for acoustic immittance measurements at low frequencies (i.e., at 226 Hz). When the task is to calibrate probe levels above 8 kHz, the 2 cm³ coupler and the artificial ear have limitations. A significant problem in 2 cm³ couplers conforming to standards is that the coupler is used with a reference microphone with a 1 in. diameter. This diameter is large compared to the diameter of the ear canal and large also compared to the acoustic wavelength at 16 kHz. The artificial ear was not designed for use at these high frequencies because the human impedance data on which its design is based do not encompass such high frequencies. An alternative and simpler coupler with acoustic properties appropriate for calibration across the audio frequency range is that of a long rigid-walled cylindrical tube, into which the source and microphone transducers are inserted in a leak-free manner.

Suppose that the sound source outputs a transient of a given duration D. This transient travels down the tube away from the source, is reflected at its far end, and travels back toward the source end to the measurement microphone with a round-trip travel time T_rt. If the measurement time is longer than D and less than T_rt, then the microphone response includes only the incident signal. There are no standing waves, so that the corresponding spectrum of the measured sound pressure has no maxima or minima associated with standing waves. This property has been used in studies measuring the ear-canal acoustic reflectance (Keefe, 1997; Keefe and Simmons, 2003). Such an anechoic, or reflectionless, coupler is well suited for probe calibration at high frequencies by eliminating the variability within the coupler due to standing waves.

A cylindrical brass tube of length 91.4 cm served as the anechoic termination; the tube was closed at its far end to prevent contamination from room noise. The tube had a circular cross-sectional diameter (8.02 mm), similar to the diameter of an adult human ear canal. A probe assembly, composed of a pair of insert earphones (ER-2, Etymotic) and microphone (ER-10B+, Etymotic), was inserted into one end of the tube. This probe assembly was also used in the CEOAE measurements. The round-trip travel time in this tube was approximately 5.3 ms. When windowed to include slightly less than the first 5.3 ms of the response, the microphone recorded the pressure response associated only with the outgoing, or incident, acoustic wave.

Stimuli were digitally generated and recorded at a sample rate f_s=44 100 Hz (sample period T=1∕f_s) using a computer, Digital Audio Labs 24 bit sound card (CardDeluxe), and custom software. The ER-10B+ microphone frequency response provided by the manufacturer was flat to within +1.8 dB up to 8 kHz with a nominal sensitivity level of −26 dB (re 1 V∕Pa). Above 8 kHz, there was one maximum and one minimum in sensitivity relative to this nominal sensitivity.1 The manufacturer’s calibration of frequency-dependent sensitivity was used in this study for all spectral results. The microphone preamplifier was used with +20 dB gain, which boosted the effective sensitivity level to −6 dB (re 1 V∕Pa). No phase calibration was provided for this microphone so that the pressure phase response above 8 kHz was approximated by the phase response of the voltage signal recorded by the analog-to-digital converter (ADC) of the sound card. Thus, the waveform plots reported in Fig. 3 of an output waveform from the microphone preamplifier and of a nonlinear residual CEOAE waveform, are voltage waveforms that have been scaled to pressure waveforms by the nominal sensitivity of −6 dB. Otherwise, all results reported herein, including CEOAE envelope delays, were independent of microphone phase sensitivity.

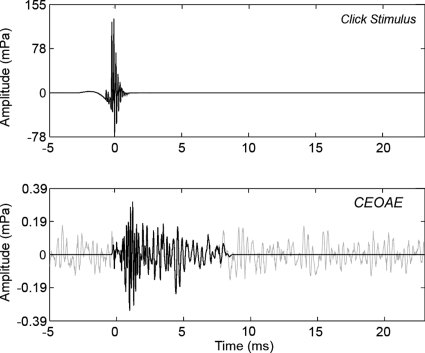
Figure 3.

Waveforms of time-averaged click stimulus (top) and CEOAE response (bottom). Zero on the time axis is set to the centroid of the click. The full CEOAE response is shown in gray, which is the waveform of the nonlinear residual. The windowed portion of the CEOAE extends from 0 to 8.3 ms and is expected to contain energy from 2 to 16 kHz (shown in black). The windowed portion was used in subsequent analyses in this paper.

ADC voltage waveforms were time averaged and analyzed spectrally after applying the frequency-dependent microphone sensitivity. Although a departure from previous work on CEOAEs, the sound level of the CEOAE was calculated using the sound-exposure spectrum level (SEL spectrum), which is a standard means of calculating the sound level of a transient (ANSI S1.1, 1994). The Appendix describes the implementation of the SEL spectrum and its relation to the SPL spectrum. The SEL spectrum was calculated using the windowed time-averaged pressure waveform sequence p[n] at sample n, which was zero padded out to N=1024 samples. Using this buffer length N, the discrete Fourier transform (DFT) of p[n] was P[k]. The band SEL spectrum L_Eb in the kth frequency bin was calculated as follows, which is based on an averaging time NT equal to the DFT buffer length,

$$L_{Eb}=10{\log }_{10}\left(\frac{\frac{2}{N^2}{\mid P\left[k\right]\mid }^2}{P_{\mathrm{ref}}^2}\right).$$ (1)

The click was designed using a method modified from Agullo et al. (1995). The microphone output voltage waveform was measured at discrete-time samples n in response to an electrical delta-function input from the digital-to-analog converter (DAC). This was the voltage impulse response h[n] of the measurement system. A finite impulse response (FIR) filter was designed using the Kaiser window technique to create a short-duration impulse response g[n] for a signal with a passband from 0.5 to 16 kHz and stop bands at 0.043 and 17 kHz. An inverse filtering technique was used to find the electrical input x[n] such that the voltage output response g[n] of the microphone was a multiple of this filter shape, that is, to find x[n] such that g[n]=h[n]^*x[n], where * represents convolution. A MATLAB implementation of a conjugate gradient method (Hansen, 2001) was used to find a stable solution for the electrical input. The resulting acoustic click spectrum recorded in the anechoic tube was approximately flat from 0.5 out to 16 kHz. The stimulus waveform so devised did not include the frequency variation of the recording microphone (ER-10B+) so that the actual pressure spectrum was inversely proportional to the maximum and minimum in microphone sensitivity described in footnote 1. These variations in microphone sensitivity level were within +2 dB at all third octave frequencies up to 12.7 kHz, but the sensitivity level was reduced by 5.2 dB at 16 kHz compared to the microphone preamplifier output voltage spectrum recorded by the ADC.

A possible source of measurement error is the close proximity of the microphone and earphone tubes in the probe assembly, which can lead to evanescent-mode effects in some situations (Burkhard and Sachs, 1977; Rabinowitz, 1981; Huang et al., 1998, 2000). The manufacturer provides the ability to modify the ER-10B+ probe by extending the sound tube further beyond the microphone tube in order to reduce evanescent effects. An extension of 5 mm is consistent with Burkhard and Sachs (1977) and is recommended by the manufacturer (Etymotic), but the 1∕4 wavelength of a 16 kHz tone is only 5.4 mm. Thus, a 5 mm extension is longer than what would be desirable for high-frequency measurements in the ear canal and what would complicate the interpretation of pressures measured near the tympanic membrane. Features of the Etymotic ER-10B+ microphone frequency response have been described along with acoustic studies of its 5 mm extension tube (Siegel, 2007).

Probe responses were measured using lesser extensions of 4 and 2 mm, which are generally consistent with recommendations in Keefe and Benade (1980), as well as using a zero-length extension (0 mm) to examine contributions of nonplanar and evanescent modes. The click stimulus was recorded using the ER-10B+ probe assembly with no extension and with extensions (ER10B-3∕ER7-14C, Etymotic) of 0, 2, and 4 mm. In addition to moving the earphone port further away from the microphone (in the 2 and 4 mm cases), the extension also reduced the cross-sectional area of the aperture. Adding an extension replaced the usual 255 of 1.35 mm inner-diameter tubing with a slightly shorter segment of inner diameter 1.35 mm coupled to a pair of short segments with inner diameters of 0.86 and 0.5 mm.

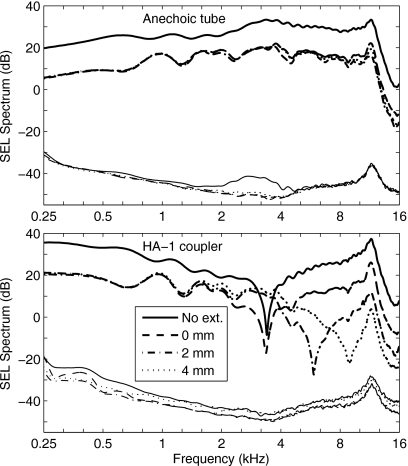
Spectral results are shown for recordings in the anechoic tube (Fig. 1, top) and a 2 cm³ coupler (Fig. 1, bottom). The 2 cm³ coupler used in all measurements was an HA-1 coupler as specified in ANSI 3.7 (1995). Each spectrum was calculated based on the waveform truncated to eliminate all reflected signals from the end of the tube and zero padded out to 1024 samples. The top panel of Fig. 1 shows that for the spectrum measured in the anechoic tube, the main effect of any extension was to attenuate the SEL spectrum compared to the no-extension condition. This was due to greater viscothermal dissipation within the reduced area of the plastic tube within the capillary. Aside from overall attenuation, the SEL spectrum varied little with extension length in the anechoic tube.

Figure 1.

Comparison of click spectra measured in the anechoic tube (top panel) and in a 2 cm³ (HA-1) coupler (bottom panel). In each panel the thicker lines toward the top show the signal SEL spectrum, and the thinner lines near the bottom show the noise SEL spectrum. The noise SEL is the standard error of the mean and is extremely low due to the large number of averages (N=4050). The legend indicates the length of the ER-10B+ extension tube associated with each spectra, or No ext. for the no-extension condition, which is the subsequent default configuration of the ER-10B+ used in the study.

The bottom panel of Fig. 1 shows that for the spectrum measured in the 2 cm³ coupler, there were level differences as large as 50 dB between the conditions. The SEL spectrum for the no-extension condition was higher than the SEL spectrum for all extension conditions at low frequencies up to 3 kHz, while the SEL spectral differences for the three extension conditions were within a few dB up to 2 kHz and much larger above 2 kHz. This large variability shows that the 2 cm³ coupler should not be used with the ER-2∕ER-10B+ probe assembly to assess stimulus level above 2 kHz. The diameter (18–21 mm) of the cylindrical cavity comprising the main volume of the 2 cm³ coupler [HA-1 as described in ANSI S3.7 (1995)] is large compared to its length (5.4–7.3 mm), which enhances the acoustical effect of the evanescent modes. In addition to an overall attenuation of the SEL spectrum, large differences appear as the sound tube is extended, especially in the location of notch frequencies between 3 and 8 kHz. A comparison of the top and bottom panels in Fig. 1 shows that the spectra measured in the anechoic tube were much smoother across frequenies than those measured in the 2 cm³ coupler. The anechoic tube removed standing-wave effects in calibration, making it more accurate in calibrating at higher frequencies. When used in real-ear tests, the sound field in the ear canal includes this calibrated incident-pressure signal and the reflected pressure signal from the tympanic membrane. The complex sum of these pressures in the ear canal forms standing waves in the ear-canal pressure that vary with the measurement location of the microphone and the source reflectance of the probe. The present method provides a measure of the incident pressure delivered to the ear, as further described below.

Based on these responses, the ER-10B+ was used in subsequent CEOAE and audiometric measurements using the no-extension configuration. This provided a SEL spectrum that was approximately 13 dB larger than in any of the configurations with extensions. This increased sound level was useful in measuring CEOAE responses with limited signal-to-noise ratios (SNRs). Another benefit was that there was no need to adjust the plastic tubing to a particular extension distance, which would have been a source of variability between subjects.

The main difficulty with higher-order evanescent mode interactions in ear-canal or tube measurements arises from the fact that the total input impedance measured at the surface of the probe is the sum of the input impedance associated with the plane-wave acoustic excitation in the ear canal and the input impedance associated with the evanescent modes, which acts as an inertance (Keefe and Benade, 1980). That is, the plane-wave and evanescent-mode impedances act in series. A reactance that is inertance dominated increases linearly with frequency, so that the effects of evanescent modes grow in importance at high frequencies. Evanescent-mode effects become important when the inertive reactance is on the order of the magnitude of the plane-wave impedance. This occurs first near the minima of the input reactance, which occur at frequencies near pressure minima as predicted by models of plane acoustic waves in cylindrical ducts. These are the frequencies of the sharp minima in the 2 cm³ coupler responses (see bottom panel of Fig. 1). At frequencies away from impedance minima, the plane-wave impedance dominates and the evanescent-mode effects are negligible. This means that there will be isolated narrow ranges of frequency in practical ear-canal measurements at high frequencies in which evanescent-mode effects can play a role. Because the middle ear is much more efficient at absorbing sound energy than are the hard walls of a coupler, the pressure minima are not as deep so that the effects of evanescent modes are smaller than in coupler measurements.

Restricting attention to the no-extension configuration of the ER-10B+ probe (including ER-2 earphones), the SEL spectrum in the 2 cm³ coupler was measured both by the probe microphone and by the reference microphone, i.e., the 1 in. Bruel and Kjaer microphone (type 4144) used in the HA-1 coupler specified in ANSI S3.7 (1995). The reference microphone was used with a sound level meter (Bruel and Kjaer type 2231). Responses were measured using both the click stimulus used in the CEOAE procedure and using tone bursts that were similar to those used in the ML threshold procedure, but of longer duration to provide time to read the visual display of the sound level meter. All measurements using the visual display of the sound level meter were an average of three measurements. The individual calibration provided by Bruel and Kjaer of the sensitivity of the reference microphone was used in all spectral analyses in this study, including frequency-dependent variations in sensitivity important at higher frequencies up to 16 kHz.

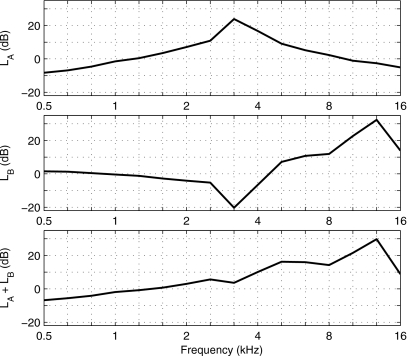
Three relevant transfer functions are defined and plotted in Fig. 2. The top panel shows the transfer-function level L_A between the probe-microphone response in the anechoic tube relative to the probe-microphone response in the 2 cm³ coupler. This transfer function shows the effect of acoustic termination on probe response. L_A was measured as the difference in the third-octave averaged sound level of the click responses. The click stimulus was the appropriate choice because it has a sufficiently short duration that the tube acts as an anechoic termination. This would not be the case for the tone-burst stimulus. L_A in the top panel of Fig. 2 was negative below 1.2 kHz, which means that the sound level measured by the ER-10B+ was less in the anechoic tube than in the compliance-dominated 2 cm³ coupler at low frequencies. The maximum in L_A near 3.2 kHz was created by a minimum in the sound level in the 2 cm³ coupler (bottom panel of Fig. 1, no-extension condition).

Figure 2.

1∕3-octave averaged transfer-function levels are plotted as follows. Top: L_A for the ER-10B+ in the anechoic tube re its level in the 2 cm³ coupler. Middle: L_B for the ER-10B+ in the 2 cm³ coupler re the level of a 1 in. Bruel and Kjaer microphone in the 2 cm³ coupler. Bottom: L_A+L_B. Frequency-dependent sensitivities have been applied to each microphone response in each panel.

The middle panel shows the transfer-function level L_B measured in the 2 cm³ coupler by the probe microphone relative to that measured by the reference microphone. The tone-burst stimulus was the appropriate choice because earphones are calibrated using the SPL measured by the reference microphone according to ANSI S3.6 (2004). The probe-microphone response was recorded in the 2 cm³ coupler by the computer measurement system and converted to SPL using the peak-to-peak pressure waveform difference during the steady-state portion of each frequency-specific tone burst. L_B was measured as the difference in these SPLs to represent the variability in SPL within the 2 cm³ coupler between the two measurement locations. L_B in the middle panel of Fig. 2 approached 0 dB at the lowest measurement frequencies to within measurement precision. The absolute value of L_B assessed level differences within the 2 cm³ coupler and did not exceed 5.3 dB at any frequency up to 2.5 kHz. However, strong spatial effects were present within the coupler above 2.5 kHz. A zero crossing in L_B occurred near 4.5 kHz, and L_B was as large as 33 dB at 12.7 kHz. Acoustic calibrations of probe microphones using the HA-1 coupler and its reference microphone strongly depend on spatial variations in sound field above 2.5 kHz.

The sum of these transfer-function levels, L_A+L_B, describes the relationship between sound level measured by the ER-10B+ microphone in the anechoic tube relative to the sound level measured in the HA-1 coupler by the 1 in. Bruel and Kjaer microphone (bottom panel, Fig. 2). The L_A+L_B increased with increasing frequency up to 30 dB at 12.7 kHz and decreased to 9 dB at 16 kHz. Because these are transfer functions, they can be used to adjust either SEL or SPL spectra.

These transfer-function measurements do not directly calibrate the probe microphone with respect to a reference microphone at high frequencies, inasmuch as a reference microphone was not incorporated into the anechoic coupler. One such approach is described in Siegel (2007). The present system with its anechoic probe termination provides an incident-pressure stimulus for use in calibrating behavioral thresholds. A power-based system for calibrating thresholds would require a measurement of the power absorbed by the middle ear (e.g., Keefe et al., (1993), but this method would require wideband aural acoustic admittance or related transfer-function measurements and would still not quantify any power internally lost within the middle ear that is not absorbed by the cochlea. The incident-pressure calibration is simpler in that it requires only sound level measurements of the incident signal, yet it provides a high-frequency calibration that is not influenced by standing waves in the ear canal. An incident-pressure calibration in a long tube is also applicable to time-gated tonal or noise signals, as long as their duration is less than the round-trip travel time within the tube.

METHODS

Subjects

Responses included in the analyses were obtained from 49 ears (24 left and 25 right ears) of 29 normal-hearing subjects (25 females and 4 males), in whom the mean age ±1 standard deviation (SD) was 20.5±3.4 years over an age range of 14–29 years. All subjects had pure-tone air-conduction thresholds <15 dB HL at octave frequencies from 0.5–8 and 226 Hz tympanograms within normal limits. During testing, subjects were seated comfortably inside a sound-attenuated booth. The experimental protocol was approved by the Institutional Review Board at Boys Town National Research Hospital, and written informed consent was obtained from all participants.

Behavioral threshold-measurement procedures

Behavioral hearing thresholds were measured using the adaptive ML procedure in a yes-no task at octave frequencies from 0.5 to 4 kHz and at 11 third-octave frequencies from 4 to 16 kHz. Each tone-burst stimulus had a total duration of 250 ms, which included 25 ms onset and offset ramps using cosine-squared envelopes. The threshold procedure was automated, and subjects provided responses using a custom-built response box that included text feedback via a visual display. The feedback indicated whether a yes or no response had been recorded on the previous trial and alerted the subject to the upcoming trial. The system waited after each stimulus presentation (gated tone or silence) until the subject depressed the Yes or No button.

The ML threshold was determined first at 0.5 kHz and then at other frequencies in ascending order. One reason for testing in this order is that all subjects were presented with stimuli in their suprathreshold range at the beginning of the test and finished with the frequencies above 8 kHz for which a tone might be inaudible. Any effect of test order was outside the scope of this study.

Two runs of the adaptive yes-no threshold procedure were performed, each run composed of 15 trials with four initial trials in which levels were set as described above in a manner that was independent of the subject responses. Three catch trials were included in the last 11 trials of each run. If the SD in the threshold between the two runs did not exceed 3 dB, the mean threshold was saved as the threshold estimate, and the test moved to the next frequency. Otherwise, a new run was performed, and the mean and SD of the threshold were again calculated. The mean threshold was stored whenever the 3 dB criterion was attained. If five runs were performed at this frequency without reaching the criterion, data collection was halted at this frequency, the mean frequency was saved as the threshold estimate across the pair of successive runs with the lowest SD, and the test proceeded to the next frequency.

Initial data collection at 0.5 kHz was considered a training run. The automated threshold test was paused when the criterion at 0.5 kHz was attained or after five runs. The operator then provided verbal feedback to the subject that the criterion had been attained, and, if so, data collection continued under the subject’s control at the next test frequency. If the criterion was not obtained after five runs, the operator so informed the subject, repeated the instructions on the use of the response box, and asked if tones were audible. Then, the threshold was again measured at 0.5 kHz (after discarding the old data), and this feedback step was repeated until the subject was either trained to criterion performance or excluded from the study.

The ML thresholds measured using the ER-2 earphones joined to the ER-10B+ with no coupling extension tube (see “No ext.” curve in top panel of Fig. 1) were compared to clinical thresholds (GSI-33 audiometer) measured at octave frequencies up to 8 kHz. The clinical thresholds were each calibrated in HL according to ANSI S3.6 (2004) using the 1 in. microphone in the 2 cm³ coupler. Thus, behavioral threshold and CEOAEs were measured with the same probe. Clinical thresholds at each frequency took approximately 0.5 min to acquire, and ML thresholds for two runs took approximately 1.5 min.

CEOAE measurement paradigm

CEOAEs were collected using a nonlinear residual method (Keefe, 1998) based on three responses (sample duration of 1124 samples or 25.5 ms), each elicited using a different stimulus. The first stimulus (s₁) was presented through a first earphone, followed by a presentation of the second stimulus (s₂) though a second earphone. Then both stimuli were presented simultaneously (s_1,2), each through its own earphone. The ear-canal sound pressure p₁ was measured in response to stimulus s₁, p₂ to stimulus s₂, and p_1,2 to stimulus s_1,2. The nonlinear residual, p_d, was extracted by calculating p_d=p₁+p₂−p_1,2. By this process, the linear-system responses to the stimuli were canceled along with any isochannel system distortion, leaving only the nonlinear residual, which was interpreted as a biological response, i.e., as the OAE, in the absence of any system intermodulation distortion. Such system distortion was assessed from coupler recordings in an artificial ear (Bruel and Kjaer type 4157) that approximated the impedance of an average adult human ear (IEC 711 standard). This distortion level never exceeded the measured noise level.

The click stimulus described above was presented as s₁, the “probe click.” The same click presented at a level of 15 dB above s₁ was used as s₂, the “second click.” Based on SF OAE studies (Dreisbach et al., 1998; Shera and Guinan, Jr., 1999; Schairer et al., 2003), a second signal with level 15 dB above the probe level is sufficient to substantially fully recover the SFOAE. Kalluri and Shera (2007) considered compression and suppression methods of extracting SFOAEs, and this CEOAE method likely involves both mechanisms, as well as a distortion mechanism (Withnell et al., 2008) further described below. Measurements in human ears (Konrad-Martin and Keefe, 2005; Kalluri and Shera, 2007) provide evidence over limited ranges of frequencies and moderate levels that SFOAEs and CEOAEs are generated by the same underlying cochlear mechanism, as predicted by the coherent reflection emission theory (Shera and Guinan, Jr., 1999). This suggests that a CEOAE response may be interpreted over these limited ranges as a superposition of SFOAE responses at frequencies within the passband of the CEOAE (this interpretation is revisited in Sec. 6). This source equivalence between SFOAE and CEOAE responses in human ears suggested the use of the simultaneous presentation of clicks differing in level by 15 dB. Previous CEOAE measurements based on the nonlinear residual technique of the present study used equal levels for the click (and chirp) stimuli s₁ and s₂ (Keefe and Ling, 1998), which resulted in slightly lower SNR levels than in the present study because of a less complete extraction of the CEOAE.

The overall duration of each recording buffer was 1124×3 samples, or 76.5 ms. This is slightly less than the typical buffer duration (80 ms) used in clinical CEOAE tests, which is comprised of three elementary buffers of a repeated click and a fourth elementary buffer of a click at three times the amplitude and opposite polarity (Kemp et al., 1990). The levels of the click stimuli were calculated in peak equivalent SPL (peSPL), which equals the SPL of a continuous tone having the same peak-to-peak pressure amplitude as the maximum peak-to-peak pressure amplitude of the click waveform.2 Probe clicks were presented in 6 dB steps at levels from 43 to 73 dB peSPL. Levels were always presented in order from highest to lowest level. For each level, M=4050 independent buffers were collected (duration of 5.2 min). The CEOAE signal and noise sound levels were calculated using the coherent and incoherent averaging procedures described in the Appendix of Schairer et al. (2003) and expressed as SEL spectra (see Appendix)

The CEOAE test time for each subject was approximately 1 h. During CEOAE testing within the booth, subjects typically viewed a television program using a closed-caption DVD (i.e., without audible sound), which helped them remain awake and alert. To reduce variability associated with probe placement, the probe was not removed from the ear during the test session unless it inadvertently needed refitting.

CEOAE post hoc analysis

Data were analyzed using custom MATLAB software. Artifact rejection was used to detect and reject data buffers contaminated by intermittent noise that were outliers in the sense of Hoaglin et al. (1983). The data were first filtered using a high-pass FIR filter (0.354 kHz cutoff, 0.5 kHz passband lower frequency, 5.7 ms group delay) to remove low-frequency noise below the analysis band, and the total energy in each buffer was calculated. Individual responses with energy >2.25 times the interquartile range (IQR) of the buffer set were discarded. This method of post hoc artifact rejection resulted in an average of N=3690 buffers retained for each recording; e.g., 8.7% of buffers were rejected on average across subjects with a SD of 4%.

In order to elicit the best possible high-frequency emissions, relatively high click levels were used. The combination of higher click levels and a nonlinear residual paradigm results in the possibility of middle-ear muscle (MEM) reflex activation, which could be mistaken for OAEs. If present, the MEM reflex would tend to affect the nonlinear residual response at lower frequencies. Further, many subjects had synchronous spontaneous otoacoustic emissions (SSOAEs) present below 2 kHz. It was therefore decided to limit the CEOAE spectral analysis to frequencies ⩾2 kHz. This decision was consistent with the fact that CEOAE spectra below 2 kHz are well understood. However, as described later, CEOAE latency measurements were extended downward to 1 kHz.

A time-domain window encompassing the higher frequencies in the CEOAE waveform was devised for the CEOAE spectral analyses as follows: The window onset was positioned at the centroid of the click stimulus; this onset occurred at t=0 ms in the click stimulus response plotted in Fig. 3 (top panel). Based on data from Shera et al. (2002), the expected group delay for a 2 kHz SFOAE is 7 ms, with an upper 95% confidence interval of 8.3 ms. The duration of the window was therefore chosen to be 8.3 ms. The effects of this window onset and duration are evident in the CEOAE waveform plotted as a black line in the bottom panel of Fig. 3. The window was gated on and off using half cosine-squared windows of duration equal to three periods of the expected CEOAE frequency. The dominant frequency at the onset was expected to be on the order of 16 kHz (period of 0.0625 ms), so the window was gated on over a duration of 0.187 ms. The dominant frequency at the offset was expected to be on the order of 2 kHz (period of 0.5 ms), so its window was gated off over a duration of 1.5 ms. This windowing had the added benefit of reducing the noise floor by eliminating the noise in the rest of the CEOAE response (Whitehead et al., 1995a), which occurred primarily at frequencies below 2 kHz. The original CEOAE waveform calculated as the nonlinear residual is plotted as the gray line in the lower panel in Fig. 3. The windowed CEOAE waveform (black line in the lower panel in Fig. 3) was further analyzed using the DFT. In particular, the windowed waveform has its initial sample at the centroid of the click stimulus response (t=0 ms) and was zero padded out to a duration of 1024 samples.

CEOAE delays were examined in the time domain using overlapping third-octave bandpass filters, with center and edge frequencies computed according to ANSI S1.11 (2004). A Kaiser-based window method was used to design the filters. Filter order decreased as center frequency and bandwidth increased. The filters spanned four octaves (1–16 kHz), and the filter orders ranged from 500 to 32, which corresponded to filter group delays of 11.3 to 0.7 ms, respectively. Each subject’s mean CEOAE waveform was bandpass filtered with each of the 13 third-octave filters. The group delays of the filters were subtracted from the filtered waveforms to ensure correct temporal alignment. A Hilbert transform was computed on each filtered waveform, and the temporal envelopes were computed as the magnitude of the transform.

RESULTS

CEOAE spectra

Figure 4 shows the median across subjects of the CEOAE SEL spectra for the six highest click levels that were analyzed (solid lines with circle symbols), with the corresponding median noise SEL at these click levels (dashed lines). The CEOAE spectra show an orderly increase in level with stimulus level, while the noise SEL was independent of click level. The CEOAE levels shown in Fig. 4 were above the noise floor for third-octave frequencies in the range of 2–8 kHz for all the stimulus click levels shown. A decreased CEOAE level at higher stimulus levels was evident above 8 kHz. At frequencies of 10–16 kHz, only the highest click levels (67 and 73 dB peSPL) resulted in CEOAE levels more than 4 dB above the noise SPL. Subsequent analysis therefore concentrates on CEOAEs elicited at the highest click stimulus level, which resulted in the largest SNRs.

Figure 4.

Median CEOAE SEL spectra (1∕3 octave average) for each of six click stimulus levels are plotted with increasing line thickness for increasing stimulus level. The peSPL of each click stimulus is specified in the legend. The median noise SEL spectra (1∕3 octave average) are also plotted (dashed lines). The line thickness is the same for the noise levels because they had no level dependence.

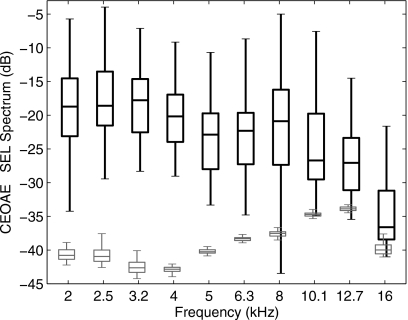
Figure 5 shows the variability across subjects of CEOAE signal and noise SEL spectra recorded using the highest click level (73 dB peSPL) as a box and whiskers plot. The “box” represents the IQR of the distributions of SEL. The IQRs for CEOAE signal SEL spectra were similar for frequencies of 2–16 kHz. The IQRs for noise levels were also similar across this frequency range. However, it was necessary to filter out an intermittent narrow-band noise spike in the microphone output near 15 kHz, which was present in some coupler recordings and some ear recordings, but not in others. This was a measurement system artifact and not a noise source of biological origin. The noise levels in Fig. 5 in the 16 kHz third octave represent the output after this exclusion of noise-contaminated bins (it should also be noted that data were analyzed only in the lower half of the third octave at 16 kHz).

Figure 5.

Box and whiskers plots of the CEOAE SEL signal and noise spectra elicited at the highest click level (73 dB peSPL) are shown for N=49 ear responses. The black plot with thicker lines shows the CEOAE SEL spectrum, and the gray plot shows the noise SEL spectrum. The boxes show the lower quartile, median, and upper quartile values. The whiskers extend from each end of the boxes to show the extent of the rest of the data, with the maximum length being the lesser of the full range of SEL spectrum and 1.5 times the IQR. Outliers are not plotted, and signal and noise plots are slightly displaced horizontally to clarify the main features of the box plots.

Measurements made in the artificial ear and in human subjects suggest that a 3 dB SNR is an appropriate value for detecting the presence of an emission. CEOAES were present using this criterion between 2 and 6.3 kHz for all ears tested. At center frequencies of 8, 10.1, 12.7, and 16 kHz, CEOAEs were present in 92%, 78%, 66%, and 52% of ears, respectively.

CEOAE latency

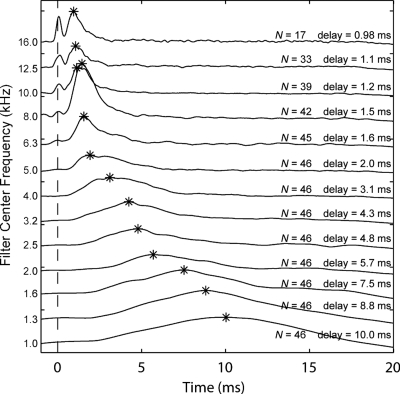
The CEOAE latency of each third-octave filtered CEOAE output was calculated as the time corresponding to a maximum in the group-averaged temporal envelope of the CEOAE output waveform with respect to the time of the maximum temporal envelope of the click stimulus. When the energy in the temporal envelopes was averaged across subjects at each time step, results at the highest stimulus level (73 dB peSPL) showed the expected decrease in CEOAE latency with increase in filter center frequency (Fig. 6). The CEOAE latency is represented by an asterisk above the envelope response of each third-octave frequency. For frequencies higher than those previously reported for CEOAEs, the latency decreased from 2.0 down to 0.98 ms as frequency increased from 5 up to 16 kHz.

Figure 6.

Mean 1∕3-octave filtered CEOAE waveform envelopes as a function of time. Data are from the highest stimulus level used (73 dB peSPL). Tracings are offset on the y-axis for clarity and arranged by filter center frequency in decreasing order. Only recordings with a SNR >3 dB were included in the averages. The number of ears (N) included in the mean is indicated for each tracing. The vertical dashed line indicates the stimulus onset. The peak of each envelope is indicated by an asterisk, and the corresponding delay (in ms) relative to stimulus onset is also displayed.

An envelope peak centered at t=0 was evident in the filter outputs at center frequencies at and above 8 kHz (Fig. 6). This energy was due to stimulus artifact in the click presented at t=0 (i.e., see Fig. 3). In terms of interpretation of CEOAE recordings, the peaks aligned at t=0 were ignored as unrelated to cochlear mechanics. The envelope peaks at later times in these high-frequency filter outputs provided a direct measure of CEOAE latency.

The CEOAE latencies derived from the mean envelope peaks at a stimulus level of 73 dB peSPL are replotted in Fig. 7 in units of the number of periods at each filter center frequency. The vertical error bars, which indicate the latencies at the half-power bandwidths of the peaks, provide a measure of the variability of latencies of the averaged group data. SFOAE latency data from Shera et al. (2002) (dashed lines show mean ±1 confidence interval) and Schairer et al. (2006) (thick solid line) are overlaid for comparison. Latencies in the present study were consistent with the predictions of Shera et al. (2002) and the measurements of Schairer et al. (2006) for frequencies between 1 and 2 kHz. Between 2 and 4 kHz, CEOAE latencies were slightly shorter than predicted by Shera et al. (2002) and slightly longer than measured by Schairer et al. (2006), but all latencies agreed to within measurement variability (the variability in Schairer et al.(2006) is reported in their article but not plotted in Fig. 7). At frequencies >5 kHz, the present latency data were shorter than the results of Shera et al. (2002). The cause of these differences is unknown, but possible explanations include differences in emission type (CEOAE versus SFOAE), differences in effective stimulus levels, differences in methodologies, and∕or the presence of multiple components contributing to the measured latency. The role of level-dependent multiple components in CEOAEs is discussed below.

Figure 7.

Group means of CEOAE latency (thin solid lines and open circle symbols) are plotted nondimensionally in units of the number of periods at the filter center frequency. Data are for CEOAEs recorded at the highest stimulus level (73 dB peSPL). Vertical error bars indicate the latencies at the half-power bandwidths of the envelope peaks. The broken lines show the mean and 95% confidence intervals of SFOAE latencies reported by Shera et al. (2002) for stimulus levels of 40 dB SPL. The thick solid line shows the mean latencies of SFOAE latencies reported by Schairer et al. (2006) for stimulus levels of 40 dB SPL [variability not plotted for clarity but are shown in Schairer et al. (2006)].

When averaged group latency data in the present study were compared across stimulus levels, a trend of decreasing CEOAE latency with increasing level was seen. This effect has been reported previously (e.g., Prieve et al., 1996; Tognola et al., 1997). However, most previous studies with human subjects have removed the first 2.5 ms of the ear-canal CEOAE recording prior to analysis in order to avoid stimulus artifact (Kemp et al., 1990). The techniques used in the present study allowed the earlier portions of the CEOAE to be included in the analysis. These group results are not shown here because of the following properties observed in responses in individual ears.

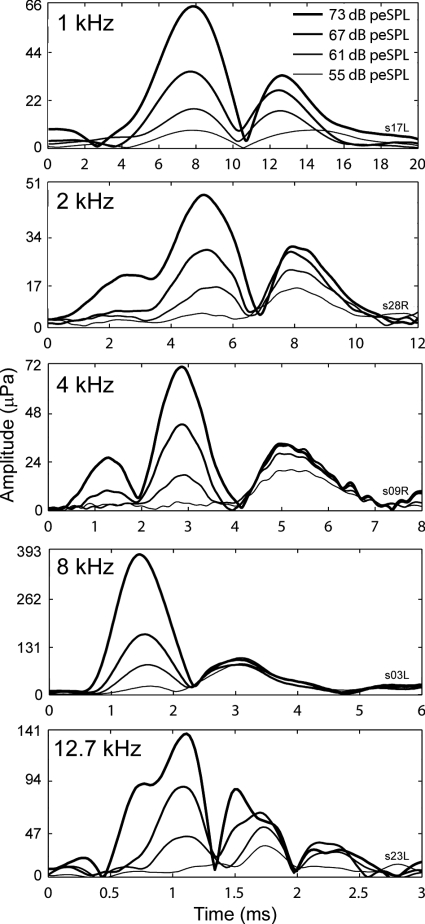
Examination of individual subjects’ data contributing to the group results in Figs. 67 suggested that there are two initial components to the CEOAEs: a longer-delay component that tends to dominate at lower stimulus levels and a shorter-delay component that dominates at higher levels. Examples of such individual-subject data are shown in Fig. 8. On average, the longer and shorter delays differed by a factor of approximately 1.6. A comparison of the envelope amplitudes of the earlier and later sources of individual-subject data suggested differences in growth as a function of stimulus level. Longer-delay components showed compressive growth, while shorter-delay components showed a more nearly linear growth. This is evident in the individual-ear responses plotted in Fig. 8.

Figure 8.

1∕3-octave filtered CEOAE waveform envelopes as a function of time and stimulus level. Panels show increasing filter center frequency (kHz). The tracings in each panel are from a different subject. The plotting axes in each panel encompass different ranges to allow the examination of salient details. No synchronized spontaneous OAEs were present in the data shown.

In order to examine group data, growth was quantified as follows: Plots similar to the panels in Fig. 8 were produced, and the main delay components (peaks) were visually identified. Each component consisted of the responses to four stimulus levels. In some subjects, four peaks were identified at a particular stimulus level. In other subjects, the responses to lower stimulus levels were below the noise floor. Wherever pairs of peaks at adjacent stimulus levels were identified in an ear, the peak amplitude at the current stimulus amplitude was divided by the peak amplitude at the next lower stimulus amplitude; this lower stimulus amplitude was one-half the amplitude of the current stimulus (i.e., −6 dB in relative level). The mean of these ratios was taken as the average growth of the CEOAE residual for that component. These average growth values were normalized so that a value of 1 indicated linear growth, <1 indicated compressive growth, and >1 indicated expansive growth. A value of 0.5 represented full saturation, i.e., no change in emission level as stimulus increased. A value of 2 indicated growth at twice the rate of linear growth, i.e., a fourfold increase in amplitude for each doubling of stimulus amplitude.

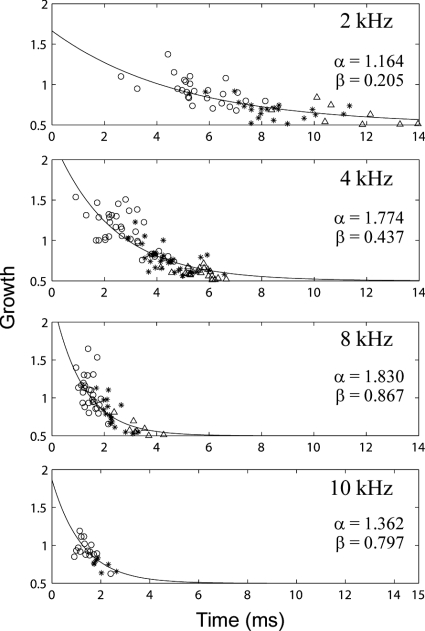
Figure 9 shows scatter plots of growth values plotted as a function of component delay using data from the four filter center frequencies (2, 4, 8, and 10 kHz) used in these group analyses. Data are also grouped by component number, with open circles, asterisks, and open triangles showing growth values from the first, second, and third components, respectively. The growth rate of the CEOAE residuals was more compressive as component delays increased. CEOAE residuals were sometimes fully saturated (a growth value of 0.5), but they never showed negative growth. Because the growth decayed approximately exponentially with component delay, the data were fitted with an exponential function of the form

$$f\left(x\right)=\alpha \exp (-\beta x)+0.5,$$ (2)

where x is peak delay in milliseconds. Values of α and β were determined for each frequency using an iterative nonlinear least squares fitting procedure with bisquares weighting (MATLAB CURVE FITTING TOOLBOX 1.2.1).

Figure 9.

Growth in peaks of emission as a function of peak delay. From top to bottom, panels show increasing filter center frequency. Open circles, asterisks, and open triangles show growth values from the first, second, and third components, respectively. α and β are the parameters of the exponential fit (solid line).

Note that the CEOAE temporal envelopes described above are envelopes of the nonlinear residual extracted from the measured waveforms (as described in Sec. 4C). Thus, an apparent linear growth in the envelope amplitude in Figs. 89 corresponds to a quadratic growth in the total CEOAE. The relevant property of the shorter-delay components is that their growth was faster than compressive growth. The growth patterns of the later components are consistent with a coherent reflection mechanism on the basilar membrane (Zweig and Shera, 1995; Prieve et al., 1996; Kalluri and Shera, 2007), as would be the result of a compressive-growth basilar-membrane input-output function. The more linear or expansive-growth patterns of the earlier components in the CEOAE residual are consistent with a nonlinear distortion source (Withnell et al., 2008). Components with the longest latencies may also have included effects of one or more internal reflections within the cochlea between its base and tonotopic place.

An important observation regarding both short- and long-delay components is that although their relative dominance shifted as a function of stimulus level, there was essentially no change in the delay of the envelope of either component as a function of level. This pattern is evident in Fig. 8. Group data were examined using a strategy similar to that described above. The main delay components were identified, each consisting of responses to four stimulus levels (55, 61, 67, and 73 dB peSPL). Wherever two or more peaks were identified, the maximum amplitude of each peak was recorded. A linear regression line was fitted to the points, with its slope indicating the rate of change in delay per doubling of stimulus amplitude.

Because earlier and later components had different growth rates, it was hypothesized that they might show different changes in delay as a function of stimulus level. Accordingly, individual-ear data were visually grouped by component number, with the earliest component designated as component 1. Some subjects had only one component identified, while others had two or three. A few subjects had four components, but fourth components were not considered in this analysis. The data comprising component 1, as a group, showed expansive or linear growth. The data comprising component 2 were linear or compressive, and the data comprising component 3 were mostly compressive in growth. These group patterns were similar to the individual patterns in Fig. 8. Data were statistically analyzed for three components at each of 2, 4, and 8 kHz and at 10 kHz for a total of 11 components tested. T-tests were performed on each component to test the null hypothesis that component delay was independent of stimulus level. A false discovery rate adjustment (Benjamini and Hochberg, 1995) was made to control for the proportion of falsely rejected hypotheses when conducting multiple significance tests. Three of the 11 groups were significantly different from zero at the 5% level: Component 1 at 2 and 8 kHz and component 2 at 4 kHz each had decreased latency with increasing stimulus level. The significant effects were small compared to the component latency: the component shifts were −0.058, −0.038, and −0.026 ms per 6 dB relative increase in stimulus SPL. In other words, the change in delay seen between a stimulus of 55 dB peSPL and a stimulus of 73 dB peSPL was on the order of 0.16 ms.

Summarizing the results of group data analysis, it was found that earlier-occurring components tended to grow expansively, consistent with a distortion mechanism, and showed a small but significant decrease in delay as the stimulus level increased. Later-occurring components tended to grow compressively, consistent with a coherent reflection mechanism, and showed no change in delay as a function of stimulus level.

Maximum-likelihood thresholds

Air-conduction thresholds obtained using the ML procedure were compared with air-conduction thresholds obtained using standard clinical procedures at frequencies up to 8 kHz at which both procedures were used. Figure 10 shows scatter plots of the clinical versus the ML audiometric thresholds for octave frequencies between 0.5 and 8 kHz, with brackets indicating a range of +1 SD. For these results, the HL reference for the probe (as well as the clinical system) was based on a calibration in the HA-1 coupler according to ANSI S3.6 (2004). The mean clinical and ML thresholds measured using the 250 ms tone bursts were within ±1 SD at 0.5, 1, and 2 kHz, but the mean ML thresholds were slightly lower at 4 and 8 kHz.

Figure 10.

Scatter plots of clinical vs the maximum-likelihood audiometric thresholds (in HL) for five frequencies. Individual ear thresholds are shown as open gray circles. The mean ±1 SD of the thresholds is plotted as bars in black. Median thresholds are shown as black filled circles.

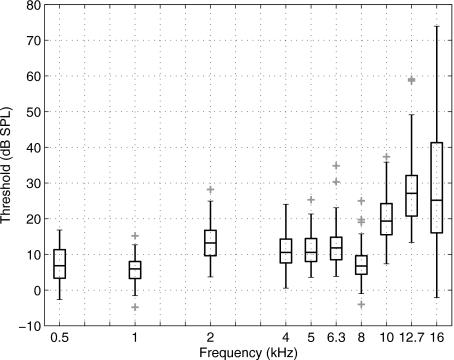
ML thresholds were also analyzed at frequencies up to 16 kHz based on the reference SPL in the anechoic tube, as determined using measurements in the HA-1 coupler and the transfer function L_A+L_B (see Fig. 2). Box and whisker plots of the ML threshold SPL are shown in Fig. 11. The median of this threshold SPL is defined at each frequency as the reference equivalent threshold sound pressure level (RETSPL) based on the incident-pressure procedure.

Figure 11.

ML thresholds expressed as the incident SPL at the threshold (i.e., the SPL on each tone burst that would be measured in the anechoic tube), as referenced to the calibration of the ER10‐B+ and ER-2 earphones in the no-extension probe condition. These thresholds are shown as a box and whiskers plot, with each outlier plotted using a plus symbol (+).

While subjects were included only if their clinical thresholds were <15 dB HL up to 8 kHz, there was no clinical reference available at higher frequencies. Consequently, a more elevated and wider range of hearing was expected and observed; e.g., the results in Fig. 11 show a 77 dB range in thresholds measured at 16 kHz. At frequencies >8 kHz, the median SPL threshold increased with frequency, in qualitative agreement with previous high-frequency audiometric studies (Green et al., 1987; Stelmachowicz et al., 1989a, 1986). The ML threshold technique had similar efficiency at all frequencies, and thresholds at high frequencies were no more complicated to measure than at low frequencies. The RETSPL calibrated according to the ER-10B+ microphone in the HA-1 coupler would be unduly influenced by the high-frequency standing waves evident in the transfer function L_B between this microphone and the reference microphone (see middle panel of Fig. 2). These standing waves produce a total variation of over 50 dB in L_B across frequency.

The significance of these results is that the determination of the incident-pressure RETSPL in a group of young normal-hearing listeners, as measured by measurements in the anechoic tube using the ER-10B+ microphone, makes possible behavioral audiometry and OAE measurements using the same probe to frequencies as high as 16 kHz.

The CEOAE SEL spectrum decreased with increasing ML threshold at 8 and 10.1 kHz, and associated correlations accounted for 28% and 43%, respectively, of the total variance. This supports the view that a reduction in the cochlear source strength of the emission was associated with an elevated threshold. While similar trends were evident at 12.7 and 16 kHz, no significant correlation was found at either frequency. One contributing factor to the absence of such a relationship may be the low SNRs at 12.7 and 16 kHz (see Figs. 45).

DISCUSSION

CEOAE spectra

The problem of calibrating the sound stimulus at high audio frequencies was successfully addressed by measurements in a long smooth-walled rigid tube. Such a tube functioned in an anechoic manner over sufficiently long recording times that it was possible to measure the incident sound level without the contaminating effects of acoustic standing waves. This enabled specification of the stimulus SPL over a broad frequency range, 0.25–16 kHz. An efficient ML procedure to measure audiometric threshold based on a yes-no task resulted in similar results to clinical audiometry up to 8 kHz and provided audiometric results at higher frequencies that were qualitatively similar to those in previous reports. An advantage in our procedures was that it was based on the use of insert earphones, which are routinely used to measure audiograms at lower frequencies and which are used to measure OAEs.

The experiments demonstrated that CEOAEs can be recorded in some otologically normal adult ears up to 16 kHz. Such responses serve as a noninvasive probe of cochlear mechanics at the base of the basilar membrane. Previous CEOAE measurements are restricted to an upper frequency of approximately 5 kHz. This frequency limitation was a property of the recording technique (and any probe transducer limitations) rather than any limitation in the ability of the human cochlea to produce a CEOAE response at higher frequencies. The ability to measure a CEOAE response up to 16 kHz has potential clinical applications as an objective physiological screening test for high-frequency sensorineural hearing loss.

While the methods described in this paper resulted in measurable high-frequency CEOAEs in many subjects, the SPL of the emissions was reduced at frequencies above 8 kHz (see median responses in Fig. 5). There are several possible reasons for this. First, the microphone sensitivity was reduced at 16 kHz, so that the stimulus SPL was reduced at the highest frequencies. Second, subject inclusion criterion specified that hearing thresholds be within normal limits only up to 8 kHz. Our results suggest that subjects had varying degrees of hearing sensitivity above 8 kHz. Stelmachowicz et al. (1989a, 1989b) compiled normative thresholds between 8 and 20 kHz as a function of age. They showed that age-related threshold shifts were greatest above 8 kHz and tended to begin starting in the second decade of life. The participants in this study had a mean (SD of) age of 20.5+3.4 years, with ages symmetrically distributed around the mean. Thus, many subjects could be expected to have had a hearing loss above 8 kHz. The increased measurement variability in the high-frequency thresholds shown in Fig. 11 supports this expectation. This variability probably reflects the changing thresholds within a subject pool spanning 15 years.

A third reason that may account for the decrease in CEOAE SPL above 8 kHz relates to the relative ability of the middle ear to transmit sound energy at higher frequencies. Middle-ear transmission measurements in human temporal bones show a decrease with frequency above about 1 kHz for both forward and reverse transmission (Puria et al., 1997; Puria, 2003). Interestingly, CEOAE SPL spectra do not closely resemble the round-trip middle-ear pressure transfer function, at least between 2 and 6 kHz where they appear to decline with frequency at a slower rate (Smurzynski and Kim, 1992). One explanation is that the mechanisms generating the CEOAEs are frequency dependent (Puria, 2003). Alternatively, indirect measurements using OAEs suggest a broader middle-ear transfer function, more consistent with the levels of the emissions, as described in Keefe (2007). These indirect measurements showed a rolloff between 4 and 8 kHz. Such indirect middle-ear transmission estimates have not been reported for frequencies above 8 kHz. Additional direct measurements of middle-ear transmission in human temporal bones are also needed to better understand the high-frequency regime relevant to the CEOAE measurements in the present study.

The sound level of the stimulus used in this experiment was relatively flat in frequency up to approximately 11 kHz and rolled off at higher frequencies (Fig. 1, top panel). Due to an additional rolloff in the forward middle-ear transfer function at high frequencies, stimulation of the cochlea at places corresponding to frequencies above 8 kHz may not have been as great as stimulation at places corresponding to lower frequencies. It might be preferable to increase the stimulus energies at and above 8 kHz in future studies.

The incident power in the ear canal, which is the integral of the incident acoustic intensity flowing through the cross-sectional area at a given location and proportional to the square of the incident pressure, is not influenced by standing waves and thus is well suited as a calibration standard for audiometric and CEOAE measurements. Nevertheless, the acoustic pressure is markedly influenced by these standing waves depending on the measurement location of the microphone within the ear canal. This has been a topic of concern in studies of OAEs at higher frequencies (Siegel, 1994; Whitehead et al., 1995b). Siegel (2007) reviewed issues related to OAE probe calibration and measurements at high frequencies. The distinctive feature of the incident-pressure approach used in the present study to measure OAEs at high frequencies is that it does not require a measurement of an aural acoustic transfer function such as admittance or reflectance. At high frequencies in the ear canal, a small shift in the OAE probe sound source or microphone can produce a large shift near a frequency at which a standing-wave minimum is present. However a small shift in the OAE probe produces no change in the incident pressure, at least to the extent that variations in the cross-section area of the ear canal are small. In any case, such area changes might produce effects on the order of a couple dB, whereas standing waves may produce SPL variations as large as 20 dB (Siegel, 1994). Studies of the repeatability of CEOAEs at high frequencies need to be performed, but specifying the stimulus level as incident pressure may reduce the variability of CEOAE levels, especially after frequency averaging over third octaves. The variation in the incident-pressure SPL was small below 11 kHz (see the No ext. curve in the top plot of Fig. 1).

Measuring an aural acoustic transfer function would allow calculation of the power absorbed from the OAE stimulus by the middle ear (and by ear-canal walls, particularly in young infants) (Keefe et al., 1993). This power absorbtion is closely related to acoustic intensity flow within the ear canal (Neely and Gorga, 1998; Farmer-Fedor and Rabbitt, 2002). It is outside the scope of the present work to consider the additional information that may be gained by combined measurements of OAEs and aural acoustic transfer functions in the same ear, but it is an area of current interest (Keefe, 2007; Scheperle et al., 2008).

CEOAE delays

Individual subjects’ data suggested that there are at least two components to the CEOAEs: a compressive-growth, longer-delay component that tends to dominate at lower stimulus levels and a linear-growth, shorter-delay component that dominates at higher levels (Fig. 8). Some subjects showed additional early and∕or late peaks (e.g., Fig. 8, 4 kHz panel and 12.5 kHz panel).

The growth pattern and delay of the later components are mainly consistent with a coherent reflection mechanism (Zweig and Shera, 1995; Prieve et al., 1996; Kalluri and Shera, 2007). This mechanism incorporates a linear, spatially distributed set of reflections of the basilar-membrane traveling wave that are coherently filtered at a given frequency by the tall broad peak in the basilar-membrane displacement envelope near the tonotopic place (i.e., the place on the basilar membrane at which its displacement for a tone at a particular frequency is maximal). The saturating nonlinearity in the CEOAE components associated with coherent reflection arises from the saturating gain characteristics of outer hair cell motion.

Although there were small decreases in latency as a function of stimulus level for the early component, a much larger effect was the shift in dominance from later to earlier components as stimulus level increased. No change in latency was found for later components. This finding is consistent with Konrad-Martin and Keefe (2005) (their Fig. 6) and Carvalho et al. (2003), who reported similar results for the later-occurring component. Thus, the CEOAE latency based on the entire response decreased with increasing stimulus level, but this was due to a change in the relative proportion of the energies of the short-latency and long-latency components. These results extend the work of Carvalho et al. (2003) by reporting that phase changes coupled with near-peak invariance is seen for both early and late components, as well as at frequencies up to 12 kHz. Above 12 kHz, a component with a longer compressive-growth delay was not identified. This may have been due to poorer SNRs, a difference in CEOAE generation at these higher frequencies, or a temporal overlap between the early and late components.

These results have implications for theories concerning the generation of CEOAEs. Kalluri and Shera (2007) suggested that CEOAEs (at least those occurring later than 5 ms poststimulus delivery) are generated by a coherent reflection mechanism present in independent channels, as opposed to being generated by intermodulation distortion between channels. A nonlinear generalization of the coherent reflection mechanism would predict that the delay of the (later) component should decrease with increasing stimulus level due to compressive growth of the traveling wave on the basilar membrane with increasing stimulus level, whereas the present finding is that this delay was approximately constant with increasing level. While the theory of coherent reflection mechanism, as originally proposed (Zweig and Shera, 1995), was used to interpret SFOAE data only at a low stimulus level (40 dB SPL), it is widely thought that this theory may apply to OAEs at higher stimulus levels. The idea is that the peak of the excitation pattern on the basilar membrane is shifted basally and the phase delay to tonotopic place is reduced with increasing stimulus level (Recio and Rhode, 2000; Lin and Guinan, 2000; de Boer and Nuttall, 2000; though see also Moore and Glasberg, 2003). The net result from both effects would be a reduction in the OAE delay with increasing level. The finding that the delay of the later CEOAE component is approximately constant is not in accord with this nonlinear generalization of coherent reflection theory.

Schairer et al. (2006) reported that SFOAE delays decreased approximately uniformly over frequencies of 0.5–4 kHz by a factor of 1∕2 with increasing stimulus level over a 20 dB range. This is in apparent agreement with the coherent reflection theory, as generalized to include the compressive nonlinear of basilar-membrane mechanics. It is unknown the extent to which undetected multiple components may have contributed to the calculated SFOAE delays, which were calculated using the phase gradient at the frequency of the tonal stimulus. The phase-gradient method requires the assumption of a single-component SFOAE. If, as suggested by Kalluri and Shera (2007), CEOAEs and SFOAEs share a common mechanism, this assumption might not hold for SFOAEs at higher stimulus levels. Future studies should examine SFOAEs for the presence of multiple components, but the relative latency changes with increasing stimulus level of individual CEOAE components in the present study appear smaller than the relative latency changes of SFOAEs reported in Schairer et al. (2006). While multiple components of CEOAE latency were identified through differing nonlinear rates of growth, the present measurements did not allow identification of the origination regions within the cochlea of the components that contributed to our ear-canal measurements.

The approximately linear growth of the earlier component of the CEOAE nonlinear residual is consistent with a nonlinear distortion source. Such a linear growth in the CEOAE residual corresponds to a quadratic growth in the total CEOAE and is not consistent with the saturating growth of a coherent reflection model. The presence of a nonlinear distortion component in the early CEOAE is in agreement with recent work by Withnell et al. (2008), who used the relatively shallow phase gradient of the early time-windowed response to infer a distortion-generated component. Our data suggest some potential complications with the phase-gradient method. Some subjects showed evidence of multiple early linear—or expansive-growth peaks (e.g., Fig. 8, 4 and 12.5 kHz panels). The relationship between the relatively invariant envelope peak latencies in the present study and the time shifts inferred from the phase-gradient method has not been well characterized. These issues raise questions regarding absolute delay values obtained by the phase-gradient method and suggest that further study is needed. Nevertheless, regardless of these measurement issues, the two studies agree that a distortion component is present in human CEOAEs.

Basilar-membrane mechanical responses to clicks measured at the cochlear base in chinchilla (Recio et al., 1998) show a “two-lobed” waveform envelope that mainly grows compressively with level, consistent with the dominant CEOAE response growth properties in the present study. However, at high click levels, the earliest envelope peak on the basilar membrane has a faster, almost linear rate of growth than later envelope peaks. Basilar-membrane responses are measured on a small region of the basilar membrane, whereas a CEOAE, even after bandpass filtering, is likely to integrate over a spatially extended region of the basilar membrane. Nevertheless, a high-frequency OAE response is likely generated from sources near the basal end of the cochlea. The variations in rates of growth of response in the basal region of the basilar membrane may be related to the level dependence observed in our CEOAE latency results. Dominance of a shorter-latency source region in basilar-membrane mechanics would shift the CEOAE envelope peak to shorter latencies, as was observed in the present study. Further research is needed to better understand relationships between click-evoked OAE responses and basilar-membrane responses.

Behavioral threshold prediction using CEOAEs

Having established that high-frequency CEOAE responses can be measured in some otologically normal ears, it remains to be determined whether such responses can be used to detect the presence of a high-frequency hearing loss in a population of subjects with varying degrees of sensorineural hearing loss. Analyses at 8 and 10.1 kHz showed that CEOAE SEL was reduced in ears with slightly elevated high-frequency thresholds. While this is a promising result, more studies are needed in subjects with a broader range of thresholds.

An important use for high-frequency audiometry has been monitoring for ototoxic hearing loss. Since ototoxic hearing loss affects the high frequencies first, an OAE detection paradigm measuring OAEs at frequencies >8 kHz has the potential to lead to earlier detection. Such a paradigm might not be effective for older patients who already have high-frequency hearing loss but may be advantageous for younger patients. If future studies show that high-frequency CEOAEs can detect a high-frequency sensorineural hearing loss, related future studies might examine the feasibility of monitoring high-frequency CEOAEs in patients receiving ototoxic medications who are at risk for hearing loss and compare the relative efficacy of high-frequency CEOAEs with DPOAEs and SFOAEs.

CONCLUSIONS

The problem of characterizing the acoustic source level of a probe designed for ear-canal measurements at high frequencies was solved by an incident-pressure calibration procedure based on reference measurements in a long cylindrical tube, which functioned as an acoustically anechoic termination. High-frequency behavioral thresholds up to 16 kHz were measured using this calibrated source based on an efficient ML procedure. The results confirmed previous research showing a wide variation in audiometric levels above 8 kHz in a population of subjects with normal audiometry at lower frequencies. In teenage and young-adult subjects with normal hearing up to 8 kHz, CEOAEs were obtained at frequencies up to 16 kHz. The CEOAE SEL spectrum decreased with increasing audiometric threshold in the third octaves centered at 8 and 10.1 kHz, which suggests the possibility that high-frequency CEOAEs may be useful in a test to detect high-frequency sensorineural hearing loss. Third-octave filtered CEOAE residual waveform envelopes showed an earlier linear-growth component, which implies a quadratic growth in the total CEOAE waveform, and a later compressive-growth component consistent with nonlinear compression acting on basilar-membrane mechanics. The envelope delays of earlier components showed small but statistically significant decreases in latency with increases in level. The envelope delays of later components were invariant with level. CEOAE latency based on the entire response decreased with increasing stimulus level, but this was mostly due to a change in the relative proportion of energies of earlier and later components.

APPENDIX: SOUND LEVEL SPECIFICATION FOR TRANSIENT-EVOKED OTOACOUSTIC EMISSIONS

The specification of the sound level of the stimulus and response for transient-evoked OAEs, which include CEOAEs, differs somewhat from that for tonal-evoked OAEs such as SFOAEs and DPOAEs. For example, the measured SPL of a sinusoidal tone is substantially independent of its measurement duration, whereas the SPL of a transient such as a click decreases with increasing measurement duration. This appendix describes how sound levels are reported for transient responses measured using discrete-time signal processing based on the DFT. These generally correspond to definitions of sound levels for transient responses measured using continuous-time signal processing based on the Fourier transform (Young, 1970; Pierce, 1989). These relationships have significance for understanding differences in sound levels reported for transient-evoked and tone-evoked OAEs.

The sound exposure E from a transient pressure waveform p(t) in a continuous-time representation and from a pressure finite sequence p[n] in a discrete-time representation with sample period T and buffer length of N samples is

$$E={\int }_0^{NT}dt{\mid p\left(t\right)\mid }^2=T\sum _{n=0}^{N-1}{\mid p\left[n\right]\mid }^2,$$ (A1)

with the integral or sum extending over the time duration NT of the measurement and with n representing the sample number. The effective duration of the transient is assumed less than NT (else a larger N would be used). A SEL L_E is defined as

$$L_E=10{\log }_{10}\left(\frac{E}{P_{\mathrm{ref}}^2{T}_{\mathrm{ref}}}\right),$$ (A2)

in which the reference pressure is P_ref=2×10⁻⁵ Pa and the reference averaging time T_ref may be arbitrarily specified with a default value of 1 s in continuous-time analysis. The SEL quantifies the level (in dB) of a transient sound.

P[k] denotes the DFT of p[n] at the kth frequency bin with center frequency f_k=k∕(NT), e.g., as defined in Oppenheim and Schafer (1989). Because p[n] is real, the so-called Parseval relation associated with the DFT for even N is

$$\sum _{n=0}^{N-1}{\mid p\left[n\right]\mid }^2=\frac{1}{N}\sum _{k=0}^{N-1}{\mid P\left[k\right]\mid }^2=\frac{1}{N}(\sum _{k=1}^{N∕2-1}2{\mid P\left[k\right]\mid }^2+{\mid P\left[0\right]\mid }^2+{\mid P[N∕2]\mid }^2).$$ (A3)

The spectral terms at k=0 and k=N∕2 are outside the measurement bandwidth and are thus discarded in the following. Using Eqs. A1, A2, A3, the SEL within the measurement bandwidth is

$$L_E=10{\log }_{10}\left(\frac{\frac{T}{N}\sum _{k=1}^{N∕2-1}2{\mid P\left[k\right]\mid }^2}{P_{\mathrm{ref}}^2{T}_{\mathrm{ref}}}\right).$$ (A4)

Generalizing the above equation to the kth spectral frequency, a band sound-exposure spectrum level L_Eb, or SEL spectrum, is defined by

$$L_{Eb}=10{\log }_{10}\left(\frac{\frac{T}{N}2{\mid P\left[k\right]\mid }^2}{P_{\mathrm{ref}}^2{T}_{\mathrm{ref}}}\right)=10{\log }_{10}\left(\frac{\frac{2}{N^2}{\mid P\left[k\right]\mid }^2∕\Delta f}{P_{\mathrm{ref}}^2{T}_{\mathrm{ref}}}\right),$$ (A5)

with the latter defined for reasons described below. The DFT bandwidth of each spectral bin is Δf=(NT)⁻¹. Other band SELs can be defined over octaves or other averaging bandwidths using an appropriate partial sum over multiple DFT frequency bins in place of the sum used in Eq. A4, as was used in the present work to calculate the third-octave band SEL spectra.

The SEL spectrum of a single transient is related to the SPL spectrum of a periodic sequence of transients, which has a period equal to the duration NT of the single transient. Alternatively, the finite sequence p[n] of length N might be sampled from an underlying random signal, and a periodic sequence might be formed to facilitate use of the DFT in periodogram analysis (Oppenheim and Schafer, 1989). Using a terminology similar to that in ANSI S1.1 (1994) for the continuous-time signal analysis, a band sound pressure spectrum level L_pbs is

$$L_{\mathit{pbs}}=10{\log }_{10}\left(\frac{\frac{2}{N^2}{\mid P\left[k\right]\mid }^2∕\Delta f}{P_{\mathrm{ref}}^2∕{\Delta }_{\mathrm{ref}}f}\right),$$ (A6)

in which the reference bandwidth is Δ_reff with a default value of 1 Hz. The L_pbs with this default is the SPL spectrum (re 1 Hz bandwidth). In the numerator, the kth spectral band component $\frac{2}{N^2}{\mid P\left[k\right]\mid }^2$ may be produced by an underlying continuous distribution of frequency components so that its spectral density over the bandwidth Δf is $\frac{2}{N^2}{\mid P\left[k\right]\mid }^2∕\Delta f$. For a sinusoid of frequency f_k, the SPL L_p can be written as

$$L_p=10{\log }_{10}\left(\frac{\frac{2}{N^2}{\mid P\left[k\right]\mid }^2}{P_{\mathrm{ref}}^2}\right),$$ (A7)

so that L_p=L_pbs+10 log₁₀(Δf∕Δ_reff).

A comparison of Eqs. A5, A6 shows that the SEL spectrum (re 1 s averaging time) of a transient sound is numerically equal to the SPL spectrum (re 1 Hz bandwidth) of the repeated transient sound. This would require that the duration NT of the underlying DFT be 1 s, which is not typically the case in practical measurements. A convenient choice for discrete-time measurements using the DFT is that the reference averaging time is equal to the DFT buffer length, i.e., T_ref=NT. For example, this is appropriate for a click train with period NT. The SEL spectrum for this choice of T_ref simplifies to

$$L_{Eb}=10{\log }_{10}\left(\frac{\frac{2}{N^2}{\mid P\left[k\right]\mid }^2}{P_{\mathrm{ref}}^2}\right).$$ (A8)

The relationship between the SEL spectrum of the single transient and the SPL spectrum of the periodic sequence of this transient is

$$L_{Eb}=L_{\mathit{pbs}}-10{\log }_{10}\left(NT\right).$$ (A9)

The observation that the right-hand sides of Eqs. A7, A8 are equal carries no special significance because they correspond to different types of measurements.

The actual stimulus presentation in the CEOAE measurement was not a periodic sequence of equal-amplitude clicks but, as described in Sec. 4D, used three click stimuli of varying amplitude with an interclick interval of 25.5 ms. Specifying the transient sound level using the SPL spectrum must also include the conditions under which the SPL should be interpreted. The simpler choice used in the present study specifies the transient sound level using the SEL spectrum based on Eq. A8.