Assessing time-dependent association between scalp EEG and muscle activation: a functional random-effects model approach

Abstract

This study investigates time-dependent associations between source strength estimated from high-density scalp electroencephalogram (EEG) and force of voluntary handgrip contraction at different intensity levels. We first estimate source strength from raw EEG signals collected during voluntary muscle contractions at different levels and then propose a functional random-effects model approach in which both functional fixed effects and functional random effects are considered for the data. Two estimation procedures for the functional model are discussed. The first estimation procedure is a two-step method which involves no iterations. It can flexibly use different smoothing methods and smoothing parameters. The second estimation procedure benefits from the connection between linear mixed models and regression splines and can be fitted using existing software. Functional ANOVA is then suggested to assess the experimental effects from the functional point of view. The statistical analysis shows that the time-dependent source strength function exhibits a nonlinear feature, where a bump is detected around the force onset time. However, there is the lack of significant variations in source strength on different force levels and different cortical areas. The proposed functional random-effects model procedure can be applied to other types of functional data in neuroscience.

1. Introduction

Nowadays, more and more neuroscience data sets are collected in the form of functional samples due to recent technological advances, where the basic unit of observation can be viewed as a curve or in general a function. For example, observations are time-series curves or images in the data from computerized electroencephalograph (EEG) or functional magnetic resonance imaging (fMRI). Functional data analysis (FDA) is a new and active area in statistical research and has become an increasingly important analytical tool for these type of complex data. One of the most important techniques in FDA is functional regression modeling. These models can be based on either functional predictors or functional responses (See Ramsay and Silverman (2002, 2005), Guo (2002, 2004), Fan and Zhang (2000), and Yao et al. (2005) for numerous applications).

Proportional relationship between brain signals and muscle output has been reported by studies involving single-cell recordings in the brain (Evarts, 1968; Conrad et al., 1977; Fetz and Cheney, 1980), positron emission tomography (PET) (Dettmers et al., 2001), fMRI (Thickbroom et al., 1998; Dai et al., 2001; Cramer et al., 2002), and EEG-derived movement-related cortical potential (MRCP) (Siemionow et al., 2000). This relationship is important in understanding motor control mechanisms and in providing guidance for neuromuscular rehabilitation. However, most of the studies either examined the relationship only at one time point or based on an averaged cortical signal across the entire time course of the motor action. It is expected that brain activation patterns differ among various time periods (e.g., preparation vs. execution periods) during a motor control process. Thus, it is of interest to examine whether the relationship between the levels of brain and muscle activation would also differ from one phase of movement control to another. In the experiment we will present, subjects performed isometric handgrip contractions of the right arm at three different intensity levels. Signals of the handgrip force, electromyographic (EMG) from the finger flexor and extensor muscles and 64-channel EEG were acquired simultaneously over the time across preparation, execution and sustaining phases at each level of the handgrip. The complex data from the multiple modalities are in the form of functional samples. The main aim of this paper is to provide a functional random-effects model approach to assess the time-dependent association between source strength estimated from high-density scalp EEG acquired during voluntary handgrip contractions at different intensity handgrip force levels. It will be shown that the proposed method can be useful for modeling other types of functional data in neuroscience.

We now summarize the contents of the rest of this paper. In section 2, we address our experiment designs and discuss how source strength of the raw EEG signals are estimated. In section 3, we propose a functional random-effects model approach for modeling time-dependent association between source strength and level of muscle activation and other design factors. Two estimation procedures for the functional model are discussed here: a two-step method and a regression spline method. We then discuss a functional analysis of variance (ANOVA) approach based on the model for the statistical inference of the design factors. In section 4, we present analysis results based on the proposed model. In section 5, we close this paper with conclusion remarks.

2. Experiment and data preprocessing

2.1. Subjects and Motor Task

Eight right-handed subjects (4 men and 4 woman, age = 31 2 yrs) participated in the study. The experimental procedures were approved by the Institutional Review Board at the Cleveland Clinic. All subjects gave informed consent prior to the participation.

During the experiment, subjects performed isometric handgrip contractions of the right arm at three intensity levels: 40%, 60% and 80% maximal voluntary contraction (MVC) forces. At each force level, the subjects performed 20 handgrip trials. Special precautions were taken to minimize noise in the data during the experiments. Muscle fatigue was minimized by allowing sufficient rest between adjacent trials. The length of the inter-trial rest period was controlled by the subjects themselves, i.e., they started the next trial when they felt comfortable and completely rested. The inter-trial rest period was, on average about 20s with the period being longer when stronger force (e.g., 80% MVC) was exerted.

2.2. Data Recording

Force

The handgrip force was sensed by a pressure transducer (EPX-N1 250 PSI, Entran Devices, Inc., Fairfield, NJ), acquired a Spike 2 data acquisition system (version 3.05, Cambridge Electronic Design, Ltd., Cambridge, UK), and stored on a hard disk of a laptop computer. The sampling rate for the force data acquisition was 100 Hz.

EMG

Surface Electromyographic (EMG) signals were measured from the flexor digitorum profundus (FDP), flexor digitorum superficialis (FDS) and extensor digitorum (ED) muscles of the right arm. Bipolar electrodes (8-mm recording diameter) were attached to the skin overlying as close as possible to the belly of each muscle. The electrodes were connected to the amplifiers directed to the Spike 2 data acquisition system. The EMG signal sampling rate was 2000 Hz.

EEG

A 64-channel NeuroScan EEG system (version 4.2, NeuroScan, El Paso, Texas, USA) was used to acquire EEG signals from the scalp. A Quik-Cap elastic nylon cap that held 64 surface electrodes was placed on the scalp for EEG data recording. Conducting gel was injected into each electrode to connect the recording surface of the electrode with the scalp. Impedance was controlled below 10,000 ohms. All the EEG electrodes were referenced to the common linked earlobes and the signals were amplified (X75,000), low-pass filtered (0.05–50 Hz), and digitized (2,000 sample/s).

2.3. Data preprocessing

The force and EMG data were processed using house-coded programs within the Spike 2 software package. The force onset time was set at the 10% handgrip MVC force rise from the baseline in each trial. The actual force at each target level was measured by averaging the data points in each trial when the force was steady and then averaging across the trials at each target level before performing the group averaging. Given that the force of isometric muscle contraction and the associated EMG are highly correlated, including either variable would yield very similar results. We picked the force in the statistical modeling because the aim of the study was to detect the relationship between the force and source strength.

The raw EEG data were visually inspected and trials with substantial artifacts due to eye blinks or head movements were excluded (the removed trial number ranges from 0 to 4 per subject). Both EEG data preprocessing and the low-resolution electromagnetic tomography (LORETA) current density estimation were performed using Curry software package (version 4.5, Neuro Scan Labs, Virginia, USA).

Estimation of current densities using LORETA

For each subject at each force level, the EEG signals were aligned with the force onset and then averaged across trials. The averaged EEG data were baseline corrected using baseline data from −3000ms to −2500ms. Subsequently, an independent component analysis (ICA) was applied to the data. Only the main components (signal-to-noise ratio (SNR) > 1, SNR was estimated by the default method in Curry, which was estimated from the 20% of samples with the lowest mean global field/potential power) were chosen for the source reconstruction. A 3-layer (conductivities of the scalp and brain: 0.033S/m, and the skull: 0.0042S/m) triangle-node boundary element model (BEM) (Fuchs et al., 1998, Fuchs et al., 2002) based on the MNI (Montral Neurological Institute) brain MRI was used to overlay the sources. Distributed current density model using LORETA with L1 norm method was applied to the ICA-preprocessed data. In addition, the sources were constrained to the reconstructed layer of the folded cortex with 6926 nodes using a rotating model (Basile et al., 2004; Yao et al., 2005).

Current Density Analysis

Source localization was analyzed at 24 different time points: −3000ms, −2800ms, −2200ms, −2100ms, −2000ms, −1000ms, −900ms, −800ms, −700ms, −600ms, −500ms, −400ms, −300ms, −200ms, −100ms, 0ms, 100ms, 200ms, 500ms, 800ms, 1000ms, 2000ms, 2500ms, 3000ms (time 0 is Force onset time) throughout the planning, execution, and sustaining phases of the handgrip muscle contraction at each force level in each subject. The time points were selected based on motor planning, execution and maintenance phases of the muscle contraction. Each source had 7 parameters: location (x, y, z), orientation (x_o, y_o, z_o) and current density (CD).

Since each source needed to be identified at its anatomical location under Talairach coordinate for further analysis, several steps were taken to transform CurryV4.5 coordinate to it. The Talairach coordinate system is a standard reference for identification of brain structures which specified locations relative to their distance from the anterior commisure (AC) (Talairach and Tournoux, 1988). In the analysis, transformation of the SPM99/MNI (X, Y, Z) coordinates from the Curry coordinates (x, y, z) was first obtained as follows (the MNI image dataset has a 1.8-mm voxel size in Curry V4.5, while the MNI brain originally had a voxel size of 2 mm):

$$\begin{array}{l}X=(120mm-x)·2/1.8\\ Y=(102mm-y)·2/1.8\\ Z=(z-100mm)·2/1.8\end{array}$$

Second, transformation of the SPM99/MNI coordinates (X, Y, Z) to the Talairach coordinates (X′, Y′, Z′) was performed (see, http://www.mrc-cbu.cam.ac.uk/Imaging/Common/mnispace.shtml): Above the AC (Z ≥ 0):

$$\begin{array}{l}{X}^{\prime }=0.9900X\\ Y^{\prime }=0.9688Y+0.0460Z\\ Z^{\prime }=-0.0485Y+0.9189Z\end{array}$$

Below the AC (Z < 0):

$$\begin{array}{l}{X}^{\prime }=0.9900X\\ Y^{\prime }=0.9688Y+0.0420Z\\ Z^{\prime }=-0.0485Y+0.8390Z\end{array}$$

Third, after establishing the position of each source on the Talairach coordinate, the anatomical label was obtained through the Talairach Daemon search for each source location. Thus, all the sources in the Broadmanns areas 1, 2 and 3 (primary sensory cortex [S1]), area 4 (primary motor cortex [M1]) and area 6 (premotor [PM] and supplementary motor area [SMA]) were identified. (We chose the three Broadmanns areas based on their well known role in modulating muscle activities.) In our data sets, there is an “area” factor which contains five “area” levels.

Within each area the vector-averaged current densities (VACD) were calculated for each subject according to the following formula:

$$\text{VACD}=\sqrt{\frac{1}{B}\sum _{i=1}^B\left[{(C{D}_i·X_{oi})}^2+{(C{D}_i·Y_{oi})}^2+{(C{D}_i·Z_{oi})}^2\right]},$$

where B is the total number of sources in the analyzed area and (X_oi, Y_oi, Z_oi) is the orientation of the ith source.

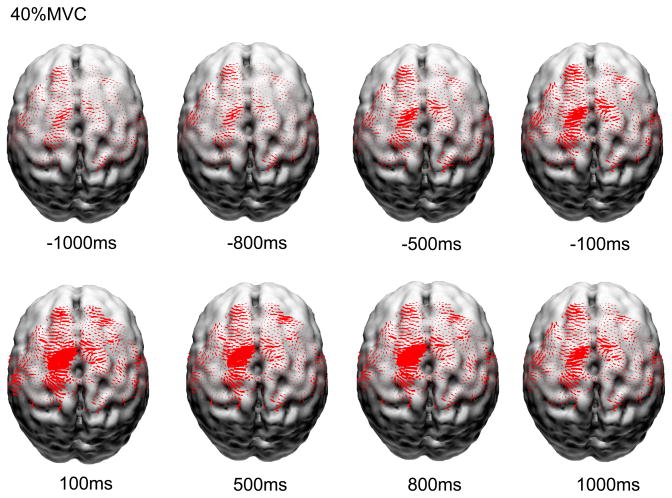
The overall averaged current densities of these five major sensorimotor areas at the three force levels at time of −2200ms, −2100ms and −2000ms were used as the normalization factor for each subject. The purpose of this normalization was to reduce the confounding effects of possible wide variation of global neuronal activity among subjects. Finally, the VACD at each time point was normalized by this normalization factor. This normalized VACD was the “source strength” for further statistical analysis with functional random-effects model. Figure 1 displays reconstructed normalized and averaged cortical currents at 40% maximal voluntary contraction force level of 8 subjects along the muscle contraction time. The size of the red areas is proportional to the local current density. Only currents in Broadmanns area 1, 2, 3, 4 and 6 are shown here. It is noted that the current density exhibited non-linear increase from muscle contraction preparation time to execution time.

Figure 1.

Reconstructed normalized and averaged cortical currents at 40% maximal voluntary contraction force level of 8 subjects along the muscle contraction time. The size of the red areas is proportional to the local current density. Only currents in Broadmanns area 1, 2, 3, 4 and 6 are shown here.

3. Functional random-effects model

As we discussed in the previous section, we have obtained the estimated source strength (i.e. normalized VACD) from raw scalp EEG by current density analysis. We now focus on our primary goal for this study: modeling the time-dependent association between estimated source strength and force levels of handgrip contraction and/or other explanatory variables. Like most studies in neuroscience research, functional curves of subjects in our study are repeatedly measured from a cluster or multi-level sampling design (e.g. different force levels and different cortical areas) so that time-varying causal relationships between the responses and explanatory variables of interest can be modeled. One may consider to formulate our data with functional linear model (Ramsay and Silverman, 2005), an extension of a linear model to the functional context. However, the model appears insufficient since it cannot consider the important features in our sampling design, such as the between-subject/within-subject variation. In conventional longitudinal data analysis, random-effects are often necessary when the observations are not obtained by simple random sampling but come from a cluster or multi-level sampling design (Diggle et al., 2002). This design may induce additional sources of variation that need to be taken into accounted by the model. Random-effects models are primarily used to describe relationships between a response variable and some covariates in data that are grouped according to one or more classification factors (Pinheiro and Bates, 2000). By associating common random effects to observations sharing the same level of a classification factor, the models flexibly represent the covariance structure induced by the grouping of the data.

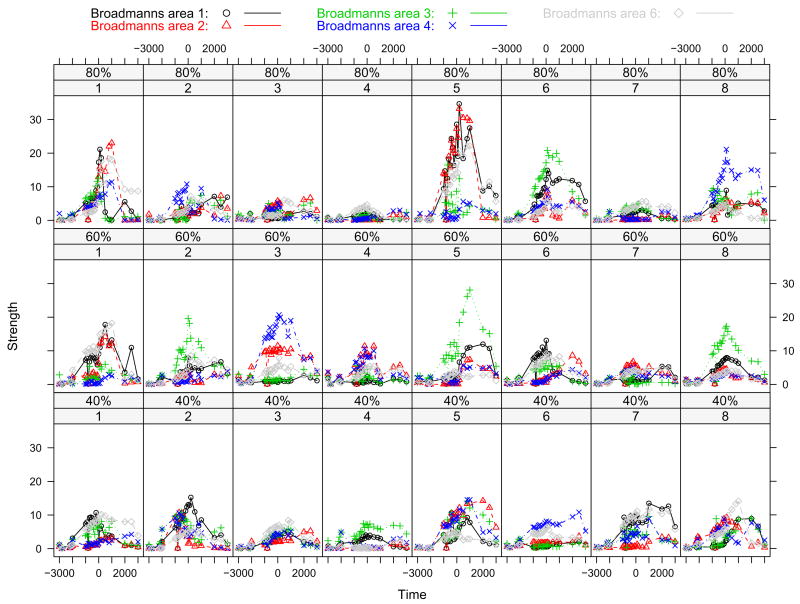
Figure 2 shows source strength versus time for eight subjects by different force level. Data points from time −1000ms to 1000ms are displayed here. In the figure, each column represents one subject and each row represents one force level. Source strengths for five different cortical areas under same conditions are plotted within one sub-plot by different symbols. It is noted that sample curves vary greatly over subjects. The eight different subjects represent a sample from the population about which we wish to make inference so we need random effects to model the “subject” factor. Hence, for the functional data we have, this leads to a functional random-effects model.

Figure 2.

Source strength versus time for eight subjects by different force level. Source strengths for five different cortical areas under same condition are plotted within one sub-plot by different symbols. Broadmanns area 1, 2, 3, 4, and 6 are denoted by circle with black, triangle with red, plus with green, cross with blue, and diamond with gray, respectively.

The basic philosophy of functional data analysis is to think of observed data functions as single entities, rather than merely as a sequence of individual observations. To formulate the problem, we first give the following notation: let us denote i = 1, · · ·, n the index of the subjects (n=8 in our study); let j = 1, · · ·, m denote the level of force (we have three force levels here: 40%, 60% and 80% maximal voluntary contraction (MVC) forces); let k = 1, · · ·, l denote the index of cortical areas (l = 5 in our data set). To quantify the between-subject/within-subject variation in our sampling design, the following functional random-effects model is motivated:

$$y_{\mathit{ijk}}(t)=\mu (t)+{\alpha }_j(t)+{\theta }_k(t)+{\eta }_{jk}(t)+u_i(t)+{\epsilon }_{\mathit{ijk}}(t)$$ (1)

The function μ(t) is the grand mean function, and therefore indicates the average source strength profile across all subjects. The terms α_j(t) are the specific effects on source strength of being in the force level j. The terms θ_k(t) are the specific effects on source strength of being in the cortical area k. The terms η_jk(t) are the specific interaction effects between the force level j and the cortical area k. To be able to identify them uniquely, we require that they satisfy the following constraint

$$\begin{array}{l}\sum _j{\alpha }_j(t)=0,\sum _k{\theta }_k(t)=0,\\ \sum _j{\eta }_{jk}(t)=0,\sum _k{\eta }_{jk}(t)=0,\text{for}\forall t.\end{array}$$

u_i(t) is the random effect function for the ith subject (i.e. “subject-specific” deviation from the grand mean function). The residual function ε_ijk(t) is the unexplained variation specific to the ith subject under jth strength level at the kth location. μ(t), α_j(t), θ_k(t) and η_jk(t) are fixed effects, which are parameters associated with an entire population or with certain repeatable levels of experimental factors; u_i(t) are the random effects, which are associated with individual experimental units drawn at random from a population. It is generally assumed that u_i(t) are i.i.d realizations of an underlying Gaussian process with mean function 0 and covariance function γ(s, t), and ε_ijk(t) are i.i.d realizations of an uncorrelated white noise process with mean function 0 and variance function σ²(t)I_{s=t}. Here γ(s, t) quantifies the between-subject variation while the σ²(t) quantifies the with-in subject variation.

The above functional random-effects model (1) can be written more compactly in matrix notation,

$$\mathit{y}(t)=\mathit{X}\mathit{\beta }(t)+\mathit{Zu}(t)+\mathit{\epsilon }(t),$$ (2)

which it is a general setting for functional mixed model. X is known as the N × p design matrix (N = n × m × l and p = 1 + (m − 1) + (l − 1) + (m −1)(l−1) in our case). It specifies values of fixed effects corresponding to each parameter for each observation. For categorical effects the values of zero and one are used to denote the absence and presence of effect categories, and for covariate effects the variable values themselves are used in X. Z is a second design matrix with the dimension N × q giving the values of random effects corresponding to each observation. It is specified in exactly the same way as X was for the fixed effects, except that an intercept term is not included (q = n in our case). β(t) = [β₁(t), β₂(t), · · ·, β_p(t)]^T are the coefficient functions of the fixed-effects component (which are parameters associated with an entire population and with certain repeatable levels of experimental factors), and u(t) = [u₁(t), u₂(t), · · ·, u_q(t)]^T are the coefficient functions of the random-effects component (which are associated with individual experimental units drawn at random from a population). u(t) is associated with a Gaussian process with covariance Γ,

$$\mathit{u}(t)\sim GP(0,\mathbf{\Gamma })$$ (3)

The above functional random-effects can also be termed as a functional mixed model, which is a natural extension from the standard functional linear model where the functional data are permitted to exhibit functional correlation and non-constant variability. The functional mixed model, therefore, provides us with the flexibility of modeling not only the means of our functional data (as in the standard functional linear model) but their functional variances and functional covariances as well. Functional mixed-effect was first proposed by Guo (2002) and was fit using a smoothing spline method. A wavelet-based method was proposed by Morris and Carroll (2006). Wu et al. (2003) fit a special case of the mixed-effects varying-coefficient models using a regression spline method. In this paper, we would like to focus on stable and flexible algorithms for practical uses. Two flexible estimation procedures for the functional model are discussed here. The first estimation procedure is a two-step method which involves no iterations. It can flexibly use different smoothing methods and smoothing parameters. The second estimation procedure benefits from the connection between linear mixed models and regression splines and can be fitted using existing software.

3.1. Two-step approach

As pointed out by Ramsay and Silverman (2005), the basic philosophy of functional data analysis is to think of observed data functions as single entities. Functional data are usually observed and recorded discretely as V pairs (t₁, y₁), · · ·, (t_v, y_v), · · · (t_V, y_V), and y_v is a snapshot of the function at time t_v, possibly blurred by measurement error. It is noted that V can be different over subjects or other experimental settings. Basis expansion is an important tool to represent functions in functional data analysis. Basis function procedures represent a function y by a linear expansion $y(t)\approx \stackrel{\sim }{y}(t)={\sum }_{s=1}^S{\lambda }_s{\phi }_s(t)$ (or in matrix form y(t) ≈ ỹ (t) = Λφ(t)) in terms of S known basis function φ_s. B-splines are the most common choice of approximation system for non-periodic functional data and/or parameters.

Our first estimation procedure is adapted from the idea of Fan and Zhang (2000)’s two-step method to estimate time-varying coefficients in a time-varying coefficient model for longitudinal data. The two-step method is so named since it includes an “estimation step” and a “smoothing step”. In the first point-wise estimation step, one calculates the raw estimates of the coefficient functions via fitting a standard linear mixed regression model. Let τ₁, τ₂, · · ·, τ_V be a suitable grid of values of t. For each given time τ_v, v = 1, · · ·, V, one fit the standard linear mixed model,

$${\stackrel{\sim }{y}}_{\mathit{ijk}}({\tau }_v)=\mu ({\tau }_v)+{\alpha }_j({\tau }_v)+{\theta }_k({\tau }_v)+{\eta }_{jk}({\tau }_v)+u_i({\tau }_v)+{\epsilon }_{\mathit{ijk}}({\tau }_v).$$

In the second smoothing step, one smoothes the estimates from the first step to obtain the smooth estimates of the coefficient functions via using one of existing smoothing techniques such as local polynomial smoothing, smoothing splines, penalized splines, or orthogonal series. For example, one can smooth the force level effect coefficients separately: {τ_v, α_j(τ_v)}, v = 1, 2, · · ·, V, to obtain the refined estimated functions α̂_j(t), j = 1, · · ·, m in model (1).

We have been assuming that the response variable ỹ(t) is a results of basis expansion of the discrete data. The basis expansion is very important when functional data are obtained from unequally spaced time points for different subjects. With the balanced design as in our study, one can fit the raw data in the first step. i.e. go straight from the raw response values to estimate the regression coefficients and smooth them in the second step. An advantage of the two-step method is that it is simple to understand and easy to implement. The method is very flexible because it not only allows different smoothing methods to be used for different coefficient functions but also allows different smoothing parameters selected by different methods.

3.2. Estimating with regularized basis expansions

As we previously mentioned, it is common to represent functions by basis expansion system in functional data analysis. Basis expansion can be used not only for functional responses but also for functional coefficients of predictors. Let us now assume that the response function y(t), the fixed-effect coefficient function β(t), and the fixed-effect coefficient function u(t) in model (2) are approximately expressed in basis expansion form as the coefficients of a B-spline or a truncated power basis. Assume that we have the following regression spline bases:

$$\begin{array}{l}\mathit{y}(t)\approx \stackrel{\sim }{\mathit{y}}(t)=\mathbf{\Lambda }(t)\mathit{\phi },\\ \mathit{\beta }(t)\approx \stackrel{\sim }{\mathit{\beta }}(t)=\mathbf{\Theta }(t)\mathit{\eta },\\ \mathit{u}(t)\approx \stackrel{\sim }{\mathit{u}}(t)=\mathbf{\Psi }(t)\mathit{\xi },\end{array}$$

where the S_y-vector φ contains the linearly independent basis functions; the N × S_y matrix contains the coefficient of expansion. Similarly, η and ξ are S_β and S_u vectors; Θ and Ψ are p × S_β and q × S_u matrices, respectively. We may choose to use the same basis for response functions and coefficient functions and consequently some of what follows becomes simpler. However, we need to keep the different basis systems in most cases of real data analysis.

Note that the element of S_u-vector ξ are i.i.d. copies of a normal random variable with mean 0 and some covariance matrix R. A direct connection between R and Γ is

$$\mathbf{\Gamma }(s,t)\approx \mathbf{\Psi }{(s)}^T\mathit{R}\mathbf{\Psi }(t).$$

Let τ₁, τ₂, · · ·, τ_V be the distinct (equal-space) design time points we specify. Similar to the two-step method, we can directly use raw response data and original time points when we have balanced designs. Model (2) can be approximately expressed as a standard linear mixed-effects model:

$${\mathbf{\Gamma }}_v\mathit{\phi }={\mathit{W}}_v\mathit{\eta }+{\mathit{D}}_v\mathit{\xi }+{\mathit{\epsilon }}_v,v=1,\cdots ,V$$ (4)

where W_v = XΘ(τ_v), D_v = ZΨ(τ_v), ξ ~ N(0,R), and ε ~ N(0, σ²I).

For given bases Λ, Θ, and Ψ, the model (4) can be fitted using the maximum likelihood or restricted maximum likelihood method by the SAS procedure Proc Mixed or R/Splus library nlme. The covariance matrix R may be specified as unstructured or with some special structure. The numbers of basis functions play the role of smoothing parameters. Usually, the choice of basis function systems is not as crucial as the determination of smoothing parameters. We use B-splines basis here due to its stability and speediness in calculations and easy implementation when using existing software. The AIC and BIC rules of linear mixed models can be used to select the smoothing parameters.

3.3. Statistical inference and functional ANOVA

The fitting of the functional model is not the ultimate goal of the analysis. We are primarily interested in drawing inferences on the fixed effects in the model, in order to generalize results obtained from a specific sample to the general population from which the sample was taken. In general, for each parameter function β_i(t) in β(t), i = 1, · · ·, p, one is concerned with testing the following hypothesis.

$$H_0:{\beta }_i(t)=0vs.H_1:{\beta }_i(t)\ne 0.$$

Wu et al. (2003) fit a special case of time-varying coefficient model using a regression spline method and discussed approximate Wald test for the above hypothesis, where the test statistic is approximated by a χ² distribution. However, as noted early by Dempster et al. (1981), the Wald test statistics are based on estimated standard errors which underestimate the true variability in β̂_i. This downward bias can be resolved by using approximate F tests as in standard linear mixed models. Here, we propose a functional analysis of variance (ANOVA) approach to make inference based on the functional random-effects model. The associated functional ANOVA plot allows us to visually evaluate the fit and examine the fixed effects over time.

To perform functional ANOVA for a specific factor (i.e. force level effect or cortical area effect), let L be a known matrix associated with the testing factor, we can consider a more general hypothesis,

$$H_0:\mathit{L}\mathit{\beta }(t)=0vs.H_1:\mathit{L}\mathit{\beta }(t)\ne 0.$$

Essentially the functional ANOVA problem can be considered as really a univariate ANOVA problem for each specific value of t.

With the two-step method, we calculate β̂(t) with a suitable grid of values of t, and the F-statistic for a given τ_v,

$$F_1({\tau }_v)=\frac{\widehat{\mathit{\beta }}{({\tau }_v)}^T{\mathit{L}}^T{(\mathit{L}{\widehat{\mathit{C}}}_1({\tau }_v){\mathit{L}}^T)}^{-1}\mathit{L}\widehat{\mathit{\beta }}({\tau }_v)}{\text{rank}(\mathit{L})}$$ (5)

Ĉ₁(τ_v) is the familiar generalized least-squares estimate of the variance-covariance matrix for β(τ_v) based on the fitted linear mixed model at the time point τ_v. F₁(τ_v) in (5) has an approximate F-distribution with rank(L) numerator degrees of freedom and denominator degrees of freedom estimated from the data. To obtain F-statistic functions, one can interpolate between these values from the grid of time points.

With the regression spline methods, if coefficient functions β(t) are smooth enough and smoothing parameters appropriately selected, β̃(t) will approximate β(t) very well. The basis function approximation errors can be ignored for practical purposes, hence, inferences regarding β(t) can be based on β̃(t). Under the regression spline approximation, the hypothesis Lβ(τ_v) = 0 for a given τ_v is approximately equivalent to LΘ(τ_v)η = 0. Therefore, an F-test based on an approximate F-statistic is

$$F_2({\tau }_v)=\frac{{\widehat{\mathit{\eta }}}^T{(\mathit{L}\mathbf{\Theta }({\tau }_v))}^T{[\mathit{L}\mathbf{\Theta }({\tau }_v){\widehat{\mathit{C}}}_2{(\mathit{L}\mathbf{\Theta }({\tau }_v))}^T]}^{-1}\mathit{L}\mathbf{\Theta }({\tau }_v)\widehat{\mathit{\eta }}}{\text{rank}(\mathit{L}\mathbf{\Theta }({\tau }_v))}$$ (6)

where Ĉ₂ is the generalized least-squares estimate of the variance-covariance matrix for η based on the model (4). F₂(t₀) in (6) has an approximate F-distribution with rank(LΘ(τ_v)) numerator degrees of freedom and denominator degrees of freedom estimated from the data. With the grid of time points τ₁, τ₂, · · ·, τ_V, we can obtain the plots of smooth F-statistic functions.

4. Results

Statistical analysis based on the proposed functional random-effects model shows a significant and consistent time-dependent source strength change pattern in different phases of the voluntary muscle contraction at all force levels. The source strength increased at the preparation phase, peaked around the fatigue onset time and decreased in the sustaining phase. There was no significant difference of source strength among the three force levels and the five cortical areas. These results show clear time-dependent cortical activation during voluntary hand muscle activity planning and execution.

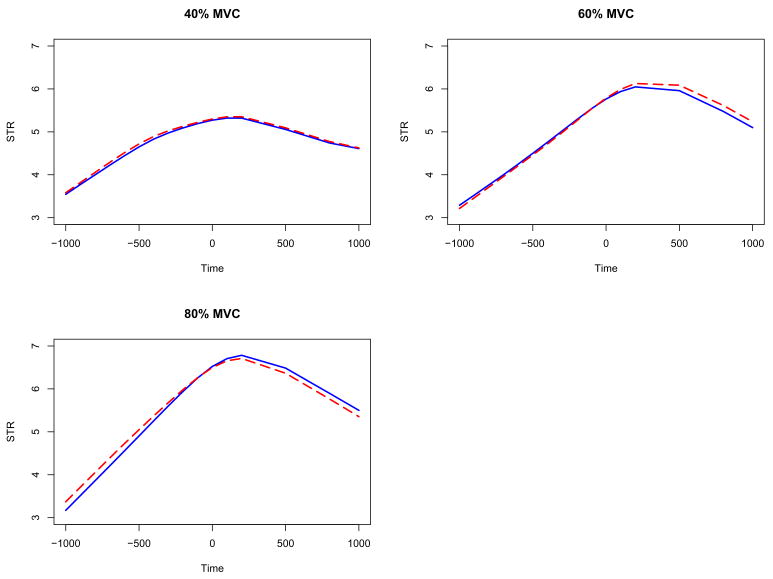
Figure 3 displays the resulting estimated effects μ(t) + α_j(t) for the three force levels. The solid curves are estimated from the two-step method and the dashed curves are estimated from the regression spline method. It is noted that the two estimating methods show the consistent results. We observe consistent time-dependent source strength changing patterns at all force levels. The curves are more complex than the constant or a linear function. The source strength increased at the preparation phase, peaked around the force onset time and decreased in the sustaining phase.

Figure 3.

The estimated composite effects μ(t) + α_j(t) for the strength functions in the functional random-effects model: the solid curves are estimated from the two-step method and the dashed curves are estimated from the regression spline method.

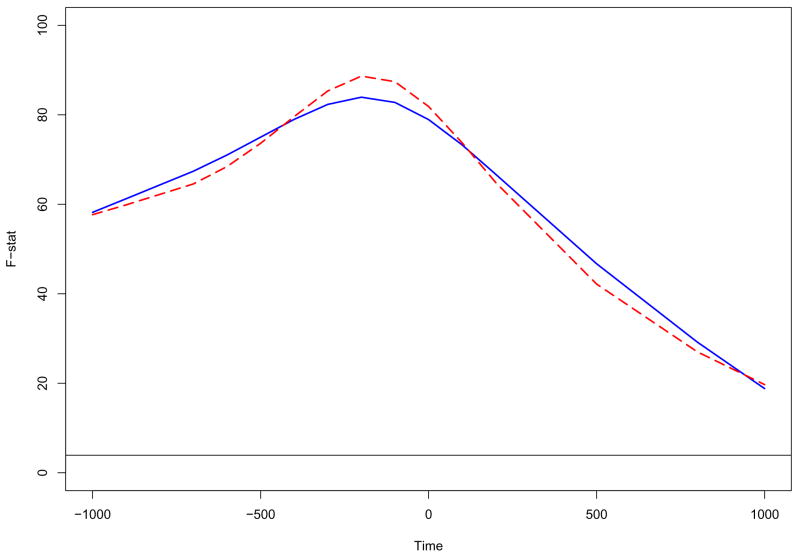
In estimating and plotting the individual force level effects, we have taken our first step towards achieving the goal of characterizing the source strength pattern in each force level. We shall next investigate the fixed effects of the model through Functional ANOVA. We first perform functional ANOVA for the grand mean function μ(t) of the source strength. The functional ANOVA curve (the solid line) based on the two-step estimation method is shown in the figure 4. The horizontal line indicates the 5% signification level for the F-distribution with 1 and 145 degrees of freedom. We can see that the F-statistic is everywhere substantially above the 5% significance level of 3.91. It is noticed that the F-statistic function exhibits a nonlinear feature, where a bump is detected around the force onset time. This indicates that the source strengths are strongly greater than zero around the force onset time. Figure 4 also displays the F-statistic function estimated by the regression spline method (the dashed curve). It is noted that the estimated curve is consistent to that based on the two-step method.

Figure 4.

Functional ANOVA plot for the grand mean function μ(t) based on the different methods: the solid curves are estimated from the two-step method and the dashed curves are estimated from the regression spline method. The horizontal line indicates the 5% signification level for the F-distribution with 1 and 145 degrees of freedom.

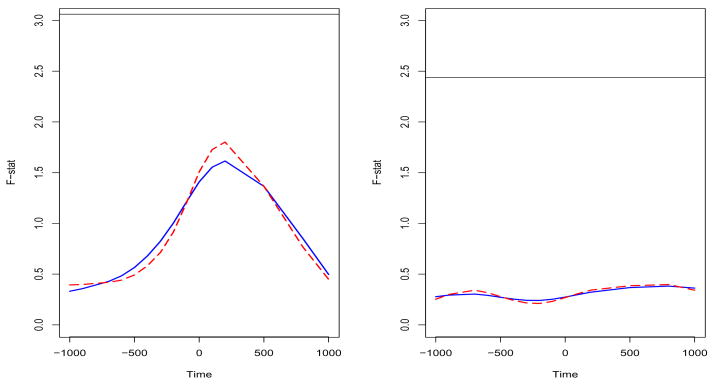
Functional ANOVA is also performed for the force level effect α_j(t), the cortical area effect θ_k(t), and their interaction η_jk(t). It is shown from the result that there is no significant difference of source strength among the three force levels, different cortical areas and their interaction. Figure 5 visually displays the F-statistic function plots for the force level effect α_j(t) and the cortical area effect θ_k(t). We can see that, based on the two-step estimation method, the F-statistic is everywhere lower than 5% significance level for both the force level effect and the cortical area effect (the solid lines). Thus, both the force level and cortical area had no significant effect on the source strength. However, it is interesting to notice that the patterns of two F-statistic functions are very different although there is no significant difference of source strength for both effects. The pattern of the F-statistic function for the force level effect is similar to that of the grand mean, while the F-statistic function of the cortical area effect is close to a constant. The result illustrates that, although there is no significant difference, there is more variation around the force onset time for the different force level. Similiar to the functional ANOVA for the grand mean function, we also calculate the F-statistic functions (the dashed curves in the figure 5) for the force level effect and the cortical area effect based on the regression spline method. The resulting functions are also close to that based on the two-step method.

Figure 5.

Functional ANOVA for the fixed effects based on the different methods: the solid curves are estimated from the two-step method and the dashed curves are estimated from the regression spline method. The left panel is the result of the force level effect α_j(t). The horizontal lines indicate the 5% signification level for the F-distribution with 2 and 145 degrees of freedom. The right panel is the result of the cortical area effect θ_k(t). The horizontal lines indicate the 5% signification level for the F-distribution with 4 and 145 degrees of freedom.

5. Concluding remarks

We present a new statistical procedure for analyzing functional data from a study of neural control of movement. We first address how to estimate source strength from the raw EEG data and then propose a functional random-effects model approach to model the data. Two flexible estimation procedures, the two-step method and the regression spline method, are discussed here. Both estimation procedures give consistent results in our data analysis. The two-step method is so named because it includes a “raw estimation step” and a “smoothing step”. The advantage of this method is that it is easy to implement and involves no iterations. The smoothing step can flexibly use different smoothing methods and smoothing parameters. The method can handle huge data sets easily. Yet, a drawback of the two-step method is that the estimation may be problematic when sample size of a study is really small. It is noted that we need to form the design matrix at each distinct time point. It is possible that the rank of design matrix will be less than the number of the parameters to be estimated in such case. Hence, we may fail to obtain the raw estimators. In the regression spline method, the use of basis function expansions gives us continuous control over smoothness while still allowing as much high frequency detail in the model as the data obtain. A drawback of the spline method is that it requires intensive computations for large data sets. Also, smoothing parameter selection is more difficult than that based on the two-step method. However, the spline method can handle the small sample study because we form the design matrix using data of all time points and we will have enough degree of freedom to solve the model.

We also perform functional ANOVA based on the fitted functional model, which allows us to assess the experimental effects from the functional point of view. Functional data analysis shows a significant and consistent time-dependent source strength change pattern in different phases of the voluntary muscle contraction at all force levels. The result confirms clear time-dependent cortical activation during voluntary hand muscle activity planning and execution.

It is noted that more and more neuroscience studies collect data as functional form. Functional data have been distinguished from longitudinal data until very recently (Zhao et al., 2004; Ramsay and Silverman, 2005). In reality, functional data often can point to longitudinal data with dense time grids, where one can understand within-subject repeated measures as discrete samples from a functional curve over the studied time interval. A curve for each subjects response can be obtained via smoothing techniques in connecting the discrete data points and then these subjects’ response curves can be modeled by functional regression or other functional models. The functional random-effect model discussed here can be applied to, for instance, multi-subject fMRI study or multi-channel neural signal analysis. With time-dependent coefficients, functional random-effects model captures the time-varying exposure-response relationship, thus providing the functional data with intuitive interpretations. With time-dependent random effects, the model allows functional between-subject/within-subject variation. The estimated coefficient function plots and functional ANOVA plots vividly reveal how the effect of a predictor can change along the time axis. Most importantly, functional random-effects model, requiring few assumptions, draws more robust conclusions as it has features similar to nonparametric methods.