Tactile intensity and population codes

Abstract

An important question in neuroscience is how different aspects of a stimulus are encoded at different stages of neural processing. In this review, I discuss studies investigating the peripheral neural code for perceived intensity in touch. One of the recurrent themes in this line of research is that information about stimulus intensity is encoded in the activity of populations of neurons. Not only is information integrated across afferents of given type, but information is also combined across submodalities to yield a unified percept of stimulus intensity. The convergence of information stemming from multiple submodalities is particularly interesting in light of the fact that tactile these are generally thought to be parallel sensory channels with distinct sensory functions and little cross-channel interactions. I discuss implications of a recently proposed model of intensity coding for psychophysical functions and for the coding of intensity in cortex. I also briefly review the peripheral coding of intensity in other sensory modalities.

Perceived intensity and integration within and across submodalities

Intensity is a basic perceptual dimension in the sense that any two stimuli can be compared along the intensive continuum as long as they impinge upon the same sensory sheet (the retina, the cochlea, the olfactory epithelium, etc.). For instance, the brightness of two objects or the loudness of two sounds can be readily compared (see [1], e.g.). Our experience with tactile stimuli – perceiving a puff of air, a light tap or a strong nudge –suggests that tactile intensity is a unitary percept; however, this belief may not be as straightforward as one might initially suppose. Indeed, the skin is innervated by a variety of receptors, several of which subserve the sense of “discriminative touch,” within which perceived (tactile) intensity is subsumed. The retina comprises four types of photoreceptors, so the presence of multiple receptor types is not what separates the sense of touch from its visual counterpart. The important distinction is that input from the four photoreceptors has long been known to converge, even within the retina itself, whereas input from low-threshold mechanoreceptive afferents is thought to remain segregated through at least the first cortical processing stage [2]. In fact, the four populations of low-threshold mechanoreceptive afferents are commonly thought to form the inputs to four distinct sensory channels in touch [3]. However, when contacting everyday objects, all four mechanoreceptive channels are more often than not activated. The study of the perception of intensity allows us to investigate how information stemming from these four channels is combined to yield a unitary percept of stimulus intensity.

Each of the three main types of low-threshold mechanoreceptive afferents innervating the glabrous skin is ascribed a distinct function (see [4;5] for reviews) and evokes a distinctive sensation when stimulated [6]. Slowly adapting type 1 (SA1) fibers, which innervate Merkel receptors, are thought to mediate fine form perception and coarse texture perception; stimulation of individual SA1 fibers elicits a sensation of pressure. Rapidly adapting (RA) fibers, which innervate Meissner corpuscles, mediate motion detection, coarse form perception and the perception of flutter; stimulation of RA fibers evokes a sensation of flutter. Pacinian (PC) fibers, named after the corpuscles they innervate, are implicated in fine texture perception (see [7] for a review) and the perception of textures through a tool [8]; stimulation of these fibers evokes sensations of vibration or tickle. The fourth population of low-threshold mechanoreceptive afferents, slowly adapting type 2 (SA2) fibers associated with Ruffini cylinders, is thought to mediate the perception of skin stretch and may be involved in the perception of hand conformation [9]. However, stimulation of individual SA2 afferents does not elicit any sensation, and doubt has been cast as to whether they actually innervate Ruffini cylinders [10]. Furthermore, Ruffini cylinders are absent from the glabrous skin of macaques [11], on which many relevant neurophysiological experiments have been carried out. Be that as it may, different aspects of the stimulus are thought to be encoded by different populations of mechanoreceptive afferents.

Not only must information be combined across submodalities in order for a unitary percept of stimulus intensity to be achieved, but information conveyed by individual afferents of a given type must be integrated. Indeed, responses of individual mechanoreceptive fibers cannot account for perceived intensity [12-14]. In the laboratory, the most common tactile stimulus used in the study of intensity coding is a vibration. Psychophysical judgments of perceived intensity are closely associated with vibration amplitude. When trying to correlate psychophysical and neurophysiological results, an important observation is that perceived intensity of a vibratory stimulus increases smoothly with stimulus amplitude [12-19]. As will be shown, this result has direct implications for the possible codes of intensity. The response of a mechanoreceptive afferent to a vibratory stimulus is typically a piece-wise linear function of its amplitude (Figure 1)[12;14;20]: As the amplitude of the stimulus increases beyond the afferent’s absolute threshold (I₀), its response increases until the afferent produces one spike per stimulus cycle (at amplitude I₁), at which point the afferent is said to be entrained to the stimulus. Then, over a range of amplitudes (between I₁ and I₂), the fiber remains entrained. Over this range of amplitudes, then, the afferent conveys no information about changes in stimulus amplitude. Beyond I₂, the fiber spikes more than once per cycle until it reaches I₃, at which point it reaches a second response plateau, over which it spikes twice per stimulus cycle. In contrast to afferent responses, perceived intensity is a smooth increasing function of amplitude [12-19]. Mountcastle and colleagues found that no aspect of the responses of individual afferent fibers progressively increased with vibratory intensity and so signals from individual afferents could not account for perceived intensity [12].

Figure 1.

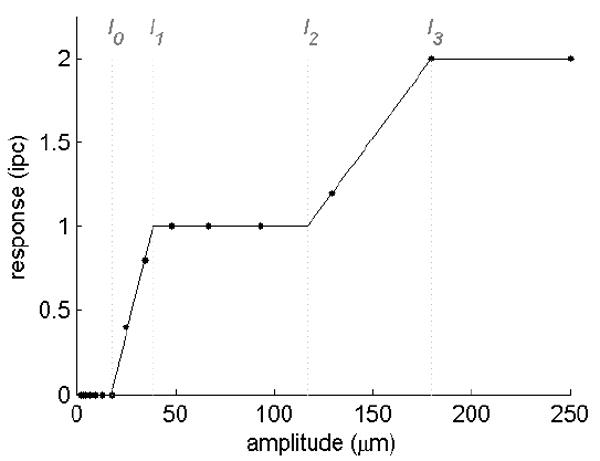
Responses (in impulses per stimulus cycle) of a typical SA1 afferent to 10-Hz sinusoids varying in amplitude from 2.5 to 250μm. Over wide ranges of amplitude (from about 40 to 115μm, for instance), the afferent’s response does not change with changes in stimulus amplitude.

Thus, the neural coding of perceived intensity at the somatosensory periphery is mediated by populations of afferents and peripheral signals must be integrated both within and across submodalities.

The neural code for perceived intensity at the somatosensory periphery

In a seminal study, Johnson [13] explored the possibility that perceived intensity relied on the response of a population of afferents. His approach consisted of reconstructing the responses of a population of RA afferents to a set of 40-Hz vibrations varying in amplitude. In a parallel psychophysical experiment, he had subjects rate the intensity of these same vibratory stimuli. He then devised a set of hypotheses relating population response to perceived intensity and assessed whether each hypothesis could account for subjects’ ratings. These hypotheses, each a possible neural code for perceived intensity, included: 1) The population firing rate; 2) firing rates for subpopulations of afferents whose RFs were within a certain radius of the locus of stimulation (radii of 2, 4, 6, and 8mm) 3) total number of active fibers; 4) total number of fibers producing one or more spike per cycle; 5) total number of fibers producing two or more spikes per cycle. To reconstruct the population response, Johnson recorded the responses evoked in individual RA afferents by each stimulus while positioning the stimulator at varying distances from its receptive field (RF). One important result from these measurements was that a stimulus excites afferents whose RFs are not under the stimulus probe and the decline in efficacy is an inverse square function of the distance between the center of the stimulating probe and the center of the RF. Johnson found that several neural codes accounted linearly for the ratings of subjective intensity, namely the total populations firing rate and the various codes based on the total number of active fibers (independently of the criterion for activity).

An important assumption underlying this approach is that the relevant aspect of the neural activity should exhibit a linear relationship with the subjective experience to which it gives rise [21;22]. The ultimate test of the validity of a hypothetical neural code, however, is its falsifiability [23] and its consistency: Can it be tested experimentally? Can it account for new data? Are there data with which it is inconsistent? From this perspective, no neural code can be proven to be correct. Rather, neural codes are or are not consistent with the available data.

A further assumption underlying this approach comparing human psychophysical judgments with the neural responses in monkeys is that somatosensory processing is comparable in the two species. The validity of this assumption was tested by Mountcastle and colleagues [24], who showed that vibratory detection and discrimination thresholds are similar in humans and monkeys.

Johnson’s [13] study was a landmark study in that it was one of the first to relate perception to the response of a population of neurons. His approach was later fruitfully applied to the investigation of the neural codes underlying other perceptual dimensions, for instance tactile roughness [25-28].

However, Johnson was unable to isolate the peripheral neural code for perceived intensity as several neural codes were linearly predictive of the subjects’ psychophysical ratings. Thus, Johnson’s psychophysical and neurophysiological data did not sufficiently constrain the proposed neural coding hypotheses. Another limitation in Johnson’s study was that he only investigated the role of RA afferents in the perception of stimulus intensity. The proposed codes might prove adequate in accounting for stimuli that activate only RA afferents; however, as noted, skin contact typically generates activity in several populations of afferents. That the responses of individual populations of afferents cannot account for perceived intensity seems to follow from the fact that each population of afferents can be selectively stimulated given the right choice of stimulus while all stimuli can be judged along a single intensive continuum. In other words, a stimulus that excites only PC fibers can be effortlessly compared in subjective intensity to one that excites only SA1 afferents. In addition, most stimuli excite all three populations of mechanoreceptive afferents, so a unitary percept of perceived intensity is likely to involve integrating information from multiple tactile submodalities.

Cohen and Vierck [29] presented preliminary evidence that perceived intensity cannot be solely explained in terms of the responses of a single population of afferents. They presented human subjects with trapezoidal indentations and found that the transient portions of the indentation were perceived as more intense than the sustained period: That the sustained period evokes a sensation (that can be judged along the intensive continuum) implicates SA1 fibers in the perception of intensity, as these are the only afferents that respond during this stimulus epoch; that the offset of the stimulus evokes a more intense percept than does the sustained portion of the stimulus implicates RA (or PC) fibers, as only these afferents respond during this stimulus period. That the responses in the SA1 population could not account for the perceived intensity of trapezoidal indentations was consistent with results from a previous study [30]. Along those lines, Hollins and Roy [19] proposed that the perceived intensity of a vibrotactile stimulus is determined by the activity in the three mechanoreceptive channels (SA1, RA and PC) but that the channel whose signal is weakest is partially reduced by cross-channel suppression.

In order to further elucidate the peripheral neural code underlying perceived intensity, we carried out a paired psychophysical/neurophysiological study [14] using an approach similar to Johnson’s [13]. Our study differed from his in two important ways, however. First, in order to more strongly constrain our neural coding hypotheses, we used a wide variety of stimuli – including simple sinusoids, diharmonic stimuli (consisting of two superimposed sinusoids), and non-repeating noise sequences – (Figure 2) that varied both in intensity and in frequency content. Because perceived intensity depends on both stimulus amplitude and stimulus frequency, we reasoned that this more complex stimulus space would constrain theories about the neural code more strongly than one in which only stimulus amplitude varies. Second, we investigated the contributions of all three populations of low-threshold mechanoreceptive afferents to perceived intensity. Importantly, the sensitivity of each of the three populations of afferents differs depending on the stimulus frequency [12;20] so we expected manipulations of the frequency content of the stimuli to affect afferent responses differently depending on their type (see below).

Figure 2.

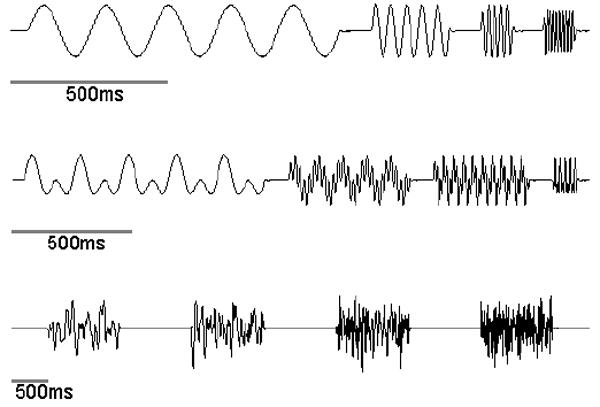
Four exemplars of the three types of stimuli presented by Muniak et al. [14]. Top: Sinusoids at 5, 20, 50 and 100Hz. Middle: Diharmonic waves (two superimposed sinusoids) with frequency components 5Hz + 10Hz, 10Hz + 50Hz, 25Hz + 75Hz, and 50Hz + 100Hz. Bottom: Noise stimuli with the low frequency cut-off at 5Hz and the high-frequency cut-off at 10, 25, 50 and 100Hz.

Our approach consisted of recording the responses of SA1, RA and PC afferents to sinusoids, diharmonic stimuli, and non-repeating noise sequences varying in intensity and frequency content. We then presented a subset of these stimuli to the index finger of human subjects and had them rate their perceived intensity. Stimuli were selected so that they differentially excited the three populations of afferents. In other words, some stimuli (comprising low-frequency components) preferentially excited SA1 afferents, others (with intermediate-frequency components) evoked the strongest responses in RA afferents, while still others (that included high frequency components) stimulated PC fibers most robustly.

Figure 3 shows the responses of five afferents of each type to sinusoidal stimuli at 4 frequencies and 2 amplitudes. Several important properties of the peripheral response can be seen in this figure. First, as the amplitude of the stimulus increases, two aspects of the peripheral neural response change: 1) The firing rate of individual afferents increases (see for instance the blue SA1 fiber’s response to the 5Hz stimuli); 2) More fibers are recruited (for instance, the red SA1 fiber does not respond to the 35-μm 5-Hz stimulus but responds robustly at 250μm). The second important property that can be gleaned from the figure is that the frequency sensitivity differs across afferents. Specifically, SA1 fibers are most sensitive at low frequencies of stimulation, PC fibers at high frequencies, and RA afferents at intermediate frequencies.

Figure 3.

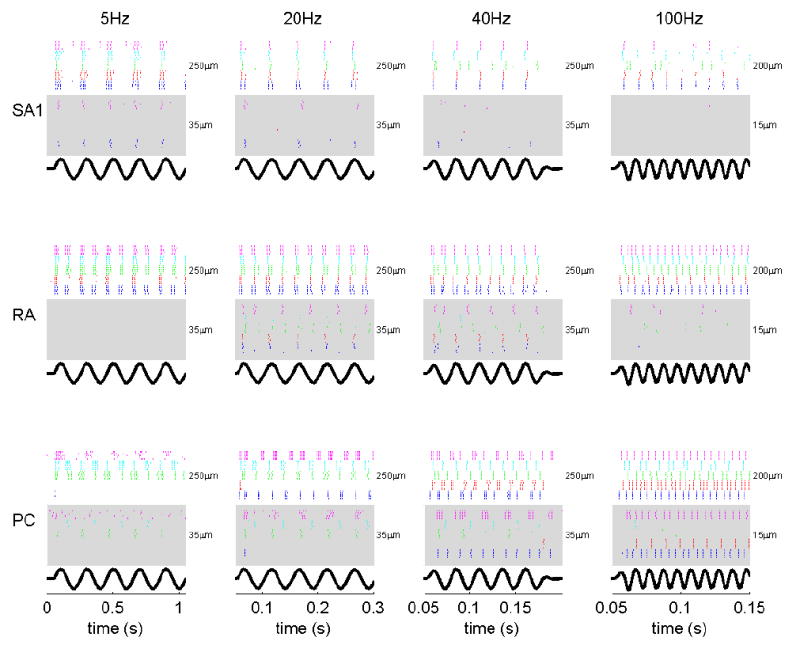
Responses of five neurons of each type to vibratory stimuli at 4 frequencies and 2 amplitudes. Each row of plots shows the response of a different type of afferent; each column of plots shows reponses to sinusoids at different frequencies. For each afferent of each type, whose responses are shown in one of five colors (blue, red, green, magenta and cyan), the stimulus (shown at the bottom of each plot) was presented five times. At each frequency, responses are shown for stimuli at two amplitudes: Responses to the low amplitude-stimulus are shown in the shaded area, responses to the high-amplitude stimulus are shown in the non-shaded area. Amplitudes are shown to the right of the corresponding raster plots.

The initial step in our analysis was to characterize the relationship between the responses of populations of afferents and stimulus intensity. To that end, we derived functions relating the mean firing rate of each afferent type as a function of stimulus intensity. The mean response evoked in a sample of afferents (of a given type) can be taken as the expected value of the response in any given afferent of that type. For all afferents, mean firing rate was a rectified logarithmic function of stimulus amplitude. The slopes and intercepts of these functions varied depending on the frequency content of the stimulus and on the afferent type (Figure 5). From these mean- rate functions, we derived predictions from neural codes based on afferent firing rates.

Figure 5.

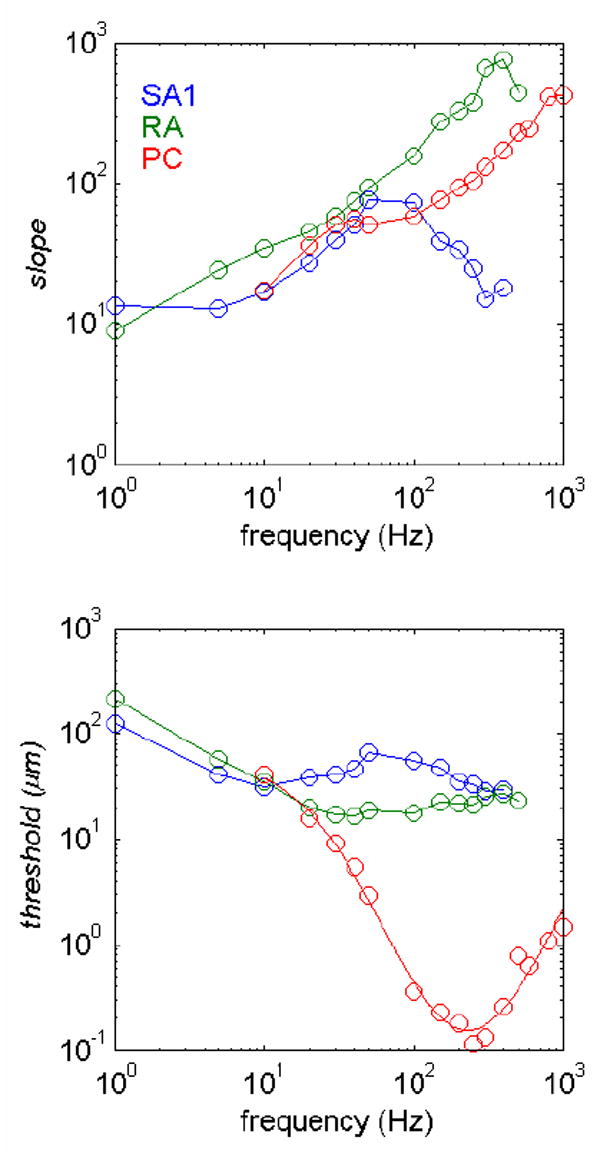
Slopes and intercepts (thresholds) of the rate-intensity functions of SA1, RA and PC fibers as a function of frequency. The form of the function was f(a) = [α(log(a) − log(β))] ⁺where f(a) is the firing rate evoked by a stimulus of amplitude a and α and β are parameters fit to the mean rate-intensity functions obtained at each frequency for each type of afferent. The plus (+) sign denotes rectification (if f(a) < 0, f(a) is set to 0). As can be seen from the figure, SA1 afferents are most sensitive at the low frequencies, PC fibers at the high frequencies, and RA afferents at intermediate frequencies.

Johnson [13] showed that a vibratory stimulus is equally efficacious at activating afferents whose RFs are located in the “hot zone,” i.e. the area of skin that is within 1mm of the locus of stimulation (Figure 4). In other words, the effective area of stimulation includes the area covered by the stimulating probe and an additional 1-mm region around the probe. Thus, the mean firing rate of individual afferents whose RFs are located in the “hot zone” multiplied by the number of afferents in the “hot zone” constitutes an estimate of the total response of afferents in the “hot zone.” As shown by Johnson [13], the ability of the stimulus to activate an RA afferent drops as an inverse square function of the distance between the center of its RF and the edge of the “hot zone” (Figure 4). Because SA1 and RA fibers have similar RF geometries, we used the same model for both populations of afferents. The total response (i.e., in the entire fingerpad or beyond) evoked by each stimulus in these two populations of afferents (SA1 and RA), then, can be estimated from the inverse-square relationship and the (rectified) logarithmic functions relating expected firing rate to stimulus intensity.

Figure 4.

The black area shows the spatial extent of the “hot zone,” centered on the locus of stimulation, the spatial extent of which is denoted by a yellow patch. Over the “hot zone,” the effective amplitude remains constant. The effective amplitude then drops off as and inverse square function of distance from the “hot zone.” The green shading shows the drop-off of the effective stimulus amplitude as a function of distance from the center of the stimulating probe. According to the population coding hypothesis, responses of afferents whose RFs are in the black, yellow and green regions contribute to perceived intensity; according to the “hot zone” model, only afferents whose RFs are in the black and yellow regions contribute to the perception of stimulus intensity.

Unlike SA1 and RA afferents, PC fibers have large RFs, over which their sensitivity is relatively homogenous [31]. We therefore assumed that sensitivity was constant over the entire RF and used as an estimate of the population response the mean response multiplied by the estimated number of active PC afferents.

An important result in our study was that the firing rate of afferents (of a given type) whose RFs were located at or near the locus of stimulation (i.e., in the “hot zone”) was a logarithmic function of stimulus amplitude. In contrast, the firing rate across an entire population of afferents (of a given type) was a linear function of amplitude. That the “hot zone” and population codes yielded different relationships between response and stimulus intensity suggested that the two codes might yield different predictions and thus be empirically distinguishable.

Based on these data and the assumptions articulated above, we tested a set of eight hypotheses as to the aspect of the neural response that determines perceived intensity. These hypotheses, summarized in Table 1, could be classified into two categories. The first category of hypotheses included neural codes based on the firing rates of individual afferents or in populations of afferents (of the same type or of different types). The second category of hypotheses encompassed neural codes based on the number of active fibers (of the same type or across types), or recruitment codes. In some models, responses were integrated over the entire population of afferents (of a given type or across types); in others, only responses of afferents whose RFs were located under or near the stimulator (i.e., in what we dubbed the “hot zone”) contributed to the perceived intensity.

Table 1.

Summary of neural codes.

Neural code	Outcome
1. Firing rate of individual afferents (SA1, RA, PC)	Rejected because individual rate-intensity functions comprise long entrainment plateaus.
2. Firing rate of afferents of a given type whose RFs are located in the “hot zone”	SA1, R2 = 0.68 RA, R2 = 0.89 PC, R2 = 0.74*
3. Firing rate of afferents whose RFs are located in the “hot zone,” weighted by type	R2 = 0.97
4. Number of afferents of each type activated in the “hot zone”	Rejected because the number of recruited afferents plateaus at low stimulus intensities.
5. Estimated total firing rate of afferents of a given type	SA1, R2 = 0.56 RA, R2 = 0.80 PC, R2 = 0.74*
6. Weighted total estimated firing rate across afferent types	R2 = 0.96
7. Estimated number of active afferents of each type	SA1, R2 = 0.10 RA, R2 = 0.51 PC, R2 = 0.54
8. Estimated weighted number of active afferents	R2 = 0.86

^*Codes are computed identically due to the nature of PC RFs.

We then evaluated the extent to which each possible neural code could account for the psychophysical data. For instance, we plotted the relationship between the psychophysical measures, perceived intensities, of the sinusoidal, diharmonic or noise stimuli against the firing rate evoked in the population of RA afferents whose RFs were located under the probe (Figure 6b). We found the relationship to be linear and to account for 89% of the variance in the intensity ratings. Thus, consistent with Johnson’s findings, RA firing rates were good predictors of perceived intensity. However, many stimuli that elicited positive ratings of perceived intensity were assigned a (predicted) rating of zero, because RA afferents did not respond to those stimuli. In order to obtain predictions for models based on the responses of the three populations of afferents, we performed multiple regressions with the perceived intensity ratings as the dependent variable, and the relevant aspect of the neural response (number of active fibers, total population firing rate, etc.) for each afferent type as the predictors.

Figure 6.

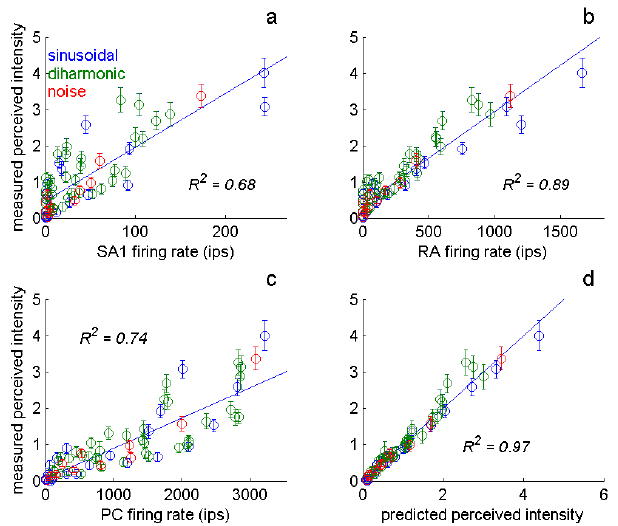
Predictions derived from the “hot zone” codes. a-c) Perceived intensity plotted against the firing rates evoked in SA1 (a), RA (b) and PC (c) fibers whose RFs are located in the “hot zone.” The strength and linearity of the relationship between the mean rate evoked in each population of afferents and perceived intensity reveals the degree to which the “hot zone” model is predictive of perceived intensity if only signals from a single population contribute to the perception of stimulus intensity. All three populations of fibers yield good fits when considered individually, but no one population accounts for all aspects of perceived intensity. d) Predictions derived from the multiple regression of perceived intensity on firing rates of afferents whose RFs are located in the “hot zone.” Note that predictions obtained from the total population response were similar to those derived from the “hot zone” hypothesis (R² was 0.97 for the “hot zone” model and 0.95 for the population model).

Certain codes could be eliminated after preliminary examination of the data. For instance, as discussed above, codes based on the firing rates of individual afferents were eliminated because the rate-intensity functions of individual afferent fibers exhibited long entrainment plateaus. Similarly, the number of active fibers in the “hot zone” was not a tenable code for intensity because this quantity plateaued at low stimulus amplitudes (whereas judgments of perceived intensity do not). After the examination of all eight possible neural codes, we found that only two codes made predictions consistent with the data. The first was the firing rate of afferents whose RFs were located in the “hot zone,” weighted by afferent type; the second was the total population firing rate, weighted by afferent type. Importantly, according to both hypotheses, all three populations of afferents significantly contribute to the perceived intensity of the stimuli. A major conclusion of this study, then, was that perceived intensity is determined by the activity evoked in all three populations of afferents. That the two codes – hot zone and population – yielded comparable predictions was somewhat surprising given that one involved a linear and the other a logarithmic relationship between neural response and stimulus amplitude.

For the “hot zone” and population models, we can estimate from the regression weights the relative contribution of individual spikes evoked by a stimulus to its perceived intensity. According to the “hot zone” model, an SA1 spike is weighted 11 times more strongly than is an RA spike and 16 times more strongly than a PC spike. According to the population model, an SA1 spike is weighted 6.5 times more than an RA spike, and a PC spike is weighted 6.25 times more than an SA1 spike. PC spikes are highly weighted in the population model because the population of active PC fibers is much smaller than its SA1 and RA counterparts. The relatively weak weighting of RA spikes may at first seem surprising given that a single action potential in a single RA fiber can be detected whereas several spikes must be evoked in SA1 or PC fibers for a conscious sensation to be elicited [6]. Note, however, that RA afferents most densely innervate the skin and are highly excitable relative to SA1 fibers, so the overall level of activity across the population of RA fibers is high relative to its SA1 counterpart. Thus, if individual RA spikes were highly weighted, the SA1 response would be drowned out. Furthermore, detection threshold and perceived intensity are aspects of perception whose neural determinants may be different.

Implications of the neural code for psychophysical functions relating perceived intensity to stimulus amplitude

Psychophysical functions relating the perceived intensity of sinusoids to their amplitude have been measured in a number of studies. Perceived intensity was modeled as a power function of stimulus intensity [15;17] or as a two-branched function, the second branch a power function with exponent about 1 [16;19;32]. In some studies, the power function exponent was found to decrease with stimulus frequency [15;17] but not in others [16;19;32].

The model makes specific predictions as to the shape of the psychophysical function relating the perceived intensity of sinusoids to their amplitude. Specifically, the shape of the function is a three branched function of amplitude: The first branch corresponds to stimuli the perception of which is mediated by a single population of afferents (the most sensitive population at that stimulus frequency); the second branch corresponds to stimuli that excite two populations of afferents; the third corresponds to stimuli that activate all three afferent populations. According to the “hot zone” model, each branch is logarithmic, whereas the population model implies linear branches.

In some studies [16;19], slopes of the intensity functions have been found to be steeper at lower stimulus intensities than at high stimulus intensities. One possibility is that the steep portion of the curves corresponds to stimuli mediated primarily by RA afferents, which yield the steepest rate-intensity functions (Figure 5). The slopes become shallower as SA1 and PC afferents are recruited.

Another implication of the model is that the decrease in exponent observed at the high frequencies (>100Hz) by some investigators [15;17] is due to a progressively larger contribution of PC afferents to perceived intensity (Figure 7). First, at high vibratory frequencies, PC responses become increasingly dominant relative to SA1 and RA responses. Second, PC rate-intensity functions tend to be shallower than their RA counterparts. To the extent that the PC response contributes to perceived intensity, then, the slope of the function relating perceived intensity to stimulus amplitude will be shallower. When the PC component is excluded from the model (i.e., when perceived intensity is predicted solely on the basis of SA1 and RA responses), the psychophysical functions no longer become shallower at higher frequencies.

Figure 7.

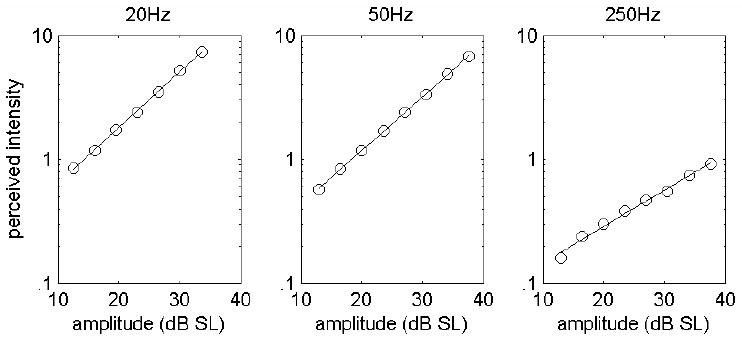
Predicted perceived intensity for sinusoids at 20, 50 and 250Hz. As the stimulus frequency increases, the exponent of the power function relating perceived intensity to stimulus amplitude decreases as has been shown in extant psychophysical studies. Predictions are derived from the hypothesis that the total population firing rate determines perceived intensity. To obscure the multiple branches of individual functions, we generated 10 sets of predictions at each frequency, each with 20% jitter around the mean slopes and intercepts of the measured SA1, RA and PC rate-intensity functions (see text) to simulate variability across subjects. Each point is the mean of 10 simulated responses. The fitted exponents were 0.92, 0.88 and 0.45 [c.f. 15;17]. The dependence of the exponent on stimulus frequency disappears when the PC contribution is eliminated.

That the decrease in power function exponent is not observed in some studies [16;19;32] suggests that the contribution of the PC response to perceived intensity was diminished in those studies. Hollins and Roy used a 2.5-mm contactor with a fixed surround, which prevented the lateral spread of vibration; the stimulated region was thus much smaller than that in other studies. Given that PC afferents exhibit spatial summation [33;34], the use of such a small contactor with a surround may explain the relatively weaker PC signal in this study. Note however that spatial summation in the PC system has been shown to lead to a decrement in threshold but not an increment in subjective magnitude [35] so the question remains open as to why Hollins and Roy obtained the same exponent at all frequencies. In the two other studies that showed no change of exponent with stimulus frequency [16;32], stimuli were applied to the thenar eminence. The responses of the three populations of afferents may thus be weighted differently in the determination of perceived intensity depending on the body region they innervate. Specifically, PC input may be weighted relatively less on the palm than at the fingertip (Note that the ratio of PC fibers to SA1 and RA fibers is higher on the palm than on the tip [36], so the inconsistency across studies cannot be straightforwardly explained by differences in innervation densities). That input from different fibers is weighted differently depending on the locus of stimulation is consistent with the finding that a single spike in an RA fiber whose RF is located on the fingertip elicits a conscious sensation, whereas multiple spikes are required to elicit a conscious sensation from an RA fiber whose RF is located on the palm [6](with the caveat that detection and perceived intensity are two different aspects of perception). Furthermore, psychophysical functions relating subjective magnitude to stimulus amplitude have been found to differ across body regions [37].

The neural code for perceived intensity in somatosensory cortex

One of the goals of sensory neuroscience is to determine how each aspect of the stimulus is encoded at each processing stage. For all sensory modalities, establishing the peripheral neural code at the sensory periphery is more straightforward than doing so in cortex because, in the former, there are a few populations of relatively homogeneous neurons (with the exception of the olfactory epithelium), whereas the latter is characterized by a variety of neuronal populations that widely vary in their response properties. It is no surprise, therefore, that the neural code for perceived intensity in cortex has yet to be elucidated. The responses of many neurons in primary somatosensory cortex are negatively accelerating functions of stimulus amplitude, the slopes of which differ across frequencies [2]; the same is found in secondary somatosensory cortex (Supratim Ray, personal communication). To date, no attempt has been made to systematically assess the relationship between the responses of neurons in primary somatosensory cortex and the perceived intensity of the stimuli that evoke them.

The two proposed peripheral neural codes for perceived intensity – “hot zone” and population – seem at first glance to imply that the corresponding cortical code will be straightforward: Given that cortical neurons integrate information across the body surface, one might expect that the overall firing rate across cortical neurons may be the neural code for perceived intensity. This issue merits closer scrutiny, however. For instance, the “hot zone” model implies that the activity of peripheral afferents outside of the “hot zone” is disregarded in the determination of perceived intensity. The process by which this takes place is not straightforward. Interestingly, the dynamics of the cortical response to vibratory stimulation suggest a cortical implementation of the “hot zone” model that develops over time. Indeed, the pattern of activation evoked in primary somatosensory cortex by vibratory stimulation has been shown to become more spatially restricted over time [38]. Given the somatotopic organization of SI, this spatial funneling of the response may reflect a network dynamic that culminates in the activation of a population of neurons whose RFs are confined to the “hot zone.” For short-duration stimuli, then, the pattern of activation in cortex could be produced by input from the entire afferent population. For long-duration stimuli, input from afferents whose RFs are outside of the “hot zone” is pruned, leaving only input from the “hot zone.” Furthermore, the activation within the cortical “hot zone” increases with increases in stimulus amplitude whereas the size of this cortical region does not [39], consistent with the “hot zone” model. That the activated region is independent of stimulus amplitude seems inconsistent with the hypothesis that perceived intensity is determined by the size of the population that is activated by a stimulus (the recruitment hypothesis). Indeed, the spatial extent of the peripheral population of active fibers increases with increased stimulus amplitude; one might therefore expect that this expansion would be reflected in cortex as well.

These cortical dynamics operate over the span of multiple seconds, whereas the duration of the stimuli presented in the aforementioned psychophysical experiments was 1 second or less. It is therefore not clear the extent to which these dynamic phenomena influenced our results or those of others investigating the perception of intensity. An intriguing possibility is that the initial code for perceived intensity is a population code (given the initial widespread activity consistent with population coding) and that this code morphs into a “hot zone” code as the stimulus extends in time. If this is the case, the perceived intensity of short-duration stimuli (on the order of 1 second) should be a three-branched linear function of amplitude, whereas the perceived intensity of long-duration stimuli (> 5-10 seconds) should be a three-branched logarithmic function of amplitude.

Another issue that the model does not address is the time course of temporal integration. Indeed, vibratory stimuli evoke peripheral responses that are essentially stable over time. The only instability in the peripheral neural response is due to vibratory adaptation, a progressive desensitization of the afferents over time [40]. However, vibratory adaptation operates with time constants on the order of tens of seconds [41] so had little to no impact on the present results. In contrast to vibratory stimuli, however, trapezoidal indentations evoke highly dynamic responses in afferents [42]. Specifically, SA1 afferents exhibit a strong response at the onset of the stimulus, then a slowly decaying response to the sustained phase of the stimulus whereas RA afferents only respond to the transient portions of the stimulus (i.e., its onset and offset). The temporal profiles of the perceived intensities of trapezoidal indentations are highly dynamic as well [29;43], with the transient portion of the stimulus perceived as more intense than the sustained portion. Importantly, no linear combination of the temporal profile of afferent responses can account for the temporal profile of the perceived intensity; specifically, the difference in the strength of the transient and sustained neural responses is much greater than the difference in perceived intensities between these stimulus epochs. Cohen and Vierck conclude that peripheral neural signals are integrated centrally over time to yield percepts of intensity. The length of the integration window remains to be established, as the relationship between perceived intensity and stimulus duration has not been investigated (although the effect of stimulus duration on detection threshold has, see [44;45], as has the effect of stimulus duration on intensity discrimination, see [46]).

A third issue that remains to be resolved is how information is integrated across tactile submodalities in cortex. The evidence suggests that the various tactile submodalities remain relatively segregated in SI [47]. However, some neurons have been shown to receive input from both SA1 and RA fibers, even in area 3b, the earliest cortical processing stage [48;49]. Thus, perceived intensity might be encoded in SI by trimodal neurons (i.e., neurons that receive input from the three populations of afferents); another possibility is that neurons upstream from area 3b receive signals originating from the three submodalities. For instance, neurons in the second somatosensory cortex, which receives direct and indirect input from area 3b, exhibit both SA-like and RA-like responses [50]. Further experiments will be required to address these questions.

Finally, we reject codes based on recruitment and propose that perceived intensity relies on a rate code across a population of neurons (whether across the entire population or across afferents whose RFs are in the “hot zone”). However, stimuli that are equated in perceived intensity can nonetheless be distinguished on the basis of their frequency content [51;52]. At the somatosensory periphery, information about stimulus frequency is thought to be encoded in the temporal profile of afferent responses to vibratory stimuli: Indeed, afferents become entrained to the stimulus and the mean interval between spikes or bursts of spikes varies inversely with stimulus frequency [12;53;54]. In cortex, however, information about stimulus frequency is thought to be conveyed through a rate code [55]; indeed, the mean firing rate of cortical neurons conveys information about stimulus frequency more faithfully than does the periodicity in their responses. If perceived intensity is also encoded as a rate code in cortex, then it remains to be elucidated how the temporal and intensive properties of the stimulus can both be encoded in the firing rates of cortical neurons.

Peripheral code of perceived intensity in other sensory modalities

In vision, signals from individual retinal ganglion cells are not correlated with brightness and it is unlikely that brightness is explicitly encoded in the response of the population of ganglion cell fibers since the perceived brightness of an area of visual field is influenced by the properties of other regions of the visual field. For instance, in brightness induction [56], the perceived brightness of a static gray field changes as the luminance of the surrounding areas is modulated, a change that is not reflected in the responses of ganglion cells [57]. Brightness perception likely involves interactions on a larger spatial scale than those observed in the retina [58].

In audition, loudness has long been thought to be determined by the total spike count evoked in the auditory nerve by a stimulus [59]. However, recent evidence is at odds with this neural coding hypothesis. Specifically, the “spike count hypothesis” yields erroneous predictions as to the slope of loudness-intensity functions, with increasingly discrepant predictions as the stimulus frequency increases [60]. One possibility is that signals emanating from fibers that innervate different regions of the basilar membrane are weighted differently.

Little is known about the coding of intensity in the olfactory nerve. However, indirect evidence suggests that perceived intensity of an odorant may be a function of the overall activity it evokes in the olfactory epithelium [61]. Intensity coding in olfaction is particularly interesting in that it involves hundreds of different olfactory receptors. Furthermore, individual odorants can yield different olfactory sensations depending on their concentrations; for instance, indole has a putrid odor at high concentrations but a floral one when diluted.

The peripheral neural code for gustatory intensity has not been explicitly investigated. As might be expected, responses of gustatory afferents increase as the concentration (intensity) of the tastant increases [62]. Furthermore, the difference in firing rates (measured in rats) evoked by two tastants that are just discriminable (i.e., are one ‘just noticeable difference’ apart, as measured in humans) is constant across the range of concentrations, as Werner and Mountcastle have found to be the case in tactile intensity discrimination [21]. Note, however, that sensation magnitude cannot be inferred from discriminability [63-65].

Thus, the peripheral neural code for perceived intensity remains an open question in three other sensory modalities. In vision, the question is moot as perceived intensity is strongly influenced by central mechanisms. Perhaps the approach adopted in the somatosensory modality can be fruitfully applied to other senses.

Summary

How information is coded in the activity of populations of neurons is a critical question in neuroscience. The study of simple sensory continua like perceived intensity allows us to address this important issue quantitatively. The conclusion after three decades of research on the peripheral neural code for perceived intensity is that the location of a stimulus along this sensory continuum is determined by the firing rates it evokes in the three populations of afferents, weighted by afferent type. The question remains whether only afferents whose RFs are at or near the locus of stimulation (i.e., in the “hot zone”) determine perceived intensity or whether the entire afferent population plays a role. Both hypotheses are consistent with extant data. Importantly, neural codes based on recruitment are not supported because they do not account for the data as well as codes based on firing rate and seem to be inconsistent with the pattern of activity evoked in cortex by vibratory stimuli.

A simple model relating perceived intensity to the activity evoked in the three afferent populations accurately predicts many aspects of perception. The question remains how this perceptual continuum is encoded in somatosensory cortex. Of particular interest is how information from the three tactile submodalities (SA1, RA and PC) is integrated to form a unitary percept. Furthermore, as was suggested by Mountcastle [12] and first explored by Johnson [13], to achieve an understanding of perception, it is necessary to understand how populations of neurons encode different aspects of the sensory environment. Because the problem of population coding is a complex one, it seems sensible to approach the problem as it relates to simple sensory continua such as perceived intensity.