Abstract
The mammalian inner ear uses its sensory hair cells to detect and amplify incoming sound. It is unclear whether cochlear amplification arises uniquely from a voltage-dependent mechanism (electromotility) associated with outer hair cells (OHCs) or whether other mechanisms are necessary, for the voltage response of OHCs is apparently attenuated excessively by the membrane electrical filter. The cochlea contains many thousands of hair cells organized in extensive arrays, embedded in an electrically coupled system of supporting cells. We have therefore constructed a multi-element, large-scale computational model of cochlear sound transduction to study the underlying potassium (K+) recirculation. We have included experimentally determined parameters of cochlear macromechanics, which govern sound transduction, and data on hair cells' electrical parameters including tonotopical variation in the membrane conductance of OHCs. In agreement with the experiment, the model predicts an exponential decay of extracellular longitudinal K+ current spread. In contrast to the predictions from isolated cells, it also predicts low attenuation of the OHC transmembrane receptor potential (−5 dB per decade) in the 0.2–30 kHz range. This suggests that OHC electromotility could be driven by the transmembrane potential. Furthermore, the OHC electromotility could serve as a single amplification mechanism over the entire hearing range.
Keywords: cochlea, potassium, recirculation, hair cell, outer hair cell amplification
1. Introduction
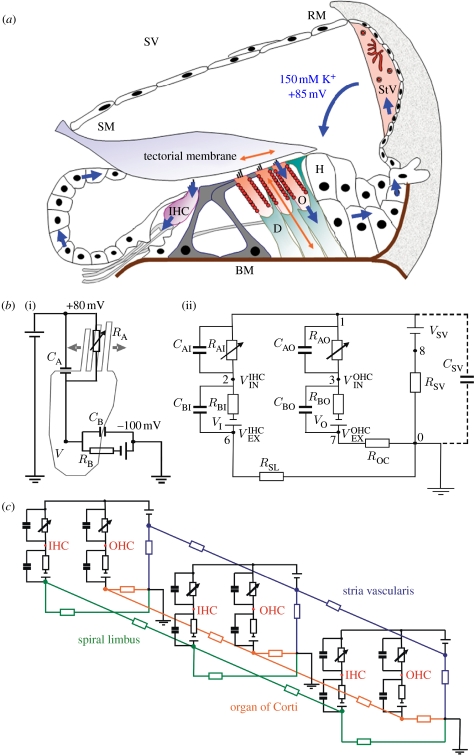
In first steps in hearing, the cochlea converts sound waves coming from the outside of the ear into electrical activity of the auditory nerve. The critical structure involved in this transduction process is the organ of Corti, an array of sensory and non-sensory cells located along the basilar membrane (BM), a dividing partition of the cochlear duct. Mechanical BM displacement activates mechanoelectrical transduction (MET) channels located in the apical membrane of the hair cells. The resulting flow of current, carried by potassium ions, initiates the cascade of neural events leading to hearing. The cochlea also contains a specific population of hair cells, the outer hair cells (OHCs), which is thought to amplify the BM motion. A further feature of the cochlea is a metabolically driven circulation of potassium ions (i.e. K+) around the sensory epithelium. The circulation is derived from an unusually high extracellular K+ concentration (typically 140 mM) in the scala media (figure 1a). Half of the electrical potential driving K+ from the scala media into the sensory hair cells arises from the endocochlear potential (EP) (+80 mV) generated in this compartment.
Figure 1.
Construction of the model of cochlear K+ recirculation. (a) Schematic of the organ of Corti with inner hair cell (IHC), OHCs (O), Hensen's cells (H), Deiters' cells (D) and Reissner's membrane (RM). Potassium is actively transported from the stria vascularis (StV) into the scala media (SM) and circulates through the OHC and IHC upon sound stimulation. From them potassium is released to Deiters' cells and recycled back to the StV. (b)(i) Equivalent electrical circuit of a single hair cell and (ii) a cochlear cross section from (a). VSV, the battery representing the EP generated by the StV; RSV, resistor representing the overall electrical resistance of the StV per single cross section; RAO, resistor of the OHC apical membrane modulated by the BM displacement; CAO, the capacitance of the OHC apical membrane; , the OHC intracellular receptor potential; RBO, resistor of the OHC basolateral membrane; CBO, the capacitance of the OHC basolateral membrane; ROC, resistor representing the overall resistance of the organ of Corti per single cross section; RSL, resistor representing the overall resistance of spiral limbus per single cross section; CSV, the capacitance of the cell membranes of the stria vascularis. The electrical components in the IHC mesh are labelled similarly. For simplicity, only one OHC and one inner hair cell per cross section are shown. (c) The three-dimensional equivalent electrical circuit of the whole cochlea built from the element circuit in (b) by its longitudinal electrical coupling in the selected nodes.
The K+ circulation in the cochlea is thought to be tightly regulated in the inner compartment of the cochlea by a transport network in the stria vascularis of the cochlea (Wangemann 2006). In the OHC case, K+ passes through the transduction channels and is released into the intercellular space of organ of Corti through several types of K+ channel at the base of the hair cell. These channels include KCNQ4 channels (Kharkovets et al. 2006) and calcium-activated SK and BK channels (Marcotti et al. 2004). From there, K+ is taken up by the supporting cells via the K–Cl cotransporters (Boettger et al. 2002). The supporting cells of the organ of Corti form an extensive epithelial tissue gap-junction system that is essential for buffering extracellular K+ ions in the organ of Corti into the perilymph (Kikuchi et al. 2000). From perilymph, K+ is actively pumped by the K+/Na+ ATPase and K+/Na+/2Cl− cotransporter back into the type II fibrocytes of the spiral ligament and from there back via the stria vascularis into the scala media by a connective tissue gap-junction system (figure 1). The potassium recirculation pathway through the second class of mammalian hair cells, the inner hair cells (IHCs), is less well understood, although an extensive epithelial tissue gap-junction system also exists between cells of the spiral limbus, and the barrier formed by the pillar cells of the tunnel of Corti (Jagger & Forge 2006) suggests that IHC-related potassium is also recycled by an independent pathway more medially through the spiral limbus.
Although electrophysiological approaches have proved helpful in studying the K+ transport mechanisms at a molecular and cellular level, there is a bottleneck when trying to integrate the single-cell properties into a system description of cochlear homeostasis. There are only a limited number of studies of the total extracellular cochlear current flow in the in vivo system (e.g. Zidanic & Brownell 1990). In addition, many of the electrical changes occur at frequencies that are close to the limits or even exceed those accessible by current electrophysiological techniques. As a consequence, it is still not resolved as to how cochlear amplification occurs. Frequency tuning in the mammalian cochlea (ranging from below 100 Hz to more than 100 kHz in some species) is likely to arise from a specialized electromotile property of the OHCs. Yet it has been argued that the electrical time constant of the cell would cause any rapid change in the intracellular potential in the cells to be filtered out (Ashmore 2008).
To investigate whether OHC electromotility can indeed be driven by the potentials arising from mechanotransduction in the cells, we have developed a large-scale computational model of the cochlear sound-evoked K+ flow. We have focused on the transmembrane potential generated across the OHC basolateral membrane, rather than the extracellular voltage gradients generated between the scala media and the fluid spaces of the organ of Corti (Dallos & Evans 1995). This model ‘laboratory’ allows us to study the distributions of potential within the cochlea not readily accessible through experiment. First, in response to a sound stimulus, the BM displacement pattern is generated by using a model of cochlear macroscopic mechanics based on anatomical reconstruction of the cochlear duct. The model incorporates physiologically realistic assumptions about cochlear mechanics (Mammano & Nobili 1993). Subsequently, the frequency-specific K+ currents and receptor potentials in hair cells can be calculated. In this way, the model describes the transduction of sound into electrical potentials performed by the cochlea. The underlying experimental data used here are derived primarily from guinea-pig (table 1).
Table 1.
Experimental values for parameters of isolated hair cells.
| component | value | reference |
|---|---|---|
| R AI | 40 MΩ | calculated from RBI |
| R BI | 120 MΩ | Raybould et al. (2001) |
| R AO | 24 MΩ (base) 1250 MΩ (apex) | calculated from RBO |
| R BO | 10 MΩ (base) 500 MΩ (apex) | Mammano & Ashmore (1996) |
| C AI | 1 pF | Lopez-Poveda & Eustaquio-Martin (2006) |
| C BI | 10 pF | Raybould et al. (2001) |
| C BO | 15 pF (base) 45 pF (apex) | Housley & Ashmore (1992) |
| V SV | +80 mV | Bekesy (1952) |
| V K | −100 mV | Nernst potential for K+ (Ospeck et al. 2003) |
| −45 mV | Russell & Sellick (1978) | |
| −70 mV | Cody & Russell (1987) |
The model we develop predicts a longitudinal spread of current decaying exponentially along the length of the cochlea. This is in agreement with the measurements of the cochlear microphonic (CM), an extracellular potential arising from sound transduction by the hair cells (Tasaki 1957; Misrahy et al. 1958). Furthermore, the model is used to assess the problem of low-pass filtering of the OHC receptor potential due to electrical filtering by cell membrane. The filtering has been a significant objection to cochlear amplification originating from OHC motility at high frequencies. Time and frequency simulations presented here show that the tonotopic variation of the OHC membrane conductance (Mammano & Ashmore 1996; Preyer et al. 1996) keeps the attenuation of the OHC transmembrane potential at a relatively low level (−5 dB per decade) in the 0.2–30 kHz frequency range. We also find that the capacitance of the non-sensory cells in the stria vascularis does not compromise this potential even though this is a circuit element attenuating electrical responses. The findings suggest that OHC electromotility could be driven by the transmembrane potential without requiring extracellular voltage gradients generated between the scala media and the fluid spaces of the organ of Corti. Furthermore, the results indicate that OHC electromotility could serve as the basis for voltage-dependent amplification over the entire hearing range of mammals.
2. Methods
2.1 Circuit description
To capture the way in which the cochlea separates an input sound into a frequency-specific map, the duct was discretized into 300 cross sections perpendicular to the longitudinal (tonotopic) axis of the cochlea. Each section contained one set of parallel IHCs and OHCs (figure 1a). This approximation grid proved adequate to synthesize macroscopic cochlear mechanics realistically and, consequently, the electrical responses generated by the sound stimulus inside the hair cells.
To treat the potassium flow as an electrical current, each cross section was reduced to a standardized electrical circuit (figure 1b). This circuit consists of passive electrical elements involving resistances, capacitances and batteries (Dallos 1983, 1984). It represents radial electrical flow through the hair cells and supporting cells in a single cochlear cross section. The modified nodal analysis (MNA) approach used (see below) provides a flexible method to describe the electrical circuit at any desired level of complexity. However, the computational cost of a very elaborate model can be considerable. To focus on how the RC characteristics of the IHC and OHC membranes determine the cochlear electrical response to sound stimulus, hair cells were represented in the model in relatively fine detail. Other cochlear compartments, such as the stria vascularis or spiral limbus, are incorporated more schematically to keep the model robustness within a computationally reasonable scale. In principle, further elaborations are possible.
In the model, OHCs and IHCs contribute two independent subcircuits. This separation is based on the compartmentalization of the organ of Corti by the pillar cells of the tunnel of Corti, which form a barrier for gap-junction mediated ionic flow (Jagger & Forge 2006). The hair cells' apical membrane resistances and capacitances are represented by RAO, CAO and RAI, CAI for OHC and IHC, respectively. Since the stereocilial conductance (=1/RA) depends on the activation state of the MET channels (He et al. 2004), the resistances RAO and RAI are modulated by the BM displacement generated by an acoustic stimulus. Electrical resistance of the hair cells' basolateral membrane is represented by resistor RBO and RBI for OHCs and IHCs, respectively. Similarly, the basolateral membrane capacitances are represented by capacitor CBO and CBI. The potassium concentration gradient across the hair cell membrane (140 mM internally and 2.7 mM externally in perilymph) provides additional Nernstian driving force for K+ ions. It is included in the circuit by a battery EK=−100 mV (shown as VI and VO in figure 1b for IHCs and OHCs, respectively). The electrical resistance of the gap-junction system of the organ of Corti, connecting the OHCs with a perilymph ground (0 mV), is represented by a simple resistor ROC. The EP in the scala media, EEP, was represented by battery VSV in series with a resistance RSV representing the gap-junction system of the stria vascularis, and no further detailed modelling was attempted at this stage. Similarly, the IHC is connected with the perilymph by a resistor RSL representing a hypothetical involvement of the gap-junction system of the spiral limbus in K+ recirculation from IHCs.
Several nodes in the circuit in figure 1b have a physiological meaning. Thus node 1 represents the endolymphatic space above the hair cells where the CM is normally measured. The nodes 2 and 3 correspond to the IHC and OHC intracellular spaces with a receptor potential and , respectively, and would be the potentials measured with an intracellular microelectrode. Similarly, the nodes 6 and 7 represent the extracellular space outside the IHC and OHC in the organ of Corti with extracellular potentials and , respectively.
The longitudinal K+ flow between individual cross sections (i.e. along the cochlear tonotopic axis) is accounted for in the model by the electrical resistive coupling between cross sections (figure 1c). This mimics the in vivo situation and the three-dimensional nature of the corresponding gap-junction systems in the stria vascularis, the organ of Corti and the spiral limbus.
The present model splits the cochlea longitudinally into 300 sections and divides each section into six compartments (scala media, IHCs, OHCs, extracellular space near IHCs, extracellular space near OHCs and the stria vascularis). A related cochlear three-dimensional electrical model but with the membrane capacitances omitted was developed by Strelioff (1973), and such models have been used to assess the performance of cochlear implants (Suesserman & Spelman 1993).
2.2 Circuit parameters
The parameters for basolateral membranes of hair cells in single section (RBI, CBI and RBO, CBO for IHCs and OHCs, respectively) were derived from measurements of input resistance and capacitance of isolated cells (table 1; multiple literature sources) using estimation procedures (Dallos & Evans 1995). The values were scaled to account for 18 OHCs and 6 IHCs per section (assuming the length of guinea-pig cochlea as 18 mm, and a spacing of 10 μm within a hair cell row). Longitudinal parameters were also scaled to allow for the coarseness of the discretization. Experimentally, RBO increases by 50-fold from the base to apex (Housley & Ashmore 1992; Mammano & Ashmore 1996). However, this feature is implemented only in the frequency-domain simulations to keep the computational load in the time-domain model within reasonable limits. The capacitance of the OHC basolateral membrane, CBO, varies only by a factor of 3 from cochlear base to apex (Housley & Ashmore 1992). For numerical simplicity, it was kept constant in all cochlear cross sections as well as for the IHC basolateral membrane RBI and CBI (Raybould et al. 2001). The nonlinear capacitance of the OHC basolateral membrane was not implemented as potential excursions used in the model, and the capacitance changes are small and the nonlinear capacitance is thus effectively linearized.
Apical resistances RAI and RAO were calculated from the basolateral values. The standing MET channel conductance equal to 0.1 (IHC) and 0.5 (OHC) of the maximal value was assumed. To calculate the input displacement and phase, the OHC stereocilia were taken as attached to the tectorial membrane (Cody & Russell 1987). It was assumed that MET channel opening depended on the BM displacement as a Boltzmann function (figure 2b). For simulations in both time and frequency domains, the amplitudes and phases of the BM displacement were computed from a model that gives realistic mechanical tuning (Mammano & Nobili 1993). Thus the input for a single frequency controls RAI and RAO significantly in approximately 10–20% of the sections and not just in a single section. Values for apical capacitances CAO and CAI were derived from basolateral values using the hair cell structural and electrical data (Dallos & Evans 1995; Lopez-Poveda & Eustaquio-Martin 2006).
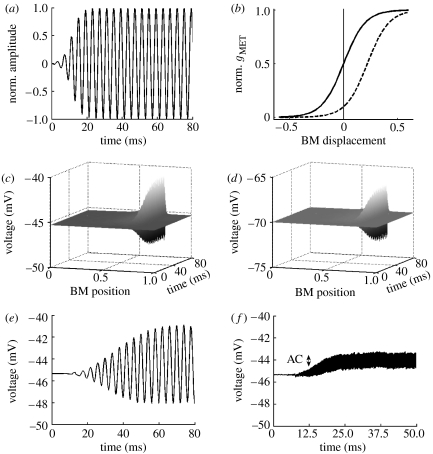
Figure 2.
Input–output relations of the model. (a) The normalized 250 Hz acoustic signal of 80 ms duration as the model input. (b) The normalized mechanoelectrical transducer channel activation as a function of BM displacement for both OHCs (solid curve) and IHCs (dashed curve). The activation gMET is described by the Boltzmann function gMET=gMET,max/(1+exp(−(x−x0)/d)), where x is the displacement of the BM (all units in μm), x0 is the BM displacement at which the MET channel is half activated (0 and 0.22 for OHCs and IHCs, respectively) and d determines the width of the transition range. For both OHCs and IHCs, d=0.1 (Kennedy et al. 2005). (c) The time course of the IHC receptor potential (the node 2, , in figure 1b) along the cochlear axis in response to a 250 Hz stimulus. The BM position is divided into 300 cross sections longitudinally coupled, extending from the cochlear base (BM position=0) to the apex (BM position=1). (d) Similar to (c) but for OHCs (the node 3, , in figure 1b). (e,f) The time course of the receptor potential at IHCs tuned to 250 and 5000 Hz, respectively. The AC voltage component attenuates with increasing frequency (from 3.4 mV at 250 Hz to 1.1 mV at 5000 Hz, or 9.6 dB attenuation). A similar behaviour is observed in the experimental data (Palmer & Russell 1986). Predicted responses in this and subsequent figures correspond to the acoustic stimulus of relatively low intensity (20–40 dB), allowing the linear approximations in the model.
The magnitudes of radial resistances in the potassium recycling pathway through the non-sensory cells ROC, RSL and RSV were chosen to obtain the standing IHC and OHC intracellular potentials of approximately −45 mV and −70 mV, respectively (Russell & Sellick 1978; Cody & Russell 1987). They are in reasonable agreement with the values determined experimentally from anaesthetized guinea-pigs (Misrahy et al. 1958; Johnstone et al. 1966). Magnitudes of longitudinal resistances do not have any apparent cellular correlate due to the longitudinal coarse graining used in the model (300 cross sections represent 3000 rows of hair cells). The magnitudes were chosen to obtain ratios of mechanical and electrical tuning close to experimental values (Fridberger et al. 2004).
Although the capacitance of the recycling pathway through the non-sensory cells is not commonly included in the cochlear electrical circuits due to uncertainly about its magnitude, an additional capacitor CSV was added to the circuit in some simulations (between nodes 0 and 1 in figure 1b) to investigate the effect of this capacitance (Cannon 1976).
The set of circuit parameters used in the simulations are listed in table 2.
Table 2.
Parameters used in simulations. (‘Node 1’ and ‘node 2’ indicate the location of the element in the circuit in figure 1b and ‘value’ indicates its electrical magnitude. ‘Connectivity’ indicates whether the node is coupled to the corresponding nodes in the adjacent cross sections; if defined a value for the longitudinal resistor (equivalent to a gap-junctional resistance) is given. Bracketed values for RAO and RBO are those used for simulations with constant OHC conductances along the tonotopic axis. For sources of the values, see table 1.)
| component | node 1 | node 2 | value | connectivity |
|---|---|---|---|---|
| R AI | 1 | 2 | 6.7 MΩ | – |
| R BI | 2 | 4 | 20 MΩ | – |
| R AO | 1 | 3 | 1.4 (8.3) MΩ | – |
| R BO | 3 | 5 | 0.6 (3.3) MΩ | – |
| C AI | 1 | 2 | 6 pF | – |
| C BI | 2 | 6 | 60 pF | – |
| C AO | 1 | 3 | 10.5 pF | – |
| C BO | 3 | 7 | 176 pF | – |
| C SV | 1 | 0 | 0–5 nF | – |
| V SV | 1 | 8 | 80 mV | – |
| V I | 4 | 6 | −100 mV | – |
| V O | 5 | 7 | −100 mV | – |
| R SV | 8 | 0 | 0.1 MΩ | 0.3 MΩ |
| R SL | 6 | 0 | 6.7 MΩ | 20 MΩ |
| R OC | 7 | 0 | 0.1 MΩ | 0.35 MΩ |
2.3 Implementation in the time domain
To determine the pattern of current flow within the cochlear equivalent electrical circuit (figure 1c), we developed the solution techniques based on MNA (Litovski & Zwolinski 1997) and modified from SCAM (developed by E. Cheever; http://www.swarthmore.edu/NatSci/echeeve1/). MNA allows elements and their connectivities within a circuit of arbitrary complexity to be written down as a table and then to be mapped into a connectivity matrix. Within this approach, the time course of ion flow is described by a set of differential algebraic equations (DAEs) of index 1 as they can be represented as
| (2.1) |
where C is the (singular) matrix of capacitances and G is the matrix of conductances (including the time-independent membrane conductances and the time-dependent contribution from the mechanotransducer channels gMET). I is the vector of independent current and voltage sources and includes the stria vascularis potential and the hair cell Nernstian potentials. V is the unknown vector of potentials at each node of the circuit. Both C and G matrices constructed following the MNA rules are very large. Even in the coarse-grain parametrization used here for a cochlear circuit from figure 1c with eight nodes and three independent voltage sources in each of the 300 electrically coupled cross sections, C and G matrices have dimensions 3300×3300. The system of equations (equation (2.1)) was solved in Matlab v. 7 (Mathworks, Natick, MA).
2.4 Implementation in the frequency domain
The calculation of the frequency dependence of the receptor potential ΔV can be simplified by making two assumptions about ΔV. These are as follows: (i) linear approximations are valid, i.e. the sound-evoked transducer channel conductance gMET is much smaller than the resting conductance G0 (gMET≪G0) and (ii) gMET is of the sinusoidal form
| (2.2) |
where γ(x) is the magnitude; ω (=2πf) is the angular frequency of the sound stimulus and θ(x) is the phase difference between the displacement of the stapes and BM at position x. Under these conditions, the receptor potential ΔV is sinusoidal as well (ΔV=|ΔV|e−jωt) and can be considered as a small perturbation of the steady-state solution V0 of equation (2.1) (i.e. the solution of −GV0+I=0). A set of DAEs (equation (2.1)) can then be reduced to a system of algebraic equations using complex representation and matrix form (see appendix A)
| (2.3) |
where etc. signifies matrix inversion. Therefore, to determine the frequency dependence of the receptor potential magnitude |ΔV| in the linear approximation, it is sufficient to find only , γejθ and (jωC−G0)−1. The magnitude γ(x) and phase θ(x) of the MET channel conductance gMET along the cochlear tonotopic axis depend on the longitudinal pattern of the BM displacement induced by sound stimulus. This pattern is determined numerically using an implementation of the cochlear macroscopic mechanics (Mammano & Nobili 1993).
3. Results
3.1 Time-domain simulation
The time-domain model calculates the time course of receptor currents and potentials generated by acoustic stimulus. The intracellular receptor potential generated by a sound consisting of a single frequency (f=250 Hz; figure 2a) is elicited only in a small population of hair cells in the cochlear segment where BM is tuned (figure 2c,d for IHCs, OHCs, respectively).
The responses of IHCs and OHCs to more complex acoustic signals (five tones with frequencies of 300, 600, 1200, 2400 and 4800 Hz) are depicted in figure 3a,b, respectively. The figures show that currents traversing the cells depend on the cell position along the cochlea. The attenuation of the steady-state amplitude with increasing frequency is, for the set of chosen parameters, more pronounced in OHCs than IHCs. This can be traced to the differences in the membrane time constants Rm·Cm between the cells (table 2), as well as in the activation of the transducer channels (figure 2b). The difference between OHC and IHC receptor currents reflects the diverse physiological function of these two cell types where IHCs act as sensory cells and OHCs have a role in sound amplification.
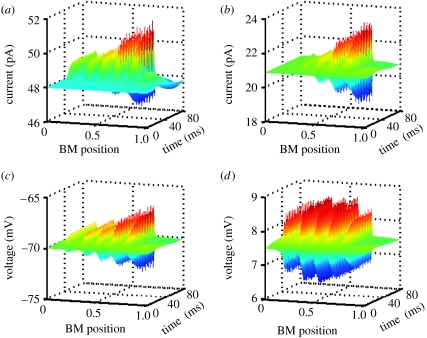
Figure 3.
Time-domain simulations. (a) The time course of the currents flowing through IHCs in response to a complex sound stimulus, a superposition of equal amplitude tones with frequencies 300, 600, 1200, 2400 and 4800 Hz. The current amplitude in IHCs tuned to higher frequencies (towards the cochlear base, BM position=0) is clearly attenuated. (b) Similar to (a) but calculated for the OHCs. (c,d) Attenuation of the OHC receptor potentials. (c) Intracellular but not (d) extracellular OHC receptor potential is attenuated with the increasing frequency of sound stimulus.
The attenuation of current amplitude is also reflected by intracellular receptor potentials. Figure 3c demonstrates low-pass filtering in the case of OHCs (node 3, , in the circuit at figure 1b). This is not the case for the extracellular OHC potential (node 7, , in the circuit at figure 1b) as figure 3d depicts relatively stable amplitude for all frequencies. This low attenuation can be attributed to two distinct mechanisms. The first mechanism is when extracellular current does not pass through the membrane and the potential, developed across a pure resistor, is therefore not filtered (Fridberger et al. 2004). A second mechanism arises when current can pass through the OHC apical and basolateral membranes with their RC filtering properties cancelling each other, a situation proposed to occur for the extracellular potential in hair cells in microchamber experiments (Dallos & Evans 1995). The attenuation of the intracellular potential arises mainly from the reduction of AC component (figure 2e,f).
3.2 Frequency-domain simulation
With any more complex parametrization of the cochlear circuits, the complexity of time-domain calculations makes it more difficult to analyse cochlear responses to sound over a broad frequency range. There are notable gradients in the values of the parameters along the cochlea, which are cumbersome to include in the time-domain calculations. For example, the OHC basolateral conductance gBO(=1/RBO) is experimentally not constant but increases towards the basal (or high-frequency) end of the cochlea (Mammano & Ashmore 1996; Preyer et al. 1996). In both mammalian and turtle cochleae, it is highly probable that the maximum transducer conductance also covaries along the cochlea (Ricci et al. 2003).
In order to study the effects of parameter variation along the cochlea efficiently, we developed a linearized frequency-domain model, calculating the potential responses in the steady state at single frequencies. We first consider the situation analysed previously for the time domain, keeping the RAO and RBO constant. Figure 4a,c shows how the hair cell receptor potential ΔV at its best frequency varies with that frequency. This is the gain function for both IHCs and OHCs. The gain functions for intracellular, extracellular and transmembrane (intracellular–extracellular) receptor potentials are comparable to those obtained experimentally (Kossl & Russell 1992; Fridberger et al. 2004). The gain functions of a single hair cell represent a limiting case when the hair cell is removed from the cochlear network. In this case the isolated hair cell has a simple equivalent circuit (figure 1b(i)).
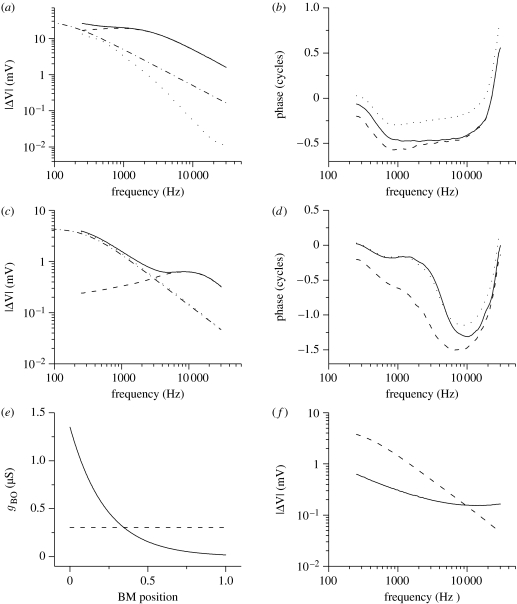
Figure 4.
Frequency-domain simulations. (a) The IHC gain function, representing the IHC receptor potential at the best frequency and how it varies with that frequency. (b) The accumulation of the IHC phase lag at the best frequency. For each frequency point, the phase lag accumulated at the characteristic position is displayed. Lags for intracellular, extracellular and transmembrane potentials are plotted. (c) The OHC gain function. (d) The accumulation of the OHC phase lag at the best frequency. Solid curve, intracellular potential; dashed curve, extracellular potential; dotted curve, transmembrane; dot-dashed line, single cell potential. (e) Assumed dependence of the OHC basolateral conductance gBO on the cochlear tonotopic position. gBO was kept either constant (gBO=300 nS) as in the time-domain simulations or varied exponentially from gBO=1200 nS at cochlear base (BM position=0) to gBO=25 nS at apex (BM position=1) as observed experimentally (Mammano & Ashmore 1996). OHC apical resistance was treated similarly. (f) The OHC transmembrane gain function is shown for variable basolateral and for constant OHC conductance. Dashed curve, constant conductance; solid curve, variable conductance.
First consider the case of an IHC (figure 4a). Insertion of a single cell into the cochlear electrical network shifts its corner frequency fc (i.e. the frequency at which the receptor potential equals of its low-frequency limit) of both intracellular and extracellular receptor potentials. The corner frequency shifts from approximately 200 Hz for a single cell to approximately 1500 Hz for a cell in a network (figure 4b). This is accompanied by a reduction of the receptor potential attenuation with frequency. In an isolated IHC, the anticipated attenuation would be approximately −20 dB per decade (−6 dB per octave), whereas we compute approximately −10 dB per decade for the networked IHCs in the 0.2–30 kHz range. This reduction in slope, producing a larger receptor potential than would be expected at higher frequencies, comes about as longitudinal coupling between sections and provides parallel connectivity of the hair cell resistors. This results in the decrease of the overall cochlear resistance and thus in the reduction of the effective overall time constant τeff of the cochlear electrical circuit. As a result, the corner frequency (fc=1/2·π·τeff) is increased. The IHC transmembrane receptor potential exhibits approximately −28 dB per decade attenuation in the same frequency range and a corner frequency of approximately 400 Hz.
In the case of an OHC in the cochlear electrical network, the extracellular receptor potential (figure 4c) exhibits a broadband filtering in the 0.2–30 kHz range with the maximum at approximately 9 kHz. This absence of attenuation is a consequence of two factors. First, the apical membrane RC filter in series with that of the basolateral membrane minimizes the membrane filtering (Dallos & Evans 1995). This effect is stronger for OHCs than for IHCs due to differences in their membrane time constants. Second, the longitudinal resistive coupling modifies the overall cochlear impedance. Thus, the extracellular receptor potential in the cochlear electrical network is broadband rather than quasi-all-pass filtered as determined for an isolated OHC (Dallos & Evans 1995). The OHC transmembrane potential, critical for the theories of electromotility (Brownell et al. 1985; Kachar et al. 1986; Ashmore 1987), is still attenuated by approximately −20 dB per decade (the corner frequency fc is approx. 500 Hz). This arises from substantial attenuation of the intracellular potential (approx. −10 dB per decade). For comparison, a single OHC cell has attenuation of approximately −20 dB per decade in the same frequency range and a corner frequency fc of approximately 300 Hz.
Figure 4b,d deals with the phase of the IHC and OHC receptor potentials, respectively. They show that phase lag accumulation at the best frequency depends on the frequency between 0.2 and 30 kHz. In the case of the IHCs, the phase accumulation is the largest in the mid-frequency region. The OHCs show the largest phase accumulation in the higher frequency region, as does the mechanical stimulus (Greenwood 1977; Mammano & Nobili 1993). The difference between the cell types arises from different time constants of IHC and OHC membranes.
To decide whether the other factors could affect OHC attenuation, we investigated the effect on the transmembrane potential by varying the longitudinal apical and basal OHC conductances (1/RAO, 1/RBO). When the conductances increased monotonically towards the basal (high frequency) end of the cochlea (figure 4e), the attenuation of the receptor potentials was significantly reduced to approximately −5 dB per decade in the 0.2–30 kHz range (figure 4f). Because in the model but , this effect can be explained as arising from less alternating current shunting at the cochlear base and thus less attenuation of the receptor potential. The corner frequency for the OHC attenuation was approximately 500 Hz.
These findings together suggest that electrically networked hair cells in functional cochlea can exhibit much smaller attenuation of their receptor potentials, and higher corner frequencies, than is commonly presumed. We conclude that arguments based on the membrane time constants of isolated hair cells are probably misleading in describing the electrical properties of hair cells in a coupled network.
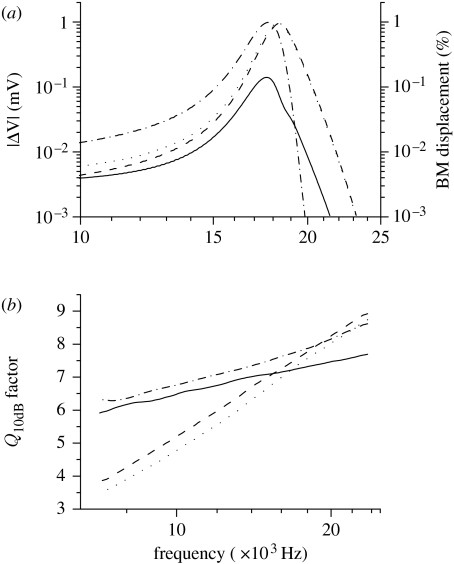
The tuning of receptor potential facilitated by the longitudinal coupling is analysed in figure 5. Figure 5a shows an example of how the OHC receptor potential generated at the 17.9 kHz position depends on the stimulus frequency. Tuning curves for intracellular, extracellular and transmembrane potentials are all plotted together with the mechanical tuning of the BM generating these responses. Similar results can also be found for IHCs (data not shown). These data were used to derive the frequency dependence of the Q10 dB quality factor, defined as the best frequency divided by the bandwidth of the tuning curve 10 dB below the peak. The values of the Q10 dB factor in the 7–23 kHz range for the OHC electrical and mechanical tuning are shown in figure 5b. The values are in good agreement with the experimental estimates of tuning of the BM (Kossl & Russell 1992; Robles & Ruggero 2001). The difference between electrical and mechanical Q10 dB factors is in line with the experimental observation of better mechanical frequency selectivity (Fridberger et al. 2004). The difference arises in the model from the longitudinal electrical coupling, allowing current to spread along the tonotopic axis away from the best frequency point. With the exception of the most basal regions, transmembrane potential is tuned with a higher Q10 dB than the extracellular potential. Thus an electromotile mechanism, dependent on transmembrane potential, could generate sharper tuning than the one dependent on field potentials alone.
Figure 5.
Frequency selectivity of the OHC receptor potential. (a) The frequency dependence of the steady-state amplitude of OHC receptor potential in the best position of 17.9 kHz (solid curve, transmembrane potential; dashed curve, extracellular potential; dotted curve, intracellular potential) and of mechanical BM displacement (dot-dashed curve). (b) The frequency dependence of quality factor Q10 dB describing the sharpness of the frequency selectivity of OHC receptor potentials (solid curve, transmembrane potential; dashed curve, extracellular potential; dotted curve, intracellular potential) and of BM mechanical tuning (dot-dashed curve).
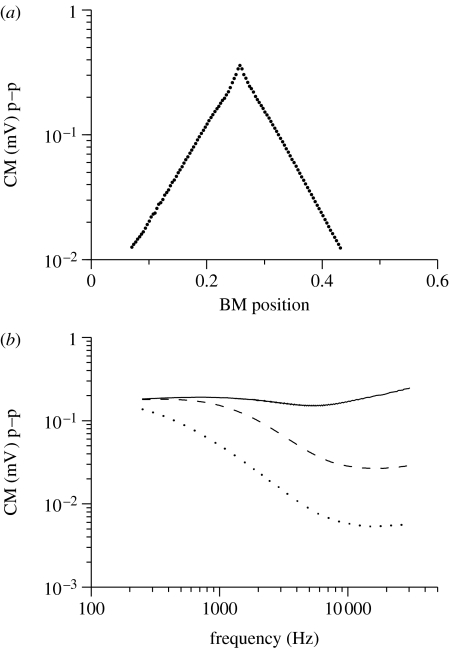
The model also demonstrates how the longitudinal spread of current determines the measured CM (Tasaki 1957; Misrahy et al. 1958). In the model, CM is the extracellular potential at node 1 (figure 1b). To estimate the range of the CM spread from a single cross section, an artificial BM displacement pattern with unity magnitude at a single cross section (best frequency=17.9 kHz) and 0 for all others was used as the input signal. Figure 6a shows that the extracellular longitudinal spread is characterized by an exponential decay constant of 1 mm in agreement with the estimates from CM measurements (Kletsky & Zwislocki 1979).
Figure 6.
The longitudinal spread of the CM. The CM is the stimulus-driven extracellular potential at node 1 in figure 1b (scala media). The input was a BM displacement pattern with unity magnitude at a single cross section corresponding to the best frequency=17.9 kHz, and 0 for all other sections. Peak-to-peak (p–p) CM amplitudes are plotted. (a) The magnitude of the CM decays exponentially along the cochlea with the space constant of 1 mm. (b) The dependence of the CM amplitude on the frequency of the sound stimulus and on the magnitude of the total capacitance of the non-sensory cells in the stria vascularis CSV. Solid curve, 0.1 nF; dashed curve, 1 nF; dotted curve, 5 nF.
Finally, the model was used to evaluate the contribution of the electrical capacitance of the non-sensory cells in the stria vascularis. Although their capacitance is commonly neglected in the cochlear equivalent electrical circuits, there is some experimental evidence indicating that it could significantly shunt the extracellular potentials at high frequency and compromise the voltage-driven cochlear amplifier performance (Cannon 1976; Mountain & Cody 1999). The addition of the capacitor CSV into the circuit (figure 1b) indeed increased the attenuation of the CM (figure 6b). When CSV=5 nF, the attenuation of approximately −12 dB per decade obtained is in good agreement with the experimentally determined CM magnitude in four different cochlear turns (Honrubia et al. 1973). Importantly, even this relatively large capacitance did not have any noticeable effect on the attenuation of the OHC transmembrane potential (data not shown). Thus, the capacitance of the non-sensory cells in the stria vascularis does not affect the OHCs' transmembrane potential critical for their electromotility.
4. Discussion
Despite a growing and detailed knowledge of molecular constituents of the potassium circulation loop (Wangemann 2006), the nature of many properties of the global interaction between cells in the cochlea is unclear. This is largely due to the experimental difficulties arising from monitoring a relatively inaccessible three-dimensional structure at multiple points. Of particular interest is the question of how, if at all, the K+ recycles back to the stria vascularis. This large-scale computational model addresses this point by treating potassium flow as electrical current in a network of the cochlea. Strictly, the transduction current is not a pure K+ current as a fraction is carried also by calcium (Ricci & Fettiplace 1998). However, Ca2+ is effectively removed from stereocilia by a plasma-membrane calcium pump PMCA2 (Lumpkin & Hudspeth 1998; Yamoah et al. 1998) and therefore the current has been treated here as essentially a K+ flux. As a result, only the K+-specific conductances and electrochemical driving forces need to be considered in the model.
This design of cochlear equivalent electrical circuit is based on the emerging molecular details of the potassium recirculation pathways facilitated by recent fundamental advances in the field of cochlear genetics (Petit 2006; Wangemann 2006). It differs in one detail from more traditional schemas (Dallos 1983, 1984) based on the cochlear electroanatomy and developed within the electrical engineering framework. In modelling the radial flow in the organ of Corti (figure 1b), the extracellular spaces surrounding IHCs and OHCs are not directly connected. This is motivated by recent experiments with genetically modified animals. Genetic deletion of potassium cotransporters or gap junctions in the adjacent supporting cells leads to prolonged depolarization of hair cells and their apoptosis resulting in animal deafness (Boettger et al. 2002; Cohen-Salmon et al. 2002). These findings suggest that excessive potassium released by hair cells upon sound stimulation is absorbed by supporting cells rather than diffusing away through the extracellular space in the tunnel of Corti. Experimental evidence that the OHCs' receptor currents affect the extracellular potential near the IHCs (Cody & Mountain 1989) is accommodated in the model by extensive longitudinal networking as the variation of the OHC receptor currents (by changing ROC values) affects the frequency tuning of the IHC receptor potential (data not shown).
The sound stimulus was included in the model by implementing realistic cochlear mechanics of the BM as the input to the gating of the mechanotransducer conductances. Owing to the linear approximation used and computational load associated with larger stimulations, the model, as it stands, predicts responses to sound stimuli at relatively low intensity (20–40 dB) where nonlinearities are less important. However, despite these restrictions, this model of cochlear transduction provides a powerful tool to analyse cochlear electrical responses to a sound stimulus.
The model reproduces reasonably well the experimental findings regarding conventional radial flow of current within the hair cells in a single cross section, the CM currents spread longitudinally along the tonotopic axis and its attenuation and also the frequency selectivity of receptor potentials. Furthermore, the model predicts that the tonotopic variation in the OHC conductance is essential for maintaining low attenuation of the OHC potential. The frequency dependence of the receptor potential ΔV for a single hair cell can be described by equation (4.1),
| (4.1) |
where ΔV is the receptor potential elicited by a change in the transducer channel conductance (=1/ΔRA) induced by sound stimulus of angular frequency ω(=1/2πf); V is the standing potential in the absence of any sound stimulus; VEP is the EP; VK is the Nernst potential for potassium; and j=(−1)1/2. The equation is a consequence of the hair cell electrical configuration (the RC filter of the apical cell membrane in series with that of the basolateral cell membrane; see appendix A). It represents a quasi-all-pass filter for the extracellular receptor potential as the filtering by apical and basolateral membranes effectively cancels each other (Dallos & Evans 1995). However, the transmembrane receptor potential remains the hypothetical driving force for the OHC electromotility. This potential would still be attenuated due to low-pass filtering of the intracellular receptor potential. As its corner frequency depends on the RC time constant, the experimentally established gradient of the OHC conductances along the cochlea would effectively increase the corner frequency and thus reduce the attenuation of both intracellular and, importantly, transmembrane potentials. Thus OHC electromotility can be driven by the transmembrane potential without requiring extracellular voltage gradients generated between the scala media and the fluid spaces of the organ of Corti (Dallos & Evans 1995).
The relatively slight attenuation we find for the potential across the OHC membrane (−5 dB per decade in the 200–30 000 Hz range) supports the possibility that the cochlear amplification is driven by somatic motility of the OHC powered by a voltage-dependent motor protein, prestin (Brownell et al. 1985; Zheng et al. 2000; Oliver et al. 2001; Lu et al. 2006; Gao et al. 2007). The proposal that prestin could provide force at acoustic frequencies has been questioned as it might be inferred from isolated hair cell measurements that forces at high frequencies are severely attenuated (as 1/f) above a corner frequency fc at approximately 300 Hz, and, for this reason, active hair bundle movement (Martin & Hudspeth 1999; Chan & Hudspeth 2005; Kennedy et al. 2005) has been proposed as an alternative driver of amplification. Our simulations predict that the voltage-driven prestin-based OHC amplification may be able to operate over a much wider frequency range than generally thought. This result is in line with the general robustness of the OHC morphology which allows the cells, if appropriately stimulated, to operate at frequencies higher than 50 kHz (Frank et al. 1999). Indeed there is evidence that there are unlikely to be significant limitations on the operating range for the motor molecule itself (Gale & Ashmore 1997). The emergent properties of this large-scale computational model could thus reconcile the discrepancy between the electrical properties and the mechanical requirements of cochlear processing at acoustic frequencies.
Acknowledgments
We thank A. Gardner-Medwin for discussion throughout the project and S. Strahl for programming suggestions. This research was supported by European Commission FP6 Integrated Project EUROHEAR, LSHG-CT-20054-512063.
Appendix A
A.1 Derivation of equation (2.3)
MNA of a circuit in figure 1c leads to a set of DAEs,
| (2.1) |
Suppose V0 is a steady-state solution that satisfies
| (A1) |
and that the MET channel conductance gMET is much smaller than the resting conductance G0(gMET≪G0). Then the sound-evoked receptor potential can be considered as a small perturbation ΔV of the steady-state solution V0(ΔV≪V0),
| (A2) |
| (A3) |
Substituting G and V in equation (2.1) gives
| (A4) |
which using equation (A 1) and treating gMET ΔV as negligible gives
| (A5) |
As we want to solve for the receptor potential ΔV(f) at a frequency f=ω/2π, we can presume the solution in the form ΔV=|ΔV|e−jωt where |ΔV| and ω are the magnitude and anglar frequency, respectively. Similarly, the conductance gMET of MET channel at a given BM position would be gMET=γe−jωt+θ where θ is the phase difference between the displacement of the stapes and BM at a given position. Substitution in equation (A 5) gives
| (A6) |
which can be rewritten to give equation (2.3)
| (2.3) |
A.2 Derivation of equation (4.1)
In case of a single cell (figure 1b(i)), the intracellular potential V is given by
| (A7) |
where ZA=RA/(1+jωRACA) and ZB=RB/(1+jωRBCB) are the impedances of apical and basolateral membranes, respectively. Consequently, the variation of the potential dV due to the change in the apical membrane impedance dZA is
| (A8) |
and because the change in the apical impedance dZA depends on the change in the MET channel conductance, dRA is
| (A9) |
equation (A 8) can be rewritten to give equation (4.1)
| (4.1) |
References
- Ashmore J.F. A fast motile response in guinea-pig outer hair cells: the cellular basis of the cochlear amplifier. J. Physiol. 1987;388:323–347. doi: 10.1113/jphysiol.1987.sp016617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashmore J. Cochlear outer hair cell motility. Physiol. Rev. 2008;88:173–210. doi: 10.1152/physrev.00044.2006. [DOI] [PubMed] [Google Scholar]
- Bekesy G. Direct observation of the vibrations of the cochlear partition under a microscope. Acta Otolaryngol. 1952;42:197–201. doi: 10.3109/00016485209120346. [DOI] [PubMed] [Google Scholar]
- Boettger T., Hubner C.A., Maier H., Rust M.B., Beck F.X., Jentsch T.J. Deafness and renal tubular acidosis in mice lacking the K–Cl co-transporter Kcc4. Nature. 2002;416:874–878. doi: 10.1038/416874a. [DOI] [PubMed] [Google Scholar]
- Brownell W.E., Bader C.R., Bertrand D., De Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- Cannon, M. W. J. 1976 Electrical impedances, current pathways, and voltage sources in the guinea pig cochlea. In Institute for sensory research. Syracuse, NY: Syracuse University.
- Chan D.K., Hudspeth A.J. Ca2+ current-driven nonlinear amplification by the mammalian cochlea in vitro. Nat. Neurosci. 2005;8:149–155. doi: 10.1038/nn1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cody A.R., Mountain D.C. Low-frequency responses of inner hair cells: evidence for a mechanical origin of peak splitting. Hear Res. 1989;41:89–99. doi: 10.1016/0378-5955(89)90002-6. [DOI] [PubMed] [Google Scholar]
- Cody A.R., Russell I.J. The response of hair cells in the basal turn of the guinea-pig cochlea to tones. J. Physiol. 1987;383:551–569. doi: 10.1113/jphysiol.1987.sp016428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen-Salmon M., et al. Targeted ablation of connexin26 in the inner ear epithelial gap junction network causes hearing impairment and cell death. Curr. Biol. 2002;12:1106–1111. doi: 10.1016/S0960-9822(02)00904-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dallos P. Some electrical circuit properties of the organ of Corti. I. Analysis without reactive elements. Hear Res. 1983;12:89–119. doi: 10.1016/0378-5955(83)90120-X. [DOI] [PubMed] [Google Scholar]
- Dallos P. Some electrical circuit properties of the organ of Corti. II. Analysis including reactive elements. Hear Res. 1984;14:281–291. doi: 10.1016/0378-5955(84)90055-8. [DOI] [PubMed] [Google Scholar]
- Dallos P., Evans B.N. High-frequency motility of outer hair cells and the cochlear amplifier. Science. 1995;267:2006–2009. doi: 10.1126/science.7701325. [DOI] [PubMed] [Google Scholar]
- Frank G., Hemmert W., Gummer A.W. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc. Natl Acad. Sci. USA. 1999;96:4420–4425. doi: 10.1073/pnas.96.8.4420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fridberger A., De Monvel J.B., Zheng J., Hu N., Zou Y., Ren T., Nuttall A. Organ of Corti potentials and the motion of the basilar membrane. J. Neurosci. 2004;24:10 057–10 063. doi: 10.1523/JNEUROSCI.2711-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale J.E., Ashmore J.F. An intrinsic frequency limit to the cochlear amplifier. Nature. 1997;389:63–66. doi: 10.1038/37968. [DOI] [PubMed] [Google Scholar]
- Gao J., et al. Prestin-based outer hair cell electromotility in knockin mice does not appear to adjust the operating point of a cilia-based amplifier. Proc. Natl Acad. Sci. USA. 2007;104:12 542–12 547. doi: 10.1073/pnas.0700356104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenwood D. Empirical travel time functions on the basilar membrane. In: In E.F., Evans J.P.W., editors. Psychophysics and physiology of hearing. Academic; London, UK: 1977. pp. 43–53. [Google Scholar]
- He D.Z., Jia S., Dallos P. Mechanoelectrical transduction of adult outer hair cells studied in a gerbil hemicochlea. Nature. 2004;429:766–770. doi: 10.1038/nature02591. [DOI] [PubMed] [Google Scholar]
- Honrubia V., Strelioff D., Ward P.H. A quantitative study of cochlear potentials along the scala media of the guinea pig. J. Acoust. Soc. Am. 1973;54:600–609. doi: 10.1121/1.1913639. [DOI] [PubMed] [Google Scholar]
- Housley G.D., Ashmore J.F. Ionic currents of outer hair cells isolated from the guinea-pig cochlea. J. Physiol. 1992;448:73–98. doi: 10.1113/jphysiol.1992.sp019030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jagger D.J., Forge A. Compartmentalized and signal-selective gap junctional coupling in the hearing cochlea. J. Neurosci. 2006;26:1260–1268. doi: 10.1523/JNEUROSCI.4278-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnstone B.M., Johnstone J.R., Pugsley I.D. Membrane resistance in endolymphatic walls of the first turn of the guinea-pig cochlea. J. Acoust. Soc. Am. 1966;40:1398–1404. doi: 10.1121/1.1910239. [DOI] [PubMed] [Google Scholar]
- Kachar B., Brownell W.E., Altschuler R., Fex J. Electrokinetic shape changes of cochlear outer hair cells. Nature. 1986;322:365–368. doi: 10.1038/322365a0. [DOI] [PubMed] [Google Scholar]
- Kennedy H.J., Crawford A.C., Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433:880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- Kharkovets T., et al. Mice with altered KCNQ4 K+ channels implicate sensory outer hair cells in human progressive deafness. Embo J. 2006;25:642–652. doi: 10.1038/sj.emboj.7600951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kikuchi T., Adams J.C., Miyabe Y., So E., Kobayashi T. Potassium ion recycling pathway via gap junction systems in the mammalian cochlea and its interruption in hereditary nonsyndromic deafness. Med. Electron Microsc. 2000;33:51–56. doi: 10.1007/s007950070001. [DOI] [PubMed] [Google Scholar]
- Kletsky E.J., Zwislocki J.J. Cochlear-microphonics versus hair-cell tuning in the cochlea. J. Acoust. Soc. Am. 1979;65:S84. doi: 10.1121/1.2017471. [DOI] [Google Scholar]
- Kossl M., Russell I.J. The phase and magnitude of hair cell receptor potentials and frequency tuning in the guinea pig cochlea. J. Neurosci. 1992;12:1575–1586. doi: 10.1523/JNEUROSCI.12-05-01575.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litovski V., Zwolinski M. Kluwer Academic Publishers; Boston, MA: 1997. VLSI circuit simulation and optimization. [Google Scholar]
- Lopez-Poveda E.A., Eustaquio-Martin A. A biophysical model of the inner hair cell: the contribution of potassium currents to peripheral auditory compression. J. Assoc. Res. Otolaryngol. 2006;7:218–235. doi: 10.1007/s10162-006-0037-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T.K., Zhak S., Dallos P., Sarpeshkar R. Fast cochlear amplification with slow outer hair cells. Hear Res. 2006;214:45–67. doi: 10.1016/j.heares.2006.01.018. [DOI] [PubMed] [Google Scholar]
- Lumpkin E.A., Hudspeth A.J. Regulation of free Ca2+ concentration in hair-cell stereocilia. J. Neurosci. 1998;18:6300–6318. doi: 10.1523/JNEUROSCI.18-16-06300.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mammano F., Ashmore J.F. Differential expression of outer hair cell potassium currents in the isolated cochlea of the guinea-pig. J. Physiol. 1996;496(Pt 3):639–646. doi: 10.1113/jphysiol.1996.sp021715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mammano F., Nobili R. Biophysics of the cochlea: linear approximation. J. Acoust. Soc. Am. 1993;93:3320–3332. doi: 10.1121/1.405716. [DOI] [PubMed] [Google Scholar]
- Marcotti W., Johnson S.L., Kros C.J. Effects of intracellular stores and extracellular Ca2+ on Ca2+-activated K+ currents in mature mouse inner hair cells. J. Physiol. 2004;557:613–633. doi: 10.1113/jphysiol.2003.060137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin P., Hudspeth A.J. Active hair-bundle movements can amplify a hair cell's response to oscillatory mechanical stimuli. Proc. Natl Acad. Sci. USA. 1999;96:14 306–14 311. doi: 10.1073/pnas.96.25.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misrahy G.A., Hildreth K.M., Shinabarger E.W., Gannon W.J. Electrical properties of wall of endolymphatic space of the cochlea (guinea pig) Am. J. Physiol. 1958;194:396–402. doi: 10.1152/ajplegacy.1958.194.2.396. [DOI] [PubMed] [Google Scholar]
- Mountain D.C., Cody A.R. Multiple modes of inner hair cell stimulation. Hear Res. 1999;132:1–14. doi: 10.1016/S0378-5955(99)00013-1. [DOI] [PubMed] [Google Scholar]
- Oliver D., He D.Z., Klocker N., Ludwig J., Schulte U., Waldegger S., Ruppersberg J.P., Dallos P., Fakler B. Intracellular anions as the voltage sensor of prestin, the outer hair cell motor protein. Science. 2001;292:2340–2343. doi: 10.1126/science.1060939. [DOI] [PubMed] [Google Scholar]
- Ospeck M., Dong X.-X., Iwasa K.H. Limiting frequency of the cochlear amplifier based on electromotility of outer hair cells. Biophys. J. 2003;84:739–749. doi: 10.1016/S0006-3495(03)74893-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer A.R., Russell I.J. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear Res. 1986;24:1–15. doi: 10.1016/0378-5955(86)90002-X. [DOI] [PubMed] [Google Scholar]
- Petit C. From deafness genes to hearing mechanisms: harmony and counterpoint. Trends Mol. Med. 2006;12:57–64. doi: 10.1016/j.molmed.2005.12.006. [DOI] [PubMed] [Google Scholar]
- Preyer S., Renz S., Hemmert W., Zenner H., Gummer A. Receptor potential of outer hair cells isolated from base to apex of the adult guinea-pig cochlea: implications for cochlear tuning mechanism. Auditory Neurosci. 1996;2:145–157. doi: 10.1177/107385849600200309. [DOI] [Google Scholar]
- Raybould N.P., Jagger D.J., Housley G.D. Positional analysis of guinea pig inner hair cell membrane conductances: implications for regulation of the membrane filter. J. Assoc. Res. Otolaryngol. 2001;2:362–376. doi: 10.1007/s101620010087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci A.J., Fettiplace R. Calcium permeation of the turtle hair cell mechanotransducer channel and its relation to the composition of endolymph. J. Physiol. 1998;506(Pt 1):159–173. doi: 10.1111/j.1469-7793.1998.159bx.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci A.J., Crawford A.C., Fettiplace R. Tonotopic variation in the conductance of the hair cell mechanotransducer channel. Neuron. 2003;40:983–990. doi: 10.1016/S0896-6273(03)00721-9. [DOI] [PubMed] [Google Scholar]
- Robles L., Ruggero M.A. Mechanics of the mammalian cochlea. Physiol. Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell I.J., Sellick P.M. Intracellular studies of hair cells in the mammalian cochlea. J. Physiol. 1978;284:261–290. doi: 10.1113/jphysiol.1978.sp012540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strelioff D. A computer simulation of the generation and distribution of cochlear potentials. J. Acoust. Soc. Am. 1973;54:620–629. doi: 10.1121/1.1913642. [DOI] [PubMed] [Google Scholar]
- Suesserman M.F., Spelman F.A. Lumped-parameter model for in vivo cochlear stimulation. IEEE Trans. Biomed. Eng. 1993;40:237–245. doi: 10.1109/10.216407. [DOI] [PubMed] [Google Scholar]
- Tasaki I. Hearing. Annu. Rev. Physiol. 1957;19:417–438. doi: 10.1146/annurev.ph.19.030157.002221. [DOI] [PubMed] [Google Scholar]
- Wangemann P. Supporting sensory transduction: cochlear fluid homeostasis and the endocochlear potential. J. Physiol. 2006;576:11–21. doi: 10.1113/jphysiol.2006.112888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamoah E.N., Lumpkin E.A., Dumont R.A., Smith P.J., Hudspeth A.J., Gillespie P.G. Plasma membrane Ca2+-ATPase extrudes Ca2+ from hair cell stereocilia. J. Neurosci. 1998;18:610–624. doi: 10.1523/JNEUROSCI.18-02-00610.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng J., Shen W., He D.Z., Long K.B., Madison L.D., Dallos P. Prestin is the motor protein of cochlear outer hair cells. Nature. 2000;405:149–155. doi: 10.1038/35012009. [DOI] [PubMed] [Google Scholar]
- Zidanic M., Brownell W.E. Fine structure of the intracochlear potential field. I. The silent current. Biophys. J. 1990;57:1253–1268. doi: 10.1016/S0006-3495(90)82644-8. [DOI] [PMC free article] [PubMed] [Google Scholar]