Abstract
High-dimensional (HD) NMR spectra have poorer digital resolution than low-dimensional (LD) spectra, for a fixed amount of experiment time. This has led to “reduced-dimensionality” strategies, in which several LD projections of the HD NMR spectrum are acquired, each with higher digital resolution; an approximate HD spectrum is then inferred by some means. We propose a strategy that moves in the opposite direction, by adding more time dimensions to increase the information content of the data set, even if only a very sparse time grid is used in each dimension. The full HD time-domain data can be analyzed by the Filter Diagonalization Method (FDM), yielding very narrow resonances along all of the frequency axes, even those with sparse sampling. Integrating over the added dimensions of HD FDM NMR spectra reconstitutes LD spectra with enhanced resolution, often more quickly than direct acquisition of the LD spectrum with a larger number of grid points in each of the fewer dimensions. If the extra dimensions do not appear in the final spectrum, and are used solely to boost information content, we propose the moniker hidden-dimension NMR. This work shows that HD peaks have unmistakable frequency signatures that can be detected as single HD objects by an appropriate algorithm, even though their patterns would be tricky for a human operator to visualize or recognize, and even if digital resolution in an HD FT spectrum is very coarse compared with natural line widths.
1. Introduction
The resolving power of high-dimensional (HD) NMR spectra has been instrumental in solution protein structure elucidation [1–4], now allowing large, interesting proteins and complexes to be studied [5–8]. High-dimensional (HD) NMR data sets have time-domain data with 3–5 dimensions and 2–4 interferometric or “indirect” time variables, tk. The direct acquisition time, tACQ, is for data collection, yielding a complex data set C(t1,t2,t3,…,tACQ). Data are usually acquired over a regular time grid for each of the t1, t2, etc., independently and then transformed into 3-5D spectra S(F1,F2,F3,…FACQ) in which each dimension has independent digital resolution SW1/N1,SW2/N2,…, SWACQ/NACQ. This sampling strategy suffers from a multiplicative time penalty arising from the need for adequate digital resolution in each spectral dimension independently. The total number of indirect points, NTOT, and hence the minimum experiment time TMIN (assuming adequate sensitivity) increases rapidly as the number of indirect dimensions is increased:
| (1) |
A 4D experiment of size 64×64×64×NACQ, with a minimum two-step phase cycle and acquisition of both N- and P-type data sets for each of the three indirect dimensions, would require 221 ~ 2.1 million transients, taking 24.3 days at 1 Hz repetition rate. Even 64 points may be marginal at high magnetic field, where the spectral widths for both 13C/15N expand to quite a few kHz, and 13C/15N line widths may be surprisingly narrow when optimized pulse sequences exploiting the TROSY effect [9–11] are used.
Strategies to speed up data collection have been proposed. Most involve reducing the dimensionality of the spectrum by taking various cross-sections or subsets of time-domain points [12–16], often corresponding to integral projections in the frequency spectrum. In FT spectra, extending acquisition in a kth orthogonal dimension cannot possibly improve the resolution of the integral projection in which this same dimension is integrated over. The integral projection along a frequency axis yields essentially the first point of the associated time-domain interferogram; the value of the first point does not depend on how many subsequent time points are acquired. This independence of the resolution of projections in FT spectra is shown in Figure 1.
Figure 1.
(a) A noise-free 2D spectrum at low resolution, showing the integral projections at the margins. Neither of the orthogonal projections allows a full count of the number of peaks in the 2D plane. (b) The same spectrum as in (a) but with superior vertical resolution, allowing two peaks to be resolved. The horizontal spectrum obtained from the vertical integral projection remains identical to the previous case, because in FT spectra the two frequency dimensions are independent.
While the digital resolution in any orthogonal frequency dimension is not altered in an FT spectrum, there is clearly far more information in the higher-dimensional spectrum provided it can be analyzed in the higher-dimensional space: degeneracies are resolved, the number of resonances can be tallied more completely, and the line shapes of the various peaks can yield a wealth of useful information. In short, the resolution of the HD spectrum with n dimensions is best assessed in n dimensions. It is mostly an artifact of display technology and limitations of the human mind that necessitates contouring planes or plotting traces to inspect the spectrum. The extra dimensions unravel overlap, by separating and visualizing each resonance. Integrating over any dimension is clearly counter-productive to this aim.
With certain assumptions about the nature of the data, it may be possible to do far better than FT methods, and materially change the resolution in one orthogonal dimension– or all the other dimensions. For example, if one were to assume that peaks of interest were already resolved in a 2D spectrum derived from a projection of a 3D spectrum, then the additional frequency information in the 3rd dimension for each resolved peak could be retrieved with very few additional points in the 3rd time dimension, using parametric fitting of the data to a model with a single peak at unknown frequency [17]. Likewise, with aggressive non-linear methods, a small number of nD projections may allow more accurate inference of peak positions in (n+1)D spectrum than is possible by straightforward Fourier Transformation. The utility of these more aggressive methods may also depend on whether simply peak position and total number of peaks, or detailed line shape, intensity and line widths are of interest. For some assignment tasks the exact intensity of each peak is relatively unimportant compared to the exact frequency coordinates, whereas in NOE experiments the peak intensities clearly matter.
Rather different altogether is the case in which the lower-dimensional data is poorly resolved, is somewhat noisy, or in which it is not clear whether or not there is overlap. In this case, aggressive processing may result in a possibly misleading HD spectrum. This is shown schematically in Fig. 2, where the simple noise-free 2D spectrum of Fig. 1 is reconstituted using the two coordinate projections, by taking the minimum ordinate at each position, the lower-value algorithm [14]. Obviously this result could be improved with more 1D projections, and this example is for illustration only, and certainly not as an example of the best practice of the method. However, even many such projections fail to reconstruct the true 2D spectrum. With more complex experimental data containing significant noise, genuine peaks may be lost, or artifacts introduced, limiting the utility of the rapid acquisition for the task at hand, which is to gain rapid and accurate information about the sample under study.
Figure 2.
(a) Integral projections obtained from a 2D spectrum, the high-resolution case of Fig.1. (b) A 2D spectrum obtained from the two integral projections, by the “lower bound” algorithm, in which the 2D spectral grid points are set according to the formula S(n,m) = Min{Ih(m),Iv(n)}, where Ih is the horizontal projection and Iv the vertical projection. Clearly, two projections are insufficient to reconstruct the true 2D spectrum in this example.
2. Results
2.1 Theory
2.1.1 A simple case of one versus two dimensions
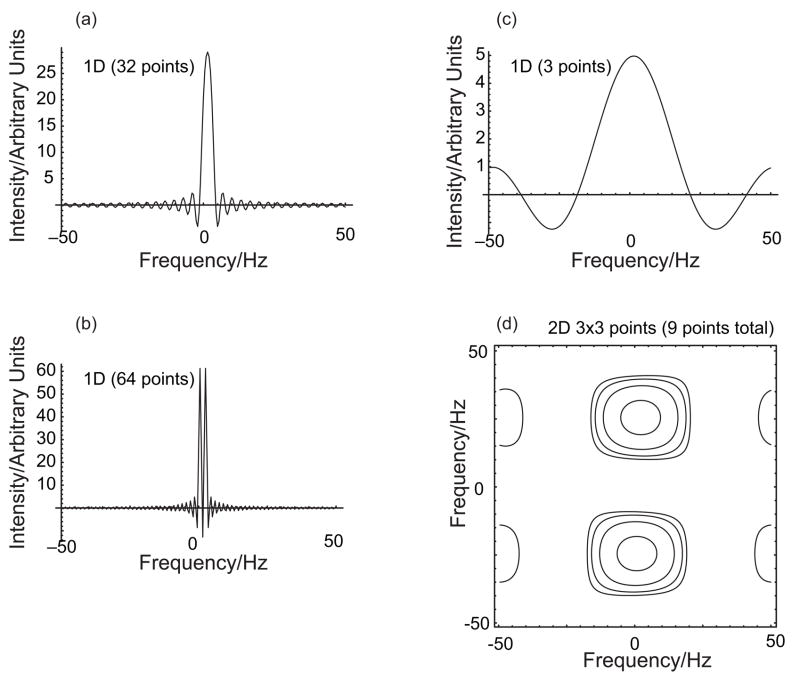
Suppose, with acquisition time Tk, that two peaks are unresolved in some dimension k of a conventional multidimensional FT spectrum. If the full width at half maximum, Dw, of each peak is much less than 1/Tk, then their frequency spacing Df must be somewhat less than 1/Tk, i.e., the limited acquisition is limiting the resolution. What is the chance of resolving these two peaks by increasing Tk? Clearly, if the two peaks happen to be nearly degenerate (Δf ≪ Δw) then increasing Tk is fruitless. However, if these same two peaks are displayed as a function of two dimensions, and the line positions in the second dimension are not tightly correlated with those in the first, then acquiring data in this new dimension, even over the entire 2D time grid, might be more efficient than acquiring an ever longer signal in the first dimension alone. This is shown schematically in Fig. 3, where two peaks are separated by 2.0 Hz in the horizontal dimension. With a spectral width of 100 Hz, about 64 pts are required to resolve them using a 1D data set. However, if they were separated by 50 Hz in a second dimension, just a 3×3 time grid suffices to indicate clearly the presence of at least two peaks using a 100 Hz spectral width in each dimension, even by conventional FT analysis (with extensive zero-filling). Taking into account the necessity of using both N/P (or sin/cos) data sets to achieve absorption line shapes, a total of 18 points is the minimum for the 2D realization. This compares very favorably to 64, reducing the number of required points by a factor of almost four. If these data were to be fit to two peaks, rather than simply transformed into a spectrum, both could be extracted quite accurately, even in the presence of some noise, for the 2D case. In the 1D case, noise would necessitate more than 64 pts to get anything like the same reliability for frequency, line width, and amplitude. The displacement of the peaks in the additional dimension facilitates their free and clear characterization, just as the reduced E. COSY multiplet patterns allow the measurement of J-couplings that are far too small to observe directly [18]. This example serves to illustrate an important point that bears emphasizing: HD NMR spectra have higher intrinsic resolution than their lower-dimensional pieces. Once the idea of independent 1D transformations is abandoned, the HD paradigm becomes ever more compelling, as very short data sets can exploit the uncorrelated line positions in, e.g., protein backbone assignment experiments even though none of the constituent 1D projections show any resolved features at all.
Figure 3.
A comparison of the amount of data needed to resolve two peaks that are very close in one frequency dimension and quite well separated in a second orthogonal frequency dimension. (a) A 1D projection using 32 time-domain points, zero-filled extensively before FT. The two peaks are unresolved. (b) The same as (a) but with 64 data points. The two peaks are resolved. (c) The same as (a) but with only three data points (before zero-filling). The two peaks are completely unresolved. (d) A 3×3 2D FT spectrum, extensively zero-filled in both dimensions. Because the peaks are widely separated in the second dimension, they are resolved with only 9 data points total (18 points to obtain an absorption-mode spectrum), even with FT analysis only. The large sinc-wiggles explain the features at the horizontal edges. Using parametric methods that try to identify actual peaks, or otherwise avoid the transform-limited line widths, the well-separated 2D peaks are much easier to identify accurately than the overlapping 1D peaks, especially in the presence of noise.
2.1.2 The one-dimensional filter diagonalization method
The Filter Diagonalization Method (FDM) is a data analysis technique that has been in the literature for a number of years, and employed for 1D [19], 2D [20–22], 3D [23] and 4D [24,25] NMR experiments of various kinds. The systematic development of the equations, numerical aspects, and performance issues of FDM have been reviewed [26]. Our brief, qualitative treatment here is to allow issues arising later on to be addressed clearly and to make the surprising results understandable.
In the one-dimensional case, FDM efficiently and reliably solves the problem of fitting a complex time signal of N points, sampled on a uniform time grid, in terms of a linear combination of M complex sinusoids:
| (2) |
with complex amplitudes dk (integral and phase) and complex frequencies ω̃k (position and width) over a spectral width SW=τ−1. The line shape from Eq. (2) is Lorentzian; the discrete infinite Fourier transform can be computed analytically [26] by introducing uk= exp(iω̃kτ) and z=exp(2πifτ) and summing a geometric series:
| (3) |
The number of peaks comprising the fit is M = N/2, half the number of frequency grid points that would occur in a non-zero-filled FT spectrum. The amplitudes and frequencies are obtained by an eigenvalue problem whose input matrix elements depend only on the discrete measured data points cn. We assume that some initial state Φ0 evolves in time and that its autocorrelation function generates the signal:
| (4) |
where a complex symmetric inner product,
| (5) |
allows for arbitrary signal phase. Diagonalizing Û is then equivalent to determining both dk and uk for each peak:
| (6) |
| (7) |
and Û itself, by translating the initial state in discrete time steps, can generate other (non-orthogonal, unnormalized) states that can be used to make up a basis {Φn}:
| (8) |
Using the evolution operator itself to construct the basis is attractive because it should yield exactly the states that are needed to describe the dynamics. Simple representations of the unit matrix, 1̂ or U(0) and Û or U(1) are obtained from the measured data [26] using this primitive basis {Φn}:
| (9) |
| (10) |
| (11) |
| (12) |
These data matrices also arise in the formulation of parametric Linear Prediction (LP) [27], which is closely related to FDM. The eigenvalue problem
| (13) |
is then written
| (14) |
It is essential to include the matrix representation for the identity operator because the basis {Φn} is not orthonormal. With the eigenvalues and eigenvectors in hand, the spectrum is then computed by Eqs. (3) and (7). Equation (14) is a generalized eigenvalue problem that has a number of library routines available to solve it. Matrix diagonalization is one of the best-studied algorithms and has been optimized extensively, making this approach efficient compared to any attempt to directly fit the FID as damped sinusoids using a nonlinear least squares routine. Nevertheless, for realistic data sets, the U matrices are (a) dense; (b) huge; and (c) possibly ill-conditioned (Hankel structure). FDM overcomes some of these problems by making linear combinations of the M time-like basis functions Φk to form frequency-like basis functions Ψ(fk) at M equally-spaced frequency grid points across the spectral width, fk = k(SW/M) − SW/2, k = 0,…, M−1:
| (15) |
When we evaluate matrix elements of the U operators between basis functions Ψ(fk) and Ψ(fj) at widely different frequencies, the values are small compared to those near the diagonal– much smaller than some intermediate point cj in the FID, which would be the corresponding value between the Φ basis functions. Indeed, the Hankel structure of Eqs. (9) and (11) ensure that very large matrix elements can occur far from the diagonal, as values along the anti-diagonal direction are identical. The Fourier basis thus disentangles the structure of the matrices to make them easier to diagonalize, in the same way the FT separates out peaks in the spectrum, making them easier to recognize than the interfering sinusoids and noise comprising the raw FID. Small off-diagonal matrix elements, which often refer mostly to noise, can be neglected according to time-independent perturbation theory when there is a large frequency difference between the states involved. This allows the giant matrix problem to yield to a divide-and-conquer strategy in which smaller submatrices, near the diagonal, are diagonalized sequentially. Each submatrix corresponds to a small frequency window. The spectra are calculated over each window by Eq. (3) or a number of other similar formulas [26] and then smoothly summed up. In our implementation of multi-window FDM we overlap adjacent windows by 50% and use a cos2 weighting function to stitch the spectral estimates together into a full spectrum [22], but this is somewhat arbitrary. The spectra so obtained are usually surprisingly insensitive to the details of the window size. This insensitivity is a prerequisite for reliable results.
This background is important to facilitate understanding the resolving power of FDM. Clearly, there are at most M peaks. If the true spectrum contains more than M distinct peaks then the fit cannot possibly be perfect. However, when there is no noise, no degenerate frequencies in any of the dimension, and the data conforms exactly to the model, then the fit obtained by FDM is perfect whenever the true number of peaks K is less than M. There is a sudden “phase transition” in which the spectrum crystallizes into clear view and then remains constant as more data is acquired. When the calculation is over one window, the number of local basis functions in the window should be greater than the number of signal peaks in the same window. These simple arguments get more complex when there are very large peaks outside the window, but there are ways to handle this situation smoothly.
Sadly, in the presence of even small noise amplitudes, the number of peaks is always essentially M or more. Noise does not repeat, does not follow any pattern, and cannot be cast as a certain fixed number of Lorentzian peaks, so that real data must appear as some number of “peaks” that is always at least M, frustrating FDM convergence somewhat. What effect will this have on the attainable resolution? The short answer is that if the number of signal peaks K is less than M, and the noise amplitude is much smaller than any of these peaks, then both the fit and the resolution are excellent. As noise increases, it may tend to dominate, forcing precious potential peaks to be “squandered” fitting the local noise instead. There appears to be no ironclad guarantee, in this case, that the output of the generalized eigenvalue problem is the best fit, in terms of Lorentzian peaks and, even if it were, that the best fit would result in the most useful spectral estimate. Even with a perfect fit the spectral estimate may not be accurate in the information we seek: line positions, intensities, etc. of signal peaks, because the perfect fit includes the noise. This makes the quality of the fit itself a potentially distracting criterion. It is well known in the LP literature that the case M ≫ K mitigates the influence of the noise. In FDM, this can be seen clearly by visualizing the grid of basis functions in frequency. Qualitatively, a reasonable guideline might be that the density of basis functions should be high enough that there is at least one grid basis function Ψ(fk) between the frequency centers of any pair of peaks we wish to resolve. The sampling must be of the order of the inverse frequency separation to achieve this density. The same is true in FT spectroscopy, although in the FT case the sampling must be long enough whether or not there is significant noise, and the line shape may still be transform limited, broad, and show sinc-wiggles. In FDM the line shape is always Lorentzian, and the accuracy of the width depends on the noise; when the latter is low, the former can be accurate. Sharp, narrow resonance lines with good resolution and accurate intensities will result.
It might seem possible to “zero fill” the basis Ψ (f) by adding more frequency coordinates between the existing fk, using Eq. (14) to calculate additional functions, and thereby increasing the potential to pick up and ultimately discount any noise features. However, the phrase “zero fill” here suggests the problem: as the frequencies become substantially closer than the natural grid fk, the functions Ψ (f) just become more linearly dependent, making U(0) closer to singular. The way the generalized eigenvalue problem is numerically handled means that linear dependence is not fatal to the algorithm, but artificially increasing the basis density without increasing the information content of the signal does not yield any notable improvement in resolution, either.
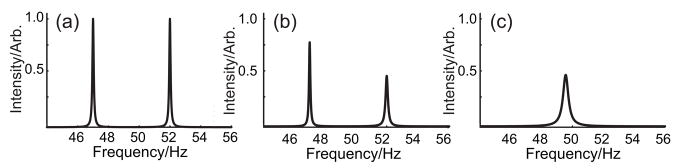
Figure 4 shows a simple but illustrative 1D benchmark problem in which the object is to resolve the two sharp Lorentzian lines in the presence of varying amounts of noise and with varying numbers of points in the FID. When the noise level is extremely low, just two Fourier basis functions (one at the edge of the spectrum, and one in the center) from only four time-domain data points can still detect the small phase/amplitude shifts that occur when the FID is left-shifted by one point, allowing the lines to be calculated fairly accurately by Eq. (10). This case is analogous to being able to open a weightless door by pushing very near the hinge. Although each basis function has a frequency center, they are fairly delocalized when only four data points comprise the FID. Noise quickly destroys the ability to resolve the two peaks as quickly, as shown in the third panel.
Figure 4.
Deterioration of a high-resolution FDM spectrum as a function of the percentage of noise added. Two narrow Lorentzian lines are located at 47 and 52 Hz, with identical amplitude, phase, and line width. The Nyquist range is 200 Hz and only four points of the synthetic FID were generated. (a) No noise. The two peaks are recovered quantitatively with only four points. (b) 0.1% random time-domain noise. Both lines have appreciable errors in line width, but not phase, frequency or amplitude (integral). (c) 1.0% random time-domain noise. The sparse data is now insufficient to resolve the two lines. A broadened peak near the mean frequency, and with line width much narrower than the original frequency separation, is the result. Only the amplitude of the noise is altered. The particular realization is otherwise identical to that in (b). With other noise realizations, the results may show narrower or broader lines, and slight errors in the integral as well.
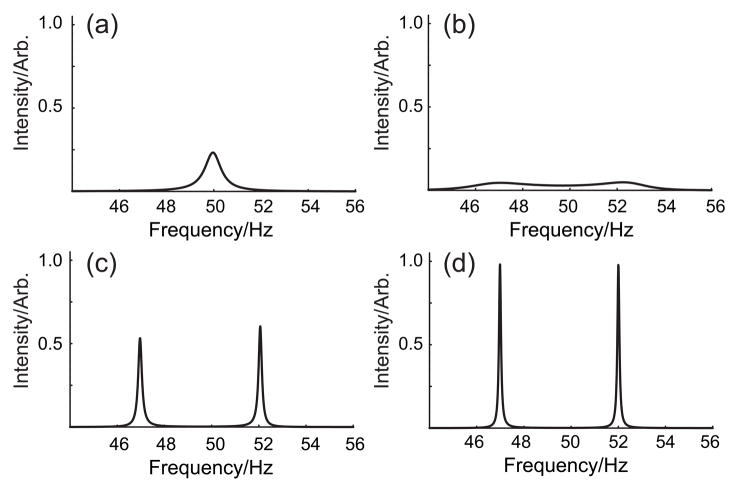
As the noise increases it pays to have a higher density of basis functions, i.e. sample more data and, in particular, having the local basis function density be of the order of the peak spacing can be quite important. (If the aforementioned door is heavy, using the handle is imperative.) The FDM behavior, shown in Fig. 5, is quite different from that of the FT spectrum. The FT spectrum requires a data length of the order of the inverse width of the peaks to really deliver all the potential resolution, and this requirement is independent of the noise, or peak spacing. It also necessitates a much longer acquisition time whenever the peaks are narrow.
Figure 5.
Behavior of the high-resolution FDM spectrum as a function of the number of data points acquired. Two narrow Lorentzian lines are located at 47 and 52 Hz, with identical amplitude, phase, and line width. The Nyquist range is 200 Hz but only the relevant region is displayed. (a) 8 points. (b) 16 points. (c) 32 points. (d) 64 points. The noise amplitude was about 1% in the time domain. For a peak spacing of 5 Hz in a 200 Hz spectral width, ~40 Fourier basis functions would be an estimate of the density needed to resolve the two peaks. This in turn would necessitate ~80 time-domain data points. In fact two features emerge with only 8 Fourier basis functions (b), although the result is only convincing with 16 Fourier basis functions (c) and the line widths are only correct when 32 Fourier basis functions can be used (d). This is close to the estimate of 40 based on the argument that the local density be of the order of the frequency separation of the features to be resolved. The actual details depend on the percentage of noise added.
2.1.3 Issues in Multidimensional FDM
Suppose that a two-dimensional signal C(t1,t2) is obtained, in which each of the one-dimensional projections shows substantial overlap. What is the possibility of obtaining a fully resolved 2D spectrum using FDM? Following the earlier discussion, the number of 2D basis functions must exceed the number of 2D peaks. However, the former is proportional to the product of the number of recorded data points
| (16) |
so that the 2D basis set can be very large if just one dimension has good digitization, N2 ≫ N1. In most NMR experiments this can be the direct detection dimension, that is, N2 = NACQ. By contrast, Fourier transformation along the direct dimension gives N2 uncorrelated 1D FDM calculations, each with 1D basis size at most N1/2. If N1 is not large, then the result may be poor for any F1 trace that happens to contain more than N1/2 peaks. Peaks are not confined to a single data point in F2. A given 2D peak will appear as a 1D peak multiple times, on adjacent F2 traces along the F1 dimension. Large peaks may have significant intensity on many points in F2, limiting the number of weaker 1D peaks that can be identified accurately. The 1D peaks in F1 for adjacent F2 points also may not align precisely. By contrast, a 2D FDM calculation of a 2D peak, wherever it is, appears only once in the 2D plane, requiring only one 2D basis function to pin it down, and it cannot look like anything except a 2D peak. This, in a nutshell, is why partial Fourier transformation can be counterproductive compared to an up-front multidimensional method, and why it may be possible to increase the dimensionality of the data set and still reduce overall acquisition time. The total nD basis size can become enormous as the number of dimensions increases: an 8×8×8×4096 4D data set requires the solution of four generalized eigenvalue problems of the form of Eq. (14), each with 128k×128k matrices containing ~17.2 billion matrix elements. It is only with the advent of FDM that it is possible to entertain problems of this enormous numerical scale.
2.1.4 Block Sampling and Deliberate Aliasing
Non-uniform sampling (NUS) is a strategy to acquire a longer interferogram, using the same number of points, by relaxing the requirement to sample time points on a uniform grid at the Nyquist rate. Instead, some points are effectively skipped in favor of others at greater evolution times. There must be a trade off, of course, as very long evolution times have vanishing signal intensity and hence little useful information. “Randomly” sampled data cannot be processed by standard FT methods, but can be handled using Maximum Entropy (MaxEnt) processing [27–29]. But consider a block sampling strategy, in which a certain number of points N2 are sampled uniformly at dwell time t2, and then a gap Mt is introduced (usually M ≫ N2) a further N2 points are sampled, and the process repeated N1 times. A 1D signal C(n2t2 + n1Mt2), n2 = 0,…N2−1, n1 = 0,…N1−1, is obtained. We can, however, consider the signal instead as a pseudo-2D signal:
| (17) |
Figure 6 shows a comparison between uniform sampling, non-uniform sampling, block sampling, and a 1D block-sampled data set considered as a pseudo-2D data set. Processed as a two-dimensional signal, which is now sampled uniformly on a two-dimensional time grid, conventional 2D FDM can be used for analysis; there are no issues with unwanted artifacts, and the smaller spectral width in the new, hidden, dimension means that the basis function density in the new dimension will be higher than it was in the first dimension. This strategy is potentially useful when the peaks cluster into groups, i. e. a number of closely spaced peaks and then areas without peaks. Many kinds of NMR spectra show these features. The first dimension then establishes the true chemical shift values over the true spectral width, and the second dimension boosts the resolution so that all peaks are distinct and resolved. Once the narrow 2D resonances are identified, the second dimension can be integrated over, giving back the original 1D spectrum with the correct frequencies, and higher resolution. This block sampling strategy is thus adapted to the different frequency scales in the spectrum.
Figure 6.
Various sampling strategies. (a) Uniform sampling at the Nyquist rate. (b) Non-uniform sampling where, for simplicity, the points are still obtained at integer multiples of the dwell time used in (a). (c) A block sampling strategy, in which data are acquired in a repeating pattern in which multiple data points are skipped. (d) Rearrangement of the block sampled 1D data into a 2D data set in which there are no missing data points but the spectral width in the new dimension is M times smaller than the Nyquist range.
Maximum entropy has also been used to create “virtual dimensions” in which the width of lines are plotted in a second dimension, with the line position plotted in the first one, thereby apparently increasing resolution [30]. The difference with the approach here is that the data itself is interpreted as a higher-dimensional signal, rather than simply displaying the data in a higher-dimensional plot in which different parameters are shown in the orthogonal dimensions.
It should be clear that sampling points further out in the data set can markedly improve the resolution, much as the NUS strategy. It is also possible to “fill in” the missing data points. The samples are all on the same time grid, so that if all points are sampled a conventional signal results. This option is not usually exploited in the NUS case, where samples are often obtained with a random sampling schedule weighted by the expected properties of the FID. The fully sampled 1D signal will have the best attainable resolution, as it contains the most information. However, it may be possible to obtain a similar result more rapidly, and check its reliability, by incrementally sampling another set of points that gradually increases the block size N2. If the spectral features do not change much when additional points are taken, then they have converged to within the prevailing signal to noise ratio (SNR), and acquisition can be terminated.
The strategy shown in Fig. 6 has a couple of subtleties. First, complementary N-and P-type data are not available in the hidden dimension when the latter results from omitting blocks of data. A conventional FT spectrum would thus show “phase-twist” [34] line shapes in the hidden dimension plane. Using multidimensional FDM, only one data set is required: the fit is to a single phase-modulated multidimensional signal. In this case, only the P-type data is available by simply skipping intervening points, but this apparent deficiency is largely irrelevant as long as methods other than FT are used to analyze the data.
We should note that the analysis of incomplete or “gapped” data has a long history in both engineering [32] and astrophysics [33]. The approach here, in which a particular kind of block-sampled data is recast as a higher-dimensional signal has not, to our knowledge, been described elsewhere.
The one disadvantage to expanding the dimensionality lies with the factor of 2 in the denominator in Eq. (16). The first set of block sampled points gives a 1D basis of size M1. Adding a second block at a much later time gives a 2D basis size that is also just M1. The second block establishes the peaks as 2D, rather than 1D, but will not necessarily contribute to improved resolution because both the size of the basis and the number of peaks have remained fixed. The noise will have been reduced, but the noise would also have been reduced by simply sampling twice as long, without skipping any data points, and doing so would give a 1D basis of size 2M1 which, in principle, would have the capability to characterize twice as many signal peaks. In benchmark problems where peaks are nearly uniformly dispersed across a known spectral width, the 1D sampling strategy is the most efficient. However, when peaks cluster markedly, the block sampling strategy, with the introduction of a hidden dimension, outperforms. This should not be any great surprise: the more that is known about the data, the better the sampling strategy can be. In particular, some protein experiments can exploit the known position of resonances in the 15N-1H plane, obtained from an initial 2D HSQC spectrum [34], to resolve closely-spaced peaks in other dimensions much more rapidly and with better sensitivity, compared to extending the sampling along these other dimensions in the usual way.
2.2 Examples of Hidden Dimension Spectra
One common example of spectral features with different scales is that of a 1D proton spectrum of a small molecule. At high field, the chemical shift separation is much larger than the scalar coupling, and resolved multiplets are observed. The spectrum therefore has signal peaks that are clustered near each other, and then larger frequency regions devoid of signals. Although there is no application for incomplete sampling of a 1D FID, it provides a straightforward way to demonstrate the potential advantage of a hidden dimension.
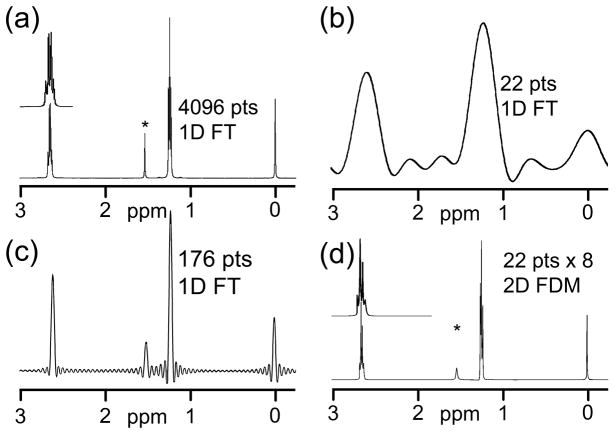
Figure 7 shows the upfield region of the 1D spectrum of ethylbenzene. With 4096 data points in the FID, 7(a), individual peaks in each multiplet are resolved. Using only the first 22 points, 7(b) leads to an FT spectrum, after zero-filling, in which peaks are very wide, and show sinc-function oscillations in the baseline. Roughly speaking, if there are rather less than eleven groups of peaks, then a 2D spectrum with just 22 points along the first dimension, and enough points in the hidden dimension to characterize the number of peaks within each group, should suffice. This is indeed the case, as shown in Fig. 7(c). A 2D FDM calculation using a 22×8 data set, followed by integration over the hidden dimension, is able to recover almost all the original information in the full data set. In this case, only 176 points out of 4096 are actually needed to obtain a decent spectrum, a potential times savings of nearly 23-fold if this were a multidimensional spectrum.
Figure 7.
A simple example showing how to boost the resolution by using a hidden dimension. (a) Conventional upfield 1H FT spectrum of a standard ethylbenzene sample using 4096 data points. The multiplets are resolved. (b) The same FID as in (a) but using only the first 22 points, replacing the others with zeroes. Very wide transform-limited line shapes are apparent. (c) The result of a 2D FDM calculation using 8 blocks of 22 points (from the same FID again), each block separated by a gap of 490 points so that the last block is near the end of the 4096 point data record. The 2D FDM spectrum was calculated and then the hidden dimension, in which the true frequencies are aliased many times, was then integrated out. Even though only 176 points were used in the calculation, the resolution and the relative intensities are quite good, and the multiplet structure is again visible.
Another case in which the hidden dimension idea can be employed is in a conventional 13C-1H HSQC. In some compounds the carbon-13 lines can be very close compared to the entire survey spectral width. Using conventional sampling, it may be time-consuming to resolve the individual 13C resonances if the corresponding multiplets in the proton dimension are also close, or overlapping. In this case, a viable strategy is to collect a block of data using the short dwell time corresponding to the full 13C spectral width, and process it to observe whether signals appear clustered or uniformly distributed, or perhaps whether there is some ambiguity in some crowded parts of the 2D spectrum. Knowing the approximate maximum peak frequency difference, an appropriate gap can be introduced (of the order of the inverse of this frequency difference) and block sampling initiated. After four such blocks the 3D FDM spectrum can be calculated, and the additional dimension integrated out. It is usually a quick matter to decide whether one, two, or more 13C resonances are present.
Figure 8 shows an example from a zoomed region of the 13C-1H HSQC of cholesteryl acetate. The assignment is indicated. There are two close diastereotopic methyl groups, Me26 and Me27, with 13C resonances near 23 ppm, and with partially overlapping proton resonances (the proton couplings are not resolved). Resolving these two correlations in a single survey-mode 2DFT spectrum is a time-consuming challenge. With 256 points in the 13C dimension, the resolution is too poor to detect anything but a slight hint of two 13C frequencies, but with 512 points the expected two peaks emerge. Using 6 blocks of just 16 points (96 increments total), the 2D projection of the 3D FDM calculation is able to definitely resolve the two close peaks.
Figure 8.
Top: the structure of cholesteryl acetate, with conventional numbering of the carbons. Bottom: a zoomed region of a survey HSQC in the upfield methyl region. The carbon-13 spectral width was 16340 Hz. (a) Conventional 2D FT spectrum using 256 increments in the 13C dimension (~64 Hz resolution). The two close peaks near 23 ppm are unresolved. (b) Same as (a) but with 512 increments (~32 Hz resolution). The two peaks near 23 ppm are resolved. (c) 2D projections of a 3D FDM calculation using 16 points over the 16340 Hz spectral width, and 6 increments over a hidden dimension of 100 Hz. In the hidden dimension, the three basis functions per 100 Hz are enough to boost the resolution so that two peaks are observed– with only 96 increments total. For the FT spectra both N- and P-type data were needed to obtain absorption-mode line shapes. The 3D FDM data set used only P-type data in each of the 13C dimensions. The time taken to acquire these data sets, based on the same minimum phase cycling and identical relaxation delays was (a) 158 min. (b) 316 min. and (c) 30 min., showing a factor of ten improvement in throughput by using a hidden dimension and FDM.
Of course it is not necessary that the hidden dimension simply be one of the existing indirect dimensions over a smaller spectral width. It could equally well be an entirely different, independent dimension in which the resolution is better than the plane under consideration. Once again, the multidimensional nature of FDM may make a 3D experiment, in which the extra dimension boosts the information content, a superior strategy to a 2D experiment in which many increments may be needed to resolve close peaks. When the pulse sequence already contains fixed delays for magnetization transfer, the hidden dimension can be a constant-time evolution during one of these fixed delays, thus optimizing both sensitivity and resolution simultaneously. If the peak positions in the hidden dimension are known beforehand, from a preliminary experiment, then this information can be exploited to narrow the spectral width while still avoiding the possibility of aliasing one peak directly upon another one. If the peak positions are unknown, the full Nyquist range should be used in the hidden dimension.
As an illustrative example, suppose a high-resolution rendition of the 1HN(i)-13C′(i−1) plane of labeled protein were of interest. As this is one of the planes of a 3D HNCO [31] experiment, the most natural course would be to fix the 15N dimension, at tN = 0, and increment the 13C′ dimension until sufficient resolution is achieved. This 2D experiment should not be too time consuming. However, as the pulse sequence must have fixed delays to allow 15N magnetization to be transferred to and from the directly bonded carbonyl carbon, incrementing the 13C′ dimension farther and farther out can cause more magnetization losses due to transverse relaxation. In the 3D experiment, the necessary fixed delays are used to encode the 15N chemical shift in a so-called “constant-time” evolution [35–37], avoiding any additional delays that would be necessary in the alternative “real-time” experiment [38]. It thus may make sense to use the 15N fixed delay, which must be present in any event, as a hidden dimension to resolve peaks in the 1HN(i)-13C′(i−1) plane rather than using 13C′ evolution to do so. If, in addition, the 15N resonance frequencies are known, a smaller spectral width can be chosen in the 15N dimension, making sure that peaks with nearly degenerate 1H frequencies are not accidentally aliased on top of each other in the nitrogen dimension. If no information on the 15N-1H plane is available, then the full Nyquist range must be used. However, the number of increments in the hidden dimension can still be very small.
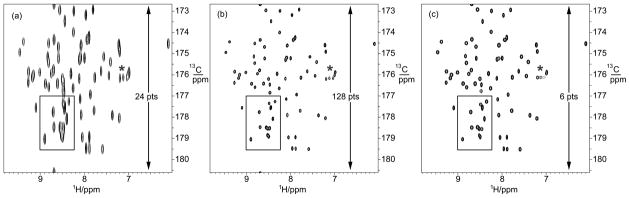
Figures 9 and 10 shows that this strategy bears fruit. Obtaining the 1HN(i)-13C′(i−1) plane by a conventional 2D strategy, using 24 C′ increments, results in a reasonable 2D FT spectrum that has a couple of congested regions near 8.5 ppm in the proton dimension. By comparison, a 4×6 (15N×13C′) 3D data set, in which the 15N hidden dimension is integrated over, clearly reveals resolved peaks in the same region. Increasing the 2D acquisition to 128 C′ increments reveals similar information but is a much longer experiment. Applying 2D FDM to the 24-increment data set likewise fails to completely resolve the region in question.
Figure 9.
The 1HN(i)-13C′(i −1) plane of human ubiquitin obtained using various numbers of 13C′ increments. See the experimental section for details. In each panel, the starred group of peaks are from arginine sidechains, and are folded into the spectral region in the 13C dimension. (a) Conventional 2D FT spectrum using 24 increments in the 13C dimension. The boxed region is unresolved. Only the zero-time increment in the 15N dimension, which was fixed, was used. (b) Same as (a) but with 128 13C′ increments. The boxed region shows much-enhanced resolution. (c) 2D projections of a 3D FDM calculation using 6 13C′ increments and 4 15N increments. The data were obtained using constant-time evolution in both indirect dimensions. The 15N constant time (2T in the literature) was the usual 12.4 ms required for magnetization transfer. Using the known positions of peaks in the 1HN-15N plane, a spectral width of 659 Hz (13.2 ppm) was employed in the 15N dimension. The 13C constant time 2T was 8.0 ms. Although only 24 joint increments were taken, the resolution rivals that of the much longer experiment in (b). Using the full Nyquist range (36 ppm) in the 15N dimension gives somewhat inferior results, although using 6 15N increments, rather than 4, again allows the full 3D spectrum, with high resolution along each dimension, to be obtained.
Figure 10.
A more detailed view of the boxed regions in Fig. 9, showing the comparison between (a) 24 C′ increments only, (b) 128 C′ increments only, and (c) 6 C′ increments and 4 15N increments. The first two panels are FT spectra, and the third is a 3D FDM spectrum in which the 15N dimension has been integrated out to give the 2D spectrum shown.
Figure 10 shows zoomed views of the boxed regions of Fig. 9, to show the details of the improvement in resolution.
3. Experimental
All spectra were obtained at 500 MHz on a Varian UnityPlus NMR spectrometer with a conventional (room temperature) 5 mm HCN triax gradient Varian probe. Sample volumes were approximately 800 ml. The ethylbenzene sample was the 0.1% ASTM standard proton sensitivity sample. The cholesteryl acetate sample was approximately 50 mM in CDCl3. The ubiquitin sample was 1 mM in 90%/10% H2O/D2O at pH 4.7. Standard pulse sequences were used for the experiments, except that BIP [39] inversion pulses were substituted in pairs for conventional 180° pulses and care was taken to suppress artifacts that could arise from unwanted magnetization transfers, as described previously [40]. The spectra are completely representative of what could be obtained in any modern facility. At higher field and with superior sensitivity, our approach will perform even better than shown herein. Further details of all the experimental conditions, including files for the BIP pulses that were employed, can be found in the Supplementary Material.
4. Discussion
We have shown that there are cases in which there is much to gain by exploiting the full HD spectrum. Hidden dimensions, either employing severe aliasing over a smaller spectral width, or a different nuclear spin species altogether, can boost the content of the HD data set. While none of the 1D or 2D FT projections of the data shown in Fig. 9 (c) show resolved features with so few increments in the 15N and 13C dimensions, the full 3D object is fully resolved by FDM, allowing post hoc high-resolution 1D or 2D projections to be calculated if they are of interest. The flexibility of FDM, in which all the data work together to determine the HD peak positions, makes it possible to sample fewer points along dimensions that are unfavorable for sensitivity reasons, and yet still obtain good resolution. The onset of the sudden convergence of FDM, once the number of multidimensional basis functions and the underlying SNR are adequate, gives this approach a measure of reliability that is not addressed as easily by a disjoint collection of lower-dimensional projections.
Of course, there are natural limits to employing HD spectra. If too many magnetization transfers, all of which may require delays to effect, are needed, then sensitivity may suffer even if resolution is boosted. In the extreme case of many dimensions there may be too little SNR to employ FDM analysis at all. However, when an unused dimension is already present along with the associated delays, as in the HN(CO)CA experiment [36], the methods described here are quite applicable and may lead to superior resolution for the same instrument time.
There is an interesting connection between orderly skipping of data points and the resulting density of basis functions in a higher-dimensional space. Our results seem to indicate that, for unknown peak dispositions within a given Nyquist range, simple uniform sampling is usually the best option for FDM. When peaks cluster narrowly or appear in groups, or if some specific question regarding close unresolved features is to be settled, then block sampling may offer some distinct advantages.
5. Conclusions
Filter Diagonalization can be a speedy and effective way to analyze NMR data that has sufficient SNR and is well matched to the assumption of a finite number of multidimensional Lorentzian peaks. The ability of FDM to process just P-type data and still obtain absorption-mode line shapes is useful in hidden dimension spectra, where in some cases the corresponding N-type data set is not readily obtained. Although the FDM algorithm does not use prior knowledge per se, if peak positions are thought to be known from a previous experiment, they can be exploited to narrow down the spectral range, allowing aliasing to occur as long as no accidental degeneracies result. Optimizing data acquisition in this way allows surprisingly short time-domain data sets to deliver very high resolution spectra, and will be generally useful for a large class of commonly-used NMR experiments.
Supplementary Material
Acknowledgments
This research was made possible by support from the National Science Foundation, CHE-0703182, and by a UC Discovery Grant BIO05-10533. B. D. N. thanks the UCI School of Physical Sciences for partial support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Oschkinat H, Griesinger C, Kraulis PJ, Sørensen OW, Ernst RR, Gronenborn AM, Clore GM. Three-dimensional NMR spectroscopy of a protein in solution. Nature. 1988;332:374–376. doi: 10.1038/332374a0. [DOI] [PubMed] [Google Scholar]
- 2.Zuiderweg ER, Fesik SW. Heteronuclear three-dimensional NMR spectroscopy of the inflammatory protein C5a. Biochemistry. 1989;28:2387–2391. doi: 10.1021/bi00432a008. [DOI] [PubMed] [Google Scholar]
- 3.Marion D, Driscoll PC, Kay LE, Wingfield PT, Bax A, Gronenborn AM, Clore GM. Overcoming the overlap problem in the assignment of 1H NMR spectra of larger proteins by use of three-dimensional heteronuclear 1H-15N Hartmann-Hahn-multiple quantum coherence and nuclear Overhauser-multiple quantum coherence spectroscopy: application to interleukin 1 beta. Biochemistry. 1989;28:6150–6156. doi: 10.1021/bi00441a004. [DOI] [PubMed] [Google Scholar]
- 4.Ikura M, Kay LE, Bax A. A novel approach for sequential assignment of 1H, 13C, and 15N spectra of proteins: heteronuclear triple-resonance three-dimensional NMR spectroscopy. Application to calmodulin. Biochemistry. 1990;29:4659–4667. doi: 10.1021/bi00471a022. [DOI] [PubMed] [Google Scholar]
- 5.Kay LE. NMR studies of protein structure and dynamics. J Magn Reson. 2005;173:193–207. doi: 10.1016/j.jmr.2004.11.021. [DOI] [PubMed] [Google Scholar]
- 6.Grishaev A, Tugarinov V, Kay LE, Trewhella J, Bax A. Refined solution structure of the 82-kDa enzyme malate synthase G from joint NMR and synchrotron SAXS restraints. J Biomol NMR. 2008;40:95–106. doi: 10.1007/s10858-007-9211-5. [DOI] [PubMed] [Google Scholar]
- 7.Placzek WJ, Almeida MS, Wüthrich K. NMR structure and functional characterization of a human cancer-related nucleoside triphosphatase. J Mol Biol. 2007;367:788–801. doi: 10.1016/j.jmb.2007.01.001. [DOI] [PubMed] [Google Scholar]
- 8.Tsodikov OV, Ivanov D, Orelli B, Staresincic L, Shoshani I, Oberman R, Schärer OD, Wagner G, Ellenberger T. Structural basis for the recruitment of ERCC1-XPF to nucleotide excision repair complexes by XPA. EMBO J. 2007;26:4768–4776. doi: 10.1038/sj.emboj.7601894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pervushin K, Riek R, Wider G, Wüthrich K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicateds and avenue to NMR structures of very large biological macromolecules in solution. Proc Nat Acad Sci USA. 1997;94:12366–12371. doi: 10.1073/pnas.94.23.12366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pervushin K, Riek R, Wider G, Wüthrich K. Transverse relaxation-optimized spectroscopy (TROSY) for NMR studies of aromatic spin systems in C-13-labeled proteins. J Am Chem Soc. 1998;120:6394–6400. [Google Scholar]
- 11.Wider G. NMR techniques used with very large biological macromolecules in solution. Methods Enzymol. 2005;394:382–398. doi: 10.1016/S0076-6879(05)94015-9. [DOI] [PubMed] [Google Scholar]
- 12.Kim S, Syzperski T. GFT NMR, a new approach to rapidly obtain precise high-dimensional NMR spectral information. J Am Chem Soc. 2003;125:1385–1393. doi: 10.1021/ja028197d. [DOI] [PubMed] [Google Scholar]
- 13.Kupce E, Freeman R. New methods for fast multidimensional NMR. J Biomol NMR. 2003;27:101–113. doi: 10.1023/a:1024960302926. [DOI] [PubMed] [Google Scholar]
- 14.Kupce E, Freeman R. Projection-reconstruction technique for speeding up multidimensional NMR spectroscopy. J Am Chem Soc. 2004;126:6429–6440. doi: 10.1021/ja049432q. [DOI] [PubMed] [Google Scholar]
- 15.Mobli M, Stern AS, Hoch JC. Spectral reconstruction methods in fast NMR: Reduced dimensionality, random sampling and maximum entropy. J Magn Reson. 2006;182:96–105. doi: 10.1016/j.jmr.2006.06.007. [DOI] [PubMed] [Google Scholar]
- 16.Coggins BE, Zhou P. PR-CALC: A program for the reconstruction of NMR spectra from projections. J Biomol NMR. 2006;34:179–195. doi: 10.1007/s10858-006-0020-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lippens G, Bodart PR, Taulelle F, Amoureux JP. Restricted linear least square treatment processing of heteronuclear spectra of biomolecules using the ANAFOR strategy. J Magn Reson. 2003;161:174–182. doi: 10.1016/s1090-7807(03)00005-3. [DOI] [PubMed] [Google Scholar]
- 18.Griesinger C, Sørensen OW, Ernst RR. Practical aspects of the E-COSY technique. Measurement of scalar spin spin coupling constants in peptides. J Magn Reson. 1987;75:474–492. [Google Scholar]
- 19.Hu H, Van QN, Mandelshtam VA, Shaka AJ. Reference deconvolution, phase correction, and line listing of NMR spectra by the 1D filter diagonalization method. J Magn Reson. 1998;134:76–87. doi: 10.1006/jmre.1998.1516. [DOI] [PubMed] [Google Scholar]
- 20.Mandelshtam VA, Taylor HS, Shaka AJ. Application of the filter diagonalization method to one- and two-dimensional NMR spectra. J Magn Reson. 1998;133:304–312. doi: 10.1006/jmre.1998.1476. [DOI] [PubMed] [Google Scholar]
- 21.Chen J, Mandelshtam VA, Shaka AJ. Regularization of the two-dimensional filter diagonalization method: FDM2K. J Magn Reson. 2000;146:363–368. doi: 10.1006/jmre.2000.2155. [DOI] [PubMed] [Google Scholar]
- 22.Chen J, De Angelis AA, Mandelshtam VA, Shaka AJ. Progress on the two-dimensional filter diagonalization method. An efficient doubling scheme for two-dimensional constant-time NMR. J Magn Reson. 2003;162:74–89. doi: 10.1016/s1090-7807(03)00045-4. [DOI] [PubMed] [Google Scholar]
- 23.Chen J, Nietlispach DN, Shaka AJ, Mandelshtam VA. Ultra-high resolution 3D NMR spectra from limited-size data sets. J Magn Reson. 2004;169:215–224. doi: 10.1016/j.jmr.2004.04.017. [DOI] [PubMed] [Google Scholar]
- 24.Armstrong GS, Mandelshtam VA, Shaka AJ, Bendiak B. Rapid high-resolution four-dimensional NMR spectroscopy using the filter diagonalization method and its advantages for detailed structural elucidation of oligosaccharides. J Magn Reson. 2005;173:160–168. doi: 10.1016/j.jmr.2004.11.027. [DOI] [PubMed] [Google Scholar]
- 25.Armstrong GS, Bendiak B. High-resolution four-dimensional carbon-correlated H-1-H-1 ROESY experiments employing isotags and the filter diagonalization method for effective assignment of glycosidic linkages in oligosaccharides. J Magn Reson. 2006;181:79–88. doi: 10.1016/j.jmr.2006.03.017. [DOI] [PubMed] [Google Scholar]
- 26.Mandelshtam VA. FDM: the filter diagonalization method for data processing in NMR experiments. Prog NMR Spectrosc. 2001;38:159–196. [Google Scholar]
- 27.Hoch JC, Stern AS. NMR data processing. Chapter 4 Wiley-Liss; New York: 1996. [Google Scholar]
- 28.Mobli M, Maciejewski MW, Gryk MR, Hoch JC. Automatic maximum entropy spectral reconstruction in NMR. J Biomol NMR. 2007;39:133–139. doi: 10.1007/s10858-007-9180-8. [DOI] [PubMed] [Google Scholar]
- 29.Frueh DP, Sun ZY, Vosburg DA, Walsh CT, Hoch JC, Wagner G. Non-uniformly sampled double-TROSY hNcaNH experiments for NMR sequential assignments of large proteins. J Am Chem Soc. 2006;128:5757–5763. doi: 10.1021/ja0584222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bodenhausen G, Freeman R, Niedermeyer R, Turner DL. Double fourier transformation in high-resolution NMR. J Magn Reson. 1977;26:133–164. [Google Scholar]
- 31.Sibisi S. Two-dimensional reconstructions from one-dimensional data by maximum entropy. Nature. 1983;301:134–136. [Google Scholar]
- 32.Welch PD. The use of fast Fourier transforms for the estimation of power spectra: A method based on time averaging over short modified periodograms. IEEE Transactions on Audio and Electroacoustics. 1967;15:70–73. [Google Scholar]
- 33.Högbom JA. Aperture synthesis with a nonregular distribution of interferometer baselines. Astron Astrophys Suppl. 1974;15:417–424. [Google Scholar]
- 34.Rubin D, Bodenhausen G. Natural abundance N-15 NMR by enhanced heteronuclear spectroscopy. Chem Phys Lett. 1980;69:185–189. [Google Scholar]
- 35.Kay LE, Ikura M, Tschudin R, Bax A. Three-dimensional triple-resonance NMR spectroscopy of isotopically enriched proteins. J Magn Reson. 1990;89:496–514. doi: 10.1016/j.jmr.2011.09.004. [DOI] [PubMed] [Google Scholar]
- 36.Bax A, Freeman R. Investigation of complex networks of spin-spin coupling by two-dimensional NMR. J Magn Reson. 1981;44:542–561. [Google Scholar]
- 37.Powers R, Gronenborn AM, Clore GM, Bax A. Three-dimensional triple-resonance NMR of C-13/N-15-enriched proteins using constant-time evolution. J Magn Reson. 1991;94:209–213. [Google Scholar]
- 38.Sattler M, Schleucher J, Griesinger C. Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients. Prog Nucl Mag Res Sp. 1999;34:93–158. [Google Scholar]
- 39.Smith MA, Hu H, Shaka AJ. Improved broadband inversion performance for NMR in liquids. J Magn Reson. 2001;151:269–283. [Google Scholar]
- 40.Keppetipola S, Kudlicki W, Nguyen BD, Meng X, Donovan K, Shaka AJ. From gene to HSQC in under five hours: high-throughput NMR proteomics. J Am Chem Soc. 2006;128:4508–4509. doi: 10.1021/ja0580791. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.