Bayesian Analysis of Mass Spectrometry Proteomics Data using Wavelet Based Functional Mixed Models

Abstract

In this paper, we analyze MALDI-TOF mass spectrometry proteomic data using Bayesian wavelet-based functional mixed models. By modeling mass spectra as functions, this approach avoids reliance on peak detection methods. The flexibility of this framework in modeling non-parametric fixed and random effect functions enables it to model the effects of multiple factors simultaneously, allowing one to perform inference on multiple factors of interest using the same model fit, while adjusting for clinical or experimental covariates that may affect both the intensities and locations of peaks in the spectra. From the model output, we identify spectral regions that are differentially expressed across experimental conditions, while controlling the Bayesian FDR, in a way that takes both statistical and clinical significance into account. We apply this method to two cancer studies.

1 Introduction

Proteomic methods simultaneously detect and measure the expression of hundreds or thousands of proteins present in a biological sample, and are gaining increased attention in biomedical research. One popular proteomic method is matrix assisted laser desorption and ionization, time-of-flight mass spectrometry (MALDI-TOF).

In a MALDI-TOF experiment, a biological sample of interest is first mixed with an energy-absorbing matrix substance, and the mixture is placed on a steel plate. A commonly used variant of MALDI-TOF, called surface enhanced laser desorption and ionization (SELDI-TOF), incorporates additional chemistry on the surface of the metal plate to bind specific classes of proteins. The plate is then placed into a vacuum chamber, where a laser strikes the plate, desorbing ionized peptides from the sample. An electric field accelerates the particles into a potential free flight tube through which they travel at a constant velocity until striking a detector plate.

The detector plate records the abundance of particles striking it over a series of short, fixed intervals of time indexed by t = (t₁,…,t_T), yielding the proteomic spectrum y(t). Using basic physics principles, a quadratic transformation can be used to map the time axis t to a set of corresponding mass-to-charge ratios (m/z) x. Each spectrum is characterized by numerous peaks, which correspond to proteins or protein fragments (polypeptides) present in the sample. Depending on the proteomic makeup of the sample, proteins may also be manifest as infection points on the shoulders of large peaks. Since most ions have equal charges (+1), the value of spectrum y(x) at a peak is a rough measure of the abundance of some molecule in the sample having a molecular mass of x Daltons. The first column of Figure 1 contains two raw spectra from a MALDI-TOF instrument. In this paper, we consider two example data sets from cancer studies conducted at the University of Texas MD Anderson Cancer Center.

Figure 1. Sample Spectra.

The first column contains raw MALDI-TOF spectra from normal and pancreatic cancer patients, respectively, from the example data set. The second column shows the same spectra after preprocessing by baseline correction, normalization, and denoising. The final column contains normal and pancreatic cancer spectra randomly drawn from the posterior predictive distribution based on fitting the wavelet-based functional mixed model to the example data set. Note that the model does a good job of generating MALDI-TOF-like functions.

Pancreatic Cancer Experiment

In this study, blood serum was taken from 139 pancreatic cancer patients and 117 healthy controls. The blood serum was fractionated using 25% acetonitrile elutions optimized using myoglobin, then run on a MALDI-TOF instrument to obtain a proteomic spectrum for each sample. For this analysis, we consider the region of the spectra between x = 4,000 and 40,000 Daltons, containing 12,096 observations per spectrum. These 256 samples were run in four different blocks over a period of several months. More specifics of the experiment can be found in Koomen, et al. (2005). Our primary goal is to identify regions of the spectra that are differentially expressed between pancreatic cancer patients and healthy controls, regions corresponding to proteins that may serve as blood serum biomarkers of pancreatic cancer.

Some recent case studies (Baggerly et al. 2003, 2004, Sorace and Zhan 2004, Hu, et al. 2005, Coombes, et al. 2005a, Villanueva, et al. 2005, Conrads and Veenstra 2005) have demonstrated that MALDI-TOF instruments can be very sensitive to experimental conditions, even varying over time within the same laboratory. These differences can manifest in systematic changes in both the intensities and locations of the peaks (i.e. both the y and x axes), and are sometimes larger in magnitude than the biological effects of interest. Thus, it is important for us to adequately model the block effects if we are to properly analyze these data.

Organ-by-Cell Line Experiment

In this study, a tumor from one of two cancer cell lines was implanted into either the brain or lungs of 16 nude mice. The cell lines were A375P, a human melanoma cancer cell line with low metastatic potential, and PC3MM2, a highly metastatic human prostate cancer cell line. After a period of time, blood serum was extracted and then placed on a SELDI chip. This chip was run on the SELDI-TOF instrument twice, once using a low laser intensity and the other using a high laser intensity. This resulted in a total of 32 spectra, two per mouse. Here, we considered the part of the spectrum between x = 2,000 and 14,000 Daltons, a range that included 7,985 observations per spectrum.

Our primary goals are to assess whether differential protein expression, if present, is more tightly coupled to the host organ site or to the donor cell line type, and to identify regions of the spectra differentially expressed by organ site, by cell line, and/or their interaction. Typically, spectra from different laser intensities are analyzed separately, which is inefficient since spectra from both laser intensities contain information on the same proteins. We want to perform these analyses combining information across the two laser intensities, requiring us to model an effect of laser intensity on both the location (x axis) and intensity (y axis) of the peaks, and to account for correlation between spectra obtained from the same mouse.

It is common to use a two-step approach to analyze mass spectrometry data (Baggerly, et al. 2003, Yasui, et al. 2003, Coombes, et al. 2003, 2005b, Morris, et al. 2005c). First, some type of feature detection algorithm is applied to identify peaks in the spectra. A quantification is then obtained for each peak and each spectrum, e.g., by taking the intensity at a local maximum or computing the area under the peak. Assuming there are p peaks and N spectra, this results in a p × N matrix of protein expression levels that is somewhat analogous to the matrix of mRNA expression levels obtained after preprocessing microarray data. Second, this matrix is analyzed using methods similar to those used for microarrays to identify peaks differentially expressed across experimental conditions.

This two-step approach is intuitive since it focuses on the peaks, the most scientifically relevant features of the spectra, and convenient, since it can borrow from a wide array of available methods developed for microarrays. However, it also has disadvantages. First, important information can be lost in the reduction from the full spectrum to the set of detected peaks. Since group comparisons are only performed after peak detection, this approach will miss important differences in low intensity peaks or on shoulders of peaks whenever the peak detection algorithm fails to detect them. Second, this approach affords no natural way to account for experimental effects that impact both the x and y axes of the spectra.

An alternative to the two-step approach described above is to model the spectra as functions, in the spirit of functional data analysis (Ramsay and Silverman 1997). Billheimer (2005) took this approach, and this is the approach we take in this paper. Mass spectra are irregular functions with many peaks, and so require flexible modeling and spatially adaptive regularization to represent accurately. Our work is based on the Bayesian implementation of the wavelet-based functional mixed model introduced by Morris and Carroll (2006), which involves a generalization of the linear mixed model equation to the setting of potentially irregular functional data. In modeling the entire spectrum, this method has the potential to identify differences at locations missed by peak detection algorithms. Further, the method's flexible nonparametric representation of the fixed and random effects allows it to model the functional effects of a number of factors simultaneously, including factors of interest as well as nuisance factors related to the experimental design. As we will demonstrate, these nonparametrically modeled effects can account for differences on both the x and y axes of the spectra, allowing data to be combined across laser intensities, blocks, or other experimental factors. The output of the method can be used to compute posterior probabilities to identify regions of interest within the spectra that take both statistical and practical significance into account, while controlling the Bayesian false discovery rate (FDR) at a specified level.

The remainder of the paper is organized as follows. In Section 2, we describe some preprocessing steps that must be performed before analyzing MALDI-TOF data. Section 3 describes the functional mixed model upon which our method is based, and explains how model specification should proceed for MALDI-TOF data. In Section 4, we introduce wavelets, describe our Bayesian wavelet-based method for fitting the functional mixed model, and explain how to use its output to identify significant regions of the spectra. We present results from analysis of the example data sets in Section 5, and conclude with a discussion of the strengths and weaknesses of this approach in Section 6.

2 Preprocessing MALDI-TOF Data

A number of preprocessing steps must be performed before modeling MALDI-TOF or SELDI-TOF data, regardless of the ultimate approach used for inference. It has been shown that inadequate or ineffective preprocessing can make it difficult to extract meaningful biological information from the data (Sorace and Zhan, 2003; Baggerly et al., 2003, 2004). These steps include baseline correction, normalization, denoising, and transformation. The baseline, frequently seen in MALDI-TOF and SELDI-TOF spectra, is a smooth underlying function that is thought to be largely due to a large cloud of particles striking the detector in the early part of the experiment (Malyarenko, et al. 2004). This baseline artifact must be removed. Normalization refers to a constant multiplicative factor that is used to adjust for spectrum-specific factors, for example to adjust for different amounts of total protein ionized and desorbed from the sample. Denoising is used to remove white noise, which is largely due to electronic noise from the detector, from the spectrum. In recent years, various methods have been proposed to deal with these issues. Here, we use the methods described by Coombes, et al. (2005b). The first two columns of Figure 1 contain a raw spectrum and corresponding preprocessed MALDI spectrum from a cancer sample and a control sample, and demonstrate the effects of preprocessing.

It is often useful to transform the spectral intensities in order to reduce the skewness in their distribution. Some options that appear to work well include the log transformation and the cube root transformation (Coombes, et al. 2005b, Billheimer 2005). Here, we choose the log₂ transformation since it leads to nice interpretations in terms of fold change. For example, a difference of one in this scale corresponds to a two-fold increase in intensity.

The presence of zero intensities makes it necessary to add a small positive constant ∈ to each intensity before taking the log. This constant shrinks any fold-change estimates towards 1, with stronger shrinkage at lower intensities. See the unpublished document at http://biostatistics.mdanderson.org/Morris/papers.html for details of this shrinkage and an elicitation procedure for ∈. Using this procedure, we choose ∈ = 0.25, which guarantees that given a fold-change difference of 2 at spectral locations with intensities of at least 0.10, the fold-change estimate will be no less than 1.8, and at spectral intensities of 1.00 or more, the fold-change estimate will be no less than 1.975. Effectively, this choice leads to very little shrinkage in regions of the spectra surrounding the true protein peaks, but reduces the possibility that spurious differences will be detected at very low intensities because of the log scale.

3 Functional Mixed Models

Suppose we observe N functions Y_i(t),i = 1,…,n, all defined on the closed interval Ƭ ∈ ℜ¹. In MALDI-TOF data, these functions are the preprocessed, log-transformed spectra on the time axis t. A functional mixed model for these data is given by

$$Y_i(t)={\displaystyle \sum _{j=1}^p{X}_{ij}{B}_j(t)+{\displaystyle \sum _{k=1}^m{Z}_{ik}{U}_k(t)+E_i(t),}}$$ (1)

where X_ij are covariates, B_j(t) are functional fixed effects, Z_ik are elements of the design matrix for functional random effects U_k(t), and E_i(t) are residual error processes. We assume that U_k(t) are independent and identically distributed (iid) mean-zero Gaussian processes with covariance surface Q(t₁, t₂), and E_i(t) are iid mean-zero Gaussian processes with covariance surface S(t₁, t₂), with U_k(t) and E_i(t) assumed to be independent. The matrix Q is the covariance function for the random effect functions U_k(t),k = 1,…,m, and S is the covariance function for the residual error processes for the N curves, after conditioning on the fixed and random effects. One may allow different strata h = 1,…,H to have their own covariance matrices Q_h and S_h by splitting the random effect functions and residual error processes into blocks. This model is a special case of the one discussed by Morris and Carroll (2006), and is also like the functional mixed model introduced by Guo (2002).

Covariates {X_.j,j = 1,…,p}, discrete or continuous, are specified for any factors we want to model. Each functional coefficient β_j(t) describes the effect of the corresponding factor at location t of the spectrum. The covariates can include a column of 1's for an overall mean spectrum, continuous or discrete variables of interest, clinical or experimental covariates for which one would like to adjust, and any interactions among these factors. As in linear mixed models, absent constraints one must take care in parameterizing the X_.j so the resulting design matrix X = (X_.1,…,X_.p) has full column rank.

When the spectra are not iid, functional random effects provide a flexible mechanism for modeling correlation among spectra. For example, individual-level random effect functions can be specified when multiple spectra are obtained from the same individual, and additional random effect functions can be specified for other clustering units such as blocks or laboratories when the spectra are obtained over a long period of time or at many different locations. The covariance matrices Q and S can be allowed to vary by some stratification factor, for example to allow the spectra from pancreatic cancer patients and healthy controls to have different covariance structures.

Suppose all observed functions are sampled on the same equally spaced grid t = (t_l; l = 1,…,T) of length T. Let Y be the n × T matrix containing the observed functions on the grid, with each row containing one observed spectrum on the grid t. A discrete, matrix-based version of this mixed model can be written as

$$Y=XB+ZU+E.$$ (2)

The matrix X is an n × p design matrix of covariates; B is a p × T matrix whose rows contain the corresponding fixed effect functions on the grid t. B_jl denotes the effect of the covariate in column j of X on the response at time t_l. The matrix U is an m × T matrix whose rows contain random effect functions on the grid t, and Z is the corresponding n × m design matrix. Each row of the n × T matrix E contains the residual error process for the corresponding observed spectrum. We assume that the rows of U are iid MVN(0,Q) and the rows of E are iid MVN(0, S), independent of U, with Q and S being T × T covariance matrices that are discrete evaluations of the covariance surfaces in (1) on the grid.

Note that this model places no restrictions on the form of the fixed or random effect functions, which is important for MALDI-TOF data since we expect their true form should be very irregular and spiky. Although their high dimensionality precludes unstructured representation, it is also important to allow flexibility in the forms of Q and S, since irregular and spiky curve-to-curve deviations imply irregularity in these matrices, as well.

Guo (2002) introduced a smoothing spline representation of this model in which the matrices Q and S are assumed to follow a particular fixed covariance structure based on the reproducing kernel for the spline. Smoothing splines are better suited to smoother functions than those encountered in MALDI-TOF. Also, Guo (2002) makes assumptions on the Q and S matrices that are not flexible enough to accommodate the complex types of curve-to-curve deviations encountered for spiky, irregular MALDI-TOF data. Morris and Carroll (2006) introduced a Bayesian wavelet-based method for fitting this model which uses wavelet shrinkage for regularization and allows more flexible structures for Q and S, and thus is better suited for these data. The third column of Figure 1 contains spectra randomly generated from the posterior predictive distribution of this model fit to the pancreatic cancer example data set, and illustrates that the model is flexible enough to generate functional data characteristic of MALDI-TOF.

4 Analysis of MALDI-TOF Data Using Wavelet-Based Functional Mixed Models

Wavelets are useful for modeling spiky functional data as encountered in MALDI-TOF. We briefly overview wavelets and wavelet regression, describe the Bayesian wavelet-based approach for fitting the functional mixed model introduced by Morris and Carroll (2006), which extended the work of Morris, et al. (2003), and describe how to use this method to analyze MALDI-TOF data.

Wavelets and Wavelet Regression

Wavelets are families of basis functions that can be used to represent other functions, often very parsimoniously. A wavelet series approximation for a function y(t) is given by $y(t)={\displaystyle {\sum }_k{c}_{J,k}{\varphi }_{J,k}(t)+{\displaystyle {\sum }_{j=1}^J{\displaystyle {\sum }_k{d}_{j,k}{\psi }_{j,k}(t),}}}$ where J is the number of scales, and k ranges from 1 to K_j , the number of coefficients at scale j. We define the scale index j such that higher j refers to a coarser level of detail. The functions ϕ_J,k(t) and ψ_j,k(t) are father and mother wavelet basis functions that are dilations and translations of a father and mother wavelet function, ϕ(t) and ψ(t), respectively, with ϕ_j,k (t) = 2^−j/2 ϕ(2^−jt – k) and ψ_j,k(t) = 2^−j/2ψ(2^−jt – k. These wavelet coefficients comprise a location-scale decomposition of the curve, with j indexing the scales and k indexing the locations within each scale. The coefficients c_J,k,d_J,k,…,d_1,k are the wavelet coefficients. The c_J,k are called the smooth coefficients, and represent smooth behavior of the function at coarse scale J, and the d_j,k are called the detail coefficients, representing deviations of the function at scale j, where a smaller j corresponds to a finer scale. The wavelet coefficients at scale j essentially correspond to the differences of averages of 2^j−1 time units, spaced 2^j units apart. In addition, by examining the phase properties of the wavelet bases, we can associate each wavelet coefficient on each scale with a specific set of time points.

Theoretically, each coefficient can be computed by taking the inner product of the function and the corresponding wavelet basis function, although in practice more efficient approaches are used. If the function is sampled on an equally spaced grid of length T, then the coefficients may be computed using a pyramid-based algorithm implementing the discrete wavelet transform (DWT) in just O(T) operations. Applying the DWT to a row vector of observations y produces a row vector of wavelet coefficients d = (c_J,1,…,c_J,KJ, d_J,1,…,d_J,KJ, d_J-1,1,…,d₁,K₁ ). This transformation is a linear projection, so it may also be represented by matrix multiplication, d = yW′, with W′ being the DWT projection matrix. Similarly, the inverse discrete wavelet transform (IDWT) may be used to project wavelet coefficients back into the data space, and can also be represented by matrix multiplication by the IDWT projection matrix W, the transpose of the DWT projection matrix. We use the method implemented in the Matlab Wavelet Toolbox (Misiti, et al. 2000) for computing the DWT; other implementations could be used as well.

Wavelets can be used to perform nonparametric regression using the following three-step procedure. Assume y_l = f(t_l) + e_l, for an equally spaced grid {t_l, l = 1,…,T}. First, noisy data y are projected into the wavelet domain using the DWT, yielding empirical wavelet coefficients d. The coefficients are then thresholded by setting to zero any coefficients smaller in magnitude than a specified threshold, and/or nonlinearly shrunken towards zero using one of a number of possible frequentist or Bayesian approaches. This yields estimates of the true wavelet coefficients, which would be the wavelet coefficients for the regression mean function f if there were no noise. Finally, these estimates are projected back to the original data domain using the IDWT, yielding a denoised nonparametric estimate of the true function. Since most signals may be represented by a small number of wavelet coefficients, yet white noise is distributed equally among all wavelet coefficients, this procedure yields denoised function estimates that tend to retain dominant local features of the function. We refer to this property as adaptive regularization, since the function is regularized (i.e., denoised or smoothed) in a way that adapts to the characteristics of the function. This property makes the procedure useful for modeling spatially heterogeneous functions like MALDI-TOF spectra with many local features like peaks.

Wavelet-Based Modeling of Functional Mixed Model

Morris and Carroll (2006) introduced a similar three-step procedure to fit the functional mixed model discussed in Section 3. First, the DWT is used to compute the wavelet coefficients for the N spectra, effectively projecting the spectra into the wavelet space. Second, a Markov chain Monte Carlo simulation is performed to obtain posterior samples of the model parameters in a wavelet-space version of the functional mixed model. Third, the IDWT is applied to the posterior samples, yielding posterior samples of the parameters in the data-space functional mixed model (2), which are then used to perform Bayesian inference. The wavelet space modeling allows parsimonious yet flexible modeling of the covariance matrices Q and S, leading to computationally efficient code and providing a natural mechanism for adaptively regularizing the random and fixed effect functions.

The projection in the first step is accomplished by applying the discrete wavelet transform (DWT) to each row of Y , yielding a matrix of wavelet coefficients D = YW′, where W′ is the DWT projection matrix. Row i of D contains the wavelet coefficients for spectrum i, with the columns corresponding to individual wavelet coefficients and double-indexed by scale j and location k. It is easy to show that the wavelet-space version of model (2) is

$$D=X{B}^{*}+Z{U}^{*}+E^{*},$$ (3)

where each row of B* = BW′ contains the wavelet coefficients corresponding to one of the fixed effect functions, each row of U* = UW′ contains the wavelet coefficients for a random effect function, and E* = EW′ contains the wavelet-space residuals. The rows of U* and E* remain independent mean-zero Gaussian distributions, but with covariance matrices Q* = WQW′ and S* = WSW′.

Motivated by the whitening property of the wavelet transform, many wavelet regression methods in the single-function setting assume that the wavelet coefficients for a given function are mutually independent. In this context, this corresponds to making Q* and S* diagonal matrices. Allowing the variance components to differ across both wavelet scale j and location k yields Q* = diag(q_jk) and S* = diag(s_jk). This assumption reduces the dimensionality of Q and S from T(T + 1)/2 to T, while still accommodating a reasonably wide range of nonstationary within-profile covariance structures for both the random effects and residual error processes. For example, it allows heteroscedasticity and differing degrees of smoothness for different regions of the curves, which are important characteristics of these matrices for MALDI-TOF spectra. Figure 1 in Morris and Carroll (2006) illustrates this point.

MCMC For Fitting the Model

Next, a Markov chain Monte Carlo scheme is used to generate posterior samples for quantities of model (3). We use vague proper priors for the variance components and independent mixture priors for the elements of B*. Specifically, the prior for $B_{ijk,}^{*}$, the wavelet coefficient at scale j and location k for fixed effect function i, is a spike-slab prior given by $B_{ijk}^{*}={\gamma }_{ijk}$ Normal(0, τ_ij)+(1−γ_ijk)δ₀, with γ_ijk ~ Bernoulli(π_ij) and δ₀ being a point mass at zero. This prior is commonly used in Bayesian implementations of wavelet regression, including those by Clyde, Parmigiani and Vidakovic (1998) and Abramovich, Sapatinas, and Silverman (1998). Use of this mixture prior causes the posterior mean estimates of the $B_{ijk}^{*}$ to be nonlinearly shrunken towards zero, which results in adaptively regularized estimates of the fixed effect functions. The parameters τ_ij and π_ij are regularization parameters that determine the relative trade-off of variance and bias in the nonparametric estimation. They may either be prespecified or estimated from the data using an empirical Bayes method; see Morris and Carroll (2006) for details.

There are three major steps in the MCMC scheme. Let Ω be the set of all covariance parameters indexing the matrices Q* and S*. The first step is a series of Gibbs steps to sample from the distribution of the fixed effect functions' wavelet coefficients conditional on the variance components and the data, f(B*|Ω,D), which is a mixture of a point mass at zero and a Gaussian distribution. See Morris and Carroll (2006) for the expressions for the mixing parameters, means, and variances of these distributions. The second step is to sample from the distribution of the variance components conditional on the fixed effects and data, f(Ω|B*,D). We accomplish this using a series of random walk Metropolis-Hastings steps, one for every combination of (j, k). We estimate each proposal variance from the data by multiplying an estimate of the variance of the MLE by 1.5. An automatic procedure for selecting the proposal variances was necessary in order for our MCMC scheme to be automated and thus computationally feasible to implement in this very high-dimensional, highly-parameterized setting. Note that we work with the marginalized likelihood with the random effects U* integrated out when we update the fixed effects B* and variance components Ω. This greatly improves the computational efficiency and convergence properties of the sampler over a simple Gibbs sampler that also conditions on the random effects. The stationary distribution for these first two steps is f(B*,Ω|D). The third step is a series of Gibbs steps to update the random effects' wavelet coefficients from their complete conditional distribution, f(U*|B*,Ω,D), which is a Gaussian distribution. Note that this step is optional, and only necessary if one is specifically interested in estimating the random effect functions.

Posterior samples for each fixed effect function, $\{{\mathbf{B}}_i^{(g)},g=1,\dots ,G\}$, on the grid t are then obtained by applying the IDWT to the posterior samples of the corresponding complete set of wavelet coefficients ${\mathbf{B}}_i^{*(g)}=[B_{i11}^{*(g)},\dots ,B_{iJ{K}_J}^{*(g)}]$. A similar approach can be used for the random effects U_i and the covariance matrices Q and S, if desired. Code to fit the wavelet-based functional mixed model is freely available at the following URL: http://biostatistics.mdanderson.org/Morris/papers.html.

Identifying Significant Regions of Spectra

Our primary goal is to identify regions of the spectra that are differentially expressed across factors of interest, which can subsequently be mapped to proteins that may serve as useful biomarkers. In microarrays, two classical approaches for handling differential expression are (i) identify all genes with a fold-change difference of at least δ and (ii) identify genes that differ significantly across treatment groups according to a statistical hypothesis test. Option (i) is intuitive to many researchers but lacks statistical rigor since it ignores the variability in the data, and option (ii) only focuses on statistical significance, ignoring practical significance, since it is typically based on a null hypothesis of equality. In the present MALDI-TOF context, we identify differentially expressed regions of the spectra in a way that considers both statistical and practical significance.

Suppose we are interested in identifying biomarkers that have at least a δ-fold intensity change between treatment groups. Given posterior samples of the corresponding fixed effect function $\{{\mathbf{B}}_i^{(g)},g=1,\dots ,G\}$ , we compute the pointwise posterior probabilities of at least a δ-fold intensity change as $p_{il}=\mathrm{Pr}\{|{\mathbf{B}}_i(t_l)|>{\text{log}}_2(\delta )|Y\}\approx G^{-1}{\displaystyle {\sum }_{g=1}^{G}I\{|{\mathbf{B}}_i^{(g)}(t_l)|>}{\text{log}}_2(\delta )\}$ for (t_l, l = 1,…,T). We replace any p_il = 1 with 1−(2*G)⁻¹. These posterior probabilities can be also computed for any contrast involving the fixed effect functions, $A^{(g)}={\displaystyle {\sum }_{i=1}^p{C}_i{\mathbf{B}}_i^{(g)}}$, or similar posterior probabilities can be computed for linear combinations of spectral locations, e.g. if one wanted to detect peaks and look at areas under peaks.

Given a choice of α, we then flag the set of locations ψ_i = {t_l : p_il > ϕ_α} as significant spectral regions for factor i. In order to obtain ϕ_α;, we first sort {p_il, l = 1,…,T} in descending order to obtain {p(_l),l = 1,…,T}. Then ϕα = p(λ), where $\lambda ={\text{max}[l}^{*}:{\displaystyle {\sum }_{l=1}^{l^{*}}\{1-p_{(l)}\}\le \alpha ]}$. The threshold ϕα is a cutpoint on the posterior probabilities that controls the expected Bayesian FDR at level α, in the sense that on average we expect ≤ 100α% of the locations in the set ψ_i to have a true δ-fold difference in expression, as estimated by the wavelet-based functional mixed model. That is, if L=length(ψ_i), then L⁻¹ Σ_tl∈ψ_i Pr{|B_i(t_l)| ≤ log₂(δ)|Y } ≤ α. If p* factors are to be investigated simultaneously, it is possible to either use one common threshold ϕα or separate thresholds for each factor, {ϕ_I,α, i = 1,…,p*}. This use of Bayesian FDR is similar in spirit to the approach used by Newton, et al. (2004).

Peak Detection

While it is unnecessary to perform peak detection in this context, some people may want to restrict attention to the peaks in the data. Morris, et al. (2005) describe a peak detection approach and demonstrate that performing peak detection on the mean spectrum results in greater sensitivity and specificity than the usual approach of performing peak detection on the individual spectra. Since the mean spectrum is easily obtainable from the functional mixed model either as a fixed effect function or a linear combination of fixed effect functions, it is easy to adapt the procedure described in that paper to detect and quantify peaks in this setting, if desired. This peak detection can be done as a postprocessing step after the functional mixed modeling. The posterior probabilities of differential expression can then be computed for each peak, and a threshold of significance determined using the procedure described above.

5 Analysis of Example Data

For both examples, we modeled the spectra on the time scale t but plotted results on the biologically meaningful mass-per-unit-charge scale (m/z, x). In our wavelet-space modeling, we chose the Daubechies wavelet with vanishing 4^th moments and performed the DWT down to J = 10 and J = 9 levels for two examples, respectively. Other wavelet bases were examined and yielded equivalent results. We used a modified empirical Bayes procedure (Morris and Carroll, 2006) to estimate the shrinkage hyperparameters π_ij and τ_ij,i = 1,…,5,j = 1,…,10, constraining τ ≥ 10 so there would be less bias in the estimation of peak heights, which we believed to be important in this context. We did almost no shrinkage (π ≈ 1, τ = 1000) for the highest wavelet level or the scaling coefficients. For each example, we ran 10 parallel chains, each consisting of 1000 iterations after a burn-in of 1000, and we kept every 5 for a total of G = 2000 MCMC samples for our analyses. All chains appear to have converged, as indicated by the trace plots available as supplementary material on http://biostatistics.mdanderson.org/Morris/papers.html. In the pancreatic cancer example, the median and 99% credible interval for the Metropolis Hastings acceptance probabilities across the roughly 12,000 covariance parameters were 0.22 and (0.11,0.31), respectively, and for the organ-by-cell line example with roughly 8,000 covariance parameters, they were 0.17 and (0.05, 0.51), respectively.

We explored the possible identities of the flagged peaks by running the estimated m/z values of the corresponding peaks through TagIdent, a searchable database (available at http://us.expasy.org/tools/tagident.html) that contains the molecular masses and pH for proteins observed in various species. For the organ by cell line example, we searched for proteins emanating from both the source (human) and the host (mouse) whose molecular masses were within the estimated mass accuracy (0.3%) of the instrument from the nearest peak or most significant location of each flagged region. This only gives an educated guess at what the protein identity of the peak could be; it is necessary to perform an additional MS/MS experiment in order to rigorously validate the protein identity.

Pancreatic Cancer Example

The design matrix for this data set of N = 256 spectra was chosen to have p = 5 columns, the first column indicating cancer (=1) or normal (= −1) status, and corresponding to a functional cancer main effect B₁(t) describing the difference between the mean log₂ intensities of cancer and normal spectra at time t. The final four columns indicate the time blocks, and correspond to mean spectra for the respective time blocks (B_i(t),i = 2,…,5). The block effects between block i and i′ can be constructed by B_i(t) − B_i′(t). No functional random effects were specified. The residual covariance matrix S was allowed to vary across cancer status.

The top two panels of Figure 2 contain posterior means and 95% credible intervals for the cancer main effect function and the corresponding pointwise posterior probabilities of at least 1.5-fold expression. The dots in the plots correspond to the 227 peaks detected on the posterior mean for the overall mean spectrum $\widehat{\mu }(t)={(4G)}^{-1}{\displaystyle {\sum }_{g=1}^G{\displaystyle {\sum }_{i=2}^5{B}_i^{(g)}(t)}}$. The horizontal line indicates the threshold on the posterior probabilities ϕ₁₀ = 0.595 corresponding to an expected Bayesian FDR at 0.10. There were a total of 506 spectral locations contained within 16 contiguous regions that were flagged as significant. Analyzing the peaks, we find 26/227 were flagged as significant. A list containing the significant regions and peaks, and a plot of the overall mean spectrum with detected peaks are available as supplementary material at http://biostatistics.mdanderson.org/Morris/papers.html.

Figure 2. Fixed Effect Curves.

(a) and (c): Posterior mean and 95% pointwise posterior credible bands for cancer main effect, pancreatic cancer example, and organ main effect, organ-by-cell-line example, respectively. The green lines indicate 1.5-fold and 2.0-fold differences in the two examples, respectively, and the dots indicate peaks detected using the average spectrum. (b) and (d): Pointwise posterior probabilities of (b) 1.5-fold difference in cancer/normal in pancreatic cancer example and (d) 2.0-fold difference in brain/lung in organ-by-cell-line example. The red dots indicate detected peaks, and the green lines mark the flagged regions. The yellow dotted lines indicate the threshold for flagging a location as significant, controlling the expected Bayesian FDR to be less than 0.10 and 0.05 in the two examples, respectively.

The most significant effects were observed in the regions (i) (17230D, 17311D), (ii) (8730D, 8787D), (iii) (11314D, 12037D), with maximum posterior mean fold-change differences of 1/2.46, 1/2.20, 2.77, respectively, between cancers and normals. The maximum fold-change differences for all three of these regions were located at peaks. These were also all identified in Koomen, et al. (2005). In that paper, they reported MS/MS results confirming the identity of (i) as a fragment of apolipoprotein A-I or apolipoprotein glutamine-I, and the cluster of 7 peaks in (iii) as serum amyloid A. Based on TagIdent, region (ii) may correspond to complement C4-A or C4-B(precursor), 8764.07D, mediators of inflammatory processes that circulate in the blood.

One peak (4284D) found to be statistically significant and highlighted by Koomen, et al. (2005) had a very small fold-change estimate (1.22), and was not flagged by our analysis. Also interesting was the region (8671D, 8684D) that was on the upslope of a very abundant peak at 8688D. The peak itself was not flagged (p=0.186), but this region was, with a a maximum fold-change of 1/1.70 at 8679 (p=0.968). It is possible that this result is driven by protein at 8679D whose peak is not visible because of its proximity to the extremely abundant peak at 8688D. An MS/MS experiment would have to be done to investigate this possibility.

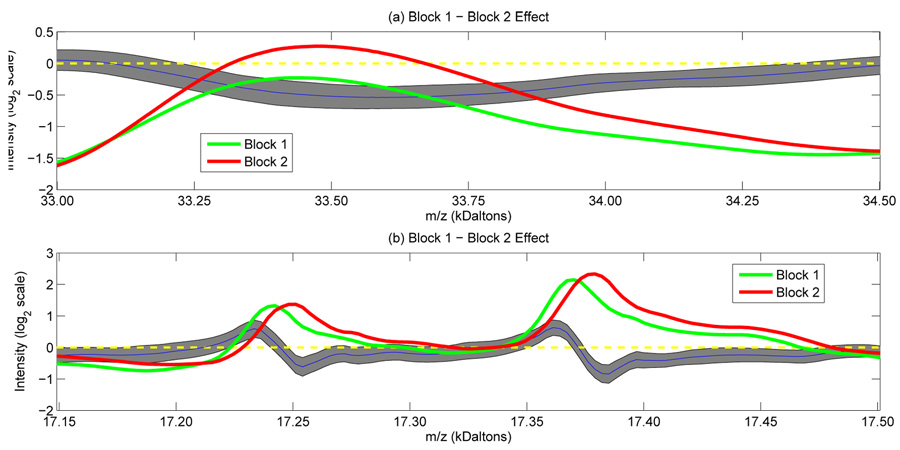
Plots of the block effects (in supplementary material) demonstrate that they affect both the location and intensity of peaks, and are of similar magnitude to the cancer main effect. Figure 3 illustrates the block effect (block 1 – block 2) in the neighborhood of some prominent peaks. The nonparametrically modeled block effects were able to capture both shifts in intensity {Figure 3(a)} and shifts in location {Figure 3(b)}. Note that changes in the x axis appear as pulses in the nonparametric block effects. These features served to calibrate the x and y axes across blocks so they were comparable, allowing spectra from different blocks to be pooled for a combined analysis.

Figure 3. Block Effects.

Plot of the mean spectra for blocks 1 (green line) and 2 (red line), along with the posterior mean and 95% pointwise posterior bounds for the block 1 – block 2 effect (blue and black lines) near (a) the peak at 33,482 and (b) the twin peaks at 17,245 and 17,376. (a) illustrates that the nonparametric functional effect can model changes in intensity, and (b) shows that the pulse-like features of the nonparametric effect account for systematic shifts in location.

Organ-by-Cell-Line Example

The design matrix for this set of N = 32 spectra had p = 5 columns. We used a cell means model for the factorial design, so the first four columns contained indicators of the 4 organ-by-cell-line groups with corresponding mean functions B_i(t), i = 1,…,4, ordered brain-A375P, brain-PC3MM2, lung-A375P, and lung-PC3MM2. From these, the overall mean spectrum 0.25 ${\displaystyle {\sum }_{i=1}^4{B}_i(t)}$, the organ main effect function B₁(t) + B₂(t) − B₃(t) − B₄(t), cell-line main effect function B₁(t)−B₂(t)+B₃(t)−B₄(t), and the organ-by-cell line interaction function B_t(t) − B₂(t) − B₃(t) + B₄(t) were constructed. Column 5 indicated whether a low (−1) or high (1) laser intensity setting was used in generating the given spectrum. The Z matrix had m = 16 columns, with Z_ij = 1 if spectrum i came from animal j, with corresponding mouse-level random effect functions U_k(t), k = 1,…,16.

The bottom two panels of Figure 2 contain the posterior means and 95% credible intervals for the organ main effect function and corresponding pointwise posterior probabilities of at least 2-fold difference, respectively. The threshold on the posterior probabilities based on setting the expected Bayesian FDR of 0.05 was ϕ₀₅ = 0.874. Equivalent plots for the cell line and interaction effects are available as supplementary material. We flagged 1393/7985 of the spectral locations in 41 contiguous regions for the organ main effect, 798/7985 in 25 contiguous regions for the cell line main effect, and 594/7985 in 18 contiguous regions for the organ-by-cell line interaction effect. Of the 101 detected peaks, we flagged 40 as significant, 13 for organ alone, 13 for cell-line, 1 for both organ and cell-line, and 13 for the interaction. Table 1 contains information for the top 10 most significant regions, all of which contained locations with posterior probabilities p_l > 0.9995. The complete list of significant regions and peaks is available as supplementary material.

Table 1.

Selected flagged regions from organ by cell line example. Location of selected region (in Daltons per coulomb) is given, along with which effect was deemed significant, estimated maximum fold change difference within the region, and a description of the effect. These effects comprise all those with pl > 0.9995.

Region	Effect type	max FC	Comment
3866.3–3971.3	organ	1/93.9	Only in brain-injected mice
3658.3–3739.0	organ	1/118.5	Only in brain-injected mice
9902.6–10044.0	organ	46.1	Only in lung-injected mice
4762.2–4874.8	interaction	1/13.7	PC3MM2>A375P, especially brain
4748.2–4868.3	cell-line	1/39.7	PC3MM2>A375P
3743.4-3565.3	organ	1/35.0	Brain>Lung
4952.6–5008.2	organ	1/32.8	Brain>Lung
4519.9–4697.5	organ	27.5	Lung>Brain
5051.3–5093.3	cell-line	1/23.5	PC3MM2>A375P
3993.4–4061.3	organ	21.0	Lung>Brain (on upslope of peak)
10912–11269	interaction	1/16.4	Brain>Lung for A375P only

The strongest differences observed were between organ groups. The largest estimated fold changes were observed in the regions [3658.3, 3739] and [3866.3, 3971.3]. These regions each contain a peak that is strongly present in all mice with tumors injected into their brains, but absent from those injected in their lungs. The region [3866.3, 3971.3] is represented in figure 4(a) and (c). This region may correspond to a calcitonin gene-related peptide II precursor (CGRP-II, 3882.34 D), a peptide in the mouse proteome that dilates blood vessels in the brain and has been observed to be abundant in the central nervous system (http://www.expasy.org/uniprot/Q99MP3). The region [3658.3, 3739.0] may correspond to a precursor of amyloid beta A4 protein in the mouse proteome (3717.10 D) that "functions as a cell surface receptor and performs physiological functions on the surface of neurons relevant to neurite growth, neuronal adhesion and axonogenesis. Involved in cell mobility and transcription regulation through protein-protein interactions " (http://www.expasy.org/uniprot/P12023). Another flagged region [10912,11269] may also correspond to a precursor of the same protein (11050.64 D). These results may represent important responses within the hosts to the tumor implantation in their brains.

Figure 4. Select Results.

(a) and (b) Plot of organ main effect function in selected regions. The green and red lines are the organ-specific mean spectra on the untransformed intensity scale, the blue and black lines are the posterior mean and pointwise 95% posterior bounds for the organ main effect on the log₂ intensity scale. The yellow dotted line at 0 and the cyan dotted lines at +/−1 are provided for reference. (c) and (d) Pointwise posterior probabilities of 2-fold difference in intensity. The red dots indicate peaks detected in the mean spectrum, and the yellow dotted line indicates the threshold on pointwise posterior probabilities chosen so the expected Bayesian FDR<0.05. The green lines in the plot indicate regions flagged as significant.

There were some significant effects that would not have been detected had we restricted our attention to the peaks. The significant organ effect in the region [3993.4, 4061.3], with maximum fold change difference of 21.0, is on the upslope of a peak, but the peak value itself was not significant. Also, the region [7618.3, 7650.5] was flagged for an organ effect, being specific to brain-injected mice.

Inspection of the overall mean spectrum (see black line in Figure 4(b)) reveals that this region contains an inflection point near 7620 on the overall mean spectrum near a larger peak at 7580.1, and the peak is not differentially expressed. The protein neurogranin in the human proteome, with a molecular weight of 7618.47 Daltons, is active in synaptic development and remodeling in the brain. No peak was detected in the region [7618.3, 7650.5], so this potential discovery would not have been made had we restricted attention to the peaks.

Of the 25 regions flagged as significantly different across cell lines, 22 of them were overexpressed in the metastatic PC3MM2 cell line relative to the non-metastatic A375P cell line. Plots of the laser intensity effect (in supplementary material) reveal systematic differences between the low and high laser intensity spectra that affect both the locations and intensities of peaks. Our nonparametric laser intensity effect was able to model this difference, allowing us to pool data from both laser intensities for this analysis.

6 Discussion

We have demonstrated how to use the Bayesian wavelet-based functional mixed model to model MALDI-TOF proteomics data. This method appears well suited to this context, for several reasons: the functional mixed model is very flexible; it is able to simultaneously model nonparametric functional effects for many covariates simultaneously, both factors of interest and nuisance factors such as block effects. The nonparametric functional effects for nuisance factors are flexible enough to account for systematic changes in both the location and intensity of peaks in the spectra. Further, the random effect functions can be used to model correlation among spectra that might be induced by the experimental design. The wavelet-based modeling approach works well for modeling functional data with many local features like MALDI-TOF peaks since it results in adaptive regularization of the fixed effect functions, avoids attenuation of the effects at the peaks, and is reasonably flexible in modeling the between-curve covariance structures, accommodating autocovariance structures induced by peaks and heteroscedasticity allowing different between-spectrum variances for different peaks.

We applied this method to two cancer proteomic studies, and identified spectral regions that were differentially expressed and may correspond to potential biomarkers. Many of these regions contained peaks, but several would not have been found had attention been restricted to peaks alone. Another benefit of our approach is that both statistical and practical significance were considered in identifying potential biomarkers.

In the pancreatic cancer example, this method was able to model nonparametric block effects that served to calibrate the x and y axes across blocks, making spectra from the different time blocks comparable and enabling them to be pooled for a common analysis. In a similar fashion, the incorporation of the nonparametric laser intensity effect in the organ-by-cell line example allowed us to account for systematic differences in spectral intensity and peak locations between the high and low laser intensity spectra. Along with the nonparametric random effects accounting for the correlation between spectra from the same animal, this allowed us to pool data across laser intensities for a common analysis, potentially increasing our power for detecting differentially expressed proteins.

While the method is complex, it is relatively straightforward to implement using the code freely available at http://biostatistics.mdanderson.org/Morris/papers.html. The user only needs to construct a matrix Y containing the preprocessed spectral intensities for the N spectra in the study and specify the design matrices X and Z. Starting values, empirical Bayes and vague proper priors, and proposal variances are all automatically computed by the program and can be used without any user input. Default choices for wavelet basis and levels of decomposition are also automatically computed and can be used, if desired. The code provides posterior samples and summary statistics for all quantities in the functional mixed model, from which Bayesian inference can be done in a straightforward fashion. The method is computationally intensive, but the code has been optimized to be able to handle very large data sets, and parallel processing can further speed the computations when it is available. For example, on average each chain of 2000 MCMC iterations for our pancreatic cancer example with 256 spectra and 12,096 observations per spectra took under an hour to run. In our analysis, we ran 10 of these chains in parallel using Condor (http://www.cs.wisc.edu/condor), parallel processing freeware that shared the job among roughly 10 Pentium IV computers in a Windows network.

Wavelet-based functional mixed models show great promise for the analysis of MALDI-TOF proteomic data. This approach may also prove useful for analyzing data from other biomedical platforms that generate irregular functional data.