Abstract
Mathematics performance at 7 years as assessed by teachers using UK national curriculum criteria has been found to be highly heritable. For almost 3000 pairs of 7-year-old same-sex twins, we used multivariate genetic analysis to investigate the extent to which these genetic effects on mathematics performance overlap with genetic effects on reading and general intelligence (g) as predicted by the ‘generalist genes’ hypothesis. We found substantial genetic overlap between mathematics and reading (genetic correlation=0.74) and between mathematics and g (0.67). These findings support the ‘generalist genes’ hypothesis that most of the genes that contribute to individual differences in mathematics are the same genes that affect reading and g. Nonetheless, the genetic correlations are less than unity and about a third of the genetic variance on mathematics is independent of reading and g, suggesting that there are also some genes whose effects are specific to mathematics.
1. Introduction
It is hard to overestimate the importance of adequate mathematical ability in a society that requires a high degree of technical competence from its citizens. Continuous technological advances, workforce expectations, the competitive economic advantages that can be acquired from high levels of mathematical literacy, and simply the requirements of successful adult living, all drive the need to improve the standard of mathematical ability and to decrease the rate of mathematical underachievement. The importance of adequate mathematical ability is becoming increasingly recognized by society and is reflected in new government and commercial initiatives, such as Maths Year 2000 initiative and Maths@Work project, as well as reports on the importance of mathematics and assessments of current levels of numeracy (e.g. Smith, 2004).
Unfortunately, what is clear from a wide range of studies conducted in different countries is that a significant number of children demonstrate poor achievement in mathematics (Mazzocco & Myers, 2003). The prevalence of mathematical disability, defined as scoring at least 2 years below grade level in arithmetic in the presence of normal intelligence, is estimated as approximately 6% in school children (e.g. Gross-Tsur, Manor, & Shalev, 1996). This estimate is similar to the reported frequency of reading disability (Mazzocco & Myers, 2003). For this reason, the study of mathematical ability is worthy of a research effort similar in scope to that devoted to the study of reading ability. However, to date the body of research on reading ability by far exceeds that on mathematical ability.
As a result, the literature is only beginning to address the important question of how genes and environments influence mathematical ability and disability. The few twin and adoption studies of mathematics performance have reported a wide range of heritabilities from 0.20 to 0.90 (reviewed in Oliver et al., 2004). In a recent report based on the same dataset used in the present study, both mathematics ability and disability at 7 years assessed by teachers using UK National Curriculum criteria during the second year of elementary school showed genetic influence in between the extremes of previous estimates (0.65) (Oliver et al., 2004).
A ‘generalist genes’ theory of learning abilities and disabilities has recently been proposed which predicts that most genetic effects for scholastic achievement and cognitive abilities are general rather than specific (Plomin & Kovas, in press). That is, the genes that affect one area of learning, such as mathematics performance, are largely the same genes that affect other abilities, although there are some genetic effects that are specific to each ability. The main purpose of the present study is to test the ‘generalist genes’ theory in relation to mathematics performance. We used multivariate genetic analysis to assess the extent to which genetic effects on mathematics performance at 7 years of age overlap with genetic effects on reading performance and g. The same analysis indicates whether there are significant specific genetic effects on mathematics performance independent of reading and g.
Mathematics performance covaries phenotypically with reading and with g (Alarcón, Knopik, & DeFries, 2000; Hecht, Torgesen, Wagner, & Rashotte, 2001; Jordan & Oettinger Montani, 1997; Knopik & DeFries, 1999), but the etiology of this covariation remains poorly understood. Even though individual differences in mathematics, reading and g are influenced by genes, it is possible that completely different sets of genes affect each of these three domains. Multivariate genetic analysis, which addresses the etiology of the covariance between traits rather than the variance of each trait considered on its own, can estimate the extent to which the genetic factors that influence individual differences in mathematics are also involved in shaping reading and g. Multivariate genetic analysis estimates the genetic correlation that represents the extent to which genetic effects on one trait are correlated with genetic effects on another trait independent of the heritability of traits (Plomin, DeFries, McClearn, & McGuffin, 2001). That is, the genetic correlation can be high when heritability is low and vice versa. The genetic correlation can be thought of as the probability that if a gene were found to be associated with one trait, the same gene would also be associated with the other trait.
Three multivariate genetic studies addressing the issue of genetic overlap between mathematics and reading suggest substantial overlap. The first study of genetic overlap between mathematics and reading included 146 MZ and 132 DZ twin pairs from 6 to 12 years of age assessed on the Metropolitan Achievement Tests of mathematics and reading (Thompson, Detterman, & Plomin, 1991). A genetic correlation of 0.98 was reported between mathematics and reading. However, wide confidence intervals surround genetic correlations, especially in modest sample sizes as in this study, although the data presented in this 1991 report do not permit an estimate of the confidence interval. In the only other twin study of the genetic overlap between mathematics and reading, a genetic correlation of 0.47 was found in a study of 220 MZ and 135 DZ twin pairs aged from 8 to 20 years (Knopik & DeFries, 1999). In an adoption study, the genetic correlation between reading and mathematical performance was 0.80 in a parent–offspring analysis (Wadsworth, DeFries, Fulker, & Plomin, 1995a) and 0.83 in a sibling analysis (Wadsworth, DeFries, Fulker, & Plomin, 1995b). One of these studies also explored the extent to which mathematics performance overlaps genetically with g. In a report based on 319 MZ and 251 DZ twin pairs aged from 8 to 20 years, the genetic correlation between latent factors of mathematics and g was 0.95 (Alarcón et al., 2000). The same estimate was obtained in a sample selected for learning deficits. Several studies indicate that reading and g also show substantial genetic correlations (Harlaar, Hayiou-Thomas, & Plomin, 2005; Knopik & DeFries, 1999; Wainwright et al., 2004).
The only multivariate genetic study that simultaneously included mathematics, reading and a measure of g (verbal IQ only) also included phonological decoding in a study based on 196 MZ and 155 same-sex DZ twin pairs aged from 8 to 20 years (Light, DeFries, & Olson, 1998). A genetic correlation of 0.36 was found between mathematics and reading with approximately 82% of this correlation being due to genetic factors that also influence verbal IQ and phonological decoding ability. Some specific genetic influence was found for mathematics independent of reading, verbal IQ and phonological decoding.
The present study uses multivariate genetic analyses of data from a large sample of 7-year-old twins to test the ‘generalist genes’ hypothesis, which predicts that most genetic effects on mathematics performance overlap in their effects on reading and g. This is the first large multivariate genetic study to assess children of the same age when they just began their formal education in mathematics and to include g as measured by both verbal and non-verbal tests.
2. Method
2.1. Participants and procedure
Participants were part of the Twins’ Early Development Study (TEDS), a longitudinal study involving a representative sample of all twins born in England and Wales in 1994, 1995, and 1996. The twins’ language, cognitive and behavior development have been assessed by parental questionnaires at 2, 3 and 4 years of age (Trouton, Spinath, & Plomin, 2002). Data from 4737 pairs of twins born between January 1994 and August 1995 were analyzed for this study. The following exclusion criteria were used: specific medical syndromes such as Down’s syndrome and other chromosomal anomalies, cystic fibrosis, cerebral palsy, hearing loss, autism spectrum disorder, organic brain damage, extreme outliers for birth weight, gestational age, maternal alcohol consumption during pregnancy, and special care after birth. In addition, participants for this sample were selected to be white in order to control for the effect of ethnic stratification in future molecular genetic studies. After the exclusions the sample consisted of 4319 pairs of twins. Further 145 pairs of twins for whom English was not the first language spoken at home were excluded from the sample. Finally, in order to avoid confounding of the genetic results with possible sex-differences in the measured traits, only the data from same-sex twins were selected for further analyses (N =2875 pairs). The final sample consisted of 1500 pairs of MZ twins and 1375 pairs of DZ twins.
Zygosity was ascertained by parental ratings with an error rate not exceeding 5%, as validated by DNA typing (for details see Freeman et al., 2003). The representativeness of the sample against UK population data and against the participants lost due to attrition was assessed and was found satisfactory (see Harlaar, Spinath, Dale, & Plomin, 2005; Spinath, Walker, Saudino, & Plomin, submitted for publication).
2.2. Testing procedures
Informed consent was obtained in writing from all of the families who agreed to take part in the study.
2.3. Measures
2.3.1. Mathematics
Mathematical ability was measured by teachers’ assessments on UK National Curriculum (NC) Key Stage 1 criteria for mathematical attainment (QCA Key Stage 1 Handbook, 1999, 2003). The assessments were obtained by postal questionnaire during the spring semester. The teachers assessed three aspects of mathematical ability: Using and applying mathematics; Numbers; and Shapes, space and measures, using a 5-point scale based on the teacher’s knowledge of the child’s mathematics achievement over the academic year (see Oliver et al., 2004 for full details of the scale). The three scales are highly correlated—their average intercorrelation is 0.81 and a factor analysis of the three scales indicated that the principal component accounted for 87.2% of the variance (Oliver et al., 2004). Based on these findings, we created a mathematics composite mean score by summing standardized scores for the three scales.
Although it would be desirable to complement the teacher assessment scores with test scores, this was not feasible for this large sample. Nevertheless, teacher assessments have been shown to be valid measures of academic achievement, particularly for mathematics, reading and language (Hoge & Coladarci, 1989). Cross-tabulation analyses on a nationwide sample of 600,000 children indicate that agreement between NC teacher assessments of reading and scores on group-administered NC reading tests at Key Stage 1 is good (Cohen’s Kappa=0.80; Dale, Harlaar, & Plomin, in press). Indeed, teacher assessment is arguably one of the best available scores of academic ability and is free from some of the biases introduced by tests (e.g. Good & Salvia, 1988; Marks, 1990). The full NC evaluation system combines teacher-assessed performance with tasks and tests administered throughout a year that are used to inform the teachers. However, the final levels are decided by teachers, which places greater emphasis on teachers’ judgments about children’s progress throughout the year. Thus, tests provide standard “snapshots” of academic achievement throughout Key Stage, whereas the teacher assessment takes into account evidence of achievement on such tests and a range of other contexts, including that gained through discussion and observation (QCA Key Stage 1 Handbook, 1999, 2003). It is therefore possible that teacher assessments may be a more accurate indicator of performance and a greater emphasis on teacher assessment has been recently suggested (QCA Key Stage 1 Evaluation Report; Qualifications & Curriculum Authority, 2001) (see Oliver et al., 2004 for more discussion of the validity of teacher assessment).
2.3.2. Reading
The Test of Word Reading Efficiency (TOWRE, Form B; Torgesen, Wagner, & Rashotte, 1999) was administered to children over the telephone. Twins were individually assessed by telephone using test stimuli that had been mailed to families in a sealed package with separate instructions that the package should not be opened until the time of testing. The same tester, who was blind to zygosity, assessed both twins in a pair within the same test session. The TOWRE is a measure of word recognition ability comprising two subtests: Sight-word Efficiency (SWE), which assesses fluency and accuracy in sight word reading, and Phonemic Decoding Efficiency (PDE), which assesses phonemic decoding. The two subtests have been shown to correlate substantially in both telephone (Dale et al., in press) and in-person administration (Torgesen et al., 1999). The scores from the two subtests were standardized and summed.
General reading achievement was also measured by teachers’ assessments on UK National Curriculum (NC) Key Stage 1 criteria for reading attainment (QCA Key Stage 1 Handbook, 1999, 2003). These criteria are linked to the National Literacy Strategy (NLS), a statutory reading curriculum that provides literacy goals and instruction guidelines for teachers in England and Wales (DfEE, 1998). The rating scale requires teachers to rate children’s reading on a five-point scale based on their knowledge of the child’s reading achievement over the academic year (see Harlaar, Dale, & Plomin, in press, for full details of this scale). Teacher assessments were obtained by postal questionnaire during the spring semester. The validity of these ratings are supported by the findings of high agreement (r =0.69) between year-long teacher assessments of reading based on UK National Curriculum criteria, which assess diverse reading processes, and the TOWRE total score, which specifically assesses reading accuracy, for the data presented here (Dale et al., in press). Multivariate genetic analyses of the data reported here also showed substantial genetic covariance between the two ways of assessing reading ability (Harlaar, Dale et al., in press). We combined the z-scores from the composite TOWRE scores and from the teacher assessment into one composite reading score. When the teacher score were not available, only the TOWRE score was used.
2.3.3. General cognitive ability
Verbal and non-verbal cognitive measures designed to yield an index of general cognitive ability (g) were administered over the telephone using the same procedure as described in the previous section on reading. The battery included two verbal measures—Vocabulary and Similarities subtests of the Wechsler Intelligence Scale for Children (WISC-III-UK; Wechsler, 1992); and two non-verbal measures—Picture Completion subtest from the Wechsler Scale and Conceptual Grouping from the McCarthy Scales of Children’s Abilities (MCSA; McCarthy, 1972). Scores from our telephone adaptations of these standard cognitive tests have been shown to be substantially correlated with both subtest and composite scores from in-person assessments using the Stanford-Binet Intelligence Scale (Thorndike, Hagen, & Sattler, 1986) in 6- to 8-year-olds (Petrill, Rempell, Oliver, & Plomin, 2002). Total scores on each subtest were converted to z-scores relative to the whole sample and a composite g score was created based on these scores.
2.4. Analyses
2.4.1. Phenotypic analyses
Phenotypic relationships between the three composites were explored with Pearson correlation.
2.4.2. Genetic analysis
The twin method, one of the major tools of quantitative genetic research, addresses the origins of individual differences by estimating the proportion of variance that can be attributed to genetic, shared, and nonshared-environment factors (Plomin et al., 2001). In the case of complex traits that are likely to be influenced by multiple factors, the genetic component of variance refers to the influence of alleles at all gene loci that affect the trait. The similarity between twins for any particular trait can be due to a common set of genes. It may also be due to the ‘shared environment’, which refers to environmental influences that contribute to the similarity between co-twins. For example, twins experience similar conditions during gestation have the same socio-economic status, live in the same family, and usually go to the same school. These factors could reasonably be expected to increase similarity between co-twins. ‘Nonshared environment’ refers to any aspect of environmental influence that shapes a given trait in such a way as to make co-twins different from each other, including measurement error. Intuitively, such influences are likely to stem from aspects of environment that are specific to an individual, such as traumas and diseases, idiosyncratic experiences, different peers, differential treatment by the parents and teachers, and different perceptions of such influences.
Genetic influence can be estimated by comparing intraclass correlations for identical (monozygotic, MZ) twins, who are genetically identical, and fraternal (dizygotic, DZ) twins, whose genetic relatedness is on average 0.50. The relatedness for shared (common) environmental influences is assumed to be 1.0 for both MZ and DZ twin pairs who grow up in the same family because they experience similar prenatal and postnatal environments. Structural equation model fitting is a more comprehensive way of estimating variance components based on the same principles. For example, variations on the full ACE model can be used for analyses of individual differences, which apportion the phenotypic variance into genetic (A), shared environmental (C), and nonshared environmental (E) components, assuming no effects of non-additive genetics or non-random mating. The ACE parameters and their confidence intervals can be estimated by fitting the models to variance/covariance matrices using the model-fitting program Mx (Neale, 1997).
These principles can be extended to determine the etiology of the covariance between traits. In contrast to univariate quantitative genetic analysis that decomposes the variance of a single trait into genetic and environmental sources of variance, multivariate genetic analysis decomposes the covariance between traits into genetic and environmental sources of covariance (Martin & Eaves, 1977). In other words, multivariate genetic analysis assesses genetic and environmental factors responsible for the phenotypic correlation between two traits. For example, if the same genes affect different traits, a genetic correlation will be observed between the traits. Such effects of the same genes on different traits are called pleiotropy.
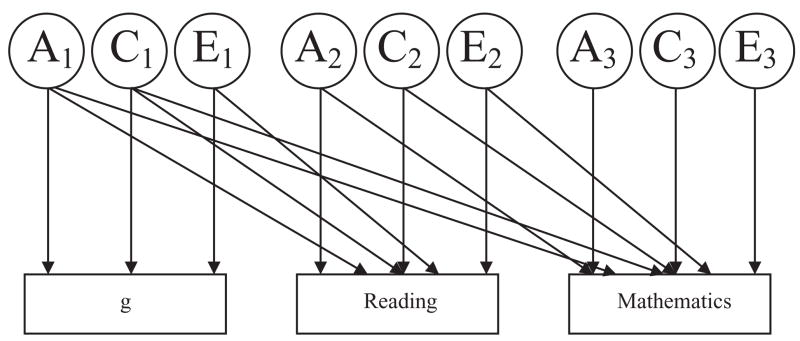
For twin studies, multivariate genetic analysis is based on cross-trait twin correlations for two or more traits. That is, one twin’s X is correlated with the co-twin’s Y. The phenotypic covariance between two traits is attributed to their genetic overlap to the extent that the MZ cross-trait twin correlation exceeds the DZ cross-trait twin correlation. Shared environmental influences are indicated to the extent that DZ twins’ correlation is more than half of the MZ correlation. As with the univariate analyses, structural equation modeling, based on the same principles, is used as a more comprehensive way of estimating the proportion of covariance. As illustrated in Fig. 1, a trivariate Cholesky decomposition model was fit to the variance–covariance matrices derived from the data to test for common and independent genetic and environmental effects on variance in mathematics, reading, and general cognitive ability. The Cholesky procedure is similar to hierarchical regression analyses in non-genetic studies, where the independent contribution of a predictor variable is assessed after accounting for its shared variance with other predictor variables. Our particular interest in the shared and specific etiology of the individual differences in mathematical ability was reflected in the order in which the variables were entered in the analysis. The order was also determined by the logical assumption that g is the most general ability of the three and is therefore likely to have shared etiology with the other two abilities to a large extent. Thus, g was entered in the analysis first, followed by reading and then mathematics (see Loehlin, 1996 for discussion of the Cholesky procedure). Mathematics was entered last so that the independent influences on this trait could be assessed. We used a three-factor model in which the first factor assessed genetic and shared and non-shared environmental influences on general cognitive ability some of which also influence reading and mathematics. The second factor represents genetic and shared and non-shared environmental influences on reading that are not shared with general cognitive ability, but are shared with mathematics. The third factor estimates genetic and shared and non-shared environmental influences unique to mathematics. The model also allowed us to estimate the proportions of the total variance attributable to genetic and environmental factors for each of the composites.
Fig. 1.
Trivariate analysis (Cholesky path model) of g, reading and mathematics at 7 years in TEDS. Full model. The three measured variables (rectangles) are g, reading, and mathematics and the latent variables (circles) represent A (additive genetic), C (common or shared environment) and E (nonshared environment) estimates. See text for more detailed explanation.
In addition we transformed the paths from the model to obtain the estimates of genetic, shared, and non-shared environmental correlations between each pair of factors. Genetic correlations index the extent to which the sum of genetic influences on one measure correlates with the sum of genetic influences on a second measure. In other words, genetic correlations indicate the extent to which individual differences in the two measures reflect the same genetic influences. We also estimated the proportion of the phenotypic covariance between X and Y that can be attributed to genetic covariance between X and Y, which is bivariate heritability, the genetic correlation weighted by the product of the square roots of the heritabilities of X and Y and divided by the phenotypic correlation between the two traits (Plomin & DeFries, 1979). Shared and nonshared environmental correlations were also estimated.
The overall fit of the model can be evaluated using three indices. The χ2 statistic, where degrees of freedom equal the number of observed correlations minus the number of estimated parameters, indicates the fit of the full model with a low value indicating good fit. However, the χ2 statistic is inflated with large sample sizes. The other two indices–Akaike’s information criterion (AIC=χ2–2df; Akaike, 1987) and the root mean square error of approximation (RMSEA)–give more interpretable estimates of fit for large samples, with lower values representing better-fitting models.
3. Results
3.1. Descriptive statistics and further exclusions
To allow for comparisons between the different measures, the three composites (mathematics, reading, and g) were separately standardized using the means and standard deviations of the entire sample (after medical and ethnic exclusions described in the method section) so that each test had zero mean and unit variance for the total sample of 8638 twins, although the means and standard deviations in the first column of Table 1 differ slightly from zero mean and unit variance after the exclusion of opposite-sex twins. The three composites have normal or near normal unimodal score distributions. Descriptive statistics for the three composites (standardized scores) are summarized in Table 1. It can be seen that MZ twins have slightly lower means than DZ twins, which may be due to greater perinatal complications of MZ twins (Lenneberg, 1967). Analysis of variance revealed a significant main effect of zygosity for all three composites favoring DZ twins. However, the effect size (η2) of zygosity is very small, accounting for less than 1% of the variance. A significant main effect of sex was found only for the reading composite, showing that girls generally performed significantly better than boys. However, this effect was also negligible, accounting for 0.2% of the variance. Sex-by-zygosity interaction was slight but significant for the mathematics and reading composites (but not g), showing that the performance of MZ male twins was the worst. It should be noted that these small significant group differences stem from the statistical power of our large sample and are unlikely to reflect any meaningful differences.
Table 1.
Means (standard deviations) and ANOVA results by sex and zygosity for the three composites
| All |
MZ |
DZ |
Males |
Females |
ANOVA |
|||
|---|---|---|---|---|---|---|---|---|
| M (SD) | M (SD) | M (SD) | M (SD) | M (SD) | Sex | Zyg | Sex*Zyg | |
| Mathematics | −0.01 (0.98) | −0.04 (0.99) | 0.02 (0.98) | 0.00 (10.00) | −0.02 (0.92) | p =0.452 | p =0.038 | p =0.033 |
| n =4612 | n =2406 | n =2206 | n =2214 | n =2398 | η2=0.000 | η2=0.001 | η2=0.001 | |
| Reading | −0.05 (0.95) | −0.09 (0.97) | −0.01 (0.93) | −0.14 (10.00) | 0.03 (0.90) | p =0.000 | p =0.001 | p =0.012 |
| n =5907 | n =3086 | n =2821 | n =2788 | n =3119 | η2=0.008 | η2=0.002 | η2=0.001 | |
| g | −0.01 (0.99) | −0.04 (0.98) | 0.03 (10.00) | −0.02 (10.00) | 0.01 (0.98) | p =0.201 | p =0.003 | p =0.576 |
| n =5650 | n =2950 | n =2700 | n =2663 | n =2987 | η2=0.000 | η2=0.002 | η2=0.000 | |
Each score was standardized on the basis of the whole sample after general exclusions (described in the text) and composites were made on the basis of these scores. Statistics reported here are based on the scores from the same sex twins only. MZ=monozygotic twins, DZ=dizygotic twins (same sex only), Males =all male twins, Females=all female twins. The n represents the numbers of individuals.
The results were corrected for age and sex differences so that they do not contribute to twin resemblance, which is standard in analyses of twin data (McGue & Bouchard, 1984). Although all children were tested at 7 years of age, the results could be affected even by small differences in age at the time of testing at this important stage of development. Six pairs of twins for whom data were not available on the date when the teacher questionnaire was returned were excluded from the mathematics composite. One pair of twins for whom the date of the telephone interview was missing was excluded from the g composite.
Also excluded from further analyses were 908 pairs in which one or both twins had missing data on any of the three composites, which is primarily due to teachers failing to return the questionnaires. This particularly affected the numbers of individuals with complete data on mathematics since teacher assessment was the only measure of mathematical ability used in this study. In order to avoid the possibility that our results were affected by very extreme scores, 34 pairs in which one or both twins scored 3 or more standard deviations below or above the mean on any of the three measures were excluded. All further phenotypic and genetic analyses were performed on the sample of 999 MZ and 928 same-sex DZ pairs for the mathematics composite, 1002 MZ and 931 same-sex DZ pairs for the reading composite, and 1002 MZ and 930 same-sex DZ pairs of twins for the g composite.
3.2. Phenotypic analyses
In our phenotypic explorations of the data, we found a substantial correlation between mathematics and reading (r =0.68, n =1927, p <0.01), and moderate correlations between mathematics and g (r =0.40, n =1926, p <0.01) and between reading and g (r =0.44, n =1932, p <0.01).
3.3. Genetic analyses
Twin correlations for the three composites are shown in Table 2. The results for mathematics are the same as those previously reported for a slightly different sample (Oliver et al., 2004). The twin correlations of 0.75 for MZ and 0.43 for DZ suggest very substantial genetic influence and modest shared environmental influence. The results for reading and g are also similar to those reported previously for this sample (Harlaar et al., 2005).
Table 2.
Intraclass correlations for Mathematics, Reading and g for twins by zygosity
| MZ | DZ | |
|---|---|---|
| Mathematics | 0.75** (n =999) | 0.43** (n =928) |
| Reading | 0.85** (n =1002) | 0.50** (n =931) |
| g | 0.67** (n =1002) | 0.50** (n =930) |
n refers to number of twin pairs.
p <0.010.
The novel aspect of the present study is its multivariate genetic analysis of mathematics as it relates to reading and g. Individual and cross-trait twin intraclass correlations for the three composites are presented in Table 3. The cross-trait twin correlations for MZ twins are nearly as great as the phenotypic correlations for individuals which create a ceiling for the MZ cross-trait twin correlations. The MZ cross-trait twin correlations are significantly greater than for DZ twins between mathematics and reading and between mathematics and g, suggesting genetic overlap between them. Consistent with the univariate results, little shared environmental influence is indicated, particularly for covariation between mathematics and reading, where the DZ correlations are almost exactly half of the MZ correlations. Because reading also shows genetic overlap with g, a trivariate analysis that considers all three composites simultaneously is needed to investigate whether there is any genetic variance specific to mathematics independent of both g and reading.
Table 3.
Cross-trait twin correlations (number of pairs) for Mathematics, Reading and g for twins by zygosity
| MZ | DZ | Same individual | |
|---|---|---|---|
| Twin 1 Mathematics | 0.60** | 0.33** | 0.68** |
| Twin 2 Reading | (n =999) | (n =928) | (n =1928) |
| Twin 1 Mathematics | 0.37** | 0.24** | 0.40** |
| Twin 2 g | (n =999) | (n =927) | (n =1927) |
| Twin 1 Reading | 0.40** | 0.29** | 0.44** |
| Twin 2 g | (n =1002) | (n =930) | (n =1933) |
Correlations for the same individual were done for one twin out of each pair (randomly selected).
p <0.010.
The Cholesky decomposition model was fit to the variance–covariance matrices derived from the data. As can be seen from the model-fit statistics, shown in Table 4, the full model fit the data well. Table 4 also shows the proportions of the total variance in each factor due to genetics (A), shared environment (C), and nonshared environment (E). These univariate ACE estimates are similar to those published previously (Harlaar, Spinath et al., 2005; Oliver et al., 2004). Both reading and mathematics show substantial A and modest C and E. g shows moderate A, C and E.
Table 4.
Model-fitting fit statistics and parameter estimates (95% confidence intervals in parentheses) for Mathematics, Reading, and g
| Measure | A | C | E |
|---|---|---|---|
| Mathematics | 0.67 (0.57–0.77) | 0.09 (0.00–0.18) | 0.24 (0.22–0.27) |
| Reading | 0.69 (0.60–0.78) | 0.17 (0.07–0.25) | 0.15 (0.14–0.17) |
| g | 0.33 (0.23–0.44) | 0.33 (0.24–0.42) | 0.33 (0.30–0.37) |
Model: ACE: A=additive genetic influence; C=shared environmental influence; E=nonshared environmental influence0. Three fit indices are reported: Chi-square (χ2), Akaike’s information criterion, (AIC; Akaike, 1987) and root mean square estimation of fit (RMSEA). Model fit: χ2=320.83; df =24; p =0.11; AIC=−15.17; RMSEA=0.180. The univariate estimates were obtained from the trivariate model fitting, which is reflected in the degrees of freedom.
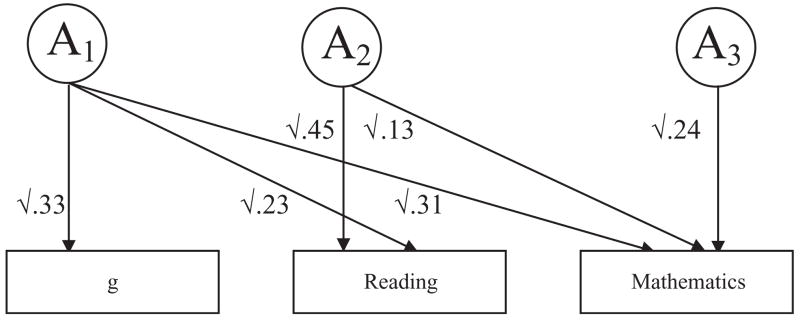
The main results from the multivariate model fitting are presented in Table 5. The total variance of the three composites is partitioned into common and independent ACE influences. Fig. 2 illustrates the Cholesky results, concentrating just on the genetic influences. The first latent factor (A1) shows significant genetic effects on g (0.33), some of which also affect reading (0.23) and mathematics (0.31). The second latent factor (A2) shows additional genetic effects that are independent of g but affect both reading (0.45) and mathematics (0.13). A3 shows significant genetic effects on mathematics (0.24) that are independent of g and reading. Another way of looking at these results is that the Cholesky model divides the genetic influence on mathematics into three components: 0.31+0.13+0.24=0.68, which is within rounding error of the heritability of mathematics shown in Table 4 (0.67). Nearly half (0.31/0.68=0.46) of the genetic influence on mathematics is in common with genetic influence on g and reading. About 20% (0.13/0.68) of the genetic influence on mathematics covaries with genetic influence on reading independent of g. Finally, more than a third (0.24/0.68) of the genetic influence on mathematics is specific to mathematics—that is, independent of both g and reading.
Table 5.
Standardized Cholesky squared path estimates (CIs) for g, Reading, and Mathematics indicating proportions of genetic (A), shared-environmental (C) and nonshared-environmental (E) influences on each trait that are shared with or independent of other traits
| Path | g | Reading | Maths |
|---|---|---|---|
| A1 | 0.33 (0.23–0.44) | 0.23 (0.14–0.36) | 0.31 (0.18–0.47) |
| C1 | 0.33 (0.24–0.42) | 0.04 (0.01–0.10) | 0.00 (0.00–0.03) |
| E1 | 0.33 (0.30–0.37) | 0.00 (0.00–0.01) | 0.00 (0.00–0.01) |
| A2 | 0.45 (0.33–0.56) | 0.13 (0.04–0.22) | |
| C2 | 0.12 (0.04–0.20) | 0.05 (0.00–0.13) | |
| E2 | 0.15 (0.13–0.16) | 0.04 (0.03–0.05) | |
| A3 | 0.24 (0.15–0.32) | ||
| C3 | 0.04 (0.00–0.10) | ||
| E3 | 0.20 (0.18–0.22) |
The three-factor model allows for: (1) A, C, and E effects on g, some of which also influence reading and mathematics (A1, C1, E1); (2) A, C, E effects on reading that are shared with mathematics but not shared with g (A2, C2, E2); (3) and A, C, and E effects unique to mathematics (A3, C3, E3).
Fig. 2.
Genetic results from the trivariate Cholesky decomposition.
It can be seen from Table 5 that the shared environmental influences on mathematics and reading are very small, as shown in the univariate analyses earlier. The path coefficients in the model are therefore also small, as they show the proportion of total variance that can be attributed to C, for these measures. The shared environmental influences on individual differences in g are moderate but almost entirely specific to g, as indicated by very small path coefficients from g to reading and mathematics. Nonshared environmental influences contributed modestly (moderately for g) to the individual differences. Most of the E effects were specific to each measure, as indicated by very small coefficients for the paths connecting the variables.
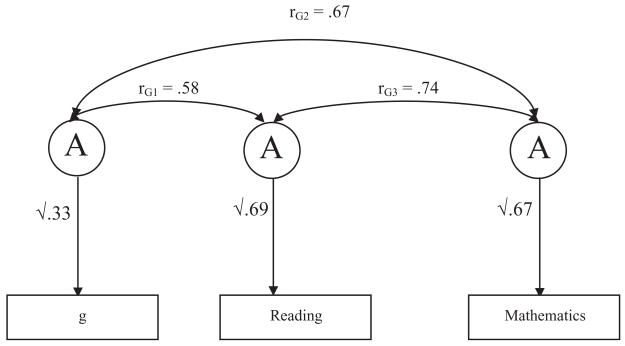
Table 6 shows the genetic, shared environmental, and non-shared environmental correlations and their confidence intervals for mathematics, reading, and g, estimated from the Cholesky model fitting. It can be seen that the bivariate correlations reflect the substantial genetic overlap between the three areas of ability, with genetic correlations ranging from 0.58 to 0.74 (illustrated in Fig. 3). As shown in Table 6, shared environmental bivariate correlations (0.21–0.74) show that, whatever tiny effects of shared environment there are, they are probably shared to a large extent for mathematics and reading; and less so for g. It should be noted, however, that the confidence intervals around these three estimates are very wide (due to the very small overall effect of C) and therefore no firm conclusions can be drawn from them. The non-shared environmental bivariate correlations are modest to moderate (0.11–0.39), suggesting that the effects of the shared environment are primarily specific to each trait, with the highest contribution to covariation between mathematics and reading.
Table 6.
Genetic, shared environmental, and non-shared environmental correlations for g, Reading, and Mathematics; and proportion of phenotypic correlation (rP) between these variables mediated by A, C, and E (95% CIs in parentheses)
| g and Reading | G and Mathematics | Reading and Mathematics | |
|---|---|---|---|
| Correlation | |||
| rA | 0.58 (0.46–0.72) | 0.67 (0.53–0.83) | 0.74 (0.68–0.80) |
| rC | 0.50 (0.23–0.76) | 0.21 (–0.58–0.91) | 0.74 (0.15–10.00) |
| rE | 0.14 (0.08–0.20) | 0.11 (0.05–0.17) | 0.39 (0.34–0.45) |
| Mediation of rP | |||
| A (axayrA/rP) | 0.65 (0.49–0.83) | 0.83 (0.63–10.00) | 0.76 (0.64–0.88) |
| C (cxcyrC/rP) | 0.27 (0.11–0.43) | 0.09 (30.11–0.27) | 0.13 (0.01–0.25) |
| E (exeyrE/rP) | 0.08 (0.04–0.11) | 0.08 (0.03–0.13) | 0.11 (0.09–0.13) |
rA, rC, rE =genetic, shared environmental, non-shared environmental correlations.
Fig. 3.
Proportions of the total variance attributable to genetic influences for each trait are indicated by the paths leading from the latent genetic factors to the measured traits. Correlations between the latent genetic influences on each trait (transformed Cholesky parameters) are denoted by rG and are represented by the double-headed arrows.
Table 6 also shows the proportion of phenotypic correlations (rP) between these variables mediated by A, C, and E (bivariate heritabilities and environmentalities), derived from the results of the Cholesky analysis. For example, the bivariate heritability between mathematics and reading is 0.76 (CI=0.64–0.88), which means that 76% of the phenotypic correlation of 0.68 between mathematics and reading is mediated genetically. It can be seen that these phenotypic correlations are primarily mediated by genetic factors for all three composites with bivariate heritabilities ranging from 0.65 to 0.83. Shared and non-shared environmental factors contributed only modestly to the phenotypic correlations (0.09–0.27 and 0.08–0.11, respectively).
4. Discussion
We investigated the extent to which genetic influences on mathematics performance also affect reading and g, as predicted by the generalist genes hypothesis. The results supported the generalist genes hypothesis in that the genetic correlations are 0.74 between mathematics and reading and 0.67 between mathematics and g. This finding implies that most of the genes that contribute to individual differences in mathematics ability also affect reading and g. Of course not all of the genetic effects are general: a third of the total genetic variance in mathematics is specific to mathematics. However, the more surprising finding is that most of the genetic action is general rather than specific to mathematics. That is, a common set of genes affects mathematics, reading and g. In addition, there are some genetic effects shared between mathematics and reading that are independent of g.
The results of the present study have several implications. The most straightforward implication is for molecular genetics: When the genes associated with any of these traits are identified, some of these genes will also be related to the other traits; and in the case of mathematics and reading, the overlap is expected to be very large. Finding generalist genes will facilitate research that attempts to understand the cognitive and brain systems responsible for the genetic overlap between mathematics, reading, and g.
One of the main reasons for such overlap is likely to be the complexity of these domains as assessed behaviorally. A great variety of non-specific abilities, such as long-term memory, working memory and attention are involved in mathematical ability as well as in reading and g. For example, if the ability to retrieve arithmetic facts and word meanings from long-term memory rely on the same mechanisms, comorbid mathematical and reading disabilities and correlated abilities should be expected. Phonological processing abilities and verbal IQ have also been implicated as a link between reading and mathematics in that they seem to explain most of the covariance between the two traits (e.g. Hecht et al., 2001; Light et al., 1998). Visuo-spatial ability, which has been implicated in at least some forms of mathematical disability (Geary, 2004), may also be involved in some aspects of general cognitive ability. Although many brain and cognitive processes are likely to contribute to the phenotypic overlap among different cognitive abilities and g, the point of the present results is that the same set of genes is largely responsible for genetic influence in these seemingly diverse domains (for more discussion on this issue see Plomin & Kovas, in press).
One might be tempted to say that what is in common between mathematics and reading is intelligence. However, our view is that this does not take us much farther in terms of understanding mechanisms because we do not know what the g factor is any more than we know what causes the general factor that pervades learning disabilities and abilities. It will be difficult to resolve these issues of the nature of the g factor and its relationship to learning disabilities and abilities at the behavioral or cognitive levels of analysis. As Spearman noted in 1927, ultimate understanding of the g factor “must needs come from the most profound and detailed direct study of the human brain in its purely physical and chemical aspects” (Spearman, 1927 p. 403). However, even the neural level of analysis cannot definitively disentangle causation from correlation because behavior can affect the brain as well as the brain affecting behavior. DNA is not subject to this direction of effects confusion—neural, cognitive and behavioral functioning does not change the structure of DNA. For this reason, we suggest that finding generalist genes associated with learning disabilities and abilities will be particularly useful in clarifying the nature of the g factor and its relationship to learning disabilities and abilities. Identifying these generalist genes will make it possible to investigate gene expression, proteomic and neural mechanisms by which these genes ultimately have their pleiotropic effects on learning disabilities and abilities as well as on the g factor (Plomin & Kovas, in press).
It should be emphasized that our results also show some genetic specificity for mathematics performance. Again, many cognitive processes might mediate this effect. For example, research in cognitive psychology and neuropsychology has identified a specific ability to assess and compare approximate numerosities, which does not depend on the modality in which the numerical information is presented. This ability seems to be separate from formally learned aspects of mathematics, such as exact calculations (e.g. Russell & Ginsburg, 1984; Xu & Spelke, 2000). This number-processing ability appears to emerge in infants at a very early age is present in animals (Landerl, Bevan, & Butterworth, 2004), and has specific parietal brain areas associated with it (e.g. Dehaene, Molko, Cohen, & Wilson, 2004; Dehaene, Piazza, Pinel, & Cohen, 2003). Another unique aspect of mathematics might be the ability to calculate small exact numerosities, which can also be demonstrated in infants (Xu, 2003). These two processes have been shown to be differentiated in the brain (e.g. Dehaene et al., 2004, 2003). It is possible that these abilities have etiologies unique to mathematics. Future research on the specificity of mathematics development will be facilitated by the use of more refined measures of mathematics, including tasks that have been specifically developed to assess ostensibly mathematics-specific processes such as calculation of approximate and exact small numerosities.
Another important implication of this study is the need to examine critically the role of environmental factors in the development of individual differences in mathematical ability. It should be emphasized that our finding of substantial heritability on individual differences in mathematics does not imply limited malleability of mathematical achievement overall. First, our results indicate that environmental influences are important—heritabilities are not 100%. However, environmental influences are largely not shared by children growing up in the same families and attending the same school. More generally, quantitative genetic results only describe genetic and environmental influences as they exist in a particular sample at a particular time. Even if a trait is highly heritable, a new environmental intervention such as a novel educational program, could have a major impact on children’s mathematics learning.
Moreover, finding that the salient environmental influences are nonshared has far-reaching implications for investigations of educationally relevant environments. It is commonly believed that environments, such as home environment and formal education, play an important role in shaping individual differences in mathematics and other cognitive abilities. In the field of educational psychology some environmental variables, such as aspects of classroom environment, teaching styles, and school environment, have been identified as significantly related to mathematical learning (e.g. Turner et al., 2002). Although the present study does not implicate specific environments, the important feature of the results is the modest effects of shared aspects of both home and school environments. The results suggest that shared environmental influences account for less than 10% of variance in mathematical ability as assessed by the teachers. In addition, an important multivariate finding is that approximately 70% of these shared environmental influences are the same as those affecting reading. This is not surprising if we assume that at least some of the variance is due to teachers, since both reading and mathematics are taught by the same teacher at this age.
Interestingly, the kind of influences that make the two twins in the same family, school, and class different rather than similar were found to be mostly ability-specific in this study. In other words, what makes a child perform similarly across the domains is largely due to genetic influences; most environmental influences act in a way as to make a child perform differently across the domains. To date none of these domain-specific environmental influences have been discovered.
What are the implications of these findings for educational research and practice? One direction for research is to identify the nonshared environmental factors that are experienced differently by twins, even identical twins, even in the same classroom and that contribute to differences in children’s relative performances in mathematics and reading. In terms of genetics, we suggest that the generalist genes hypothesis has received such consistent support that it would be useful to begin to consider its implications for teaching mathematics and reading. The immediate reaction is likely to be to focus on the smaller group of children with specific impairments, for example, children with problems in learning mathematics but whose performance in reading and general cognitive ability is not impaired. However, in reading where specific reading disability has been a focus of research, the difficulties of such discrepancy models have been increasingly recognized (e.g. Fletcher, Francis, Rourke, Shaywitz, & Shaywitz, 1992). The consistent support for the generalist genes hypothesis suggests that there is merit in focusing on what is in common between problems in reading and mathematics and their relationship with general cognitive ability. As noted earlier, investigation of the mechanisms responsible for this overlap will be facilitated when generalist genes are identified.
It should be noted that our environmental results may not generalize beyond the population of England and Wales. Most notably, having a common national curriculum as in the UK might lead to decrease in variation in mathematical ability, with the relative role of environment being smaller and the relative role of genetic influences being larger than in countries with different educational practices.
Potential assessment limitations of the present study should also be mentioned. It is important to demonstrate that the observed correlations between the traits are not due to the way the traits are measured. For example, if reading is necessary for the assessment of mathematics and general cognitive ability, then we would expect the traits to correlate simply for this reason. In our study, general cognitive ability was assessed over the telephone and reading was not involved in this assessment. Mathematics was assessed by teachers based on the pupil’s performance over the whole academic year, and it is unlikely that such measure can be seriously confounded by reading ability. Nonetheless, the use of teacher ratings for both mathematics and reading could inflate the overlap between them and with g if for example teachers’ ratings of mathematics and reading are influenced by their general impression of the children’s intelligence. For this reason, we are currently collecting data from children as well as teachers in order to directly test the validity of the teacher assessments and to enrich our findings.
To conclude, the study reported here has contributed to understanding the etiology of individual differences in mathematical ability by conducting the first multivariate genetic analysis using the data on mathematics, reading and general verbal and nonverbal cognitive ability from a large population-based sample of twins. The results of this study can be used to inform future multidisciplinary investigations in this area aimed to clarify the genetic and environmental mechanisms that underlie individual differences in mathematical cognition. A better understanding of these mechanisms will have important implications for mathematics education as well as diagnosis and prevention of mathematical learning disability.
Acknowledgments
We gratefully acknowledge the ongoing contribution of the parents and children in the Twins’ Early Development Study (TEDS). TEDS is supported by a programme grant (G9424799) from the UK Medical Research Council and our work on mathematics is supported in part by the US National Institute of Child Health and Human Development and the Office of Special Education and Rehabilitative Services (HD 46167).
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52:317–332. [Google Scholar]
- Alarcón M, Knopik VS, DeFries JC. Covariation of mathematics achievement and general cognitive ability in twins. Journal of School Psychology. 2000;38:63–77. [Google Scholar]
- Dale PS, Harlaar N, Plomin R. Correspondence between telephone and teacher assessments of reading: I. Substantial correspondence for a sample of 5808 children and for extremes. Reading and Writing: An Interdisciplinary Journal in press. [Google Scholar]
- Dehaene S, Molko N, Cohen L, Wilson AJ. Arithmetic and the brain. Current Opinion in Neurobiology. 2004;14:218–224. doi: 10.1016/j.conb.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cognitive Neuropsychology. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- DfEE. The national literacy strategy: Framework for teaching. London: HMSO; 1998. [Google Scholar]
- Fletcher JM, Francis DJ, Rourke BP, Shaywitz SE, Shaywitz BA. The validity of discrepancy-based definitions of reading disabilities. Journal of Learning Disabilities. 1992;25:555–561. doi: 10.1177/002221949202500903. [DOI] [PubMed] [Google Scholar]
- Freeman B, Smith N, Curtis C, Huckett L, Mill J, Craig IW. DNA from buccal swabs recruited by mail: Evaluation of storage effects on long-term stability and suitability for multiplex polymerase chain reaction genotyping. Behavioral Genetics. 2003;33(1):67–72. doi: 10.1023/a:1021055617738. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematics and learning disabilities. Journal of Learning Disabilities. 2004;37(1):4–15. doi: 10.1177/00222194040370010201. [DOI] [PubMed] [Google Scholar]
- Good RH, III, Salvia J. Curriculum bias in published, norm-referenced reading tests: Demonstrable effects. School Psychology Review. 1988;17(1):51–60. [Google Scholar]
- Gross-Tsur V, Manor O, Shalev RS. Developmental Medicine and Child Neurology. 1996;38:25–33. doi: 10.1111/j.1469-8749.1996.tb15029.x. [DOI] [PubMed] [Google Scholar]
- Harlaar N, Dale PS, Plomin R. Correspondence between telephone testing and teacher assessments of reading skills in a sample of 7-year-old twins: II. Strong genetic overlap. Reading and Writing: An Interdisciplinary Journal in press. [Google Scholar]
- Harlaar N, Hayiou-Thomas ME, Plomin R. Reading and general cognitive ability: A multivariate analysis of 7-year-old twins. Scientific Studies of Reading. 2005;9:197–218. [Google Scholar]
- Harlaar N, Spinath FM, Dale PS, Plomin R. Genetic influences on early word recognition abilities and disabilities: A study of 7-year-old twins. Journal of Child Psychology and Psychiatry. 2005;46:373–384. doi: 10.1111/j.1469-7610.2004.00358.x. [DOI] [PubMed] [Google Scholar]
- Hecht SA, Torgesen JK, Wagner RK, Rashotte CA. The relations between phonological processing abilities and emerging individual differences in mathematical skills: A longitudinal study from second to fifth grades. Journal of Experimental Child Psychology. 2001;79:192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Hoge RD, Coladarci T. Teacher-based judgements of academic achievement: A review of literature. Review of Educational Research. 1989;59(3):297–313. [Google Scholar]
- Jordan C, Oettinger Montani T. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997;30(6):624–634. 684. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
- Knopik VS, DeFries JC. Etiology of covariation between reading and mathematics performance: A twin study. Twin Research. 1999;2:226–234. doi: 10.1375/136905299320565906. [DOI] [PubMed] [Google Scholar]
- Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8–9-year-old students. Cognition. 2004;93:99–125. doi: 10.1016/j.cognition.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Lenneberg EH. Biological foundations of language. New York: John Wiley & Sons; 1967. [Google Scholar]
- Light JG, DeFries JC, Olson RK. Multivariate behavioral analysis of achievement and cognitive measures in reading-disabled and control twin pairs. Human Biology. 1998;70:215–237. [PubMed] [Google Scholar]
- Loehlin JC. The Cholesky approach: A cautionary note. Behavior Genetics. 1996;26(1):65–69. [Google Scholar]
- Marks D. Cautions in interpreting district-wide standardized mathematics achievement test results. Journal of Educational Research. 1990;83:349–354. [Google Scholar]
- Martin NG, Eaves LJ. The genetical analysis of covariance structure. Heredity. 1977;38:79–95. doi: 10.1038/hdy.1977.9. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Myers GF. Complexities in identifying and defining mathematics learning disability in the primary school age years. Annals of Dyslexia. 2003;53:218–253. doi: 10.1007/s11881-003-0011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy D. McCarthy scales of children’s abilities. New York: The Psychological Corporation; 1972. [Google Scholar]
- McGue M, Bouchard TJ. Adjustment of twin data for the effects of age and sex. Behavior Genetics. 1984;14:325–343. doi: 10.1007/BF01080045. [DOI] [PubMed] [Google Scholar]
- Neale MC. Mx: Statistical modeling. Box 126 MCV, Richmond, VA 23298: Department of Psychiatry; 1997. [Google Scholar]
- Oliver B, Harlaar N, Hayiou-Thomas ME, Kovas Y, Walker SO, Petrill SA, et al. A twin study of teacher-reported mathematics performance and low performance in 7-year-olds. Journal of Educational Psychology. 2004;96(3):504–517. [Google Scholar]
- Petrill SA, Rempell J, Oliver B, Plomin R. Testing cognitive abilities by telephone in a sample of 6- to 8-year-olds. Intelligence. 2002;30:353–360. [Google Scholar]
- Plomin R, DeFries JC. Multivariate behavioral genetic analysis of twin data on scholastic abilities. Behavior Genetics. 1979;9:505–517. doi: 10.1007/BF01067347. [DOI] [PubMed] [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioural genetics. 4. New York: Worth; 2001. [Google Scholar]
- Plomin R, Kovas Y. Generalist genes and learning disabilities. Psychological Bulletin. doi: 10.1037/0033-2909.131.4.592. in press. [DOI] [PubMed] [Google Scholar]
- Qualifications and Curriculum Authority. QCA Key Stage 1: Assessment and reporting arrangements. Great Britain: Qualifications and Curriculum Authority; 1999. ( www.qca.org.uk/ca/tests) [Google Scholar]
- Qualifications and Curriculum Authority. Report to QCA on the evaluation of statutory assessment in 2001 Key Stage 1. Great Britain: Qualifications and Curriculum Authority; 2001. ( www.qca.org.uk/ca/tests) [Google Scholar]
- Qualifications and Curriculum Authority. QCA Key Stage 1: Assessment and reporting arrangements. Great Britain: Qualifications and Curriculum Authority; 2003. ( www.qca.org.uk/ca/tests) [Google Scholar]
- Russell RL, Ginsburg HP. Cognitive analysis of children’s mathematics difficulties. Cognition and Instruction. 1984;1(2):217–244. [Google Scholar]
- Smith A. Making mathematics count: The report of Professor Adrian Smith’s Inquiry into Post-14 Mathematics Education. DfES 2004 [Google Scholar]
- Spearman C. The abilities of man. London: Macmillan; 1927. [Google Scholar]
- Spinath FM, Walker SO, Saudino KJ, Plomin R. Genetic influences on teacher assessed academic achievement and general cognitive ability: A bivariate twin study in 7-year-old twins. Intelligence submitted for publication. [Google Scholar]
- Thompson LA, Detterman DK, Plomin R. Associations between cognitive abilities and scholastic achievement: Genetic overlap but environmental differences. Psychological Science. 1991;2:158–165. [Google Scholar]
- Thorndike RL, Hagen EP, Sattler JM. Guide for administering and scoring the fourth edition: Stanford-Binet Intelligence Scale. Chicago, IL: Riverside; 1986. [Google Scholar]
- Torgesen JK, Wagner RK, Rashotte CA. Test of Word Reading Efficiency (TOWRE) Austin, TX: Pro-ed; 1999. [Google Scholar]
- Trouton A, Spinath FM, Plomin R. Twins Early Development Study (TEDS): A multivariate longitudinal genetic investigation of language, cognition and behaviour problems in childhood. Twin Research. 2002;5:444–448. doi: 10.1375/136905202320906255. [DOI] [PubMed] [Google Scholar]
- Turner JC, Midgley C, Meyer DK, Gheen M, Anderman EM, Kang Y, et al. The classroom environment and students’ reports of avoidance strategies in mathematics: A multimethod study. Journal of Educational Psychology. 2002;94(1):88–106. [Google Scholar]
- Wadsworth SJ, DeFries JC, Fulker DW, Plomin R. Cognitive ability and academic achievement in the Colorado Adoption Project: A multivariate genetic analysis of parent–offspring and sibling data. Behavior Genetics. 1995a;25:1–15. doi: 10.1007/BF02197237. [DOI] [PubMed] [Google Scholar]
- Wadsworth SJ, DeFries JC, Fulker DW, Plomin R. Covariation among measures of cognitive ability and academic achievement in the Colorado Adoption Project: Sibling analysis. Personality and Individual Differences. 1995b;18:63–73. [Google Scholar]
- Wainwright M, Wright MJ, Geffen GM, Geffen LB, Luciano M, Martin NG. Genetic and environmental sources of covariance between reading tests used in neuropsychological assessment and IQ subtests. Behavior Genetics. 2004;34:365–376. doi: 10.1023/B:BEGE.0000023642.34853.cb. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Wechsler intelligence scale for children. 3. London: The Psychological Corporation; 1992. [Google Scholar]
- Xu F. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]