Multi-finger Prehension: An overview

Abstract

This paper reviews the available experimental evidence on what people do when they grasp an object with several digits and then manipulate it. In addition to the Introduction, the paper includes three parts each addressing a specific aspect of multi-finger prehension. Part II discusses manipulation forces, i.e. the resultant force and moment of force exerted on the object, and the digits contribution to such force production. Part III deals with internal forces defined as forces that cancel each other and do not disturb object equilibrium. The role of the internal forces in maintaining the object stability is discussed with respect to such issues as slip prevention, tilt prevention and resistance to perturbations. Part IV is devoted to the motor control of prehension. It covers such topics as prehension synergies, chain effects, the principle of superposition, inter-finger connection matrices and reconstruction of neural commands, mechanical advantage of the fingers, and the simultaneous digit adjustment to several mutually reinforcing or conflicting demands.

I. Introduction

People interact with various objects everyday—utensils, glasses containing liquid, tools, door handles, a computer mouse, etc. The performers face three sequential challenges (reviewed in MacKenzie, Iberall 1994), they: (a) decide on how to grasp the object – depending on the object shape, size and the performance goal the performers grasp objects differently (Cutkosky, Howe 1990; Cesari, Newell 1999, 2000, 2002; Hershkovitz, Tasch, Teboulle 1995; Hershkovitz, Tasch, Teboulle, Tzelgov 1997; Hershkovitz, Teboulle 1998; Rosenbaum, Halloran, Cohen 2006), (b) execute reach-to-grasp movements (movement before contact is reviewed in Bennett, Castiello, 1994; Castiello, 2005), and (c) manipulate the grasped objects – exert forces on them and change their position, i.e. orientation and location, in space. This paper deals with the latter task, object manipulation.

Multi-finger grasps are mechanically redundant: the variables immediately controlled by the performer (forces and moments at the fingertips and fingertip displacements) outnumber the degrees of freedom of a solid object, maximally 6 (three force and three moment components in statics, and three linear and three angular displacements in kinematics). For comparison, in five-digit grasps, the total number of the force and moment components at the digit tips equals thirty (5 digits × 6 force and moment component at a digit contact). Therefore identical resultant forces on the object can be exerted by different sets of the individual digit forces. Since all the forces at the digit-tip interfaces and object movement can be recorded, multi-finger prehension is a convenient action for studying the problem of motor redundancy, the Bernstein problem (Bernstein 1967). An expectation is that the central controller uses analogous strategies to confront motor redundancy in many tasks, e.g. similar strategies are used to control redundant muscles acting at the joints and redundant fingers acting on the object (Li, Latash, Zatsiorsky 1998a). Of course, this similarity is only a hypothesis.

The present review is mainly limited to the prismatic precision grip, i.e. a grip by the tips of the digits in which the thumb and the fingers oppose each other (Figure 1). In such a grasp all grasping surfaces are parallel to each other and the normal digit forces are in the plane of grasp, an imagined plane that includes (or is close to) all the points of force application of the involved digits. The forces of the fingers opposing the thumb can be reduced to a resultant force and a moment of force. This is equivalent to replacing a set of fingers with a virtual finger, VF (Arbib, Iberall, Lyons 1985, Iberall 1987). A VF generates the same mechanical effect as a set of actual fingers. In various research, either individual digit forces are analyzed (the IF level) or the thumb and VF forces are only addressed (the VF level).

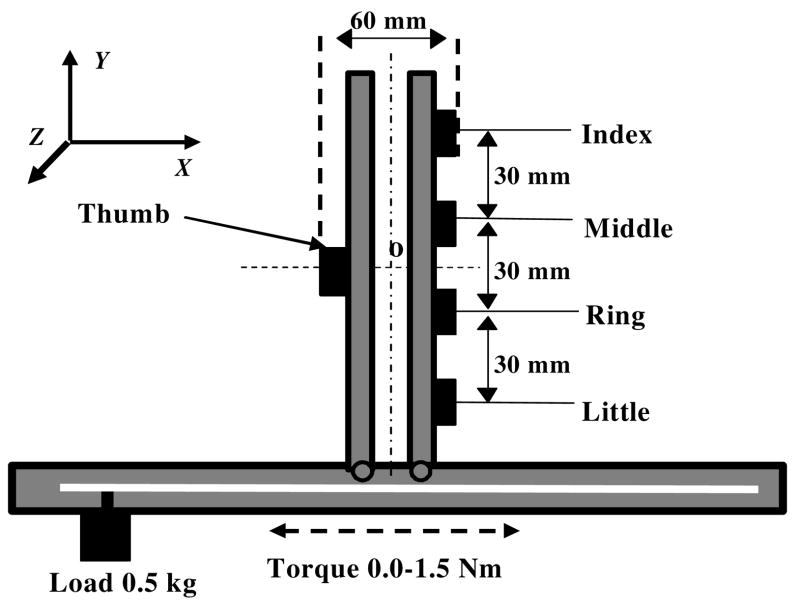
Figure 1.

Experimental ‘inverted-T’ handle/beam apparatus commonly used to study the prismatic precision grip. Five six-component force sensors (black rectangles) are used to register individual digit forces. During testing the suspended load was varied among the trials. The load displacement along the horizontal bar created torques from 0 N·m to 1.5 N·m in both directions. The torques are in the plane of the grasp. While forces in all three directions were recorded the forces in Z direction were very small and, if not mentioned otherwise, were neglected. When the handle is oriented vertically the force components in the X and Y directions are the normal and shear, (or tangential) forces, respectively. (Reprinted by permission from V.M. Zatsiorsky, F. Gao, and M.L. Latash (2003a) Finger force vectors in multi-finger prehension. J Biomech 36: 1745-1749.)

During data collection, in addition to the handle orientation and displacement (acceleration), two main groups of variables are recorded: (a) digit force vectors (Figure 2 A) and (b) displacement of the points of application of digit forces on the sensors (Figure 2 B).

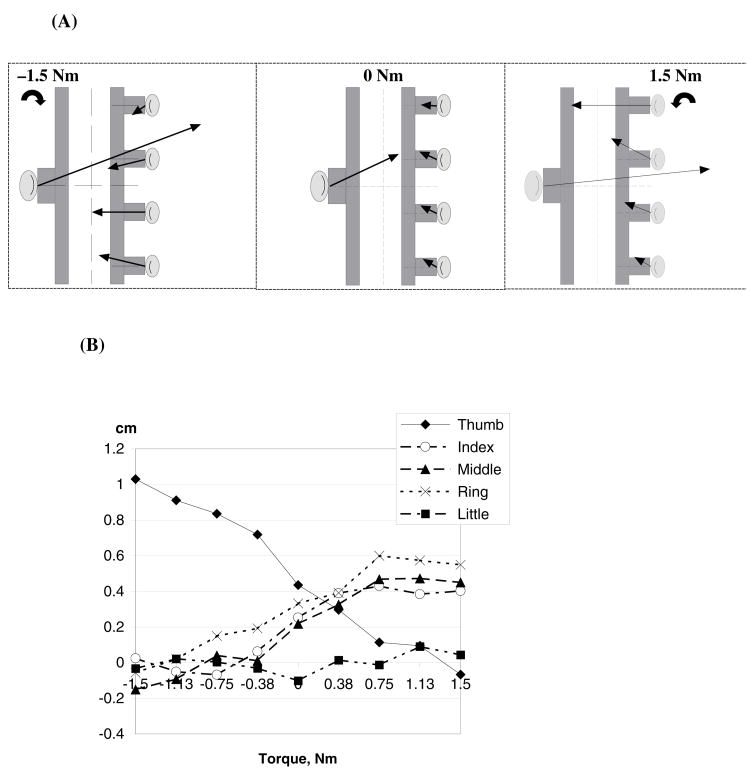
Figure 2.

Representative examples of digit force vectors (A) and displacement of the points of digit force application on the sensor surface (B). The handle (total weight 15.71 N) was maintained vertically at rest in the air at three different torques exerted on the handle, −1.5 Nm, 0 Nm (no torque), and 1.5 Nm. The torques were applied to the handle about an axis perpendicular to the plane of the page. The subjects were instructed to exert minimal force on the handle. The positive and negative direction of the torque refers to the resistive torque exerted by the subject (which is in the opposite direction to the external torque due to the loading). The supination torque efforts are negative and the pronation torque efforts are positive.

(A) The thin arrows originating at the five force sensors represent the corresponding digit forces; they are in proportion to force magnitude and along the line of force action. The two thick curved arrows indicate the subject efforts either in supination (−1.5 Nm, the arrow on the left) or in pronation (1.5 Nm, on the right), group average data. In this and future references, if not mentioned otherwise, the sensors are covered by 100-grit sandpaper (friction coefficient ≈ 1.40–1.52).

(B) Displacement of the point of application of digit forces in the vertical direction at the various torque levels. The results are for an individual subject (average of ten trials). Note that the displacement can be as large as 10 mm. (Adapted by permission from V.M. Zatsiorsky, F. Gao, and M.L. Latash. Finger force vectors in multi-finger prehension. Journal of Biomechanics, 2003, 36:1745–1749).

Following classical mechanics, all digit forces exerted on the object can be reduced to a generalized resultant force which includes three force components along the orthogonal axes (X-axis, Y-axis, Z-axis) and three moment components about these axes. A 6-component vector of the resultant force and moment is commonly called the manipulation force.

An internal force is a set of contact forces which can be applied to an object without disturbing its equilibrium (Mason, Salisbury 1985; Murray, Li, Sastry 1994). The elements of an internal force vector act in opposite directions, thus canceling each other and, hence, do not contribute to the manipulation force. The best known example of an internal force is the grasp force, two equal and opposite normal forces exerted by the thumb and VF against each other. Another example is equal and opposite tangential forces exerted by any two fingers. The resultant of such forces would be zero. Note that an internal force is not a single force; it is a set of forces and moments that, when act together, generate a zero resultant force and a zero resultant moment. The dimensionality of such a vector equals the total number of the digit forces and moments, i.e. thirty in five-digit grasps (some of the elements of an internal force vector can be zero). A performer can choose innumerable combinations of the internal force elements provided that they cancel each other.

The manipulation force is prescribed by the task mechanics; without exerting a required manipulation force the task will not be performed. The internal forces allow for much freedom. The force elements can be of different magnitude (provided that they negate each other’s effects) and there can be many internal forces, e.g. in 5-digit grasps there are 24 independent sets of internal forces that can be combined in different linear combinations (Gao, Latash, Zatsiorsky 2005b).

The remainder of this paper consists of three parts. Parts II and III review experimental data on what people do when they manipulate objects. These parts concentrate on the Manipulation Force and Internal Forces, respectively. Part IV deals with Prehension Control and addresses several governing principles of the control in multi-finger prehension tasks. In other words, Parts II and III cover motor behavior aspects of multi-finger prehension while Part IV focuses on motor control issues.

In ensuing parts, the following symbols are used: f is a digit force; F is resultant force acting on the handle; M is a moment of force exerted on the handle; superscripts n and t designate the normal and tangential force components, respectively; symbols T, I, M, R and L designate the thumb, index, middle, ring and little fingers, respectively; subscript i designates an arbitrary digit (i =1, 2…5). Hence, the symbol $f_I^n$ indicates the normal force of the index finger and the symbol Mⁿ is the moment of normal forces. The term torque is used to designate a rotational effect of the external load exerted on the handle while the term moment of force (or moment for brevity) is used for the rotational effect of performer’s efforts. The IMRL set is referred to as ‘fingers’ and the TIMRL set is referred to as ‘digits’.

II. Manipulation force

Consider tasks that require producing a non-zero manipulation force or moment on a hand-held object. The topic of interest is the contribution of individual fingers to the resultant force and moment. The data on the normal and tangential forces will be presented separately. In contrast to the tangential forces, the normal finger forces have different moment arms with respect to the thumb as a pivot, and hence finger forces of the same magnitude exerted by different fingers would generate different moments. The tangential finger forces of the same magnitude generate similar moments.

II.1. Normal force production

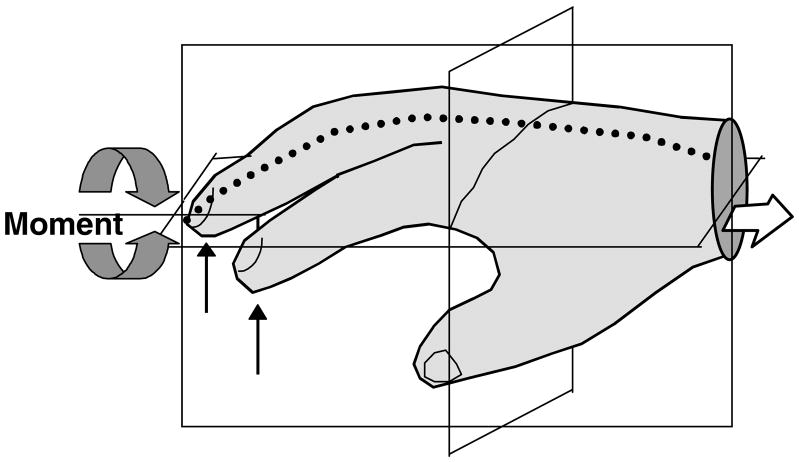
In prismatic grasps, normal finger forces produce a moment in the direction of either pronation (e.g. the index finger) or supination (e.g. the little finger). Imagine a longitudinal axis perpendicular to the transverse plane of the hand (Figure). Finger forces that do not pass through this axis generate a moment with respect to it. This auxiliary moment was termed a secondary moment (Li, Latash, Zatsiorsky 1998 a, b). It was found that the forces generated by the fingers in a four-finger pressing task produce a zero total moment with respect to a line passing approximately along the ulnar side of the middle finger (the neutral line of the hand). As a result, the set of finger forces can be reduced to a single resultant force normal to the hand neutral line. In pressing tasks, the central controller activates individual fingers such that the secondary moment is minimal or zero (the principle of minimization of the secondary moment,Li, Latash, Zatsiorsky 1998b). The principle imposes an additional constraint on the digit forces. However, when a desired total force in a 4-finger pressing task has to be produced, the central controller still has two degrees of freedom left to manipulate. The principle helps to explain: (a) the force sharing pattern between the normal finger forces in the pressing and grasping tasks, (b) independency of the force sharing percentage on the total force magnitude, and (c) high linear correlations between the finger forces during the transient periods. In cases (b) and (c) maintaining consistent force sharing among fingers is the simplest strategy for the CNS to keep the secondary moment unchanged.

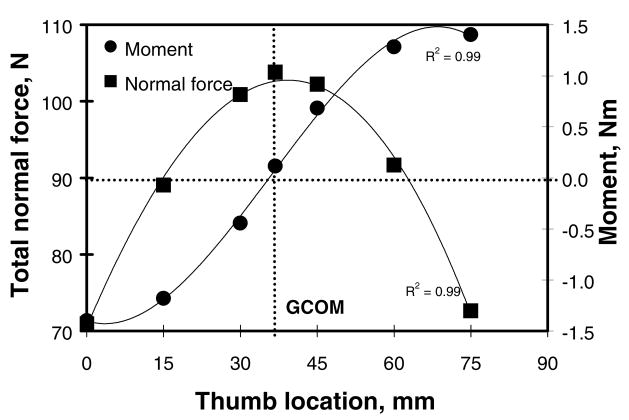
The neutral line in the grip task is similar to that of the pressing tasks (Li, Latash, Zatsiorsky 1998b). In the grasping tasks with different thumb locations, when the thumb was along the neutral line: (a) the moment due to the normal finger forces was zero; (b) the total normal force applied to the gripping object was maximal (Figure 4); (c) the relative peak normal force (% of the maximal force exerted by the digit in its single-finger task) was similar for all the fingers. This position was also preferred by the subjects as most comfortable.

Figure 4.

Total normal force and moment of the normal forces at different thumb locations (averaged across subject values, N; n =10). The experiment included three parts. Part 1: Grip with the thumb at different locations. With the thumb at a specified location, the handle was lifted and gripped maximally. In various trials, the thumb location was changed systematically from the level of the index finger down to the level of the little finger at a 15 mm step. The six data sets at abscissa of 0, 15, 30, 45, 60, and 75 mm are for the six fixed thumb locations. Part 2: Press with the four fingers. The firmly secured handle was oriented vertically. The subjects were asked to press as hard as possible with all four fingers. Part 3. Selection of the comfortable thumb position. The subjects were asked to choose the most convenient thumb position in the prismatic grasps. The vertical dotted line indicates the comfortable thumb location (GCOM). (Adapted by permission from Z.-M. Li, M.L. Latash, K.M. Newell, and V.M. Zatsiorsky Motor redundancy during maximal voluntary contraction in four-finger tasks. Exp Brain Res. 1998b; 122(1):71–77.)

The principle of minimization of the secondary moment is valid only for force production with several fingers. It is overridden when a force and a moment on the object must be produced.

When people exert force on the environment, both the magnitude and direction of the force vectors have to be controlled. When the force is exerted by several fingers, as in multi-finger grasping, the direction of the individual finger forces differs from the resultant force direction. The finger force vectors are in dissimilar directions but they compensate for each other (Figure 5). The desired direction of the total force is achieved by a synergic adjustment of the finger forces.

Figure 5.

Finger forces in a task of exerting a 4-finger force in a prescribed direction. The angles are in the flexion-extension plane. Visual feedback of the IMRL force was provided. The force polygon is obtained by adding tail-to-head the individual finger forces. Group average data are shown (n =9). Note the large difference in the direction of the index and little finger forces. Reprinted by permission from F. Gao, M.L. Latash, and V.M. Zatsiorsky. Control of finger force direction in the flexion-extension plane. Experimental Brain Research, 2005, 161: 307–315.

II.2. Tangential force production

Tangential force is the component of a contact force acting in parallel to the contacted surface. Frequently f^ts are the only functional forces that contribute to the manipulation force (e.g. holding a glass of water, turning a doorknob) while fⁿs are incidental to task success, they contribute to the internal force vector. Although the decomposition of the contact force into its normal and tangential components is always possible, it might be misleading for studying equilibrium of the bodies of arbitrary shape. For example, when the contact surfaces are not parallel and local curvatures at contacts are different (e.g. holding a football near one of its tips), mechanical equilibrium cannot be readily defined in terms of the local normal and tangential forces. The present discussion is however limited to the prismatic grasps with parallel contact surfaces.

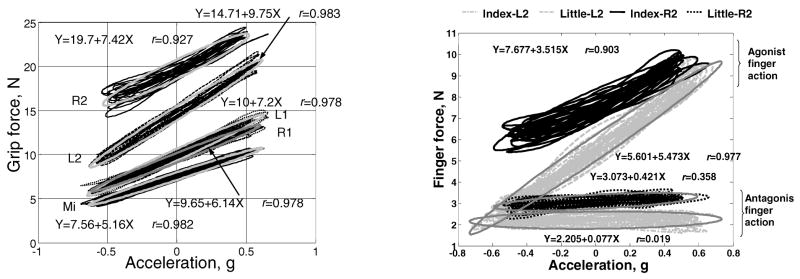
In prismatic grasps, the total tangential force, commonly referred to as load, is shared between the thumb and the four fingers, the VF. The VF tangential force is shared among the fingers. The sharing (in percent of the VF tangential force) does not depend on the load magnitude but strongly depends on the load direction, radial or ulnar (Pataky, Latash, Zatsiorsky 2004a). Note that the task is redundant: one VF force could be shared among four fingers in many different ways.

In passive mechanical structures, the load sharing among the redundant effectors is determined by the material and geometric properties of the effectors such that minimum elastic potential energy is stored in the system (e.g. Rumann 1991). Thus, in the absence of active force production (by joint actuators), redundancy would be solved by the passive properties of the system. Robotic grippers, for example, do not have actuators that produce tangential forces; the force sharing is solely due to structural deformation of the fingers. In contrast, people generate active (muscle) finger forces in the radial or ulnar directions and hence can regulate tangential force sharing. As an example see again Figure 2a, where during the supination torque effort (left panel) the index finger force is directed downward while the little finger force is directed upward. Such opposite force directions cannot be explained by the material properties of the fingers. They are due to the active finger adduction at the metacarpophalangeal (MCP) joints. It seems that finger opposition, i.e. spreading the fingers apart – abduction, or squeezing the fingers together – adduction (Pataky, Latash, Zatsiorsky 2007b), is used during prehension. The tangential forces generated due to the finger opposition are the internal forces, provided that they cancel each other. When finger tangential forces are in opposite directions, the concept of the VF force sharing cannot be immediately applied.

II.3. Torque production

In most everyday tasks people produce torques on the objects (eating with a spoon, drinking from a glass, turning a door handle, etc.). Different mechanisms of torque production are used when objects are (a) in the air (drinking from a glass) or (b) mechanically fixed (turning a door handle).

II.3.1. Moment production on free objects

Moment production in the plane of grasp

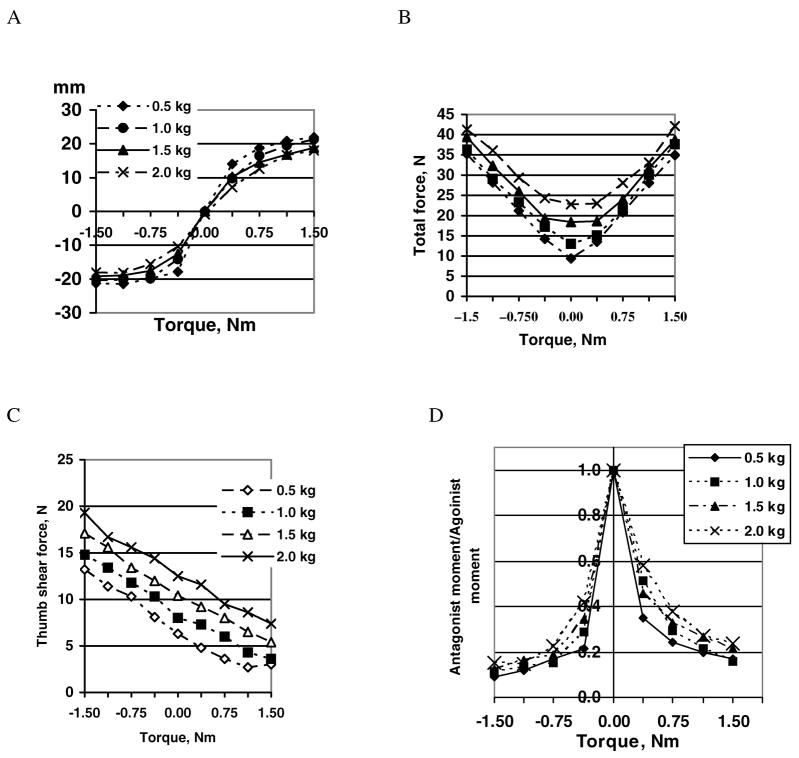
Both the normal and tangential digit forces can generate moments on the object and hence contribute to the total moment production (Figure 6). For a given object geometry, the contribution of the moments of the normal and tangential forces does not depend either on the external load or on the moment magnitude and direction, in pronation or supination (Figure 7). Hence, for a given grasp, the percentage distribution of the total moment between its normal and tangential components is invariant. At the handle width of 56.5 mm their contributions are approximately equal (Zatsiorsky, Gregory, Latash 2002a).

Figure 6.

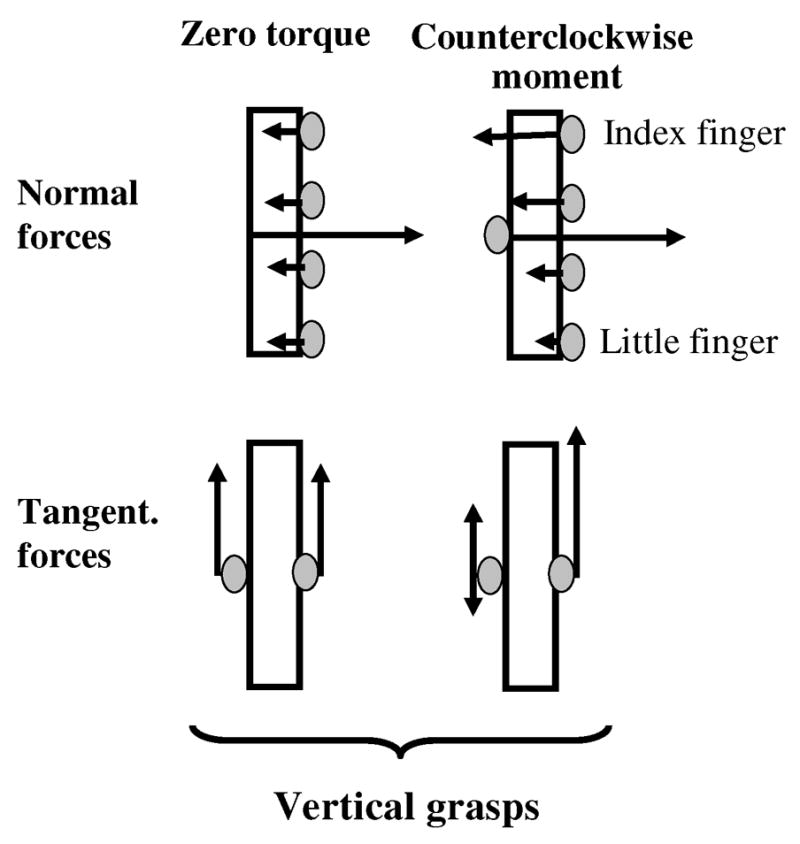
Normal and tangential digit forces during torque production, a schematic. Upper panel - normal forces; bottom panel - tangential forces. In the upper panel, the forces are drawn as vectors with their origin at the digit sensors. In the bottom panel, the tangential digit forces are represented by one vector (the VF force). The moment of the thumb and VF tangential forces is proportional to the difference in the magnitude of the forces. Note that the thumb force can be either in upward or downward direction. During the moment generation in the counterclockwise direction (pronation), the normal forces of index and middle fingers produce moments in pronation, i.e. in the required direction. Such fingers are called torque agonists. The ring and little fingers work in this task as torque antagonists: they generate moments in the opposite direction, clockwise.

Figure 7.

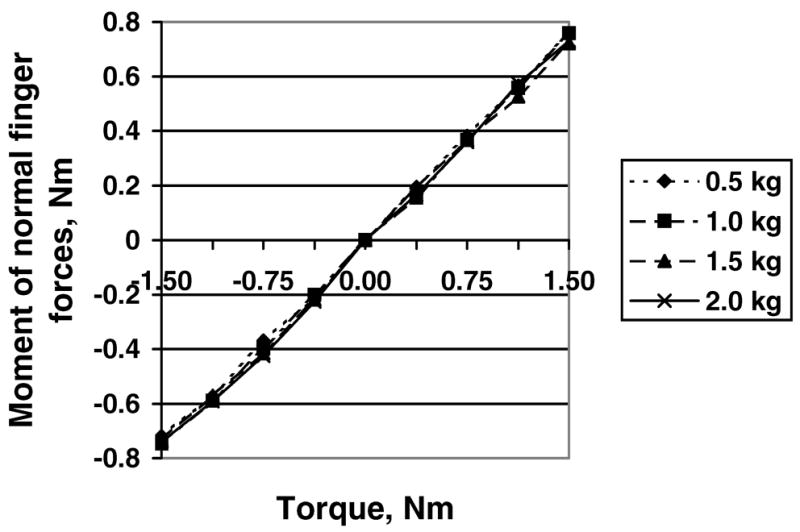
Relations between the external torque generated by the suspended load (abscissa) and the moment produced by the normal forces of the fingers, Mⁿ (ordinate). Group average data are shown (n=10). The data are for four different loads. The coefficients of the regression equations Mⁿ =a+b(Torque) are: for load 0.5 kg, slope b=0.451, intercept a = 0.06; load 1.0 kg, b=0.473, a = 0.02; load 1.5 kg, b=0.492, a = −0.01; load 2.0 kg, b=0.504, a = −0.01. Note that the intercepts are very small; hence the regression lines pass very close to the origin of the system of coordinates. Consequently, the percentage contribution of Mⁿ into the total moment exerted on the object by the performers remains constant. Since the sum Mⁿ + M^t equals the total moment, the percentage contribution of Mⁿ into the total moment is also invariant. (Adapted by permission from V.M. Zatsiorsky, R.W. Gregory, and M.L. Latash. Force and torque production in static multifinger prehension: biomechanics and control. I. Biomechanics. Biological Cybernetics, 2002, 87:50–57.)

The moment of the normal forces can be viewed as the product of the VF normal force and its moment arm with respect to the thumb as a pivot. The VF moment arm equals the shortest vertical distance between the VF and thumb normal forces. During static equilibrium these forces are equal in magnitude (otherwise the handle would accelerate in the direction of the larger force) but they usually not act along the same line. Therefore, they form a force couple that generates a free moment remaining unchanged under parallel translation (see for instance Zatsiorsky, 2002, p. 20). The moments of the tangential and normal forces can be added to obtain the total moment exerted by the performer (Total moment, M^TOT = M^t+Mⁿ).

Small moments (under 0.75 Nm) are controlled mainly by changes of the moment arm, i.e. the relative position of the points of the VF and thumb force application. This is achieved by displacing the point of application of the VF force (Figure 8 A), i.e. by redistributing the VF force among the individual fingers, as well as by displacing the point of application of the thumb force (see Figure 2B above). Large moments (those over 0.75 Nm) are primarily produced by changes in the magnitude of the VF and thumb normal forces. The normal forces increase with the moment magnitude but do not depend on moment direction (Figure 8 B). The thumb and VF tangential forces change with the moment in a linear fashion (Figure 8 C). During static equilibrium the sum of the thumb and VF tangential forces remains constant (it equals the supported load). An increase or decrease of the thumb force is always accompanied by equal opposite changes of the VF force (not shown in the figure).

Figure 8.

Digit forces and moments for different external torques and loads. Group average data are shown (n = 10). (A) The position of the point of application of the VF normal force. The zero position corresponds to the application of the VF resultant force at the center of the thumb force sensor. (B) The VF normal force. (C). The thumb tangential (shear) force. Note that in panel C curves are almost parallel, which signifies the lack of interaction between the LOAD and TORQUE factors. (D) ‘Antagonist/agonist moment’ ratio. The ratio for the zero torque conditions was estimated from the equilibrium requirements under the assumption that the normal forces of the two pairs of agonist and antagonist fingers were equal. Antagonist moments were observed over the entire range of load-torque combinations. (Adapted by permission from V.M. Zatsiorsky, R.W.Gregory, and M.L.Latash. Force and torque production in static multifinger prehension: biomechanics and control. I. Biomechanics. Biological Cybernetics, 2002, 87:50–57.)

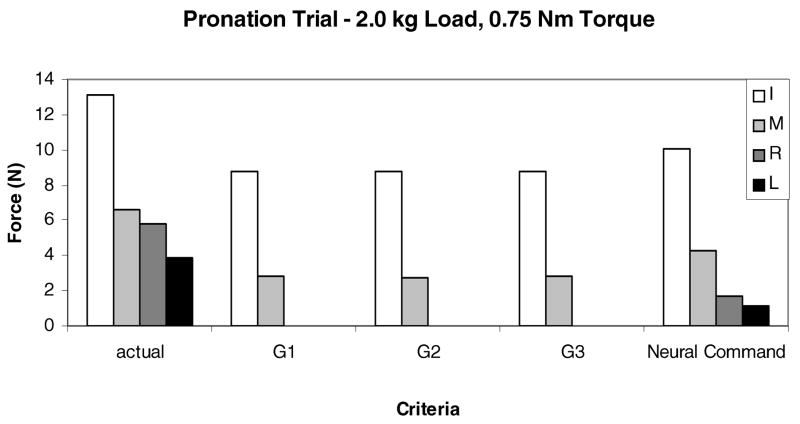
Two findings with respect to moment production should be noted: (a) When both the torque and load change systematically among the trials, the force of the ‘peripheral’ fingers (index and little) depends mainly on the torque while the force exerted by the ‘central’ fingers (middle and ring) depends both on the load and torque (not shown in the figure). (b) Fingers that produce a moment in the opposite direction to the required direction, e.g. generate moment in supination when the pronation moment is required, are regularly active. Hence, both agonist and antagonist moments are exerted (Figure 8D). The antagonist moments should be counterbalanced by the increased activity of the agonist fingers, those that generate moment in the desired direction. Such a pattern of coordination requires additional effort and seems inefficient. This finding is discussed later in this paper.

Moment production in the plane orthogonal to the plane of grasp

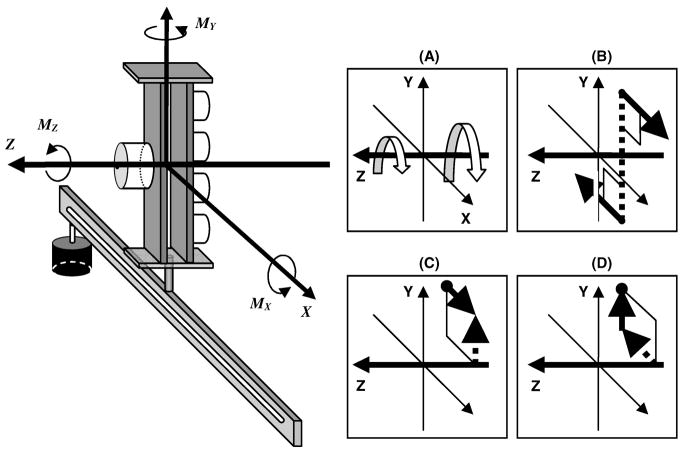
The task is similar to holding a book vertically in the air where the center of mass of the book is located farther from the hand than the points of digit contacts (Figure 9, left panel; Shim, Latash, Zatsiorsky 2005a.). In such tasks, the total moment about the Z-axis (M_Z) has four sources (Figure 9, right panels): (a) thumb and fingers local free moments, (b) moment of a VF couple acting in the X-Y plane (a free VF moment), (c) moment of the VF tangential horizontal force (acting in the X-direction), and (d) moment of the VF vertical force (acting in the Y-direction). The percentage contribution of the four sources into the total moment is invariant. It does not depend on the torque magnitude (cf. with Figure 7 where a similarly consistent distribution of the total moment between the moments of the normal and tangential force in the planar tasks is illustrated).

Figure 9. Experimental setup (left panel) and sources of the total moment by digits about the Z-axis (right panels).

Left panel: Thumb and finger sensors (shown as white cylinders) were attached to vertical aluminum bars, and a movable load (shown as a black cylinder) was attached to the long aluminum bar. M_X, M_Y and M_Z are the moments with respect to the global X-, Y- and Zaxes, respectively. By suspending the load at various locations along the horizontal bar, the different external torques about the Z-axis were exerted on the handle. The subjects were required to maintain the handle at rest.

Right panel. Sources of the M_Z. Line arrows are the forces and the dotted arrows are the moment arms, as described in the body of the text.

(Adapted by permission from J.E. Shim, M.L. Latash, and V.M. Zatsiorsky.

Prehension synergies in three dimensions. Journal of Neurophysiology, 2005a, 93: 766–776.)

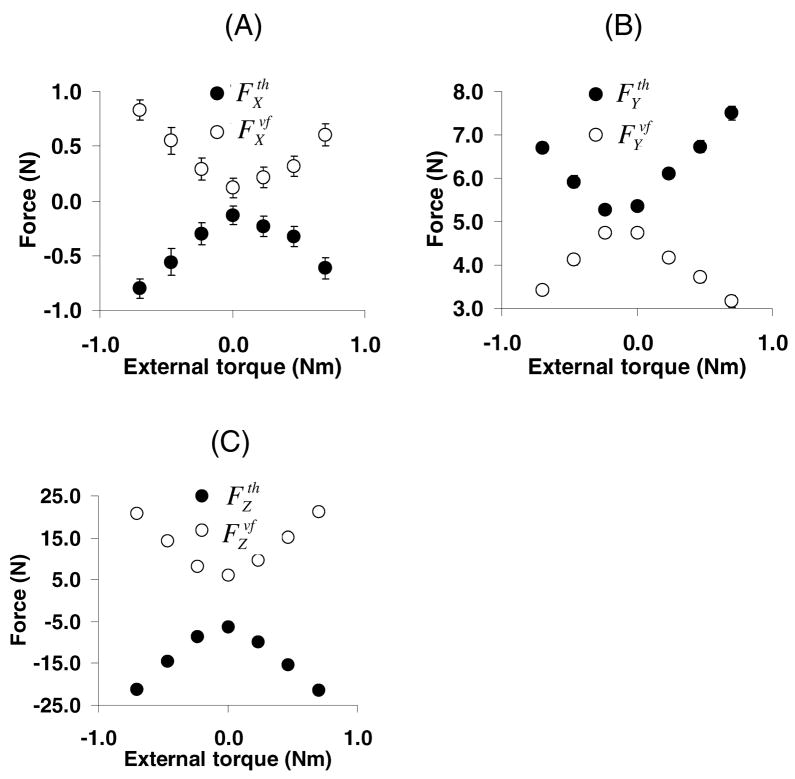
The studied task is essentially 2-dimensional in a sense that the external torque is exerted in one plane and the equilibrium could be achieved solely by generating resistive torque in that plane. However, the force components in all three directions changed systematically with the external torques, i.e. the CNS reacted to a 2-dimentional task with a 3-dimensional response (Figure 10).

Figure 10.

Relations among forces under different external torques at the VF level. A: thumb and VF forces along the X-axis. B: thumb and VF forces along the Y-axis. C: thumb and VF forces along the Z-axis. (Adapted by permission from J.E. Shim, M.L. Latash, and V.M. Zatsiorsky. Prehension synergies in three dimensions. Journal of Neurophysiology, 2005a, 93: 766–776.)

II.3.2. Moment production on a mechanically fixed object

The tasks discussed in this section are analogous to rotating a door handle and are quite common in everyday life. As compared to holding a free object, such tasks have one essential distinction. When a free object is held statically in the air, the forces and moments exerted on the object are constrained by the equilibrium equations. Specifically, to maintain the equilibrium, the resultant horizontal force exerted on the object must equal zero. The resultant vertical force must equal the weight of the object and the resultant moment should equal the external moment applied to the handle. In contrast, when a handle is affixed to an external support, the forces exerted on the handle can be of any magnitude. In this sense, the task is much less constrained and the finger forces are selected by the performer based on principles that are not dictated by mechanics.

It is known from mechanics that an arbitrary set of forces acting on a rigid body can be reduced to a resultant force and a force couple, i.e. two equal and opposite forces that generate a moment (see, for instance, Zatsiorsky 2002). A force couple generates a moment (free moment, Mfree) about any axis that is not in the plane of the couple. When several fingers act on a hand-held object and produce a moment M about a fixed axis, the moment M is due both to the resultant force F acting on the handle and free moment: M = Mfree + l × F, where l is the moment arm of force F.

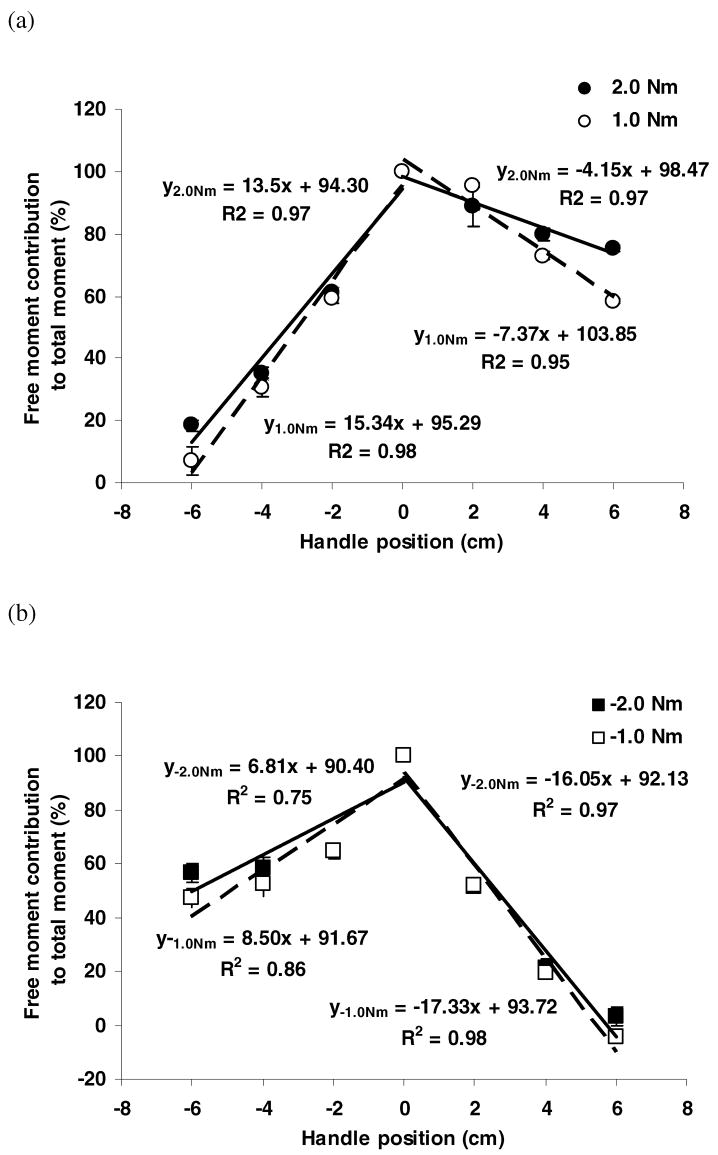
Humans exert moments on mechanically fixed objects by using two complementary mechanisms: (a) the resultant force (its moment effect equals l × F) and (b) a free moment Mfree which is created by the pronation or supination efforts (Shim et al. 2004). The relative contribution of the l × F and Mfree into the total moment M is illustrated in Figure 11. The Mfree contribution is 100% when the neutral line of the hand is located exactly at the level of the moment axis. There exists a point of zero free moment (PZFM) at which the contribution of the free moment to the total moment is zero. In the intermediate grasp locations, the performers select a mixture of these two strategies such that the contribution of these strategies scales linearly with the distance to the moment axis. The linearity of such a scaling is not prescribed by the task mechanics. It is a consequence of certain motor control mechanisms which are presently unknown.

Figure 11.

Free moment contribution to the total moment, %, as a function of the position of the neutral line of the hand from the moment axis (handle position). The handle was oriented vertically and its position with respect to the axis of rotation changed in different trials either in upward (positive) or downward (negative) directions. (a) Positive moment production (pronation efforts); (b) negative moment production (supination efforts). Averaged across subjects data are presented with standard error bars. To find the PZFMs, the regression lines should be extrapolated to the level of the zero contribution of the free moment. (Adapted by permission from J.K. Shim, M.L. Latash, and V.M. Zatsiorsky (2004) Finger coordination during moment production on a mechanically fixed object. Experimental Brain Research, 2004, 157: 457–467.)

III. Internal forces and grasp stability

The manipulation force vector and the vector of the internal force are mathematically independent (Kerr, Roth 1986; Yoshikawa, Nagai 1991). Practically this means that the central controller can change manipulation force without changing the internal force and vice versa (Yoshikawa 1990; Yoshikawa, Nagai 1991; Gao, Latash, Zatsiorsky 2005b). This opportunity is realized in robotics manipulators where the manipulation force and the internal forces are controlled separately (e.g., Zuo, Qian 2000); the control is said to be decoupled. The decoupled control requires less computational resources; the controller does not have to bother about online adjustments of the grasp force to object acceleration and/or orientation. However, this strategy requires exerting unnecessarily large forces and is, in this sense, uneconomical. People do not use this option. Available data suggest that the CNS prefers to face larger computational costs rather than produce excessive forces. In contrast to robots, people adjust the internal forces to the manipulation forces during the object transport (Smith, Soechting 2005; Gao, Latash, Zatsiorsky 2005 b, c; Zatsiorsky, Gao, Latash 2005).

Manipulation forces are prescribed by the task mechanics, for instance to keep an object at rest the vertical forces should equal the object weight. In contrast, the internal forces are forces of choice. As already mentioned, in multi-finger grasps there are many internal forces, too many to analyze each individually. However, for planar tasks performed with mechanically unconstrained objects and analyzed at the VF level, there exist only two internal forces: the grasp force and the internal moment. This claim has been proved mathematically (Gao, Latash, Zatsiorsky 2005b).

Whatever the task is the grasps should be stable. Grasp stability refers to slip prevention (the objects should not be dropped), tilt prevention (object orientation in space should be properly maintained), and perturbation resistance, respectively. Slip prevention is achieved mainly by modulating the grasp force while the tilt prevention is achieved via a proper modulation of the components of the internal moment (discussed further in III.2). Performers are free to select the values of: (a) normal thumb and VF forces, provided that the forces are equal in magnitude and sufficient to prevent slipping; and (b) Mⁿ and M^t, provided that their sum equals the external torque. Perturbation resistance depends on the pattern of perturbation (to be discussed further).

III.1 Slip prevention

The conditions for slip prevention depend on the task. This section addresses the following tasks: (1) the object is oriented vertically and is at rest; (2) the object is non-vertically oriented, and (3) a vertically oriented object is moved in (3a) vertical direction or (3b) horizontal direction. Note that only when a vertically oriented object is at rest or is being moved vertically the thumb and VF normal forces are equal. The forces cancel each other and are collectively called the grasp force. In all other cases, such as a non-vertical handle orientation or during object acceleration in a horizontal direction, the forces are not equal and hence cannot be called the grasp force.

III.1.1. A vertically oriented object at static equilibrium

To prevent slip of a vertically oriented object, $f_i^n$ produced by each digit should be sufficiently large, above the slipping threshold. In the literature, the relation between the normal and tangential forces is usually characterized by either the Fⁿ/F^t ratio or the percent difference between the actual normal force and the minimal normal force to prevent slippage known as the safety margin, SM (Westling, Johansson, 1984).:

$$S{M}_i=\frac{\left(f_i^n-\mid f_i^t/{\mu }_i\mid \right)}{f_i^n}\times 100\%$$ [1]

where μ_i is the coefficient of friction at the i digit contact.

The grasp force increases with object weight (Johansson, Westling 1984; Winstein, Abbs, Petashnick 1991; Kinoshita, Kawai, Ikuta 1995, Monzee, Lamarre, Smith 2003) and the tangential torque, i.e. the torque in the tangential plane at the digit-surface interface (Kinoshita, Backstrom, Flanagan, Johansson 1997; Goodwin, Jenmalm, Johansson 1998). The relation between the grasp force and the load is linear (Kinoshita et al. 1995, Monzee et al. 2003; Zatsiorsky, Gao, Latash 2005). Grasp force increases with a decrease in friction resulting in higher grip force to load force ratios at low friction while the SM is relatively constant (Johansson, Westling 1984; Cole, Johansson, 1993; Cadoret, Smith 1996; Burstedt, Flanagan, Johansson 1999). The friction-related scaling effect is neither task-specific (Cole and Johansson 1993) nor grip configuration-specific (Burstedt et al. 1999; Kinoshita et al. 1995). The grasp force adjustments to friction are triggered by cutaneous sensation (Johansson, Westling 1984, 1987; Johansson 1996, 1998, 2002; Edin, Westling, Johansson 1992; Edin, Johansson 1995; Cole, Johansson 1993; Forssberg, Eliasson, Kinoshita, Westling, Johansson 1995; Birznieks, Burstedt, Edin, Johansson 1998).

When the friction at the two sides of the object is different, e.g. it is high under the thumb and low under the fingers, the grip force falls between the forces seen for the high friction and low friction conditions applied for all digits (Aoki, Niu, Latash, Zatsiorsky 2006). Performers also decrease tangential forces at the low friction contacts. As a result, if not instructed to maintain the object orientation vertical, subjects tilt the handheld object toward the side with lower friction conditions (Edin et al. 1992).

When subjects grasp objects with different surfaces underneath each digit (a complex friction pattern), they scale the grip to load force ratio based on the local friction condition at each digit (Burstedt, Flanagan, Johansson 1999 a, b; Edin et al. 1992;Quaney, Cole 2004). It has been concluded that the coordination of digit-tip forces during human manipulation emerges from independent neural networks controlling each engaged digit (Burstedt, Edin, Johansson 1997).

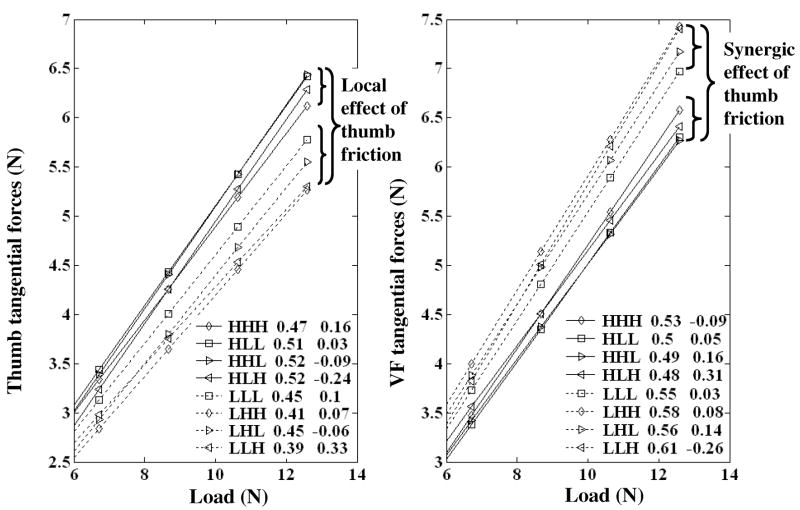
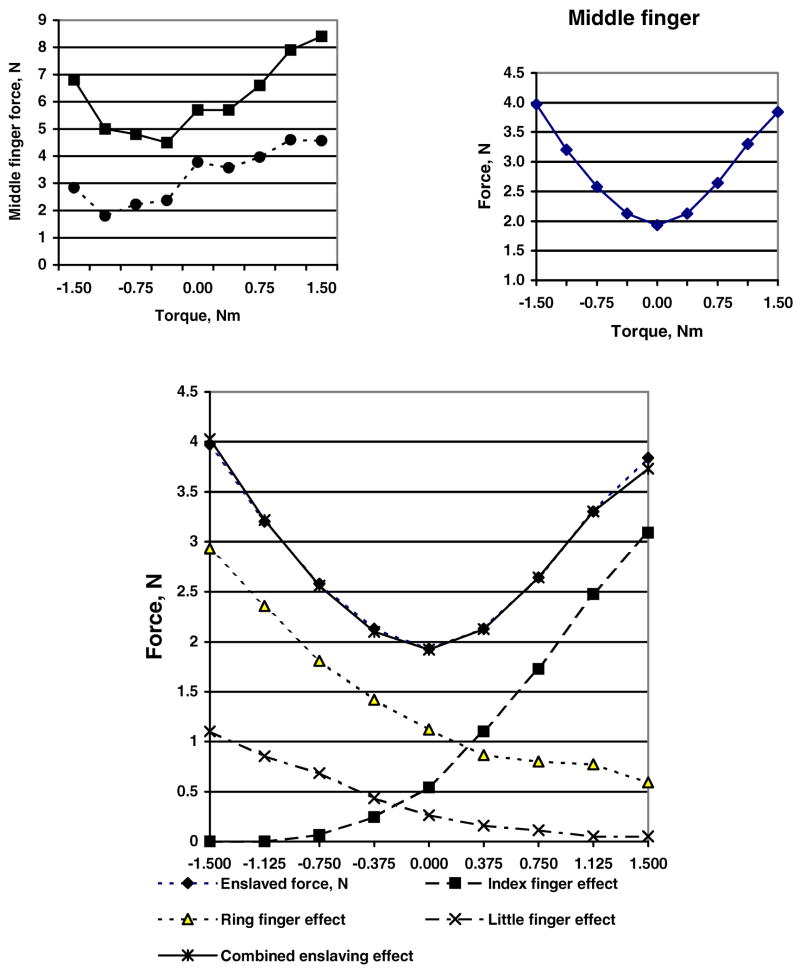
For the grasps with complex friction patterns, the local and synergic reactions of the individual digits to the friction and load alterations can be discerned. In the present context, the term local designates responses that start and end at the same digit, i.e. an effect of friction at a given digit on the force exerted by this digit. The term synergic refers to changes of finger C force in response to changes in friction for finger A and/or B (Aoki et al. 2006; Aoki, Latash, Zatsiorsky 2007; Zatsiorsky, Gao, Latash 2006). In experiments performed by Niu, Latash, Zatsiorsky (2007) subjects statically held a handle in a three-digit prismatic grasp. The friction under each digit was either high or low, resulting in eight friction conditions. When friction under a digit was low, its respective tangential force decreased and the normal force increased (local effects). Digit forces were also adjusted to friction at other digits (synergic effects). The synergic effects were directed to maintain the handle equilibrium. For instance, to keep the total tangential force constant, the tangential forces of the thumb and fingers changed in opposite directions (Figure 12). The normal digit forces also demonstrated local and synergic effects. The tangential force adjustments to the local friction support the notion that the VF tangential force sharing is under neural control; the sharing percentage is not determined solely by the passive mechanical properties of the individual fingers.

Figure 12.

Tangential forces of the thumb (left panel) and VF (right panel) as a function of the load and friction, high (H) or low (L), in three-digit grasps. The eight friction conditions were HHH, HLL, HHL, HLH, LLL, LHH, LHL, and LLH, where the letters correspond to the friction condition for the thumb, index and middle fingers, respectively. The difference between the high and low friction was approximately threefold. The friction sets with the thumb at the low friction contact (LLL, LHH, LHL and LLH) are printed with dotted lines. The solid lines represent the tasks with the high friction contact at the thumb. In the left panel, two smaller figure brackets show the synergic effects, i.e. the effect of friction at other digits on the thumb force. The numbers in the bottom right insets are the regression coefficients and intercepts (the regression model $f_i^t=a_i+k_i^{(1)}L$. was used for computations). Note the small values of the intercepts. Compare the right and the left panels: the thumb friction, H or L, induced opposite changes of the thumb and VF forces. Reprinted by permission from Niu X, Latash ML, and Zatsiorsky VM (2007) Prehension synergies in the grasps with complex friction patterns: local vs. synergic effects and the template control. Journal of Neurophysiology (in press).

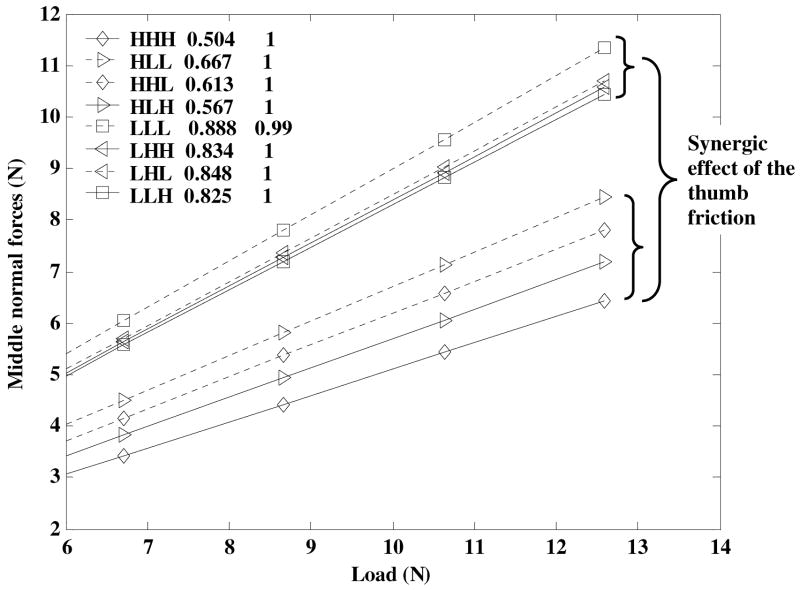
A triple-product model of the digit force control (Niu et al. 2007) describes the experimental data quite accurately. According to the model, the relation between the forces and loads is $f_i^n=k_i^{(2)}{k}_i^{(1)}L$ where $f_i^n$ is normal force of digit i, L is the load (newtons), $k_i^{(1)}$ is a dimensionless coefficient representing sharing the total tangential force among the digits ( $\sum k_i^{(1)}=1.0$), and $k_i^{(2)}$ is a coefficient representing the relation between the tangential and normal forces of digit i (the overall friction equivalent, OFE). The OFEs were influenced both by the local and synergic effects. The three-element sets of $k_i^{(2)}{k}_i^{(1)}$ products (the grasping templates) equal the digit forces at a unit load. The templates are scaled with the load magnitude. The essence of the model is that operations of grasping control are performed in sequence: (1) the coefficients $k_i^{(1)}$ and hence the tangential forces at each digit are determined, (2) based on the tangential forces and friction values at all digits the CNS determines the OFEs, i.e. the $k_i^{(2)}$ coefficients, and (3) the triple products $f_i^n=k_i^{(2)}{k}_i^{(1)}L$ are computed. The model accurately describes the experimental data (see Figure 13 as an example).

Figure 13.

Dependence of the middle finger normal force on the load for different friction sets. Group averages are shown. The numbers in the figure are the $k_i^{(3)}$ coefficients and the coefficients of correlation squared (all r²≥0.98). The dotted lines designate the low friction contact at the middle finger. The two groups of the regression lines were mainly distinguished by the friction at the thumb (the synergic effect). The two small figure brackets show the local friction effect, i.e. the force variations induced by the high or low friction contact at the middle finger. At a given thumb friction, the forces were larger at the low friction contact at the middle finger. Adapted by permission from Niu X, Latash ML, and Zatsiorsky VM (2007) Prehension synergies in the grasps with complex friction patterns: local vs. synergic effects and the template control. Journal of Neurophysiology (in press).

III.1.2. A non-vertically oriented object at rest

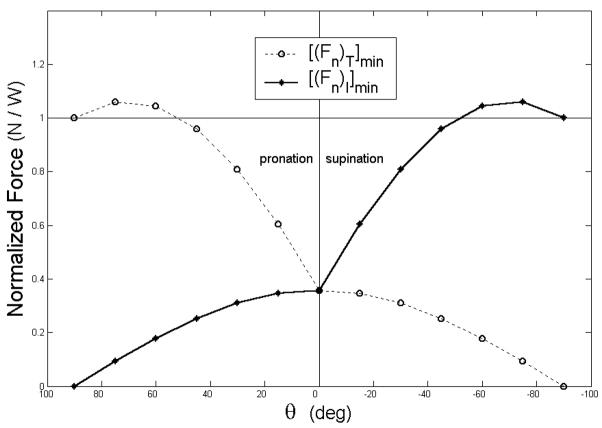
When the object is rotated from the vertical orientation, e.g. when a glass filled with water is tilted during drinking, the normal digit forces are not horizontal anymore and the tangential forces are not vertical. The thumb Fⁿ no longer equals the VF Fⁿ; therefore the notion of SM (equation 1) cannot be applied. The Fⁿ of the thumb in supinated postures and of the fingers in pronated postures will exert force in the downward direction, contribute to the object weight, and hence acts as a force antagonist. Because the agonist digits (those that support the object weight) always exert a larger normal force than the force antagonists, the slipping prevention is achieved by a sufficiently large normal force of the antagonist digits. The minimal forces necessary to prevent slipping and support the object for a simplified case of zero Mⁿ are shown in Figure 14. Even this simple and idealized model has inherently highly complex mechanics. The relations presented in the figure are nonlinear. There is a discontinuity in each digit’s behavior at the θ = 0.

Figure 14.

The minimum normal forces to prevent slipping and support load for a pinch grasp performed with the T and I digits. By assumption, the normal forces exert no net moment. Results of mathematical modeling. θ is an inclination angle. Adapted by permission from Pataky TC, Latash ML, and Zatsiorsky VM (2004b) Prehension synergies during nonvertical grasping, II: Modeling and optimization. Biol Cybern. 91: 231–242.

The CNS must adjust digit forces to these requirements. The adjustments are perfectly coordinated and highly reproducible (Figure 15).

Figure 15.

Normal internal force (ordinate) as a function of the sine of the handle orientation angle (abscissa). The force is normalized by object weight (corresponding to the masses of 830, 1080 or 1330 g) and hence is dimensionless. Group average data are shown. Note that the curves to the right (supination) and to the left (pronation) on the zero inclination line are slightly concave and do not converge to the zero force levels. (Adapted by permission from T.C. Pataky, M.L. Latash, and V.M. Zatsiorsky. Prehension synergies during nonvertical grasping, I: experimental observations. Biological Cybernetics, 2004, 91: 148–158.)

When normalized by object weight, the force-orientation relations for various supported loads were remarkably alike. The forces did not change as a sine or cosine function of orientation. This conclusion agrees well with the results of mathematical modeling of the non-vertical grasping (Pataky, Latash, Zatsiorsky 2004a).

III. 1.3 Motion of a vertically oriented object, zero-torque tasks

Vertical motion

This is the only object manipulation task that has been investigated in detail. When people move a vertically oriented object up or down, an inertial force acts in the vertical direction in addition to the gravity force. The load force (L, tangential force) in this case equals L=W+ma, where W is the weight, m is mass of the object and a is its acceleration.

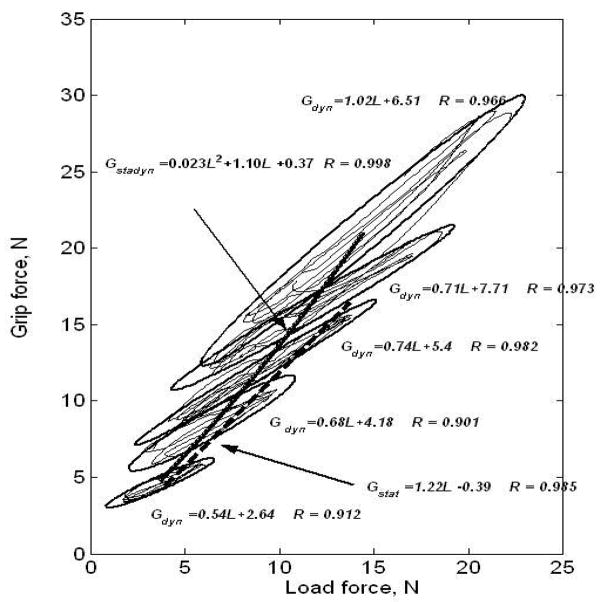
The digit forces—at the VF-thumb level—during such a manipulation produce both compensated normal forces (grasp force) and compensated rotational actions (internal moment, reviewed later in the text). When the load force increases, the grasp force (F_G) also increases (Johansson, Westling 1984), apparently to prevent slip. The grasp force-load force relation (reviewed in Flanagan, Johansson 2002) is so strong that people increase F_G in parallel with L even when F_G is already much above the slipping threshold, e.g. when before lifting the object a performer purposefully grasps the object with a high force (Flanagan, Wing 1995). A relation between F_G and L forces during lifting an object, a grasping synergy (Zatsiorsky, Latash 2004), develops at an early age (Forssberg et al. 1991; Blank, Breitenbach, Nitschke, Heizer, Letzgus, Hermsdorfer 2001) and is a sign of skilled hand function (see Gordon 2001 for review). The grasp force is modulated by the weight of the object (Johansson, Westling 1984; Winstein, Abbs, Petashnick 1991), abrupt load perturbations (Cole, Abbs 1988; Eliasson, Forssberg, Ikuta, Apel, Westling, Johansson 1995, Serrien, Kaluzny, Wicki, Wiesendanger 1999), friction conditions (Cole, Johansson 1993; Cadoret, Smith 1996; Burstedt et. al. 1999a, b), tangential torques (Kinoshita et. al. 1997), gravity changes during parabolic flights (McIntyre, Berthoz, Lacquaniti 1998; Hermsdorfer, Marquardt, Philipp, Zierdt, Nowak, Glasauer, Mai 1999a; Augurelle, Penta, White, Thonnard 2003a), and inertial forces that act during shaking and point-to-point arm movements (Flanagan, Wing 1993, 1995; Flanagan, Tresilian 1994; Kinoshita, Kawai, Ikuta, Teraoka 1996) as well as during locomotion (Gysin, Kaminski, Gordon 2003). During similar manipulations, the grasp forces are larger in senior adults (Kinoshita, Francis 1996; Cole, Rotella 2002) and patients with neurological disorders (Gordon, Duff 1999; Babin-Ratté, Sirigu, Gilles, Wing 1999; Hermsdorfer, Ulrich, Marquardt, Goldenberg, Mai 1999b; Serrien, Wiesendanger 1999a, b; Fellows, Noth, Schwarz 1998; Fellows, Ernst, Schwarz, Topper, Noth 2001; Fellows, Noth 2004). Local skin anesthesia and digit cooling make the coordination of the load and grasp force less precise but does not change the general pattern of coordination (Nowak, Hermsdorfer, Glasauer, Philipp, Meyer, Mai 2001; Monzee, Lamarre, Smith 2003; Nowak, Hermsdörfer 2003). Based on these observations, it has been concluded that the grasp force-load force coupling is mainly controlled by a feed-forward mechanism: A central controller regulates the grasp force according to the expected load force (Johansson, Westling 1984; Flanagan, Wing 1995) while feedback mechanisms triggered by cutaneous sensors act if an assessment of an expected load force happens to be erroneous.

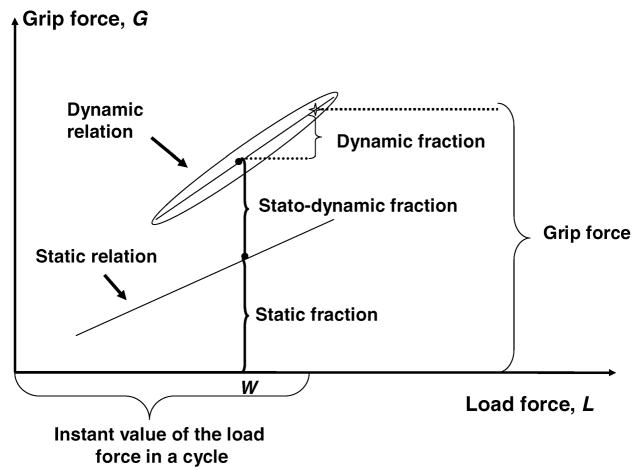
According to basic physics, the local effects induced by gravity and acceleration are identical and cannot be separated by any physical experiment, e.g. physics in a gravitational field are equivalent to physics in an accelerating spacecraft (the so-called equivalence principle, Einstein 1907). However, changes of object weight or acceleration cause different modulations of the grasp force in humans (Zatsiorsky, Gao, Latash 2005). The grasp force during object manipulation can be expanded intro three fractions (Figure 16): (a) Static fraction reflects grasp force related to holding a load statically. (b) Stato-dynamic fraction reflects a steady change in the grasp force when the same load is moved cyclically. (c) Dynamic fraction is due to the acceleration-related adjustments of the grasp force during oscillation cycles.

Figure 16.

Expanding the grasp force into the three fractions, a schematic. In the experiment, the subjects oscillated the object in the vertical direction. In the figure, an instant value of the grasp force is represented as the sum of the static, stato-dynamic and dynamic fractions. W is the object weight. The static relation is represented by a straight line. To obtain the static relation the subjects held at rest objects of different weight. The dynamic relation is represented by an ellipse. The relation is a grasp force-load force plot recorded in a single trial. (Reprinted by permission from V.M. Zatsiorsky, F. Gao, and M.L. Latash. Motor control goes beyond physics: differential effects of gravity and inertia on finger forces during manipulation of hand-held objects. Experimental Brain Research. 2005, 162: 300–308).

The slope of the relation between the grasp force and the load force is steeper for the static fraction than for the dynamic fraction. The stato-dynamic fraction increases with the frequency and load. The slopes of the dynamic grasp force-load force relations decrease with the frequency of load motion and, as a rule, increase with the load. Hence, when adjusting grasp force to task requirements, the central controller takes into account not only the expected magnitude of the load force but also such factors as whether the force is gravitational or inertial and the contributions of the object mass and acceleration into the inertial force (Figure 17). It is not presently known whether the different responses to gravity and acceleration during purposeful manipulation arise from the motor control of the task or they have other origins at different levels (cognitive, volitional, etc).

Figure 17.

Static, dynamic and stato-dynamic relations between the grasp and load forces. The inertial forces are due to an oscillation of the vertically oriented handle at 1.5 Hz over about 10 cm in the vertical plane. The weights are 3.8, 6.3, 8.8, 11.3, and 13.8 N. Data from a representative subject are shown. W is the object weight and the load force is L=W+ma. The broken line represents the static load-grasp force relation; the solid line represents the stato-dynamic relation, and the ellipses illustrate the dynamic relations between the variable load force and the grasping force. Reprinted by permission from V.M. Zatsiorsky, F. Gao, and M.L. Latash. Motor control goes beyond physics: differential effects of gravity and inertia on finger forces during manipulation of hand-held objects. Experimental Brain Research. 2005, 162: 300–308.

Horizontal motion

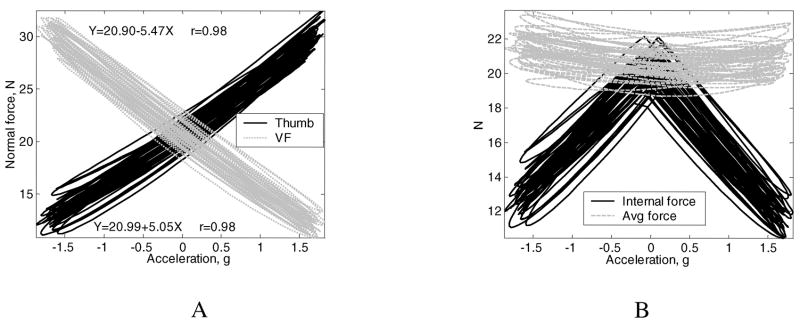
The horizontal transport of a vertically oriented object has been studied by Smith and Soechting (2005) and by Gao, Latash, Zatsiorsky (2005). In the first study, subjects held an object in a tripod grasp from above and moved it in a horizontal plane in various directions; in the second study, a prismatic grasp was used. In both studies, the grasping forces reached a peak near the time of peak velocity when the object acceleration was equal or close to zero (Figure 18). Note that at the extreme points of the oscillatory movements, the force exerted in the opposite direction to the manipulation force was low and hence the slip was mainly prevented by the large manipulation force. It would be interesting to know whether similar coordination pattern is used in tennis and golf strokes. Do people grasp the implement stronger at the instances of minimal acceleration?

Figure 18.

Normal forces of the thumb and VF (A) and internal force and average normal force (B) versus the handle acceleration in the horizontal direction. Data shown are from a representative trial. The load was 11.3 N, the frequency was 3 Hz. Adapted from F. Gao, M.L. Latash, and V.M. Zatsiorsky. Internal forces during object manipulation. Experimental Brain Research. 2005, 165: 69–83.

III.2 Tilt prevention

Tilt prevention is achieved by an appropriate combination of two contributors to the rotational hand action: (a) moment of the tangential forces M^t that results from unequal thumb and VF tangential forces, and (b) moment of the normal forces. The moment of the normal forces Mⁿ is due to the normal forces of the thumb and VF.

In multi-digit grasps: (a) both Mⁿ and M^t are always present; (b) in the zero-torque tasks at rest Mⁿ and M^t act in opposite directions and cancel each other (Shim, Latash, Zatsiorsky 2003; Gao, Latash, Zatsiorsky 2005b, c); (c) during the object manipulation Mⁿ and M^t change in synchrony in opposite directions and cancel each other (Gao et al. 2005b; Figure 19); (d) in non-zero torque tasks Mⁿ and M^t act in the same direction assisting each other (Zatsiorsky, Gregory, Latash 2002a). When Mⁿ and M^t cancel each other they constitute an internal force, or more specifically an internal moment.

Figure 19.

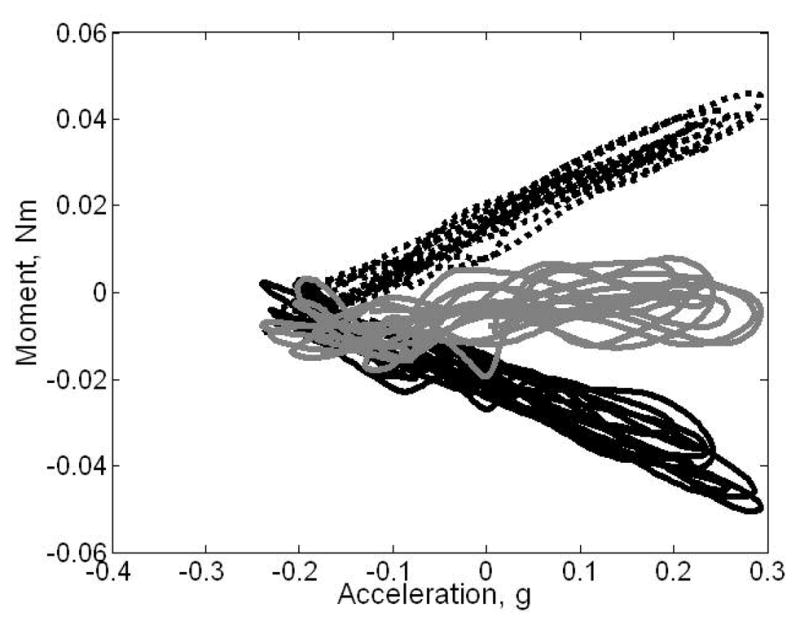
Internal and resultant moments during horizontal oscillation of a horizontally oriented handle (frequency 1 Hz, weight 6.3 N). Data from a representative trial are shown. Dotted black line – moment of tangential forces; solid black line – moment of the normal forces; gray line –the total moment. During the manipulation, both Mⁿ and M^t change in synchrony while the total moment remains relatively constant. Adapted by permission from F. Gao, M.L. Latash, and V.M. Zatsiorsky. Internal forces during object manipulation. Experimental Brain Research. 2005, 165: 69–83.

III.3 Resistance to perturbation

In cases of external mechanical perturbations, digit forces have to adjust to ensure grasp stability. A common assumption is that stability is achieved by spring-like reactions at joints; the reactions are due to both elastic properties of the muscle and tendons and the short-latency stretch reflexes. If the assumption is correct, grasp stability can be characterized by the grasp stiffness, which was successfully measured by Van Doren (1998) and by Friedman and Flash (2007). In the first study, the grasp stiffness was estimated in the plane of grasp; in the second study it was computed in three dimensions (the stiffness ellipsoids were computed). A new hypothesis has however been offered recently suggesting that immediate responses to perturbations in many situations assist rather than resist the perturbation and are, therefore, destabilizing (Hazan 2005). Our data agree with this new hypothesis.

In our experiments, subjects grasped a customized motorized handle with five digits and held it statically in the air (Zatsiorsky, Gao, Latash 2006). The handle width either increased (expanded) or decreased (contracted) at a rate of 1.0, 1.5, or 2.0 mm/s, while the subjects were asked to ignore the handle width changes and their attention was distracted. (they were asked to count down from a large number in their mind). External torques of 0.0, 0.25, and 0.5 Nm were applied to the handle in two directions while the subjects resisted the torques by exerting the pronation moments (positive, counterclockwise) or supination moments (negative, clockwise), respectively.

In all the tasks, the normal VF and thumb forces increased with the handle expansion and decreased with the handle contraction. Similar behavior was seen for the thumb tangential force. In contrast, the VF tangential force decreased with the handle expansion and increased with the handle contraction. The changes in the tangential forces assisted the moment perturbations in the tasks requiring exertion of the supination moments and acted against the moment perturbation in the pronation effort tasks. In the former tasks, the equilibrium was maintained by the changes of the moment of normal forces, while in the latter tasks the equilibrium was maintained by the changes of the moment of the tangential forces. The Mⁿ behavior followed a simple algebraic rule; it could be represented as the product of positive and negative entries (Table 1). The changes of M^t were always opposite to the Mⁿ changes.

Table 1.

Effects of the handle expansion and contraction on the magnitudes of the moments of the normal (Mⁿ) and tangential (M^t) forces in the pronation (+) and supination (−) effort tasks.

[From V.M, Zatsiorsky, F. Gao, and M.L. Latash (2006) Prehension stability: Experiments with expanding and contracting handle. Journal of Neurophysiology 95: 2513–2529.]

Initial torque effort	Handle expansion (+)		Handle contraction (−)
	Moment of normal forces	Moment of tangential forces	Moment of normal forces	Moment of tangential forces
Pronation (positive, +)	Increases, (+, +)	Decreases, −(+, +)	Decreases, (+,−)	Increases, −(+,−)
Supination (negative, −)	Decreases, (−,+)	Increases, −(−,+)	Increases, (−, −)	Decreases, − (−, −)

Note. The Mⁿ and M^t behavior is represented as products of positive and negative entries. The pronation and handle expansion entries are considered positive, and the supination entries are considered negative. Hence, the expression (+,+) signifies handle expansion in pronation tasks; it yields the Mⁿ increase. The (+,−) combination, i.e. a handle increase during supination tasks, results in decreasing the Mⁿ magnitude. The values in other cells are interpreted in a similar way.

Handle expansion/contraction does not affect the load force and external torque acting on the handle, i.e. it does not immediately perturb the handle equilibrium. The simplest strategy for the performer to prevent slip and tilt, e.g. in zero-torque tasks, would be to do nothing, i.e. to not change the digit forces. However, in all the tasks, numerous interrelated adjustments of the individual digit forces and moments to the perturbation occurred. The adjustments of digit forces to handle width changes may be viewed as coming from two sources. First, there are local spring-like adjustments of individual digit forces and moments due to both mechanical properties of the digits and the action of spinal reflexes. These spring-like reactions mainly contribute to perturbing the rotational equilibrium of the object rather than to maintaining it. Second, there are tilt-preventing adjustments defined by the common task constraints that unite the digits into a task-specific synergy.

IV. Prehension control

As in any motor control research, main goals of prehension studies are not to describe the behavior but, ultimately, to offer an explanation of experimental findings, i.e. to formulate a limited set of hypotheses, rules, and principles that can account for and predict observable behavior. This section addresses several such governing principles applicable to various prehension tasks. We should admit that we are presently at the very beginning of this endeavor and many experimental findings have no explanation.

Prehension is controlled: (a) in a hierarchical fashion and (b) as a set of synergies. At least two levels of control can be distinguished. At an upper level (the VF-thumb level), an apposition space is created between the thumb and a virtual finger and their forces are specified. At the level of individual fingers (the IF level), VF action is used to define the forces exerted by individual fingers. Such a hierarchical control provides computational advantages; this conclusion was supported by neural network modeling (Gao, Latash, Zatsiorsky 2004).

IV.1 Prehension synergies and chain effects

Prehension synergies have been identified as conjoint changes in finger forces and moments during multi-finger gripping tasks (Santello, Soechting 2000; Rearick., Santello 2002;Baud-Bovy, Soechting 2002; Zatsiorsky, Gao, Latash 2003b; Zatsiorsky, Latash 2004; Pataky, Latash, Zatsiorsky 2004a, b; Shim, Latash, Zatsiorsky 2003, 2005a, b). Some of these adjustments are dictated by mechanics, whereas others are results of choice by the CNS.

To study prehension synergies, researchers have so far employed five experimental techniques, they: (a) inflicted external perturbations (Cole, Abbs 1987, 1988; Zatsiorsky et al. 2006); (b) inflicted self-perturbations— the subjects varied the number of grasping fingers during prehension (Budgeon, 2007); (c) recorded correlations among output variables in single trials of long duration (Santello, Soechting 2000; Vaillancourt, Slifkin, Newell 2002); (d) varied the task parameters, in particular the object geometry, resisted torque and/or load (Zatsiorsky, Gregory, Latash 2002a, b; Zatsiorsky, Gao, Latash 2003) and (e) studied trial-to-trial variability (Shim, Latash, Zatsiorsky 2003, 2005b; Shim, Park 2007).

A general conclusion from all these studies is that during prehension the individual digit force variations are always interrelated; i.e. they manifest the prehension synergies. For instance, people do not perform the same prehension task in one and the same way; in each trial, the digit forces are different. However, a change in one elemental variable is compensated by an adjustment in another variable such that the total output is constant (Figure 20).

Figure 20.

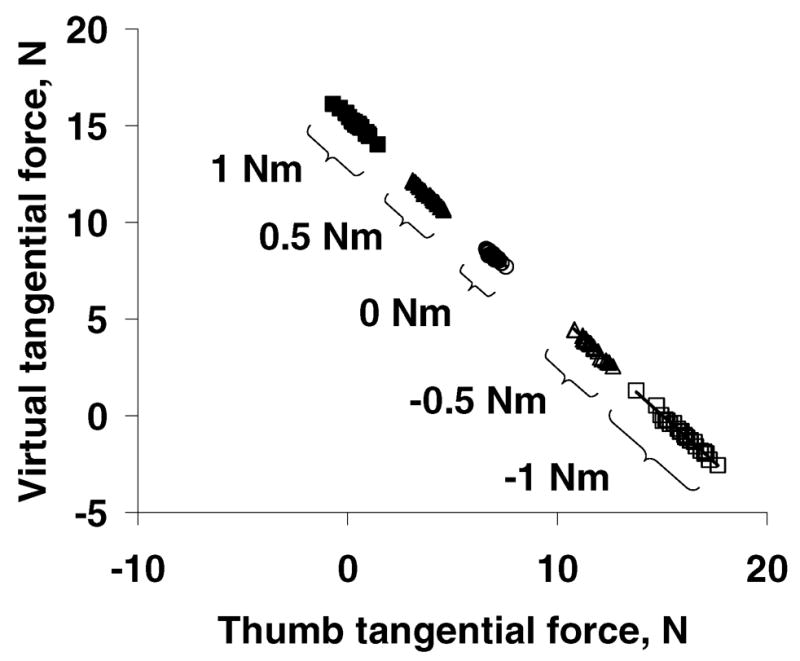
Tangential forces of the thumb versus tangential forces of the virtual finger across 25 trials. Data from a representative subject are shown. The subjects performed 25 trials at each of the external torques −1.0 Nm, −0.5 Nm, 0 Nm, 0.5 Nm and 1.0 Nm while the total load was always 14.9 N. In individual trials the forces were different. However, they were along the same line such that their sum was always constant. All the coefficients of correlation were −1.00. Because the moment of the tangential forces is proportional to the difference between the tangential forces, different location of the forces along the line is indicative of the different moment of tangential forces. The trial-to-trial variations of the moment of tangential forces were compensated by the matching changes of the moments of normal forces (not shown in the figure). Adapted by permission from J.K. Shim, M.L. Latash, and V.M. Zatsiorsky (2003). Prehension synergies: tria-to-trial variability and hierarchical organization of stable performance. Experimental Brain Research. 2003, 152: 173–184.

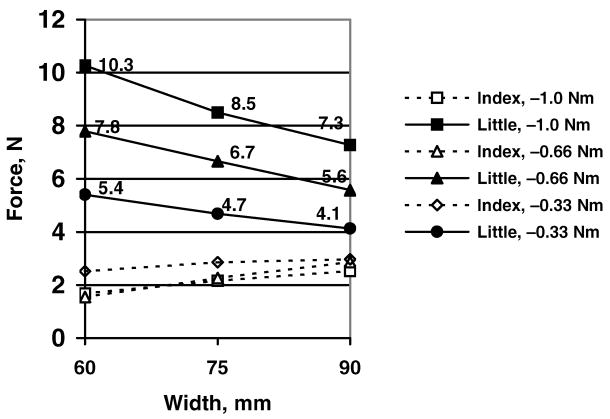
If several elemental variables are involved, the relations among the variables—e.g. individual digit forces, displacements of the points of their application, moments of the normal and tangential forces, etc.—can be explained and predicted by chain effects (Zatsiorsky, Gregory, Latash 2002b; Zatsiorsky, Gao, Latash 2003b; Shim, Latash, Zatsiorsky 2003, 2005a, b). The chain effects are sequences of local cause-effect adjustments necessitated by the task mechanics. The word ‘sequence’ in the above definition does not imply a chronological order; it only refers to the cause-effect relations. The chain effects arise from the necessity to find a solution that simultaneously satisfies a variety of constraints. Similar situation occurs in the control of the muscles serving the index finger (Valero-Cuevas, Zajac, Burgar 1998; Valero-Cuevas 2005). One example of the chain effects is presented in Figure 21: an increase in the handle width during the supination efforts across the trials causes —after several chain effects—a decrease in the little finger force and an increase in the index finger force. Specifically, an increase of the handle width induced the following effects: (a) tangential forces remained unchanged, (b) the same tangential forces produced a larger moment M^t, (c) the increased M^t was compensated by a smaller moment of the normal forces Mⁿ, and (d) the normal finger forces were rearranged to generate a smaller moment (Zatsiorsky et al. 2002a, b): the little finger force decreased and the index finger force increased.

Figure 21.

The normal forces of the index and little fingers at the different widths of the handle during the supination efforts of −1.0, −0.66 and −0.33 Nm. When the width increases, the force of the little finger decreases and the force of the index finger increases. As a result the moment of the normal forces decreases. The forces of the ‘central’ fingers (middle and the ring) that have the smaller moment arms do not change systematically. To avoid a messy picture these forces are not shown in the figure. (Reprinted by permission from V.M. Zatsiorsky, R.W. Gregory, and M.L. Latash. Force and torque production in static multifinger prehension: biomechanics and control. I. Biomechanics. Biological Cybernetics, 2002, 87:50–57.)

Other possible examples of chain effects are:

1. Adjustments to friction. In a recent experiment (Aoki et al. 2006), four friction conditions were tested, two symmetric conditions (1- high friction under the thumb & high friction under the fingers, 2- low & low friction) and two asymmetric conditions (3- high & low friction, 4- low & high friction). Subjects exerted smaller tangential forces at the surfaces with lower friction. Compared to symmetric tasks, in asymmetric tasks the sharing percentage of the individual normal digit forces changed. For the zero torque tasks this fact was explained by the following chain effects: (1) the subjects decreased the tangential force of the thumb or VF that was in contact with the surface with lower friction; (2) to maintain the sum of the tangential forces constant they also increased the tangential force at the side with higher friction; (3) these opposite tangential force changes generated M^t; (4) the M^t was compensated by an opposite Mⁿ; and (5) to produce the Mⁿ, normal forces of the individual fingers were rearranged.

2. Reaction to changes in the object size during the trial (see section III.3 above). In all the tasks, the sharing percentage of the normal finger force varied and the point of application of the VF normal force was displaced. The following chain effects explain some of the findings: increasing/decreasing the handle width changed the moment arms of the tangential forces → the M^t changed → to maintain the total moment constant, Mⁿ should undergo opposite changes → the individual normal finger forces were adjusted.

3. In three dimensions, an increase of the external torque in one direction changes the forces exerted in all three directions (see Figure 10). A set of chain effects explains this finding (Shim, Latash, Zatsiorsky 2005a). Omitting the details, the chain effects can be explained in the following way. The forces change because the line of action of the VF normal force acting in Z direction is not collinear with the line of action of the thumb normal force (this major experimental finding could not be predicted from the grasp mechanics). The VF and the thumb normal forces are equal in magnitude; they form a force couple that generates rotational effects about the X- and Y-axes. To preserve the rotational equilibrium of the handle, the moments of the couple must be counterbalanced. It is achieved by moments generated by the X- and Y-force components. Thus, the systematic relations in 3-D are mechanically necessary.

IV.2. Prehension control at the VF level and the principle of superposition

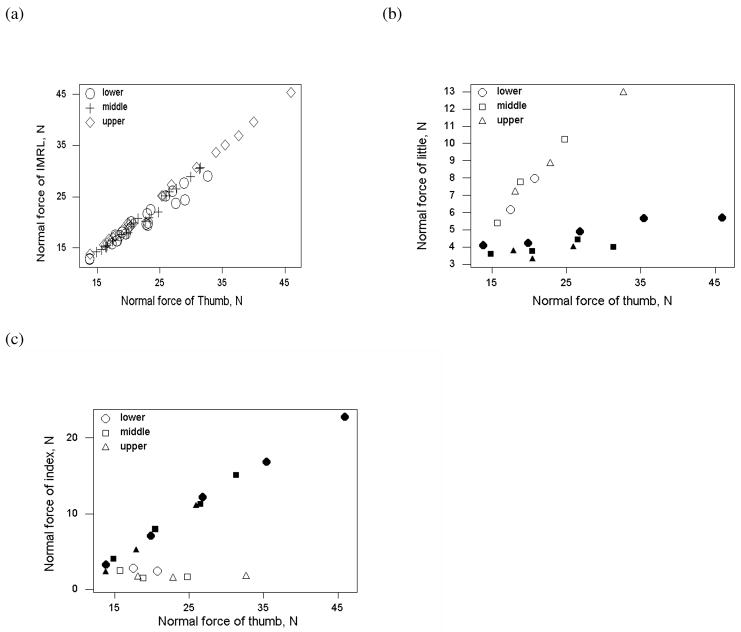
There are substantial differences between the VF and IF forces: (a) The force directions are as a rule dissimilar. The IF forces can be exerted in disparate directions such that only their resultant (i.e. VF) force is in the desired direction (see Figure 5). (b) VF and IF forces adjust differently to modified task conditions (Figure 22). (c) IF forces are much more variable than VF forces (Shim et al. 2005a, b). In all the above examples, the desired performance at the VF level is achieved by a synergetic co-variation among elemental variables at the IF level.

Figure 22.

The relations between the normal forces of the thumb and the fingers. (a) the virtual finger force, (b) the little finger force, (c) the index finger force. Open symbols represent supination efforts and the closed symbols represent pronation efforts. Note the difference between the (a) panel and other two panels. The thumb transducer position was varied across trials: (a) middle position - the center line of the thumb sensor was at the midpoint of the handle; (b) bottom position - the center line of the thumb sensor was at the midpoint between the center lines of the ring and little finger sensors; and (c) upper position - situated at the midpoint between the center lines of the index and middle finger sensors. Group average data are shown. Adapted by permission from V.M. Zatsiorsky, F. Gao, and M.L. Latash. Prehension synergies: Effects of object geometry and prescribed torques. Experimental Brain Research, 2003, 148: 77–87.

According to the principle of superposition, as suggested in robotics (Arimoto, Tahara, Yamaguchi, Nguyen, Han 2001), some skilled actions can be decomposed into several elemental actions that can be controlled independently by several controllers. It has been shown that dexterous manipulation of an object by two soft-tip robot fingers can be realized by a linear superposition of two commands, one command for the stable grasping and the second one for regulating the orientation of the object. In robotics, such a decoupled control decreases the computation time.

When applied to human performers and multi-finger grasps, the principle claims that forces and moments during prehension are defined by two independent commands: “Grasp the object stronger/weaker to prevent slipping” and “Maintain the rotational equilibrium of the object”. The effects of the two commands are summed up. The commands correspond to the two internal forces discussed previously, the grip force and the internal moment. The following evidence supports the validity of the principle for human grasping:

(A) When the resisted load and torque change in a systematic manner, both LOAD and TORQUE factors show highly significant effects on most elemental variables, while the interaction LOAD×TORQUE is not significant. The finger force changes associated with manipulation of one of the factors do not depend on the magnitude (level) of the other factor (see again Figure 8C above). The lack of the statistically significant interaction effects implies an additive action of the LOAD and TORQUE commands.

(B) Studies of trial-to-trial variability of digit forces in planar tasks (Shim et al. 2003; Zatsiorsky, Latash, Gao, Shim 2004) were performed with the subjects keeping the handle at rest in the air while applying minimal grasping effort. The subjects performed 25 trials at each of the five external torques: −1.0 Nm, −0.5 Nm, 0 Nm, 0.5 Nm and 1.0 Nm.

All the efforts were made to assure stable grasping and performance. Nevertheless, the digit forces varied across repetitive trials at the same external torque (see Figure 20). All the elemental variables at the VF-thumb level formed two subsets (Figure 23). The variables within each subset highly correlated with each other over repetitions of a task while the variables from different subsets did not correlate. The first subset included normal forces of the thumb and VF. The second subset included tangential forces of the thumb and VF, the moments produced by the tangential and normal forces, and the moment arm of the VF normal force, i.e. the projected vertical distance between the points of application of the VF and thumb normal forces. In particular, trial-to-trial changes of the VF normal force $F_{vf}^n$ did not correlate with the variations of the moment of the normal force $M_{vf}^n$ (Figure 23 A-2). Because moment of the VF normal force is the product of this force and its moment arm, this lack of correlation is counter-intuitive. In contrast, a high correlation between $M_{vf}^n$ and the tangential force of the thumb (or VF) was discovered (Figure 23 B-4).

Figure 23.

Interrelations among the experimental variables over 25 trials. The data are from a representative subject. F and M designate the force and moment; superscripts n and t refer to the normal and tangential force components; subscripts th and vf refer to the thumb and virtual finger, respectively. A-1: $F_{th}^n$ correlated closely with $F_{vf}^n$. This correlation was expected: in static tasks $F_{th}^n$ and $F_{vf}^n$ cancel each other. These two forces represent the first subset of variables mentioned in the text. A-2: $F_{vf}^n$ versus $M_{vf}^n$. The correlation coefficients are close to zero. B-1: $F_{th}^t$ versus $F_{vf}^t$. The values of $F_{th}^t$ and $F_{vf}^t$ are on a straight line. This correlation was expected because $F_{th}^t+F_{vf}^t=\text{Constant}(\text{weight}\text{of}\text{handle})$. The different location of $F_{th}^t$ and $F_{vf}^t$ values along the straight line signifies the different magnitude of M^t. B-2: $F_{vf}^t$ versus $M^t[M^t=0.5(F_{vf}^t-F_{th}^v)d$, where d = 68 mm]. As the sum $F_{th}^t$ and $F_{vf}^t$ is constant a change in one of these forces determines the difference between their values and, hence, the moment that these force produce. B-3: M^t versus $M_{vf}^n$. B-4: $M_{vf}^n$ versus $F_{th}^t$. The variables in the panels B ( $F_{th}^t,F_{vf}^t,M^t,M_{vf}^n$) plus moment arm of the VF normal force constitute the second subset of variables mentioned in the text. The curved arrows signify the sequence of events resulting in the high correlation between $F_{th}^t$ and $M_{vf}^n$ (‘chain effects’). Such a correlation does not exist between $F_{vf}^n$ and $M_{vf}^n$, see panel A-2. (Reprinted by permission from V.M. Zatsiorsky, M.L. Latash, F. Gao, and J.K. Shim. The principle of superposition in human prehension. Robotica, 2004, 22: 231–234.)

Functionally, fine-tuning of the variables of the first subset prevents the object from slipping out of the hand and from moving in the horizontal direction. Conjoint adjustments of the variables of the second subset maintain the torque and vertical orientation of the handle constant (they also prevent the object from moving in the vertical direction). Hence the data conform to the principle of superposition: Preventing the object from slipping out of the hand and maintaining the object orientation are controlled by two separate commands whose effects on elemental variables do not interact with each other.

(C) The principle of superposition was shown to be valid for prehension in three dimensions (Shim et al. 2005b). The sets of elemental variables associated with moment production about the vertical axis in the grasp plane and the axis orthogonal to the grasp plane consisted of two non-correlated subsets each; one subset of variables was related to the control of grasping forces (grasp control) and the other subset was associated with the control of the orientation of the hand-held object (torque control).

(D) The principle is also valid for grasping circular objects (Shim, Park 2007). Principal component analysis showed that the elemental variables are combined into two groups: one group related to grasping stability control (normal force control) and the other group associated with rotational equilibrium control (tangential force control). These findings support the principle of superposition.

In summary, the variability of the elemental variables during prehension is: (a) inter-compensated in the sense that negative correlations among variables cancel the variability effect on the total outcome, e.g. on the resultant force or moment acting on the hand-held object (a note on terminology: in mathematical parlance, a completely compensated variability represents a null space of variables); and (b) is organized in two null spaces.

The variability and inter-compensation indicate that the CNS, in contrast to the common assumption, does not employ a unique optimal solution for a given task. An assumption is that the CNS performs motor tasks—whether it is walking (reviewed in Prilutsky, Zatsiorsky 2002), pedaling (Kautz, Hull 1995; Raasch, Zajac, Ma, Levine 1997), arm pointing (Flash, Hogan 1985; Uno, Kawato, Suzuki 1989; Dornay, Uno, Kawato, Suzuki 1996), manual lifting (Dysart, Woldstad 1996; Chang, Brown, Bloswick, Hsiang 2001), or prehension (Buss, Hashimoto, Moore 1996; Buss, Faybusovich, Moore 1998; Hershkovitz, Tasch, Teboulle, Tzelgov 1997; Zatsiorsky, Gregory, Latash 2002b, Pataky, Latash, Zatsiorsky 2004b; Lee, Zhang 2005; Aoki et al. 2006)—in an optimal way, by minimizing a certain cost function, is broadly accepted. However, as follows from the presented data, the optimization at best identifies only null spaces of the solutions, whereas other mechanisms take care of the fine-tuning of the motor variables to the task requirements.

IV.3. Prehension control at the IF level

We limit our discussion to two issues: (A) finger interdependence and (B) the mechanical advantage hypothesis.

IV.3.1. Finger interdependence, inter-finger connection matrices, and reconstruction of neural commands

Finger forces exerted during prehension are constrained by the finger interdependence (reviewed in Schieber, Santello, 2004). Finger interdependence is manifested as (a) force deficit and (b) finger enslaving. The above terms describe the following phenomena: (a) Force deficit — peak force generated by a finger in a multi-finger maximal voluntary contraction (MVC) task is smaller than its peak force in the single-finger MVC task. The deficit increases with the number of explicitly involved (master) fingers (Li, Latash, Zatsiorsky 1998a). (b) Enslaving—fingers that are not required to produce any force by instruction are involuntary activated (Kilbreath, Gandevia 1994; Li, Latash, Newell, Zatsiorsky 1998b; Zatsiorsky, Li, Latash. 2000; Kilbreath, Gorman, Raymond, Gandevia 2002). To demonstrate the enslaving turn your palm up and wiggle the ring finger. You will see that other fingers also move.

Finger interdependence can be described by inter-finger connection matrices that relate central commands to individual fingers with actual finger forces via a matrix equation (Zatsiorsky, Li, Latash, 1998; Li, Zatsiorsky, Latash, Bose 2002; Danion, Schöner, Latash, Li, Scholz, Zatsiorsky, 2003; Gao, Li S, Li ZM, Latash, Zatsiorsky 2003; Latash, Gao, Zatsiorsky 2003a):

$$\mathbf{F}=[\mathbf{W}]\mathbf{c}$$ [2]

where F is a (4×1) vector of the normal finger forces, [W] is a (4×4) inter-finger connection matrix whose elements depend on the number of fingers involved in the task, and c is a (4×1) vector of the central (neural) commands. The elements of vector c equal 1.0 if the finger is intended to produce maximal force (maximal voluntary activation) or 0.0 if the finger is not intended to produce force (no voluntary activation). Similar matrices were also computed for the finger interaction during maximal radial and ulnar deviation efforts (Pataky, Latash, Zatsiorsky 2007a).

For computing matrix [W] the maximal finger forces exerted in different tasks are recorded: the subjects are instructed to press on force sensors as hard as possible with either one two, three or four fingers, using all possible finger combinations. Then, the inter-finger connection matrices are computed by artificial neural networks (Zatsiorsky, Li, Latash 1998; Li, Zatsiorsky, Latash, Bose 2002; Gao, Latash, Zatsiorsky 2003, 2004; Latash, Gao, Zatsiorsky 2003a) or they are estimated by simple algebraic equations (Danion et al, 2003). The described approach led to the concept of finger modes that are arrays of finger forces caused by a single command to one of the fingers. Consider the following matrix that was computed in one of the studies (Zatsiorsky et al. 1998); the matrix is valid for the IMRL tasks:

$$\mathbf{F}=[\mathbf{W}]\mathbf{c}=\left[\begin{array}{cccc}25.075& 2.275& 0.95& 0.925\\ 3.55& 17.35& 3.4& 0.875\\ 2.25& 5.05& 13.9& 2.275\\ 2.2& 1.9& 4.0& 11.5\end{array}\right][\mathbf{c}]$$ [3]

The elements of the matrix are the weight coefficients. When multiplied by commands c_i they represent: (a) elements on the main diagonal: the forces exerted by finger i in response to the command sent to this finger (direct, or master, forces); (b) elements in rows: force of finger i due to the commands sent to all the fingers (sum of the direct and enslaved forces); and (c) elements in the columns: forces exerted by all four fingers due to a command sent to one of the fingers (a mode).

Force generated by a finger in prehension arises from a command sent to this finger (‘direct’ finger force) as well as from the commands sent to other fingers (enslaved force). The direct finger forces can be computed as the product w_ii c_i (i =1, 2, 3, 4) where w_ii is a diagonal element of the weight matrix, and c_i is a command intensity to this finger. To perform these computations, commands c_i to individual fingers should be known. In other words, the command vector c should be reconstructed. If matrix [W] is known and actual finger forces in a prehension task are recorded, the vector of neural commands c is reconstructed by inverting equation (1): c = [W]⁻¹F (Zatsiorsky, Gregory, Latash 2002b). Note that matrix [W] is 4×4 and is always invertible.

When the vector c is reconstructed, forces generated by individual fingers can be decomposed into components that are due to (a) direct commands to the targeted fingers, and (b) the enslaving effects, i.e. the commands sent to other fingers (Figure 23).

Force deficit and enslaving, originally discovered in maximal pressing tasks, exist also in prehension tasks with submaximal force production. Force deficit is manifested as the necessity to use a larger command intensity in order to generate a given force magnitude by a digit when another digit is active, as compared to force production by the first digit alone. Due to the enslaving, fingers that generate moment in the direction opposite to the direction required by the task (torque antagonists) are often activated (see Figure 8 D), even though such activation is mechanically not efficient (Zatsiorsky et al. 2002b). When mathematical optimization methods were applied to determine whether the force patterns observed in human prehension agree with certain optimization criteria, the cost functions based on finger forces were not able to predict the activation of the torque antagonists. In contrast, the command minimization predicted the presence and magnitude (approximately) of the antagonist forces (Figure 25). The criterion based on neural commands exhibited better performance because it accounts for enslaving effects while other criteria do not.

Figure 25.

Comparison of the actual force data with the force patterns predicted by different optimization criteria. The norms of the following vectors were employed as cost functions: G₁: Finger forces. G2: Finger forces normalized with respect to the maximal forces measured in single-finger tasks. G3: Finger forces normalized with respect to the maximal forces measured in a four-finger (IMRL) task. For the neural commands, the following objective function was optimized

$$G_4={\left(\sum _{i=1}^{i=4}{(c_i)}^p\right)}^{1/p}\to min(p=1,2\dots 15)$$

The norm powers from 1 to 15 were explored. The presented data are for p=3. Criteria G₁, G₂ and G₃ did not predict well antagonist moments. (Adapted by permission from V.M. Zatsiorsky, R.W. Gregory, and M.L. Latash. (2002b) Force and torque production in static multifinger prehension. II. Control. Biological Cybernetics, 87: 40–49.)

There is an apparent similarity between finger enslaving and the recently discovered lateral transmission of muscle forces (myo-fascial force transmission as opposed to the myo-tendinous transmission, Huijing 1998, 1999) when the force exerted by muscle fibers is transmitted to the bone not only via the muscle tendon but also via muscle sheaths, neighboring connective and muscle tissues, etc.

IV.3.2. Mechanical advantage of the fingers during moment production

Mechanical advantage of a finger, i.e. its moment arm during moment production, may affect the degree of that finger involvement during prehension tasks. There is a certain analogy between controlling the finger and muscle involvement. In particular, it has been reported that the EMG activity of a one-joint muscle is proportional to its moment arm at the joint (Buchanan, Almdale, Lewis, Rymer 1986; Buchanan, Rovai, Rymer 1989; Flanders, Soechting 1990, Nichols 1994, Kuo 1994; Prilutsky 2000).

During the moment production, fingers with larger moment arms have been shown to produce larger forces (Zatsiorsky et al. 2002a). When holding an object statically in the air against different loads and torques, the normal forces of the ‘peripheral’ (index and little) fingers, i.e. the fingers with the larger moment arms, depend mainly on the torque while the forces exerted by the ‘central’ (middle and ring) fingers depend both on the load and torque. During tasks in three dimensions (Shim et al. 2005a), fingers with a larger mechanical advantage also generated or resisted larger forces. When the task is to produce a moment on a mechanically fixed object, the mechanical advantage hypothesis was successful in explaining some of the data but could not cope with other findings (Shim, Latash, Zatsiorsky 2004a).

IV. 4. Combined effects of prehension adjustments to different factors

When manipulating hand-held objects, the performers adjust digit forces to (a) the load force and its modulation associated with the handle acceleration; (b) the external torque and its modulation; (c) the object orientation in the gravity field; (c) friction at the digit tips; (d) the object size (which is typically constant but can be varied as it was done in our recent experiments with the expanding or collapsing handles, Zatsiorsky et al. 2006), and some other variables. Some of these variables can vary at the same time. The variations may require similar or opposite adjustments. For instance, an increase of the object weight and a decrease in friction both require a larger gripping force while a decrease of the load and a decrease in friction require opposite grasp force changes, a force decrease and increase, respectively The question is: How does the CNS respond to combinations of similar and opposite requirements?

We would like to suggest the following postulate that we formulate in a slogan-like manner: Adjustment to the sum equals the sum of the adjustments. (We admit that this formulation mimics a well known in mechanics theorem of moments: Moment of the sum equals the sum of the moments.)

Here are a few examples suggesting that the above postulate is valid.

(A) In experiments with different friction at different digit tips (Aoki et al. 2006), tangential forces were always smaller at the side with lower friction than at the side with higher friction. The difference between the thumb and VF tangential forces generated a moment of the tangential forces (‘friction-induced moment’). The friction-induced moment and the moment counterbalancing the external torque (‘equilibrium-necessitated moment’) could be in the same or in opposite directions. At non-zero torque conditions, when the two moments were in the same direction, the contribution of the moment of tangential forces to the total moment was large, and the contribution of the normal forces was relatively low. In contrast, when the two moments were in opposite directions, the contribution of the moment of tangential forces to the total moment was markedly decreased, which was compensated by an increase in the moment of normal forces. These apparently complicated results were explained as the result of summation of the friction-related and torque-related components of the central commands to the individual digits.

(B) Hand-held objects commonly exert on the hand not only a load force but also an external torque (Gao, Latash, Zatsiorsky 2006). Imagine that the handle shown in Figure 1 is being moved in the vertical direction. During the motion both the load L and moment M change in proportion to object acceleration. Such a task would impose conflicting demands on the individual normal finger forces. To maintain a sufficiently high and constant safety margin the grasp force—the force generated by all the fingers—should change in synchrony with load force. In contrast, to compensate for the moment increase— to maintain the rotational equilibrium of the object—the forces of only the agonist fingers should rise with acceleration. The increased force of the antagonist fingers leads to an increase in the moment acting on the handle and hence, if not compensated, would induce the handle rotation. The question is how does the CNS sort out these two conflicting demands?

It has been found that (a) the grasp force increases both with the acceleration and the torque (Figure 26, left panel) and (b) when the fingers work as torque agonists the finger force increases with the acceleration while when the fingers work as torque antagonists the forces stay put (see Figure 26, right panel).

Figure 26.

The dependence of the finger forces on object acceleration at different torques. Data from a representative subject are shown. Vertical oscillation of the handle, frequency 2 Hz. Left panel: the grasp force at different torques. Right panel: the index and little finger normal forces. The torques are described by the location of the object’s center of mass with respect to the grasp, Mi – middle (zero torque), R - right, L - left, 1 designates 1/6 Nm, 2 corresponds to 1/3 Nm. As an example, the symbol R2 represents the load location to the right of the center that results in the moment of −1/3 Nm. Such a moment—as seen from the subject—is in the clockwise direction (negative). To counterbalance this external moment/torque the subject should exert a counterclockwise (pronation, positive) moment of equal magnitude. Note: (1) in the left panel—the grasp force increases both with the acceleration and the torque; (2) in the right panel – when the fingers work as torque agonists the finger force increases with the acceleration; when the fingers work as torque antagonists the forces stay put. (Adapted from F. Gao, M.L. Latash, and V.M. Zatsiorsky. Maintaining rotational equilibrium during object manipulation: linear behavior of a highly non-linear system. Experimental Brain Research, 2006, 169(4):519–531).

The results were explained by the superposition of two commands aimed at the slip prevention and tilt prevention, respectively. The first command, whose intensity is proportional to the load force, results in stronger/weaker contractions of all involved fingers and hence in a change in grasping force. This command represents the load effect. The second command, representing the torque effects, results in potentiation of the flexion command to the agonist fingers and inhibition of the commands to the antagonist fingers. For that reason, the force of the agonist fingers increases and the force of the antagonist fingers decreases. The forces exerted by the agonist fingers scaled with the handle acceleration while the forces of the antagonist fingers did not change much or even remained constant. For the antagonist fingers, the load effects were cancelled by the oppositely directed torque effects of equal magnitude. These experimental findings and their explanation agree well with both the above postulate and the principle of superposition.

V. Summary

1. Multi-finger prehension is mechanically redundant: the same resultant forces and moments on a hand-held object can be exerted in many different ways. In research, either individual digit forces are analyzed (the IF level) or a set of fingers opposing the thumb is reduced to one virtual finger (VF), an imagined finger that generates the same mechanical effect as a set of actual fingers (the VF level).

2. The forces on the object are classified as manipulation force (resultant force and moment) and internal forces (the forces that cancel each other and consequently do not perturb the object equilibrium). The central controller can change manipulation forces without changing the internal forces and vice versa. This opportunity is realized in contemporary robotic manipulators where the manipulation force and the internal forces are controlled separately. People do not use this option; they adjust the internal force to the manipulation force.

3. When exerting manipulation force using several fingers, performers do the following.

   • (3a) While exerting normal finger forces (flexion finger forces):

     • Obey the principle of minimization of secondary moment.

     • Control the direction of a VF force vector by a synergetic adjustment of the individual finger force vectors that are pointing in dissimilar directions.

   • (3b) While exerting tangential finger forces: actively control the finger forces in the ulnar/radial directions. While the passive finger resistance to the tangential forces cannot be disregarded, it does not account completely for the tangential force sharing among the fingers.

   • (3c) While exerting moment on the object:

     • When the torque is in the plane of the grasp: both the moments of the normal and tangential forces contribute to the total moment. The percentage contribution of the above moments into the total moment is invariant with respect to the supported load, torque magnitude and direction. The invariance is not necessitated by the task mechanics and represents choice by the central controller.

     • When external torque is in a plane perpendicular to the plane of grasp, the resisting moment is generated by four sources: (a) thumb and finger local free moments, (b) a free VF moment, (c) moment of the VF tangential horizontal force, and (d) moment of the VF vertical force. The percentage contribution of these sources into the total moment is invariant with respect to torque magnitude and direction. Systematic changes of the digit forces in all three directions take place; the CNS controls a two-dimensional task with three-dimensional adjustments.

     • Humans use two complementary sources to generate torque on a mechanically fixed object: (a) resultant force and (b) free moment that is created by the pronation or supination efforts. Their relative contribution scales linearly with the distance of the neutral line of the hand to the moment axis. The linearity is not prescribed by the task mechanics; it is a consequence of a certain motor control strategy.

4. Internal forces exerted on hand-held objects are numerous. In planar tasks analyzed at the VF level, two internal forces exist: the grasp force and the internal moment. The internal forces are mainly involved in maintaining grasp stability: slip prevention, tilt prevention, and resistance to perturbations.

   • (4a) Slip prevention.

     • Vertically oriented object at rest. Slip prevention is achieved by proper adjustments of the grasp force, the two opposite and equal normal forces of the thumb and VF that cancel each other. When the friction at the individual digit contacts is different, the performers adjust not only the normal forces but also the tangential forces to the friction. The different tangential forces at the thumb and VF generate a moment of the tangential forces. To prevent tilt, the latter moment is counterbalanced by a changed moment of the normal forces. The grasping templates that correspond to digit forces for a unitary load are linearly scaled with the load magnitude.

       The local and synergic responses are discerned. Term local designates responses that start and end at the same digit, i.e. an effect of friction at a given digit on the force exerted by this digit. The term synergic refers to changes of finger force in response to changes in friction under a different finger. The synergic effects are directed to maintain the handle equilibrium.

     • Non-vertically oriented object at rest. When the grasped object is not oriented vertically, the normal forces of the thumb and VF are not equal anymore and such concepts as grasp force and safety margin cannot be immediately applied. When normalized by object weight, the force-inclination angle relations are invariant with respect to load magnitude. The forces could not be represented as linear functions of the sine or cosine of the orientation angle.

     • Vertically oriented object during movement. During vertical movements, the grasp force changes in synchrony with the load force (object acceleration). The grasp force is maximal at the instances of maximal acceleration. The grasp force can be expanded intro three fractions: (a) the static fraction - the force related to holding the load statically; (b) the stato-dynamic fraction that reflects a steady change in the grasp force when the same load is moved cyclically; and (c) the dynamic fraction due to the acceleration-related adjustments of the grasp force during oscillation. The grasp force is adjusted to the same load force differently, depending on whether the latter force is gravitational or inertial and whether changes in the inertial force are due to changes in the object mass or acceleration.

       In contrast to vertical object motion, during horizontal motion the internal normal force (which at rest is called the grasp force) is maximal at the instances of minimal acceleration.

   • (4b) Tilt prevention is achieved by opposite and matching changes of the moments of the normal and tangential forces, which make up the internal moment.

   • (4c) Resistance to perturbations. The results of the experiments with the expanding or collapsing handle agree with the hypothesis (Hazan 2005) that immediate responses to perturbations assist rather than resist the perturbation and are, therefore, destabilizing.

5. During prehension, the individual digit force variations are always interrelated; i.e. they manifest the prehension synergies. Prehension synergies are identified as conjoint changes in finger forces and moments during multi-finger tasks. Some of these adjustments are dictated by mechanics, whereas others are results of choice by the CNS.

6. Relations among the variables comprising a prehension synergy can be explained and predicted by chain effects. The chain effects are sequences of local cause-effect adjustments necessitated by the task mechanics. The chain effects arise from the necessity to find a solution that simultaneously satisfies a variety of constraints. Numerous examples of the chain effects have been presented.

7. There are substantial differences between the VF and IF forces: (a) The IF forces may be exerted in disparate directions such that only their resultant (i.e. VF) force is in the desired direction. (b) VF and IF forces adjust differently to modified task conditions. (c) IF forces are much more variable than VF forces.

8. According to the principle of superposition, suggested in robotics, some skilled actions can be decomposed into several elemental actions that can be controlled independently. When applied to human performers and multi-finger grasps, the principle claims that forces and moments during prehension are defined by two independent commands: “Grasp the object stronger/weaker to prevent slipping” and “Maintain the rotational equilibrium of the object”. The effects of the two commands are summed up. The validity of the principle has been confirmed in several experiments.

9. Finger forces exerted during prehension are constrained by the finger interdependence, in particular force deficit and finger enslaving. The finger interdependence can be described by inter-finger connection matrices that relate central commands to individual fingers with actual finger forces. Knowledge of the matrix allows for reconstructing the commands sent to individual digits. The method of command reconstruction is presented.

10. Force generated by a finger during prehension arises from a command sent to this finger (‘direct’ finger force) as well as from commands sent to other fingers (enslaved force). Due to the enslaving, fingers that generate moment in the direction opposite to the direction required by the task are active, even though such activation is not mechanically efficient.

11. Mechanical advantage of a finger, i.e. its moment arm during moment production, affects the degree of that finger’s involvement. During moment production, fingers with larger moment arms produce larger forces.

12. When manipulating hand-held objects, the performers adjust digit forces to many variables requiring similar or opposite adjustments. To explain the diverse adjustments the following postulate is suggested: Adjustment to the sum equals the sum of the adjustments. The examples confirming validity of the postulate are presented.

13. There are evident analogies between the facts discovered in studies of prehension and in other fields of motor control and biomechanics. For instance, there is an analogy between the mechanical advantage of a finger and mechanical advantage of a muscle, finger enslaving and the myo-fascial force transmission, etc. The multi-finger prehension is an advantageous object for studying motor redundancy problem in general: all the involved forces and displacement can be directly measured.

Figure 3.

Three cardinal planes of the hand. Adapted by permission from Z.-M.Li, M.L. Latash, and V.M. Zatsiorsky (1998a) Force sharing among fingers as a model of the redundancy problem. Experimental Brain Research 119: 276–286.

Figure 24.

Decomposition of the normal forces of the middle finger during holding a 2.0 kg load at different external torques (Zatsiorsky et al. 2002). The data are from a representative subject.

Upper left panel. Actual and ‘direct’ finger forces. The direct forces (dashed line) were computed as the products of the diagonal elements of the inter-finger connection matrix times the corresponding finger commands.

Upper right panel. Enslaved forces, i.e. the difference between the actual and ‘direct’ forces.

Bottom panel. Decomposition of the enslaving effects. Effects of the commands to other fingers on the middle finger force are presented.

(Adapted by permission from V.M. Zatsiorsky, R.W. Gregory, and M.L. Latash. (2002b) Force and torque production in static multifinger prehension. II. Control. Biological Cybernetics, 87: 40–49.)