EMPLOYING TOPOGRAPHICAL HEIGHT MAP IN COLONIC POLYP MEASUREMENT AND FALSE POSITIVE REDUCTION

Abstract

CT Colonography (CTC) is an emerging minimally invasive technique for screening and diagnosing colon cancers. Computer Aided Detection (CAD) techniques can increase sensitivity and reduce false positives. Inspired by the way radiologists detect polyps via 3D virtual fly-through in CTC, we borrowed the idea from geographic information systems to employ topographical height map in colonic polyp measurement and false positive reduction. After a curvature based filtering and a 3D CT feature classifier, a height map is computed for each detection using a ray-casting algorithm. We design a concentric index to characterize the concentric pattern in polyp height map based on the fact that polyps are protrusions from the colon wall and round in shape. The height map is optimized through a multi-scale spiral spherical search to maximize the concentric index. We derive several topographic features from the map and compute texture features based on wavelet decomposition. We then send the features to a committee of support vector machines for classification. We have trained our method on 394 patients (71 polyps) and tested it on 792 patients (226 polyps). Results showed that we can achieve 95% sensitivity at 2.4 false positives per patient and the height map features can reduce false positives by more than 50%. We compute the polyp height and width measurements and correlate them with manual measurements. The Pearson correlations are 0.74 (p=0.11) and 0.75 (p=0.17) for height and width, respectively.

1. INTRODUCTION

Colorectal cancer is the second leading cause of cancer death in the United States, estimated to claim 56,290 lives in 2005 alone [1]. Screening is currently the most suitable method for early detection and eventually removal of colonic polyps. CT colonography (CTC) is a minimally invasive technique and can be used to detect both pre-cancerous polyps and colon cancers. The accuracy of CTC is reported by some investigators to be as good as that of traditional optical colonoscopy (OC) [2]. One characteristic used to predict the malignancy risk of a polyp is its size including the height and width [3] [4]. Polyp size is usually determined by making a linear measurement during optical colonoscopy. In this paper, we propose a novel technique to employ topographical height map in polyp detection and measurement.

Computer aided detection (CAD) of colonic polyps using CTC have been under investigation in the past decade. Most systems used features computed from the original CT data set. Summers et al. [5] extracted features based on surface curvature. Yao et al. [6] employed a deformable model to segment polyps and thus obtain quantitative features. Paik et al. [7] proposed a surface normal overlap method to detect round shape objects such as colonic polyps. Nappi and Yoshida [8] [9] extracted the directional gradient concentration from the volume data. They noticed that the directional gradient for polyps concentrated while other structures did not. Zhao et al. [10] extended the scalar curvature to lines of curvature for polyp detection. Sundaram et al [11] further smoothed the curvature and shape estimation using a geometry processing approach. Hong et al. [12] proposed a pipeline by integrating texture and shape analysis on a flattened colon. Bhotika et al [13] combined simple geometric shapes such as spherical and cylindrical structures to represent and differentiate polyps and folds. Gokturk et al. [14] proposed a random orthogonal shape sections method which combined the information from many random images to generate reliable signatures of shape. Dijkers et al. [15] developed a technique based on surface patch growing to segment and measure polyp. Konukoglu et al. [16] used level set evolution to enhance spherical polyp structure as a pre-processing step to improve the performance.

None of the above methods made use of the knowledge of the way radiologists detect polyps. Radiologists read CTC studies in mainly two ways. One is 2D scan-through, where radiologists scan through 2D slices and form 3D pictures in their brain. Another is 3D fly-through, where computer graphics techniques are employed to reconstruct the 3D surface of the colon from the CT data and the radiologist navigates through the colon along the center line. One investigation suggested that radiologists can achieve higher diagnostic accuracy in 3D fly-through than in 2D scan-through [2]. This observation prompts us to explore ways to extract features from 3D colon fly-through which can be used to distinguish polyps from normal colon surface. Li et al [17] [18] proposed a method based on 2D endoluminal projection images. They computed the projection images using graphical snapshot through an optimized viewpoint and derived wavelet coefficients as texture features for classification. In this paper we propose an approach based on topographic height map, which is potentially more robust.

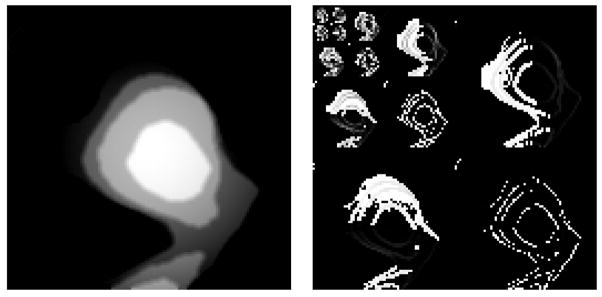
Height maps are commonly used in geographic information systems (GIS), where they are also called digital elevation models [19]. Remote sensing techniques such as radar or LIDAR are applied to determine the distance from the sensor to an object or surface. Similar idea has also been applied in range imaging [20], where structure lights coupled with calibrated optical cameras are employed to reconstruct the depth features of a surface. The distance or depth is then converted to elevation data. The elevation data can be used to recognize structures in a terrain [21]. For instance, mountains usually have higher elevation than their surrounding regions. Figure 1a is the aerial view of Mt. St. Helens from NASA’s WorldWind (http://worldwind.arc.nasa.gov/screenshots-sl.html). The viewer can easily recognize the mountain just from the height contrast of mountain and plain by navigating the landscape. The same strategy can be employed in polyp detection. Colonic polyps are abnormal growths protruding outward from the colon wall, and are characteristically round in shape. In contrast, haustral folds and other normal colonic structures tend to be circumferential and ridge-shaped. The main idea is that the colon surface can be viewed as a terrain and polyps as mountains (bumps) on the terrain. The unique topographic features of mountains (bumps) can assist us in distinguishing polyps from the rest of the colon surface. Figure 1b is a picture from a 3D fly-through of CTC. We notice the similarity between polyps in CTC fly through and mountains in terrain navigation. In the case of CT colonography, we can survey the colon surface by placing a camera above the detections. Using the ray casting technique, we compute the distance from the camera to the surface. The inverted distance can be converted to the elevation height from the base of the polyp. The height data is then digitized and stored in a 2D grid. Due to the special characteristics of polyps, their height map will present concentric patterns and other topographic features. Figure 2 shows one CT slice of a polyp, its 3D endoluminal view and height map.

Figure 1. Terrain surface and colon surface.

a) aerial view of Mount St Helens from NASA’s WorldWind

b) 3D endoluminal view from a fly-through in CTC of a 8-mm polyp

Figure 2. Colonic polyp and height map.

a) 2D CT slice of a 10mm polyp, b) 3D endoluminal view, c) Height map

There are two main applications for the height map technique: one is the CAD system for polyp detection, another is the measurement of polyp size. The paper is organized as follows. In section 2, we first describe our approach to apply the height map in our CAD pipeline. We then describe the methods in height map generation, topographic feature computation, view direction optimization, and polyp height and width measurement. In section 3, we present the CAD results in both the training sets and independent test sets. We also analyze the correlation and agreement between the manual height and width measurements and those derived from the height map. Finally we provide some discussions in section 4.

Some initial results from this paper were previously published in two conference papers [22] [23]. In this paper, we improve our technique by introducing virtual flattening techniques, and new topographic features based on principal component analysis. We also conduct much more thorough validation experiments and analysis and provide more discussions.

2. METHODS AND MATERIALS

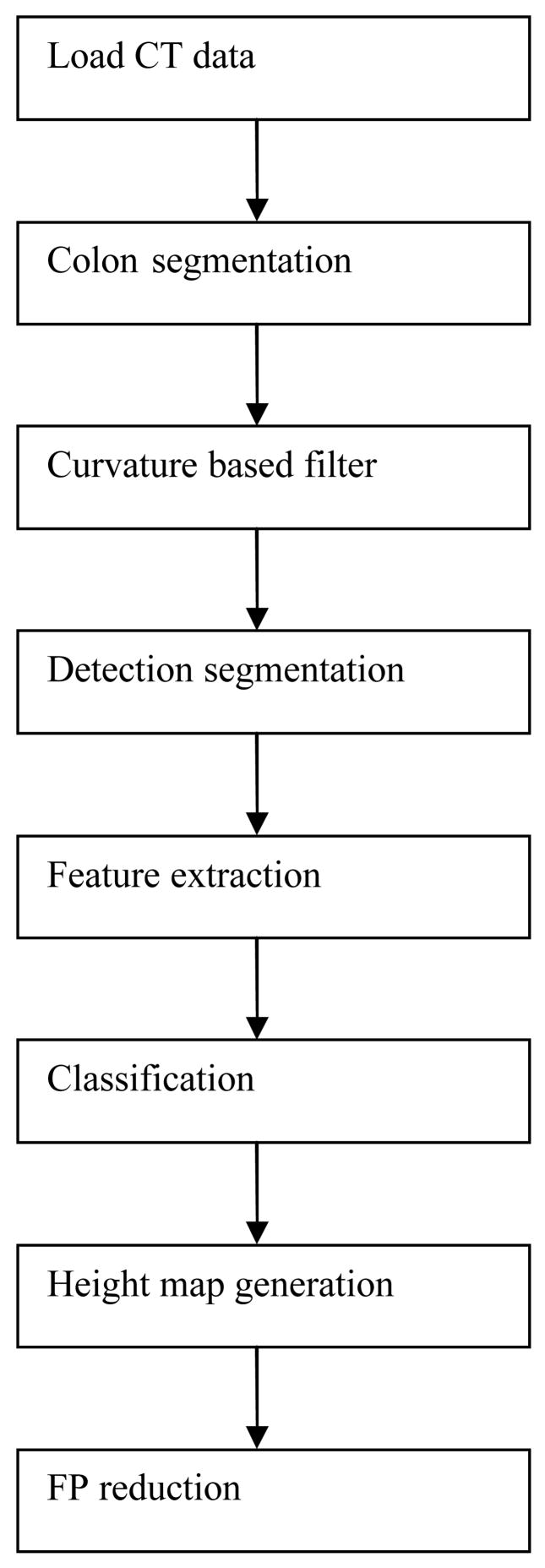
The pipeline of our CAD system is illustrated in Figure 3. First a CTC data set is loaded into the program. The colon surface is extracted using fuzzy connectness and iso-surface techniques [5]. A curvature filter is applied to every vertex on the surface to exclude approximate 90% of the colon surface from further consideration. The vertices passing the filter are then clustered according to their connectivity and curvature attributes, and the centroid of each cluster is treated as one detection. The detections are then sent to a segmenter for computation of boundaries, 3D shape, and attenuation features. These features are then fed to a classifier (support vector machine). A height map is generated for each detection passed through the classifier. Topographic and texture features are computed for a second classification to reduce the number of false positive detections. This pipeline has three classification stages: surface curvature filter, CT feature classifier and height map feature classifier. This paper is focused on the height map stage. The details of the first two stages can be found in [6, 24].

Figure 3.

CAD pipeline

2.1 Height map generation

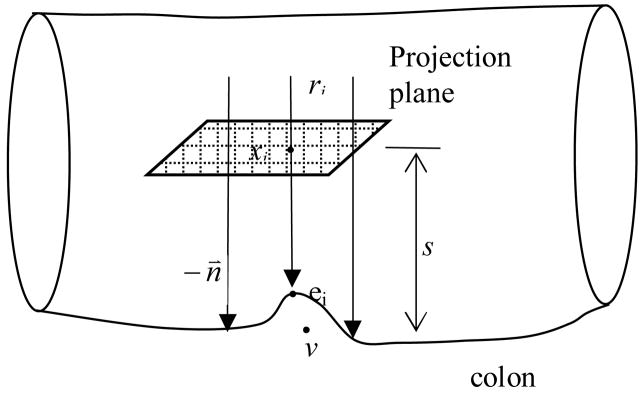
The approach to generate a height map is illustrated in Figure 4. The method is based on a ray casting technique. For every detection, a projection plane is defined and placed over it. The projection plane is determined by its normal, its distance to the colon surface and the location of the detection, and is represented as

Figure 4.

Height map generation based on ray casting

$$\mathbf{P}(\stackrel{\rightharpoonup }{n},v,s):\stackrel{\rightharpoonup }{n}\circ (x-(v+\stackrel{\rightharpoonup }{n}·s))=0$$ (1)

Here P is the projection plane, n⃑ is the unit normal of the plane, v is the detection location, s is the distance from the plane to the detection, x is any point on the plane, ○ is dot product of two 3D vectors. We use orthogonal projection to avoid the projection distortion associated with perspective projection. For every point x_i on the projection plane, a ray r_i is cast onto the colon surface. The point that ray r_i encounters the colon surface is e_i. The equation for the projection ray is

$$e_i=x_i-\stackrel{\rightharpoonup }{n}·d_i$$ (2)

here d_i is the distance between x_i and e_i, which is recorded at x_i, and n⃑ is the unit normal of the plane. We use an implicit iso-surface associated with the colon surface in the 3D image to locate point e_i. The iso-value in use is −700 HU.

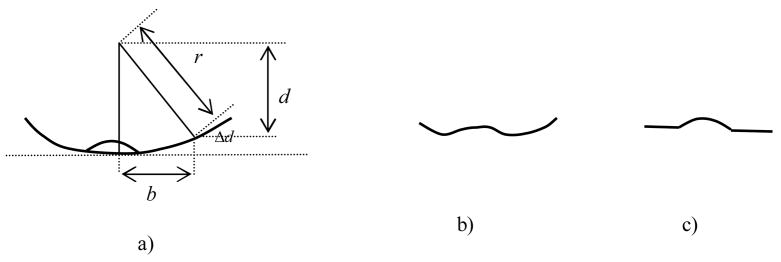
Since colon is a curved tubular structure and orthogonal projection is used, the height values for pixels off the center of the map are artificially higher than they actually are (Figure 5). We need to flatten the colon to get precise height measurement. We virtually flatten the colon by compensating the height distance measurement according to the distance to the center of the map. The process is illustrated in Figure 5 and equation 3,

Figure 5. Virtual colon flattening.

a) virtual colon flattening, b) height profile before flattening, c) height profile after flattening

$$\begin{array}{l}\mathrm{\Delta }d=r-\sqrt{r^2-b^2}\\ d^{\prime }=d+\mathrm{\Delta }d\end{array}$$ (3)

here r is the radius of the colon tube, b is the distance to the center of the map, d is the measured height distance, d′ is the adjusted height distance. The radius of the colon section can be computed from the center line to the colon surface. Figure 5a shows the virtual colon flattening. Figure 5b is the height profile before the flattening. We can see that the height contrast between polyp and its surrounding region is smaller than the real value. This effect can be significant especially for flat polyps. Figure 5c is the height profile after the flattening.

After the distance map to the projection plane is computed and compensated, we normalize and convert the distance map to a digitized height map using the following equation,

$$h_i={d_c}^{\prime }-{d_i}^{\prime }+maxD$$ (4)

where d_i′ and h_i are the height distance and height value at pixel i, maxD is the maximum distance in the distance map, and d_c is the distance in the center of the map. In this way the height map is normalized to a banded range around the center of the height map, which is the height value for the candidate location. The height map is converted to a raster image where the image intensity indicates the height. The brighter the pixel is, the higher the height is. The physical size of the height map is 25mm * 25mm, and it is sampled in a 128*128 image grid. A typical height map is shown in Figure 2c.

2.2 Topographic features

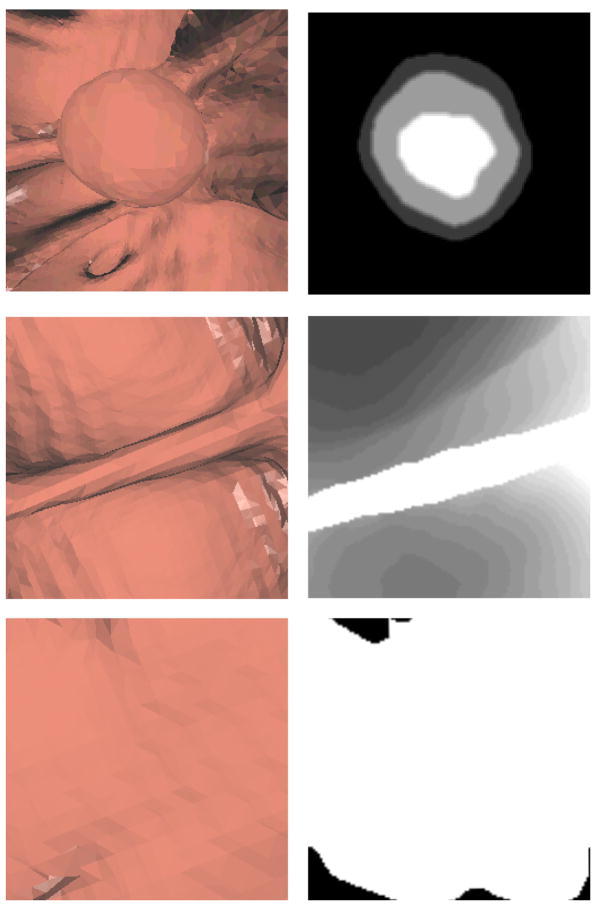
The height differential and directional slopes in the height map reveal the topographic features of a terrain surface. In the case of a polyp with ideal semi-spherical shape, the slope from its apex to the base should be homogeneous and big in every direction. In the case of haustral fold, the slopes are big in the directions perpendicular to the ridge and small in the directions parallel to the ridge. In the normal flat colon surface, the slopes are generally small in all directions. Figure 6 demonstratesthe height map and 3D endoluminal view of polyp, haustral fold and normal colon surface. We notice that the polyp height map presents a concentric pattern, while the other two do not.

Figure 6. Height map of structures in CTC.

Left: 3D endoluminal view; Right: height map

First row: a 14-mm polyp; second row: haustral fold; third row: flat colon surface.

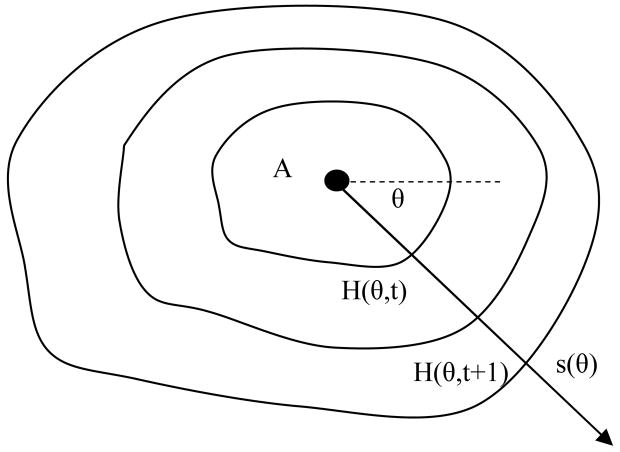
Just like identifying a mountain in a terrain, first we locate the apex in the height map. The height map is centered at the location of the detection, i.e. the height of the center of the map is the height of the point passing through the casting ray of the detection point (v in Figure 4). Therefore we conduct the search for the apex in the center of the height map. In the case where there is a plateau, the center of the plateau is used. From the peak, we compute the directional slope for every direction defined by angle θ(Figure 7). The computation is done by accumulating the height difference along the direction θ,

Figure 7. Directional slope computation.

A is the Apex

$$\begin{array}{l}s(\theta )=\sum _{t=\mathrm{1..}n}(H(\theta ,t)-H(\theta ,t+1))=H(\theta ,0)-H(\theta ,n)\\ H(\theta ,t)=h(A+r{(\theta )}^{\ast }t)\\ r(\theta )=(cos\theta ,sin\theta )\end{array}$$ (5)

where s(θ) is the accumulative directional slope at angle θ, A=(A_x, A_y) is the coordinate of the apex, t is the time step, h(.) is the height value retrieved from the height map through linear interpolation, H(θ, t) is the height value represented by angle and step. θ goes from 0 to 360 degree. n is the number of steps to accumulate the height difference, which is determined by a sliding transition window technique (Section 2.4). We use 18 degree interval in current system. Figure 7 illustrates how the directional slopes are computed. Several topographic features can be derived from the directional slopes. The mean M(s) and standard deviation STD(s) of directional accumulative slopes in all directions are among the most useful ones.

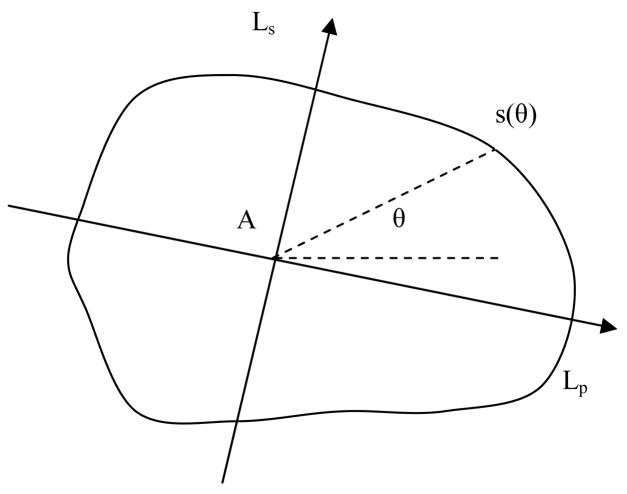
To further explore the characteristics of slope changes in all directions, we transform the directional accumulative slopes into a contour in a polar coordinate system centered at the apex. The angular coordinate is the slope direction (angle) and the radial coordinate is the accumulative slope (Figure 8). We name this contour the slope contour. The slope contour summarizes the characteristics of the slope distribution. We perform a principal component analysis [25] on the slope contour and compute the principal and secondary axes of the contour. The lengths of the principal and secondary axes (L_p, L_s) and the slope aspect ratio AS=L_p/L_s are computed as topographic features. We also compute the compactness = 4π(area)/(perimeter)² as an additional feature. These features are translation, rotation and scale invariant.

Figure 8.

Slope contour

A is Apex

2.3 Concentric index and projection direction optimization

In the ray casting method, different projection directions could produce very different height maps. Figure 9 shows height maps of the same polyp in Figure 2 from different projection directions. The middle one is the optimal projection where the projection plane is placed right over the polyp. It demonstrates a concentric pattern, which is also the pattern to distinguish polyps from other colon surfaces (Figure 6). We design a concentric index to gauge this pattern,

Figure 9.

Height maps of the same polyp in Figure 2 from different projection directions

$$CI=M(s)-\mathit{STD}(s)$$ (6)

where CI is the concentric index, M(s) and STD(s) are the mean and standard deviation of accumulative directional slopes. A height map with bigger and more homogeneous directional slopes in all directions tends to have higher concentric index. Figure 9 marks the CI values from different projection directions.

We optimize the projection direction by maximizing the concentric index. The projection plane is determined by its normal (projection direction) and its distance to the colon surface. Since we use orthogonal projection, the distance does not affect the height map generation. However, if the plane is too far from the detection, it may be behind the opposite colon wall and the polyp may be occluded; on the other hand, if the plane is too close to the detection, it may cut across the polyp and thus the height map is not complete. We place the plane 10mm from the detection as default, and move the plane closer if it is behind the opposite wall. The optimization process can be written as,

$$\underset{\stackrel{\rightharpoonup }{n}}{argmax}(CI(P(\stackrel{\rightharpoonup }{n},v,s))$$ (7)

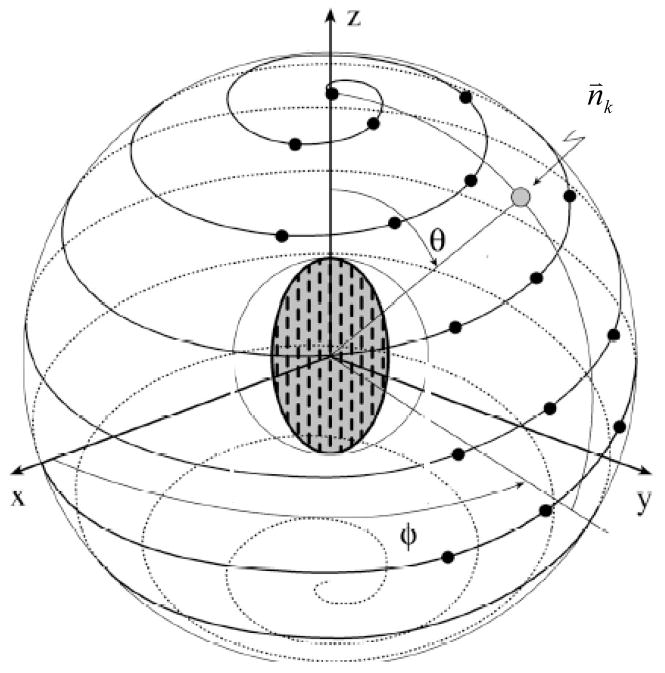
Here CI is the concentric index of the height map generated from the projection plane P, n⃑ is the normal of the plane, v is the detection location, s is the distance from plane to detection. Since v and s are known, the only variable to optimize is n⃑. We sample all possible projection directions to select the optimal direction. One way to generate the set of all directions in 3D space is the spiral-point technique [26], which produces uniformly distributed points on a sphere. The spherical coordinate (θ, ϕ) defines the projection direction. The k^th direction generated by this technique is,

$$\begin{array}{l}{b}_k=-1+\frac{2(k-1)}{(N-1)}\\ {\theta }_k=arccos(b_k)\\ {\varphi }_k=\left({\varphi }_{k-1}+\frac{3.6}{\sqrt{N(1-b_k^2)}}\right)mod2\pi \\ {\stackrel{\rightharpoonup }{n}}_k=(sin{\theta }_{k}cos{\varphi }_k,sin{\theta }_{k}sin{\varphi }_k,cos{\theta }_k)\end{array}$$ (8)

here N is the total number of projection directions, 1≤k≤N, n⃑_k is a projection direction, 0≤θ≤π, 0≤ϕ≤2π. The spiral point technique is illustrated in Figure 10. The number of directions N is determined by the angle interval between adjacent directions, which is approximately $N={\left(\frac{218.4}{\alpha }\right)}^2$ (α is the angle interval). For instance, the method generates 1908 directions at 5-degree angle interval. Each direction requires one height map generation and evaluation, which takes about 0.03 second in our system. Therefore, it takes about 1908*0.03 = 57 seconds to exhaustively search all directions at 5-degree interval. The CAD system typically generates about 50 detections per data set at this stage. It will take 3000 seconds (about 50 minutes) for just the projection optimization alone, which makes the exhaustive search not practical. In order to improve the time efficiency, we propose a multi-scale spherical search scheme. In this scheme, the search starts with a big angle interval and decreases the angle interval in following iterations. A full range search (0≤θ≤π, 0≤ϕ≤2π) is conducted at the coarsest scale. After that, a local search is conducted in the neighborhood of the direction obtained from the previous scale. The range of neighborhood is twice of the angle interval in the previous scale. We use a 3-scale searching scheme, with 30, 10 and 5 degree intervals at each scale. The first scale takes (218.4/30)² = 53 evaluations, the second scale of refinement at 10 degree intervals takes (30/10*2+1)²=49 evaluations, and the third scale of refinement at 5 degree intervals takes (10/5*2+1)²=25 evaluations. Altogether it takes at most 53+49+25=127 height map evaluations for this scheme. To further limit the search, if a projection plane is out of the lumen which indicates projecting from the back of the polyp, it should be excluded from further consideration. The multi-scale searching technique is robust. The interval for the first scale is 30-degree, and we also add a 30-degree margin on both sides in the second scale. It then covers 3*30=90 degrees for any chosen projection angle, which is ¼ of the angle span. Furthermore, polyps usually have one side against the colon wall, which makes almost half of the projection angles invalid. We have compared the multi-scale search with the exhaustive search for 20 polyps and obtained the same projection angles for both methods.

Figure 10.

Spiral point technique

2.4 Polyp Height and Width Measurement

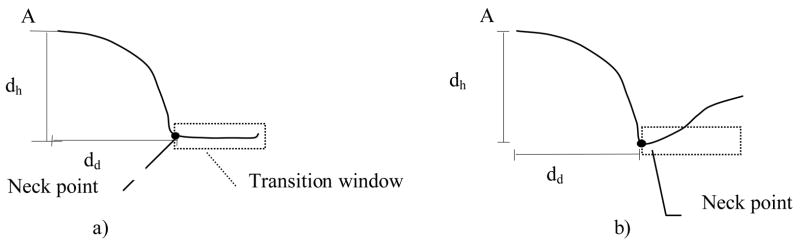
Height and width are two important characteristics of a polyp. Their measurement is not trivial since the polyp orientation and the boundary between polyp and normal colon are hard to determine. The height map can be used to address this problem. To conduct the measurement, we need to locate the tip and base of a polyp in the height map. The highest point in the center of the height map is used as the tip of the polyp. We define the interface between the polyp surface and its surrounding colon region as the polyp neck. The neck can be detected by examining the directional height profile. We use the same approach in Section 2.2 to generate the directional height profile by shooting rays in all directions from the tip of the polyp. Starting from the highest point in the center of the height map (the polyp tip), we sample the height value along a specified direction to plot the height profile. The neck location occurs in two scenarios in the height profile (Figure 11). In the first case (Figure 11a), the neck location is at where the changes of the height values are smaller than a height threshold (t_h) for a certain distance (distance threshold, t_d). In the second case (Figure 11b), the neck location lies at where the height value starts to increase. The first case indicates that the portion of polyp rests on a flat colon region, while the second case implies that the portion of polyp touches other structures such as haustral folds. We define a transition window to identify the two scenarios in the height profile. The height of the transition window is the height threshold (t_h) and the width is distance threshold (t_d). The transition window is slid along the height profile and stops in the following two scenarios when it reaches the neck point: 1) the heights of all points in the window are within a range,

Figure 11. Directional height profile and transition window.

a) scenario 1: polyp connects to normal colon surface

b) scenario 2: polyp next to other structures or the arch of colon is highly curved. A is apex of the height map.

$$\mid h_i-h_j\mid <t_h,\forall i\in W,\forall j\in W$$ (9)

here W is the transition window, i, j are points in the window, and h_i and h_j are heights of points i and j in the height profile; or 2) the heights of all points in the window are bigger than that of the first point in the window,

$$h_j\ge h_k,\forall j\in W$$ (10)

here W is the transition window, k is the first point in the window, j is any other point in the window. The size of the transition window is currently set as t_h=1mm and t_d=4mm. The size of the window allows us to handle polyps with plateaus as large as 8mm without triggering the termination of the sliding transition window.

Figure 12d shows the polyp tip and neck points in two height maps. For each neck point, we can compute its relative height to the tip (d_h) and its span distance along the profile (d_d) from the tip. The polyp height is the average height difference between polyp tip and polyp neck points, and the polyp width is the average of span distances. They are computed as

Figure 12. Examples of polyp height map.

a) 2D transverse slice; b) 3D surface rendering; c) Height map; d) Height map with tip and neck locations (dark dot is the tip, bright dots are the neck locations)

First row: a 10mm adenoma polyp; Manual measurement: height=5.9 mm, width=8.6mm; Height map measurement: height=3.67mm, width=9.02mm.

Second row: a 6mm hyperplastic polyp; Manual measurement: height=3.0 mm, width=4.7mm; Height map measurement: height=3.22mm, width=5.98mm.

$$\begin{array}{l}PH=\underset{i=\mathrm{1..}N}{\mathit{AVG}}({d_h}^i)\\ PW=\underset{\begin{array}{l}i=\mathrm{1..}N/2\\ j=i+N/2\end{array}}{\mathit{AVG}}({d_d}^i+{d_d}^j)\end{array}$$ (11)

Here PH is the polyp height, PW is the polyp width, N is the total number of directions in the evaluation, d_hⁱ are d_dⁱ are the height and distance of i^th neck point. We use 20 directions at 18-degree angle interval. We also compute the maximum and minimum width of the polyp. Considering artifacts and outliers, we exclude the top 10% and bottom 10% of {d_h} and {d_d} values in the evaluation of height and width. Essentially, the height measurement is the depth of protrusion from the colon wall and width measurement is the projected 2D spread.

2.4 Texture features based on wavelet decomposition

The height maps of polyps demonstrate concentric patterns that differentiate them from other structures. These patterns can be extracted by texture analysis. Texture analysis based on wavelet decomposition has been applied in identifying forgery of paintings [27]. Wavelet is a set of functions to represent a given signal sequence by its frequency components. In 2D images, it allows us to analyze the signal in different image scales. We are able to extract multiple scales of frequency information (edge, boundaries) from the height map. We use a Haar kernel and conduct a four-level wavelet decomposition on the height map. Each level has sub-bands in vertical, horizontal and diagonal directions. Figure 13 show a wavelet decomposition of one height map. We compute six statistics features for each sub-band coefficients (mean, variance, skewness, kurtosis, energy and entropy). We therefore obtain 78 (13*6) texture features from each map.

Figure 13. Wavelet decomposition.

a) height map; b) four-level wavelet decomposition

2.5 Feature selection and classifier

We use a committee of support vector machines (SVM) [28] as our classifier. SVM is a supervised machine learning technique which defines a hyperplane to separate data in different classes. SVM in higher dimensional space can lead to more accurate classification, but in the meantime also increases the complexity of the model and may lead to overtraining of the data and decrease the generality of the model. Hence, we developed a committee of SVMs to balance the power of the classifier and the generality of the model. In the committee, each SVM is established in a low dimensional feature space and their classification values are combined to reach the committee decision. We used a SumProb [29] strategy in compiling the committee decision, where the normalized distance to the decision boundary for each SVM is summed up as the decision function.

The feature space has 90 features (12 topographic and 78 wavelet features). The topographic features are listed in Table 1. They are put in 3 categories. We employed a forward stepwise feature selection method [30] to select a pool of good performing feature vectors. We then applied another stepwise method to form a SVM committee. The configuration of the committee was determined by an ANOVA analysis. The committee has five members, and each member has four features. The details of the SVM committee used in this paper can be found in [30]. Table 2 lists the selected features in one committee formed by using our training set. The wavelet features start with “w_”, and the number at the end of feature name indicates the wavelet sub-band. The rest are topographic features. Both topographic features and wavelet features are used in the committee. Some features are repeated for different members.

Table 1.

List of topographic features

Feature category	Feature name
Directional slope statistics	meanSlope, stdSlope, minSlope, maxSlope, concentric index
Slope Contour	principal axis, secondary axis, aspect ratio, radius, compactness
Dimension	height, width

Table 2.

Selected features in an SVM committee

Feature name
radius, height, w_entropy5, w_mean11
meanSlope, width, w_mean2, w_ entropy8
height, width, aspectRatio, w_kurtosis10
meanSlope, width, concentricIndex, w_entropy9
minSlope, secondaryAxis, w_entropy7, w_STD9,

The final classifier is created using a 10-fold scheme. At each fold, 9/10 of training cases are used and an SVM committee with five SVM members is created. After that, we put all members in the ten SVM committees in a big committee as the final classifier. Therefore, the final committee has 5*10=50 SVM members.

2.6 Data specification and experiments

The CTC data were acquired as follows. Patients underwent 24-hour colonic preparation consisting of oral administration of 90 mL sodium phosphate, 10 mg bisacodyl, 500mL barium (2.1% by weight), and 120 mL diatrizoate meglumine and diatrizoate sodium given in divided doses [31]. Each patient was scanned in both supine and prone positions. CT scanning parameters included 1.25- to 2.5-mm section collimation and 1-mm reconstruction interval. The patients also underwent optical colonoscopy on the same day of the CTC. After the CTC data was transferred to a workstation, the polyps were manually identified and segmented by a consensus panel consisting of a research trainee and an experienced radiologist to delineate the polyp border in an axial view of the CTC. The manual segmentation was used as the reference standard for CAD training and validation.

We used separate training and test data sets. The classifier was created using the training set and a 10-fold cross validation. The classifier was then independently validated on a separate test set. Free response receiver operating characteristics (FROC) curves were used to evaluate the performance. The evaluations were conducted in two polyp size categories of clinical importance: >=10mm, and between 6mm and 9mm. Polyps <6mm are not thought to be clinically important [32]. In order to test the effectiveness of the height map, the performances were compared with and without the height map classification phase.

We also manually measured the height and width of polyps. Manual measurements were made with a measurement tool in the Viatronix V3D software (research version 1.3.0.0; Viatronix, Stony Brook, NY). Minimum and maximum widths were measured for each polyp in the 3D view in Viatronix. An ellipse was used to model each polyp from a birds-eye view. The minor axis of the ellipse corresponds to the minimum width and the major axis corresponds to the maximum width. The height of the polyps from the colonic wall was measured in the 2D cross-sectional view in Viatronix. The cross-sectional plane was chosen so that it was perpendicular to the polyp base. The height was measured as the length from the peak to the neck of the polyp. The manual measurement was conducted twice by the same operator in a two-week time interval and the mean of two measurements was used. We conducted experiments to evaluate the correlation and agreement of height map and manual measurements using regression and Bland-Altman analysis [33]. Figure 12 shows two examples of polyp height maps and their measurements.

3. RESULTS

The patient population consisted of 1186 adults between 40 and 79 years of age at 3 medical institutions. In total, there were 226 polyps larger than 6mm. We divided the data into independent training and test sets. Table 3 lists the distribution of CTC studies and polyps in the training and test sets.

Table 3.

Data distribution

	Total patients	Polyps >=6mm	>=10mm	6–9 mm
Training set	394	71	25	46
Test set	792	155	43	112
Total	1186	226	68	158

3.1 CAD results

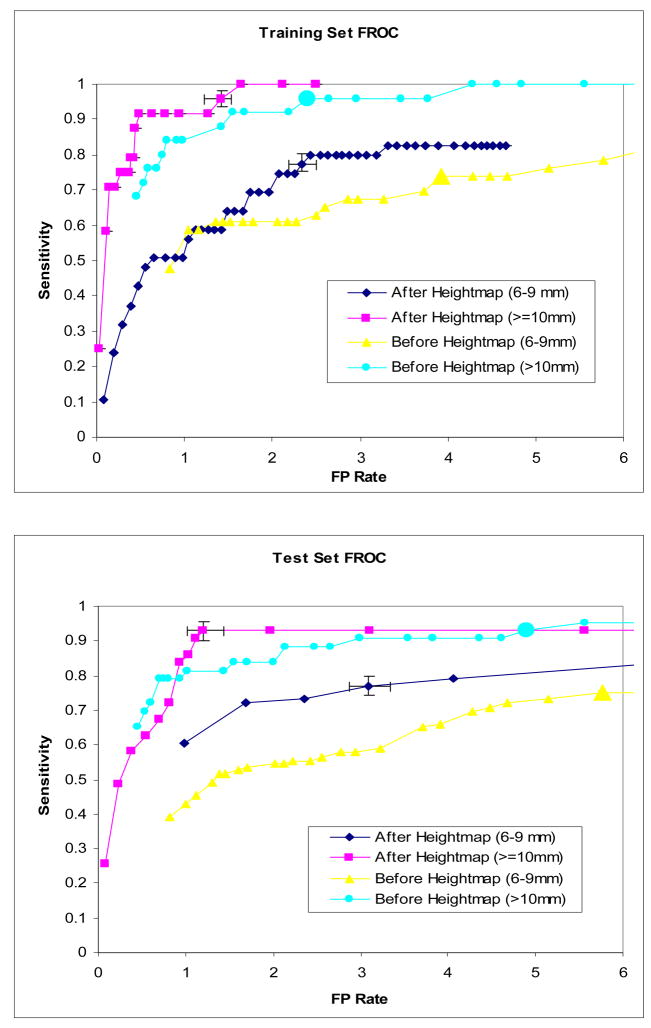
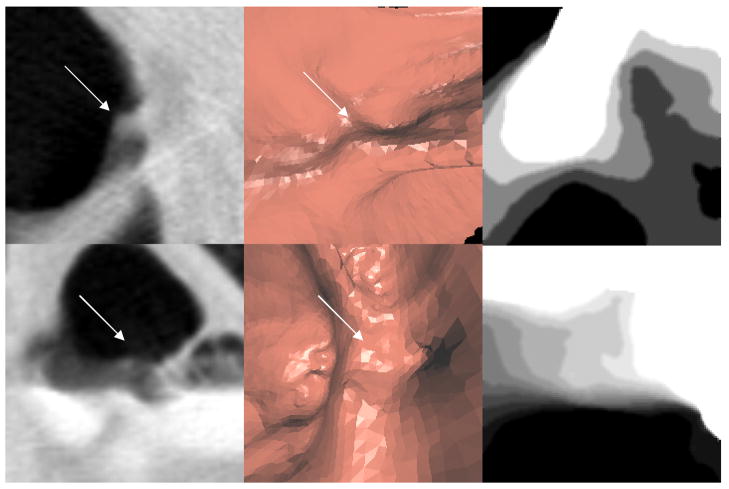
Figure 14 shows the FROC curves of the training and test sets. The operating point is indicated on the plot (big markers). The sensitivity and false positive (FP) rate were calculated for only the detections that passed the initial curvature filter. We also performed 100 iterations of bootstrap to get the error bars on the FROC curve at the operating point. We compared the results before and after the height map features were applied in the classification (Table 4). We also showed the 95% confidence interval for height map CAD. For polyps>=10mm, the FP rate was reduced from 2.65 to 1.42 at 96% sensitivity in the training set and from 4.9 to 1.2 at 93% sensitivity in the test set. For polyps between 6–9mm, the FP rate was reduced from 5.14 to 2.33 at 77% sensitivity for polyps in the training set, and from 6.86 to 3.1 at 76% sensitivity in the test set. Most false positive detections eliminated by the height map classifier are fold structures and artifacts created by fluid interface. Figure 15 shows two of these examples.

Figure 14.

FROC curve of CAD system

Table 4.

Performance comparison before and after height map is applied

	Before height map		After height map
	Sensitivity	False positive rate	Sensitivity	False positive rate
Training set (6–9 mm)	0.761	5.14	0.773 (0.755–0.802)	2.33 (2.18–2.50)
Training set (>=10mm)	0.96	2.65	0.958 (0..935–0.973)	1.42 (1.23–1.54)
Test set (6–9 mm)	0.759	6.86	0.769 (0.756–0.792)	3.09 (2.87–3.34)
Test set (>=10mm)	0.93	4.9	0.930 (0.901–0.957)	1.2 (1.02– 1.43)

Figure 15. Examples of false positive detections eliminated by height map features.

First row: false positive on fold; second row: false positive on fluid interface

First Column: 2D view; second column: 3D view; third row: height map

3.2 Height and width measurements

We randomly selected 50 polyps and manually measured their height and width in a reader study to assess the conspicuity of polyps [34]. Those polyps are varied in size, histology, shape and location. Table 5 lists the categorization of the measured polyps.

Table 5.

Polyp categories

Size	6mm (31)	8mm (13)	10mm (6)
Histology	Adenoma (37)	Hyperplastic (13)	Carcinoma (0)
Shape	Sessile (39)	Pedunculated (8)	Flat (3)
Fold	On fold (17)	Not no fold (33)

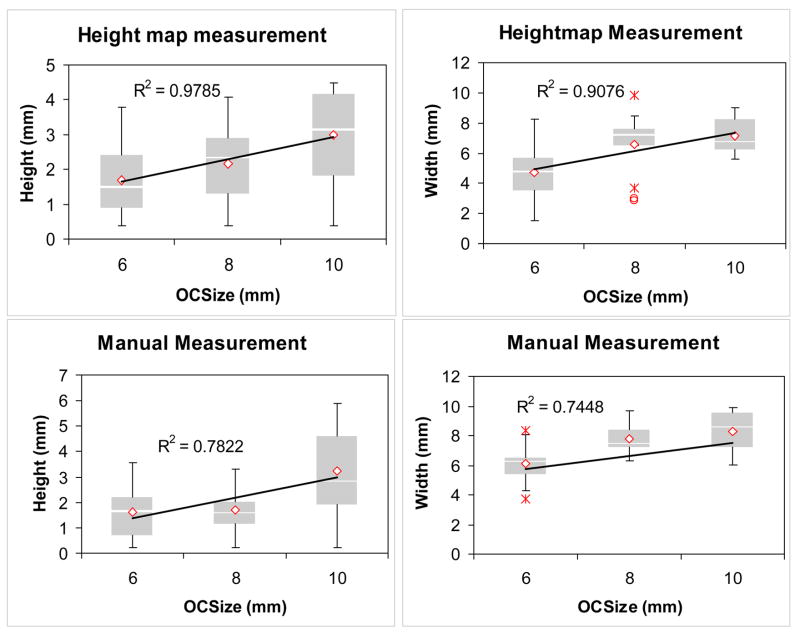
We first validate the height and width against the categorized OC size measurement. Figure 16 shows the Box-Whisker plots of the correlation. The regression trend line of the mean of each category is also displayed. It indicates that heightmap measurements correlate better with OC size than the manual measurements.

Figure 16.

Box-whisker plots show correlation of polyp size measured in OC and height measurement using height map (upper left), width measurement using height map (upper right), manual height measurement (lower left), and manual width measurement (lower right).

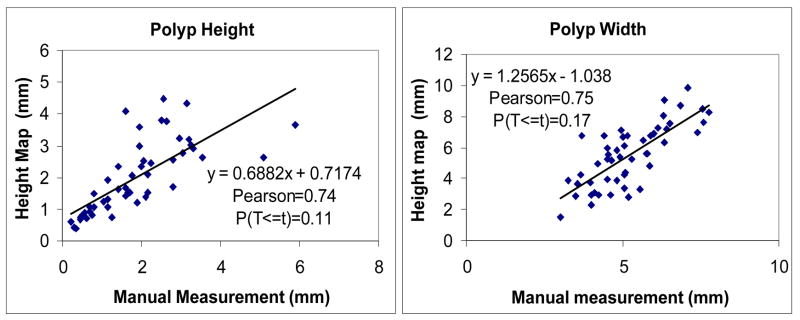
The correlations of height map and manual measurements are shown in Figure 17. The paired t-test for the height measurement shows that the Pearson correlation is 0.74, P(T<=t) is 0.11. The paired t-test for the width measurement shows that Pearson correlation is 0.75, p(T<=t) is 0.17. The regression analysis shows that we get fairly good polyp height and width correlations. However, the correlation is not statistically significant. One possible reason is that the height map measurements and manual measurements do not exactly measure the same thing. The manual measurement requires a subjectively chosen perpendicular cross plane, while the height map method automatically optimizes the best plane for measurement.

Figure 17.

Paired t-test of between manual and height map measurements

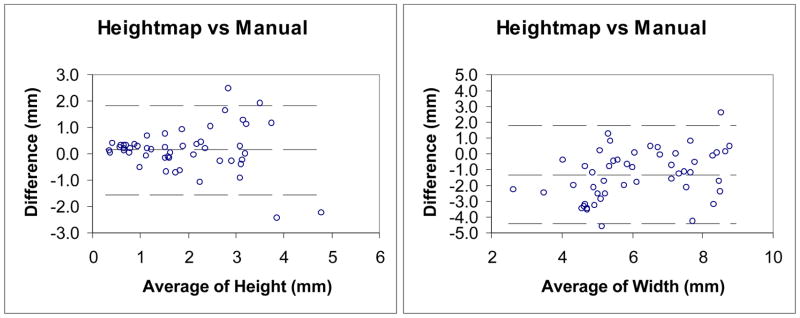
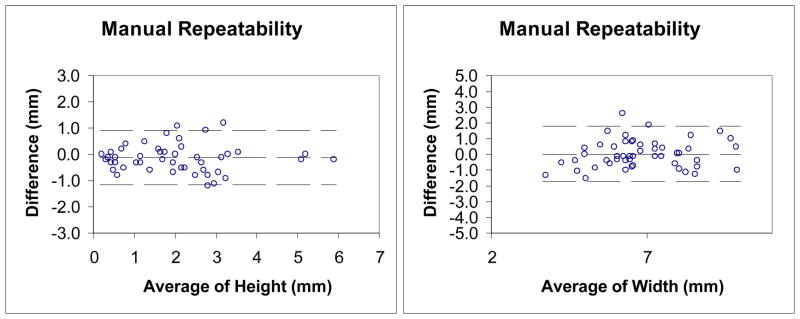
We then conducted Bland-Altman analysis to evaluate the agreement of the two measurements and the repeatability of two manual measurements. Figure 18 shows the Bland-Altman plot of height and width measurement between the height map technique and the manual technique. Figure 19 shows the Bland-Altman plot of the two repeated manual height and width measurements. Table 6 lists the agreement of the Bland-Altman analysis in Figure 18–19. The results indicate the agreement between the two methods is relatively low. Since we achieve high correlations in paired t-tests, this means that there is a systematic difference between these two techniques. The agreement of width measurement is better than that of height measurement. These observations may be explained by the way the manual measurements are conducted. For the height measurement, a perpendicular plane needs to be chosen, which is not an easy manual task. Another observation is that the agreement of height measurement from manual and height map method is comparable to the repeatability agreement of two manual height measurements. This further indicates that manual height measurement is subjective.

Figure 18.

Bland-Altman plots of inter-method agreement of height and width measurements

Figure 19.

Bland-Altman plots of repeatability agreement of manual height and width measurements

Table 6.

Bland-Altman analysis of inter-method agreement and repeatability of manual measurements

Measurement	Mean Difference (mm)	95% Bland-Altman Limits of Agreement (mm)	rValue
Inter-method
Height	0.1	−1.5, 1.8	0.09
Width	−1.3	−4.3, 1.7	0.43
Repeatability
Height	−0.1	−1.1, 0.9	0.04
Width	0.0	−1.7, 1.8	0.15

4. DISCUSSION AND CONCLUSION

We proposed a novel technique to distinguish colonic polyps from normal colon surfaces based on topographical height maps. The novelty of this technique is that in addition to using the original 3D CT image, it uses height maps which reveal several visual properties that radiologists perceive to detect polyps. The technique can reduce false positives by more than 50%, and work well for both big polyps (>=10mm) and medium sized polyps (6–9mm).

The 2D endoluminal projection image technique proposed by Li et al. [17] [18] is close to our height map method in the sense that we both try to mimic the radiologist’s detection process. 2D endoluminal projection is more visually realistic compared to height map. However, the endoluminal projection method has several limitations. Firstly, lighting condition plays an important role in the image formation and is difficult to optimize. Secondly, excessive and complex background could influence the feature extraction for the main structures in the scene (polyps in this case). Thirdly, texture features are dependent on the in-plane rotation and translation of the projection plane. The height map approach handles these issues. The height map generation does not rely on any lighting condition. A height threshold can be applied to filter out most of the background. Topographic features based on the directional slopes from the apex to the base of a polyp are invariant to in-plane scale, translation and rotation. The height map is a 2D map. However 3D information is still preserved in the map since height value is stored at each pixel grid. This enables us to compute 3D features such as height, spread, and slope. Furthermore, we can also apply the wavelet transform to extract texture features of the polyp pattern, which cannot be easily computed from the 3D data directly. The Harr wavelet is currently used in our method, which is not rotation invariant. However since we are looking for concentric texture pattern for polyps, directional analysis is not necessary.

Instead of using the height map classifier as a post-processing step to reduce false positive detections, we can combine the features from 3D CT data and height map features to form a hybrid classifier. The benefit of this scheme is that it may improve the sensitivity. However, it requires height map evaluation on all detections before the second stage of classification, which may be too computationally expensive since the second stage classification typically eliminates 90% of false detections. Furthermore, putting all features together may over-train the classifier. The two-stage classifiers in current system are trained separately. The height map classifier is trained on the data from the first stage classifier (Figure 3). One can argue that the performance improvement in the two-stage classifiers could be attributed to increased classifier complexity. However, since we validated our system using separate test sets and obtained the same improvement, this indicated that the system was not over-trained.

The height map is generated using the ray casting technique. Both orthogonal and perspective projections were investigated. We chose the orthogonal projection since it is invariant to the projection distance and can preserve polyp size information. Another advantage is that only the projection direction needs to be set in the orthogonal projection, which makes the optimization much simpler. Orthogonal projection is also much more efficient to compute since we can pre-compute the projection rays. We adopted a simple virtual flattening algorithm to compensate the artificial height difference caused by the curved colon surface. Unlike the flattening techniques in [35] [36] [37], our virtual flattening operation is limited to a small local neighborhood around the polyp. In Equation 3, r is generally much bigger than b (5 to 10 times), so Δd is a small value. Therefore the geometric distortion associated with most flattening algorithms is insignificant in our method.

The concentric pattern of the polyp can be presented only when the projection direction is parallel to the polyp elevation direction. Choosing the correct projection direction is essential. The concentric index based on the directional slope is proven to be an effective metric. Other metrics such as image entropy to maximize the information in the map have also been employed in computer vision in trying to get the optimal projection angle [38]. However, in our case, more information does not equal stronger differentiating power. We search the entire projection direction space through a multi-scale scheme. An optimization algorithm such as gradient descent and Powell’s method [39] can be applied to improve the efficiency.

In future work, more topographic features such as profile curvatures, ridge lines and incident radiation could be computed and applied in the classification. A more precise concentric index will also be investigated. We are also working on using the height map features to evaluate polyp conspicuity.