Bayes pulmonary embolism assisted diagnosis: a new expert system for clinical use

Abstract

Background

The diagnosis of pulmonary embolism demands flexible decision models, both for the presence of clinical confounders and for the variability of local diagnostic resources. As Bayesian networks fully meet this requirement, Bayes Pulmonary embolism Assisted Diagnosis (BayPAD), a probabilistic expert systems focused on pulmonary embolism, was developed.

Methods

To quantitatively validate and improve BayPAD, the system was applied to 750 patients from a prospective study done in an Italian tertiary hospital where the true pulmonary embolism status was confirmed using pulmonary angiography or ruled out with a lung scan. The proportion of correct diagnoses made by BayPAD (accuracy) and the correctness of the pulmonary embolism probabilities predicted by the model (calibration) were calculated. The calibration was evaluated according to the Cox regression–calibration model.

Results

Before refining the model, accuracy was 88.6%. Once refined, accuracy was 97.2% and 98%, respectively, in the training and validation samples. According to Cox analysis, calibration was satisfactory, despite a tendency to exaggerate the effect of the findings on the probability of pulmonary embolism. The lack of some investigations (like Spiral computed tomographic scan and Lower limbs doppler ultrasounds) in the pool of available data often prevents BayPAD from reaching the diagnosis without invasive procedures.

Conclusions

BayPAD offers clinicians a flexible and accurate strategy to diagnose pulmonary embolism. Simple to use, the system performs case‐based reasoning to optimise the use of resources available within a particular hospital. Bayesian networks are expected to have a prominent role in the clinical management of complex diagnostic problems in the near future.

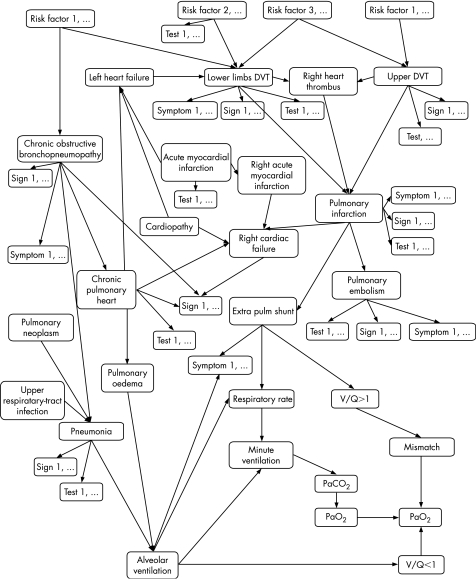
Despite the recent improvements in diagnostic methods for thromboembolism, the diagnosis of pulmonary embolism remains challenging.¹,²,³,⁴,⁵,⁶,⁷,⁸ Reasons include the high cost of accurate examinations, the different risk perception with techniques based on contrast media (like pulmonary angiography,⁹ phlebography and spiral computed tomographic scan¹⁰,¹¹), and the variability in terms of practical availability and even the performance of qualified people.¹²,¹³ Moreover, some observations may have a negative or positive effect on the value of further ascertainments, explaining why, for instance, pulmonary embolism can be hard to diagnose in patients with other cardiorespiratory diseases.¹⁴,¹⁵,¹⁶,¹⁷ Thus, the diagnosis of pulmonary embolism cannot be made without combining and interpreting a collection of investigations.¹⁸ One innovative approach to see how different findings influence medical hypotheses is offered by Bayesian or probabilistic networks.¹⁹,²⁰ These can assist a decision flexibly, depending on the examinations that are available among a large range of choices.²¹,²² To exploit these innovations in the diagnosis of pulmonary embolism, we developed Bayes Pulmonary embolism Assisted Diagnosis (BayPAD), an evidence‐based expert system²³ composed of a probabilistic network focused on thromboembolic disease (fig 1). Once a patient's findings are entered, the model provides the probability of pulmonary embolism and the information content of examinations still to be carried out. The information content is related to the ability of an examination to reduce the uncertainty about a diagnostic hypothesis, and can be assessed by the mutual information measure.²⁴ The BayPAD suggestions are tailored to each patient's characteristics and each centre's facilities. The system was extensively validated through different steps, covering face and content validity, and qualitative comparison with independent experts' suggestions.

Figure 1 A simplified Bayesian network showing the main pathophysiological relationships in the diagnostic reasoning focused on a suspected pulmonary embolism event. For the sake of clarity, observable findings have been given a generic label of symptom, sign, test or risk factor, and their association with the rest of the variables has been omitted.

Here we used the data collected in the Prospective Investigative Study of Acute Pulmonary Embolism Diagnosis (PISA‐PED) study on the diagnosis of pulmonary embolism²⁵ to quantitatively validate and further improve the system. As BayPAD was designed to help doctors in correctly classifying suspected thromboembolic events, the primary index of performance is diagnostic accuracy, split into its two dimensions: sensitivity and specificity. Given that the model also indicates the probability of the disease, we analysed the “calibration”, which evaluates the degree of correspondence between the estimated probability produced by the model and the patient's true disease status.

Methods

Data

The PISA‐PED study was a prospective observational study completed at an Italian tertiary hospital in 1996 on 750 consecutive patients. Eligibility was based on the clinical judgement of suspected pulmonary embolism according to six on‐call pulmonary doctors, all of whom had experience with diagnosis of the disease.²⁵ From the whole study population, a first group of 500 patients were randomly selected to further develop the model (training sample), with the second group of 250 patients employed only to evaluate the validity of the refined model (validation sample). In all patients pulmonary embolism was confirmed by pulmonary angiography, or was ruled out when a lung scan showed no perfusional defects. In the training sample, perfusion lung scans were normal or near normal in 105 of 500 (21%) patients and abnormal in 395 (79%). Angiograms were positive for pulmonary embolism in 200 (40%) patients and negative in 191 (38%). In four patients who died before angiography could be done, the diagnosis was established at autopsy. Two of these patients had pulmonary embolism. Patients were aged 63.8 (14.5) years (range 15–91 years); 243 (49%) of them were men. Most patients (85%) were hospitalised at the time of study entry (table 1).²⁶

Table 1 Characteristics of the first 500 patients enrolled in the Prospective Investigative Study of Acute Pulmonary Embolism Diagnosis Study.

	n (%)
Dyspnoea	345 (69)
Chest pain	240 (48)
Fainting	91 (18)
Palpitations	82 (16)
Hospitalisation	437 (85)
Surgery*	197 (39)
Bone fractures (lower limbs)*	82 (16)
Pre‐existing diseases
Cardiovascular	149 (30)
Pulmonary	86 (17)
Neoplastic	79 (16)
Endocrine	53 (11)

*Within 4 weeks of study entry.

Table 2 displays the variables of diagnostic interest the BayPAD system is able to cope with, as well as those available in the PISA‐PED database.

Table 2 Variables selected in the validation analysis.

Variables	BayPAD included in the network	Available in the PISA‐PED Study	Selected for the validation
Pre‐existing disease
Chronic cardiovascular disease	Yes	Yes	Yes
Chronic pulmonary disease	Yes	Yes	Yes
Cancer	Yes	Yes	Yes
Hereditary DVT predisposing factors	Yes	No	No
Risk factors
Age	Yes	Yes	Yes
Sex	Yes	Yes	Yes
Immobilisation	Yes	Yes	Yes
Cigarette smoking	Yes	No	No
Central line	Yes	No	No
Surgery	Yes	Yes	Yes
Pregnancy	Yes	Yes	Yes
Chronic venous insufficiency	Yes	Yes	Yes
Oestrogen intake	Yes	Yes	Yes
Bone fractures	Yes	Yes	Yes
DVT prophylaxis	Yes	No	No
Symptoms
Dyspnoea	Yes	Yes	Yes
Orthopnoea	Yes	Yes	Yes
Fainting	Yes	Yes	Yes
Chest pain	Yes	Yes	Yes
Haemoptysis	Yes	Yes	Yes
Agitation	Yes	No	No
Lower limb discomfort	Yes	No	No
Cough	Yes	No	No
Signs
Lower limb unilateral oedema	Yes	Yes	Yes
Cyanosis	Yes	No	No
Fever>38 °C	No	Yes	No
Bronchospasmus	Yes	Yes	Yes
Systolic blood pressure	Yes	No	No
Tachypnoea	Yes	Yes	Yes
Tachycardia	No	Yes	No
Cardiac failure signs	Yes	Yes	Yes
Shock	Yes	No	No
Laboratory findings
D‐dimer test	Yes	No	No
paO2	Yes	Yes	Yes
paCO2	Yes	Yes	Yes
CK‐MB enzymes	Yes	No	No
ECG findings
ECG right heart overload signs	Yes	Yes	Yes
ECG acute myocardial infarction signs	Yes	No	No
Chest x rays
Consolidation (infarction)	Yes	Yes	Yes
Consolidation (no infarction)	No	Yes	No
Plate‐like atelectasis	No	Yes	No
Pulmonary oedema	Yes	Yes	Yes
Elevation of half of the diaphragm	Yes	Yes	Yes
Unilateral pleural effusion	Yes	No	No
Pulmonary oligaemia	No	Yes	No
Amputation of hilar artery	No	Yes	No
Pneumonia	Yes	No	No
Imaging
Doppler ultrasounds of the lower limbs	Yes	No	No
Echocardiographic signs of pulmonary embolism	Yes	No	No
Ventilation/perfusion lung scan	Yes	No	No
Perfusion lung scan	Yes	Yes	Yes
Phlebography	Yes	No	No
Spiral CT scan	Yes	No	No
Pulmonary angiography	Yes	Yes	Yes

BayPAD, Bayes Pulmonary embolism Assisted Diagnosis; CK‐MB, Creatine Kinase; CT, Computed tomography; DVT, Deep venous thrombosis; ECG, electrocardiogram; PISA‐PED, Prospective Investigative Study of Acute Pulmonary Embolism Diagnosis.

As the BayPAD system had 48 variables and the PISA‐PED 34, the model could not be validated completely. Regardless of this limit, the bayesian characteristic of the network enables us to deal with missing information, without the need to input any observation merely because it is contemplated by the model. This feature explains the adaptability of the system to the diagnostic resources of a particular hospital or ward, and it is also what makes this retrospective analysis methodologically feasible.

Overall, six variables were present in the PISA‐PED study but not in our model. Five variables (“chest pain”, “pregnancy”, “surgery”, “electrocardiographic signs of right heart overload” and “pulmonary embolism”) were expressed with more details in the network than in the study (three‐level v two‐level variables). To use the PISA‐PED data, we simplified the network in these variables. The opposite happened for “perfusion lung scan”, which was a three‐level variable in the PISA‐PED Study (“no perfusional defects”, “segmental defect” and “not segmental defect”) but binary in the original network (“normal” and “abnormal”). The model was extended accordingly. Eventually, 28 variables were available for the validation analysis (table 2).

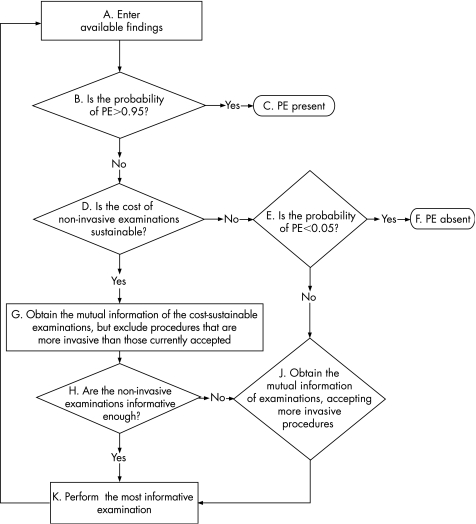
Data were processed following the algorithm through which BayPAD implements its strategy (fig 2). The diagnostic criteria are based on two probabilistic cut‐offs: probability >95% to confirm pulmonary embolism and <5% to exclude pulmonary embolism, provided that all the examinations whose costs divided by the probability of pulmonary embolism do not exceed a conventional boundary of €3500 were already done.²³ Once applied, these criteria become clearly asymmetric and more sensitive to false negatives, as many diagnostic procedures remain cost‐sustainable even for probabilities <5%. BayPAD suggests pulmonary angiography when the information content of the examinations not carried out is too low to allow a diagnostic conclusion (fig 2). As a result, we had the final BayPAD diagnosis for each patient and one predicted probability of pulmonary embolism for each patient step (fig 3, where the algorithm has been applied to two real clinical examples). Patients whose diagnosis was reached by asking for this “standard” were identified.

Figure 2 The Bayes Pulmonary embolism Assisted Diagnosis (BayPAD) strategy: the algorithm implementing the BayPAD diagnostic strategy on the PISA‐PED cases.

Figure 3. Bayes Pulmonary embolism Assisted Diagnosis (BayPAD) working with two real clinical examples. The algorithm steps presented in fig 2 are indicated in brackets.

Hardware requirements for the analysis consist of a central processing unit of at least 233 MHz and 64 Mb random access memory.

Diagnostic performance

BayPAD's ability to classify cases correctly was assessed from sensitivity, specificity and overall diagnostic accuracy. We computed these indicators for the whole sample and for the subsample of patients whose diagnosis was reached without pulmonary angiography.

To measure how well the model was calibrated, we adopted the approach introduced by Cox.²⁷ Labelling p the probabilities computed by the model, a logistic regression was done with the outcome of pulmonary embolism as the dependent variable and the natural logarithm transformation of the ratio p/(1‐p) as the independent regressor (ie, the ordinary logit transformation). If the accuracy of p is faultless, the estimates of the intercept and the slope are 0 and 1, respectively. An intercept different from 0 would show a systematic disagreement between the probabilities produced by the model and the proportion of pulmonary embolism cases. A positive slope lower or higher than 1 would show the predicted probabilities, respectively, increasing or decreasing compared with the observed density of pulmonary embolism events. A null slope would mean that predicted probabilities are completely independent of the outcomes, whereas a negative slope would prove a negative association.²⁸

Finally, a calibration curve was drawn by plotting deciles of predicted probabilities against the corresponding proportion of pulmonary embolism events.

Refinement and validation of the model

As diagnostic accuracy is sensitive to biases affecting predicted probabilities, the network was refined by looking at its calibration in the 500 cases representing the training sample. We followed the approach suggested by Miller et al.²⁸ Firstly, a sensitivity analysis was performed by excluding cases with identical characteristics. As a result, each case was associated with a measure of its effect on calibration, considering both Cox parameters. Secondly, these measures played the part of dependent variable in two separate linear regression models, where the influential patient's characteristics (on calibration) were identified. Finally, the network parameters related to these characteristics were reappraised and tuned, keeping a modification only when it conformed to the medical literature and enhanced the validity of the model. As the structure of the network represents the cause–effect relationships among variables (fig 1), if an improvement was attainable with structural changes, these were discussed and allowed only if consistent with the pathophysiological understanding of pulmonary embolism. Such a conservative approach in changing the probabilistic network was adopted to reduce the chance of overfitting the PISA‐PED data. The process was repeated until influential variables and convincing refinements could be detected.

Diagnostic performance was evaluated on both the original and the refined model, with the additional employment of a validation (250 cases) sample as it concerns the latter.

Results

The original network

Among the 500 cases provided by the training sample, there were 40.4% of pulmonary embolism cases. BayPAD made a correct diagnosis in 88.6% of the cases (accuracy), with 17 false negative and 40 false positive cases. This figure can be divided into 91.6% (95% CI 86.9 to 94.7) cases of correct diagnosis among true pulmonary embolism cases (sensitivity) and 86.6% (95% CI 82.2 to 90) cases of correct diagnosis among truly non‐pulmonary embolism cases (specificity); 152 (30.4%) cases required pulmonary angiography to reach the final diagnosis. In the subgroup in which pulmonary angiography was not used, accuracy was 83.6%, sensitivity 88.8% and specificity 79.6%.

When the BayPAD strategy was applied to the data, each case passed through an average of 3.3 further ascertainments before the final diagnosis, producing a total of 1660 steps where predicted probabilities were computed. Cox analysis indicated that the intercept was −0.234 (95% CI –0.364 to –0.104), significantly different from 0 (p<0.001), and the slope 0.2091 (95% CI 0.182 to 0.236), significantly different from 1 (p<0.001).

The refined network

Several phases of parameter tuning were done to increase the validity of the model. Most of them affected the quantitative strength of associations between variables, and others the increase in the number of discrete intervals for continuous variables (like paO₂ and paCO₂). Structural changes were introduced to account for previously neglected associations, like that for “bone fractures”, found to be an extra explanation of “unilateral oedema”.

After refinement, BayPAD showed 97.2% accuracy in the 500 cases of the training sample, with six false‐negative and eight false‐positive cases. Sensitivity and specificity were 97.0% (95% CI 94.2 to 98.7) and 97.3% (95% CI 95.2 to 98.7); 187 (37%) cases required pulmonary angiography to reach the final diagnosis. Accuracy was 96.0%, with 96.0% sensitivity and 95.9% specificity in the subgroup in which pulmonary angiography was not needed.

Concerning calibration, the intercept and slope of the Cox approach were, respectively, –0.05 (95% CI –0.08 to 0.18), not significantly different from 0 (p = 0.47), and 0.62 (95% CI 0.56 to 0.68), significantly different from 1 (p<0.001).

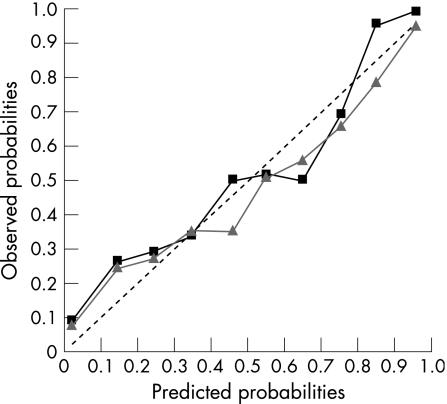
Figure 4 shows the calibration curve of the refined model. Each decile had more than five expected cases of pulmonary embolism.

Figure 4 The calibration curve with observed probabilities (frequencies) of pulmonary embolism events plotted against predicted probabilities of the same event. Data are grouped into deciles according to the predicted probabilities. The dotted line represents perfect calibration, whereas the green (with triangles) and the blue (with squares) curves, respectively, refer to the training and validation samples.

The validation sample showed a proportion of pulmonary embolism cases (41.6%) comparable to that which emerged from the training sample. BayPAD delivered an accurate diagnosis in 98% of the 250 cases, with four false‐negative and one false‐positive cases. Sensitivity and specificity were 96.1% and 99.3%; pulmonary angiography was required for 79 (31%) cases. Sensitivity and specificity were 94.5% and 98.9% in the subgroup in which pulmonary angiography was not needed. The intercept and slope of the Cox regression–calibration model were, respectively, 0.31 (95% CI 0.10 to 0.52), significantly different from 0 (p = 0.003), and 0.70 (95% CI 0.61 to 0.80), significantly different from 1 (p<0.001).

Discussion

BayPAD is an expert system based on a probabilistic network whose structure represents the “state of the art” on the pathophysiological understanding of thromboembolism (fig 1). Thus, within its automated diagnostic reasoning, the system acknowledges which part of the network is relevant to a decision, given the specific patient's findings. On the basis of the causal relationships between events, a virtually infinite number of clinical scenarios can be dealt with, whereas the computation to identify the most appropriate examination takes just a few milliseconds.¹⁹ Conversely, in guidelines based on decision trees, whether or not an examination is appropriate is established through a limited set of predefined patient's findings. So if the performance of these algorithms proves to be satisfactory at a population level, they are often inappropriate when applied to the clinical investigation of individual problems.²⁹

The other popular aid to medical diagnosis is scoring systems, indicating the need for further ascertainments according to the predicted probability of the diagnosis. However, they overlook the possible influence of available findings on the results of the examinations suggested. As an example, recent surgery increases the risk of pulmonary embolism, but it also reduces the specificity of the D‐dimer test ³⁰; again, previous cardiopathy makes an echocardiography or an ECG more sensitive to an embolic episode, because in these patients a haemodynamically relevant pulmonary embolism is more likely.¹⁷,³¹ In the BayPAD model, these phenomena are taken into account. Finally, the Bayesian nature of the probabilistic network allows BayPAD to deal with missing information.³²

The consequent flexibility makes it possible to deal with the problem of optimal exploitation of available diagnostic resources. This is important, as resources are usually so differently distributed among the clinical settings where pulmonary embolism is a challenge that it is hard to expect widespread acceptance of any guideline on the basis of a fixed set of examinations.¹³ The potential value of probabilistic networks in this field has been theoretically accepted,²¹,²²,³³ but their successful application obviously depends on their diagnostic accuracy over different contexts. Usually, to validate a prediction model, all the variables considered must be collected, without missing. However, a Bayesian Network can be regarded as the assemblage of smaller networks, allowing independent validation of each part. Such an approach is safe as long as the structure of the network represents the causal relationships among the events included in the model.³⁴ Consequently, even a quite old database like PISA‐PED is of value for a validation purpose. Indeed, although some important tests are lacking (eg, computed tomographic scan or D‐dimer), the PISA‐PED data allowed the assessment of the most complex part of the model. Moreover, since in a Bayesian Network the overall proportion of an event depends on the conditional observations included, the large set of variables considered in BayPAD makes the possible difference between the validation sample and another population of interest relatively unimportant. As a matter of fact, BayPAD, after its refinement based on the PISA‐PED data, still returns a proportion of pulmonary embolism cases before any observation is introduced which is around 1%. This resembles the prevalence of pulmonary embolism in a general hospital, rather than the prevalence expected given a clinical suspicion of pulmonary embolism, like in the PISA‐PED study.

Here the assessment of the system passed through the evaluation of two major properties: predicting a reliable probability of pulmonary embolism for a specific patient, and distinguishing between true and false cases of pulmonary embolism. These are closely related, as the second is obtained through a couple of probabilistic cut‐offs that are expected to be reliable. Therefore, the calibration of BayPAD has been examined first, providing the only evidence used to refine the model.

Rather than looking at a qualitative response in the calibration of our model, like within a significance testing framework,³⁵,³⁶ our aim was to see how accurate the probabilities predicted by the model were. The approach introduced by Cox provided us with this quantitative insight.²⁷ Once applied to the original network, the analysis gave an intercept of –0.23, meaning that, on average, the probability of pulmonary embolism exceeded its observed frequency. Instead, the slope of 0.21 showed a tendency of the low probabilities to be too low and that of the high probabilities to be too high, resulting in overconfidence in the diagnosis. Looking at the effect of this calibration on the diagnostic accuracy in the studied population, we found correct classification for 88.6% of the suspected cases.

The complete independence of the PISA‐PED study from the development of the model, the heterogeneity of the sources in the medical literature fuelling the network's knowledge³⁷ and the qualitative assessment of the network's behaviour as its sole former validation²³ make this figure encouraging. However, this estimation is also inconsistent with the probabilistic values adopted to authorise a diagnosis, which would allow <10% of diagnostic errors. As expected, this inadequacy was treated as a model recalibration problem. After the refinement analysis, the slope parameter moved near to its ideal value of 1, both in the training and in the validation sample (0.62 and 0.70, respectively). This means that the original tendency to exaggerate the effect of the observations on the pulmonary embolism hypothesis has been greatly reduced. The intercept parameter, on the other hand, shows that, in the validation sample, the predicted probabilities tend to be overall too low. Particularly, an intercept of 0.3 entails for predicted probability around 50% to be undersized of 7%.

How the residual bias affects the diagnostic accuracy is easily visualised on the calibration curve (fig 4). Misclassified cases became <10% (2.8% and 2%, respectively, in the training and validation samples), and this remains true when accuracy was measured in the 347 cases where pulmonary angiography was not suggested (4%). The lack of important investigations in the pool of available data (table 2) often prevented BayPAD from suggesting minimally invasive but still informative tests, with the result that pulmonary angiography was suggested for about one third of the patients. The many investigations not contemplated in the PISA‐PED study include Doppler ultrasound of the lower limbs, echocardiography, D‐dimer and spiral computed tomographic scan. As these procedures are available in most hospitals, the resulting proportion of pulmonary angiography seems not to reflect the behaviour of BayPAD, once introduced in the clinical setting (eg, fig 3 shows two real cases where BayPAD evaluates the appropriateness of D‐dimer and spiral computed tomographic scan). Moreover, given the progress achieved by the latest multidetector computed tomographic scans,³⁸ this technique is expected to replace pulmonary angiography in most instances, while still supporting the diagnostic engine with similar precision. To confirm this, we simulate the effect of the availability of a computed tomographic scan with 0.92 sensibility and 0.98 specificity,³,⁶ obtaining a correct diagnosis in 96% of all cases.

The literature offers a number of diagnostic strategies for the diagnosis of pulmonary embolism,²⁵,³⁹,⁴⁰,⁴¹,⁴²,⁴³,⁴⁴ but it is hard to compare their performances. Studies to validate the proposed algorithms apply different procedures to check the true diagnosis²⁵,⁴³: some are focused on the prognostic outcome rather than the diagnostic classification.⁴²,⁴⁴ They mostly differ in terms of available diagnostics,²⁵,³⁹,⁴⁰,⁴¹,⁴³ and classify patients according to a variable number of pulmonary embolism probability levels.²⁵,⁴⁰

Without perfusion lung scan, but with a clinical assessment extended to chest x rays, ECG and arterial blood samples, Miniati et al found their algorithm correct in 90% of suspected cases.²⁵ On the basis of similar findings, but with the inclusion of the ventilation/perfusion lung scan and bilateral leg vein ultrasonography, the Wells score correctly identified 96% of cases.³⁹ Another study showed a predictive accuracy for the Geneva score and a simplified version of the Wells score, both based on clinical findings alone, of 78% and 74%, respectively.⁴⁰,⁴¹

The BayPAD system deals with most of the issues raised by a complex diagnostic problem like pulmonary embolism. To the best of our knowledge, this is the first validated clinical model where the choice of a new ascertainment depends on its information content.²⁴,⁴⁵ Moreover, the probabilistic network underlying the expert system covers the largest set of examinations ever contemplated for the disease. This already enables BayPAD to deal with hypotheses other than pulmonary embolism. Such a possibility will be fully exploited in a future version, where the most appropriate ascertainment will depend on a broad spectrum of possible diagnoses, without privileging pulmonary embolism. Growing to be a multi‐purpose system, BayPAD could be accepted even in the emergency department, where time constraints and overcrowding often hamper the use of computer‐based systems.

Although a prospective investigation is still needed to evaluate BayPAD in its full potential, the results obtained with this model, even at an initial phase of its development, reserve for Bayesian networks a prominent role in the next generation of clinical decision models. This prospect sounds like a proper reply to some farsighted authors who, like Feinstein, 10 years ago advocated “appropriate scientific analyses for the unique and fundamental characteristics of clinical activities that still occur as ‘clinical judgement'”.⁴⁶

Abbreviations

BayPAD - Bayes Pulmonary embolism Assisted Diagnosis

PISA‐PED - Prospective Investigative Study of Acute Pulmonary Embolism Diagnosis