An information-bearing seed for nucleating algorithmic self-assembly

Abstract

Self-assembly creates natural mineral, chemical, and biological structures of great complexity. Often, the same starting materials have the potential to form an infinite variety of distinct structures; information in a seed molecule can determine which form is grown as well as where and when. These phenomena can be exploited to program the growth of complex supramolecular structures, as demonstrated by the algorithmic self-assembly of DNA tiles. However, the lack of effective seeds has limited the reliability and yield of algorithmic crystals. Here, we present a programmable DNA origami seed that can display up to 32 distinct binding sites and demonstrate the use of seeds to nucleate three types of algorithmic crystals. In the simplest case, the starting materials are a set of tiles that can form crystalline ribbons of any width; the seed directs assembly of a chosen width with >90% yield. Increased structural diversity is obtained by using tiles that copy a binary string from layer to layer; the seed specifies the initial string and triggers growth under near-optimal conditions where the bit copying error rate is <0.2%. Increased structural complexity is achieved by using tiles that generate a binary counting pattern; the seed specifies the initial value for the counter. Self-assembly proceeds in a one-pot annealing reaction involving up to 300 DNA strands containing >17 kb of sequence information. In sum, this work demonstrates how DNA origami seeds enable the easy, high-yield, low-error-rate growth of algorithmic crystals as a route toward programmable bottom-up fabrication.

Growth from seeds confers both flexibility and control to a synthetic method: A single process can generate a wide range of products, with the specific choice of product determined by information contained in the seed; side products can be reduced dramatically because of the presence of a nucleation barrier, resulting in high-yield synthesis; and growth can proceed under near-ideal chemical conditions, resulting in products with few defects. Mineral and chemical compounds exhibit the simplest form of seeded growth, wherein a supersaturated solution of a polymorphic material can be inoculated with seed crystals to produce large, pure crystals of the desired form (1). In nanostructure synthesis, seeds may be used to control the diameter and crystal type of carbon nanotubes and metal nanowires (2–4). Biological organisms use information-bearing seeds with amazing control over the type, place, and timing of the structures grown from the same starting materials: Minimal media consisting of glucose, nitrogen, sulfates, and salts can be seeded with a single bacterium that will convert the starting material to biomass whose structure and composition is dictated by genomic information (5). Multicellular development, where genomic information in the zygote directs the algorithmic construction of the entire organism (6, 7), demonstrates the ultimate potential of seeded growth. Accessing this potential for nonbiological synthesis requires artificial systems of intermediate complexity that retain the simplicity of nonbiological seeded growth yet exhibit the diverse programmability of biological growth.

The algorithmic self-assembly of tiles (8, 9) fills this gap by providing an interpretation of crystal growth as information processing; it is related to crystal growth by identifying tiles with molecules. In tiling theory, a tile is a geometrical shape, such as a jigsaw puzzle piece, that may be assembled with other tiles based on local matching rules. The way tiles fit together can impose complex long-range order, including shapes and patterns generated by Turing-universal computation (10–12). Such shapes and patterns go beyond familiar fixed-size, periodic, and random arrangements to include objects created algorithmically, such as fractals, binary trees, cellular automata—i.e., things that can be created by a computer program. Remarkably, to achieve such diversity, it suffices to use just 4-sided tiles on a rectilinear lattice—these are known as Wang tiles. The self-assembly process begins with an initial seed tile to which additional tiles can attach if they make sufficiently many matching contacts (8, 9). In this setting, the starting materials—a set of available tiles—is considered a program, the seed is an input to that program, and the structure produced by self-assembly is the output. Such self-assembly programs can create extremely large algorithmic structures, even when the program is small. There even exists a single universal tile set that can grow arbitrary algorithmic shapes as specified by information provided in the seed (13). Thus, algorithmic self-assembly is universal both for computation and for construction (10, 14). These features establish an analogy to developmental programs in biological organisms: “Genomic information” contained in a seed specifies a complex growth process guided by information processing.

Although the behavior of many naturally occurring molecules cannot be described within this framework, many successful artificial systems have been created by translating a set of abstract tiles that compose an abstract tiling into a set of molecules that build the desired physical structure. Tile-based self-assembly programs have been demonstrated experimentally by using DNA tiles (15) to create periodic (16–18), finite (19, 20), and algorithmic (21–23) patterns. Each DNA tile consists of multiple strands folded into a rigid unit typically displaying 4 single-stranded “sticky ends” that direct the tile's binding interactions with other tiles. Tile binding interactions are programmed (24) by choice of sticky-end sequence, relying on the affinity and specificity of Watson–Crick base-pairing. This allows the systematic molecular implementation of matching rules for arbitrary Wang tiles. Under slightly supersaturated conditions, where the rate of tile attachment is only slightly higher than the rate of dissociation, molecular self-assembly is predicted to sustain growth of algorithmic patterns with few errors (25) while preventing spontaneous nucleation of unseeded structures (26). In practice, however, insufficient control over nucleation has so far prevented high-yield synthesis of accurate algorithmic structures. Using single-stranded DNA as nuclei (22, 23, 27) resulted in high error rates (a few percent per tile or more), high spontaneous nucleation rates, and low yields of well-formed structures—which were partially attributed to the floppiness of these single-stranded seeds. Finite-sized tile assemblies and self-assembled ribbon-like crystals have also been used as seeds, with improved performance ascribed to increased rigidity, but incorporating significant amounts of specific information into such seeds remains prohibitive (28, 29). This motivates our interest in creating seeds that are (i) sufficiently well-formed to nucleate defect-free DNA tile crystals, (ii) capable of being synthesized with arbitrary information that the DNA tile programs can read as input, and (iii) straightforward to implement experimentally.

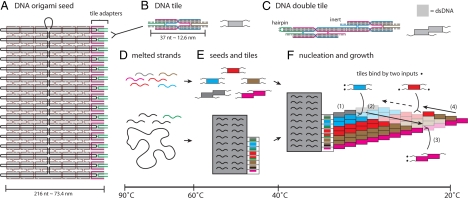
Here, we develop DNA origami rectangles (30) as information-bearing seeds that efficiently nucleate algorithmic self-assembly of DNA tile crystals. Each rectangle assembles from a single circular “scaffold strand” (a 7.3-kb M13mp18 single-stranded DNA phage genome) and 192 short “staple strands” that direct its folding into an ≈75 × 95-nm structure consisting of 32 parallel double-helical regions bound together by multiple crossover points where strands exchange helices (Fig. 1A). For the origami rectangles to serve as seeds for DNA tile crystals, we designed a set of 32 “adapter strands” that bind on the right side of the rectangle, forming 16 “tile adapters” whose local structure is identical to the DNA tile motif [Fig. 1 B and C and supporting information (SI) Figs. S1–S4]. Each adapter strand contains unique sequence elements, ensuring that the tile adapter forms at a specific location along the side of the rectangle where it presents a chosen pair of sticky ends. These sticky ends selectively bind tiles, with each tile attaching between two tile adapters. By changing the sticky-end sequences on the adapter strands, the rectangle can be programmed to specify any chosen pattern of tiles.

Fig. 1.

Molecular design and self-assembly scheme. (A) The DNA origami seed consists of a scaffold strand (black), 192 staple strands (brown), and 32 tile adapter strands (pink and green) that bind at specific locations along the scaffold strand (base pairing indicated in gray). To present different information, tile adapter strands (green) are changed to have different sticky-end sequences, blunt ends, or inert hairpins; alternatively, tile adapter strands may be omitted for unused positions. (B) Each DNA tile consists of 4 strands that self-assemble into a molecule with a double-stranded core and 4 single-stranded 5-nt sticky ends. In simplified form, we depict tiles as rectangles (inert cores) and squiggly lines (active sticky ends). Forked arrows show how tiles attach to tile adapters. (C) Each DNA double tile, structurally equivalent to 2 fused tiles, consists of 6 strands that display 4 active sticky ends; 2 helix arms end either with a hairpin or with an inactive (inert) sticky end whose sequence matches no other sticky end. (D–F) The expected sequence of self-assembly events is shown for an illustrative example; transition temperatures are approximate. Colored stripes on the seed‘s tile adapters indicate sticky ends that specify an 8-tile-wide ribbon encoding the string “01.” Ribbon growth follows a zig-zag path: (1) attachment of an upper double tile allows (2) rightward growth of the “ZIG layer” during which tiles attach by their two left sticky ends. Subsequent attachment (3) of a lower double tile allows (4) leftward growth of the “ZAG layer” during which tiles attach by their two bottom sticky ends. In this example, each zig and zag copies the pattern of “0” and “1” blocks from the preceding layer.

A typical experiment proceeds as follows. (See SI Text for details.) All strands for the seed (scaffold, staple, and adapter strands) and for the tile set (4 or 6 strands per tile species) are mixed together in buffer, heated to 90 °C, and annealed slowly to room temperature. Temperature-dependent thermodynamics and kinetics orchestrate the self-assembly process. At high temperatures, the DNA double helix is unstable and dissociates into its single-stranded form (Fig. 1D). At intermediate temperatures, the seed and individual tiles become stable because of extensive contacts between strands (at least 16 bp). However, tiles do not attach to the seed nor to each other because the two additional sticky-end contacts (totaling 10 bp) formed by each tile attachment are not thermodynamically favorable at these temperatures and concentrations (Fig. 1E). At slightly lower temperatures, below the crystal melting temperature, slightly supersaturated conditions are achieved. The attachment of a tile by two matching sticky ends becomes favorable, but attachment by a single matching sticky end remains unfavorable. Consequently, tiles now attach to the origami seed and then attach to each other to grow a crystal (Fig. 1F); in the absence of a seed, no growth is possible. For tile sets used in this work, crystals grow as long ribbons with standard-size DNA tiles (Fig. 1B) in the interior and DNA double-tiles (Fig. 1C) at the edges. Under such optimal conditions, correct growth consists strictly of favorable tile attachments that constrain tile additions to follow a zig-zag path; at each step, there is exactly one location where a tile can attach by two sticky ends simultaneously. In contrast, at even lower temperatures, a single sticky end may be sufficient for favorable attachment of a tile. At this point, tiles can attach to the ribbon at multiple locations, violating the restriction of growth to the zig-zag path and allowing incorrect partially matching tiles to attach; thus, correct algorithmic growth is no longer expected. This motivates designing tile systems so that the majority of the tiles will be incorporated into well-formed structures before the lowest temperatures are reached. Furthermore, the transition temperatures between these regimes depend on free tile concentrations, which decrease over the course of an experiment. Thus, by the time the lowest temperatures are reached, if all tile concentrations decrease sufficiently, it is possible to stay within the desired slightly supersaturated regime.

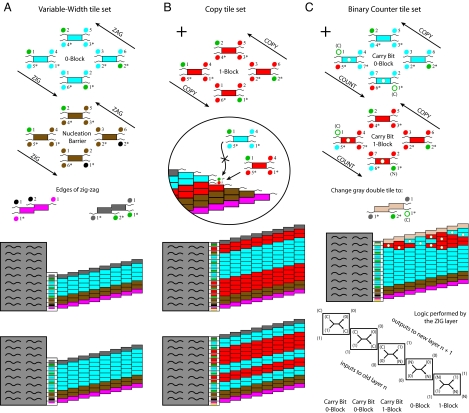
To test whether the origami rectangle could serve as a seed for crystal growth, we used a DNA tile set known to have a substantial nucleation barrier under slightly supersaturated conditions (28). These tiles, the “4-wide zig-zag tile set” (the double tiles and nucleation barrier tiles in Fig. 2A), self-assemble into 4-tile-wide ribbons. By adding another 4 tiles (“0” block tiles in Fig. 2A), we created a tile set capable of forming zig-zag ribbons of any even width greater than 2 (containing zero or more repeats of the 0 block), thus constituting a system where the crystal morphology may be determined by information specified within the seed. We call this the “Variable-Width tile set.” The rate of spontaneous nucleation decreases dramatically with width, and so, when the tiles are annealed without a seed, we expect the majority of crystals to be just 4 tiles wide. However, when annealed in the presence of seeds whose adapter tiles specify a particular width ribbon, we expect crystals of the specified width will grow off the seed—even before 4-wide ribbons nucleate spontaneously.

Fig. 2.

Logical design of tile sets and ribbons grown from example seeds. (A) Variable-Width tile set. Tiles are grouped into blocks to emphasize logical relations, but crystals grow by addition of individual tiles. Dot color and number together indicate the logic of sticky-end hybridization, with complementary sticky-ends marked by an asterisk. (B) Additional tiles for the Copy tile set. Inset shows how correct copying of information at bit boundaries depends on preferred attachment of tiles matching two sticky ends over tiles matching just one. (C) Binary Counter tile set. The 4 tiles in the COUNT layers of the “Carry Bit 1-Block” and “Carry Bit 0-Block” are added to the Copy tile set, and the gray double tile is replaced by the beige one, whose sticky end provides the initial carry bit for each new COUNT layer. (Four tiles of the Copy tile set are repeated in the Carry Bit Blocks.) White dots mark tiles receiving a carry bit. Inset indicates the logic for the COUNT layers in the example 10011 + 1 = 10100. Each rectangle indicates the logic encoded by a pair of COUNT layer tiles; arrows indicate input and output. Sequences and diagrams for all tiles and strands are in Figs. S1–S4 and the SI Appendix; details for seeds are in Figs. S5 and S6.

We therefore performed experiments with three origami seeds, specifying ribbon widths 8, 10, and 12. Each sample was prepared with a matching stoichiometry of tiles, by using more 0-block tiles for wider ribbons, so that an equal percentage of each tile type would be depleted per layer of ribbon growth, with ideally no tiles left over. For each stoichiometry, control samples without seeds were similarly prepared and analyzed (SI Text). After annealing, crystals were deposited on mica and examined by atomic force microscopy (AFM). To avoid fragmentation during deposition, some samples were ligated after assembly (31) and purified by spin filtration to remove molecules that otherwise reduce image quality. All clearly identifiable crystals in ligated samples had the expected “corn-cob pipe” morphology, although significant aggregation precluded assessment of yield (Fig. 3 A–C).

Fig. 3.

Programming ribbon width. (A–C) AFM images of ligated ribbons grown from seeds specifying 8-, 10-, and 12-tile-wide ribbons, respectively. (Scale bars: 1 μm.) (D, F, and H) Respective high-resolution AFM images of individual ribbons. (Scale bars: 50 nm.) (E, G, and I) Distribution of ribbon widths in corresponding samples of unligated ribbons (SI Text), given as the fraction of tiles found in ribbons of a given width. Solid bars indicate samples annealed with seeds. n = 41,718; 69,200; and 125,876 tiles, respectively. Dots indicate samples annealed without seeds. n = 23,524; 26,404; and 145,376 tiles, respectively. In each experiment, boundary and nucleation barrier tiles were at 100 nM each, and the repeatable block tile concentrations were proportional to their use in ribbons of the target width, i.e., 200, 300, and 400 nM, respectively. For samples with seeds, each staple strand was at 50 nM, each adapter strand was at 100 nM, and the origami scaffold strand was at 10 nM.

Because single tiles could be identified routinely in high-resolution images (Fig. 3 D, F, and H), we were able to measure the widths of individual crystals and thereby the distributions of ribbon widths in a sample, by using images of random locations on the mica surface (Fig. S7). Although the distributions of widths in all unseeded samples were peaked at the minimum width (4 tiles) as expected, the seeded samples were sharply peaked with >90% of tiles in ribbons of the seed-specified width (Fig. 3 E, G, and I). The major remaining species were crystals of the next smaller width, often because of lattice defects in the first layer of tiles. (Experiments using the same seeds but with equimolar tile concentrations produced similarly peaked distributions, but resulted in a higher fraction of unseeded crystals. These crystals presumably formed from the excess double tiles and nucleation barrier tiles remaining after seeded growth depleted the 0-block tiles. See SI Text and Fig. S8). Thus, origami seeds nucleated crystals with a highly specific target width chosen from the 7 widths (4 to 16) that could be encoded with a seed of this size. For larger seeds, the number of possible products in Variable-Width experiments is proportional to the number of tile adapters.

In principle, origami seeds can provide combinatorial information to the growing ribbon, because each tile adapter may present an independent choice of sticky ends. Such diversity can be harnessed to specify one of an exponential number of products, as a function of the number of tile adapters. To demonstrate this principle, we added 4 tiles to the Variable-Width tile set to obtain the Copy tile set, which is designed to copy arbitrary binary bit strings from layer to layer within the ribbon. These 4 tiles, the 1-block tiles in Fig. 2B, can substitute for the 0-block tiles on their upper-left and lower-right sides, but can bind only to appropriate 1-block tiles on their lower-left and upper-right sides (layer to layer). This logic permits ribbons whose cross-sections can consist of arbitrary patterns of 0- and 1-blocks while enforcing that the pattern in each layer is the same. We created 5 origami seeds to nucleate Copy ribbons with 5 distinct 6-bit patterns (of 64 possible), and annealed each with tiles adjusted to the matching stoichiometry. All seeds successfully nucleated crystals with their target pattern (Fig. 4 A–E), and information was correctly propagated from layer to layer—with occasional errors (e.g., Fig. 4F). Statistics were collected from AFM images of ribbons nucleated with the “011010” seed (Fig. S9). Within ribbons, information was copied with an error rate of 0.13% per tile. The low copying error rates can be explained partly by their logical design, which incorporates proofreading (32) and self-healing (33) features (SI Text). However, error rates were lower than in a previous demonstration of proofreading and self-healing tile sets (S. H. Park, personal communication), suggesting that origami seed-nucleated crystals grow under very slightly supersaturated conditions, which are predicted to give optimal error rates (25, 32). To our surprise, the most significant errors (occurring in 2.4% of layers) were those that changed the width of the ribbon, either by an internal lattice defect (e.g., Fig. S10) or by a double tile attaching too early, causing a premature reversal of the zig-zag path. Examination of errors on the first layer of the ribbon, where tiles attach directly to tile adapters, revealed that nucleation is not perfect: The copying error rate increased to 8% per tile and width-changing errors increased to 6% per layer. We attribute this to a slight geometric mismatch between the loosely woven tile lattice and the tightly woven origami lattice; as can be seen in Fig. 4, ribbons often appear to stretch the side of the seed to which they attach.

Fig. 4.

AFM images of ligated Copy ribbons. Binary numbers indicate the target bit pattern presented by the seeds (read top to bottom) in a given experiment. “0-Block” tiles appear gray; “1-Block” tiles contain hairpins for height contrast under AFM and appear white (Fig. S2). The yellow arrow points to a copying error in which a 1 changed to a 0. (Scale bars: 50 nm.) Strand and tile concentrations were as in Fig. 1, except for the repeatable block tiles, which were adjusted to match the target bit pattern. (e.g., for the sample with “100001” seeds, each 1-block tile was at 200 nM and each 0-block tile was at 400 nM.) Thus, an equal percentage of each tile type should be depleted per layer of zig-zag growth, with little residual material remaining after growth of seeded ribbons.

We then tested whether the information provided by an origami seed can direct the growth of a complex algorithmic pattern. We chose to implement a binary counting program because it plays a prominent role in theory investigating how algorithmic self-assembly can be used to efficiently grow large precise structures (9, 34, 35). The “Binary Counter” tile set is obtained from the Copy tile set by adding 4 tiles (Fig. 2C) that implement a ripple-carry binary increment (36) during ZIG layer growth. Starting at the upper left of the ZIG/COUNT layer, the double tile presents a “C” sticky end, representing a carry bit input that initiates the increment operation. The next tile, binding by its left two sticky ends, reads this carry bit in conjunction with information from the previous layer specifying whether the least significant bit of the counter is “0” or “1” If a 0 is read, the attaching tile (and its partner in the Carry Bit 1-Block) will output a 1 to the next layer while passing a “N” (indicating no carry bit) to the next bit to be processed in the ZIG/COUNT layer. In this case, the remainder of the ZIG/COUNT layer will simply copy the bits verbatim, because the N sticky end is the one used by the corresponding tiles in the Copy tile set. Conversely, if a 1 is read, the attaching tile and its partner will output a 0 and the carry bit “C” will be passed to the next bit in the ZIG/COUNT layer. The net effect of this ripple-carry logic is that growth in the ZIG/COUNT layer flips 1s into 0s until it reaches the first 0, which it flips to a 1, and then subsequent bits are copied unchanged—this increments the binary counter. ZAG layer growth uses exactly the same tiles as the Copy tile set, thus copying the bit pattern to the next layer while growing from the bottom right to the upper left. Thus, iterated zig-zag growth generates a binary counting pattern.

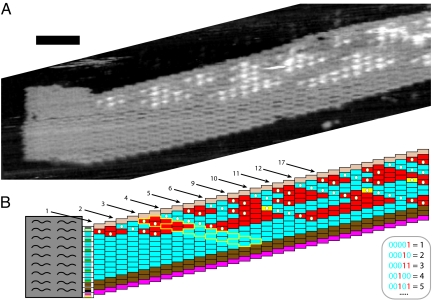
Seeds specifying the initial bit-string “00001” were annealed in the presence of all 18 Binary Counter tiles, ligated, and imaged by AFM. The correct initial pattern was nucleated in all 19 crystals that were imaged at high resolution. Fig. 5 shows a representative example and interpretation. The error rate in this crystal was 4% per block, considerably higher than that observed in the Copy ribbons. We attribute this difference to the use of proofreading and self-healing logic in the Copy ribbons; there, all information being propagated is encoded redundantly in two tiles such that a single isolated error cannot occur; to change a block from 0 to 1 requires introducing two sticky-end mismatches. This remains true for the ZAG/COPY layer in Binary Counter ribbons, but in the ZIG/COUNT layer the carry bit information is encoded by a single sticky end during growth, and a single error can cause an error in counting (SI Text). Despite the higher error rate, the crystals' ability to count successfully provides evidence that the zig-zag growth path was largely followed; unlike in the Copy ribbons, deviations from zig-zag growth will often result in disruption of the intended binary counting pattern.

Fig. 5.

Counting in binary. (A) AFM image of a ligated binary counter ribbon that counted to 17, skipping 7 and 8 and 13–16. (Scale bar: 50 nm.) See Fig. S7 O and P for wide-field views showing both isolated and aggregated assemblies and Fig. S11 for nucleation from seeds with other initial values. Origami seeds were at either 5 or 10 nM, double tiles and nucleation barrier tiles at 50 nM each, and 1-block, 0-block, and carry-bit tiles at 250 nM each. Stoichiometry was not adjusted to exactly match the intended pattern, because this is not generally feasible for algorithmic patterns. For the tiles unique to the Binary Counter tile set, the carry bit was implemented by modifying their molecular shape in addition to sticky-end sequence, in an attempt to reduce errors in carry bit calculations (Fig. S3); however, no obvious differences were discernible between experiments done with and without the shape modifications. Averaged over 16 crystals (both with and without the shape modifications), the error rate was 4.1% per block. Unlike for the Variable-Width and Copy tile set statistics, here, we did not use procedures to eliminate selection bias when estimating this error rate. (B) Interpretation of A. The AFM image only distinguishes between tiles with and without hairpins; therefore the identification of tiles was derived from an interpretation involving the fewest errors consistent with the image. Tile types are colored as in Fig. 1, except that errors are colored yellow. The seed specifies the width and starting value (“00001”) of the counter. Each diagonal of blocks, read from bottom right to top left, encodes a binary number; e.g., the blocks outlined in yellow encode “00011” = 3. (Inset gives binary to decimal conversions.) Each red tile has a hairpin visible by AFM. White dots mark tiles in the COUNT layer that receive a carry bit from their left.

The effective nucleation of Variable-Width, Copy, and Binary Counter ribbons using information-bearing origami seeds points the way to reliable and programmable bottom-up fabrication of complex molecular structures. This success was based on several principles. (i) Each tile set was capable of generating an infinite variety of distinct structures, a precondition for programmability. (ii) A designed nucleation barrier prevented the spontaneous assembly of tiles in slightly supersaturated conditions, clearing the way for high-yield seeded growth with low error rates. (iii) Information contained in the seed was propagated, and sometimes processed, during crystal growth, enacting a simple developmental program. The system developed here has already been useful for growing DNA crystals with other algorithmic patterns (37). At the same time, this work uncovers several problems that must be solved to improve the technique. (i) The rate of copying errors that changed 1 to 0 was 5–10 times higher than errors changing 0 to 1 (see Fig. S9), suggesting that modifying tiles by adding DNA hairpins as an AFM contrast agent significantly alters the crystal growth energetics. Alternative labeling methods could reduce the 1-to-0 copying error rate dramatically. (ii) Premature reversal errors and spurious nucleation errors could be reduced by adding an independent nucleation barrier on the other edge of the ribbon. (iii) Nucleation on the seed could occur more readily if the origami seed were redesigned to match the tile lattice spacing. (iv) Here, we used unequal tile concentrations to prevent excess tiles from forming undesirable side products. In contrast, theory predicts that error rates are lowest when the concentrations of all tiles are equal throughout the reaction. Low error rates and elimination of side products could be simultaneously achieved by purification of crystals before growth creates an imbalance in concentration, use of a chemostat (38), or design of a chemical buffer for tile concentrations (R. Hariadi, personal communication). (v) Implementing improved proofreading techniques (39) should further reduce logical error rates and larger block sizes may reduce internal lattice defects. Finally (vi), aggregation of crystals must be reduced. Combined with the wealth of available chemistries for attaching biomolecules and nanoparticles to DNA, an improved system for seeded growth of algorithmic crystals could be a powerful platform for programming the growth of molecularly defined structures and information-based materials.

The artificial systems developed here fill the gap between the simple seeded growth of natural crystals and the sophisticated seeded growth of biological organisms. Some natural systems also occupy this gap: Similar phenomena—seeded growth of crystals with fixed thickness, variable thickness, combinatorial layering patterns, and even complex patterns derived from local interactions—have all been observed or inferred in minerals such as rectorite, illite, kaolinite, barium ferrite, and mica (40–42). Within biology, centrioles that nucleate microtubles in the “9 + 2” arrangement to form cilia or flagella can be seen as information-bearing seeds for molecular self-assembly (43). Thus, in addition to their technical relevance, the ability to study seeded growth processes using programmable DNA systems may open up new approaches for studying fundamental natural phenomena.