The role of time and pressure on alveolar recruitment

Abstract

Inappropriate mechanical ventilation in patients with acute respiratory distress syndrome can lead to ventilator-induced lung injury (VILI) and increase the morbidity and mortality. Reopening collapsed lung units may significantly reduce VILI, but the mechanisms governing lung recruitment are unclear. We thus investigated the dynamics of lung recruitment at the alveolar level. Rats (n = 6) were anesthetized and mechanically ventilated. The lungs were then lavaged with saline to simulate acute respiratory distress syndrome (ARDS). A left thoracotomy was performed, and an in vivo microscope was placed on the lung surface. The lung was recruited to three recruitment pressures (RP) of 20, 30, or 40 cmH₂O for 40 s while subpleural alveoli were continuously filmed. Following measurement of microscopic alveolar recruitment, the lungs were excised, and macroscopic gross lung recruitment was digitally filmed. Recruitment was quantified by computer image analysis, and data were interpreted using a mathematical model. The majority of alveolar recruitment (78.3 ± 7.4 and 84.6 ± 5.1%) occurred in the first 2 s (T2) following application of RP 30 and 40, respectively. Only 51.9 ± 5.4% of the microscopic field was recruited by T2 with RP 20. There was limited recruitment from T2 to T40 at all RPs. The majority of gross lung recruitment also occurred by T2 with gradual recruitment to T40. The data were accurately predicted by a mathematical model incorporating the effects of both pressure and time. Alveolar recruitment is determined by the magnitude of recruiting pressure and length of time pressure is applied, a concept supported by our mathematical model. Such a temporal dependence of alveolar recruitment needs to be considered when recruitment maneuvers for clinical application are designed.

the clinical impact of acute lung injury (ALI) and its more hypoxemic form of acute respiratory distress syndrome (ARDS) is significant, with an estimated 17,000–43,000 deaths per year (40). It is widely believed that improper mechanical ventilation of these patients can worsen ARDS mortality through a process of ventilator-induced lung injury (VILI) (14). As a result of this concern, investigators have proposed various “protective modes” of ventilation aimed at reducing morbidity and mortality in ALI secondary to VILI (4, 5). In fact, in a landmark study by the ARDS network, lower tidal volumes and reduced plateau pressures led to a reduction in overall mortality compared with standard-of-care ventilation (1). However, one potential and undesirable consequence of lower tidal volumes is progressive collapse or “derecruitment” of dependent lung (39), with the potential for repeated alveolar recruitment and derecruitment (R/D) over time (41).

There is sufficient evidence to suggest that repeated alveolar R/D can significantly contribute to VILI (23, 24, 37, 44), presumably through a shearing stress-induced trauma to the lung parenchyma when airways and alveoli are repeatedly forced open (37, 41, 44). Moreover, Slutsky and colleagues have shown that this mechanical injury to the lung can lead to a secondary activation of systemic inflammation, which could potentially lead to downstream multi-organ dysfunction (42). Steinberg et al. used in vivo microscopy in a porcine ARDS model to support the notion that alveolar instability (R/D) leads to VILI through increased mechanical stress (44). In addition, added positive end-expiratory pressure (PEEP) can stabilize alveoli, leading to a reduction in alveolar R/D (22, 29) and a reduction in serum inflammatory mediators (3, 15). Therefore, if alveolar R/D can be prevented with protective mechanical ventilation, there may be both pulmonary and systemic benefits resulting in reduced morbidity and mortality.

One widely espoused strategy to prevent VILI is to “open the lung and keep it open”(27). This strategy first requires a recruitment maneuver to open the lung, followed by sufficient PEEP to maintain the lung in its newly open state (4). Two components believed to be critical to recruiting the lung are the magnitude of the airway pressure increase and the time that the pressure is elevated (6), the latter being the primary impetus for sustained airway pressure elevations during recruitment (4, 9, 31). As pressure is applied, lung units open according to their critical opening pressure from lowest to highest in a sequence, as defined by the “avalanche theory” of lung inflation (2). Similarly, the closure of lung units during deflation, or derecruitment, is governed by alveolar critical closing pressure. Importantly, both critical opening and closing pressures are presumed to change appreciably in ALI and ARDS (6).

Animal studies have demonstrated that temporal recruitment occurs during sustained inflation (28, 33). Understanding the pressure and time dependence of alveolar recruitment is critical to the development of optimal recruiting strategies. Bates and Irvin have developed a mathematical model in which both pressure and time play key roles in the recruitment and derecruitment of lung units (6). Thus, according to this model, alveolar units not only have critical opening and closing pressures but also characteristic opening and closing times that change in the acutely injured lung (6). This is a novel and important concept that has yet to be fully explored experimentally. We hypothesize that alveolar recruitment does not occur instantaneously when pressure is applied, but rather the recruitment is temporal, continuing gradually as the pressure is sustained.

In this study, we visually recorded the effects of an alveolar recruitment maneuver at both gross and microscopic levels over time in a lavage injured rat lung, and fit these data to a mathematical model of recruitment that incorporates both pressure and time. Recruitment of individual subpleural alveoli was visualized using in situ videomicroscopy. In the same injured lungs, gross recruitment was assessed ex vivo in terms of the amount of atelectasis visible on the pleural surface. We then interpreted these data using a mathematical model featuring distributions of critical opening pressures and opening velocities.

METHODS

Vertebrate animals.

The protocol was approved by the Committee for the Humane Use of Animals at SUNY Upstate Medical University where all the animal experiments were performed. The experiments described in this study were performed in accordance with the National Institutes of Health guidelines for the use of experimental animals in research.

Surgical preparation.

Male Sprague-Dawley rats (n = 6), weighing 371.1 ± 20.6 g received an intraperitoneal injection of ketamine (90 mg/kg) and xylazine (10 mg/kg) with additional dosing as needed to maintain anesthesia. A tracheostomy was established with a 2.5-mm pediatric endotracheal tube. A 5.0-Fr carotid arterial catheter was placed for blood gas analysis (model ABL5, Radiometer, Copenhagen, Denmark) and in-line measurement of systemic arterial pressure (TruWave, Baxter Healthcare, Irvine, CA). The external jugular vein was cannulated for fluid resuscitation and drug infusion. Paralysis was then achieved with intravenous pancuronium (0.8 mg/kg). After surgical preparation, the animals were placed on pressure control ventilation, PEEP 5 cmH₂O, and control pressure (P_control) of 15 cmH₂O, inspiratory-to-expiratory ratio of 1:2, and inspired oxygen fraction of 1.0. (Servoⁱ ventilator, Maquet, Bridgewater, NJ). A baseline blood gas was obtained, and the respiratory rate was adjusted to normalize baseline Pco₂ between 35 and 45 cmH₂O. Baseline blood pressure, blood gases, and pulmonary parameters (pH, Pco₂, Po₂, respiratory rate, and tidal volume) were obtained before injury.

Injury protocol.

Lung injury was induced with saline lavage (16 ml/kg) via the endotracheal tube until the Po₂ was ≤200 cmH₂O. Postinjury hemodynamic and pulmonary parameters were recorded. The animals were killed (barbiturate overdose, 150 mg/kg), and the left lung was exposed with a sternotomy and left thoracotomy. Great care was used not to injure the lungs during surgical exposure. The postinjury lung surface had inhomogeneous areas of gross atelectasis (Fig. 1; see movie 2 in supplemental material, which is available online at the Journal of Applied Physiology's website). The ventilator was switched to airway pressure release ventilation (APRV) or inverse ratio mode (Servoⁱ Bivent). An initial recruitment maneuver was performed at 40 cmH₂O for 40 s to normalize lung volume history before initiating the protocol.

Fig. 1.

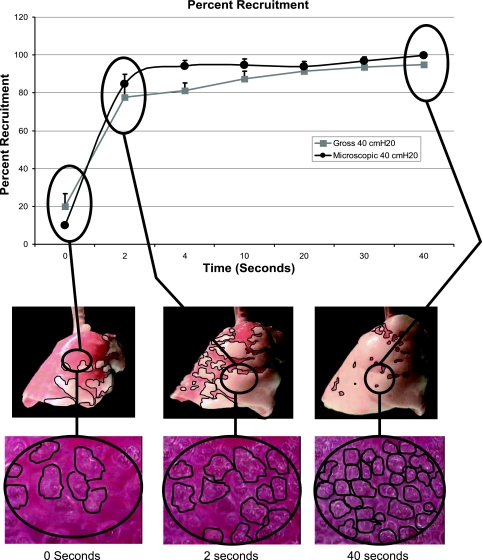
Overview of our methods for measuring and graphing both microscopic and macroscopic lung recruitment. Three photomicrographs of subpleural alveoli before the application (T0) of recruitment pressure (RP) and at 2 (T2) and 40 s (T40) after the application of RP. Note the increased number of alveoli over time at the same RP. The gross lung is also depicted at the same time periods. The dark red areas were considered atelectatic, and the light pink areas were considered inflated. Note that there was more inflated (pink) areas of lung over time at the same pressure. The blue lines demonstrate how the increase in alveolar and lung recruitment was depicted graphically.

In situ microscopy.

A microscopic coverslip mounted on a ring was lowered onto the pleural surface, and the lung was held in place by gentle suction (≤5 cmH₂O) at end inspiration for placement of an in situ videomicroscope (Olympus, epi-objective microscope with epi-illumination). Each placement of the videomicroscope was done randomly on the lung surface. Microscopic images of alveoli in the same microscopic field during the entire recruitment maneuver were viewed at a final magnification of ×130 with a color video camera (model CCD SSC-S20, Sony) and stored in digital format on a personal computer (Dell OPTIPLEX GX620). Each microscopic field measured 1.22 × 10⁶ μm².

Microscopic recruitment.

Following lung injury, the animals (n = 6) were placed on inverse ratio mode (Bivent) Pressure_top 20 cmH₂O, Pressure_rise 0 s, Time_low 0.2 s, and Time_top 1 s. The lung was allowed to derecruit for 5 min to a pressure of 5 cmH₂O to standardize the lung volume history. Sequential recruitment maneuvers were made with three different recruitment pressures (RP) of 20, 30, and 40 cmH₂O for 40 s in random order, with a derecruitment for 5 min at 5 cmH₂O between each recruitment maneuver. Video recordings of subpleural alveoli in the left lung were taken in real time with the in situ microscope throughout the 40-s recruitment periods (see movie 1 of supplemental material, available online at the Journal of Applied Physiology's website). Postexperimental video analysis was performed, and two randomly selected video frames were extracted for alveolar recruitment measurement by computer image analysis (Empire Imaging Systems, Image Pro, Syracuse, NY) at 0, 2, 5, 10, 20, 30, and 40 s during the 40-s recruitment maneuver. At each of these time points, the recruited alveoli were circled and the area (μm²) within each circle was calculated using the computer image software. All the areas of recruited alveoli were added to yield the sum area of alveolar recruitment per microscopic field. The total number of alveoli analyzed per animal using this method ranged from 2,207 to 3,549 alveoli. The data were expressed as the percentage of the entire microscopic field occupied by recruited alveoli.

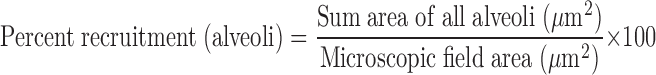Microscopic field area.

A small majority of the microscopic field area (μm²) is made up of capillaries and interstitium not incorporated into the traced alveolar area. Therefore, the lung could approach, but never achieve, 100% recruitment. The microscopic field was maintained throughout each recruitment maneuver, and then a new random field was chosen for the subsequent RP maneuver. Therefore, three random locations were used for each recruitment pressure in each animal.

Macroscopic recruitment.

Lungs (n = 5) were excised following the microscopic measurements for gross lung recruitment filming. One lung was damaged during removal and could not be used, so the number of lungs tested in the macroscopic protocol was one less than in the microscopic protocol. The lungs were suspended via the tracheostomy tube, which was attached to the ventilator (see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website). The excised lungs were ventilated using the Servoⁱ ventilator in Bivent mode with the same settings as used during the microscopic measurements. The lungs were allowed to derecruit to 5 cmH₂O between each recruitment maneuver to standardize lung volume history. This derecruitment pressure was only held for 1 min in the ex vivo lungs in an attempt to prevent drying out and desiccation that occurs when exposed to air. Desiccation of the lung was also prevented by periodically wetting with normal saline. In an identical manner to the microscopic images, photos were captured every 2 s during the 40-s recruitment maneuver.

The lungs were randomly subjected to the identical RP of 20, 30, and 40 cmH₂O and held for 40 s while gross video recording was taken (Sony digital video camera recorder, model DCR-TRV33) of the lung surface. Postexperimental video analysis was performed by computer image analysis (Empire Imaging Systems, Image Pro, Syracuse, NY) on individual photographs taken from the video recording at 0, 2, 5, 10, 20, 30, and 40 s during the 40-s recruitment maneuver. The areas of visible lung that were inflated (i.e., pink) were circled (Fig. 1, gross lung photos; see black lines circling the inflated tissue), and the area within each of these circled areas was measured (mm²) using the computer image software. All areas were added to yield the sum area of inflated lung. The data were expressed as the percentage of the entire visible lung surface that was occupied by inflated (pink) areas of lung (Fig. 1):

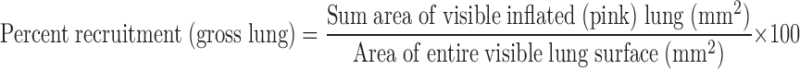Statistical analysis.

All results are presented as means ± SE. Statistical analyses were performed using a multiple-measures ANOVA, followed by pairwise means comparisons using Tukey's post hoc tests (JMP software, version 5 Cary, NC). We accepted a P value of <0.05 as statistically significant.

Modeling.

Following the original suppositions of Bates and Irvin (6), the dynamic nature of opening and closing was modeled by associating each lung unit (i.e., single independent segment of open lung) with a virtual trajectory (x) that takes values from 0 to 1. This trajectory does not correspond to any physical quantity or process, yet it is motivated by the considerations of liquid bridge formation discussed previously (6). Movement along the trajectory occurs at a velocity proportional to the difference between the pressure (P) applied to the unit and a critical opening pressure (P_o). The constant of proportionality is s_o. That is,

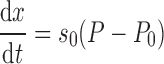(1)

The unit is either open or closed, depending on which extreme of the trajectory, either x = 1 or x = 0, was last visited. The dynamics of the model are governed by probability distribution functions for P₀ and s₀, that is

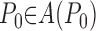(2)

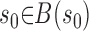(3)

The experiments reported here involved suddenly elevating a lung from 5 cmH₂O to a recruiting pressure of P_r. This leads to the eventual recruitment of a fraction F(P_r) of the lung given by

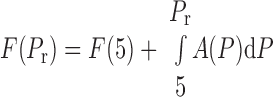(4)

where F(5) is the fraction of lung already recruited by maintaining pressure at 5 cmH₂O for an extended period of time. The fraction of recruited lung at time t, however, depends on how rapidly the individual units move from x = 0 to x = 1. The velocity of movement of a unit along its virtual trajectory is given by Eq. 1, so the time, t₀, taken to open a unit with opening pressure P₀ is

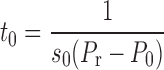(5)

Therefore, for a unit to be open at time t, it must satisfy the two conditions: P₀ < P_r and s₀ > 1/[t(P_r − P₀)]. If we assume that A and B are independent (that is, the value of s that a unit has does not influence its value of P₀), then

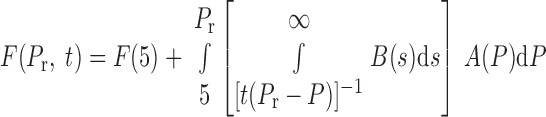(6)

Having the model simulate the time course of recruitment thus comes down to the question of choosing the distributions A(P) and B(s). The cumulative distribution of opening pressures, which is the integral of A(P) with respect to P, describes how percent recruitment at infinite time depends on P_r. Insofar as recruitment is complete by 40 s after each step change in pressure, a plot of percent recruitment at 40 s vs. P_r gives the integral of A(P) for the data of the present study.

The appropriate distribution for B(s) is less obvious. Bates and Irvin (6) used a hyperbolic distribution for B(s) in their original numerical study, but this is problematic for the analytical development of the model because the integrated area under a hyperbola between 0 and infinity is infinite, which means it cannot feasibly be used as a probability distribution function in Eq. 6. We therefore decided to make B(s) exponential, since this functional form is also monotonically decreasing but can be scaled to have unity area. That is.

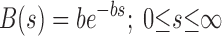(7)

We adapted Eq. 6 for the present study by incorporating the above equation for B(s) and using a functional form for A(P) that was determined from our experimental data.

RESULTS

Hemodynamic and ventilatory parameters.

Table 1 displays baseline and postinjury blood gas measurements, mean arterial blood pressure, respiratory rate, and tidal volume. The pH and Po₂ were significantly lower after injury, indicative of ARDS. There were no significant differences in tidal volume and mean arterial blood pressure (Table 1).

Table 1.

Hemodynamic and ventilatory parameters before and following lung injury

Time	pH	Pco2, Torr	Po2, Torr	MAP	RR, breaths/min	Vt, ml
Baseline	7.38±0.03	38±4.17	533.4±34.4	78.4±19.2	22.6±3.89	5.6±1.96
Postinjury	7.27±0.10*	42.1±13.4	131.7±52.7*	73.7±16.9	37.4±13.5*	5.6±1.98

Values are means ± SE. MAP, mean arterial pressure; RR, respiratory rate; Vt, tidal volume.

^*Significant difference vs. baseline (P < 0.05).

Recruitment.

Figure 1 demonstrates how both micro- and macro-recruitment were expressed graphically. Examples of subpleural alveoli at T0, T2, and T40 are shown at the bottom of the figure. Note how the number of subpleural alveoli increases with increasing time at a constant pressure, and thus the surface area of the microscopic field occupied by alveoli increases (see movie 1 of supplemental material, available online at the Journal of Applied Physiology's website). The gross lung is also shown at the same time points. The areas of obvious dark red were considered atelectatic, and the areas of obvious pink were considered inflated. Note how the amount of recruited lung (i.e., pink) increases with time at the same airway pressure (see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website). Computer image analysis was used to measure both total alveolar area (37) and area of gross lung inflation (see Macroscopic recruitment). Percent recruitment for alveoli was expressed as the percent of the microscopic field occupied by inflated alveoli and for the gross lung the percent of the visible lung surface that was occupied by inflated lung. These percentages were expressed graphically (black lines from alveoli → lung → graph) over time (graph at the top of figure).

Microscopic recruitment.

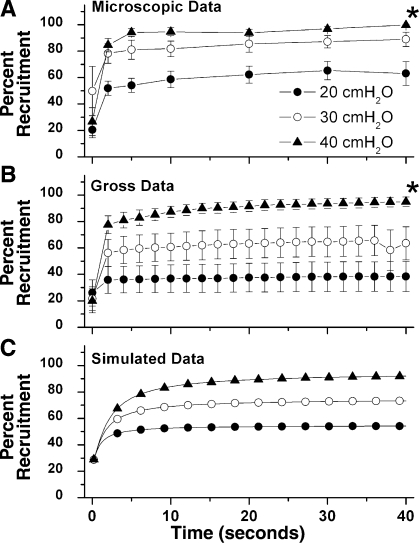
Three different RPs (20, 30, 40 cmH₂O) were applied to a lung that had been open to atmospheric pressure for 5 min. These pressures were held for a total of 40 s. The majority of alveolar recruitment occurred within the first 2 s of applied pressure with all three RPs (Table 2). A statistically significant increase in the area of recruited alveoli occurred between T0 and T2 at both RP-20 and RP-40. The increase seen during these time points at RP-30 was not significant. There was a continuous gradual recruitment thereafter with all three RPs over the 40-s inflation period (Table 3). At RP-20 and RP-40, all subsequent increases in recruitment area after T2 are significantly higher than T0 but are not significantly higher than any other time point. No significance is seen for any time points at RP-30. There was significantly more recruited alveolar area at RP-40 (99.8%) and RP-30 (89.1%) compared with RP-20 (63.1%) at 40 s (Table 2; Fig. 2A; and see movie 1 of supplemental material, available online at the Journal of Applied Physiology's website).

Table 2.

Percent alveolar recruitment in the first 2 s

RP	T0	T2	%Δ
20 cmH2O	20.5±6.0	51.9±5.4*	30.5±7.2†
30 cmH2O	49.8±18.7	78.3±7.4	47.0±10.1
40 cmH2O	26.6±10.6	84.6±5.1	66.0±10.6

Values are means ± SE. RP, recruitment pressure; T0, before application of RP; T2, 2 s after application of RP; %Δ, the percent increase in alveolar recruitment from T0 to T2.

^*Significant difference compared with other pressures (P < 0.05).

^†Significant difference compared with 40 cmH₂O (P < 0.05).

Table 3.

Percent alveolar recruitment from 2 to 40 s

RP	T2	T40	%Δ
20 cmH2O	51.9±5.4*	63.1±9.0*	20.9±4.6
30 cmH2O	78.3±7.4	89.0±5.5	12.0±2.8
40 cmH2O	84.6±5.1	99.8±0.2	15.0±5.1

Values are means ± SE. T40, 40 s after application of RP; %Δ, the percent increase in alveolar recruitment from T2 to T40.

^*Significant difference compared with other pressures (P < 0.05).

Fig. 2.

A: microscopic percent recruitment. Alveolar temporal recruitment at three different RPs (20, 30, and 40 cmH₂O). Application of a constant RP occurred immediately after time point 0 and was held for 40 s. The majority of alveolar recruitment occurs within the first 2 s (T2) during the application of each RP. Alveoli continue to recruit (positive slope) over 40 s during each RP. RP-40 recruits significantly more alveoli than RP-20 at 40 s. Data are means ± SE (*P < 0.05 vs. PR-20). B: gross whole lung recruitment at three separate RPs (20, 30, and 40 cmH₂O) over 40 s. Again, the majority of recruitment occurs within the first 2 s (T2) during each RP. There was a gradual temporal recruitment from T2 → T40 during RP. The higher the RP, the steeper the slope of the curve, suggesting increased recruitment. Data are means ± SE (*P < 0.05 vs. PR 20). C: simulated data from the mathematical model for each RP (20, 30, and 40 cmH₂O).

Whole lung gross recruitment.

Three different RPs (20, 30, 40 cmH₂0) were randomly applied for 40 s to a lung that had been open to atmospheric pressure for 1 min (Fig. 2B; and see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website). Similar to alveolar recruitment, there was significantly more recruited gross lung area at RP-40 (94.9%) compared with RP-20 (38.4%) at 40 s (see Table 5 and Fig. 2B; and see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website). A trend toward more recruited alveolar area was seen at RP-30 (63.5%), which was not significant. Similar to alveolar recruitment, the majority of gross lung recruitment occurred within the first 2 s of applied pressure with all three RPs (Table 4). This increase in gross lung recruitment was only statistically significant between T0 and T2 at PR-40. There was a continuous gradual recruitment of gross lung with all three RPs over the 40-s inflation period, with a trend toward more temporal gross lung recruitment with RP-40 compared with RP-20 or RP-30 (Table 5). RP-40 recruited more gross lung from T2 to T40 than did RP-20 or RP-30 (Table 5).

Table 5.

Percent gross lung recruitment from 2 to 40 s

RP	T2	T40	%Δ
20 cmH2O	35.8±10.2*	38.4±11.4*	2.7±1.3
30 cmH2O	56.3±10.2	63.5±12.5	7.2±2.7
40 cmH2O	77.6±6.8	94.9±3.7	17.4±6.3

Values are means ± SE.

^*Significant difference compared with 40 cmH₂O (P < 0.05).

Table 4.

Percent gross lung recruitment in the first 2 s

RP	T0	T2	%Δ
20 cmH2O	26.0±9.9	35.8±10.2†	9.8±3.2*
30 cmH2O	21.7±9.0	56.3±10.2	34.6±6.7
40 cmH2O	20.0±9.1	77.6±6.8	57.7±8.6

Values are means ± SE.

^*Significant difference compared with other pressures (P < 0.05).

^†Significant difference compared with 40 cmH₂O (P < 0.05).

Modeling.

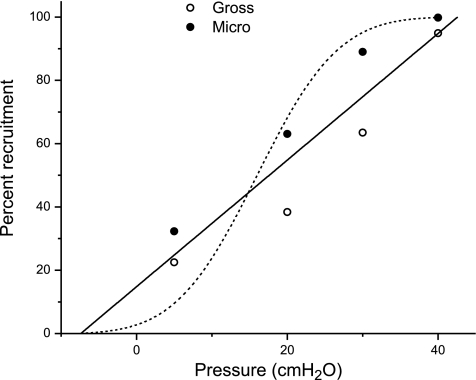
Figure 3 shows the plot of pressure against percent recruitment at 40 s (a surrogate for infinite time), for both the microscopic and gross recruitment data, together with their combined regression line given by

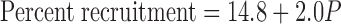(8)

The positive intercept in Eq. 8 implies that ∼15% of the alveoli are already recruited even when pressure is zero, which means that to completely collapse the lung one would have to apply a pressure of about −7 cmH₂O. Also shown in Fig. 3 is a cumulative Gaussian distribution spanning the same range of pressure as the data points (mean of the Gaussian is 16 cmH₂O, standard deviation is 12 cmH₂O). Whereas the straight line passes through the middle of the data, the cumulative Gaussian swings systematically wide of the data. This means that, rather than being Gaussian, as assumed in the original model of Bates and Irvin (6), the distribution of opening pressures pertaining to the data of the present study is roughly constant. That is, A(P) is constant between the limits −7.4 and 42.6 cmH₂O thus:

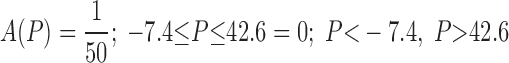(9)

With this choice for A and the equation for B (see Eq. 7), Eq. 6 now becomes

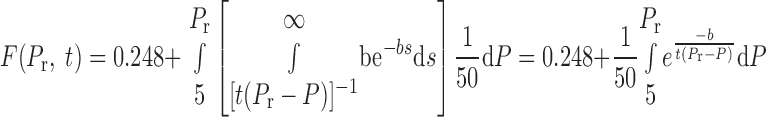(10)

so long as P_r is <42.6 cmH₂O, which is the case for the data of the present study.

Fig. 3.

Total percent recruitment against starting pressures and recruiting pressures for gross (○) and microscopic (•) recruitment. Solid line represents the least squares regression for a straight line fitted to all data points. Broken line represents an integrated Gaussian function with mean of 16 cmH₂O and a standard deviation of 12 cmH₂O.

We fit Eq. 10 to both the microscopic and gross data sets by adjusting the value of b for each set so as to minimize the sum of squared residuals between the predicted values of F and the experimental measurements for all values of t and P_r. For the microscopic data, we obtained a value of b = 0.01 s⁻¹·cmH₂O⁻¹ with a root mean-squared residual between the model predictions and the data of 8 cmH₂O. For the gross data, b = 0.10 s⁻¹·cmH₂O⁻¹ with a root mean-squared residual of 10 cmH₂O. These differences in b for the two data sets give us at least some idea of the range of values this parameter might take, given that the microscopic and gross data sets reflect only small samplings of the entire lung. Indeed, when b = 0.10 s⁻¹·cmH₂O⁻¹, the model predictions of F(P_r,t) match both the microscopic and gross percent recruitment experimental data to within the differences between the two data sets themselves. This indicates that the model has captured the essential aspects of the recruitment dynamics in the saline lavage-injured rat lung.

DISCUSSION

The data collected in the present study both by in situ microscopy and from gross pleural measurements of reversing atelectasis show that the amount of recruited lung depends both on the magnitude of the recruitment pressure and on the length of time over which this pressure is applied. This is demonstrated by the increased recruitment that occurred as the inflation pressure of the lungs was progressively increased from 5 cmH₂O to 20, 30, and 40 cmH₂O, and also by the temporal increases in recruitment that occurred out to 40 s after each step change in pressure, as shown in Fig. 2, A and B. With suitable choices for the distributions A(P) and B(s), this behavior is also predicted by a mathematical model of recruitment that incorporates pressure and time (6) as demonstrated in Fig. 2C.

There are probably several different mechanisms that can give rise to a time dependence of recruitment and derecruitment, but the best studied is the formation of liquid bridges across the lumen of small airways. It has been shown in vitro (35) that a compliant conduit lined with fluid will eventually become occluded by a liquid bridge when the pressure applied to it falls below a certain value. Closure does not take place immediately, however, because it takes time for the fluid to flow into the bridge (36). Similarly, when the pressure exceeds a certain pressure, the airway will eventually re-open, but this is proposed to take time as the fluid occluding the lumen is pushed axially and redistributed back along the walls of the conduit (19).

Nevertheless, the precise mechanisms by which recruitment takes place in the lung remain controversial. Indeed, it is still not entirely clear how changes in lung volume occur at the alveolar level during inflation. The two principal competing hypotheses are 1) expansion of individual alveoli and alveolar ducts and 2) increases in the number of open alveoli and alveolar ducts (i.e., R/D). There is evidence supporting both hypotheses (10, 18). Some investigators believe that alveolar R/D is the main mechanism of normal lung volume changes during tidal ventilation (8, 11, 42). In a slightly refined description of this model, Namati et al. demonstrated the recruitment of “daughter” alveoli once a threshold airway pressure is achieved in the feeding primary “mother” alveolus (32). Alternatively, others argue that the majority of volume change during tidal inflation is accommodated by changes in the size of the alveolar mouth (26), but not all experts accept this notion (25).

The R/D of an alveolus is generally believed to be governed by its critical opening and closing pressures (13, 32, 38). In particular, it is commonly postulated that, when the critical opening pressure of an alveolus, alveolar duct, or small airway is reached, it instantly “pops” open (2) and then continues to expand until maximally inflated. As a result, some mathematical models have focused exclusively on transmural pressure as being the sole controlling variable (23, 45). In the model by Suki et al., for example, airways pop open instantaneously once they reach their critical opening pressures, leading to avalanches of distal airway openings (46). Data from the present study, however, suggest that more precise modeling of alveolar R/D must incorporate both pressure and time. Accordingly, alveolar R/D in the present model is not instantaneous but rather occurs over a time scale that may range from seconds to minutes (6).

The alveolar opening measurements in our animal model of saline lavage show that the majority of recruitment, both microscopic and macroscopic, occurred within the first 2 s following application of all three RPs. Nevertheless, recruitment continued up to 40 s at all RPs, demonstrating the existence of a range of airspace opening rates. These data support the hypothesis of Bates and Irvin that recruitment is not instantaneous but rather has a time scale that may extend over many seconds (6). It is not intuitively obvious what the functional form for the distribution of opening velocities, B(s), should be from inspection of these data. However, in their original modeling study, Bates and Irvin (6) found that a hyperbolic distribution for s_o gave model predictions reminiscent of data in the literature. In the present study, we employed a decaying exponential function for B(s) because it has the same monotonically decreasing characteristic as the hyperbolic function but has the advantage that it can be scaled to have an area of unity (Eq. 7) and therefore conveniently serves as an analytic expression for a probability distribution function.

The notion that the lung has a distribution of regional opening pressures is not entirely novel. However, whereas other studies have suggested that this distribution is Gaussian (13, 38), the cumulative distribution of opening pressures in the present study appears to be linear. Of course there is considerable scatter in the data shown in Fig. 3, so we cannot discount the possibility that the cumulative distribution is not exactly linear. However, it is clear from Fig. 3 that the data are certainly not described by a cumulative Gaussian. Also, when a Gaussian distribution of opening pressures was used in the model, we were able to simulate recruitment-time curves that resembled the data as closely as those in Fig. 2C. This implies that the distribution of opening pressures, A(P), was close to being uniform over a wide range of pressure for the rat model of lavage injury we investigated. However, it is entirely plausible that other opening pressure distributions such as the Gaussian may be more appropriate for other different kinds of lung injury or in other species.

The similarity between the micro- and macro-recruitment during delivery of the RP-40 is striking (Fig. 2, A and B), suggesting that near maximal recruitment is achieved at this pressure. The atelectatic patches seen grossly on the pleural surface tended to disappear suddenly following lung inflation (see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website), likely corresponding to the opening of the rather large airways that supply these segments. These findings support the avalanche theory of alveolar recruitment (45). When a gross lung unit “pops” open, we can microscopically detect a large percentage of alveolar recruitment (Fig. 1). Since almost 80% of both gross and microscopic achievable recruitment occurs within 2 s during the RP-40 maneuver (77.6 and 84.6%, respectively), it is likely that our microscopic field was in a location that grossly recruited. This suggests that, as the gross lung goes from atelectatic (dark red) to inflated (pink), ∼80% of achievable alveolar recruitment occurs briskly yet still requires almost 40 s to achieve near maximal recruitment. Correspondingly, other investigators have found that up to 86% of gross lung recruitment occurs as early as within 0.5 s at 50 cmH₂O of continuous pressure (28). On the other hand, only 35.8% gross recruitment and 51.9% microscopic recruitment occurred within 2 s when applying 20 cmH₂O. During the RP-20, we observed a gradual increase in alveolar recruitment over time that never approached 80% achievable recruitment.

The greater discordance between total gross and microscopic recruitment observed at lower recruiting pressures is likely due to suboptimal resolution of the gross ex vivo lung assessment technique when recruitment is submaximal. This suggests that there is a component of microscopic alveolar recruitment occurring in the atelectatic dark red segments of lung before we can detect gross lung recruitment manifesting in an abrupt change from red to pink lung (see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website). Furthermore, in the areas that do grossly recruit, there appears to be continued microscopic recruitment over at least 40 s. Interestingly, regardless of the recruiting pressures applied, roughly 80–90% of the total achievable recruitment by 40 s was typically achieved within the first 2 s, at both the gross and the microscopic level. This suggests that, despite differences in absolute values for gross and microscopic recruitment, both processes are governed by the same physiological dynamics.

When the majority of recruitment occurs within the first 2 s of deep inflation, one also needs to consider whether such a rapid recruitment process generates increased shearing forces that could promote additional lung injury. However, Gadiali et al. demonstrated in their in vitro model that shear forces generated by rapid bubble propagation down an artificial airway lead to negligible epithelial injury compared with the vertical strain imposed on the same cells when bubbles are propagating more slowly, the latter phenomenon mimicking slower airway recruitment (47). Furthermore, others have demonstrated that, when such aggressive deep inflation is delivered infrequently, it generates negligible biotrauma compared with when it is delivered with every breath (3), possibly due to plasticity of cell membranes and a critical period of cellular recovery time (16).

The clinical relevance of these findings ultimately depends on the application of our improved understanding of alveolar recruitment dynamics to the design of maneuvers that maximize alveolar opening while minimizing mechanical stress (3). Currently, there is no clinical consensus as to the best recruitment strategy. The most commonly used strategy is the sustained application of 40 cmH₂O over 40 s (4), a technique similar to the most effective strategy employed in the present study. Clinical trials using this recruitment protocol have yielded mixed results (4, 9, 17, 21, 31). Grasso et al. used a recruitment maneuver of 40 cmH₂O for 40 s with low tidal volumes and found that only patients with early ARDS responded favorably (21). Subsequent clinical studies have corroborated the finding that significant variation in response to recruitment exists within the general ARDS population (9, 17). The most recent large randomized clinical trial using a combination of low tidal volumes, combined with high PEEP and sustained recruitment maneuvers, failed to demonstrate a significant impact on all-cause mortality (31). However, the group receiving this intervention did demonstrate a reduction in refractory hypoxemia and use of rescue therapies (31). Data from the present study suggest that, at least in our model, a 40-cmH₂O maneuver over 40 s does indeed open most of the lung, whereas 20 cmH₂O for 40 s does not.

Sustained pressure is thus clearly important in achieving maximal recruitment, but the clinical efficacy of this practice is unclear when the majority of recruitment occurs within the first 2 s of pressure application. It is not clear from our data that such a significant amount of recruitment would be achieved during the first few seconds of recruitment in all forms of injury, but previous studies do suggest this to be the case in other models as well (33). By contrast, the effect of sustained recruitment pressures on the dynamics of alveolar and small airway closure (derecruitment) is largely unknown. Although nearly 80% of maximally achievable recruitment occurs within the first 2 s of applied pressure in our model, the effect of 38 additional seconds of sustained pressure on subsequent derecruitment during the next passive exhalation is unclear. It has been shown in vitro (35) that a compliant conduit lined with fluid is eventually occluded by a liquid bridge across the lumen when applied pressure falls below a certain value. This process does not take place immediately since it takes time for the fluid to flow into the bridge. In theory, a sustained increase in airway pressure during recruitment could change the distribution of airway surface lining fluid or the distribution of surfactant at the air liquid interface such that subsequent liquid cross-bridge formation during deflation is retarded (12). Future studies need to focus on the recruitment (and anti-derecruitment) potential of applying less elevated pressures over longer periods of time, as in high-frequency oscillatory and airway pressure-release modes of ventilation or delivering higher but more cyclic recruiting pressure in conjunction with higher PEEP (7).

Caveats of the methods.

Only subpleural alveoli can be measured with our in vivo microscopic technique since our depth of field is limited to 70 μm, limiting analysis of dynamic alveolar mechanics to two dimensions. Subpleural alveolar mechanics might differ mechanically from those within the lung parenchyma since there is less structural support of subpleural alveoli. That is, subpleural alveoli are not surrounded on all sides by adjacent alveoli (i.e., one wall of a subpleural alveolus is attached to the visceral pleura rather than another alveolus), and thus these alveoli lose a degree of structural interdependence. Reduced interdependent support may cause subpleural alveoli to recruit at different pressures and with different time constants than those within the lung (30). Mead et el., however, were able to demonstrate using a lung model that the subpleural and internal alveoli are subjected to equal pressures (30). In addition to this, Gil et al. showed that the alveolar surface area-volume relation was the same between subpleural and parenchymal alveoli (20). Both of these studies support our belief that alveolar mechanics are similar between subpleural and deeper alveoli and that subpleural alveoli can be used to accurately represent the mechanics of all alveoli.

Another issue is that the suction used to stabilize the alveoli under the cover slip might alter alveolar mechanics. However, we have shown that this suction only slightly increases both alveolar size and stability; alveolar size changed from expiration to inspiration and was 1.1% with the suction and increased 8.3% without suction (34). We acknowledge that our assessment of gross lung recruitment is somewhat crude, but it is nevertheless practical for helping to corroborate our findings at the microscopic level. Assessing the change in visible lung surface color from dark red (collapsed) to pink (open) is by no means a sophisticated way of measuring lung recruitment and yields only inferential evidence for recruitment throughout the lung. Nevertheless, our technique of filming the gross visible lung surface yielded corroborative visual insight into the temporal mechanism of lung recruitment, as various segments of lung were observed popping open throughout the 40-s recruitment maneuver (see movie 2 of supplemental material, available online at the Journal of Applied Physiology's website).

Finally, alveoli may behave in a mechanically different manner when the chest is open compared with when the lung is enclosed within an intact chest wall. This could potentially affect the assessment of both micro- and macro-lung recruitment. Furthermore, the tethering effects of blood flow through neighboring alveolar capillaries on alveolar structure and function are not specifically addressed with our technique. In any case, we must accept these technical limitations since we currently have no way of performing videomicroscopy of the pleural surface with the chest wall in place.

In conclusion, this study provides direct evidence of the temporal behavior of alveolar recruitment in an animal model of ARDS. The speed, timing, and effectiveness of recruitment all depend on the magnitude of the recruitment pressure and the length of time that this pressure is applied. Mathematical modeling of our data suggests that the temporal dependence of recruitment in our model of injury is best described in terms of a linear distribution of critical opening pressures and an exponential distribution of virtual trajectory velocities for airspace opening. We believe that our findings further our understanding of the dynamic physiology of alveolar recruitment, which could influence the design and delivery of optimal recruitment maneuvers in the setting of ARDS. This will help to improve lung function while minimizing mechanical stress and potential for VILI.

GRANTS

This study was funded in part by National Heart, Lung, and Blood Institute Grant R01 HL-075593.