Nonlinear Analysis of the Dynamics of DNA Breathing

Abstract

The base pairs that encode the genetic information in DNA show large amplitude localized excitations called DNA breathing. We discuss the experimental observations of this phenomenon and its theoretical analysis. Starting from a model introduced to study the thermal denaturation of DNA, we show that it can qualitatively describe DNA breathing but is quantitatively not satisfactory. We show how the model can be modified to be quantitatively correct. This defines a nonlinear lattice model, which is interesting in itself because it has nonlinear localized excitations, forming a new class of discrete breather.

Introduction

DNA is the molecule that encodes the information that organisms need to live and reproduce themselves. Fifty years after the discovery of its double helix structure [1], it is still fascinating physicists, as well as biologists, who try to unveil its remarkable properties. In their paper, Watson and Crick wrote “it has not escaped our notice that the specific pairing we have postulated immediately suggests a possible copying mechanisms for the genetic material”. This remark attracted attention to the structure of biomolecules and it is at the origin of one fundamental dogma in biology that form is function. However, DNA is not the static entity that structural pictures show. Its fluctuations are even essential for function because the genetic information is encoded in the bases which are buried inside the structure. In order to read the code, DNA must be locally opened by breaking the pairing between its bases. Moreover, even in the absence of enzymes involved in the reading or duplication of the code, DNA undergoes large-amplitude fluctuations. The lifetime of a base pair, i.e., the time during which it stays closed, is only of the order of a few milliseconds. Experiments show that these fluctuations, known by biologists as the “breathing of DNA”, are highly localized. Here, we review the experimental observations of the fluctuational opening of DNA. Then we introduce a simple model of DNA, which describes the molecule at the mesoscale, i.e., at a scale intermediate between the atomic scale and the largest scale of the full molecule. We show that nonlinear dynamics can lead to the observed breathing, and by comparing the properties of the model with the experimental observations, we show how the original model can be refined to better describe the actual properties of DNA. This refinement leads to a nonlinear lattice model which turns out to be interesting in itself because it exhibits unusual properties which raise interesting questions for nonlinear science. This interplay between physics and biology, where physical modeling gives some hints for the understanding of DNA properties, while the biological system suggests new ideas for nonlinear science, is a reminder of the famous quotation of Stanislas Ulam: “Ask not what physics can do for biology. Ask what biology can do for physics”.

The breathing of DNA: experimental studies

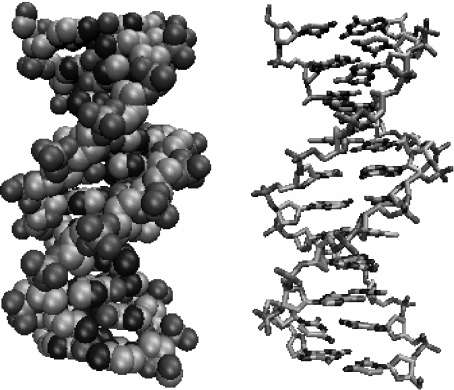
Figure 1 shows the structure of DNA. The backbone of the two entangled helices is made of a chain of phosphates and sugar groups. The two strands are linked to each other by large base plateaus, covalently bound to the sugar groups and forming pairs connected by hydrogen bonds as shown in Fig. 2. There are four possible bases, symbolized by A (adenine), T (thymine), G (guanine), C (cytosine), forming only two types of pairs, AT, linked by two hydrogen bonds, and GC, linked by three hydrogen bonds. While the covalent bonds that form the backbones and the bases are very strong, the hydrogen bonds that connect the two bases in a pair are much weaker. They can be broken by thermal fluctuations at biological temperature, exposing the bases to the surrounding solvent before the base pair closes again. It is these large fluctuations which are called the “breathing of DNA”. They are well known by biologists and, for instance, they allow flat molecules (such as some dyes) to be trapped within the DNA helix when base pairs close.

Fig. 1.

The structure of DNA in its B form in a full atomic representation (left) or in a schematic diagram showing the interatomic bonds

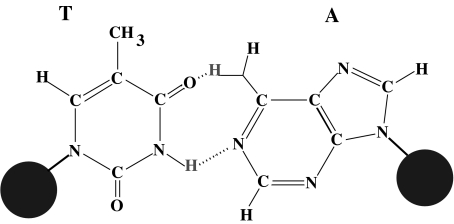
Fig. 2.

The AT base pair of DNA. The two large dots schematize the sugar-phosphate backbones. The dotted lines in the central part of the diagram indicate the hydrogen bonds that connect the two bases

The breathing of DNA can be studied accurately using proton–deuterium exchange. If DNA is dissolved into deuterated water, when the opening of a base pair exposes the protons that form the hydrogen bonds to the solvent, the so-called imino protons, those protons can be exchanged with deuterium from the water molecules of the solvent. The exchange rate can be accelerated by a catalyst. Then, NMR can be used to detect the deuterium atoms within the DNA molecule [2]. Kinetic experiments show that the lifetime of base pairs (time during which they stay closed) is in the range of milliseconds at 35° and ten times more at 0°. Lifetimes of the GC pairs linked by three hydrogen bonds are three times longer than those of the AT pairs. At biological temperatures, the experiments show that single base pair opening events are the only mode of base pair disruption. This indicates that the large-amplitude conformational change that is able to break a pair and expose a base to the solvent is a highly localized phenomenon. It should also be pointed out that these localized fluctuations are observed in artificial molecules which contain homogeneous sequences of identical base pairs. Therefore, the localization cannot be attributed to the inhomogeneity of natural DNA sequences. At higher temperatures, the picture changes. Thermal fluctuations can break the base pairs in large regions of DNA, leading to the so-called DNA bubbles, which grow when temperature is raised, until full separation of the strands. This melting transition of DNA is very sharp for homogeneous sequences. It can be easily studied because the absorption of UV light at 219 nm increases drastically when the base pairs are unstacked. The melting transition appears therefore as a sharp rise of the UV absorption of the DNA solution, which only occurs within a few degrees for a short DNA homopolymer. Depending on the sequence and salt concentration of the solution, which affects the repulsion of the charged phosphate groups of the backbone, melting occurs between 310 and 410 K [3]. This transition can be followed by differential scanning calorimetry and Raman spectroscopy [4]. The changes observed in specific Raman band frequencies and intensities as a function of temperature reveal that thermal denaturation is accompanied by disruption of base pairs, unstacking of the bases and disordering of the backbone. Furthermore, the intensity of some Raman bands at 1,240 and 1,668 cm^− 1 exhibits the same increase with temperature in the 340–360 K range as the variation of enthalpy ΔH of the denaturation transition measured by differential scanning calorimetry. This shows that there is a link between an increase of the amplitude of the vibration of the bases and DNA melting. Moreover, as melting occurs first through local opening of DNA, the experiments appear to be compatible with the following pathway to melting: one vibrational mode associated with base pair opening has an amplitude that grows locally until it becomes so large that it leads to a local opening, forming a precursor of melting.

However, the wavelength of the light used in spectroscopic experiments is so large compared to interatomic distances that standard spectroscopy cannot conclude about the localization of the motions. The great interest of DNA is that one knows how to perform local reactions at sites which can be precisely determined. This opens the possibility to observe the local dynamics of the molecule through the response of a chromophore attached to the region of interest. In [5], the authors studied the local dynamics of calf thymus double-helical DNA by measuring the visible absorption band of the cationic dye ethidium bromide, both free in solution and bound to DNA, for a temperature range 360–30 K in two different solvent conditions. The comparison of the thermal behavior of the absorption band of free and DNA-bound ethidium bromide gives information on the local dynamics of the double helix in the proximity of the chromophore. The experiments show that above 280 K, the anharmonicity of the motion of the dye increases much faster when it is bound to DNA than when it is free in solution. This is attributed to an onset of wobbling of the dye in its intercalation site, which is likely to be connected with the onset of local opening/unwinding of the double helix. The experiments clearly show that large amplitude “premelting” motions of DNA occur well below the denaturation temperature [6]. The use of a dye provides a method to probe these motions locally. However, although the experiments of [5] can probe the “micro-environment” of DNA vibrations, they do not prove that the motions observed in the vicinity of the dye are really localized in space. They could extend along the helix. But the experiments can be refined by moving the probe along the DNA molecule. This has been done with short DNA segments which form the stem of a DNA hairpin [7]. In these experiments, the probe is a combination of a fluorophore and a quencher, bound on the two strands. In the closed state, these two elements are next to each other and electronic transfer between the fluorophore and the quencher prevents fluorescence, while in the open state, fluorophore and quencher are sufficiently far apart and the fluorescence of the fluorophore is observed. Recording the autocorrelation function of the fluorescence allowed the authors of this study to investigate the dynamics of the fluctuations of small DNA bubbles, extending over a few base pairs. They showed that bubbles of 2 to 10 base pairs with lifetimes in the 50-μs range spontaneously open in double-stranded DNA at 37°C under low salt conditions (0.1 M).

Therefore, experiments using special molecular constructs, made possible by the ability of biologists and chemists to initiate reactions at well-defined sites of DNA, are very powerful. However, they can only report on the properties of the molecule at the sites of the probes. Moreover, designing the molecular constructs may be difficult. Another powerful method to investigate the properties of DNA with an excellent spatial resolution has been designed recently. It uses photoinduced reactions in DNA exposed to high-intensity UV laser pulses. This induces oxidative modifications affecting strongly the guanine bases (part of all GC pairs along the sequence). Depending on the local conformation of the molecule at the time of the pulse, two different modifications can be produced and they can be detected by standard biochemical methods. A temperature study shows that the ratio between the two modifications closely follows thermal opening of the base pairs [8]. The essential point is that this method provides local information at the sites of all GC pairs in the sequence. Thus, a single experiment provides a kind of mapping of the fluctuations along the DNA molecule. This experimental tool, which is already well tested, increases by one order of magnitude the experimental data available. It is particularly useful to tune DNA models up [9].

Nonlinear theory of the dynamics of DNA breathing

Therefore, although local observations may be challenging, the various methods which have been used to study DNA fluctuations converge to the same conclusion: at biological or room temperatures, DNA undergoes large amplitude-localized opening of the base pairs, which can exist even in homopolymers. Understanding these observations is an interesting challenge for a theoretician. Although the base pair dynamics are detected in some Raman scattering experiments, the standard analysis of Raman vibrational modes cannot be used to analyze the experiments because they are based on harmonic or weakly anharmonic modes, which are not localized. The model must include the nonlinearities which are associated with the large amplitude motions of the bases.

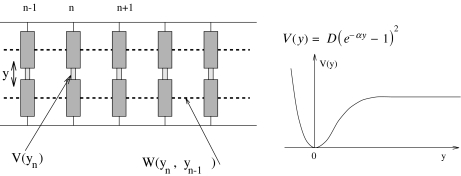
The simplest model (Fig. 3) is a model at the scale of a base pair [10] originally introduced to study the thermal denaturation of DNA. It considers a single variable for each base pair, the stretching y of the bond connecting the two bases. It is defined by its Hamiltonian

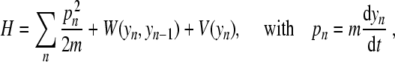1

where n is the index of a base pair and m its reduced mass. In the present study devoted to the localization process, we do not include the genetic code. All base pairs are considered to be the same to avoid any influence of disorder, which could introduce another source of localization. Therefore the results that we discuss here are only valid for homopolymers. The potential V(y) describes the interaction between the two bases in a pair. The model of DNA melting [10] uses a Morse potential

2

where D is the dissociation energy of the pair and α a parameter, homogeneous to the inverse of a length, which sets the spatial scale of the potential. This expression has been chosen because it is a standard expression for chemical bonds and, moreover, it has the appropriate qualitative shape: (a) it includes a strong repulsive part for y < 0, corresponding to the steric hindrance mentioned above; (b) it has a minimum at the equilibrium position y = 0; and (c) it becomes flat for large y, giving a force between the bases that tends to vanish, as expected when the bases are very far apart; this feature allows a complete dissociation of the base pair, which would be forbidden if we had chosen a simple harmonic potential.

Fig. 3.

The simple dynamical model for DNA nonlinear dynamics, described by the Hamiltonian (1)

The potential W(y_n, y_n − 1) describes the interaction between adjacent bases along the DNA molecule. It has several physical origins:

• the presence of the sugar-phosphate strand, which is rather rigid and connects the bases. Pulling a base out of the stack in a translational motion tends to pull the neighbors due to this link. One should notice, however, that we have not specified the three-dimensional motion of the bases in this simple model. An increase of the base pair stretching could also be obtained by rotating the bases out of the stack, around an axis parallel to the helix axis and passing through the attachment point between a base and the sugar-phosphate strand. Such a motion would not couple the bases through the strands. The potential W(y_n, y_n − 1) is an effective potential which can be viewed as averaging over the different possibilities to displace the bases.

• the direct interaction between the base pair plateaus, which is due to an overlap of the π-electron orbitals of the organic rings that make up the bases.

In a first step, a harmonic interaction W(y_n, y_n − 1) was used, but this is a crude approximation since experiments show that a base pair can open independently of its neighbors. The large relative displacements rule out a low-order expansion of the potential, and the nonlinearity of the stacking interaction should not be ignored. The appropriate shape of the potential is imposed by the sharpness of the melting transition of DNA. This sharpness is associated with an entropic effect. Opening the base pairs has an energy cost D, which is the energy required to break the base pair, but there is an entropy gain because once they are open the bases are freer to fluctuate. It is this effect which allows transitions in a one-dimensional model like DNA [11]. The model can lead to realistic melting curves if the potential W(y_n, y_n − 1) takes into account the extra freedom of the broken base pairs. This can be described [12] by choosing

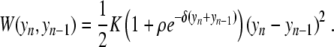3

This expression can be viewed as a harmonic interaction with a variable coupling constant. As soon as either one of the two interacting base pairs is open (not necessarily both simultaneously), the effective coupling constant drops from K′ ≈ K(1 + ρ) down to K′ ≈ K. The smaller coupling leads to an entropy increase, which promotes the transition by reducing the free energy of the open state.

Figure 4 shows the dynamics of this model when it is in contact with a thermal bath that describes the effect of the solvent on the DNA molecule. It shows characteristic features which are consistent with the experimental observations of localized openings in DNA. Some regions of the molecule appear as closed (light gray on the figure), while narrow domains, appearing as black on the figure, correspond to a few base pairs which are open. A careful examination of the figure shows that the opening is not static. The open regions often appear on the figure as dashed lines, indicating an alternation of open and closed states. This is a typical property of a nonlinear lattice such as the one that we used to model DNA fluctuations (1). These motions are actually discrete breathers [13, 14]. Such localized modes would not survive in a harmonic lattice, but due to the soft nonlinearity of the potential V, if a site vibrates with a very large amplitude its oscillation frequency is significantly lower than the resonant frequency of its unexcited neighbors. As a result, the energy transfer to the neighbors is not efficient, and the energy can stay on the excited site. A soft nonlinearity can be expected from a qualitative analysis of DNA so that, even if the model cannot claim to be fully realistic for DNA, the observations that we make on the simple model can be expected to reflect the actual properties of the molecule. The intuitive argument given above for the existence of localized oscillatory modes can be made fully rigorous, and exact solutions of this type can be proved to exist for the DNA model that we introduced [13, 15, 16]. What is important is that their existence is not tied to a specific model. Only very generic features are required, essentially that the localized mode frequency does not resonate with the frequencies of normal modes (phonons).

Fig. 4.

Numerical simulation of the DNA model in contact with a thermal bath at 270 K. The stretching of the base pairs is shown by a gray scale going from white for a closed pair to black for a fully open pair (y ≥ 2.0 Å). The vertical axis extends along the DNA chain, which has 256 base pairs in this calculation, with periodic boundary conditions. The horizontal axis corresponds to time. The time domain shown in this figure is 2 × 10^− 11 s. The parameters used for this calculation are m = 300 atomic mass units, D = 0.05254 eV, α = 4.0 Å^− 1, K = 0.01 eV Å^− 2, ρ = 3.0, δ = 0.8 Å^− 1

However, the existence of localized solutions is not sufficient to justify their observation in a physical system like DNA. A mechanism for their creation must exist, which poses the question of the localization of thermal fluctuations. At a first glance, it appears as a breaking of equipartition of energy, but this is indeed not true. The observation of Fig. 4 and the study of the system on longer timescales show that the localized modes have a finite lifetime. A mode can decay in one site, while another one appears elsewhere in the system, so that, in the long term, the energy of the thermal fluctuation is evenly distributed along a whole DNA homopolymer, as expected from statistical physics. It is, however, remarkable that, on a timescale of the order of several hundred periods of oscillations of a base pair, the distribution of the thermal fluctuations can vary significantly from place to place in the molecule. In order to give a quantitative measurement of localization, one can use local distribution functions. Let us consider a particular dynamical variable A(n,t) which depends on site n and time t. A can be the displacement field y_n(t), the kinetic energy of an oscillator 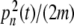, or the energy density e_n(t). The local distribution function for A, , is the normalized distribution of the values of A(n,t) within the domain n₀ − Δn / 2 ≤ n ≤ n₀ + Δn / 2, t₀ − Δt / 2 ≤ t ≤ t₀ + Δt /2. 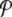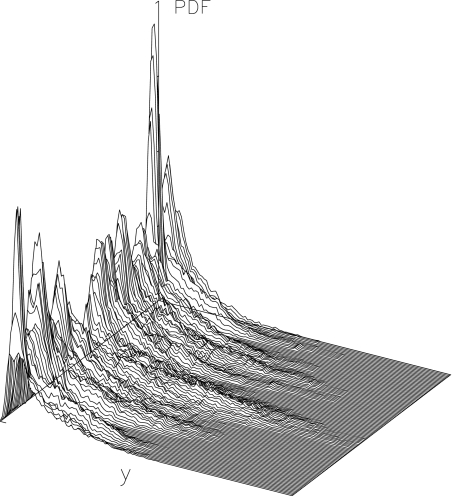In the limit Δn → ∞, or Δt → ∞, tends to the equilibrium distribution for the variable A at the temperature T of the simulation. On the contrary, for small Δn and Δt, 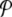depends on space. Figure 5 shows an example of this variation for the DNA model at T = 300 K, for Δn = 4, Δt = 2 × 10^− 10 s. Localization can even be measured quantitatively by calculating distances in probability space between the local distribution functions evaluated at different points [17].

Fig. 5.

Local distribution 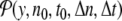for the DNA model at temperature T = 300 K. Δn = 4, Δt = 2 × 10^− 10 s. The axis extending from left to right gives the values of the displacements y, and the axis going from front to back corresponds to n₀. It extends along the 128 cells of the lattice used in the simulation, and the vertical axis corresponds to the distribution function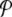

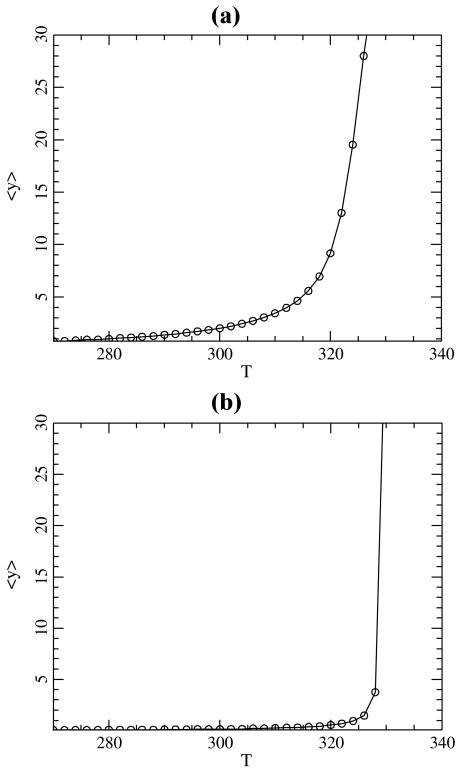
Besides the highly localized fluctuations, Fig. 4 shows the presence of larger dark spots, which correspond to open regions than span several base pairs of DNA. They correspond to the DNA bubbles, which are the precursors of the melting transition. For the simple model that we introduced, this melting transition can be studied by standard methods of statistical physics [11]. The partition function of the model can be calculated exactly by numerical methods, as well as other quantities such as the average stretching of the base pairs shown in Fig. 6a. The sharp increase of 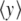observed around 335 K is due to the separation of the two DNA strands.

Fig. 6.

Average stretching of the base pairs in the DNA model described by the Hamiltonian (1) with the Morse potential (2) (a) and with the modified potential (4) (b). The parameters of the model are K = 0.01 eV Å^− 2, ρ = 3.0, δ = 0.8 Å^− 1, and D = 0.05254 eV, α = 4.0 Å^− 1 for (a) ; D = 0.0857 eV α = β = 4.0 Å^− 1, E = 4.0 eV Å^− 1 for (b)

The theoretical results presented above seem to describe the experimental results on DNA to a reasonable accuracy, and, as one cannot expect quantitative results from a model which is so simple, it is tempting to consider that the model is satisfactory. However, although a complete quantitative agreement with experiments cannot be expected, there are some aspects of the results that show that the model cannot be accepted as it is. The problem concerns the lifetime of the open states of the base pairs. With the model described by (1), (2), and (3), the opening appears as a breathing mode, i.e., although the breather can have a lifetime of hundreds of picoseconds, the base pair opens and closes with a period of the order of a picosecond. This is not in agreement with the measurements of the kinetics of the imino-proton exchanges which conclude that the lifetime of the open state is in the nanosecond range (estimations are in the range 30 to 300 ns) [18]. Thus, although the model gives statistical averages which can be fitted to experimental results for the melting curves of short DNA segments [19], its dynamics is not consistent with the observations, which suggests that it is qualitatively incorrect. Ideas to solve this discrepancy come from all-atom molecular dynamics (MD) simulations [20]. As opening is a rare event, which may extend over hundreds of nanoseconds, MD simulations, which have to study a very large number of degrees of freedom, including those of the solvent, cannot study the lifetime of the open state. But these simulations can be biased to observe the free energy pathway associated with opening. This is done by adding a geometrical constraint imposed by a bias potential that imposes a given opening. Then the fluctuations of the DNA structure are recorded for all intermediate positions. Their probability distribution, corrected from the effect of the bias, gives the free energy as a function of the opening [20]. The results are highly sensitive to the details of the solvent and counterion dynamics, but they nevertheless show that the free energy of the open state may have a shallow minimum. This is consistent with a dynamics in which the base pair may stay open for a long time rather than vibrating as a breather. Moreover, the simulations show that open bases can fluctuate a lot. Their motions include rotations, which may hinder the reclosing of the pairs, inducing an energetic barrier for closing. In a mesoscopic model, which only describes a subset of the degrees of freedom of the system, the potentials are actually free energies that take into account all the degrees of freedom which are not included in the model. Therefore, it is natural to replace the simple Morse potential by a more elaborate function which describes the effects discussed above, and particularly the barrier for reclosing. To allow analytical calculations, we have chosen the following expression

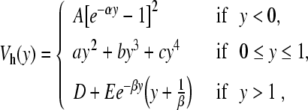4

which is determined when the parameters D, E, α, and β are selected. The other parameters are calculated to ensure the continuity of the potential and of its first and second derivatives. For y < 0, this potential is identical to a Morse potential, while for large values of y, it decreases towards D after a hump which describes the barrier for reclosing. The polynomial form for the intermediate range of y provides a smooth matching between the two domains. We choose α = β = 4.0 Å^− 1 as in the original Morse potential. 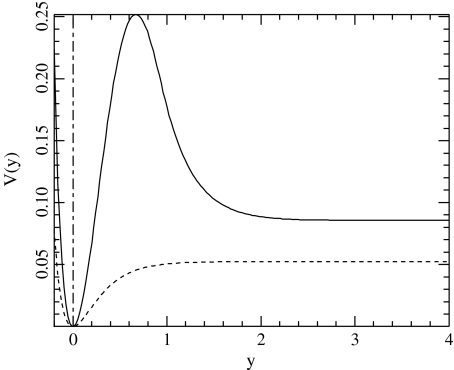The value of E = 4.0 Å^− 1 has been selected to give a decay rate for the hump that extends on the proper spatial scale, and the value of D is selected by calculating the melting temperature of the resulting DNA model, using the transfer integral method [11] to compute , as shown in Fig. 6. To obtain the same melting temperature as with the Morse potential, we have to select D = 0.0857 eV. The resulting potential is shown in Fig. 7 together with the Morse potential V(y). One can notice that the new potential has a higher value in the open state of the bases. This is determined by the condition that we imposed on the melting temperature, but it is consistent with the physics of DNA because the bases are hydrophobic. There is a significant energy cost due to their interaction with the solvent in the open state, and the new potential, which aims at a more accurate description of the free energy of the bases, has to take this into account instead of simply describing the energy cost to break a base pair, as done by the Morse potential. The melting curves for the two models are plotted in Fig. 6. Their comparison shows that the melting is much sharper with the new model. This is an interesting feature because it provides a better fit with the experimental observations on DNA homopolymers, for which the transition is known to be very sharp.

Fig. 7.

The potential 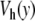for α = β = 4.0 Å^− 1, E = 4.0 Å^− 1 and D = 0.0857 eV ( solid line) and the Morse potential with α = 4.0 Å^− 1, D = 0.05254 eV (dotted line) that gives the same melting temperature for the DNA model

This new model can be used to study the dynamics of DNA at controlled temperature, as we did with the first model. Figure 8 compares the results for the Morse potential and for the new potential 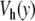. The difference is striking. For the Morse potential, the parameters for the simulation are exactly the same as those used to plot Fig. 4, but the time domain which is shown in Fig. 8 is 1,000 times longer (20 ns). At this scale, the very short lifetime of the open states given by the Morse potential shows up clearly. The results with the potential 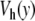are very different. First, only a few regions are affected by the opening. This is consistent with the statistical calculation of the melting curve (Fig. 6), which shows that precursor effects are small below the melting temperature. In order to evaluate the lifetimes of the open and closed states, we performed long calculations with the parameters of Fig. 8 but a total simulation time of 6.6 μs. For each base pair, we detect opening events, defined as an increase of y beyond 2.6 Å, and closing events, defined as a drop of y below 0.6 Å. They are used to compute the statistics of the lifetimes of the open and closed states. For the Morse potential, the average lifetime of an open base pair is only 0.08 ns, while it increases to 7 ns when we use the new potential, bringing it in the range measured in experiments [18]. Moreover, the open states concern only one or two consecutive bases, in agreement with the observations [2], while the Morse potential was giving larger bubbles, even well below the melting transition. The average lifetime of a closed base pair is found to be 0.4 ns for the Morse potential, whereas we get 0.4 μs when we use the new model. This value is still well below the experimental estimates of a few milliseconds [2], but the new potential nevertheless improves the results by three orders of magnitude. The origin of the discrepancy certainly comes partly from the oversimplified model that we use. However, it could also come from different thresholds to detect openings in the experiments and in the simulations. In our simulations, any opening, even as short as a 20 ps, is detected and therefore considered as an interruption of the closed state, hence shortening its lifetime. In the experiments using proton–deuterium exchange, it is likely that very short bursts of opening are not detected because they do not last long enough to allow the exchange.

Fig. 8.

Comparison of the dynamics of the model with the Morse potential V(y) (top figure) and with the modified potential with a hump 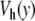(bottom figure) obtained from a numerical simulation of the models in contact with a thermal bath at 270 K. The stretching of the base pairs is shown by a gray scale going from white for a closed pair to black for a fully open pair (y ≥ 2.0 Å). The vertical axis extends along the DNA chain, which has 256 base pairs in these calculations, with periodic boundary conditions. The horizontal axis corresponds to time. The parameters used for this calculation are K = 0.01 eV Å^− 2, ρ = 3.0, δ = 0.8 Å^− 1, D = 0.05254 eV, α = 4.0 Å^− 1 for the Morse potential (top figure) and α = β = 4.0 Å^− 1, E = 4.0 Å^− 1 and D = 0.0857 eV for the potential 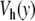(bottom figure). The total time shown in these figures is 2 × 10^− 8 s, i.e., 1,000 times longer than for Fig. 4

All these results show that replacing the Morse potential V(y) by the potential with a hump, 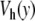, introduces a huge qualitative and quantitative change in the dynamical properties of the DNA model and brings the lifetime of the open states in the experimental range, while the original model was wrong by several orders of magnitude. This is remarkable because the changes in the potential are rather minor and by no means of several orders of magnitude.

A nonlinear model inspired by DNA

In the previous section, we have shown that attempts to describe DNA at the mesoscopic scale with a model including only one degree of freedom per base pair led us to introduce a new nonlinear lattice, with a potential which is not a simple potential well. This naturally raises the question of the mathematical properties of this new model. The initial lattice model with an on-site Morse potential had oscillatory localized solutions, the discrete breathers. A qualitative analysis of the new model suggests that it might have localized oscillatory solutions, too. In order to test this idea, we used numerical simulations of the nonlinear lattice described by the Hamiltonian

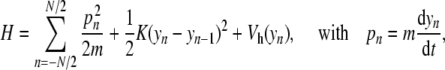5

where 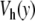is given by (4). Instead of the nonlinear coupling W(y_n,y_n − 1) introduced to describe the stacking interactions in DNA, we have chosen a harmonic interaction which simplifies the analysis, and which is identical to the interaction used in the mathematical studies of discrete breathers [13, 16]. To initiate a localized mode, we start from a lattice at equilibrium except for the central particle which has an initial position 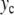(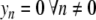, , 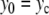p_n = 0  ∀ n). This initial condition creates a vibrational motion centered at site 0 and small amplitude linear waves which are radiated away. The simulations have been carried out with N = 512 particles, fixed boundary conditions, and a small damping on the last 32 particles at both ends of the lattice to absorb the small amplitude waves. After a transient, this process generates a steady vibrational mode. It is highly localized because the amplitude of the motion decays quickly when one moves away from the central site. Once the steady state is reached, we determine the extrema y_min and y_max of the motion of the central particle, the frequency Ω of the oscillation, and the energy of the breathing mode computed as the energy in the 20 sites around the center. Figure 9 shows the result for a coupling constant K = 0.01, corresponding to the value used for the DNA model.

Fig. 9.

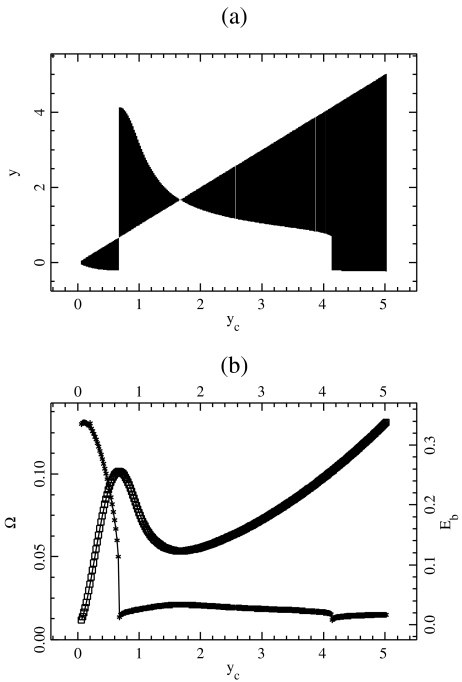
Properties of the localized oscillatory mode created by exciting one particle in the lattice described by Hamiltonian (5). The top figure (a) shows the extrema of the oscillation y_min and y_max as a function of the amplitude 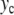of the excitation. For each value of 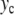a vertical line is drawn between y_min and y_max. The bottom figure (b) shows the frequency Ω (crosses) and the energy 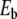(squares) of the breather versus 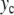. Lengths are in Å, energy in eV, and frequency in 10¹⁴ s^− 1, which are the units used for the DNA model

Figure 9 displays a rich behavior with two bifurcations in the dynamics. For a small excitation (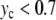), the localized modes oscillate around the minimum of the potential 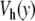located at y = 0. In this domain, the breather is very similar to breathers observed with various on-site potentials having a single minimum, and it can be studied with the same methods. A first bifurcation appears when the amplitude of the excitation is large enough to move the central particle beyond the hump of the potential. Then, the particle tends to fall downhill, moving to large values of y_max until it is brought backwards by its harmonic coupling to its neighboring particles, which are still in the potential well, close to y = 0. This leads to an oscillation which takes place entirely in the range of y which is beyond the hump of 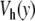. This bifurcation is associated with a sharp drop in the frequency of the breather because the oscillation no longer takes place in the narrow minimum of .

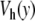When 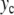is increased beyond the bifurcation, the amplitude of the oscillation decreases, until it vanishes for 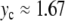and increases again. This behavior suggests that the value 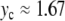corresponds to a static equilibrium of the lattice and that the breather oscillates around this static distortion of the lattice. We show below that such a static solution does indeed exist. This domain is interesting because it corresponds to a new class of discrete breathers, which oscillate around a stable excited state of the lattice. As shown below when we derive the static solution, these modes cannot be studied with the same approximate methods as usual breathers because the limit K →0 is singular.

Increasing 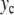even more leads to a second bifurcation because the amplitude of the motion is such that the central particle can again fall into the potential minimum, with a value y_min < 0 as for the case of small amplitude excitations, but with a very large value of y_max. This second bifurcation is also accompanied by a frequency drop. It is interesting to notice that, although the amplitude of the breather exhibits some discontinuities at the two bifurcation points, its energy 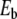is a continuous function of .

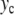Let us now give an analytical proof of the existence of this spatially localized equilibrium. It corresponds to a solution of

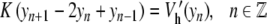6

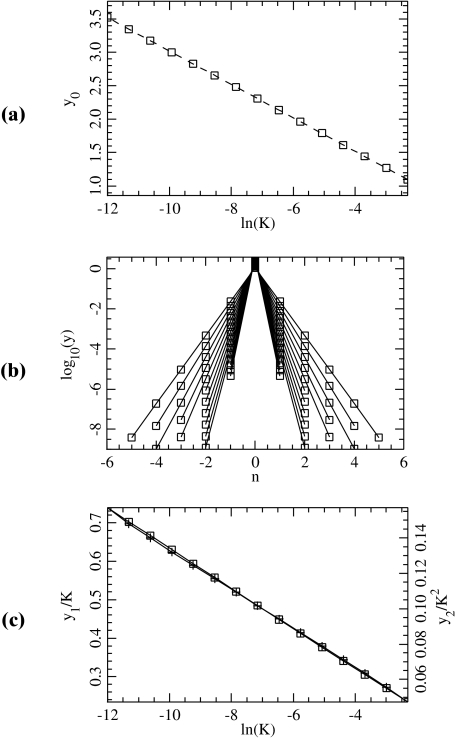
satisfying y_n →0 as n→± ∞. Equivalently, { (y_n , y_n − 1) }_{n ∈ ℤ} defines a homoclinic orbit to 0 of a two-dimensional reversible map. As illustrated in Fig. 10, when the coupling constant K varies one has in addition 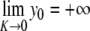and 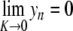for n ≠ 0.

Fig. 10.

Properties of the static solution for different values of K. a The amplitude y₀ as a function of ln (K ) (squares) and the curve y = − (1/β) ln (2 K / Eβ). b The static solution for different values of K in logarithmic scale. Only the positions of the particles near the center of the solution are shown. cy₁/K (squares, left scale) and 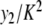(crosses, right scale)

Our existence proof is valid when K is small enough and relies on an extension to a singular case of the anticontinuum limit for maps [21, 22] (see also [23] and its references). In the classical anticontinuum limit, one starts from a well-defined solution of (6) for K = 0, for which y_n is assigned to a critical point of 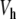for any n, and one uses the implicit function theorem to continue this solution to K ≈ 0. In our case, one of the critical points lies at infinity and the problem becomes singular for K = 0. Consequently, instead of the implicit function theorem, one has to use the contraction mapping theorem in the neighborhood of a suitable approximate solution , for which 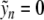if n ≠ 0. Setting n = 0 in (6), 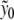can be explicitly computed due to the specific form of 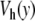for y > 1. One obtains

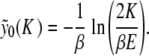7

The following result ensures the existence of an exact localized equilibrium close to 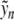(in what follows we denote by O Landau’s order symbol).

Theorem 1 There exists a constant K₀ (depending on D,E,α,β) such that for 0 < K < K₀, problem (6) admits a spatially localized solution y_n (K ) satisfying

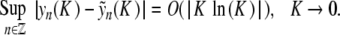8

Moreover, y_n decays to 0 exponentially as n →± ∞ and has the symmetry y_− n = y_n.

To prove Theorem 1, we set 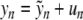and look for symmetric solutions satisfying u_− n = u_n. The sequence u = { u_n }_n ≥ 0 is searched in the Banach space ℓ_∞(ℕ₀) consisting of real, bounded sequences, endowed with the usual supremum norm || ||_∞. More precisely, we look for u in the ball B_R of radius R and center 0 in ℓ_∞(ℕ₀), where R will be fixed small enough. After elementary algebra, problem (6) can be rewritten

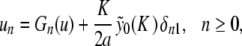9

where δ_ij denotes the usual Kronecker symbol,

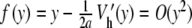. Let us note F_n (u) the right side of (9) (it consists in perturbative terms which are either or become small for K ≈ 0). If R is fixed small enough, then for all K > 0 small enough the map F : u ↦{ F_n (u) }_n ≥ 0 defines a contraction in B_R, and thus problem (9) admits a unique solution u(K ) in B_R in virtue of the contraction mapping theorem. Using the estimate || G(u) ||_∞ ≤ M || u ||_∞ (M < 1) in (9), one obtains in addition || u(K ) ||_∞ ≤ C | K ln (K ) | and an exact solution 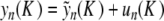of (6). Now there remains to show that y_n tends to 0 as n→± ∞. If a sequence u converges to 0 as n→ + ∞, then the same holds true for the sequence F(u). Consequently, for all k ≥ 0, the sequence 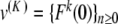tends to 0 as n→ + ∞. Since 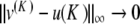as k→ + ∞ (classical property of successive approximations in the contraction mapping theorem), it follows that 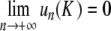. Consequently, the corresponding orbit { (y_n , y_n − 1) } of the two-dimensional map associated with (6) belongs to the stable manifold of the origin (and to its unstable manifold, since y_− n = y_n), therefore, y_n decays to 0 exponentially as n→± ∞. More precisely, we have 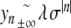, where 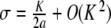denotes the stable eigenvalue associated with the hyperbolic fixed point 0. This completes the proof of Theorem 1.

Although we have restricted our attention to solutions having a single particle beyond the hump at n = 0, it is worthwhile stressing that our method could also provide localized solutions with multiple excited sites, as it the case, for example, in [23].

To end this analysis, we approximate the localized mode frequency Ω computed in Fig. 9, in the limit of small amplitude oscillations around y_n(K ) and for K ≈ 0. From estimate (8), we conclude

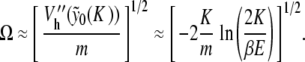For the parameter values indicated in Fig. 7 (with K = 0.01 and m = 300), this approximation yields Ω ≈ 0.021, which is in good agreement with Fig. 9 for .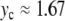

To test the results obtained in the proof of Theorem 1, we have determined the static solution numerically. It can be obtained by a simple process. We impose a fixed position y₀ to the central particle, and we relax the lattice, i.e. we determine the positions of all other particles in order to minimize the energy. Then, given the positions y_− 1, y₀ and y₁, we can compute the total force f ₀ acting on the central particle due to the potential 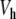and its coupling with the neighbors. For an arbitrary value of y₀, f ₀ does not vanish. But for the value of y₀ which corresponds to the static solution, f ₀ vanishes exactly. In this case, the force deriving from the potential 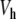is exactly compensated by the pulling exerted on the central particle by its neighbors. Therefore, finding the static solution amounts to solving the equation f ₀(y₀) = 0, with respect to y₀. Figure 10 shows the result for various values of the coupling constant K. Figure 10a shows that the approximate solution 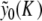given by (7) gives an excellent description of the exact static solution. Figure 10b confirms the exponential decay of y_n versus n and Fig. 10c shows that 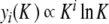(plotted for i = 1 and 2).

Conclusion

This work shows that the study of localized fluctuations in DNA is interesting both in enhancing our understanding of the physics of DNA and for the mathematical theory of nonlinear localized excitations.

Experiments show the existence of highly localized large amplitude motions of the base pairs in DNA. This raises the question of the origin of this localization. A simple model describing base pair opening only, i.e. focusing on the most relevant degree of freedom, reproduces qualitatively, and even to a fairly good quantitative accuracy, the dynamics of the localized fluctuations observed in the experiments. Although this is not a rigorous proof that the localization observed in DNA is due to nonlinear effects, we believe that this is a strong indication that it is the case. A simple model may sound less “realistic” than a very detailed description, but, when it concentrates on the main qualitative properties of the physical system of interest, it is also less likely to be wrong, because its main features are hardly questionable. In this study, we have shown, however, that the model must meet certain conditions to be acceptable. The statistical studies of equilibrium properties of DNA had already shown that the stacking interactions had to be nonlinear to allow the model to describe the sharp thermal denaturation of DNA homopolymers [10–12]. But, by focusing on the dynamical properties of the base pair fluctuations, the present study has shown, moreover, that the potential describing the interaction between the two bases in a pair must have a hump, i.e. a barrier for reclosing, to lead to the correct order of magnitude for the dynamics of the fluctuations. This is a significant improvement towards the analysis of actual DNA properties with a simple mesoscopic model.

This study also had an interesting output for the theory of nonlinear excitations because the study of DNA leads to a model which has several bifurcations and exhibits a new class of discrete breathers that do not oscillate around a ground state of the system but around a static localized distortion of the lattice. We made a first analysis of this new type of discrete breather, but it requires further investigations.