Tilting after Dutch windmills: probably no long-lived Davydov solitons in proteins

Abstract

We present a summary of picosecond pump-probe and photon echo experiments in the mid-IR at 6 μm on the protein myoglobin. The intriguing temperature dependence of the amide I band in Mb is rather similar to the temperature dependence of the amide I band of acetanilide, the molecule that launched Al Scott down the road of looking for Davydov solitons in biology. Alas, after much effort, we believe the data show that there is no long-lived Davydov soliton, at least in myoglobin.

Introduction

There are two basic divisions in almost any field of science: experiment and theory. In theory, it is often easy to think that all things are possible given a lucky combination of various parameters that may or may not be physically reasonable. It is then possible to spin fantasias in the sky that, unfortunately, while mathematically correct, have no connection with reality. On the other hand, in experiments, we can become so earthbound due to a lack of imagination that the experimenter can miss a really exciting piece of physics that unifies and explains some puzzling, profound effect. The puzzling, profound effect we want to examine in this paper is the fundamental way that chemical free energy can get possibly trapped in a protein rather than flowing ergodically into the thermodynamic limit of equal occupation of all the degrees of freedom.

Failure of equipartition into all accessible states can be achieved in at least two ways: (a) kinetically, the rate into some accessible state can be so small compared to others that the relaxation rate to equipartition can be very slow. We would expect this to happen in a system with a rough free energy landscape, a protein being an example of such a system [1]. Such a kinetic trapping of free energy is both an incoherent process and metastable: eventually, the free energy will flow into all the possible states, maximizing the entropy of the system. The flow of free energy on the free energy surface in a linear system is a “passive” process in that the surface itself is unchanged by the presence of the occupation of energy levels that constitute the surface. (b) In coherent self-trapping in anharmonic systems [2], excitation of a system to an excited quantum mechanical state results in the time-dependent alteration of the free energy surface itself: the free energy shape is changed by the presence of the excitation. This is inherently a nonlinear process and can result in extremely long lifetimes of the self-trapped state if the coherent localization that drives the localization does not disperse. The most famous example of this kind of coherent self-trapped state is called the Davydov soliton [3] and is discussed in depth in several articles in this special issue.

The experimental biological physics world originally got interested in the Davydov soliton model for coherent vibrational energy flow in proteins because of the intriguing infrared temperature dependence of molecular crystals of the amino acid analog acetanilide [4, 5]. Acetanilide, a metabolic precursor to the commercial pain reliever Tylenol, has a far simpler structure than a globular protein, but since it is an amino acid analog and forms a molecular crystal, there was hope that there would be “new physics” happening in such a molecular crystal that might map over to protein dynamics of biological relevance [17]. Acetanilide shows a strong temperature-dependent splitting of the amide-I band, and it was conjectured by Carreri et al. [4] that the new, long wavelength shifted band that appeared below 150 K was a Davydov soliton self-trapped state. This led Alywn Scott to conjecture that indeed the interactions between the acetanilide molecules in the molecular crystal formed by acetanilide had the right parameters to form a self-trapped Davydov solition at low temperatures upon absorbing an IR photon at around 6 μm, statements we will try to explain very shortly. Although one of the authors (RHA) did a very early experiment using a ps IR pump-probe, indicating there was no long-lived state in acetanalide [6], it was certainly intriguing to hope that maybe all the complex quantum mechanical machinery of Davydov just might have some relevance to biology and help explain one of the basic mysteries in biology: energy flow in a protein in the nonoptical energy scale below 1 eV.

However, the early ps IR pump-probe experiment we did was very rough and crude with a very poorly controlled ps free-electron light source. Extraordinary claims, both theoretical and experimental, require extraordinary experiments, and so we continued the hunt for long-lived vibrational states at FELIX, the remarkable free-electron laser in The Netherlands. We have written a number of papers about that work [7–9] and will confine ourselves in this paper to the end game where we finally thought we had evidence for a truly narrow, long-lived state in a protein within the amide I band and the probable crashing of that dream.

Self-trapped states, classical and quantum mechanical

The simplest (classical) example of self-trapping of vibrational energy is two anharmonic oscillators (pendula) coupled by a linear torsional spring. The Hamiltonian for these two pendula is:

1

where κ is the torsional spring constant of the coupling spring. When θ₁, θ₂ < < 1 and mgL > > κ, the problem reduces to a coupled harmonic oscillator with split normal modes and with frequency splitting . The acoustic mode where both pendula swing with phase difference 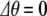lies lower in energy than the optical mode. There is no energy trapping here: energy flows back and forth between the two modes and, on average, each mode has the same energy. Things are different when we can no longer make the small angle approximation. When that happens, the frequency ω_o of the oscillators becomes a function of the angle of the maximum excursion of the oscillator θ_o, and the driving phase θ₁(t) of one of the oscillators now averages to 0 torque over time if the other oscillator is initially at rest. In that case, the energy in the large-angle excursion oscillator is “trapped” and cannot transfer much energy to the other oscillator, in spite of the coupling between the oscillators. Viewed from a spectroscopic perspective, the frequency of the large-angle oscillator is shifted out of resonance (to lower frequencies) with the small-angle oscillator as the energy of the oscillator is driven higher; as the two frequencies shift out of resonance, the energy is trapped in the vibrationally excited state, which cannot transfer its energy to the ground state if there is no dissipation (dephasing) in the system.

The simplest quantum mechanical analogy to the dynamics of a weakly coupled set of anharmonic oscillators is a two-level system, which, of course, is extremely anharmonic (there are only two levels, not a infinite ladder of them). Let the energy splitting between the ground and the excited state be 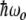, and let there be an incident-driving electric field 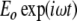driving transitions between the ground and the excited state, so that the occupation levels p₁(t) and p₂(t) change with time. If there is an electric dipole matrix element 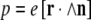connecting the two states, the occupation of the excited p₂(t) varies as [10]:

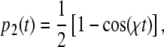2

where χ is the Rabi frequency, given by:

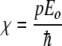3

when the incoming photon energy is exactly resonant with the energy splitting 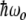. If the photon is off resonance, let 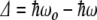be the energy difference between the splitting of the ground and excited states and the energy of the incident photons. When 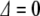, there is a full periodic inversion of the ground and excited state populations at the Rabi frequency χ, when the incident field frequency ω is detuned from the splitting frequency ω_o the amplitude of p ₂(t) becomes smaller, which is also what happens in our simple two-coupled anharmonic pendula when the amplitude dependence of the period detunes one pendulum from another...the off-resonance driving frequency results in a reduced transfer of energy to the other system. The classical and quantum systems have the same basic behavior, caused by the nonlinearity of the system and the phase difference between the driving force and the response of the excited state.

The localization of energy on one two-level system due to detuning from another two-level system is not really energy trapping because the two-level system splitting is not a function of the driving field, but it is an example of quantum mechanical coupling between two discrete anharmonic systems. The Davydov soliton that Alwyn Scott worked so hard on [11] comes out of exciton and polaron theory, and these theories come out of semiconductor physics and the concept of delocalized identical particles: band theory. A semiconductor is a material with a filled valence band and an empty conduction band with band gap 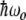of the order of 1 eV or less, so that typical semiconductors appear highly absorbing in the visible range due to allowed optical transitions. Unfortunately, most biological polymers are insulators: the band gap is at least 5 eV or so, and they are thus transparent in the visible range. One basic problem is then: to what extent can the band theories developed for localized electronic states just below the conduction band edge be applied to systems with far bigger band gaps than semiconductors? That there are fundamental problems with applying concepts that work for small band gap semiconductors to biological polymers is unfortunately a very long and sad story in biological physics. It is sad because it would be great fun and exciting to use simple fundamental quantum mechanical concepts of delocalization and actually apply them to protein polymers’ and (even better) DNA polymers’ energy transport: why, we could have very low resistance charge transport, even superconductivity in biological polymers [12], and we could go on from there to even greater excesses of quantum mechanical splendor [13, 14]. However, there are both experimental failures to observe these effects [15] and a fundamental theoretical problem: electronic states are, in fact, highly localized in biopolymers and not delocalized.

There is a reason for this localization of charge where one would hope that, somehow, the interactions between monomers (nucleic acid bases or amino acids) would conspire to give delocalization: the Mott insulator transition. The failure of simple band theory to properly predict the insulating nature of materials that naively would be considered conductors is a very old problem first addressed by Mott in his Nobel prize-winning work [16]. A Mott insulator is a metal that is an insulator: it is an insulator because the Coulomb repulsion interaction U between electrons in the material is greater than the exchange integral W, which delocalizes identical particles and, hence, lowers their kinetic energy. Roughly speaking, the Coulomb repulsion energy U(a) for two electrons situated on a simple linear lattice of spacing a is given by:

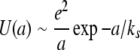4

where 1/k_s is the Thomas–Fermi screening length for an electron gas of density n_o and Fermi energy ε_F:

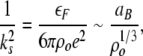5

where a_B is the Bohr radius. Because ρ_o for biological polymers is quite small, on the order of 10¹⁹ cm^− 3, the screening length is quite large, on the order of 1 nm, over 10 times the screening length of electrons in a typical metal. It is hard to go much further here quantitatively, other than to point out that, because of the low density of charge carriers in a typical biopolymer, the Coulomb energy is so large as to localize the charges, and much of the apparatus of small band gap semiconductor physics is simply wrong. If you open a typical textbook on biopolymer infrared spectroscopy, such as Mantsch and Chapman [18], you will find no talk of semiconductors or band gaps, all the discussion is purely molecular. Most of the calculations of Davydov solition dynamics use explicitly semiconductor delocalized wave functions and terminology, creating not only a gap in understanding of the difference between the dynamics of a Mott insulator and a semiconductor, but also a complete disconnection between the community of biophysicists who read Mantsch and Chapman and those who read Kittel [19], which is very unfortunate.

The two key ingredients in the Davydov scheme for energy trapping are anharmonicity in the mid-IR spectral region and “long” dephasing times to maintain the same phase coherence needed in the simple two-level quantum system. Basically, the phase coherence must last as long as the energy is to be trapped, so one would guess that phase coherence times at least on the order of 10 ps are necessary. Does a globular protein have any unusual properties in these two sectors? The anharmonicity in soliton theory is typically expressed by the quantity χ:

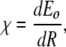6

where E_o is the vibrational energy of the amide I band (about 0.2 eV) and R is the length of the hydrogen bond that couples to the C=O stretch, which is the primary origin of the amide I transition. It really is not right, but in analogy to our anharmonic coupled oscillator, you could view 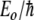as the small angle frequency of the anharmonic oscillator ω_o:

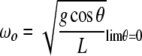7

and χ, given by

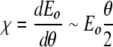8

represents a detuning of the oscillator with angle and the origin of localization of the energy in the excited oscillator.

The connection between the dependence of the anharmonicity of the system on the hydrogen bond length R and the IR spectroscopy is mapped by the temperature dependence of the red-shifted band, which is determined by the binding energy of the soliton in the theory expanded by Alwyn Scott. The binding energy E_b of the soliton is given by:

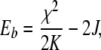9

where K is the spring constant of the C=O bond (about 13 N/m) and J is the electromagnetic strength of the coupling between adjacent amide I oscillators (about 1–2 cm^− 1) [5]. Note that J plays the role of the torsional spring in our mechanical toy, K plays the role of gravity g, and χ plays the role of the nonlinear angular dependence cosθ of the restoring force on the pendulum bob.

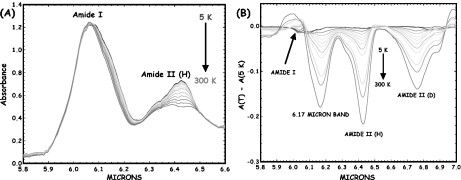
It is fairly straightforward using IR spectroscopy to make rough estimates of the anharmonicity of the α-helix amide-I bands, assuming that the temperature dependence comes from this self-trapping model, as we discussed in [20]. A truly harmonic (linear response) transition has no temperature dependence since all levels are equally spaced in energy. An anharmonic transition will show a temperature dependence since, with increasing temperature (assuming that the potential surface becomes softer with increasing energy), there should be a red shift. While the electronic transitions of semiconductors have enormous red shifts with increasing temperature, giving rise to the phenomena of thermal run-away, proteins are, in fact, rather hard harmonic oscillators within the vibrational manifold showing a rather weak temperature dependence. Figure 1 shows the temperature dependence of the amide I vibrational spectral region of the protein myoglobin (Mb) from 5 to 300 K. There is a clear anharmonicity in the amide I band (and much more in the amide II band), and a new red-shifted band appears rather similar to the acetanilide low-temperature band. If one assumes that the red-shifted band is some sort of a trapped state, as Careri and his colleagues did, then the binding energy of the state is approximately 20 cm^− 1, which translates into a χ of approximately 100 pN, in the range needed for soliton stability as discussed by Scott [21]. Note that the temperature dependence of the amide I band is such that the amide I band on the blue side of the spectrum has almost no temperature dependence. Note also that this thermal temperature dependence is different from the nonlinear optical dependence expected from driving excited states, as we discussed in Eq. 2.

Fig. 1.

a The infrared absorption spectrum of sperm whale myoglobin as a function of temperature from 5 to 300 K (blue line to red line) from 5.8 to 6.6 μm. b Difference spectra of the amide I and II regions of Mb (5 K base) as a function of temperature. The band at 6.17 μm decreases with absorbance as the temperature increases

Mb (a highly alpha-helical containing protein) thus has a long wavelength-shifted band that has a similar temperature dependence and binding energy (with the soliton model) to acetanilide. If Davydov solitons truly exist in acetanilide, and if they are biologically important for self-trapping of vibrational energy in biology, then it would appear that the simple protein myoglobin would be the place to look for them.

Experiment

The only true test of a theory is experiment. The previous section was a long-winded and simple-minded introduction to the connection between proteins, solitons, Davydov, A. Scott, and some IR spectroscopy of a globular protein (myoglobin). This part takes up where the last paper we published ended [20]: 1.5-ps pulses from the FELIX with transform-limited linewidths of 10 cm^− 1 were used to ascertain the dynamics of the amide-I band at the (mainly temperature-independent) blue side of the amide-I band (6.00 μm) and the red side of the amide-I band (6.17 μm) where one would hope to see energy trapping. While we did see a long-lived absorbance state develop at the 6.17 μm side of the amide-I band, we ascribed it to a pure thermal population of the amide-I modes and, hence, not a coherent superposition of states as is required by soliton models developed by Davydov and espoused by Scott. That would seem to put a nail in the soliton model of nonlinear trapping of vibrational energy in proteins.

However, we did a further experiment which gave rise to a very interesting signal, which we now present. The purpose of using 1.5 ps (10 cm^− 1) pulses was to enhance the time resolution of the pump-probe signals; however, that was of course obtained at the cost of spectral resolution, and if there is indeed a long-lived (say, greater than 20 ps) self-trapped coherent state, it is possible that the dynamic state generated is of very narrow line width and will not be easily seen using a spectrally broad pulse. Thus, in the interest of obtaining higher spectral resolution at the cost of time resolution, we changed the pulse width (which can be done easily at FELIX) to ~10 ps, or ~1 cm^− 1 resolution.

The result narrowing the pump line width was quite shocking: on the “blue side” of the amide-I band, where there is no temperature dependence of the absorption band, there was an apparently huge (50%!) transmission change observed at 6.05 μm, as opposed to the 5% transmission changes seen at the same pulse energy with a 1.5-ps pulse width at the same 6.05-μm wavelength. This apparently huge signal is highly wavelength-dependent, scanning across the absorption band of the protein reveals, as is revealed by scanning across the absorption band of the protien, and it is shown in Fig. 2 that the large signal occurs only in the spectral region where the amide-I absorbance is not temperature dependent.

Fig. 2.

Pump-probe signal in the frequency domain seen with 1 cm^− 1 linewidth pulse scanning through the amide I band of Mb at 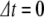 ps relative to the pump pulse. The sample absorbance is on the right, the left axis is the equivalent transmission change

One can do controls. In the time domain, the result of this narrow wavelength experiment is very puzzling on two counts. First, the signal follows the autocorrelation profile of the pulse with no long-lived “tail” after the pump-probe pulse sequence has passed through the sample. If indeed there was a long-lived state at this position in the amide-I band profile, it should not simply look like the autocorrelation of the pump and probe profiles. Secondly, since the apparent signal is over 10 times bigger in the narrow range of the zero-temperature coefficient region, one would have still expected to see anomalous effects due to a long-lived state even in the case of a short (1.5-ps) pulse.

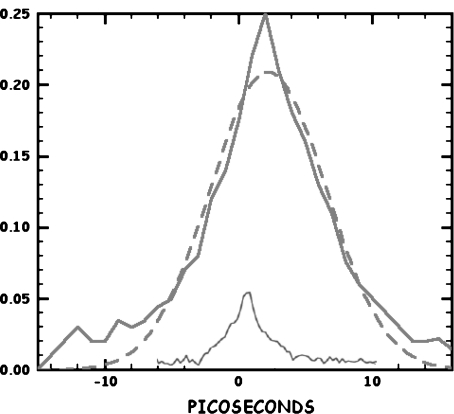
Alas, there is no long-lived state for the long pulse signal, but rather what looks like the convolution of the probe pulse with the pump pulse, so it would appear that what seems to be an exciting signal reminiscent of what is expected within the context of soliton physics is some sort of a degenerate four-wave mixing artifact [22]. That is, the coherent superposition of the pump with the probe pulse on a sample whose absorbance is a function of intensity generates a diffraction grating, which scatters the pump beam coherently (diffracts) into the probe beam. If the grating is “deep” in terms of real or imaginary index of refraction change between constructive and destructive interference lines, so much of the pump beam is scattered into the probe direction that an apparently huge “saturation” signal is observed. But, the signal is really due to the intensity of the diffractively scattered pump beam. If the lifetime of the grating which generates the four-wave mixing is short compared to the pulse width of the pump and probe beam pulses, one sees simply the convolution of the pump and the probe beams as the pulses collide to generate the grating transiently. A fit of the convolution of two Gaussian-shaped pulses to the observed long-pulse signal is shown as the dashed line in Fig. 3. The extracted FWHM of the pump pulse is ~7 ps. The fit is not a perfect fit to a Gaussian, and there is clearly a slower decay at times greater than 10 ps. The observed long time tails that do not fit the Gaussian convolution are presumably due to the true relaxation time of the vibrational excited state of the protein amide I system, which, as we have discussed earlier [8], is non-exponential, presumably due to the conformational distribution of the protein structure [1] which gives rise to a distribution of longitudinal relaxation times.

Fig. 3.

Pump-probe signal in the time domain at 6.07 μm for Mb. The response of the system to a short (1.5 ps) pulse is shown as the solid blue line, the response to long pulse response is shown by the solid red line. The fit of convolution of two Gaussian pump-probe pulses is shown by the dotted line

However, while it is consistent to assume that the large pump-probe signal is not a long lived state but rather a grating artifact on top of a short-lived saturation of the system, this grating-induced four-wave mixing explanation for the enhancement does not explain why this large signal only occurs on the temperature-independent short wavelength side of the amide I absorbance band, and only when the pulse width is narrowed. Why is that?

First, we can certainly say that the grating is not due to the temperature dependence of the amide I absorbance, since that would result in a large signal only on the long wavelength side of the amide I band where there is a large temperature dependence to the absorbance. The grating must be due to a population depletion due to Rabi pumping of a coherent vibrational excited state. Using the language of NMR and the Bloch equations, there are two parameters that characterize a coherent excited state: the longitudinal relaxation time T₁ which is a measure of the lifetime of the excited state, and the transverse relaxation time (pure dephasing time) 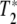, which is a measure of how long the system remains in phase [10]. It could be, as we discuss below, that the dephasing time of any coherently excited vibrations can be much shorter than the excited state relaxation times and determine the linewidths of the transition. In that case, it is a mistake to ignore a short , for many non-linear effects need the coherence times of the excitations to be long as well to be effective. A short 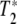can be as destructive as a short T₁ for a beautiful theory of non-linear effects in biology.

The determination of the T₁ and 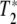’s of a state starts with the static spectroscopy of the state. If a particular transition is not heterogeneously broadened, the static Lorentzian linewidth Γ_o of the transition (in energy units of wavenumbers per centimeter) is given by [10]:

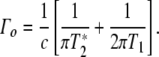10

The classic problem in proteins is of course is that static spectroscopy cannot disentangle T₁ from 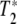, and further that the vibrational lines in the IR spectra of a protein are inhomogenously broadened due to the complex energy landscape of a protein [1] as we have mentioned. It is possible that within this distribution of lines there exist a set of states that are both spectrally narrow and have long dephasing times. In order to discover these states it is necessary to probe their dynamics by some form of site-selective spectroscopy.

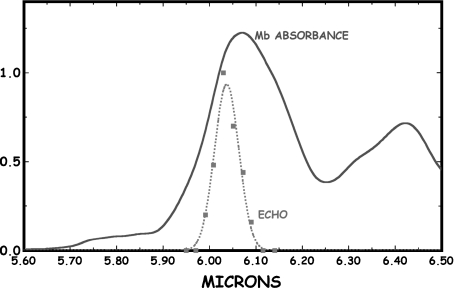
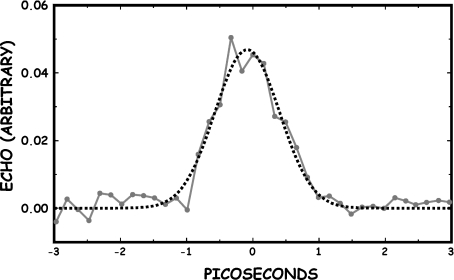
The lifetime of the coherent state creating the grating could be significantly longer than observed if the dephasing time T₂ of the presumably heterogenously broadened collection of states is sufficiently shorter than the true T₁. To test this, we did a photon echo experiment to determine if the dephasing time was shorter than the relaxation time. The photon echo experiment was not done at FELIX but rather on an OPO system constructed at Princeton University. The pulse width on this system could not be varied and was a fixed at ~2 ps. Figure 4 shows that scanning at fixed echo delay of 0 ps with a 2 ps wide pulse across the amide I band did indeed reveal an enhanced echo amplitude at the same wavelength where the pump-probe experiment showed large enhancement. Although the spectral resolution is not as high as the FELIX pump-probe experiment, the echo was seen only on the short-wavelength side of the amide I band, at the same position of the enhanced pump-probe signal. However, a scan along the time axis of the photon echo, shown in Fig. 5, reveals that the echo has no long decay times, and that whatever state is generating this coherent signal is short-lived with a lifetime of no more than several ps. If the Davydov soliton needs a long T₁ and T₂ to be of biological relevance, we have not found it, in spite of the mysteries of the blue side of the amide I.

Fig. 4.

The photon echo observed from a simple two-pulse photon echo experiment at delay =0 ps as a function of wavelength. The scale of the echo pulse amplitude is arbitrary, and we have superposed the Mb IR absorbance of the amide I band

Fig. 5.

The amplitude of the 6.07-μm echo amplitude vs delay time. The dashed line is a fit to a Gaussian

Conclusions

It is important in science to test powerful ideas developed by the theorists. Sometimes, however improbable, the ideas are correct: special and general relativity, the neutrino, the breaking of parity conservation in the weak interaction followed by CP violation come immediately to mind. Sometimes Mother Nature is not so cooperative: there seem to be no magnetic monopoles, no one has seen a proton decay yet, and maybe we will never find the axion. Davydov started the idea that vibrational energy could be self-trapped in proteins, and Alywn Scott devoted a good part of his life to exploring that idea. Scott catalyzed a huge theoretical effort that still continues to this day, but not so many experimentalists felt inclined to test all the calculations with experiments. This paper represents at least for one of us, RHA, a coda to a long and hard effort to test the Davydov soliton model in a real protein under real biological conditions. One of best things we can say about Alwyn Scott’s work was that he realized that experiment ultimately is the true test of theory and that without experiment a theory is lame, to paraphrase Einstein. We wish we could say that all the huge effort that Alwyn Scott poured in the Davydov soliton was repaid with the triumph of physics over biology, but we think such is not the case. Sometimes, when you tilt at windmills, the windmill wins. Perhaps someday we will see what Scott and Davydov were driving at as we gain ever deeper understanding of the possible functional and non-trivial connections between quantum mechanics and biology.