Abstract
If one formulates Helmholtz’s ideas about perception in terms of modern-day theories one arrives at a model of perceptual inference and learning that can explain a remarkable range of neurobiological facts. Using constructs from statistical physics it can be shown that the problems of inferring what cause our sensory input and learning causal regularities in the sensorium can be resolved using exactly the same principles. Furthermore, inference and learning can proceed in a biologically plausible fashion. The ensuing scheme rests on Empirical Bayes and hierarchical models of how sensory information is generated. The use of hierarchical models enables the brain to construct prior expectations in a dynamic and context-sensitive fashion. This scheme provides a principled way to understand many aspects of the brain’s organisation and responses.
In this paper, we suggest that these perceptual processes are just one emergent property of systems that conform to a free-energy principle. The free-energy considered here represents a bound on the surprise inherent in any exchange with the environment, under expectations encoded by its state or configuration. A system can minimise free-energy by changing its configuration to change the way it samples the environment, or to change its expectations. These changes correspond to action and perception respectively and lead to an adaptive exchange with the environment that is characteristic of biological systems. This treatment implies that the system’s state and structure encode an implicit and probabilistic model of the environment. We will look at models entailed by the brain and how minimisation of free-energy can explain its dynamics and structure.
Keywords: Variational Bayes, Free-energy, Inference, Perception, Action, Value, Learning, Attention, Selection, Hierarchical
INTRODUCTION
This paper illustrates how ideas from theoretical physics can help understand the structure and dynamics of biological systems, in particular the brain. This is not a rigorous treatment, but a series of heuristics that provide an interesting perspective on how biological systems might function. The first section motivates and describes a free-energy principle that addresses the maintenance of structural order seen in living systems. The subsequent sections use this principle to understand key functional and structural aspects of neuronal systems, with a focus on perceptual learning and inference. This work pursues an agenda established by von Helmholtz in the nineteenth century, who sought a basis for neuronal energy in his work on conservation laws in physics. This ambition underlies many energy-based approaches to neural networks (Borisyuk and Hoppensteadt 2004), including the approach described here.
Despite the latitude for disorder, the nervous system maintains an exquisite configurational and dynamic order. This order is preserved on both an evolutionary and somatic time-scale. The amount of reproducible anatomic information pertaining to the brain is now so vast it can only be organised electronically (e.g., Stephan et al 2001). Furthermore, the brain’s spatiotemporal responses, elicited experimentally, are sufficiently reproducible that they support whole fields of neuroscience (e.g., human brain mapping). The premise of this paper is that this precise structural and functional organisation is maintained by causal structure in the environment. The principles behind this maintenance and the attending neuronal mechanisms are the subject of this paper.
The analysis presented in this paper rests on some fairly mathematical and abstract approaches to understanding the behaviour of systems. These approaches were developed primarily in statistical physics and machine learning. The payoff for adopting this mathematical treatment is that many apparently diverse aspects of the brain’s structure and function can be understood in terms of one simple principle; namely the minimisation of a quantity (free-energy) that reflects the probability of sensory input, given the current state of the brain. We will see that this principle can be applied at different time-scales to explain perpetual inference, attention and learning. Furthermore, exactly the same principle can explain how we interact with, or sample, the environment; providing a principled account of adaptive behaviour. It highlights the importance of perception for action and enforces a mechanistic view of many ethological and neuronal processes. Another payoff is the disclosure of some rather counterintuitive conclusions about our brains; for example, it suggests that everything we do serves to minimise surprising exchanges with the environment (and other people); it suggests that perception plays a secondary role in optimising action; it suggests that the salience, attention and the encoding of uncertainty in the brain are all aspects of the same underlying process; it suggests the hierarchal structure of our brains is transcribed from causal hierarchies in the environment. Finally, it furnishes clear links among other important formulations of adaptive systems; for example, we will see that value, in microeconomics and reinforcement learning, is synonymous with (negative) free-energy and surprise. Similarly, adaptive fitness can be formulated in terms of free-energy, which allows one to link evolutionary and somatic timescales in terms of hierarchical co-evolution.
Many people now regard the brain as an inference machine that conforms to the same principles that govern the interrogation of scientific data (MacKay, 1956; Neisser, 1967; Ballard et al, 1983; Mumford, 1992; Kawato et al 1993; Rao and Ballard 1998; Dayan et al, 1995; Friston, 2003; Körding and Wolpert 2004; Kersten et al 2004; Friston 2005). In everyday life, these rules are applied to information obtained by sampling the world with our senses. Over the past years, we have pursued this perspective in a Bayesian framework to suggest that the brain employs hierarchical or empirical Bayes to infer the causes of its sensations. This model of brain function can explain a wide range of anatomical and physiological facts; for example, the hierarchical deployment of cortical areas, recurrent architectures using forward and backward connections and functional asymmetries in these connections (Angelucci et al, 2002a; Friston 2003). In terms of synaptic physiology, it predicts associative plasticity and, for dynamic models, spike-timing-dependent plasticity. In terms of electrophysiology it accounts for classical and extra-classical receptive field effects and long-latency or endogenous components of evoked cortical responses (Rao and Ballard, 1998; Friston 2005). It predicts the attenuation of responses encoding prediction error, with perceptual learning, and explains many phenomena like repetition suppression, mismatch negativity and the P300 in electroencephalography. In psychophysical terms, it accounts for the behavioural correlates of these physiological phenomena, e.g., priming, and global precedence (see Friston 2005 for an overview)
It is fairly easy to show that both perceptual inference and learning rest on a minimisation of free-energy (Friston 2003) or suppression of prediction error (Rao and Ballard 1998). The notion of free-energy derives from statistical physics and is used widely in machine learning to convert difficult integration problems, inherent in inference, into easier optimisation problems. This optimisation or free-energy minimisation can, in principle, be implemented using relatively simple neuronal infrastructures. The purpose of this paper is to suggest that perception is just one emergent aspect of free-energy minimisation and that a free-energy principle for the brain can explain the intimate relationship between perception and action. Furthermore, the processes entailed by the free-energy principle cover not just inference about the current state of the world but a dynamic encoding of context that bears the hallmarks of attention and perceptual salience.
The free-energy principle states that systems change to decrease their free-energy. The concept of free-energy arises in many contexts, especially physics and statistics. In thermodynamics, free-energy is a measure of the amount of work that can be extracted from a system, and is useful in engineering applications (see Streater 1993 for discussion of free-energy theorems). It is the difference between the energy and the entropy of a system. Free-energy also plays a central role in statistics, where, borrowing from statistical thermodynamics, approximate inference by variational free-energy minimization (also known as variational Bayes, or ensemble learning) has maximum likelihood and maximum a posteriori methods as special cases. It should be noted that the only link between these two uses of the term ‘free-energy’ is mathematical; i.e., both appeal to the same probabilistic fundaments. It is the second sort of free-energy, which is a measure of statistical probability distributions that we apply to the exchange of biological systems with the world. The implication is that these systems make implicit inferences about their surroundings. Previous treatments of free-energy in inference (e.g., predictive coding) have been framed as explanations or descriptions of the brain at work. In this paper, we try to go a step further by suggesting that free-energy minimisation is mandatory in biological systems and has a more fundamental status. We try to do this by presenting a series of heuristics that draw from theoretical biology and statistical thermodynamics.
Overview
This paper has three sections. In the first, we lay out the theory behind the free-energy principle, starting from a selectionist standpoint and ending with the implications of the free-energy principle for neurobiology. The second section addresses the implementation of free-energy minimisation in hierarchical neuronal architectures and concludes with a simple simulation of sensory evoked responses. This illustrates some of the key behaviours of brain-like systems that self-organise in accord with the free-energy principle. A key phenomenon; namely, suppression of prediction error by top-down predictions from higher cortical areas, is examined in the third section. In this final section, we review some key issues in neurobiology that can be understood under the free energy principle.
THEORY
In this section, we develop a series of heuristics that lead to a variational free-energy principle for biological systems and, in particular, the brain. We start with evolutionary or selectionist considerations that transform difficult questions about how biological systems operate into simpler questions about constraints on their behaviour. These constraints lead to the important notion of an ensemble density that is encoded by the state of the system. This density is used to construct a free-energy for any system that is in exchange with its environment. We then consider the implications of minimising this free-energy with regard to quantities that determine the system’s (i.e., brain’s) state and, critically, its action upon the environment. We will see that this minimisation leads naturally to perceptual inference about the world, encoding of perceptual uncertainty (i.e., attention or salience), perceptual learning about the causal structure of the environment and, finally, a principled exchange with, or sampling of, that environment.
In what follows, free-energy becomes a Lyapunov function for the brain. A Lyapunov function is a scalar function of a system’s state that decreases with time; it is also referred to colloquially as a Harmony function in the neural network literature (Prince and Smolensky, 1997). There are many examples of related energy functionals1 in the time-dependent partial differential equations literature (e.g., Kloucek, 1998). Usually, one tries to infer the Lyapunov function given a system’s structure and behaviour. However, we address the converse problem: given the Lyapunov function, what would systems that minimise free-energy look like?
Thermodynamics and biological systems
We start with an apparent anomaly: biological systems and especially neuronal systems appear to contravene the second law of thermodynamics. The second law states that the entropy of closed systems increases with time. Entropy is a measure of disorder or, more simply, the number of ways the elements of a system can be rearranged. In the physical sciences the second law of thermodynamics is fundamental and has attained almost cult status: As noted by Sir Arthur Eddington “If someone points out to you that your pet theory of the universe is in disagreement with Maxwell’s equations, then so much the worse for Maxwell’s equations. And if your theory contradicts the facts, well, sometimes these experimentalists make mistakes. But if your theory is found to be against the Second Law of Thermodynamics, I can give you no hope; there is nothing for it but to collapse in deepest humiliation” (http://en.wikipedia.org/Second_law). The fact that the second law applies only to ‘closed’ systems is quite important because biological systems are open, which means they have the opportunity to resist the second law; but how?
Thermodynamics and fluctuations
The second law applies to macroscopic or ensemble behaviour. It posits time-irreversible behaviour of a system, despite the fact that its microscopic dynamics can be time-reversible. This apparent paradox is resolved with the Fluctuation Theorem (see Evans & Searles 2002). The Fluctuation Theorem shows that the entropy of small systems can decrease but as the system’s size or the observation time gets longer, the probability of this happening decreases exponentially. The fluctuation theorem is important for non-equilibrium statistical mechanics, and includes the second law as a special case. Critically, the Fluctuation Theorem holds for dissipative, non-equilibrium systems. A dissipative system is an open system, which operates far-from-equilibrium by exchanging energy or entropy with the environment. Recently, the Fluctuation Theorem has been applied to non-equilibrium transitions between equilibrium states to show how free-energy differences can be computed from thermodynamic path integrals (Crooks 1999). Equivalent derivations for deterministic systems highlight the close relationship between non-equilibrium free-energy theorems and the Fluctuation Theorem (Evans 2003). These non-equilibrium free-energy theorems are of particular interest because they apply to dissipative systems like biological systems.
The nature of biological systems
If the Fluctuation Theorem is so fundamental, why do we see order emerging all around us? Specifically, why are living systems apparently exempt from these thermodynamic laws? How do they preserve their order (i.e., configurational entropy)2, immersed in an environment that is becoming irrevocably more disordered? The premise here is that the environment unfolds in a thermodynamically structured and lawful way and biological systems embed these laws into their anatomy. The existence of environmental order is assured, at the level of probability distributions, through thermodynamics. For example, although disorder always increases, the second law per se is invariant. This invariance is itself a source of order. In short, organisms could maintain configurational order, if they transcribed physical laws governing their environment into their structure. One might ask how this transcription occurs. However, a more basic question is not how biological systems arise, but what are they?
What is the difference between a plant and a stone? The obvious answer is that the plant is an open non-equilibrium system, exchanging matter and energy with the environment, whereas the stone is an open system that is largely at equilibrium: Morowitz computed the thermal bonding energy required to assemble a single Escherichia coli bacterium. He concluded “if equilibrium process alone were at work, the largest possible fluctuation in the history of the universe is likely to have been no longer than a small peptide” (Morowitz 1968; p68). In short, biological systems must operate far-from-equilibrium: The flow of matter and energy in open systems allows them to exchange entropy with the environment and self-organise. Self-organisation (Ashby 1947, Haken 1983) refers to the spontaneous increase in the internal organisation of open systems. Typically, self-organising systems also exhibit emergent properties. Self-organisation only occurs when the system is far-from-equilibrium (Nicolis and Prigogine 1977). The concept of self-organisation is central to the description of biological systems and also plays a key role in chemistry, where is it often taken to be synonymous with self-assembly3.
Beyond self-organisation
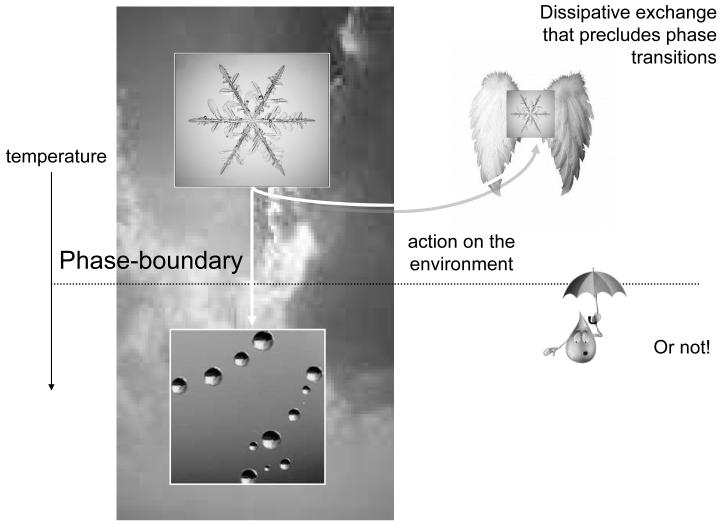
Biological systems are thermodynamically open, in the sense that they exchange energy and entropy with the environment. Furthermore, they operate far-from-equilibrium, showing self-organising behaviour (Ashby, 1947; Nicolis and Prigogine, 1977; Haken 1983; Kauffman 1993). However, biological systems are more than simply dissipative self-organising systems. They can negotiate a changing or non-stationary environment in a way that allows them to endure over substantial periods of time. This means that they avoid phase-transitions that would otherwise change their physical structure. A key aspect of biological systems is that they act upon the environment to change their position within it, or relation to it, in a way that precludes extremes of temperature, pressure or other external fields. By sampling or navigating the environment selectively, they keep their exchange within bounds and preserve their physical integrity. A fanciful example is provided in Figure 1: Here, we have taken a paradigm example of a non-biological self-organising system, namely a snowflake and endowed it with wings so that it can act on the environment. A normal snowflake will fall and encounter a phase-boundary, at which its temperature will cause it to melt. Conversely, snowflakes that maintain their altitude and regulate their temperature may survive indefinitely, with a qualitatively recognisable form. The key difference between the normal and adaptive snowflake is the ability to change their relationship with the environment and maintain thermodynamic homeostasis. Similar mechanisms can be envisaged in an evolutionary setting, wherein systems that avoid phase-transitions will be selected above those that cannot (c.f., the selection of chemotaxis in single-cell organisms). By considering the nature of biological systems in terms of selective pressure, one can replace difficult questions about how biological systems emerge with questions about what behaviours they must exhibit to exist. In other words, selection explains how biological systems arise; the only outstanding issue is what characteristics they must possess. The snowflake example suggests biological systems act upon the environment to preclude phase-transitions. It is therefore sufficient to define a principle that ensures this sort of exchange. We will see that free-energy minimisation is one such principle.
Figure 1.
Schematic highlighting the difference between dissipative, self-organising systems (like normal snowflakes) and adaptive systems (like adaptive snowflakes) that can change their relationship to the environment. By occupying a particular environmental niche, biological systems can restrict themselves to a domain that is far from phase-boundaries. The phase-boundary depicted here is a temperature phase-boundary that would cause the snowflake to melt (i.e., induce a phase-transition). In this fanciful example, we have assumed that snowflakes have been given the ability to fly and maintain their altitude (and temperature) and avoid being turned into raindrops.
A free-energy formulation
To develop these arguments formally, we need to define some quantities that describe an agent, phenotype or system, m and its exchange with the environment. This exchange rests on quantities that describe the system, the effect of the environment on the system and the effect of the system on the environment. We will denote these as λ, and α respectively. can be thought of as system states that are caused by environmental forces; for example, the state of sensory receptors. This means that can be regarded as sensory input. The quantities α represent forces exerted by effectors that act on the environment to change sensory samples. We will represent this dependency by conditioning the sensory samples on action. Sometimes, this dependency can be quite simple: for example, the activity of stretch receptors in muscle spindles is affected directly by muscular forces causing that spindle to contract. In other cases, the dependency can be more complicated; for example, the oculomotor system, controlling eye position, can influence the activity of every photoreceptor in the retina.
The tilde means that covers generalised motion in terms of high-order temporal derivatives. This allows α to change the motion or trajectory of sensory input through its higher derivatives by interacting with forces that cause . We will call these environmental causes . This formulation means that sensory input is a generalised convolution of the action and unknown or hidden causes. We will unpack these quantities later. At the moment, we will simply note that they can be high-dimensional and time-varying. See also Figure 2.
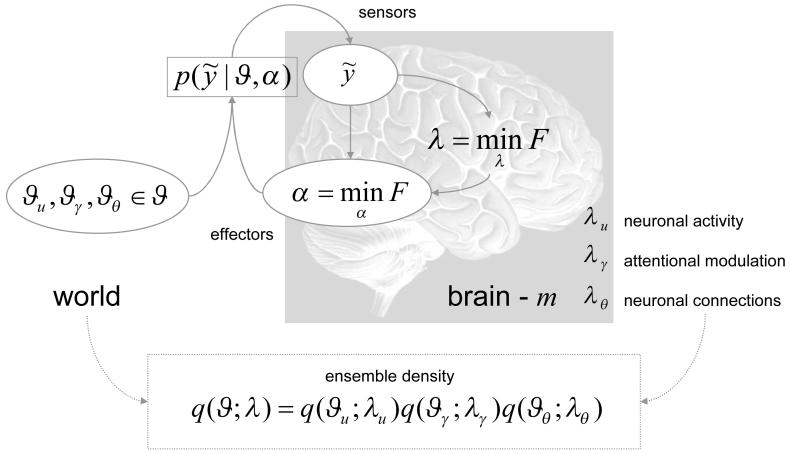
Figure 2.
Schematic detailing the quantities that define the free-energy. These quantities refer to the internal configuration of the brain and quantities that determine how a system is influenced by the environment. This influence is encoded by the variables that could correspond to sensory input or any other changes in the system state due to external environmental forces or fields. The parameters α correspond to physical states of the system that change the way the external forces act upon it or, more simply, change the way the environment is sampled. A simple example of these would be the state of ocular motor systems controlling the direction of eye gaze. is the conditional probability of sensory input given its causes, , and the state of effectors (i.e., action). is called an ensemble density and is encoded by the system’s parameters, λ. These parameters (e.g., mean or expectation) change to minimise free-energy, F and, in so doing, make the ensemble density an approximate conditional density on the causes of sensory input.
A free-energy bound
The basic premise we start with is that biological systems must keep within bounds (i.e., phase-boundaries) through adaptive changes in α. Put simply, adaptive systems or agents should minimise unlikely or surprising exchanges with the environment. We can express this more formally by requiring adaptive systems to minimise surprise, or maximise the following quantity
| 1 |
In fact, it is fairly simple to show that any member of a population, whose population density, is at equilibrium, must, on average increase (Friston et al in preparation).
The conditional surprise measures the improbability of exchange given a particular agent and its action. Each point in the space of exchange will have a measure of this sort, which will be high if the exchange is compatible with m and low if not (i.e., high in domains populated by m ). More intuitively, we would be surprised, given a particular system, to find it in some environments (e.g., a snowflake in a sauna). In a selectionist setting, the quantity could be regarded as the adaptive value of a particular exchange. From a statistical perspective, is also known as the log-evidence or marginal likelihood (marginal because it obtains by integrating out dependencies on the causes, ). These two perspectives are useful because they link selection in theoretical biology to Bayesian model selection in machine learning; we will exploit this link below by treating the system or agent as a model of its sensory input. Finally, also plays the role of the value in microeconomics and value-learning. Value-learning is a branch of computational neuroscience that deals with the reinforcement of actions and optimisation of policies. In short, for a given agent we require action to optimise4
| 2 |
where is the joint density of environmental effects and their unknown causes, conditioned an action. However, this maximisation must be accomplished by changes in action, which can only be a function of and the internal states, λ of the agent; because these are the only variables it has access to.
Clearly, the system cannot perform the integration in Eq.2 because it does not know the causes. However, it can optimise a bound on the integral using a relatively simple gradient descent. One such bound is the free-energy, which is a scalar function of sensory and internal states5
| 3 |
The inequality is an example of something called Jensen’s inequality, which follows simply from the concavity of the log function. To make this bound, a function of internal states λ , we have introduced , which is an arbitrary density function on the causes that is encoded by the system’s internal states. Usually, is called an ensemble density6 and can be regarded as the probability density that the causes would be selected from an ensemble of environments. For example, λ could be the mean and variance of a Gaussian distribution on temperature, .
The free-energy (i.e., the bound) above comprises two terms. The first is the energy expected under the ensemble density. This energy is simply the surprise or information about the joint occurrence of the sensory input and its causes. The second term is the negative entropy of the ensemble density. Notice that action can be considered causes of sensory input that are not covered by the ensemble density. In what follows, we look at the ensemble density and its role in adaptive behaviour.
The ensemble and generative densities
The free-energy formulation in Eq.3 has a fundamental implication: systems that minimise the surprise of their interactions with the environment by adaptive sampling can only do so by optimising a bound, which is a function of the system’s states. Formulating that bound in terms of Jensen’s inequality requires that function to be a probability density, which links the system’s states to the hidden causes of its sensory input. In other words, the system is compelled to represent the causes of its sensorium. This means adaptive systems, at some level, represent the state and causal architecture of the environment in which they are immersed. Conversely, this means that causal regularities in the environment are transcribed into the system’s configuration.
Note that the free-energy is defined by two densities; the ensemble density and the generative density, , from which one could generate sensory samples and their causes. The generative density factorises into a likelihood and prior density, , which specify a generative model. This means the free-energy formulation induces a generative model for any system and an ensemble density over the causes or parameters of that model. The functional form of these densities is needed to evaluate the free-energy. We will consider functional forms that may be employed by the brain in the next section. At the moment, we will just note that these forms enable the free-energy to be defined as a function, of the system’s sensory input and internal state. Figure 2 shows a schematic of the quantities introduced so far; and how they relate to each other.
The free-energy principle
The free-energy principle states that all the quantities that can change; i.e., that are part of the system, will change to minimise free-energy. These quantities are the internal parameters λ and the action parameters, α. This principle, as we will see below, is sufficient to account for adaptive exchange with the environment by ensuring a bound on adaptive value is optimised. We now consider the implications of minimising the free-energy with respect to λ and α respectively.
Perception: Optimising λ
Clearly, if action is to minimise surprise, the free-energy bound should be reasonably tight. A tight bound is assured when the free-energy is minimised with respect to internal parameters. In this case, it is fairly easy to show that the ensemble density approximates the conditional density of the environmental causes, given the sensory samples. This can be seen by rearranging Eq.3 to show the dependence of the free-energy on λ.
| 4 |
Only the second term is a function of λ ; this is a Kullback-Leibler cross-entropy or divergence that measures the difference between the ensemble density and the conditional density of the causes. Because this measure is always positive, minimising the free-energy corresponds to making the ensemble density the same as the conditional density; at which point the free-energy becomes the surprise; . This is quite a fundamental result that underlies free-energy optimisation schemes in statistical physics and machine learning and rests on the fact that the divergence cannot be less than zero (in the sense that a distance cannot be negative). This means that if one has minimised the free energy, one has implicitly minimised surprise, because the second term in Eq.4 will be zero.
Put simply, when the free-energy minimised, the ensemble density encoded by the system’s parameters becomes an approximation to the posterior probability of the causes of its sensory input. This means the system implicitly infers the causes of its sensory samples. Clearly, this approximation depends upon the physical structure of the system and the implicit form of the ensemble density; and how closely this matches the causal structure of the environment. Those systems that can match their internal structure to the causal structure of the environment will attain a tighter bound (see below).
Action: Optimising α
Changing the system to move or re-sample the environment by minimising the free-energy with respect to action enforces a sampling of the environment that is consistent with the ensemble density. This can be seen with a second rearrangement of Eq.3 that shows how the free-energy depends upon α.
| 5 |
In this instance, only the first term is a function of action. Minimising this term corresponds to maximising the log-probability of sensory input, expected under the ensemble density. In other words, the system will sample sensory inputs that are the most likely under the ensemble density. However, as we have just seen, the ensemble density approximates the conditional distribution of the causes given sensory inputs. This inherent circularity obliges the system to fulfil its own expectations. In other words, the system will expose itself selectively to causes in the environment that it expects to encounter. However, these expectations are limited to the repertoire of physical states the system can occupy, which specify the ensemble density. Therefore, systems with a low free-energy can only sample parts of the environment they can encode with their repertoire of physical states. Because the free-energy is low, the inferred causes approximate the real causes. This means the system’s physical state must be (in general) sustainable under these causes, because each system is its own existence proof (where a system can be any unit of section; i.e., a phenotype or a species). In short, low free-energy systems will look like they are responding adaptively to changes in the external or internal milieu, to maintain a homeostatic exchange with the environment.
This paper is concerned largely with perceptual inference and learning in neural systems. However, there are many intriguing issues that arise when we consider that the free-energy principle is served by sampling from the environment selectively to maximise the predictability of sensory input. This sort of behaviour is found in many biological systems, ranging from the chemotactic movement of single-cell organisms to the phototropic behaviour of plants. In nervous systems there are numerous examples of sensory homeostasis, ranging from simple reflexes that reverse proprioceptive perturbations, to smooth pursuit eye movements responsible for stabilisation of the retinal image. Heuristically, these mechanisms can be viewed as suppressing free-energy by re-sampling the environment to minimise the prediction error incurred by a mismatch between what is sampled and the prediction afforded by perceptual inference. This suggests that motor and sensory systems in the brain should be in intimate anatomic relation. This is the case at spinal, subcortical and cortical levels. For example, the primary motor and sensory cortex are juxtaposed along the central sulcus and are strongly interconnected (Huffmann & Krubitzer 2001). Similarly, at a subcortical level, the superior collicullus represents a point of convergence for sensory information (through direct projections from the retina) and visual predictions (from visual, parietal and frontal cortex to the intermediate and deep layers). Neuronal discharges in the deep layers, that initiate saccades, define motor-fields that coincide with visual receptive fields in the superficial layers (Andersen et al 1989).
In summary, the free-energy principle can be motivated, quite simply, by noting that systems that minimise their free-energy respond to environmental changes adaptively. It follows that minimisation of free-energy may be a necessary, if not sufficient, characteristic of evolutionary successful systems. The attributes that ensure biological systems minimise their free-energy can be ascribed to selective pressure, operating at somatic (i.e., the life time of the organism) or evolutionary timescales (Edelman, 1993). These attributes include the functional form of the densities entailed by the system’s architecture. Systems which fail to minimise free-energy will have sub-optimal representations or ineffective mechanisms for action and perception. These systems will not restrict themselves to specific domains of their milieu and may ultimately experience a phase-transition (e.g., death). Note that in this formulation, adaptive action depends on perception; perception per se is only necessary to ensure a tight bound on the value-function minimised by action. Before returning to selective mechanisms, we will unpack the quantities describing the system and relate their dynamics to processes in neuroscience.
The mean-field approximation
Clearly, the quantities describing hidden causes in the environment could be enormous in number and variety. A key difference among them is the timescales over which they change. We will use this distinction to partition causes into three sets that change on a timescale of milliseconds, seconds and minutes, and factorise the ensemble density in terms of marginal densities
| 6 |
This induces a partitioning of the system’s parameters into λ = λu,λγ,λθ that encode time-varying marginals of the ensemble density. The first, λu, are system quantities that change rapidly. These could correspond to neuronal activity or electromagnetic states of the brain that change with a timescale of milliseconds. The causes they encode correspond to evolving environmental states, for example, changes in the environment caused by structural instabilities or other organisms. The second partition λγ changes more slowly, over seconds. These could correspond to the kinetics of molecular signalling in neurons; for example calcium-dependent mechanisms underlying short-term changes in synaptic efficacy and classical neuromodulatory effects. The equivalent partition of causes in the environment may be contextual in nature, such as the level of radiant illumination or slowly varying fields that set the context for more rapid fluctuations in its state. Finally, λθ represent system quantities that change slowly; for example long-term changes in synaptic connections during experience-dependent plasticity, or the deployment of axons that change on a neurodevelopmental timescale. The corresponding environmental quantities are (relatively) invariant aspects of its causal architecture. These could correspond to physical laws and other structural regularities that shape our interactions with the world.
In statistical physics, the factorization in Eq.6 is known as a mean-field approximation.7 Clearly, our approximation with these marginal densities is a little arbitrary, but it helps organise the functional correlates of their respective optimisation in the nervous system. More precisely, we are assuming that the brain uses the same mean-field approximation used above because it has evolved to exploit the ensuing computational efficiency; the mean-field approximation greatly finesses the minimisation of free-energy when considering particular mechanisms. These schemes usually employ variational techniques8.
Optimising variational modes
We now revisit optimisation of system parameters that underlie perception in more detail, using the mean-field approximation. Because variational techniques predominate in this approximation, the free-energy in Eq.3 is also known as the variational free-energy and λi are called variational parameters. The mean-field factorisation means that the approximation cannot cover the effect of random fluctuations in one partition, on the fluctuations in another. However, this is not a severe limitation because these effects are modelled through mean-field effects (i.e., through the means of random fluctuations). This approximation is particularly easy to motivate in the present framework, because random fluctuations at fast timescales are unlikely to have a direct effect at slower timescales and their influence can be sensibly approximated with their average.
Using variational calculus it is simple to show (see Appendix 1) that, under the mean-field approximation above, the marginal ensemble densities have the following form
| 7 |
where is simply the log-probability of the input and its causes , expected under the ensemble density of the other partitions, q\i. We will call this the variational energy. From Eq.7 it is evident that the mode (highest point) of the ensemble density maximises the variational energy. The mode is an important variational parameter. For example, if we assume is Gaussian, then it is parameterised by two variational parameters λi = μi,Σi encoding the mode or expectation and covariance respectively. This is known as the Laplace approximation and will be used later. In what follows, we will focus on minimising the free-energy by optimizing μi; noting that there may be other variational parameters describing higher moments. Fortunately, under the Laplace approximation, the only other variational parameter required is the covariance. This has a simple form, which is an analytic function of the mode and does not need to be represented explicitly (see Friston et al 2006 and Appendix 2). We now look at the optimisation of the variational modes μi and the neurobiological and cognitive processes this optimisation entails:
Perceptual inference: Optimising μu
Minimising the free-energy with respect to neuronal states μu means maximising
| 8 |
The free-energy principle is served when the variational mode of the states (i.e., neuronal activity) changes to maximize the posterior probability of the causes. Eq.8 shows that this can be achieved, without knowing the true posterior, by maximising the expected log-likelihood and prior that specify a probabilistic generative model (second line). As mentioned above, this optimisation requires the functional form of the generative model. In the next section, we will look at hierarchical forms that are commensurate with the structure of the brain. For now, it is sufficient to note that the free-energy principle means that brain states will come to encode the most likely causes in the environment generating sensory input.
Generalised coordinates
Because states are time-varying quantities, it is important to think about what their ensemble density encodes. This includes not just the states at one moment in time but their high-order motion. In other words, a particular state of the environment and its probabilistic encoding can embody dynamics by representing the paths or trajectories of states in generalised coordinates. Generalised coordinates are a common device in physics and normally cover position and momentum.9 In the present context, a generalised state includes the current state, and its generalised motion (i.e., the state and its first, second, etc. derivatives with time), with corresponding variational modes . It is fairly simple to show (Friston, 2007) that the optimisation in Eq.8 can be achieved with a rapid gradient descent, while coupling high to low-order motion via mean-field terms
| 9 |
Here μ&u mean the rate of change of μu and κ is some suitable rate constant. The simulations in the next section use this descent scheme, which can be implemented using relatively simple neural networks. Note, when the conditional mode has found the maximum of , its gradient is zero and the motion of the mode becomes the mode of the motion; i.e., . However, it is perfectly possible, in generalised coordinates, for these quantities to differ. At the level of perception, psychophysical phenomena suggest that we use generalised coordinates, at least perceptually: for example, on stopping, after looking at scenery from a moving train, the world is perceived as moving but does not change its position. The impression that visual objects change their position in accord with their motion is something that we have learned about the world. It is also something that can be unlearned, temporarily (e.g., perceptual after-effects). We now turn to how these causal regularities are learned.
Perceptual context and attention: Optimising μγ
If we call the causes that change on an intermediate timescale, contextual, then optimizing μγ corresponds to encoding the probabilistic contingencies in which the fast dynamics of states evolve. This optimization can proceed as above; however, we can assume that the context changes sufficiently slowly that we can make the approximation, . Because, these variational parameters change more slowly than the neuronal states, the free-energy may change substantially. This means the variational parameters optimise the sum of free-energy over time10. This gives the simple gradient ascent
| 10 |
We will see later that the conditional mode μγ encoding context might correspond to the strength of lateral interactions among neurons in the brain. These lateral interactions control the relative effects of top-down and bottom-up influences on perceptual inference. This suggests that attention could be thought of in terms of optimizing contextual parameters of this sort. It is important to note that, in Eq.10, the dynamics of μγ are determined by the expectation under the ensemble density of the perceptual states. This means that it is possible for the system to adjust its internal representation of probabilistic contingencies in a way that is sensitive to the states and their history. A simple example of this, in psychology, would be the Posner paradigm, where a perceptual state, namely an orienting cue, directs visual attention to a particular part of visual space in which a target cue will be presented. In terms of the current formulation, this would correspond to a state-dependent change in the variational parameters encoding context that bias perceptual inference towards a cued part of the sensorium.
The key point here is that the mean-field approximation allows for inferences about rapidly changing perceptual states and more slowly changing context to influence each other through mean-field effects (i.e.,. the expectations in Eq.8 and Eq.10). This can proceed without representing the joint distribution in an ensemble density over state and context explicitly (c.f., Rao 2005). Another important interaction between variational parameters relates to the encoding of uncertainty. Under the Laplace assumption, this is encoded by the conditional covariances. Critically the conditional covariance of one ensemble is a function of the conditional mode of the others (see Eq.A5 in Appendix 2). In the present context, the influence of context on perceptual inference can be cast in terms of encoding uncertainty. We will look at neuronal implementations of this in the next section.
Perceptual learning: Optimising μθ
Optimizing the variational mode encoding corresponds to inferring and learning structural regularities in the environment’s causal architecture. As above, this learning can be implemented as a gradient ascent on the time integral of , which represents an expectation under the ensemble density encoding the generalised states and context.
| 11 |
In the brain, this descent can be formulated as changes in connections that are a function of pre-synaptic prediction and post-synaptic prediction error (see Friston 2003; 2005 and the next section). The ensuing learning rule conforms to simple associative plasticity or, in dynamic models, spike-timing-dependent plasticity. In the sense that optimizing the variational parameters that correspond to connection strengths in the brain encodes causal structure in the environment, this instance of free-energy minimisation corresponds to learning. The implicit change in the brain’s connectivity endows it with a memory of past interactions with the environment that affects the free-energy dynamics underlying perception and attention. This is through the mean-field effects in Eq.8 and Eq.10. Put simply, sustained exposure to environmental inputs causes the internal structure of the brain to recapitulate the causal structure of those inputs. In turn, this enables efficient perceptual inference. This formulation provides a transparent account of perceptual learning and categorization, which enables the system to remember associations and contingencies among causal states and context.
Variational action and free-energy
The integrals over time, in Eq.10 and Eq.11, speak to a more general principle that entails the minimisation of action (c.f., Hamilton’s principle of stationary action). Action is the time-integral of energy
| 12 |
Strictly speaking, all variational parameters optimise action, which is a bound on the integral of the surprise or free-energy. For time-varying variational parameters, the principle of stationary action requires the variation δqi A of action with respect to to be zero. The Fundamental Lemma of variational calculus states that 11
| 13 |
This means that the variation of the free-energy with respect to should be zero at all times. This is simply the free-energy principle (see Appendix 1). In brief, we only need to invoke variational action if some of the marginal ensemble densities do not change with time; otherwise the free-energy principle is sufficient. The variational action can also be regarded as a bound on the path-integral of adaptive value as the system’s interaction with the environment evolves (i.e., summarises the value of sensory interactions harvested over a period of time). In what follows, one can think about variational action as a generalisation of the marginal likelihood, to cover dynamic models.
Model optimisation
Hitherto, we have considered only the quantitative optimisation of variational parameters given a particular system and its implicit generative model. Exactly the same free-energy (or stationary action) principle can be applied to optimise the model itself. Different models can come from populations of systems or from qualitative changes in one system over time. A model here corresponds to a particular architecture that can be enumerated with the same set of variational parameters. Removing a part of the system or adding, for example, a synaptic connection, changes the model and the variational parameters in a qualitative or categorical fashion.
Model optimisation involves maximising the marginal likelihood (or variational action) of the model itself. In statistics and machine learning this is equivalent to Bayesian model selection, where the free-energy is used to approximate the log evidence or marginal likelihood, for a particular model, mi. This approximation can be motivated easily using Eq.4: If the system has minimised its free-energy and the divergence term is near zero, then the free-energy approaches the negative log-evidence. Therefore, modes that maintain a low free-energy (i.e., a low variational action) are likely to have a high marginal likelihood.
An evolutionary perspective might consider the variational action in terms of adaptive fitness, which is defined for any system’s exchange with the environment and is independent of its internal state, λ. An adaptive system will keep this exchange within bounds that ensure its physical integrity. Systems that fail to suppress free-energy will encounter surprising interactions with the environment that may remove them from the population. Notice that the ensuing hierarchical selection rests upon interplay between optimising the parameters of each model and optimising an ensemble of models. Optimisation at both levels is prescribed by the free-energy principle. In the theory of genetic algorithms, similar schemes are referred to as hierarchical co-evolution (e.g., Maniadakis and Trahanias, 2006). A similar relationship is found in Bayesian inference, where model selection is based on the free-energy approximation to the model evidence that is furnished by optimising the parameters of each model. In short, free-energy may be a useful surrogate for adaptive fitness in an evolutionary setting and the log-evidence in model selection.
In short, within an organism’s lifetime its parameters minimise free-energy, given the model implicit in its phenotype. At a supraordinate level, the models themselves may be selected, enabling the population to explore model space and find optimal models. This exploration depends upon the heritability of key model components, which could be viewed as priors about environmental niches the system can model.
Summary
The above arguments suggest biological systems sample their environment to fulfil expectations that are generated by the model implicit in their structure. The free-energy principle explains adaptive behaviour without invoking notions of reinforcement or operant conditioning: From the point of view of the agent, it is simply sampling the environment so that its sensory input conforms to its expectations. From its perspective, the environment is an accommodating place; fluctuations or displacements caused by environmental forces are quickly explained away by adaptive re-sampling. Because action is not encoded by the ensemble density, these adaptive responses may not be perceived. However, for someone observing this system, it will appear to respond adaptively to environmental changes and avoid adverse conditions. In other words, it will seem as if certain stimulus-response links are selectively reinforced to ensure the homeostasis of its internal milieu, where this reinforcement emerges spontaneously in the larger context of action and perception under the free-energy principle.
The assertion that adaptive systems should minimise unlikely or surprising exchanges with the environment may seem implausible at first glance. For example, one of the most likely things to happen is death; and minimizing an organism’s avoidance of death doesn’t seem very adaptive. The key thing to note here is that surprise is conditioned on the organism; it is the surprise, given the system’s expectations embodied in its phenotype or current state. Clearly, if a phenotype expects to die and it conforms to a free-energy principle, it will die. The argument is that when natural selection operates on a population, such phenotypes will disappear, leaving those that expect to live (there may be exceptions to this, if death entails progeny; other interesting exceptions are phase-transitions in developmental trajectories; e.g., in metamorphic insects).
It might be thought that the relationship between value and surprise is ambiguous; in the sense that some valuable events are surprising, whereas value is the converse of surprise. Again, this is resolved by noting that surprise is conditional on the agent. Although, wining a lottery may be improbable it is not surprising, in the sense you expected to win on entering; imagine you won a lottery that you had not entered: you would immediately think there had been a mistake (which would be unexpected and of little value). In short, surprise is distinct from improbability because is depends on expectations under the model of the environment used to evaluate probability (i.e., ln p (y) ≠ ln p(y|m) ). In this sense, it is conceptually (if not mathematically) the same as ‘Bayesian surprise’, invoked to explain visual search and the deployment of attention (Itti and Baldi 2006). The definition of Bayesian surprise rests on the divergence between the prior and conditional densities elaborated during perceptual inference. This again emphasises the role of prior expectations in shaping surprise or value. The distinction between conditional surprise and improbability suggests that, a priori we expect to be (for example) rich, are chronically surprised that we are not but value monetary gains that transiently render our expectations valid.
A further counterintuitive aspect of minimising surprise is that it seems to preclude exploratory behaviour, novelty-seeking and risk-taking. However, this is not the case. Optimisation of free-energy may engage different mechanisms at different time-scales. Below, we will focus on dynamics and gradient descent that may be used in the brain. However, at an ethological level different schemes may operate; for example, stochastic explorations of the free-energy function (c.f., genetic algorithms). This would entail sampling the environment is a stochastic fashion to find samples with the least surprise. From an observers point of view this would appear like random or exploratory behaviour. From the agent’s point of view, everything is surprising, so it might as well sample desperately until something familiar is encountered. The trade-off between exploration and exploitation is a central theme in evolutionary theory, learning theory, microeconomics and optimization theory (e.g. March 1991) and can be applied easily to free-energy functions.
In this section, we have developed a free-energy principle for the evolution of an organism’s state and structure and have touched upon minimisation of free-energy at the population level, through hierarchical selection. Minimising free-energy corresponds to optimising the organism’s configuration, which parameterises an ensemble density on the causes of sensory input and optimising the model itself in somatic or evolutionary time. Factorization of the ensemble density to cover quantities that change on different timescales provides an ontology that maps nicely onto perceptual inference, attention and learning. In the next section, we consider how the brain might instantiate the free-energy principle with a special focus on the likelihood models implied by its structure.
GENERATIVE MODELS IN THE BRAIN
In this section, we will look at how the rather abstract principles of the previous section might be applied to the brain. We have already introduced the idea that a biological structure encodes a model of its environment. We now look at the form of these models implied by the structure of the brain and try to understand how evoked responses and associative plasticity emerge naturally with minimisation of free-energy. In the current formulation, attributes or quantities describing the brain parameterise an ensemble density of environmental causes. To evaluate the free-energy of this density we need to specify the functional form of the ensemble and generative densities. We will assume a Gaussian form for the ensemble densities (i.e., the Laplace approximation), which is parameterised by its mode or expectation and covariance. The generative density is specified by its likelihood and priors. Together these constitute a generative model. If this model is specified properly, we should be able to predict, using the free-energy principle, how the brain behaves in different contexts. In a series of previous papers (e.g., Friston and Price, 2001; Friston 2003; 2005) we have described the form of hierarchical generative models that might be employed by the brain. In this section, we will cover briefly the main points again.
Perception and sensation
This section is about trying to understand cortical responses in terms of perceptual inference and learning. The specific model considered here rests on empirical Bayes, using generative models that are embodied in cortical hierarchies. This model can be regarded as a mathematical formulation of the longstanding notion (Locke 1690) that “our minds should often change the idea of its sensation into that of its judgement, and make one serve only to excite the other”. In a similar vein, Helmholtz (1860) distinguished between perception and sensation. “It may often be rather hard to say how much from perceptions as derived from the sense of sight is due directly to sensation, and how much of them, on the other hand, is due to experience and training” (see Pollen 1999). In short, there is a distinction between percepts, which are the products of recognising the causes of sensory input, and sensation per se. Recognition, i.e., inferring causes from sensation, is the inverse of generating sensory data from their causes. It follows that recognition rests on models, learned through experience, of how sensations are caused. In this section, we will consider hierarchical generative models and how cortical responses can be understood as part of the recognition process. The particular recognition scheme we will focus on is empirical Bayes, where prior expectations are abstracted from the sensory input, using a hierarchical model of how those data were caused.
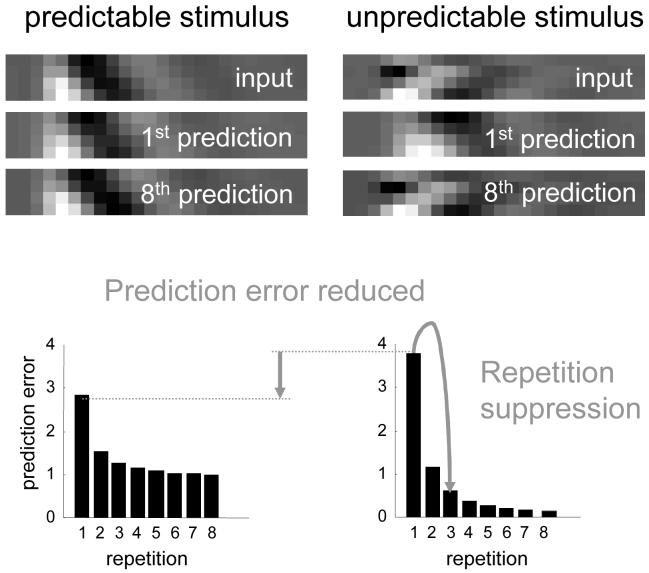
Conceptually, empirical Bayes and generative models are related to ‘analysis-by-synthesis’ (Neisser 1967). This approach to perception, from cognitive psychology, involves adapting an internal model of the world to match sensory input and was suggested by Mumford (1992) as a way of understanding hierarchical neuronal processing. The idea is reminiscent of Mackay’s epistemological automata (MacKay 1956) which perceive by comparing expected and actual sensory input (Rao 1999). These models emphasise the role of backward connections in mediating predictions of lower level input, based on the activity of higher cortical levels. Recognition is simply the process of solving an inverse problem, by jointly minimising prediction error (i.e., free energy) at all levels of the cortical hierarchy. This perspective explains many physiological and behavioural phenomena, e.g. extra-classical receptive field effects and repetition suppression in unit recordings, the mismatch negativity (MMN) and P300 in event-related potentials (ERPs), priming and global precedence effects in psychophysics. Critically, many of these emerge from the same basic principles governing inference with hierarchical generative models.
To finesse the inverse problem, posed by non-invertible generative models, constraints or priors are required. These resolve the ill-posed problems that confound recognition based on purely forward architectures. It has long been assumed that sensory units adapt to the statistical properties of the signals to which they are exposed (see Simoncelli and Olshausen 2001 for review). The Bayesian framework for perceptual inference has its origins in Helmholtz’s notion of perception as unconscious inference. Helmholtz realised that retinal images are ambiguous and that prior knowledge was required to account for perception (Kersten et al 2004). Kersten et al (2004) provide an excellent review of object perception as Bayesian inference and ask a fundamental question “Where do the priors come from? Without direct input, how does image-independent knowledge of the world get put into the visual system?” In the next subsection we answer this question and show how empirical Bayes allows most of the necessary priors to be learned and induced online, during inference.
Hierarchical dynamic models in the brain
A key architectural principle of the brain is its hierarchical organisation (Zeki and Shipp, 1988; Felleman and Van Essen, 1991; Mesulam, 1998; Hochstein and Ahissar, 2002). This organisation has been studied most thoroughly in the visual system, where cortical areas can be regarded as forming a hierarchy; with lower areas being closer to primary sensory input and higher areas adopting a multimodal or associational role. The notion of a hierarchy rests upon the distinction between forward and backward connections (Rockland and Pandya, 1979; Murphy and Sillito, 1987; Felleman and Van Essen, 1991; Sherman and Guillery, 1998; Angelucci et al, 2002a). The distinction between forward and backward connections is based on the specificity of cortical layers that are the predominant sources and origins of extrinsic connections in the brain. Forward connections arise largely in superficial pyramidal cells, in supra-granular layers and terminate in spiny stellate cells of layer four or the granular layer of a higher cortical area (Felleman and Van Essen, 1991; DeFelipe et al 2002). Conversely, backward connections arise largely from deep pyramidal cells in infra-granular layers and target cells in the infra and supra granular layers of lower cortical areas. Intrinsic connections are both intra and inter-laminar and mediate lateral interactions between neurons that are a few millimetres away. Due to convergence and divergence of extrinsic forward and backward connections, receptive fields in higher areas are generally larger than in lower areas (Zeki and Shipp, 1988). There is a key functional distinction between forward and backward connections that renders backward connections more modulatory or non-linear in their effects on neuronal responses (e.g., Sherman and Guillery, 1998). This is consistent with the deployment of voltage sensitive and non-linear NMDA receptors in the supra-granular layers (Rosier et al. 1993) that are targeted by backward connections. Typically, the synaptic dynamics of backward connections have slower time constants. This has led to the notion that forward connections are driving and illicit an obligatory response in higher levels, whereas backward connections have both driving and modulatory effects and operate over greater spatial and temporal scales.
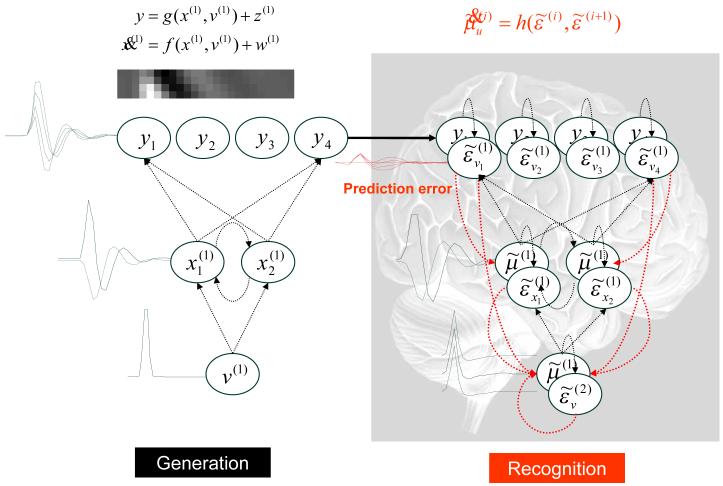
The hierarchical structure of the brain speaks to hierarchical models of sensory input. For example
| 14 |
In this model sensory states, y are caused by a non-linear function of internal states, g(x(1),v(1)) plus a random effect z(1). The dynamic states x(1) have memory and evolve according to equations of motion prescribed by the non-linear function f(x(1),v(1)). These dynamics are subject to random fluctuations w(1) and perturbations from higher levels that are generated in exactly the same way. In other words, the input to any level is the output of the level above. This means causal states v(i) link hierarchical levels and dynamic states x(i) are intrinsic to each level, linking states over time. The random fluctuations can be assumed to be Gaussian, with a covariance encoded by some hyper-parameters ,and independent across levels. The functions at each level are parameterised by . This form of hierarchical dynamical model is very generic and subsumes most models found in statistics and machine learning as special cases. These cases depend on the choice of the functions and assumptions about the form of the priors. For example, static models discount dynamic states x(i) and retain only the functions g(v(2)) (e.g., g(v(i)) = θ(i)v(i) for mixed effects models used in analysis of variance), where assumptions about the covariance of v(i) correspond to empirical priors on the causes.
This model specifies the functional form of the generative density in generalised coordinates of motion (see Appendix 3) and induces an ensemble density on the generalised states . If we assume neuronal activity is the variational mode of these states and the variational mode of the model parameters and corresponds to synaptic efficacy or connection strengths, we can write down the variational energy as a function of these modes using Eq.8; with
| 15 |
Here is a generalised prediction error for the states at the i-th level. The generalised predictions of the causal states and motion of the dynamic states are and respectively (see Appendix 3). Here, represents the generalised velocity of . are the precisions of the random fluctuations that control their amplitude and smoothness. For simplicity, we have omitted terms that depend on the conditional covariance of the parameters; this is the same approximation used by expectation maximisation (Dempster et al, 1977).
The dynamics and architecture of perceptual inference
As mentioned above, we will focus on the optimization of the ensemble density covering the states, implicit in perception or perceptual inference. From Eq.8 we obtain an expression that describes the dynamics of neuronal activity under the free-energy principle.
| 16 |
These dynamics describe how neuronal states self-organise when the brain is exposed to sensory input. The form of Eq.16 is quite revealing; it is principally a function of prediction error, namely the mismatch between the expected state of the world, at any level, and that predicted on the basis of the expected state in the level above. Critically, inference only requires the prediction error from the lower level and the higher level . This drives conditional expectations to provide a better prediction, conveyed by backward connections, to explain the prediction error away. This is the essence of the recurrent dynamics that self-organise to suppress free-energy or prediction error; i.e., recognition dynamics; .
Critically, the motion of the expected states is a linear function of the bottom-up prediction error. This is exactly what is observed physiologically, in the sense that bottom-up driving inputs elicit obligatory responses in higher levels that do not depend on other bottom-up inputs. In fact, the forward connections in Eq.16 have a simple form12
| 17 |
This comprises block diagonal repeats of the derivatives gx = ∂g/∂x (similarly for the other derivatives). D is a block matrix with identity matrices in its first diagonal that ensure the internal consistency of generalised motion. The connections are modulated by the precisions encoded by . The lateral interactions within each level have an even simpler form
| 18 |
and reduce to the precisions of the causes at that level. We will look at the biological substrate of these interactions below.
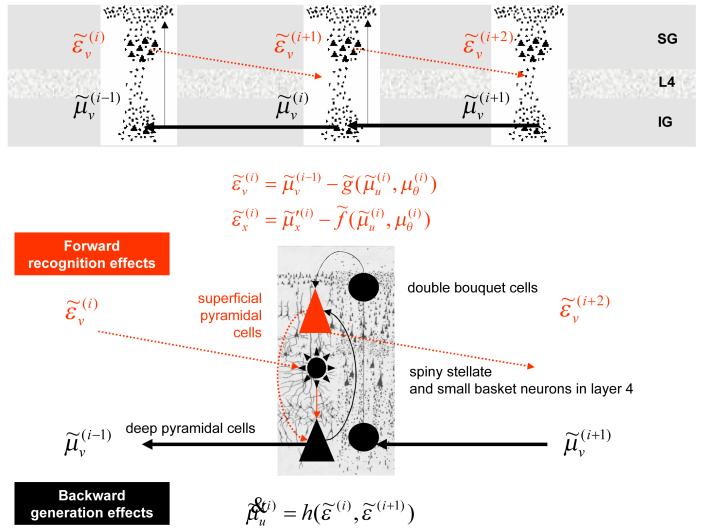
The form of Eq.16 allows us to ascribe the source of prediction error to superficial pyramidal cells, which means we can posit these as encoding prediction error. This is because the only quantity that is passed forward from one level in the hierarchy to the next is prediction error and superficial pyramidal cells are the major source of forward influences in the brain (Felleman & Van Essen 1991; Mumford 1992). Attributing this role to superficial pyramidal cells is useful because these cells are primarily responsible for the genesis of electroencephalographic (EEG) signals that can be measured non-invasively. The prediction error itself is formed by predictions conveyed by backward connections and dynamics intrinsic to the level in question. These influences embody the non-linearities implicit in and ; see Eq.17. Again, this is entirely consistent with the non-linear or modulatory role of backward connections that, in this context, model interactions among inferred states to predict lower level inferences. See Figure 3 for a schematic of the implicit neuronal architecture.
Figure 3.
Schematic detailing the neuronal architectures that encode an ensemble density on the states and parameters of hierarchical models. The upper panel shows the deployment of neurons within three cortical areas (or macro-columns). Within each area the cells are shown in relation to the laminar structure of the cortex that includes supra-granular (SG) granular (L4) and infra-granular (IG) layers The lower panel shows an enlargement of a particular area and the speculative cells of origin of forward driving connections that convey prediction error from a lower area to a higher area and the backward connections that carry predictions. These predictions try to explain away input from lower areas by suppressing the mismatch or prediction error. In this scheme, the source of forward connections is the superficial pyramidal cell population and the source of backward connections is the deep pyramidal cell population. The differential equations relate to the free-energy minimisation scheme detailed in the main text.
In short, the dynamics of the conditional modes are driven by three things. The first links generalised coordinates to ensure the motion of the mode approximates the mode of the motion. This ensures the representation of causal dynamics is internally consistent. The second is a bottom-up effect that depends upon prediction error from the level below. This can be thought of as a likelihood term. The third term, corresponding to an empirical prior, is mediated by prediction error at the current level. This is constructed using top-down predictions. An important aspect of hierarchical models is that they can construct their own empirical priors. In the statistics literature these models are known as parametric empirical Bayes models (Efron and Morris, 1973) and rely on the conditional independence of random fluctuation at each level (Kass and Steffey 1989).
In summary, the dynamics of perceptual inference at any level in the brain are moderated by top-down priors from the level above. This is recapitulated at all levels, enabling self-organisation through recurrent interactions to minimise free-energy by suppressing prediction error throughout the hierarchy. In this way, higher levels provide guidance to lower levels and ensure an internal consistency of the inferred causes of sensory input at multiple levels of description.
Perceptual attention and learning
The dynamics above describe the optimization of conditional or variational modes describing the most likely cause of sensory inputs. This is perceptual inference and corresponds to Bayesian inversion of the hierarchical generative model described in Eq.14. In this simplified scheme, in which conditional covariances have been ignored, minimising the free-energy is equivalent to suppressing hierarchical prediction error. Exactly the same treatment can be applied to changes in extrinsic and intrinsic connectivity encoding the conditional modes μγ and μθ.
As above, the changes in these modes or synaptic efficacies are relatively simple functions of prediction error and lead to forms that are recognisable as associative plasticity. Examples of these derivations, for static systems are provided in Friston (2005). The contextual variables are interesting because of their role in moderating perceptual inference. Eq.16 shows that the influence of prediction error from the level below and the current level is scaled by the precisions and that are functions of μγ. This means that the relative influence of the bottom-up likelihood term and top-down prior is controlled by modulatory influences encoded by μγ. This selective modulation of afferents is exactly the same as gain-control mechanisms that have been invoked for attention (e.g., Treue and Maunsell, 1996; Martinez-Trujillo and Treue, 2004). It is fairly simple to formulate neuronal architectures in which this gain is controlled by lateral interactions that are intrinsic to each cortical level (see Figure 3).
As noted in the previous section changes in μγ are supposed to occur at a timescale that is intermediate between the fast dynamics of the states and slow associative changes in extrinsic connections mediating the likelihood model. One could think of μγ as describing the short-term changes in synaptic efficacy, in lateral or intrinsic connections that depend upon classical neuromodulatory inputs and other slower synaptic dynamics (e.g., after-hyperpolarisation potentials, slow changes in synchronized oscillations and molecular signalling). The physiological aspects of these intermediate dynamics provide an interesting substrate for attentional mechanisms in the brain (see Schroeder et al, 2001 for review) and are not unrelated to the ideas in Yu and Dayan (2005). These authors posit a role for acetylcholine (an ascending modulatory neurotransmitter) mediating expected uncertainty. Neural modulatory neurotransmitters have, characteristically, much slower time constants, in terms of their synaptic effects, than glutamatergic neurotransmission that is employed by forward and backward extrinsic connections.
The Bayesian brain
The similarity between the form or structure of the brain and statistical models means that perceptual inference and learning lends itself nicely to a hierarchical treatment, which considers the brain as an empirical Bayesian device. The dynamics of neurons or populations are driven to minimise error at all levels of the cortical hierarchy and implicitly render themselves posterior or conditional modes (i.e. most likely values) of the causes given sensory inputs. In contradistinction to supervised learning, hierarchical prediction does not require any desired output. Unlike many information theoretic approaches they do not assume independent causes. In contrast to regularised inverse solutions (e.g. in machine vision) they do not depend on a priori constraints. These emerge spontaneously as empirical priors from higher levels.
The scheme implicit in Eq.16 sits comfortably with the hypothesis (Mumford, 1992) “on the role of the reciprocal, topographic pathways between two cortical areas, one often a ‘higher’ area dealing with more abstract information about the world, the other ‘lower’, dealing with more concrete data. The higher area attempts to fit its abstractions to the data it receives from lower areas by sending back to them from its deep pyramidal cells a template reconstruction best fitting the lower level view. The lower area attempts to reconcile the reconstruction of its view that it receives from higher areas with what it knows, sending back from its superficial pyramidal cells the features in its data which are not predicted by the higher area. The whole calculation is done with all areas working simultaneously, but with order imposed by synchronous activity in the various top-down, bottom-up loops”. We have tried to show that this sort of hierarchical prediction can be implemented in brain-like architectures using mechanisms that are biologically plausible. Furthermore, this sort of scheme arises from some basic principles concerning adaptive systems and free-energy.
Backward or feedback connections?
There is something slightly counterintuitive about generative models in the brain. In this view, cortical hierarchies are trying to generate sensory predictions from high-level causes. This means the causal structure of the world is embodied in the backward connections. Forward connections simply provide feedback by conveying prediction error to higher levels. In short, forward connections are the feedback connections. This is why we have been careful not to ascribe a functional label like ‘feedback’ to backward connections. Perceptual inference emerges from mutually informed top-down and bottom-up processes that enable sensation to constrain perception. This self-organising process is distributed throughout the hierarchy. Similar perspectives have emerged in cognitive neuroscience on the basis of psychophysical findings. For example, Reverse Hierarchy Theory distinguishes between early explicit perception and implicit low-level vision, where “our initial conscious percept - vision at a glance - matches a high-level, generalised, categorical scene interpretation, identifying “forest before trees” (Hochstein and Ahissar (2002).
Schemes based on generative models can be regarded as arising from the distinction between forward and inverse models adopted in machine vision (Ballard 1983; Kawato et al 1993). Forward models generate inputs from causes (c.f. generative models); whereas inverse models approximate the reverse transformation of inputs to causes (c.f. recognition models). This distinction embraces the non-invertability of generating processes and the ill-posed nature of inverse problems. As with all underdetermined inverse problems the role of constraints is central. In the inverse literature a priori constraints usually enter in terms of regularised solutions. For example: “Descriptions of physical properties of visible surfaces, such as their distance and the presence of edges, must be recovered from the primary image data. Computational vision aims to understand how such descriptions can be obtained from inherently ambiguous and noisy data” (Poggio et al 1985). The architectures that emerge from these schemes suggest that “Feedforward connections from the lower visual cortical area to the higher visual cortical area provide an approximated inverse model of the imaging process (optics)”. Conversely, “ the back-projection from the higher area to the lower area provides a forward model of the optics” (Kawato et al 1993). See also Harth et al (1987). This perspective highlights the importance of backward connections and the role of empirical priors during Bayesian inversion of generative models.
Summary
In conclusion, we have seen how a fairly generic hierarchical and dynamical model of environmental inputs can be transcribed onto neuronal quantities to specify the free-energy and its minimisation. This minimisation corresponds, under some simplifying assumptions, to a suppression of prediction error at all levels in a cortical hierarchy. This suppression rests upon a balance between bottom-up (likelihood) influences and top-down (prior) influences that are balanced by representations of uncertainty. In turn, these representations may be mediated by classical neural modulatory effects or slow post-synaptic cellular processes that are driven by overall levels of prediction error. Overall, this enables Bayesian inversion of a hierarchical model of sensory input that is context-sensitive and conforms to the free-energy principle. We will next illustrate the sorts of dynamics and behaviours one might expect to see in the brain, using a simple simulation.
Simulations
Generative and recognition models
Here, we describe a very simple simulation of a two-layer neuronal hierarchy to show the key features of its self-organised dynamics, when presented with a stimulus. The system is shown in Figure 4. On the left is the system used to generate sensory input and on the right is the neuronal architecture used to invert this generation; i.e., to recognise or disclose the underlying cause. The generative system used a single input (a Gaussian bump function) that excites a damped oscillatory transient in two reciprocally connected dynamic units. The output of these units is then passed through a linear mapping to four sensory channels. Note that the form of the neuronal or recognition model recapitulates the generative model: The only difference is that the causal states are driven by prediction errors which invoke the need for forward connections (depicted in red). The inferred causes, with conditional uncertainty (shown as 95% confidence intervals) concur reasonably with the real causes. The input pattern is shown as a function of time and in image format at the top of the figure. This can be thought of as either a changing visual stimulus, impinging on four photo-receptor channels or, perhaps, a formant over time-frequency in an acoustic setting.
Figure 4.
Diagram showing the generative model (left) and corresponding recognition; i.e., neuronal model (right) used in the simulations. Left panel: this is the generative model using a single cause v(1), two dynamic states and four outputs y1,K, y4. The lines denote the dependencies of the variables on each other, summarised by the equation on top (in this example both the equations were simple linear mappings). This is effectively a linear convolution model, mapping one cause to four outputs, which form the inputs to the recognition model (solid arrow). The architecture of the corresponding recognition model is shown on the right. This has a corresponding architecture, but here the prediction error units, , provide feedback. The combination of forward (red lines) and backward influences (black lines) enables recurrent dynamics that self-organise (according to the recognition equation; to suppress and hopefully eliminate prediction error, at which point the inferred causes and real causes should correspond.
This simulation can be regarded as reproducing sensory evoked transients and corresponds to Bayesian inversion of the generative model shown on the left hand side of the figure. In this context, because we used a dynamical generative model, the inversion corresponds to a deconvolution. If we allow the connection strengths in the recognition model to minimise free-energy, we are also implicitly estimating the parameters of the corresponding generative model. In machine learning and signal-processing this is known as blind deconvolution. Examples of this are shown in Figure 5. Here, we presented the same stimulus eight times and recorded the prediction error in the input or lowest level, summed over all peristimulus time. The initial values of the parameters were the same as in the generative model (those used in Figure 4). The upper panels show the stimulus and predicted input, in image format, for the first and last trial. It can be seen that both the first and eighth predictions are almost identical to the real input. This is because the connection strengths, i.e., conditional modes of the parameters (in the recognition model), started with the same values used by the generative model. Despite this, optimising the parameters enables the recognition model to encode this stimulus more efficiently, with a progressive suppression of prediction error with repeated exposure. This effect is much more marked if we use a stimulus that the recognition model has not seen before. We produced this stimulus by adding small random numbers to the parameters of the generative model. At the first presentation, the recognition model tries to perceive the input in terms of what it already knows and has experienced (c.f., an illusion); in this case, a prolonged version of the expected stimulus. This produces a large prediction error. By the eighth presentation, changes in the parameters enable it to recognise and predict the input almost exactly, with a profound suppression of prediction error with each repetition of the input.
Figure 5.
Results of repeated presentations to the simulated neural network shown in the previous figure. Left panels: the four channel sensory data used to evoke responses and the predictions from these evoked responses for the first and last of eight trials are shown on top, in image format. The corresponding prediction error (summed over the entire trial period after rectification) is shown below. As expected, there is a progressive reduction in prediction error as the system learns the most efficient causal architecture underlying the generation of sensory inputs. Right panels: exactly the same as above but now using an unpredictable or unfamiliar stimulus that was created using a slightly different generative model. Here, learning the causal architecture of this new stimulus occurs progressively over repeated presentations, leading to profound reduction in prediction error and repetition suppression.
Repetition suppression
This simple simulation shows a ubiquitous and generic aspect of free-energy minimisation schemes and indeed real brain responses; namely repetition suppression. This phenomenon describes the reduction or suppression in evoked responses on repeated presentation of stimuli. This can be seen in many contexts, ranging from the mismatch negativity in EEG research (Näätänen, 2003) to fMRI examples of face processing (see Henson et al, 2000 and Figure 6). In the next section we look more closely at this and related phenomena.
Figure 6.
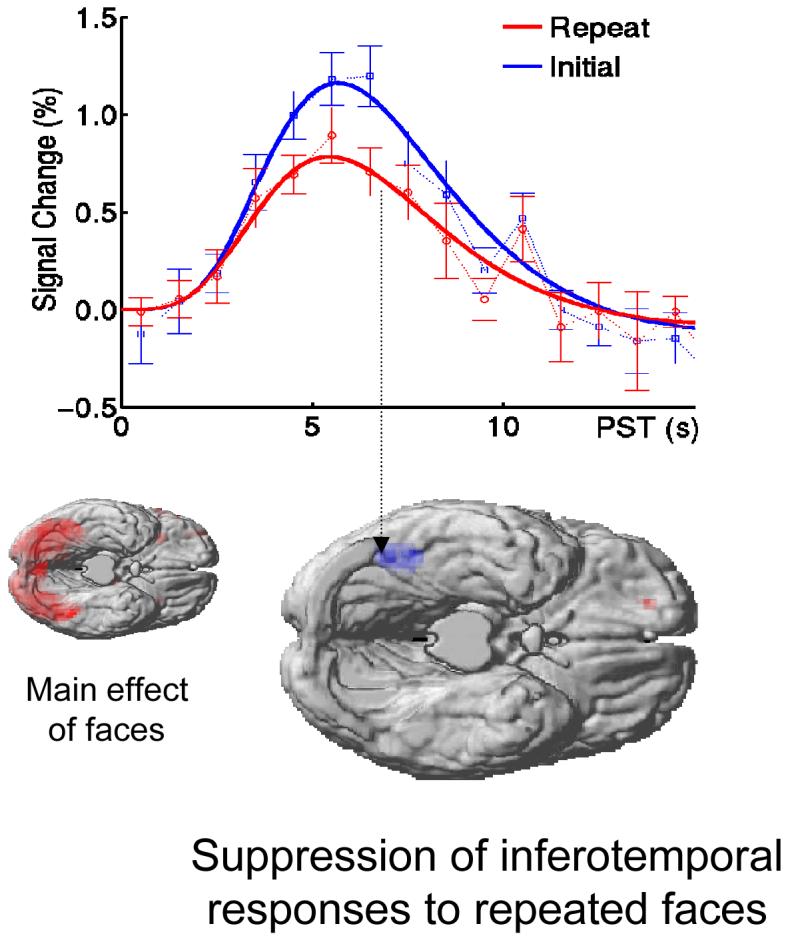
A summary of the results of an fMRI experiment reported in Henson et al (2000). The upper panel shows responses to visually presented faces for the first presentation (blue) and the second presentation (red). This is a nice example of repetition suppression as measured using fMRI. The inserts show voxels that were significantly activated by all faces (red) and those that showed significant repetition suppression in the fusiform cortex (blue).
SUPPRESSING FREE-ENERGY IN THE BRAIN
There are clearly a vast number of predictions and experiments that follow from the free-energy treatment of the previous sections. We have reviewed many of these elsewhere (e.g., Friston and Price, 2001; Friston, 2003; 2005). In this section, we review briefly some aspects of functional brain anatomy that relate to the theoretical treatment above. From the previous section, we can suggest that activity in a cortical hierarchy self-organises to minimise its free-energy through minimising prediction error. Is this sufficient to account for classical receptive fields and functional segregation seen in cortical hierarchies, such as the visual system?
Classical receptive fields
The answer is yes. We have shown previously that minimising free-energy is equivalent to maximising the mutual information between sensory inputs and neuronal activity encoding their underlying causes (Friston 2003). There have been many compelling developments in theoretical neurobiology that have used information theory (e.g. Barlow 1961, Optican and Richmond 1987, Linsker 1990, Oja 1989, Foldiak 1990). Many appeal to the principle of maximum information transfer (e.g. Linsker 1990, Atick and Redlich 1990, Bell and Sejnowski 1995). This principle has proven extremely powerful in predicting many of the basic receptive field properties of cells involved in early visual processing (e.g. Atick and Redlich 1990, Olshausen and Field 1996). This principle represents a formal statement of the common sense notion that neuronal dynamics in sensory systems should reflect, efficiently, what is going on in the environment (Barlow 1961).
Extra-classical receptive fields
Classical models (e.g. classical receptive fields) assume that evoked responses will be expressed invariably in the same units or neuronal populations, irrespective of context. However, real neuronal responses are not invariant but depend upon the context in which they are evoked. For example, visual cortical neurons have dynamic receptive fields that can change from moment to moment. A useful synthesis that highlights the anatomical substrates of context-dependent responses can be found in Angelucci et al (2002b). The key conclusion is that “feedback from extrastriate cortex (possibly together with overlap or inter-digitation of coactive lateral connectional fields within V1) can provide a large and stimulus-specific surround modulatory field. The stimulus specificity of the interactions between the centre and surround fields may be due to the orderly matching structure and different scales of intra-areal and feedback projection excitatory pathways.”
Extra-classical effects are commonplace and are generally understood in terms of the modulation of receptive field properties by backward and lateral afferents. There is clear evidence that horizontal connections in visual cortex are modulatory in nature (Hirsch and Gilbert 1991), speaking to an interaction between the functional segregation implicit in the columnar architecture of V1 and activity in remote populations. These observations suggest that lateral and backwards interactions may convey contextual information that shapes the responses of any neuron to its inputs (e.g. Phillips and Singer 1997) to confer the ability to make conditional inferences about sensory input.
The most detailed and compelling analysis of extra-classical effects, in the context of hierarchical models and predictive coding, is presented in Rao and Ballard (1999). These authors exposed a hierarchical network to natural images. The neurons developed simple-cell-like receptive fields. In addition, a subpopulation of error units showed a variety of extra-classical receptive field effects suggesting that “non-classical surround effects in the visual cortex may also result from cortico-cortical feedback as a consequence of the visual system using an efficient hierarchical strategy for encoding natural images.” One non-classical feature the authors focus on is end-stopping. Visual neurons that respond optimally to line segments of a particular length are abundant in supragranular layers and have the curious property of end-stopping or end-inhibition; vigorous responses to optimally oriented line segments are attenuated or eliminated when the line extends beyond the classical receptive field. The explanation for this effect is simple: because the hierarchy was trained on natural images, containing long line segments, the input caused by short segments could not be predicted and error responses could not be suppressed. This example makes a fundamental point: the selective response of these units does not mean they have learned to encode short line segments. Their responses reflect the fact that short line segments have not been encountered before and represent an unexpected visual input, given the context established by input beyond the classical receptive field. In short, their response signals a violation of statistical regularities that have been learned.
If these models are right, interruption of backward connections should disinhibit the response of supragranular error units that are normally suppressed by extra-classical stimuli. Rao and Ballard (1999) cite inactivation studies, of high-level visual cortex in anaesthetised monkeys, in which disinhibition of responses to surround stimuli is observed in lower areas (Hupe et al 1998). Furthermore, removal of feedback from V1 and V2 to the lateral geniculate nucleus (LGN) reduces the end-stopping of LGN cells (Murphy and Sillito 1987).
Long-latency evoked responses
In addition to explaining the form of classical receptive fields the temporal form of evoked transients is consistent with empirical (hierarchical) Bayes. This is summarised nicely by Lee and Mumford (2003); “Recent electrophysiological recordings from early visual neurons in awake behaving monkeys reveal that there are many levels of complexity in the information processing of the early visual cortex, as seen in the long latency responses of its neurons. These new findings suggest that activity in the early visual cortex is tightly coupled and highly interactive with the rest of the visual system.” Long-latency responses are used to motivate hierarchical Bayesian inference in which “the recurrent feedforward/feedback loops in the cortex serve to integrate top-down contextual priors and bottom-up observations so as to implement concurrent probabilistic inference.”
The prevalence of long-latency responses in unit recordings is mirrored in similar late components of event-related potentials (ERPs) recorded non-invasively. The cortical hierarchy in Figure 3 comprises a chain of coupled oscillators. The response of these systems, to sensory perturbation, usually conforms to a damped oscillation, emulating a succession of late components. Functionally, the activity of error units at any one level reflect states that have yet to be explained by higher-level representations and will wax and wane as higher-level causes are selected and refined. The ensuing transient provides a compelling model for the form of ERPs, which look very much like damped oscillation in the alpha range. In some instances specific components of ERPs can be identified with specific causes. For example the N170, a negative wave about 170ms after stimulus onset, is elicited by face stimuli, relative to non-face stimuli. In what follows, we focus on a few examples of late components. The emerging theme is that late components reflect inference about supraordinate or global causes at higher levels in the hierarchy.
Examples from neurophysiology
This example considers evidence for hierarchical processing in terms of single-cell responses, to visual stimuli, in the temporal cortex of behaving monkeys. If perceptual inference rests on a hierarchical generative model, then predictions that depend on the high-order attributes of a stimulus must be conferred by top-down influences. Consequently, one might expect to see the emergence of selectivity, for high-level attributes, after the initial visual response (although delays vary greatly, it typically takes about ten milliseconds for spikes to propagate from one cortical area to another). The late emergence of selectivity is seen in motion processing. A critical aspect of visual processing is the integration of local motion signals generated by moving objects. This process is complicated by the fact that local velocity measurements can differ depending on contour orientation and spatial position. Specifically, any local motion detector can measure only the component of motion perpendicular to a contour that extends beyond its field of view (Pack and Born 2001). This aperture problem is particularly relevant to direction-selective neurons early in the visual pathways, where small receptive fields permit only a limited view of a moving object. Pack and Born (2001) have shown “that neurons in the middle temporal visual area (known as MT or V5) of the macaque brain reveal a dynamic solution to the aperture problem. MT neurons initially respond primarily to the component of motion perpendicular to a contour’s orientation, but over a period of approximately 60 ms the responses gradually shift to encode the true stimulus direction, regardless of orientation”. It is interesting to note that extra-classical receptive field effects in supragranular V1 units are often manifest 80-100 milliseconds after stimulus onset, “suggesting that feedback from higher areas may be involved in mediating these effects” (Rao and Ballard 1999).
Examples from electrophysiology
In the discussion of extra-classical receptive field effects above we established that evoked responses, expressed 100ms or so after stimulus onset, could be understood in terms of a failure to suppress prediction error when the local information in the classical receptive field was incongruent with the global context, established by the surround. Exactly the same phenomena can be observed in ERPs evoked by the processing of compound stimuli that have local and global attributes (e.g. an ensemble of L shaped stimuli, arranged to form an H). For example, Han and He (2003) have shown that incongruence between global and local letters enlarged the posterior N2, a component of visually evoked responses occurring about 200ms after stimulus onset. This sort of result may be the electrophysiological correlate of the global precedence effect expressed behaviourally. The global precedence effect refers to a speeded behavioural response to a global attribute relative to local attributes and the slowing of local responses by incongruent global information (Han and He 2003).
Examples from neuroimaging
Although neuroimaging has a poor temporal resolution, the notion that V1 responses, evoked by compound stimuli, can be suppressed by congruent global information can be tested easily. Murray et al (2002) used functional MRI to measure responses in V1 and a higher object processing area, the lateral occipital complex, to visual elements that were either grouped into objects or arranged randomly. They “observed significant activity increases in the lateral occipital complex and concurrent reductions of activity in primary visual cortex when elements formed coherent shapes, suggesting that activity in early visual areas is reduced as a result of grouping processes performed in higher areas. These findings are consistent with predictive coding models of vision that postulate that inferences of high-level areas are subtracted from incoming sensory information in lower areas through cortical feedback.”
CONCLUSION
In this paper, we have considered the characteristics of biological systems, in relation to non-adaptive self-organizing and dissipative systems. Biological systems act on the environment and sample it selectively to avoid phase-transitions that will irreversibly alter their structure. This adaptive exchange can be formalised in terms of free-energy minimisation, in which both the behaviour of the organism and its internal configuration minimise its free-energy. This free-energy is a function of the ensemble density encoded by the organism’s configuration and the sensory data to which it is exposed. Minimisation of free-energy occurs through action-dependent changes in sensory input and the ensemble density implied by internal changes. Systems that fail to maintain a low free-energy will encounter surprising environmental conditions, in which the probability of finding them (i.e., surviving) is low. It may therefore be necessary, if not sufficient, for biological systems to minimise their free-energy.
The variational free-energy is not a thermodynamic free-energy but a free-energy formulated in terms of information theoretic quantities. The free-energy principle discussed here is not a consequence of thermodynamics but arises from population dynamics and selection. Put simply, systems with a low free-energy will be selected over systems with a higher free-energy. The free-energy rests on a specification of a generative model, entailed by the organism’s structure. Identifying this model enables one to predict how a system will change if it conforms to the free-energy principle. For the brain, a plausible model is a hierarchical dynamic system in which neural activity encodes the conditional modes of environmental states and its connectivity encodes the causal context in which these states evolve. Bayesian inversion of this model, to infer the causes of sensory input, is a natural consequence of minimising free-energy or, under simplifying assumptions, the suppression of prediction error.
The ideas presented in this paper have a long history, starting with the notions of neuronal energy described by Helmholtz (1860) and covering ideas like analysis by synthesis (Neisser, 1967) and more recent formulations like Bayesian inversion and predictive coding (e.g., Ballard et al, 1983; Mumford, 1992; Dayan et al, 1995; Rao & Ballard, 1998). The specific contribution of this paper is to provide a general formulation of the free-energy principle to cover both action and perception. Furthermore, this formulation can be used to connect constructs from machine learning and statistical physics with ideas from evolutionary theory theoretical neurobiology biology and microeconomics.
Acknowledgements
The Wellcome Trust funded this work. We would like to express our great thanks to Marcia Bennett for preparing this manuscript.
Appendix 1
Free-form variational density
This appendix derives the functional form of the ensemble density.
Lemma: The free-energy is maximised with respect to when
| A.1 |
where Zi is a normalisation constant (i.e., partition function). We will call the variational energy, noting its expectation under qi is the negative expected energy. , where denotes parameters not in the i-th set.
Proof: The Fundamental Lemma of variational calculus states that F is maximised with respect to qi when, and only when
| A.2 |
δqiF is the variation of the free-energy with respect to qi. From Eq.1
| A.3 |
We have lumped terms that do not depend on into ln Zi. The extremal condition is met when ∂qifi = 0, giving Eq.A.1.
Appendix 2
The conditional covariances
Under the Laplace approximation, the variational density assumes a Gaussian form qi = N(μi,Σi) with variational parameters μi and Σi, corresponding to the conditional mode and covariance of the i-th parameter set. The advantage of this approximation is that the conditional covariance can be evaluated very simply: Under the Laplace approximation the free-energy is
| A.4 |
pi is the number of parameters in the i-th set. The conditional covariances obtain as an analytic function of the modes by differentiating the free-energy and solving for zero
| A.5 |
This solution for the conditional covariances does not depend on the mean-field approximation but only on the Laplace approximation. See Friston et al (2006) for more details.
Appendix 3
Dynamic models
Here we consider the functional form of the generative density for hierarchical dynamic models of the sort described in the main text. To simplify things, we will deal with a single level and generalise to multiple levels later.
| A.6 |
The continuous nonlinear functions f(x,v) and g(x,v) of states are parameterised by . Stochastic fluctuations z(t) are assumed to be analytic such that the covariance of is well defined in generalised coordinates; similarly for random fluctuations in the states, . Under local linearity assumptions, the generalised motion is
| A.7 |
This induces a variational density on generalised causes that are necessary to generate . Here, and are predictions of the generalised response and velocity of the dynamic states , in the absence of random fluctuations. The equations on the right prescribe dynamics by coupling low and high-order motion of .
The likelihood and priors
Gaussian assumptions about the fluctuations furnish the functional form of the likelihood, , where is the precision (i.e., inverse covariance) of that controls its amplitude and smoothness. The priors are
| A.8 |
Gaussian assumptions about fluctuations in the dynamic states induce empirical priors on their generalised velocity, , where is the precision of . These impose dynamic constraints and confer memory on the states. We assume Gaussian priors on the parameters and hyperparameters13 and flat priors on the remaining states.
We now have now the functional form of the likelihood and priors of the generative model. This enables us to specify the variational energies that the modes have to optimise; from A.1
| A.9 |
Where is the generalised velocity of . So far we have assumed the priors are flat. However, we can impose a priori structure on these states using hierarchical models:
Hierarchical models
The hierarchical generalization of Eq.A.1, with y = v(0) is
| A.10 |
This induces empirical priors on the states and lends the generative density a Markov form (Kass and Steffey, 1989), through independence assumptions about the random fluctuations in different levels14.
| A.11 |
The prediction plays the role of a prior expectation on and its prior precision is estimated empirically as ; hence empirical Bayes (Efron and Morris, 1973). In short, a hierarchical form endows a model with the ability to construct its own priors. This feature is central to many inference and estimation procedures ranging from mixed-effects analyses in classical covariance component analysis to automatic relevance determination. See Friston et al (2006) for a fuller discussion of static models.
In hierarchical models, the variational energies are (omitting constants)
| A.12 |
The gradients of these quantise specify the dynamics of the variational parameters as described in the main text. Note that we have omitted terms pertaining to conditional uncertainty from the expressions for the states and parameters. This is the same approximation used in expectation maximisation and simplifies neuronal implementation considerably. In fact, Uγ = 0 when is linear in the hyperparameters, because (see Eq.A.4).
Footnotes
A functional is a function of a function.
Configurational entropy measures randomness in the distribution of matter in the same way that thermal entropy measures the distribution of energy.
The theory of dissipative structures was developed to understand structure formation in far-from-equilibrium systems. Examples include turbulence and convection in fluid dynamics (e.g., Bénard cells), percolation and reaction-diffusion systems such as the Belousov-Zhabotinsky reaction. Self-assembly is another important example from chemistry that has biological implications (e.g. for pre-biotic formation of proteins). Self-organization depends on a (reasonably) stationary environment that couples to the system to allow an appropriate exchange of entropy and energy.
Dropping the dependency on m for clarity.
<. >q means the expectation under the density q.
In statistical physics, an ‘ensemble’ denotes a fictitious collection of replicas of the system in question, each of which represents a possible state that the real system might be in.
The basic idea of a mean-field approximation is to approximate a very high dimensional probability distribution with the product of a number of simpler (marginal) densities. This is often used to cope with problems that are otherwise computationally or analytically intractable.
Variational techniques were introduced by Feynman (1972), in the context of quantum mechanics, using the path integral formulation. They have been adopted widely by the machine learning community (e.g., Hinton and von Camp, 1993; MacKay, 1995). Established statistical methods like expectation maximisation and restricted maximum likelihood (Dempster et al, 1977, Harville 1977) can be formulated in terms of free-energy (Neal and Hinton, 1998, Friston et al 2006).
Generalised coordinates include any non-standard (non-Cartesian) coordinate system applied to the analysis of a physical system. For example, a system of m particles in three dimensions may have up to 3m degrees of freedom, and therefore 3m generalised coordinates (one for each dimension of motion of each particle). A system of m rigid bodies in three dimensions may have up to 6m generalised coordinates (three axes of rotation and three axes of translation for each body).
In the simulations below, we use peristimulus time. The integral of energy over time is known as action, which means that, strictly speaking, it is variational action that is optimised (see below).
Here, and later we write ∂tA as a short form for the partial derivative ∂A/∂t ; similarly, δqA denotes the variation of A with respect to q(t).
⊗ is the Kronecker tensor product, and I denotes the identity matrix.
Noting that nonlinearities in and the functions in Eq.A.6 allow for any arbitrary transform to non-Gaussian priors.
We have omitted conditional dependence on the parameters and hyperparameters for clarity.
References
- Andersen RA. Visual and eye movement factions of the posterior parietal cortex. Annu. Rev. Neurosci. 1989;12:377–405. doi: 10.1146/annurev.ne.12.030189.002113. [DOI] [PubMed] [Google Scholar]
- Angelucci A, Levitt JB, Walton EJ, Hupe JM, Bullier J, Lund JS. Circuits for local and global signal integration in primary visual cortex. J Neurosci. 2002a;22:8633–46. doi: 10.1523/JNEUROSCI.22-19-08633.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelucci A, Levitt JB, Lund JS. Anatomical origins of the classical receptive field and modulatory surround field of single neurons in macaque visual cortical area V1. Prog. Brain Res. 2002b;136:373–88. doi: 10.1016/s0079-6123(02)36031-x. [DOI] [PubMed] [Google Scholar]
- Ashby WR. Principles of the self-organising dynamic system. J. Gen. Psychology. 1947;37:125–128. doi: 10.1080/00221309.1947.9918144. [DOI] [PubMed] [Google Scholar]
- Atick JJ, Redlich AN. Towards a theory of early visual processing. Neural Computation. 1990;2:308–320. [Google Scholar]
- Ballard DH, Hinton GE, Sejnowski TJ. Parallel visual computation. Nature. 1983;306:21–6. doi: 10.1038/306021a0. [DOI] [PubMed] [Google Scholar]
- Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith WA, editor. In sensory communication. MIT press; Cambridge MA: 1961. [Google Scholar]
- Bell AJ, Sejnowski TJ. An information maximisation approach to blind separation and blind de-convolution. Neural computation. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Borisyuk R, Hoppensteadt F. A theory of epineuronal memory. Neural Networks. 2004;17:1427–1436. doi: 10.1016/j.neunet.2004.07.006. [DOI] [PubMed] [Google Scholar]
- Crooks GE. Entropy production fluctuation theorem and the non-equilibrium work relation for free-energy differences. Phys. Rev. E. 1999;60:2721–26. doi: 10.1103/physreve.60.2721. [DOI] [PubMed] [Google Scholar]
- Dayan P, Hinton GE, Neal RM. The Helmholtz machine. Neural Computation. 1995;7:889–904. doi: 10.1162/neco.1995.7.5.889. [DOI] [PubMed] [Google Scholar]
- DeFelipe J, Alonso-Nanclares L, Arellano JI. Microstructure of the neocortex: comparative aspects. J Neurocytol. 2002;31:299–316. doi: 10.1023/a:1024130211265. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J. Roy. Stat. Soc. Series B. 1977;39:1–38. [Google Scholar]
- Edelman GM. Neural Darwinism: selection and reentrant signaling in higher brain function. Neuron. 1993;10:115–25. doi: 10.1016/0896-6273(93)90304-a. [DOI] [PubMed] [Google Scholar]
- Efron B, Morris C. Stein’s estimation rule and its competitors - an empirical Bayes approach. J. Am. Stats. Assoc. 1973;68:117–130. [Google Scholar]
- Evans DJ, Searles DJ. The fluctuation theorem. Advances in Physics. 2002;51:1529–1585. [Google Scholar]
- Evans DJ. A non-equilibrium free-energy theorem for deterministic systems. Molecular Physics. 2003;101:15551–1554. [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Feynman RP. Statistical mechanics. Benjamin; Reading MA, USA: 1972. [Google Scholar]
- Foldiak P. Forming sparse representations by local anti-Hebbian learning. Biol. Cybern. 1990;64:165–170. doi: 10.1007/BF02331346. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Price CJ. Dynamic representations and generative models of brain function. Brain Res Bull. 2001;54:275–85. doi: 10.1016/s0361-9230(00)00436-6. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Learning and inference in the brain. Neural Netw. 2003;16:1325–52. doi: 10.1016/j.neunet.2003.06.005. [DOI] [PubMed] [Google Scholar]
- Friston KJ. A theory of cortical responses. Philos Trans R Soc Lond B Biol Sci. 2005;360:815–36. doi: 10.1098/rstb.2005.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, et al. Variational Bayes and the Laplace approximation. NeuroImage. 2006;34:220–234. doi: 10.1016/j.neuroimage.2006.08.035. [DOI] [PubMed] [Google Scholar]
- Friston KJ, et al. DEM: A variational treatment of dynamic systems. 2007. in preparation. [DOI] [PubMed] [Google Scholar]
- Haken H. Synergistics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology. Third Edition Springer Verlag; 1983. [Google Scholar]
- Han S, He X. Modulation of neural activities by enhanced local selection in the processing of compound stimuli. Hum. Brain Mapp. 2003;19:273–281. doi: 10.1002/hbm.10121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harth E, Unnikrishnan KP, Pandya AS. The inversion of sensory processing by feedback pathways: a model of visual cognitive functions. Science. 1987;237:184–7. doi: 10.1126/science.3603015. [DOI] [PubMed] [Google Scholar]
- Harville DA. Maximum likelihood approaches to variance component estimation and to related problems. J. Am. Stat. Assoc. 1977;72:320–338. [Google Scholar]
- Helmholtz H. In: Handbuch der physiologischen optik. Southall JPC, editor. Vol. 3. Dover; New York: 1860/1962. English trans. [Google Scholar]
- Henson R, Shallice T, Dolan R. Neuroimaging evidence for dissociable forms of repetition priming. Science. 2000;287:1269–72. doi: 10.1126/science.287.5456.1269. [DOI] [PubMed] [Google Scholar]
- Hinton GE, von Cramp D. Keeping neural networks simple by minimising the description length of weights; Proceedings of COLT-93; 1993.pp. 5–13. [Google Scholar]
- Hirsch JA, Gilbert CD. Synaptic physiology of horizontal connections in the cat’s visual cortex. J. Neurosci. 1991;11:1800–1809. doi: 10.1523/JNEUROSCI.11-06-01800.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochstein S, Ahissar M. View from the top: Hierarchies and reverse hierarchies in the visual system. Neuron. 2002;36:791–804. doi: 10.1016/s0896-6273(02)01091-7. [DOI] [PubMed] [Google Scholar]
- Huffman KJ, Krubitzer L. Area 3a: topographic organization and cortical connections in marmoset monkeys. Cerebral Cortex. 2001;11:849–867. doi: 10.1093/cercor/11.9.849. [DOI] [PubMed] [Google Scholar]
- Hupe JM, James AC, Payne BR, Lomber SG, Girard P, Bullier J. Cortical feedback improves discrimination between figure and background by V1, V2 and V3 neurons. Nature. 1998;394:784–7. doi: 10.1038/29537. [DOI] [PubMed] [Google Scholar]
- Itti P, Baldi . Advances in Neural Information Processing Systems. Vol. 19. MIT Press; Cambridge, MA: 2006. Bayesian Surprise Attracts Human Attention; pp. 1–8. NIPS*2005. [Google Scholar]
- Jääskeläinen IP, Ahveninen J, Bonmassar G, Dale AM, Ilmoniemi RJ, Levänen S, Lin F-H, Kass RE, Steffey D. Approximate Bayesian inference in conditionally independent hierarchical models (parametric empirical Bayes models) J. Am. Stat. Assoc. 1989;407:717–726. [Google Scholar]
- Kauffman S. Self-organisation on selection in evolution. Oxford University Press; Oxford. UK: 1993. [Google Scholar]
- Kawato M, Hayakawa H, Inui T. A forward-inverse optics model of reciprocal connections between visual cortical areas. Network. 1993;4:415–422. [Google Scholar]
- Kersten D, Mamassian P, Yuille A. Object perception as Bayesian inference. Annu. Rev. Psychol. 2004;55:271–304. doi: 10.1146/annurev.psych.55.090902.142005. [DOI] [PubMed] [Google Scholar]
- Kloucek P. The computational modeling of nonequilibrium thermodynamics of the martensitic transformations. Computational Mechanics. 1998;23:239–254. [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Lee TS, Mumford D. Hierarchical Bayesian inference in the visual cortex. J. Opt. Soc. Am. Opt. Image Sc. Vis. 2003;20:1434–48. doi: 10.1364/josaa.20.001434. [DOI] [PubMed] [Google Scholar]
- Linsker R. Perceptual neural organisation: some approaches based on network models and information theory. Annu Rev Neurosci. 1990;13:257–81. doi: 10.1146/annurev.ne.13.030190.001353. [DOI] [PubMed] [Google Scholar]
- Locke J. An essay concerning human understanding. Dent; London: 1690/1976. [Google Scholar]
- MacKay DM. The epistemological problem for automata. In: Shannon CE, McCarthy J, editors. Automata Studies. Princeton University Press; Princeton, NJ: 1956. pp. 235–251. [Google Scholar]
- MacKay DJC. Free-energy minimisation algorithm for decoding and cryptoanalysis. Electronics Letters. 1995;31:445–447. [Google Scholar]
- Maniadakis M, Trahanias PE. Modelling brain emergent behaviours through coevolution of neural agents. Neural Networks. 2006;19(5):705–720. doi: 10.1016/j.neunet.2005.02.007. [DOI] [PubMed] [Google Scholar]
- March JG. Exploration and exploitation in organizational learning. Organization Science. 1991;10(1):299–316. [Google Scholar]
- Martinez-Trujillo JC, Treue S. Feature-based attention increases the selectivity of population responses in primate visual cortex. Curr. Biol. 2004;14:744–51. doi: 10.1016/j.cub.2004.04.028. [DOI] [PubMed] [Google Scholar]
- Mesulam MM. From sensation to cognition. Brain. 1998;121:1013–52. doi: 10.1093/brain/121.6.1013. [DOI] [PubMed] [Google Scholar]
- Morowitz HJ. Energy flow in biology. Academic Press; New York, USA: 1968. p. 68. [Google Scholar]
- Nicolis G, Prigogine I. Self-organisation in non-equilibrium systems. John Wiley; New York, USA: 1977. p. 24. [Google Scholar]
- Mumford D. On the computational architecture of the neocortex. II. The role of cortico-cortical loops. Biol. Cybern. 1992;66:241–51. doi: 10.1007/BF00198477. [DOI] [PubMed] [Google Scholar]
- Murphy PC, Sillito AM. Corticofugal feedback influences the generation of length tuning in the visual pathway. Nature. 1987;329:727–9. doi: 10.1038/329727a0. [DOI] [PubMed] [Google Scholar]
- Murray SO, Kersten D, Olshausen BA, Schrater P, Woods DL. Shape perception reduces activity in human primary visual cortex. Proc Natl Acad Sci USA. 2002;99:15164–9. doi: 10.1073/pnas.192579399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Näätänen R. Mismatch negativity: clinical research and possible applications. Int. J. Psychophysiology. 2003;48:179–188. doi: 10.1016/s0167-8760(03)00053-9. [DOI] [PubMed] [Google Scholar]
- Neal RM, Hinton GE. A view of the EM algorithm that justifies incremental sparse and other variants. In: Jordan MI, editor. Learning in Graphical Models. Kulver Academic Press; 1998. [Google Scholar]
- Neisser U. Cognitive psychology. Appleton-Century-Crofts; New York: 1967. [Google Scholar]
- Nicolis G, Prigogine I. Self-organisation in non-equilibrium systems. John Wiley; New York, USA: 1977. p. 24. [Google Scholar]
- Oja E. Neural networks, principal components, and subspaces. Int. J. Neural Systems. 1989;1:61–68. [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Optican L, Richmond BJ. Temporal encoding of two-dimensional patterns by single units in primate inferior cortex. II Information theoretic analysis. J Neurophysiol. 1987;57:132–146. doi: 10.1152/jn.1987.57.1.162. [DOI] [PubMed] [Google Scholar]
- Pack CC, Born RT. Temporal dynamics of a neural solution to the aperture problem in visual area MT of macaque brain. Nature. 2001;409:1040–2. doi: 10.1038/35059085. [DOI] [PubMed] [Google Scholar]
- Phillips WA, Singer W. In search of common foundations for cortical computation. Behavioural and Brain Sciences. 1997;20:57–83. doi: 10.1017/s0140525x9700160x. [DOI] [PubMed] [Google Scholar]
- Pollen DA. On the neural correlates of visual perception. Cerebral Cortex. 1999;9:4–19. doi: 10.1093/cercor/9.1.4. [DOI] [PubMed] [Google Scholar]
- Poggio T, Torre V, Koch C. Computational vision and regularisation theory. Nature. 1985;317:314–9. doi: 10.1038/317314a0. [DOI] [PubMed] [Google Scholar]
- Prince A, Smolensky P. Optimality: from neural networks to universal grammar. Science. 1997;275:1604–10. doi: 10.1126/science.275.5306.1604. [DOI] [PubMed] [Google Scholar]
- Rao RP, Ballard DH. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive field effects. Nature Neuroscience. 1998;2:79–87. doi: 10.1038/4580. [DOI] [PubMed] [Google Scholar]
- Rao RP. Bayesian inference and attentional modulation in the visual cortex. NeuroReport. 2005;16:1843–8. doi: 10.1097/01.wnr.0000183900.92901.fc. [DOI] [PubMed] [Google Scholar]
- Rockland KS, Pandya DN. Laminar origins and terminations of cortical connections of the occipital lobe in the rhesus monkey. Brain Res. 1979;179:3–20. doi: 10.1016/0006-8993(79)90485-2. [DOI] [PubMed] [Google Scholar]
- Rosier AM, Arckens L, Orban GA, Vandesande F. Laminar distribution of NMDA receptors in cat and monkey visual cortex visualized by [3H]-MK-801 binding. Journal of Comparative Neurology. 1993;335:369–380. doi: 10.1002/cne.903350307. [DOI] [PubMed] [Google Scholar]
- Sherman SM, Guillery RW. On the actions that one nerve cell can have on another: distinguishing “drivers” from “modulators”. Proc Natl Acad Sci USA. 1998;95:7121–6. doi: 10.1073/pnas.95.12.7121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder CE, Mehta AD, Foxe JJ. Determinants and mechanisms of attentional modulation of neural processing. Front Biosci. 2001;6:D672–84. doi: 10.2741/schroed. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu. Rev. Neurosci. 2001;24:1193–216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- Stephan KE, Kamper L, Bozkurt A, Burns GAPC, Young MP, Kötter R. Advanced database methodology for the Collation of Connectivity data on the Macaque brain (CoCoMac) Philosophical Transactions of the Royal Society London B: Biological Sciences. 2001;356:1159–1186. doi: 10.1098/rstb.2001.0908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streater RF. The free-energy theorem. In: Araki H, Ito KR, Kishimoto A, Ojima I, editors. Quantum and non-commutative analysis. Kluwer Press; 1993. pp. 137–147. [Google Scholar]
- Treue S, Maunsell HR. Attentional modulation of visual motion processing in cortical areas MT and MST. Nature. 1996;382:539–41. doi: 10.1038/382539a0. [DOI] [PubMed] [Google Scholar]
- Yu AJ, Dayan P. Uncertainty, neuromodulation and attention. Neuron. 2005;46:681–692. doi: 10.1016/j.neuron.2005.04.026. [DOI] [PubMed] [Google Scholar]
- Zeki S, Shipp S. The functional logic of cortical connections. Nature. 1988;335:311–317. doi: 10.1038/335311a0. [DOI] [PubMed] [Google Scholar]