The homology recognition well as an innate property of DNA structure

Abstract

Mutual recognition of homologous sequences of DNA before strand exchange is considered to be the most puzzling stage of recombination of genes. In 2001, a mechanism was suggested for a double-stranded DNA molecule to recognize from a distance its homologous match in electrolytic solution without unzipping [Kornyshev AA, Leikin S (2001) Phys Rev Lett 86:3666–3669]. Based on a theory of electrostatic interactions between helical molecules, the difference in the electrostatic interaction energy between homologous duplexes and between nonhomologous duplexes, called the recognition energy, was calculated. Here, we report a theoretical investigation of the form of the potential well that DNA molecules may feel sliding along each other. This well, the bottom of which is determined by the recognition energy, leads to trapping of the molecular tracks of the same homology in direct juxtaposition. A simple formula for the shape of the well is obtained. The well is quasi-exponential. Its half-width is determined by the helical coherence length, introduced first in the same 2001 article, the value of which, as the latest study shows, is ≈10 nm.

Decades of research into homologous recombination have unraveled many of the details concerning the transfer of information between 2 homologous sequences. By contrast, the processes by which the interacting molecules initially colocalize are largely unknown. How can 2 homologous needles find each other in the genomic haystack?

—Barzel and Kupiec (2008)

Recombination of genes is a process in which sequences are exchanged between 2 DNA molecules. In homologous recombination fragments of the same homology, those that have almost identical sequences are swapped. This makes possible gene shuffling between 2 parental copies of DNA, crucial for evolution and genetic diversity. A similar process is used in DNA repair, when the cell uses a backup copy of the genome as a template for repairs. It is generally accepted that understanding recombination of genes is one of the key challenges of the “postgenomic era” (1).

Homology Recognition Enigma

The key point in homologous recombination is the swapping of correct genes: only regions with homologous sequences should be exchanged or used as a template for repair. Recombination mistakes are known to cause a variety of severe genetic diseases (2, 3) and contribute to aging (4). Fortunately, such errors are rare. The recognition of sequence homology occurs with amazing precision. In site-specific recombination, the exchange happens at specific, designated loci recognized by the complex recombination machinery of the cell (involving multiple proteins). In homologous recombination the exchange can occur anywhere. It was established that at least 50- to 100-bp homology is required for it (see, e.g., refs. 5–7). This ensures that the fragments belong to 2 alleles of the same gene rather than to different genes. The long-range goal is an in-depth understanding of the recognition mechanism to be able to develop procedures that could further minimize these errors.

Textbooks describe that “we know only one mechanism for nucleic acids to recognize one another on the basis of sequence: complementarity between single strands” (3). The breakage of double-stranded DNA and formation of single strands mediated by specialized proteins (e.g., RecA family) is known to be the first step of homologous recombination (3). The single strand recognizes and invades a homologous double helix through hydrogen bond formation with bases, triggering further recombination events. However, such recognition achieves high efficiency only for 8–10 base fragments (8). If this were the only recognition mechanism, frequent mistakes would be inevitable.

So, might there be an initial, “snap-shot” recognition stage of recombination, at which long DNA tracks recognize each other as a whole? In their review article, Barzel and Kupiec (9), ask directly, whether homologous pairing is an innate general characteristic of the genome. Zickler in another review (10) focuses on the same point. In their articles one finds a list of publications in which this problem was addressed by biologists over an extensive time period. The quest began before the molecular understanding of genes [cf. McClintock (11), in which the author states that “there is a tendency for chromosomes to associate 2-by-2 in the prophase of meiosis”]. For example, Henikoff proposed the existence of some form of communication between homologous DNA sequences outside of the recombination process (12) and Keeney and Kleckner (13) hypothesized that “homology is sensed directly at the DNA level, guided by direct physical interactions between DNA duplexes in accessible regions … such as nucleosome-free regions.” Based on their experimental observations (14, 15), Kleckner and coworkers concluded that pairing of large, homologous chromosomes in the absence of known recombination proteins is an initial, coarse recognition step, followed by double-helix breakage and subsequent recombination steps.

The review (9) sums up the many attempts to uncover the enigma of homology recognition, but at the end of it the authors conclude: “After a long journey we are back at the starting position. The mechanism of homologous pairing has so far resisted our survey of possible explanations” (9). But this review referred exclusively to biological journals, missing some findings reported in physical literature. In 2001, an electrostatic mechanism of homology recognition of intact DNA duplexes without assistance of proteins was suggested (16). This mechanism resulted from a detailed theory of the interaction of biomolecules with helical charge patterns in solutions (17–20) which explained a number of observations of DNA aggregation and poly- and mesomorphism (21).

In ref. 16, the difference between the energy of electrostatic interaction of 2 DNAs with the same sequence text in parallel juxtaposition and that of the interaction of duplexes with unrelated (nonhomologous) sequences was calculated. This difference was termed the recognition energy. A formula was obtained for it, which revealed its dependence on the length, L, of the interacting duplexes (equal, in that derivation, to the juxtaposition length) and the interaxial separation, R, between the duplexes. The recognition energies decay exponentially with R and increases with L . It is ≥1 k_BT for sequences with >50–100 bp at a 1-nm surface-to-surface separation. This correlates with the above-mentioned observations of the low frequency of recombination events for sequences having this many or fewer base pairs (5–7).*

The values of the recognition energy, provided in ref. 16, were obtained for torsionally rigid DNA (22). Extensions of this theory (23, 24), which have included various effects of DNA elasticity, have led to somewhat smaller values, but did not change the effect qualitatively. For the simplicity of the analysis, we will consider below only rigid molecules, although we discuss in the end possible consequences of elastic effects.

The Physics of the Snap-Shot Electrostatic Recognition of Homology.

The mechanism of homology recognition (16) was further discussed in several articles (23, 24) (for a comprehensive summary, see ref. 25). However, for completeness of this article, we will briefly summarize it. Figs. 1 and 2, borrowed from the indicated references, and their captions explain the principle of recognition. Recent analysis extended the theory to other sequence-dependent distortions of DNA structure, such as tilt, roll, propeller twist, etc., and elastic properties of DNA (23, 24). Including these reduces the effective value of λ_c (27), which enhances the recognition. Current estimate of λ_c based on X-ray data from wet fibers or NMR data banks in solution is ≈100 Å (27).

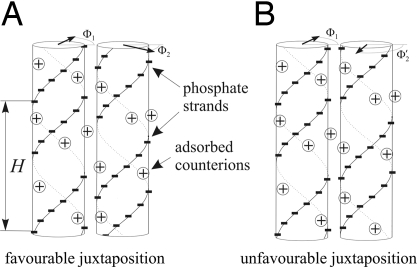
Fig. 1.

The principle of DNA mutual alignment (taken from the supplementary material of ref. 38). The azimuthal orientation of each molecule Φ_v is shown by a bold arrow in its top cross-section (drawn from the axis to the middle of the minor groove of the molecule). The alignment with strands of one molecule facing the grooves of the other one (A) leads to intermolecular attraction (or reduced repulsion) compared with relative orientations with strand-to-strand alignment (B). To realize the corresponding energy gain of favorable juxtaposition, the strands must stay in register with the grooves over the whole juxtaposition length. Sequence-dependent variations in the local helical pitch H will disrupt such register in juxtaposition of molecules with different sequences but not in juxtaposition of molecules with the same sequences as illustrated in Fig. 2.

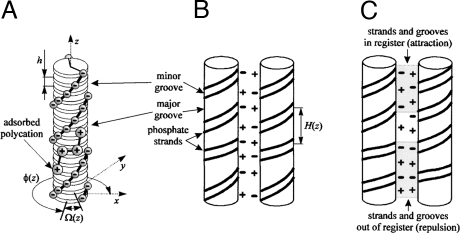
Fig. 2.

Accumulating mismatch (taken from ref. 16). (A) B-DNA sketched as a stack of base pairs (disks). Each base pair has two negatively charged phosphate groups. The base pair orientation at the altitude z is described by the azimuthal phase angle Φ(z) of the middle of the minor groove. Each combination of adjacent base pairs has a preferred twist angle Ω(z) = 〈Ω〉 = + ΔΩ(z), where 〈Ω〉 = 34–35° and $\sqrt{\langle \Delta {\Omega }^2\rangle }$ = 4–6° (22). For rigid molecules the phase angle accumulates according to the preferred twist angles between adjacent base pairs, i.e., Φ(z) = ∫₀^z Ω(z′)dz′. The deviations of the phase angle from ideal helicity accumulate along the z axis as a “random walk” over a characteristic length, called the helical coherence length λ_c = h/(ΔΩ)² [ΔΩ given in radians (16)], beyond which nonhomologous molecules cannot maintain favorable juxtaposition (B) The sequence-dependent twist modulation, Ω(z), leads to axial variation of the local helical pitch. As a result, only DNA with homologous sequences can have negatively charged strands facing positively charged grooves over a large juxtaposition length. (For visualization, the variation of H(z) is strongly exaggerated). (C) Molecules with unrelated sequences have uncorrelated twist modulations; this results in the loss of register between opposing strands and grooves, and a larger interaction energy. The loss of register takes place over the length λ_c, which determines the length of a sequence above which the double helices can sense the difference between the juxtaposition of homologous and nonhomologous tracks.

First Experiments on Double-Stranded DNA Homology Recognition.

Homology recognition between intact DNA duplexes in protein-free electrolytic solutions has been demonstrated by Baldwin et al. (28). In that work a mixture of 2 fluorescently tagged double-helical DNAs with identical nucleotide composition and length, but different sequences, was studied. These confocal microscopy experiments of fluorescently tagged DNA osmotically compressed into liquid crystalline domains (spherulites) revealed spontaneous segregation independent of the dyes. Polarizing microscopy images of the spherulites revealed patterns characteristic for cholesteric order. This has indicated that DNA duplexes in the spherulites are separated by >1 nm of water. Note that this homology segregation has been detected without the presence of any structure-altering ions in solutions, just NaCl as an electrolyte and a standard buffer. This result has been widely discussed (25, 29–33).

Inoue et al. (34) reported facilitated DNA aggregation of homologous DNA compared with that of mixtures of DNA with different sequences in aqueous electrolyte solutions with physiological concentrations of Mg²⁺. This had been detected by using electrophoretic measurements studying gel retardation of different DNA mixtures (35). Inoue et al. (34) interpreted their data in terms of a putative transient cross-hybridization between single-stranded bubbles and flipped-out bases. Despite some concerns^† and the authors' interpretation of the recognition mechanism, the results of ref. 30 may well have a similar origin to those of Baldwin et al. (28) and they may also be related to the effect predicted in ref 16.

The Subject of This Article.

The initial physical theory prescribed the existence of this recognition effect (16). But there is an unresolved question that theory should answer: What is the shape of the recognition potential well?

Previous theory (16) calculated the thermodynamic driving force for recognition as a function of the DNA–DNA interaxial separation, counterion adsorption, etc. Yet it did not specify the potential energy profile emerging when one DNA molecule in solution slides along the other, the likely process in the search for DNA homology before recombination. In other words, the theory had determined how deep the “recognition trap” was without reporting how wide it could be. Determining the shape of the well will help us to rationalize how mutual homology between molecules may be felt in a putative homology search process or in any future single-molecule “sliding” experiments.

The Shape of the Recognition Well

Homology Recognition Well for Sliding Genes.

By using the basic formulae of the theory (16) we calculate the energy profile for sliding of one long DNA molecule along another, as shown schematically in Fig. 3. The recognition well is determined by the difference between the energies of 2 homologous DNAs sliding along each other as compared with that of sliding 2 nonhomologous ones. Here, we treat the molecules as straight and rigid within the range over which we calculate their interaction. This approximation provides the deepest and, presumably, the sharpest recognition well, although we would expect that including the finite torsional flexibility of the molecules would only moderately reduce the recognition energy. The details of the derivation and the general form of the result are presented in Appendix B. In the main text we present the simplest form for the well and discuss its consequences.

Fig. 3.

A diagram of two long dsDNA sequences, denoted as molecules 1 and 2, interacting within a window of length L at interaxial separation R. Outside the juxtaposition window, the molecules' interactions are neglected (assuming that the molecules lie in close juxtaposition only over the length L). (A) Two homologous sections directly in front of each other. (B) Two homologous sections shifted by distance x. The point, d, corresponds to the location along the z axis where the relative difference of the phase angles, Φ₂(z) − Φ₁(z), between the molecules takes a value of δΦ (see Appendix B).

The geometry in question is sketched in Fig. 3. We calculate the energy over a juxtaposition length L. The sequences are shifted with respect to each other by a distance x. The total length of the molecules is considered to be much longer than the juxtaposition length and therefore “edge effects” may be neglected. As the transverse interactions between the molecules decay exponentially (17, 20), the juxtaposition window corresponds to the length over which opposite molecules may lie closely parallel to each other. L may be on the order of the DNA persistence length or larger if the genetic machinery of the cell, which may control the sliding of the molecules, provides longer juxtaposition. Because these details lie beyond our knowledge, we currently consider L as the parameter of the model.

The calculated energy of interaction between 2 such molecules shifted by distance x reads

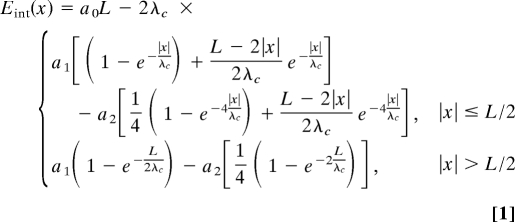where the coefficients a₀, a₁, and a₂ are Debye-screened decaying functions of interaxial separation R, depending on adsorption of counterions. The point x = 0 corresponds to the bottom of the well. Here, the homologous sections lie directly in front of each other, and

At |x| > L/2 the interaction energy reaches a plateau, E_int (L/2), given by the second row of Eq. 1. For this shift in x, the energies for homologous and nonhomologous pairs become equivalent.

The value of ΔE(L/2) ≡ E_int(L/2) − E_int(0) corresponds to the recognition energy calculated in ref. 16, slightly modified to allow for full rotation of the molecules about their long axes:

This quantity shows how much larger the interaction energy of 2 nonhomologous sections is compared with the interaction energy of homologous sections over this juxtaposition length.

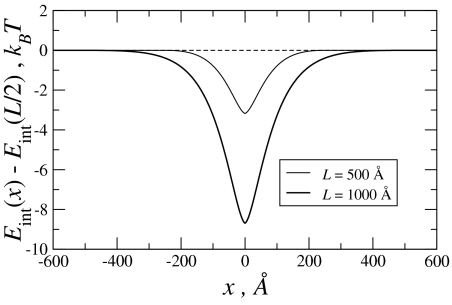
The graph of the difference in the interaction energies, δE_int(x) = E_int(x) − E_int(L/2), is shown in Fig. 4.

Fig. 4.

The recognition well for the indicated values of juxtaposition length and molecular homology length, L. The energy is given in the units of thermal energy at room temperature (0.025 eV). The parameters used in calculations are: a₁ = 3.75·10⁻⁴ eV/Å = 1.5·10⁻² k_{BT/Å, a2} = 0.875·10⁻⁴ eV/Å = 0.35·10⁻² k_{BT/Å (as in ref. 16) For λ[infi]c} we adopted an updated, shorter value [which effectively takes into a account not only twist angle, but also all other distortions of helicity and is essentially taken from experiments (27)]: λ_c ≈ 100 Å. λ_c constitutes approximately the half-width of the well.

Interaction of DNA Fragments.

One may also envision in vitro experiments in which the forces between finite-length DNA fragments, being either homologous or nonhomologous, are measured as one molecule is dragged along another at a close interaxial separation. For such experiments, the formulation outlined in the previous section needs modification.

Here, we contrast the work required to drag 2 homologous molecules of length L across each other with that required to drag 2 nonhomologous molecules along their juxtaposition. The main assumption here, different from that outlined in the previous section, is that sections of the molecules that do not overlap do not contribute to their interaction. Interactions thus only occur over an L − |x| juxtaposition length, i.e., from the left end of molecule 2 at z = x to the right end of molecule 1 at z = L (Fig. 5). For homologous fragments the phase-angle-independent a₀ term will now contribute a trivial x dependence through its proportionality to the juxtaposition length L − |x|. As a function of the molecules' lengths and the shift, x, between their ends, E_fin is given by

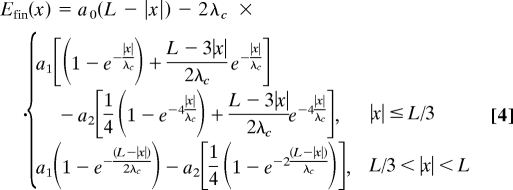For nonhomologous fragments the interaction energy is simply the lower equation of Eq. 4 for any value of the shift x. The same is true for homologous pairs with sequence texts aligned antiparallel.

Fig. 5.

A sketch of configuration for sliding DNA fragments of length L relative to each other; the fragments having the same homology. Juxtaposition length in this case is L–x, beyond which there is no interaction taken into account.

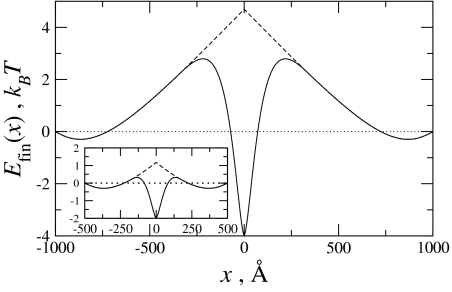
This equation for molecular fragments is similar to that for long sliding genes (Eq. 1), the primary difference being the range, |x| ≤ L/3 instead of |x| ≤ L/2, over which the energy for homologous pairs differs from that of nonhomologous pairs.^‡ However, there are also some other new features that Eq. 4 prescribes. Indeed, depending on the relative values of the electrostatic coefficients, a_n, the sliding forces could either oppose or facilitate full juxtaposition of the molecules. A plot comparing the interaction energies for homologous and nonhomologous molecules is given in Fig. 6. As shown, the interaction energy for homologous molecules is less repulsive/more attractive than their nonhomologous counterparts when the molecules approach full juxtaposition (x = 0). For the values of a_n, used in this plot, the interaction energy for homologous pairs at full juxtaposition provides a global minimum. For nonhomologous pairs, however, full juxtaposition of the molecules is disfavored. As also shown in Fig. 6, for both homologous and nonhomologous pairs there are local minima at the wings, when the overlap of the fragments is small. This is the case because for short segments on the order of the coherence length λ_c and for the chosen set of a_n values, the attractive a₁ term dominates the always-repulsive a₀ term.

Fig. 6.

The interaction energy between finite molecules of length L = 1,000 Å (Inset, L = 500 Å). Differences between nonhomologous (dashed line) and homologous (solid line) molecules appear when the shift between the pairs is L/3 from full juxtaposition (see text). Homology reduces the energetic barrier for the sliding finite molecules, and for the electrostatic coefficients used here [the same as those used in Fig. 4, with a₀ = 0.75·10⁻² k_BT/Å (16)], full juxtaposition of the homologous fragments is energetically favored.

Discussion

The shape of the recognition well for long molecules is different from the interaction of fragments of finite length. In the former case, shifting one molecule relative the other one, we get new sections of the molecules entering the juxtaposition window, the width of which is kept constant. In the latter case, increasing the shift between the molecules always decreases the juxtaposition length. This is why the interaction energy first grows and then decreases again as the juxtaposition length becomes smaller (Fig. 6, dashed curve). The reason for the secondary minima is less trivial, as discussed in Results.

Differentiating Eq. 1, we get the trapping force, F_int(x) = −d/dx E_int, i.e., the force acting against sliding one molecule along the other away from bottom of the well, F_int(x = 0) ≈ −(a₁ − 4a₂)L/λ_csgn(x), where sgn(x) = {_{−1, x < 0}^{+1, x > 0} is a sign function. The force thus jumps about the minimum of the well. The same is true for Eq. 4, but there are new terms in the force: F_int (x ≈ 0) ≈ {−L/λ_c·(a₁ − 4a₂) + a₀ − a₁ + a₂}sgn(x). This “nonanalytical” behavior is a minor artifact of the model. Calculations show that it disappears when one accounts for the natural width of the helical charged lines of the phosphate strands.^§ Taking into account DNA torsional elasticity (cf. 23, 24) is expected to further smoothen the whole potential well.

For a juxtaposition window of L = 10λ_c and the values of the electrostatic coefficients provided to generate the well for “sliding genes” in Fig. 4, an average attractive force of ≈−2 pN acts on the molecules near the center of the well, favoring full juxtaposition of the homologous molecules. And, as shown in Fig. 6 for molecular fragments with lengths L = 1,000 Å, the average force near the center of the well is ≈−1.5 pN (for homologous molecules, favoring full juxtaposition) as compared with ≈+0.3 pN (a repulsive force for nonhomologous molecules, disfavoring full juxtaposition). In both cases, for “sliding genes” and molecular fragments, these average forces near full juxtaposition scale roughly as L/λ_c, which is apparent on comparing the results for the 2 lengths shown in Figs. 4 and 6.

Conclusions

We have thus found that the homology recognition well has a quasi-exponential shape (Eq. 1, Fig. 4) and may provide a substantial trap for homologous genes to pair in front of each other, but it is not too deep for them to be trapped “forever” within the well.

The well has a half-width of helical coherence length (≈100 Å).

However, sliding of fully nonhomologous tracks will be smooth and almost friction-free. Two homologous tracks oriented in opposite directions will show the same behavior, which can be tested in single-molecule experiments.

The depth of the well itself has been studied before, and it decreases with the distance between DNA, whereas it increases with preferential accommodation of counterions in the major grove and reduced dielectric screening. The well depth also depends on the coherence length λ_c. The smaller λ_c is, the greater the difference in the interaction energies between that of homologous molecules and that of nonhomologous molecules, and the steeper is the well.

It was found, for example, that for crystallized DNA λ_c ≈ 1,000 Å as compared with λ_c ≈ 100 Å for DNA in wet fibers (27), which would most closely proximate DNA in living cells, or DNA in solutions. The longer λ_c is, the closer the DNA structure is to that of an ideal double helix. Thus, an order of magnitude enhancement of λ_c suggests that, in crystals of DNA, fragments tend to adjust torsionally to resemble ideal double helices (for the analysis of the effects of the structural adaptation in dense, hydrated DNA assemblies, see refs. 23 and 24). Note that DNA changes its conformation to “look structurally more ideal” in crystals where the interactions are very strong (at such short interaxial separations, Debye screening of Coulomb interactions is practically absent and dielectric screening may be strongly reduced). Hence, we may expect that in solutions, at relatively small interaction distances, DNA duplexes should at least notice their structural differences, whether this leads to some structural adaptation or not.

The torsional adjustments were excluded from the analysis here. We have essentially obtained the strongest effect possible. These adjustments could be incorporated at the cost of a more involved formalism that will result in nonlinear equations to be solved numerically. It is clear that, on taking account of these effects, the recognition well will be somewhat less deep and less steep.

The experiments on protein-free homology recognition, discussed in the introduction, were based on the study of spontaneous segregation of DNA of the same homology in aggregates, and as such they could not access the shape of the recognition well, although they have detected its existence. Performed deliberately in a “test tube” and in a pure electrolytic solution (28), they have demonstrated that recognition may be warranted by a physical phenomenon that may result solely from the underlying structure of DNA. Still, those experiments are only a first step. Not only should they be reproduced in different kinds of physical experiments in a test tube, but it must be also confirmed that this effect is used in cells, in which DNA interactions are complicated by the much more complex environments in the cell nuclei. Before the corresponding in vivo studies are performed, molecular biologists might not accept the conclusions from in vitro recognition experiments as a new “dogma.” But with greater confirmation of these effects in vitro, the stronger would be the impetus to perform the in vivo experiments.

We clearly understand a gap between the physical theory of the recognition well and biological reality. Indeed, the DNA environment is quite complex, where it is stored in chromatin structures (36). Approximately three quarters of eukaryotic DNA are tightly wrapped onto histones, cylindrical-like protein bodies, forming nucleosomes, further packed into larger structures. Juxtaposition of substantial DNA tracks for realization of the recognition model described above should thus require stripping DNA off histones and at least partial chromatin unfolding. Physical mechanisms that lie behind (i) temporary nucleosome unwrapping via fluctuations (which, e.g., provides DNA-binding proteins access to the ordinarily wrapped DNA portions without disrupting the nucleosomes as a whole), (ii) corkscrew sliding of histones along DNA, potentially exposing histone-free sections, and (iii) decoupling of nucleosomes for overall chromatin unfolding are currently at the center of attention of theory and experiments (37–40). We may speculate that these or similar processes might allow two chromatin complexes to partially unfold to provide a juxtaposition of long stretches of histone-free, “bare” DNA for mutual recognition [compare Kleckner's “nucleosome free regions” (13)], but how this exactly proceeds, we do not know.

Our investigation into the shape of the recognition well between stretched bare DNA molecules has been developed to rationalize the effect that possibly underpins the in vivo gene–gene recognition machinery at a stage that should follow the complicated dynamics or chromatin unwrapping. In addition, it provides a theoretical framework for designing new kinds of in vitro single molecule experiments in which homologous recognition might be probed.

Appendix A: Electrostatic Interaction Coefficients

We borrow these from ref. 20 in the same form as they were used in ref. 16:

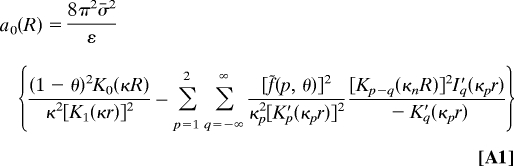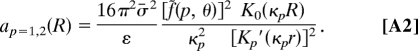The first term in a₀ is the interaction of the uniformly charged rods (41), whereas the sum of first two (p = 1, 2) helical harmonics describes the repulsion of the helical charge of one molecule with their image charges in the dielectric core of the other. Term a₁(R) is the first helical harmonic of direct charge–charge interactions.

Here, f˜(p, θ) = f₁θ + f₂(−1)^p θ − (1 − f₃θ)cos(pφ_s); I_p, K_p, I′_p, and K′_p are, respectively, the modified Bessel functions and their derivatives; r = (≈9–10 Å), the DNA radius; κ_D⁻¹, the Debye screening length in the bulk solution; ε, the solvent dielectric constant; κ_p = $\sqrt{{\kappa }^2+p^2{\left(2\pi /H\right)}^2}$, the effective reciprocal screening length of the pth DNA–DNA interaction harmonics; H, the average DNA pitch (see Fig. 2B); σ̄ = 16.8 μC/cm², the mean surface charge density of DNA phosphates; φ_s (≈ 0.4π for B-DNA), the azimuthal half-width of the B-DNA minor groove; θ, the fraction of DNA charge compensated by adsorbed cations; f_i are the fractions of counterions bound in the minor groove (f₁), in the major groove (f₂), on the phosphate strands (f₃); f₁ + f₂ + f₃ = 1.

The phosphate strands and the cations adsorbed in the grooves are considered in this approximation as infinitely thin charged spirals. One can account for a more realistic, thermally smeared, charge distribution that would slightly weaken the electrostatic interactions (20, 21). We assume that the adsorption of cations on DNA is irreversible and that no change in adsorption occurs with temperature, i.e., f and θ are T-independent (for adjustable patterns of adsorbed cations on DNAs see ref. 26). In this analysis, the value of macroscopic dielectric constant in solution between DNA is held constant, ε = 80. A more complicated picture of dielectric screening may strongly affect all of the three coefficients, but would likely only enhance the electrostatic interactions.

Appendix B: Derivation of the Formula For Interaction Energy

With a reference to Fig. 1, we adopt a slightly modified version of the formulation of ref. 16. for the evolution along the z axis of the phase difference between two rigid DNA molecules in parallel juxtaposition. The modification engenders assuming that the phase difference between the molecules at z = d is δΦ, i.e., Φ₂(d) − Φ₁(d) = δΦ (see Fig. 3):

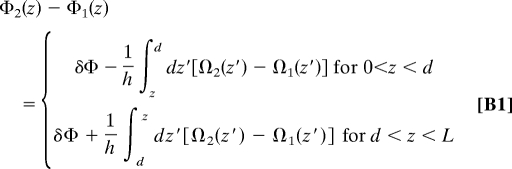where Ω_i(z) is the twist angle at an “altitude” z (see Fig. 2) of a molecule i (= 1, 2), and h ≈ 3.4 Å is the base pair step rise (distance between adjacent base pairs projected along the DNA axis). For homologous sequences, Ω₂(z′) = Ω₁(z′ − x) (see Fig. 3), and

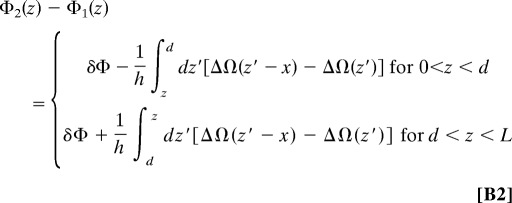where ΔΩ(z) = Ω₁(z) − 〈Ω〉 is the deviation of the twist angle from its mean value, 〈Ω〉 ≈ 34°. Eq. B2 and the following derivation of the interaction energy considers the case of long molecules with a juxtaposition over length L, but a similar derivation can be performed for the recognition of fragments by replacing L with the length over which the fragments overlap, L − |x|.

Following ref. 16, the interaction energy between the molecules within the juxtaposition length L is given by

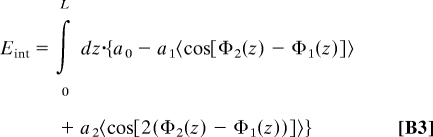where 〈⋯〉 means statistical average. We now substitute Eq. B2 into Eq. B3, and average over the long tracks of the twist angle deviations, which are assumed to obey Gaussian statistics (16, 21, 24)

where $\sqrt{\langle \Delta {\Omega }^2\rangle }$ ≈ 6° = 0.1 rad is the root-mean-square value of twist angle deviation from the average value. Carefully performing all double integrations and minimizing the resulting energy with respect to d to find the location along the molecules where their phase difference has the assumed value δΦ, we obtain

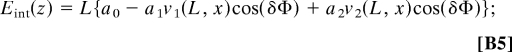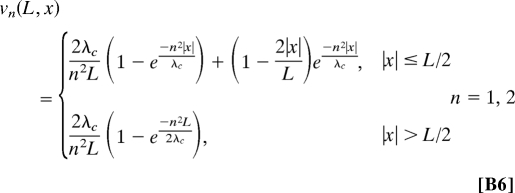where λ_c = h/〈ΔΩ²〉.

The optimal value of the phase difference δΦ may be obtained by minimizing the energy, Eq. B5, with respect to it. As long as a₁v₁(L, x) > 4a₂v₂(L, x), the minimum is given by δΦ = 0. When a₁v₁(L, x) < 4a₂v₂(L, x), δΦ = ±acos {a₁v₁ (L, x)/4a₂v₂(L, x)}. Since v₁(L, x) > v₂(L, x) for any values of the arguments, the former condition is warranted by a₁ > 4a₂, which is fulfilled unless the molecules are very close to each other (17). In principle, one may consider the other case, and the formulas given above are sufficient for this. But in this article, we limit the discussion to the case of δΦ = 0. Then Eqs. B5 and B6 give us Eq. 4 of the main text.