Analysis of the Stochastic Variation in LTQ Single Scan Mass Spectra

Abstract

A better understanding of the scan-to-scan signal intensity variation can lead to more sophisticated algorithms for database searching and de novo peptide sequencing using single scan mass spectra. In this study, we systematically studied the variation in relative intensity of m/z values in the single scan product ion mass spectra (MS²) derived from five representative precursor ions (MS¹) collected using an LTQ linear ion trap under constant flow direct infusion conditions with peptide concentrations held constant. We applied a matching algorithm based on a pair hidden Markov model to align the peaks from each scan belonging to the same m/z value prior to assessing the signal intensity variation. The most significant single contributor to scan-to-scan signal intensity variation for high abundance ions was centroider error. Our study also showed that the variation in signal intensity is higher than what would be expected if the ion statistics derived from the dual geometry electron multiplier detector followed a Poisson distribution.

High throughput proteomics requires high speed data acquisition. Signal-averaged spectra have relatively cleaner signals and therefore produce more reliable sequencing results than single scan spectra. However, collecting signal-averaged spectra is also more time-consuming, which may not be feasible for many proteomics applications that are duty cycle limited, i.e. limited by the scanning speed of the instrument and the need to collect spectra for as many peptide precursor ions as possible. The single scan spectra can be viewed statistically as components of the signal averages, i.e. the signal average with random error. In a properly functioning instrument the scan-to-scan variation on the m/z scale is small. For our LTQ it is within the manufacturer’s specification of 0.1 to 0.2 m/z units, but the peak intensities are highly variable. Due to a lack of a proper way to deal computationally with the large scan-to-scan variation in signal intensity, many currently available database matching programs, including SEQUEST¹, depend primarily on the m/z axis (is the ion present above a certain threshold or not?) to match sequences and do not make extensive use of relative abundance differences among ions within the same spectrum. However, the intensities carry additional information beyond m/z value², and incorporating this dimension of information can enhance the quality of the spectral match to a theoretical sequence calculated from a protein database. For instance, Zhang³ incorporated the similarity of intensities between the predicted spectra and the observed spectra in his reported scoring function. However, Zhang and others have normally used signal-averaged data to develop new computational approaches to using tandem mass spectrometry in conjunction with protein databases. Recent improvements in mass spectrometer technology have increased scan speed and the quality of single scan spectra to the point that their use has become practical for high throughput applications, something that was normally not done with the previous generation of commercial quadrupole ion trap mass spectrometers. Studying the noise variation in such single scan spectra can help gain a better understanding of the relationship between signal and noise in the new instruments, can facilitate extraction of the peptide sequence information the intensity carries, and can eventually improve performance of peptide sequencing/database searching software that uses single scan CID mass spectra as an input.

The noise characteristics and other fundamental aspects of detectors in mass spectrometry have been extensively studied for many years. The literature up to 1979 was summarized in the doctoral dissertation by Peterson⁴. Examples of published reviews include those by Geno⁵ and Evans⁶. Linear ion trap instrumentation, with an emphasis on mass analyzer design, has recently been reviewed by Douglas, Frank and Mao⁷. An early version of the LTQ, similar to the instrument used in our laboratory, but with a single detector geometry and less advanced electronics, has been described by Schwartz, Senko and Syka⁸. The dual detector design employed in the LTQ has been described in the manufacturer’s documentation⁹. For a properly functioning instrument of the type used here, the variation on the m/z scale is usually a small quantity (< 0.2 m/z units), and to a first approximation is independent of the m/z value under our conditions. For mass spectrometers used with conventional detectors, the intensity of a peak at a certain m/z is directly proportional to the count of ions detected within a predetermined time unit, the length of time associated with the particular scan event. Theoretically, such a detection process often follows a Poisson distribution, in which the standard deviation of intensity scales linearly with the square root of the intensity^{4, 5, 6}. More specifically, the theoretical distribution of ions forming a peak in the mass spectrum can be defined by a Poisson random variable that is determined by the physical and stochastic properties of the specific detector. In this study, we provide a systematic assessment of the noise properties of single scan spectra from the LTQ, from multiple product ion scans for five different precursor ions of different lengths, amino acid compositions and charge distributions. We believe these spectra to be adequately representative of the vast majority of peptides in our archives for purposes of studying scan-to-scan intensity variations. To correct for the slight scan-to-scan variation on the m/z axis, we applied a matching algorithm to align the ions from different scans prior to the analyses of signal intensity variation. The data were normalized so that the total intensity of all ions summed is equal to 1 on a linear scale. This normalization is more stable than the standard method of scaling the intensities so that the highest peak has intensity 100%. The aligned spectra were then used to study both variation on the m/z scale and the variation in intensity. Section 2 describes the data collection methods, the matching algorithm and other statistical methods. Section 3 presents the results and Section 4 includes discussion.

2. Methods

2.1 Data collection

Standard peptides Adrenocorticotropic Hormone Fragment 1-17 (Cat. No. A 2407), Angiotensin I (A 9650 ), Bombesin (B 4272), γ-Melanocyte Stimulating Hormone (M 9638) were purchased from Sigma (St. Louis, MO, USA). The peptides were dissolved in 40% acetonitrile (Burdick & Jackson, Muskegon, MI, USA) and 5mM NH₄HCO₃ (Sigma) in order to shift the charge state distributions to fewer charges and more abundant doubly charged ions. The peptide concentrations were adjusted to generate ion intensities of 10⁵–10⁶ counts for doubly charged precursor ions. A 100 μl gas-tight HPLC syringe (Hamilton, Reno, NV, USA) and the built-in syringe pump in the LTQ mass spectrometer (Thermo Electron Corp., San Jose, CA, USA) were used to directly infuse the peptide solutions at constant flow rate and peptide concentration. The flow-rate was 0.2 μl/min. A 1/16 inch stainless steel union (MU1XCS6, Valco, Houston, TX, USA) and a 50 cm long, 75 μm i.d. x 360 μm o.d. IntegraFrit Capillary (IF360-75-50-N-5, New Objective, Woburn, MS, USA) was used to connect the syringe and the lab-built micro ESI interface. The ESI voltage was 2.2 kV. The ion transfer capillary was set to 160 °C. The scan range was 400–2000 m/z units and scan rate was set to normal (16,700 m/z units sec⁻¹). For CID spectra (MS²), the isolation width was 3.0 m/z units and the normalized collision energy was 40%. All other parameters were default. Automatic gain control was on, thus ion injection time (maximum 300 msec) was varied such that approximately 20,000 charges were contained in the ion trap for any single injection event. Typical scan duration was 0.2–0.3 sec and 200 scans were collected for each peptide. The five precursor ions and their properties are summarized in Table 1.

Table 1.

The five precursor ions used in this study. A2 and A3 are Adrenocorticotropic Hormone Fragment 1–17 (SYSMEHFRWGKPVGKKR); AB433 is Angiotensin (DRVYIHPFHL); AB810 is modified Bombesin (pEQRLGNQWAVGHLM-NH2); and M is γ-Melanocyte Stimulating Hormone (YVMGHFRWDRFG).

	Monoisotopic Neutral Mass	Charge State	Tryptic?
A2	2093.41	+2	Yes
A3	2093.41	+3	Yes
AB433	1295.68	+3	No
AB810	1619.85	+2	No
M	1570.77	+2	No

2.2 Spectral alignment

When assessing the variation of a signal, the variation should be assessed on the peaks from the same ion in different scans. Ideally, the same ion should generate signals at exactly the same m/z location. However, the m/z locations of peaks from the same ion vary from scan to scan due to the finite performance characteristics of the scanning, detection and signal processing circuitry, including errors associated with “on-the-fly” conversion from profile to centroid data. Peaks from the same ion in different scans seldom locate at exactly the same m/z value, varying within the tolerances established for the specific instrument. Thus, a way to explicitly define a window for each observed m/z value to be studied in terms of signal intensity variation had to be established first. A straightforward solution is to split the m/z axis into small fixed windows, and evaluate the variations of the intensities in the intervals. This will be referred to as the fixed window method. However, this evaluation is not based on the signals from the same ions. The signals from the same ions may be placed into different bins in each scan and the assessment of signal intensity variation becomes inaccurate. In this study, we first attempted to match the ions using a spectral alignment algorithm, then we assessed the scan-to-scan signal intensity variation using the aligned signals. To align the spectra from all scans, typically 200, we first randomly chose a spectrum as the template, then aligned the spectrum from another scan to the template using a pairwise alignment algorithm (described in section 2.2.2) and added the peaks that do not match to any existing peaks in the first template to the updated template, then we repeated the above procedure for the next scan using the updated template until all scans were included. Due to the variation in the presence or absence of ions at each m/z value in each scan, the number of total peaks aligned varied from location to location on the m/z axis after the alignment process was completed. Throughout the rest of the paper, we refer to the m/z location of a peak on the template as an aligned location, the number of total peaks at an aligned location as sample size, and the percentage of peaks aligned at an aligned location as frequency of appearance.

2.2.1 Notation and Assumptions

Before further discussion, we first introduce some notation. We denote a signal as S, which consists of the m/z location (denoted as X) and the intensity (denoted as Y), written as S ≡ (X,Y) . Both the m/z value and the relative intensity of each signal are assumed to be identically independently distributed with a normal distribution (N):

$$X\sim N({\mu }_X,{\sigma }_X^2)\text{and}Y\sim N({\mu }_Y,{\sigma }_Y^2({\mu }_Y)),$$

where μ_X and μ_Y are the mean of m/z value and intensity, respectively, and ${\sigma }_X^2$ and ${\sigma }_Y^2$ are the variance of m/z value and intensity, respectively. The variation on the m/z axis is assumed to be independent of the m/z value and the variability of the intensity is related to the magnitude of the intensity. Hence, ${\sigma }_X^2$ is assumed to be a constant independent of the value of X or μ_X , and ${\sigma }_Y^2$ is assumed to be a function of μY . We also make the assumption that X and Y are independent.

2.2.2 Pairwise Alignment Algorithm

We developed a pairwise alignment algorithm using the pair hidden Markov model (pair HMM)¹⁰. Pair HMM is similar to the standard hidden Markov model^{11, 12}, except that it generates a pairwise alignment rather than a sequence. Just as in the standard hidden Markov model (HMM), the pair HMM contains a series of hidden states and emissions. In pair HMM, there are three hidden states: matched, inserted and deleted. Each of them can transition to any other states or itself. In our context, if spectrum A (S_A) is matched to the template spectrum (S₀), then the matched state means that a peak from spectrum A matches to a peak from the template, inserted state means that a peak from spectrum A does not have a matching peak in the template, and deleted state means a peak in the template has no match in spectrum A. The emissions are defined as the aligned signals for the two spectra, denoted as the following for the three hidden states:

$$\text{matched}:(S_0,S_A)\text{inserted}:(\varnothing ,S_A)\text{deleted}:(S_0,\varnothing )$$

where ∅ denotes that no peak in the spectrum matches to any peak in the other spectrum. In this application, there is no preference between which states the transition occurs. Hence, the transition probabilities are made all equal and independent of the state it transitions from. The hidden states form an order-0 Markov chain. Under the model and assumptions in section 2.2.1, the difference between two aligned observed signals S₀ and S_A follows the following distributions:

$$\text{matched}:X_0-X_A\sim N(0,2{\sigma }_X^2)\text{and}{Y}_0-Y_A\sim N(0,2{\sigma }_Y^2({\mu }_Y))$$

Because μ_Y is unobserved, we replace the mean of intensity with the empirical values, then the variance of Y₀ − Y_A becomes ${\sigma }_Y^2(Y_0)+{\sigma }_Y^2(Y_A)$. For notational simplicity, we denote the variance as ${\sigma }_Y^2$. When two peaks are matched, the emission probability is defined as the product of the alignment probability of m/z and the alignment probability of the intensity, as the m/z and intensity are assumed to be independent of each other. When the unmatched case (insertion or deletion) happens, we consider the missing signal as a signal with intensity lower than the detection threshold. According to our model, the probability of an unmatched case is the probability that the intensity is lower than threshold. In our model, we take the threshold equal to zero. Therefore, the emission probabilities are defined as following:

$$P((S_0,S_A)\mid \mathit{matched})=\phi (\frac{x_0-x_A}{\sqrt{2}{\sigma }_X})\phi (\frac{y_0-y_A}{{\sigma }_Y})$$ (1)

$$P((\varnothing ,S_A)\mid \mathit{inserted})=\mathrm{\Phi }(-\frac{y_A}{{\sigma }_Y})$$ (2)

$$P((S_0,\varnothing )\mid \mathit{deleted})=\mathrm{\Phi }(-\frac{y_0}{{\sigma }_Y})$$ (3)

where φ and Φ are the probability density function and cumulative density function of the standard normal distribution, respectively. Assuming that the data come from the same true spectrum, and that noise in m/z does not cause peaks to change order, the HMM above describes P(s, S₀, S_A), the joint probability of observing the two spectra and some sequence s of “matched, inserted, deleted” states. The most probable state sequence in the hidden Markov model provides the alignment between the peaks of two spectra. The standard technique for finding this most probable state sequence is a dynamic programming method¹³ called the Viterbi algorithm. In our case the Viterbi algorithm is also efficient, as will be shown in the next section. A detailed introduction to the Viterbi algorithm can be found in Rabiner and Juang¹².

2.2.3 Parameterization

Before using the algorithm, we needed to specify the parameters in the model above, i.e. σ_X and σ_Y. We also needed to specify a maximum allowed m/z distance such that only peaks within the specified interval would be allowed to match and peaks outside the interval would be ignored. We choose the maximum distance to be 0.5 m/z units. This means that only the peaks within ±0.5 m/z units from the target peak could be matched and aligned. This constraint allowed us to implement a very efficient Viterbi algorithm¹², whose running time is of the order max(n₀, n_A), where n₀, n_A are the number of peaks in the two spectra, instead of n₀ × n_A, the running time of a standard Viterbi algorithm. The standard deviation of the m/z assignment was chosen to be half this value (i.e. σ_X = 0.25). For simplicity, the standard deviation of intensity was chosen to be proportional to the observed intensity with a constant coefficient of variation (CV) of 1 for all spectra (i.e. σ_Y ( y) = y ). With this choice of the variation of Y, the deletion (or insertion) cost becomes a constant (Φ(−1/ CV) ) independent of the intensity of the peak. Our experience showed that the algorithm performs well using a wide range of values for the parameters. We also experimented with the Poisson relation ${\sigma }_Y(y)=\sqrt{y}$. The choice of variance model actually had little impact on the observed alignments. The matching algorithm was implemented in Java, and the source code is available from the authors.

2.3 Methods for analysis of signal intensity variation

It is well known that the variability of signal intensity is a function of the mean. Hence, we assume that the standard deviation of intensity ( SD_Y ) is proportional to a power θ of the mean μ_Y:

$${SD}_Y=\sigma {\mu }_Y^{\theta }$$ (4)

where θ and σ are constants independent of Y. For example, in the Poisson model θ = 0.5. Taking the log transformation of both sides will lead to a linear regression equation:

$$log({SD}_Y)=log\sigma +\theta log{\mu }_Y$$ (5)

The slope of the linear regression in (5) estimates the power θ. For ease of interpretation, we used a base 10 logarithmic transformation. Because the number of aligned peaks varies from one m/z location to another, the mean and the standard deviation at each aligned location were calculated with different sample sizes. To adjust for this variation of sample size, a weighted regression was used¹⁴. The weighting factor¹⁴ for each aligned location on the m/z axis was the number of peaks aligned at that location, denoted as m_i for the i^th aligned location. Formally, θ and σ are estimated by minimizing ${\displaystyle \sum _{i=1}^n}{m}_i{(log({SD}_{Y_i})-(log\sigma +\theta log{\overline{Y}}_i))}^2$, where m_i is the weight, n is the number of aligned locations, SD_Yi and Ȳ_i are the standard deviation and mean intensity of peaks at the i^th aligned location, respectively.

The root mean square (RMS) error was used as a summary of the variation on the m/z scale at all the aligned locations in the spectra: ${\mathit{RMS}}_X=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{m_i}}{(X_{ij}-\overline{X_i})}^2}{{\displaystyle \sum _{i=1}^n}{m}_i}}$ where m_i is the number of aligned peaks at the i^th aligned location in the template and n is the number of aligned locations in the template. It can be viewed as a weighted mean of the standard deviation of the m/z value at each aligned location with the number of peaks at an aligned location as the weight. The statistical analysis was done using the public domain software package R.

3. Results

3.1 Matching Results with the alignment algorithm

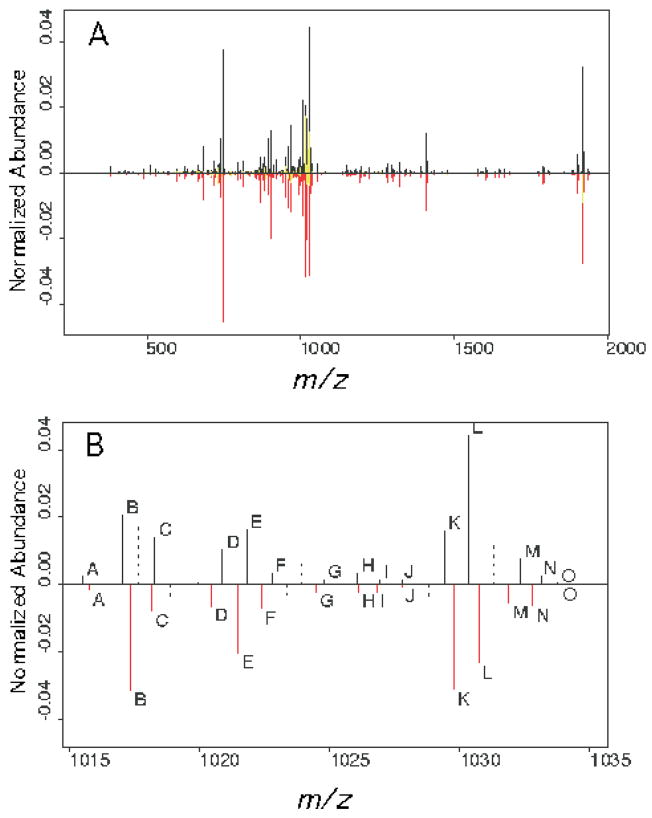
Due to a lack of certain knowledge in the CID scans about which mass peaks are derived from the same ions in each scan, we had to assess the quality of the alignment indirectly. One way was to evaluate the alignment with a simulation experiment. In the simulation experiment, the true alignment is known. Thus we could assess the mismatch rate as a criterion of the alignment quality. Since the multiple alignment is achieved using the pairwise alignment algorithm, we assessed the overall quality of the alignment by assessing the quality of the pairwise alignment. An example of a single pairwise alignment performed with two single scan CIDs from precursor A2 is shown in Figure 1. We first randomly chose a spectrum as a template, then simulated a series of spectra by adding Gaussian noise on both the m/z and the intensity axes. The amount of noise added was based on our measurements of real spectra. The noise added on the m/z axis was ε _X ~ N (0,0.14²) and the noise added on the intensity axis was ε_Y ~ N (0,(0.3y)²), where y is the intensity of the peak chosen as the template. We assessed the mismatch rate for our matching algorithm and for the fixed window method (window size = 0.5 m/z units) in 10 simulations. Our algorithm matched all the peaks correctly in all 10 simulations; the fixed window method consistently had a mismatch rate of about 20%. When we ran the simulation 100 times for both the fixed window and our matching algorithm, the mismatch rates were 22% and 0.2%, respectively. The variation between real scans is more complicated than in the simulated experiment, which only included the shift in m/z value and the shift in intensity. For example, real scans may have different numbers of peaks, and not all peaks are present in every scan, as illustrated in Figure 1. This complication results in a different frequency of alignment at different aligned locations. The significant ions are usually from the major fragmentation pathways, which consistently produce detectable signals from scan to scan. Therefore, the number of peaks aligned at those locations should be very close to the total number of scans if an alignment is good. In addition, the signals with very few peaks aligned should be noise, i.e. with low average intensities, for a good alignment. These can be used as a criterion to show the quality of alignment for real scans. Table 2 reports the average frequency of alignment of the 10 most intense signals in the CID scans for each precursor ion in Table 1 and the average intensity for different frequencies of alignment for all ions. Most of the 10 most abundant signals in each CID had a high frequency of appearance at the aligned location. Occasionally, the abundant ions appeared with low frequency. That was due to the “peak splitting” that occurs in centroid data collection mode. Section 4 contains discussion regarding centroider error. The lowest frequency groups had low average intensities, which indicated that most low frequency alignments were noise. The total number of aligned ions ranged from 701 for precursor AB433 to 2,570 for A2, with an average of 1,774.

Figure 1.

The alignment of two single scan spectra from precursor ion A2 is plotted. One spectrum is plotted in black and the other in red on the same m/z scale. The allowed matching range was +/−0.5 m/z unit. (A) The complete spectra. Misaligned peaks are colored in yellow. (B) The blowup of the region 1015–1035 m/z units. Matched peaks are plotted in solid lines and labeled with identical letters. Non-aligned peaks that fell outside the allowable window are plotted using dashed lines.

Table 2.

The normalized mean intensity of mass peaks with different frequencies of alignment. The frequency of alignment is based on the number of aligned peaks acquired over a total of 200 scans, as defined in the text.

	Mean frequency of top 10 ions	Normalized mean intensity for frequencies of spectral alignment (×10−3)
		<25%	25%–50%	50%–75%	>75%
A2	76.4%	0.266	0.452	0.859	2.236
A3	72.1%	0.480	0.724	1.334	5.493
AB433	82.5%	0.502	0.497	2.949	8.795
AB810	80.0%	0.371	0.368	0.662	7.260
M	87.6%	0.251	0.470	0.794	2.159

3.2 Variation on the m/z axis

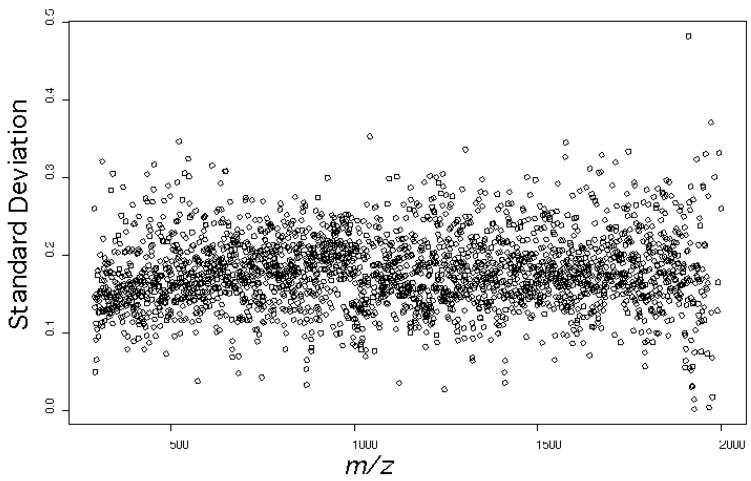
One advantage of using the matching algorithm is that it allows the assessment of variation on the m/z axis. To summarize the standard deviation, the average standard deviation and RMS were calculated over all aligned locations. The average standard deviation was within the range of 0.16 to 0.18 m/z units for all five peptides studied. The RMS error represents a weighted average of the standard deviation, and was within the range of 0.15 to 0.17 m/z units for all five peptides. Figure 2 shows the individual standard deviations for all ions used in our study as a function of m/z, which are quite consistent across the range of m/z values. As stated earlier, the most abundant peaks were matched more reliably. When only the 10 most abundant ions in each peptide CID were taken into account, the average standard deviation was reduced to a range of 0.08 to 0.11 m/z units and the RMS was reduced to 0.09 to 0.13 m/z units.

Figure 2.

Plot of m/z standard deviation as a function of m/z for all product ions derived from the five precursors shown in Table 1. The standard deviations were observed to be quite consistent across the m/z range studied.

3.3 Variation in signal intensity

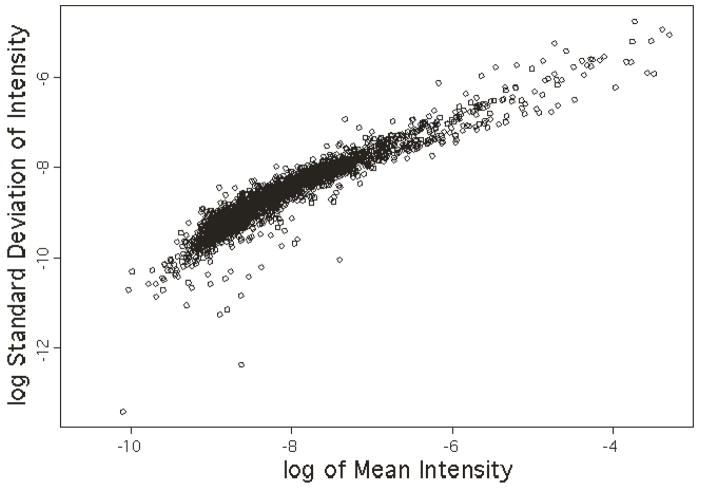
The mean, standard deviation and coefficient of variation were calculated for signal intensity at each observed m/z value using the aligned spectra. We first explored the relationship between the mean intensities and the standard deviation of intensities using weighted linear regression of the log transformed data. Figure 3 shows typical data illustrative of the linear relationship that holds except in the very low intensity region for all the CID scans studied, in this case for precursor A2. Essentially the same relationship was also observed for the other four precursor ions described in Table 1, as well as for an additional five precursor ions chosen from our archives of collision spectra derived from synthetic peptides of known sequence, analyzed on the LTQ using the same experimental conditions (data not shown). Table 3 summarizes the regression coefficients. The slope estimates the power θ in the relationship between the mean intensities and standard deviation of intensities shown in the regression equation (5). For the precursor ions studied, the slopes were all in the range of 0.7 to 0.8 and intercepts were in the range of −0.92 to 1.23 (i.e. σ was within 0.059 to 0.120), which indicates a consistent relationship between mean intensity and standard deviation of intensity regardless of the peptide sequence chosen to generate the CID scan or the individual product ions chosen for further investigation. With the five additional precursor ions noted above (data not shown), we have now studied several thousand ions contained in CID spectra that we believe are representative of the much larger population in our archives, and failed to note any significant differences from the findings noted above. While relative abundance itself has an amino acid sequence dependence that is pronounced and well known, we have not observed an obvious sequence dependence on the scan-to-scan variability of individual ions. The higher numerical values for θ indicate the variation of the signal intensity is higher than what a Poisson distribution would give. Figure 3 also indicates a relatively high variation at the low intensity end, as would be expected from low signal-to-noise ratio data.

Figure 3.

Representative scatter plot of the log transformed standard deviation of signal intensity versus the log transformed mean of signal intensity for the CID ions derived from the precursor ion A2 in Table 1. All CID spectra derived from the five precursor ions in Table 1 showed plots with similar slopes and intercepts, see Table 3. The data were normalized such that the total intensity of all ions summed is equal to one on a linear scale.

Table 3.

The regression results for the log transformed mean and standard deviation of signal intensities. The slope of the regression line is an estimate of the power θ in (5).

	Intercept	Slope	r2
A2	−1.103	0.743	0.944
A3	−0.924	0.776	0.935
AB433	−1.125	0.720	0.934
AB810	−1.231	0.708	0.939
M	−1.192	0.721	0.943

4. Discussion

The matching algorithm performed well in general and allowed us to accomplish our goal of studying variation in mass peak intensity as independently as possible of centroider errors. The data suggests that most of the abundant peaks have a high frequency of appearance (>75%) (see Table 2). However, some abundant peaks have a low frequency of appearance (<25%), with centroider errors accounting for much of the reduced frequency of appearance in the spectrum. A careful examination of the data shows that the low frequency of appearance is due to the occasional “peak splitting” effect when collecting data in centroid mode. When peak splitting happens, a mass peak that represents a single ion is split into two peaks of lesser abundance, an artifact that has been recognized since the advent of modern mass spectrometry data systems and their associated centroiding algorithms. Under our experimental conditions, such peak splitting is observed in about 2% of our single scan CID (MS²) data, i.e. 2 out of every 100 scans will have at least one mass peak showing evidence of such random centroider error. There does not seem to be an obvious dependency on either location on the m/z axis (see Figure 2) or precursor ion charge state within the range of +2 to +3 that we encounter most frequently in our proteomics work. The matching algorithm described here only aligns one of the split peaks to the same m/z assignment in other scans, and inserts the other split peak into the template as a new m/z value. The inserted split peak only aligns with other split peaks at the same location on the m/z axis (within the tolerance set in the matching algorithm), and results in a low frequency of appearance in the dataset due to the sporadic nature of the centroid split artifact. Such centroider errors have been of less practical importance historically, because of the nearly universal practice of averaging several scans of GC or LC/MS data prior to database searching or other efforts at interpretation. For the instrumentation employed in our work under constant infusion conditions, random centroider error now seems to be the single most significant factor in determining scan-to-scan variability for the most highly abundant peptide sequence ions, as they relate to the suitability of the single scan spectra for input into database search algorithms. However, the magnitude of such errors is not so high as to preclude their use. In a typical whole proteome analysis in our laboratory, almost all of the *.dta files (the files that are actually searched against the database) now consist of single scan CID spectra, a significant percentage of which are of sufficiently high quality to yield a good match with a database search algorithm, or to use for purposes of manual interpretation. This analysis ignores the confounding effects of changing peptide concentrations, proton concentrations and solvent gradients encountered under typical LC/MS conditions, where we have observed minor electrospray instabilities to play a somewhat more obvious role in spectrum relative abundance variation. Our purpose here was to examine what was ultimately limiting in terms of mass spectrometer performance, independent of variables associated with gradient elution HPLC. However, it is worth noting that when compared to conventional triple quadrupole beam instruments and 3D quadrupole ion traps, an LTQ operated under normal conditions (constant total number of charges injected, fixed well below any space-charge limit, variable ion injection time) tends to show markedly less spectral distortion as a function of scan timing during chromatographic peak elution. Operating the instrument in such a manner also tends to minimize mass discrimination effects in general, as noted in the review by Douglas and coworkers⁷.

Our results using the LTQ show that the standard deviation of the signal intensity is not the square root of the mean intensity, as what a Poisson process would suggest. Blackler et al. have also made a similar observation¹⁵. The observed values for the exponent θ in Equation (5) must be interpreted with caution. Our results, and those of Blackler et al., suggest a systematic source of noise that does not scale with the square root of the signal intensity, but the actual source of the additional noise remains unknown. However, the practical consequences in terms of overall spectral quality, detection limits and other metrics of instrument performance seem to be minimal. This is probably due at least in part to the enhanced sensitivity of the dual detector scheme, combined with the inherently wider linear dynamic range associated with 2D quadrupole ion trap instruments relative to 3D traps.