Adjusted Estimates for Time-to-Event Endpoints

Abstract

In the analysis of retrospective data or when interpreting results from a single-arm phase II clinical trial relative to historical data, it is often of interest to show plots summarizing time-to-event outcomes comparing treatment groups. If the groups being compared are imbalanced with respect to factors known to influence outcome, these plots can be misleading and seemingly incompatible with results obtained from a regression model that accounts for these imbalances. We consider ways in which covariate information can be used to obtain adjusted curves for time-to-event outcomes. We first review a common model-based method and then suggest another model-based approach that is not as reliant on model assumptions. Finally, an approach that is partially model free is suggested. Each method is applied to an example from hematopoietic cell transplantation.

1. Introduction

In the evaluation of time-to-event data derived from phase II clinical trials or retrospective studies in hematopoietic cell transplantation (HCT), Cox regression is typically used to quantify the difference in outcome between two groups. Regression analysis allows one to adjust for potential imbalances in characteristics associated with outcome that might partially explain the difference (or lack thereof) between the groups being compared. In addition to an estimate of the difference in outcome as derived from the regression model, it is often desirable to provide a graphical illustration of the difference. The most common tool for this purpose is the Kaplan-Meier estimate for survival endpoints, and cumulative incidence estimate for endpoints with competing risks; however, neither of these estimates considers information from covariates that may be imbalanced among the groups, thereby leading to curves that may not reflect the differences among the groups as measured by the regression model. A method to generate adjusted curves would therefore be desirable. Section 2 provides an example from HCT data and motivates the problem. Section 3 describes a relatively standard model-based approach, which illustrates the fitted model but falls short of achieving what we would consider to represent ‘adjusted survival’ curves. We then suggest a simple alternative that better accommodates the notion of adjustment, though still requiring some model assumptions. Section 4 proposes a method that is less dependent on the model assumptions required of the methods summarized in Section 3, and is extended to provide adjusted cumulative incidence estimates in Section 5.

2. Example from HCT

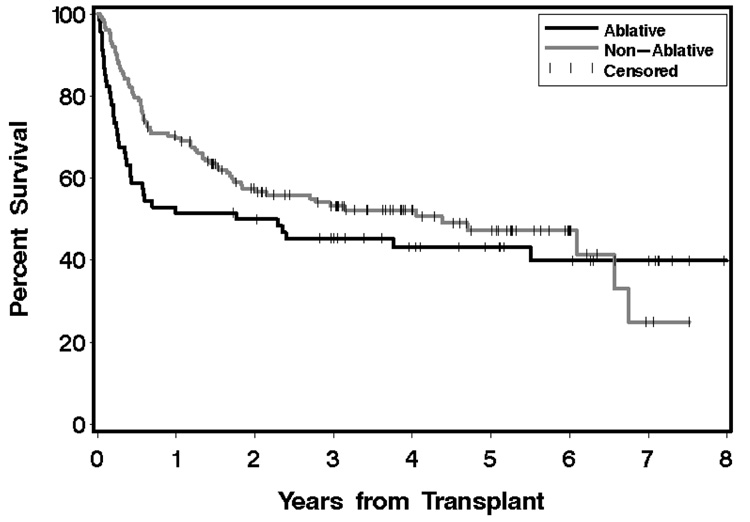
As an illustration of the problem we present an example from a retrospective data analysis that sought to compare outcomes after HCT following the use of nonmyeloablative conditioning to outcomes following conventional myeloablative conditioning in 220 patients with B-cell malignancies [non-Hodgkin lymphoma (NHL), chronic lymphocytic leukemia (CLL), and Hodgkin lymphoma (HL)], as reported previously (Sorror et al. 2008). This comparison is complicated by a number of factors, chief among them the fact that nonmyeloablative conditioning is generally offered only to older patients and to patients with pre-existing comorbidity, who are generally considered to be unsuitable for transplant with myeloablative conditioning regimens. There are also differences between these patient populations with respect to other factors that could influence outcome, including the diagnosis being treated, the use of mobilized peripheral blood (PBSC) versus bone marrow (BM) as a source of stem cells, and the use of matched sibling versus mismatched or unrelated donor grafts. Shown in Figure 1 are (unadjusted) Kaplan-Meier estimates of overall survival for the two conditioning groups.

Fig 1.

Kaplan-Meier estimates of overall survival from aretrospective study in HCT. The gray curve represents the probability of survival for patients who received a nonmyeloablative conditioning regimen, and the black curve represents the same for patients who received a myeloablative regimen. Tick marks represent censored observations.

Table 1 summarizes the characteristics of the two conditioning groups plus the results from proportional hazards models relating these factors to overall mortality and non-relapse mortality (NRM), which is defined as any death occurring in the absence of recurrence or progression of malignancy. As can be seen from this table, patients receiving nonmyeloablative conditioning are more likely to possess some factors that are associated with increased mortality when compared to patients receiving myeloablative conditioning. Although not all factors were associated with outcome in univariate analysis, they were considered as possible adjustment factors based on prior considerations and the possibility that an association was obscured by confounding factors.

Table 1.

Distribution of potential risk factors and their univariate association with overall mortality and non-relapse mortality from a Cox regression model.

		Ablative	Non-Ablative	Overall mortality	Non-relapse mortality
		(n=68)	(n=152)	(114 events)	(62 events)
		%	%	HR (95% CI)	HR (95% CI)
Diagnosis	NHL	79	53	Ref	Ref
	CLL	15	27	0.57 (0.3–0.9)	0.62 (0.3–1.2)
	HL	6	20	0.88 (0.5–1.5)	0.69 (0.3–1.5)
HCT-CI	0	41	30	Ref	Ref
	1,2	26	30	1.66 (1.0–2.8)	2.05 (1.0–4.2)
	3+	32	40	2.30 (1.4–3.7)	2.99 (1.5–5.8)
Donor	Sibling	66	55	Ref	Ref
	Other	34	45	0.98 (0.7–1.4)	1.07 (0.6–1.8)
Source	PBSC	69	99	Ref	Ref
	BM	31	1	0.83 (0.4–1.6)	0.72 (0.3–1.8)
Age	< 50	82	41	Ref	Ref
	≥50	18	59	1.15 (0.8–1.7)	1.45 (0.9–2.4)
Prior regimens	0–2	56	49	Ref	Ref
	3,4	41	37	1.54 (1.1–2.2)	1.44 (0.9–2.4)
	5+	3	14	0.74 (0.3–1.6)	0.52 (0.2–1.7)
Resistant Disease	No	34	49	Ref	Ref
	Yes	66	51	1.53 (1.0–2.3)	1.39 (0.8–2.3)

Abbreviations: NHL, non-Hodgkin lymphoma; CLL, chronic lymphocytic leukemia; HL, Hodgkin lymphoma; HCT-CI, hematopoietic cell transplant – comorbidity index; BM, bone marrow; PBSC, peripheral blood stem cells.

The results from an unadjusted Cox regression model show a modestly reduced hazard of mortality associated with nonmyeloablative conditioning relative to myeloablative conditioning [HR=0.77, 95% CI 0.5–1.4, p=0.20], as also evidenced by the curves in Figure 1. However, the HR for overall mortality adjusted for the factors in Table 1 suggests a much larger difference between the conditioning groups than is visually apparent [HR=0.50, 95% CI 0.3–0.8), p=0.008]. Given this, there is a need for some type of adjustment to the curves shown in Figure 1 so that the adjusted curves better reflect the association measured by the regression model. In the next two sections, we discuss several approaches to adjustment.

3. Model-based Approaches

We first introduce some notation that will be used throughout. Suppose we have K groups of interest, with sample size in each group denoted n_k, and sets of labels of the individuals within each group, denoted M_k k = 1,…,K. Each individual i has a vector of additional covariates, z_i, that may be related to overall survival or to some cause-specific hazard of interest.

The Cox proportional hazards model assumes that the hazard of failure associated with a set of covariates z is defined by

$$\lambda (t|z)={\lambda }_0(t)·\text{exp}(z^{\prime }\beta )$$ (1)

where λ₀ (t) is an arbitrary and unspecified baseline hazard function, and β is a vector of unknown regression parameters. Based on this model, the estimated survival for a particular set of covariates z is given by

$$\widehat{S}(t|z)={\left[{\widehat{S}}_0(t)\right]}^{\text{exp}(z^{\prime }\widehat{\beta })}$$ (2)

where Ŝ₀(t) = exp[−Λ̂₀(t)] is derived from any standard estimate of the cumulative baseline hazard function (Kalbfleisch and Prentice 1980; Breslow 1974), and β̂ is the vector of estimated coefficients from the Cox model.

Under this model, one can use equation (2) to generate an estimate of survival for any specified set of covariates. For the current example, a standard approach to illustrating the effect of the conditioning regimen “adjusted” for the other covariates, would be to fit a proportional hazards model incorporating all of the covariates in Table 1 plus an indicator of conditioning group. Then (2) would be plotted for two z vectors differing only by the presence or absence of the indicator for conditioning, for example by using the “covariates=” option in the SAS “baseline” statement within the “phreg” procedure. For the factors listed in Table 1, one could assign the average value for patients in the myeloablative group, yielding the survival estimates in Figure 2.

Fig 2.

Kaplan-Meier estimates and adjusted estimates of overall survival from a retrospective study in HCT. Solid curves represent the unadjusted (Kaplan-Meier) survival estimates for the two groups, dashed lines represent the adjusted estimates as determined from the appropriate Cox regression model. Tick marks on the Kaplan-Meier curves represent censored observations.

In our view, the adjusted curves that result from this model-based approach have some shortcomings. First, the overall shape of the unadjusted Kaplan-Meier curves is not maintained. This is due to the fact that the adjusted curves from (2) are derived from a pooled estimate of the common baseline hazard function, with the separation between curves dictated by the model-based hazard ratio estimate. Even if the proportional hazards model is completely correct, the jump points of the adjusted curves will not match those of the unadjusted curves, because the jump points reflect deaths within either group. While these curves accurately illustrate the fitted model, we believe they are too far removed from the unadjusted Kaplan-Meier curves to conform to the conventional notion of adjustment.

We propose a relatively simple adjustment method which results in jump points for the adjusted curve only when a death occurs within that group, so that the adjusted curve maintains its overall shape, although there is still dependence on a model-based hazard ratio comparing the two groups. To implement the method one first chooses one of the K groups as the reference group, and then selects a time point t_A as a point of reference for adjustment. Ideally this point is well along the time axis to the right, but before the point where excessively large jumps may occur due to small numbers of patients at risk. In a setting with two groups, suppose we choose M₁ as the reference group, Ŝ₁(t) and Ŝ₂(t) denote the unadjusted Kaplan-Meier curves for M₁ and M₂, respectively, and π̂ is the estimated adjusted hazard ratio comparing M₂ to M₁. If S̃(t) denotes the adjusted curve for M₂, then we require this curve to satisfy

$${\tilde{S}}_2(t_A)={[{\widehat{S}}_1(t_A)]}^{\widehat{\pi }},$$ (3)

that is, at time t_A we want the survival estimate for the adjusted curve for group 2 and the survival estimate for the reference group 1 to be in accordance with the adjusted hazard ratio π̂.

One way to modify Ŝ₂(t) to achieve this condition is to make a proportionate adjustment to the failure probability that yields the desired relationship at t_A and then apply that to the entire curve, so that

$${\tilde{S}}_2(t)=1-({\tilde{m}}_2/m_2)(1-{\widehat{S}}_2(t)),$$ (4)

where m̃₂ = (1−[Ŝ₁(t_A)]^π̃ and m₂ = (1 − Ŝ(t_A)). Although this adjustment method is based on the survival estimates at a single point in time, it produces reasonable results in many cases, although it is of course somewhat dependent on the choice of t_A. Also, if Ŝ₂(t) becomes small and the adjustment ratio m̃₂/m₂ is large, then S̃₂(t) can be < 0. In this case the proportionate adjustment could be based on the survival probability at t_A, rather than the failure probability.

Another alternative to (4) that avoids this possibility is to solve for π̃ to satisfy the relation [Ŝ₂(t_A)]π̃ = [Ŝ₁(t_A)]π̂. That is, π̃ is the “effective hazard ratio” that would need to be applied to Ŝ₂(t) in order to achieve the desired survival probability at t_A, and is easily solved as π̃ = π̂ · log[Ŝ₁(t_A)]/log[Ŝ₂(t_A)], with then S̃₂(t)= [Ŝ₂(t)]π̃.

In the example at hand we take t_A to be 6 years, since it represents a point relatively far along in time yet short of where the curves become obviously unstable due to small numbers at risk, and again wish to use the myeloablative group as the reference group. We have Ŝ₁(6) = 0.399 and since π̂ = 0.5 we want S̃₂ 6) = 0.399^0.5 = 0.632, so that the adjusted failure probability m̃₂ = 0.368. Since Ŝ₂ (6) = 0.473, the unadjusted failure probability at t_A is m₂ = 0.527, and S̃₂(t) is constructed by mutiplying the failure probability in group 2 by a factor of 0.368/0.527 = 0.698 at all points in time. The adjusted curve according to (4) is shown in Figure 3. The alternate adjusted curve is obtained by using an effective hazard ratio π̃ = 0.5 · log(0.399)/log(0.473) = 0.614 applied to Ŝ₂(t). The resulting curve is very similar to (4) except in the tail.

Fig 3.

Kaplan-Meier estimates and adjusted estimates of overall survival from a retrospective study in HCT. Solid curves represent the unadjusted (Kaplan-Meier) estimates for the two groups, dashed lines represent the adjusted estimates from two different methods for the nonmyeloablative group. The first dashed curve is obtained by proportionately changing the failure probability at each time; the second dashed curve is obtained by exponentiating the unadjusted curve to the appropriate power as detailed in Section 3. Tick marks on the Kaplan-Meier curves represent censored observations.

As noted above, a drawback to this simple approach is the need to choose the timepoint t_A. If the survival curves are based on groups with large sample sizes, and the risk sets do not get too small (< 10 patients per group, say), then the method is not particularly sensitive to the choice of time. When the sample sizes are small, or there is clear non-proportionality of hazards, then the choice of t_A becomes problematic and one should consider the method described below.

4. Partially Model-free Approach

Although the methods described above produce adjusted curves that retain the same appearance as the unadjusted curves, they rely on a model-based estimate of the hazard ratio, including the assumption of proportional hazards between the groups of interest. They are also subject to some arbitrariness in the choice of the adjustment time t_A. The method described below makes no modeling assumptions about the factor of interest, though it depends on modeling the hazards associated with the covariates to be adjusted for.

Using the notation above, a stratified proportional hazards model for this setting is defined by allowing the baseline hazard function to vary for each group, with other covariates modulating this hazard in a way that is common to all strata, as defined by

$${\lambda }_k(t)={\lambda }_{0k}(t)·\text{exp}(z^{\prime }\beta ),k=1,\dots ,K.$$ (5)

Although in principle one or more components of β can be allowed to vary across strata, in the present context it makes little sense to talk about ‘adjustment’ unless it is presumed that the observed survival differences among the K groups are attributable to imbalances in covariates, not to differences in covariate effects.

Given estimates of the λ_0k and β, a standard estimate of the survival function for a member of group k, with arbitrary covariate vector z, is given by

$${\widehat{S}}_k(t|z)=\text{exp}\{-{\widehat{\Lambda }}_{0k}(t)·\text{exp}(z^{\prime }\widehat{\beta })\},k=1,\dots ,K$$ (6)

where Λ_0k(t) is any standard estimator of the cumulative baseline hazard function for group k in the context of a stratified proportional hazards model (Kalbfleisch and Prentice 1980). Now define a reference group of n_A individuals with a specified set of covariates that will constitute a common point of adjustment; the set of labels for the individuals in this group is denoted M_A. In general we expect that M_A would in fact be the same as one of the existing groups M_k, and mostly likely the reference group used in Cox regression analysis, but this is not essential and M_A could instead represent some other defined population. The adjusted survival function estimate for the k^th group is simply the average of the estimated survival functions that would be obtained by applying (6) to each of the covariate vectors of the individuals in M_A

$${\tilde{S}}_k(t)=n_A^{-1}·{\displaystyle {\sum }_{i\in M_A}{\widehat{S}}_k(t|z_i),k=1,\dots ,K.}$$ (7)

This approach to adjustment is somewhat similar to adjustment procedures described by Makuch (1982) and Chang et al. (1982); however, their methods used an unstratified proportional hazards model incorporating the group variable as a covariate. Thus, like the standard approach described in Section 3, the adjusted curves are constrained to have the same shape (which matches none of the unadjusted curves) and have a constant relationship determined by the fitted model. Gail and Byar (1986) considered use of the stratified proportional hazards model for what they called “direct adjustment” of survival curves, due to the similarity to the concept of direct standardization in epidemiology. The use of the stratified proportional hazards model frees the adjustment process of an unnecessary proportional hazards assumption for the groups of interest. The shape and jump points of the adjusted survival curves will match those of the corresponding unadjusted Kaplan-Meier survival curves, and are free to cross. Zhang et al. (2007) also discuss the stratified approach. In fact, if M_A = ∪M_k, k = 1,…,K (i.e., the adjustment set comprises the entire dataset) then (7) is equivalent to their estimator (3).

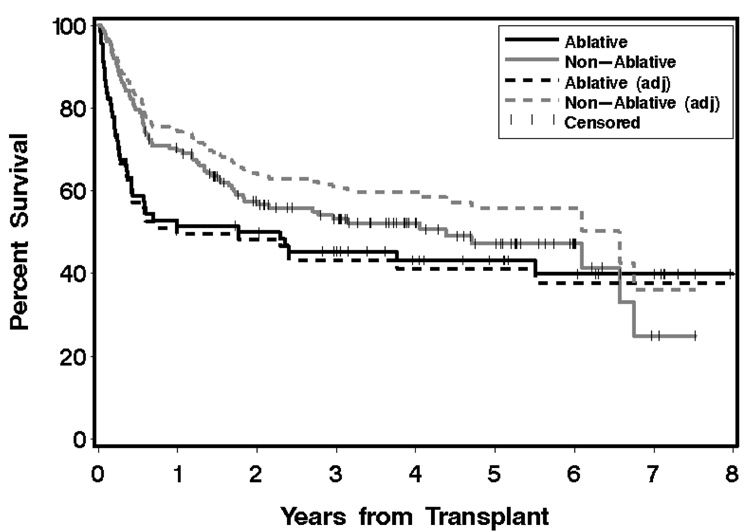
We apply this approach to the data associated with the above example, with the resulting curves shown in Figure 4, with M_A corresponding to the group receiving myeloablative conditioning. The adjusted curves now yield the hypothetical survival curves that would result if the patient characteristics of both groups had been that of the group receiving myeloablative conditioning. The adjusted curve for the latter group, as should be expected, is very close to the original curve. In fact, the visible separation observed here is larger than that typically seen when a group is adjusted to itself. The method is easily implemented in SAS and we provide the requisite code in the Appendix. A SAS macro that computes both estimates and standard errors when M_A comprises the entire dataset can be found in Zhang et al. (2007).

Fig 4.

Kaplan-Meier estimates and adjusted estimates of overall survival from a retrospective study in HCT. Solid curves represent the unadjusted (Kaplan-Meier) survival estimates for the two groups; dashed lines represent the adjusted estimates obtained from the partially model-free approach detailed in Section 4.

5. Adjusted Cumulative Incidence Estimates

In the transplant setting, it is also common to make comparisons of cause-specific hazards (for example, relapse and non-relapse mortality) and to graphically illustrate differences among groups with the use of cumulative incidence curves. The same issues of adjustment arise when groups are imbalanced with respect to factors which may influence the cause-specific hazards of interest, as would be true for the situation in Table 1.

Suppose that j indexes the J types of events, let t_i denote the event or censoring times for each individual, and let δ_i = j indicate that the event that occurred at t_i was of type j, with δ_i = 0 indicating that t_i is a censoring time. Then, the estimated cumulative incidence function for the j^th type of event in the k^th group may be written as

$${\widehat{I}}_k^j(t)={\displaystyle {\sum }_{i\in M_k:t_i\le t,{\delta }_i=j}{\widehat{S}}_k^0(t_i^{-})·[1-{\widehat{S}}_k^j(t_i)/{\widehat{S}}_k^j(t_i^{-})],k=1,\dots K,j=1,\dots ,J}$$ (8)

(Kalbfleisch and Prentice 1980) where the ${\widehat{S}}_k^0(t)$ are the Kaplan-Meier estimates of “event-free” overall survival within the k^th group, and the ${\widehat{S}}_k^j(t),j=1,\dots ,J$ are the Kaplan-Meier estimates of “cause-specific” survival, i.e., the estimates obtained by censoring for other event types except j. In general the latter are not interpretable, and are used here only as a device for computing the adjusted curves. The expression in brackets in (8) is an empirical estimate within group k of the conditional probability of a failure of type j at t_i, more commonly written as an expression like d_j(t_i)/n(t_i) (that is, the number of events of type j at t_i divided by the number of subjects still at risk at t_i); however, we have re-expressed this quantity by the equivalent representation using the cause-specific survivor functions. The adjusted estimator of the cumulative incidence function follows immediately by substituting the comparable adjusted estimator (7) for each of the ${\widehat{S}}_k^j(t)$ in (8), yielding

$${\tilde{I}}_k^j(t)={\displaystyle {\sum }_{i\in M_k:t_1\le t,{\delta }_i=j}{\tilde{S}}_k^0(t_i^{-})·[1-{\tilde{S}}_k^j(t_i)/{\tilde{S}}_k^j(t_i^{-})],k=1,\dots K,j=1,\dots J}$$ (9)

For example, ${\tilde{S}}_k^0(t)$ is the adjusted version of event-free overall survival, computed using (7). We assume that each of the adjusted components of (9) is adjusted for the same set of covariates, although of course the covariates may have different associations with each of the cause-specific hazards and with event-free survival. The choice of the covariates to adjust for will depend on the particular cumulative incidence estimates that are of interest. An alternative formulation of (9), more in the spirit of (7), would first calculate individual estimates of cumulative incidence associated with each covariate vector z_i in M_A and then average these estimates, as defined by

$$\begin{array}{c}\hfill {\tilde{I}}_k^j(t)=n_A^{-1}·{\displaystyle {\sum }_{i\in M_A}{\tilde{I}}_k^j(t|z_i)}\hfill \\ \text{where}{\tilde{I}}_k^j(t|z_i)={\displaystyle {\sum }_{l\in M_k:t_1\le t,{\delta }_l=j}{\widehat{S}}_k^0(t_l^{-}|z_i)·[1-{\widehat{S}}_k^j(t_l|z_i)/{\widehat{S}}_k^j(t_i^{-}|z_i)]}\hfill \end{array}$$ (10)

and the ${\widehat{S}}_k^j(t|z)$ are derived from stratified overall and cause-specific proportional hazards models, as in (6). The adjusted estimators (9) and (10) are generally very close, but the computational algorithm for (9) is more straightforward and the one which we recommend.

Although we find the procedures give sensible results, neither strictly satisfies the relation $1-{\tilde{S}}_k^0(t)={{\displaystyle {\sum }_{j=1}^J\tilde{I}}}_k^j(t)$ which would be true of the unadjusted estimates (8). In most cases, however, the difference is negligible except possibly in the far right tail of the curves.

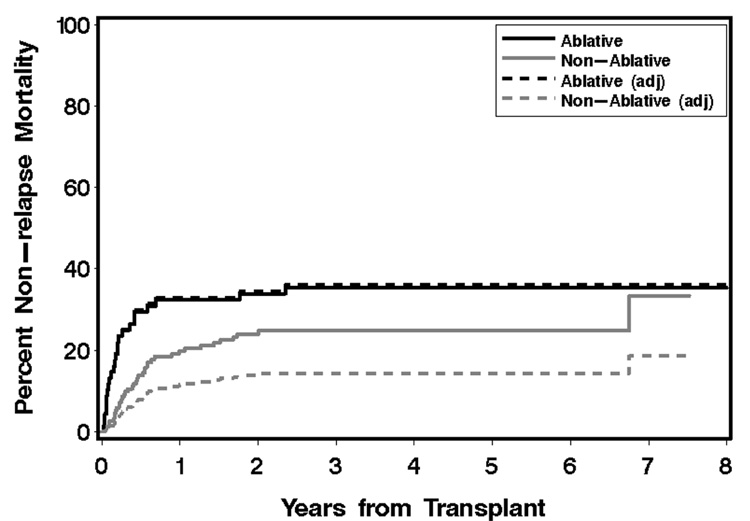
Figure 5 illustrates the same data as used above, except that now we show curves for the cumulative incidence of non-relapse mortality, which accounts for 62 of the 114 total deaths. The adjustment factors are the same as for overall mortality, and again M_A represents the group receiving myeloablative conditioning. The adjusted curve for the myeloablative group closely tracks the unadjusted curve, as should be expected. Although the unadjusted curves are consistent with a lower rate of non-relapse mortality for the nonmyeloablative group [HR=0.65, 95% CI 0.4–1.1, p=0.10], the cumulative incidence adjusted to the covariate characteristics of the myeloablative group is notably lower than the unadjusted curve and better reflects the adjusted analysis [HR=0.28, 95% CI 0.1–0.6, p=0.0003].

Fig 5.

Cumulative incidence estimates and adjusted estimates of non-relapse mortality from a retrospective study in HCT. Solid curves represent the unadjusted (cumulative incidence) non-relapse mortality estimates for the two groups, dashed lines represent the adjusted estimates obtained from the partially model-free approach detailed in Section 5.

6. Discussion

We have described several methods to obtain adjusted curves that summarize the probability of failure for time-to-event endpoints that commonly occur in HCT. Other than the first of these methods (based directly on the Cox proportional hazards model), each has the desirable feature that the adjusted curves change only with failures within the relevant group, and the adjusted curves also maintain the shape that is seen in the appropriate unadjusted curve. Regardless of the method used, it should be emphasized repeatedly that the adjusted curve is not “real”, is dependent on model assumptions, and is not in any way a surrogate for a properly designed prospective comparison. We recommend that the unadjusted estimates always be shown for comparison, either in the same or a separate figure. We argue, however, that the adjusted curves do make sense and visually provide a better reflection of the estimated differences among groups compared to use of the unadjusted curves. There are likely other reasonable methods that would yield results that intuitively make sense as well.

The methods in Section 3 provide similar results, at least for the example considered. The method in Section 4 makes fewer model assumptions, and is not dependent on the choice of a time point to anchor the adjustment. We also show how it can be extended to provide adjusted estimates of cumulative incidence curves. Because of the general relationship between cumulative incidence and cause-specific survival functions seen in (8), the methods in Section 3 could also be adapted to provide adjusted cumulative incidence estimates. We have not evaluated the properties of such a procedure, however.

While the model-based estimates differ a bit from the partially model-free estimates (and from each other), it is difficult to say that one is ‘correct’ and another ‘incorrect’ since, as emphasized above, the adjusted estimates are not real. For the particular example considered, however, all methods resulted in adjusted curves that seem reasonable representations of the group differences as measured by the regression model. In our experience, this has held true for other data sets as well, although in certain situations the estimates can differ by a fair amount in the tails, which is not unexpected. Given that the partially model-free approach requires the fewest assumptions, we prefer its use over the other methods. The model-based approach that is derived from S̃₂(t)= [Ŝ₂(t)]π̃ is very easy to implement, however, and would appear to be a reasonable approach as well.

Appendix

SAS code for calculating adjusted Kaplan-Meier estimate according to (7).

* generic data setup;
data a;
*   grp      stratification variable (eg 1=reference, 2=current);
*   daysur   survival time;
*   delsur   failure indicator;
*   z1–z5    covariates to adjust for;

* define reference covariate set as group 1;
data ref; set a; if grp eq 1;

* fit stratified Cox model, with covariate adjustment;
* ‘estsurv’ is estimated survival for each member of reference set;
proc phreg noprint data=a;
 strata grp;
 model daysur*delsur(0)=z1 z2 z3 z4 z5;
 baseline out=b covariates=ref survival=estsurv/method=emp nomean;

* average across the individuals in reference set at each time;
* ‘adjkm’ is the adjusted Kaplan-Meier estimate;
proc sort data=b; by grp daysur;
proc univariate noprint data=b; by grp daysur;
 var estsurv;
 output out=c mean=adjkm;