The Theory of Everything

Abstract

We discuss recent developments in our understanding of matter, broadly construed, and their implications for contemporary research in fundamental physics.

The Theory of Everything is a term for the ultimate theory of the universe—a set of equations capable of describing all phenomena that have been observed, or that will ever be observed (1). It is the modern incarnation of the reductionist ideal of the ancient Greeks, an approach to the natural world that has been fabulously successful in bettering the lot of mankind and continues in many people's minds to be the central paradigm of physics. A special case of this idea, and also a beautiful instance of it, is the equation of conventional nonrelativistic quantum mechanics, which describes the everyday world of human beings—air, water, rocks, fire, people, and so forth. The details of this equation are less important than the fact that it can be written down simply and is completely specified by a handful of known quantities: the charge and mass of the electron, the charges and masses of the atomic nuclei, and Planck's constant. For experts we write

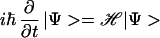1

where

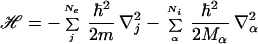2

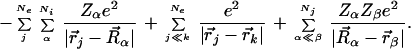The symbols Zα and Mα are the atomic number and mass of the α^th nucleus, Rα is the location of this nucleus, e and m are the electron charge and mass, r_j is the location of the j^th electron, and ℏ is Planck's constant.

Less immediate things in the universe, such as the planet Jupiter, nuclear fission, the sun, or isotopic abundances of elements in space are not described by this equation, because important elements such as gravity and nuclear interactions are missing. But except for light, which is easily included, and possibly gravity, these missing parts are irrelevant to people-scale phenomena. Eqs. 1 and 2 are, for all practical purposes, the Theory of Everything for our everyday world.

However, it is obvious glancing through this list that the Theory of Everything is not even remotely a theory of every thing (2). We know this equation is correct because it has been solved accurately for small numbers of particles (isolated atoms and small molecules) and found to agree in minute detail with experiment (3–5). However, it cannot be solved accurately when the number of particles exceeds about 10. No computer existing, or that will ever exist, can break this barrier because it is a catastrophe of dimension. If the amount of computer memory required to represent the quantum wavefunction of one particle is N then the amount required to represent the wavefunction of k particles is N^k. It is possible to perform approximate calculations for larger systems, and it is through such calculations that we have learned why atoms have the size they do, why chemical bonds have the length and strength they do, why solid matter has the elastic properties it does, why some things are transparent while others reflect or absorb light (6). With a little more experimental input for guidance it is even possible to predict atomic conformations of small molecules, simple chemical reaction rates, structural phase transitions, ferromagnetism, and sometimes even superconducting transition temperatures (7). But the schemes for approximating are not first-principles deductions but are rather art keyed to experiment, and thus tend to be the least reliable precisely when reliability is most needed, i.e., when experimental information is scarce, the physical behavior has no precedent, and the key questions have not yet been identified. There are many notorious failures of alleged ab initio computation methods, including the phase diagram of liquid ³He and the entire phenomenonology of high-temperature superconductors (8–10). Predicting protein functionality or the behavior of the human brain from these equations is patently absurd. So the triumph of the reductionism of the Greeks is a pyrrhic victory: We have succeeded in reducing all of ordinary physical behavior to a simple, correct Theory of Everything only to discover that it has revealed exactly nothing about many things of great importance.

In light of this fact it strikes a thinking person as odd that the parameters e, ℏ, and m appearing in these equations may be measured accurately in laboratory experiments involving large numbers of particles. The electron charge, for example, may be accurately measured by passing current through an electrochemical cell, plating out metal atoms, and measuring the mass deposited, the separation of the atoms in the crystal being known from x-ray diffraction (11). Simple electrical measurements performed on superconducting rings determine to high accuracy the quantity the quantum of magnetic flux hc/2e (11). A version of this phenomenon also is seen in superfluid helium, where coupling to electromagnetism is irrelevant (12). Four-point conductance measurements on semiconductors in the quantum Hall regime accurately determine the quantity e²/h (13). The magnetic field generated by a superconductor that is mechanically rotated measures e/mc (14, 15). These things are clearly true, yet they cannot be deduced by direct calculation from the Theory of Everything, for exact results cannot be predicted by approximate calculations. This point is still not understood by many professional physicists, who find it easier to believe that a deductive link exists and has only to be discovered than to face the truth that there is no link. But it is true nonetheless. Experiments of this kind work because there are higher organizing principles in nature that make them work. The Josephson quantum is exact because of the principle of continuous symmetry breaking (16). The quantum Hall effect is exact because of localization (17). Neither of these things can be deduced from microscopics, and both are transcendent, in that they would continue to be true and to lead to exact results even if the Theory of Everything were changed. Thus the existence of these effects is profoundly important, for it shows us that for at least some fundamental things in nature the Theory of Everything is irrelevant. P. W. Anderson's famous and apt description of this state of affairs is “more is different” (2).

The emergent physical phenomena regulated by higher organizing principles have a property, namely their insensitivity to microscopics, that is directly relevant to the broad question of what is knowable in the deepest sense of the term. The low-energy excitation spectrum of a conventional superconductor, for example, is completely generic and is characterized by a handful of parameters that may be determined experimentally but cannot, in general, be computed from first principles. An even more trivial example is the low-energy excitation spectrum of a conventional crystalline insulator, which consists of transverse and longitudinal sound and nothing else, regardless of details. It is rather obvious that one does not need to prove the existence of sound in a solid, for it follows from the existence of elastic moduli at long length scales, which in turn follows from the spontaneous breaking of translational and rotational symmetry characteristic of the crystalline state (16). Conversely, one therefore learns little about the atomic structure of a crystalline solid by measuring its acoustics.

The crystalline state is the simplest known example of a quantum protectorate, a stable state of matter whose generic low-energy properties are determined by a higher organizing principle and nothing else. There are many of these, the classic prototype being the Landau fermi liquid, the state of matter represented by conventional metals and normal ³He (18). Landau realized that the existence of well-defined fermionic quasiparticles at a fermi surface was a universal property of such systems independent of microscopic details, and he eventually abstracted this to the more general idea that low-energy elementary excitation spectra were generic and characteristic of distinct stable states of matter. Other important quantum protectorates include superfluidity in Bose liquids such as ⁴He and the newly discovered atomic condensates (19–21), superconductivity (22, 23), band insulation (24), ferromagnetism (25), antiferromagnetism (26), and the quantum Hall states (27). The low-energy excited quantum states of these systems are particles in exactly the same sense that the electron in the vacuum of quantum electrodynamics is a particle: They carry momentum, energy, spin, and charge, scatter off one another according to simple rules, obey fermi or bose statistics depending on their nature, and in some cases are even “relativistic,” in the sense of being described quantitively by Dirac or Klein-Gordon equations at low energy scales. Yet they are not elementary, and, as in the case of sound, simply do not exist outside the context of the stable state of matter in which they live. These quantum protectorates, with their associated emergent behavior, provide us with explicit demonstrations that the underlying microscopic theory can easily have no measurable consequences whatsoever at low energies. The nature of the underlying theory is unknowable until one raises the energy scale sufficiently to escape protection.

Thus far we have addressed the behavior of matter at comparatively low energies. But why should the universe be any different? The vacuum of space-time has a number of properties (relativity, renormalizability, gauge forces, fractional quantum numbers) that ordinary matter does not possess, and this state of affairs is alleged to be something extraordinary distinguishing the matter making up the universe from the matter we see in the laboratory (28). But this is incorrect. It has been known since the early 1970s that renormalizability is an emergent property of ordinary matter either in stable quantum phases, such as the superconducting state, or at particular zero-temperature phase transitions between such states called quantum critical points (29, 30). In either case the low-energy excitation spectrum becomes more and more generic and less and less sensitive to microscopic details as the energy scale of the measurement is lowered, until in the extreme limit of low energy all evidence of the microscopic equations vanishes away. The emergent renormalizability of quantum critical points is formally equivalent to that postulated in the standard model of elementary particles right down to the specific phrase “relevant direction” used to describe measurable quantities surviving renormalization. At least in some cases there is thought to be an emergent relativity principle in the bargain (29, 30). The rest of the strange agents in the standard model also have laboratory analogues. Particles carrying fractional quantum numbers and gauge forces between these particles occur as emergent phenomena in the fractional quantum Hall effect (17). The Higgs mechanism is nothing but superconductivity with a few technical modifications (31). Dirac fermions, spontaneous breaking of CP, and topological defects all occur in the low-energy spectrum of superfluid ³He (32–34).

Whether the universe is near a quantum critical point is not known one way or the other, for the physics of renormalization blinds one to the underlying microscopics as a matter of principle when only low-energy measurements are available. But that is exactly the point. The belief on the part of many that the renormalizability of the universe is a constraint on an underlying microscopic Theory of Everything rather than an emergent property is nothing but an unfalsifiable article of faith. But if proximity to a quantum critical point turns out to be responsible for this behavior, then just as it is impossible to infer the atomic structure of a solid by measuring long-wavelength sound, so might it be impossible to determine the true microscopic basis of the universe with the experimental tools presently at our disposal. The standard model and models based conceptually on it would be nothing but mathematically elegant phenomenological descriptions of low-energy behavior, from which, until experiments or observations could be carried out that fall outside the its region of validity, very little could be inferred about the underlying microscopic Theory of Everything. Big Bang cosmology is vulnerable to the same criticism. No one familiar with violent high-temperature phenomena would dare to infer anything about Eqs. 1 and 2 by studying explosions, for they are unstable and quite unpredictable one experiment to the next (35, 36). The assumption that the early universe should be exempt from this problem is not justified by anything except wishful thinking. It could very well turn out that the Big Bang is the ultimate emergent phenomenon, for it is impossible to miss the similarity between the large-scale structure recently discovered in the density of galaxies and the structure of styrofoam, popcorn, or puffed cereals (37, 38).

Self-organization and protection are not inherently quantum phenomena. They occur equally well in systems with temperatures or frequency scales of measurement so high that quantum effects are unobservable. Indeed the first experimental measurements of critical exponents were made on classical fluids near their liquid-vapor critical points (39). Good examples would be the spontaneous crystallization exhibited by ball bearings placed in a shallow bowl, the emission of vortices by an airplane wing (40), finite-temperature ferromagnetism, ordering phenomena in liquid crystals (41), or the spontaneous formation of micelle membranes (42). To this day the best experimental confirmations of the renormalization group come from measurements of finite-temperature critical points (43). As is the case in quantum systems, these classical ones have low-frequency dynamic properties that are regulated by principles and independent of microscopic details (44, 45). The existence of classical protectorates raises the possibility that such principles might even be at work in biology (46).

What do we learn from a closer examination of quantum and classical protectorates? First, that these are governed by emergent rules. This means, in practice, that if you are locked in a room with the system Hamiltonian, you can't figure the rules out in the absence of experiment, and hand-shaking between theory and experiment. Second, one can follow each of the ideas that explain the behavior of the protectorates we have mentioned as it evolved historically. In solid-state physics, the experimental tools available were mainly long-wavelength, so that one needed to exploit the atomic perfection of crystal lattices to infer the rules. Imperfection is always present, but time and again it was found that fundamental understanding of the emergent rules had to wait until the materials became sufficiently free of imperfection. Conventional superconductors, for which nonmagnetic impurities do not interfere appreciably with superconductivity, provide an interesting counterexample. In general it took a long time to establish that there really were higher organizing principles leading to quantum protectorates. The reason was partly materials, but also the indirectness of the information provided by experiment and the difficulty in consolidating that information, including throwing out the results of experiments that have been perfectly executed, but provide information on minute details of a particular sample, rather than on global principles that apply to all samples.

Some protectorates have prototypes for which the logical path to microscopics is at least discernable. This helped in establishing the viability of their assignment as protectorates. But we now understand that this is not always the case. For example, superfluid ³He, heavy-fermion metals, and cuprate superconductors appear to be systems in which all vestiges of this link have disappeared, and one is left with nothing but the low-energy principle itself. This problem is exacerbated when the principles of self-organization responsible for emergent behavior compete. When more than one kind of ordering is possible the system decides what to do based on subtleties that are often beyond our ken. How can one distinguish between such competition, as exists for example, in the cuprate superconductors, and a “mess”? The history of physics has shown that higher organizing principles are best identified in the limiting case in which the competition is turned off, and the key breakthroughs are almost always associated with the serendipitous discovery of such limits. Indeed, one could ask whether the laws of quantum mechanics would ever have been discovered if there had been no hydrogen atom. The laws are just as true in the methane molecule and are equally simple, but their manifestations are complicated.

The fact that the essential role played by higher organizing principles in determining emergent behavior continues to be disavowed by so many physical scientists is a poignant comment on the nature of modern science. To solid-state physicists and chemists, who are schooled in quantum mechanics and deal with it every day in the context of unpredictable electronic phenomena such as organogels (47), Kondo insulators (48), or cuprate superconductivity, the existence of these principles is so obvious that it is a cliché not discussed in polite company. However, to other kinds of scientist the idea is considered dangerous and ludicrous, for it is fundamentally at odds with the reductionist beliefs central to much of physics. But the safety that comes from acknowledging only the facts one likes is fundamentally incompatible with science. Sooner or later it must be swept away by the forces of history.

For the biologist, evolution and emergence are part of daily life. For many physicists, on the other hand, the transition from a reductionist approach may not be easy, but should, in the long run, prove highly satisfying. Living with emergence means, among other things, focusing on what experiment tells us about candidate scenarios for the way a given system might behave before attempting to explore the consequences of any specific model. This contrasts sharply with the imperative of reductionism, which requires us never to use experiment, as its objective is to construct a deductive path from the ultimate equations to the experiment without cheating. But this is unreasonable when the behavior in question is emergent, for the higher organizing principles—the core physical ideas on which the model is based—would have to be deduced from the underlying equations, and this is, in general, impossible. Repudiation of this physically unreasonable constraint is the first step down the road to fundamental discovery. No problem in physics in our time has received more attention, and with less in the way of concrete success, than that of the behavior of the cuprate superconductors, whose superconductivity was discovered serendipitously, and whose properties, especially in the underdoped region, continue to surprise (49, 50). As the high-T_c community has learned to its sorrow, deduction from microscopics has not explained, and probably cannot explain as a matter of principle, the wealth of crossover behavior discovered in the normal state of the underdoped systems, much less the remarkably high superconducting transition temperatures measured at optimal doping. Paradoxically high-T_c continues to be the most important problem in solid-state physics, and perhaps physics generally, because this very richness of behavior strongly suggests the presence of a fundamentally new and unprecedented kind of quantum emergence.

In his book “The End of Science” John Horgan (51) argues that our civilization is now facing barriers to the acquisition of knowledge so fundamental that the Golden Age of Science must be thought of as over. It is an instructive and humbling experience to attempt explaining this idea to a child. The outcome is always the same. The child eventually stops listening, smiles politely, and then runs off to explore the countless infinities of new things in his or her world. Horgan's book might more properly have been called the End of Reductionism, for it is actually a call to those of us concerned with the health of physical science to face the truth that in most respects the reductionist ideal has reached its limits as a guiding principle. Rather than a Theory of Everything we appear to face a hierarchy of Theories of Things, each emerging from its parent and evolving into its children as the energy scale is lowered. The end of reductionism is, however, not the end of science, or even the end of theoretical physics. How do proteins work their wonders? Why do magnetic insulators superconduct? Why is ³He a superfluid? Why is the electron mass in some metals stupendously large? Why do turbulent fluids display patterns? Why does black hole formation so resemble a quantum phase transition? Why do galaxies emit such enormous jets? The list is endless, and it does not include the most important questions of all, namely those raised by discoveries yet to come. The central task of theoretical physics in our time is no longer to write down the ultimate equations but rather to catalogue and understand emergent behavior in its many guises, including potentially life itself. We call this physics of the next century the study of complex adaptive matter. For better or worse we are now witnessing a transition from the science of the past, so intimately linked to reductionism, to the study of complex adaptive matter, firmly based in experiment, with its hope for providing a jumping-off point for new discoveries, new concepts, and new wisdom.