The middle way

Abstract

Mesoscopic organization in soft, hard, and biological matter is examined in the context of our present understanding of the principles responsible for emergent organized behavior (crystallinity, ferromagnetism, superconductivity, etc.) at long wavelengths in very large aggregations of particles. Particular attention is paid to the possibility that as-yet-undiscovered organizing principles might be at work at the mesoscopic scale, intermediate between atomic and macroscopic dimensions, and the implications of their discovery for biology and the physical sciences. The search for the existence and universality of such rules, the proof or disproof of organizing principles appropriate to the mesoscopic domain, is called the middle way.

Limits of Understanding

Seeing is the beginning of understanding. This may seem an obvious truism, yet it conflicts with a dogma central to much of science, that knowledge of the underlying physical laws alone is sufficient for us to understand all things, even ones that cannot be seen. But the conflict is only apparent, for the dogma is false. Although behavior of atoms and small molecules can be predicted with reasonable accuracy starting from the underlying laws of quantum mechanics, the behavior of large ones cannot, for the errors always eventually run out of control as the number of atoms increases because of exponentially increasing computer requirements. At the same time, however, very large aggregations of particles have some astonishing properties, such as the ability to levitate magnets when they are cooled to cryogenic temperatures, that are commonly acknowledged to be “understood.” How can this be? The answer is that these properties are actually caused by collective organizing principles that formally grow out of the microscopic rules but are in a real sense independent of them.

We say that superfluidity, ferromagnetism, metallic conduction, hydrodynamics, and so forth are “protected” properties of matter—generic behavior that is reliably the same one system to the next, regardless of details (1). There are more sophisticated ways of articulating this idea, such as stable fixed point of the renormalization group, but these all boil down to descriptions of behavior that emerges spontaneously and is stable against small perturbations of the underlying equations of motion. Unfortunately, the observational tools with which these principles were discovered work only at long wavelengths. Furthermore, the mathematical tools that have been used to justify the existence of protected properties from the theoretical view have focused on reaching asymptopia, the existence of a thermodynamic limit of a nearly infinite number of particles. More is clearly different (2). But we also must ask is plenty nearly enough? One could debate whether the existence of protected behavior on the macroscopic level is a fundamental truth because of quantum mechanics or is a historical accident because that is where we have had the tools to discover protectorates. However, the fact is that the length scale between atoms and small molecules on the one hand and macroscopic matter on the other is a regime into which we cannot presently see and about which we therefore know very little. This state of affairs would not be of much concern if there were a desert of physical phenomena between the very large and the very small. But, as we all know, there is life in the desert.

The miracles of nature revealed by modern molecular biology are no less astonishing than those found by physicists in macroscopic matter. Their existence leads one to question whether as-yet-undiscovered organizing principles might be at work at the mesoscopic scale, at least in living things. This is by any measure a central philosophical controversy of modern science, for a commonly held view is that there are no principles in biology except for Darwinian evolution. But what if this view is just a consequence of our inability to see? Indeed the rules of self-organization at macroscopic length scales were not self-evident at the time of their discovery and were accepted as true only after repeated confrontations with experiment left no alternative. The existence of similar rules at the mesoscopic scale would have profound implications for all of science, not just biology, for noncrystalline matter often has curious and poorly understood behavior suggestive of mesoscopic organization. It is thus a question worth asking. We call the search for the existence of mesoscopic protectorates—the proof or disproof of organizing principles appropriate to the mesoscopic domain—the middle way.

Life in the Desert

Twentieth-century science has uncovered the fact that there are numerous large molecules that carry out the processes of life. Although the functions carried out by these molecules are still very incompletely understood, they are amazing to an extent rarely appreciated by physical scientists and engineers. Proteins can catalyze a vast number of unrelated chemical reactions. They can pick out one substrate from thousands of chemically similar ones. They can act like computers executing a sequence of instructions. They can alter their activity through the presence of specific affector molecules in their environments. They can function as signals or receptors for these signals. They can be poisons. They can assemble together spontaneously to form mechanical structures like the cytoskeleton or viruses. The precedent of life allows no other conclusion than that mesoscopic objects organize themselves and function in ways unlike anything we know at very large or very small scales.

Nonbiological systems also have interesting mesoscopic behavior, although it is not as well understood. Glasses, for example, which have structure on this scale, exhibit a strange low temperature-specific heat, and at higher temperatures, memory effect, and nonergodicity, behavior also seen in protein crystals. They are unstable and age, i.e., interconvert their structures slowly over time while showing no significant changes in x-ray scattering, in contrast to the stability and time-independence of crystalline solids (3). They also exhibit a wide range of time scales of motion, including indications that entire mesoscopic regions reconfigure themselves cooperatively. All of these phenomena are organizational, in that the atomic constituents of glasses and interactions are well known, but how they cooperate to yield the observed behavior is not.

Some kinds of inanimate mesoscopic self-organization can be easily visualized, and perhaps not coincidentally are identified as understood. For example, a variety of mesoscopic structures, some of which are aptly analogous to the cellular membrane, can be formed by assembling artificial polymers in solution or amphiphiles in water-oil mixtures (4, 5). There are also spherical micelles, self-assembled droplets of surfactant, and interpenetrating networks of water and lipids closely related to structures within the Golgi apparatus (6). Such amphiphillic assemblies exhibit dynamics at a range of long time scales similar to the relaxation seen in glasses. Another instance of visible self-organization is the organogel, a simple monomer that does not crystallize easily out of solution but instead forms fibrous webs with complex internal substucture similar to those found in organic gelatins (7).

Mesoscopic organization also occurs as a purely electronic phenomenon in systems with relatively defect-free atomic lattices. For example, electrons in semiconductors engineered to the mesoscopic scale show a wealth of incipient ordering phenomena that continue to surprise. There are spin glasses, systems that exhibit remanence, hysteresis, memory, and so forth but consist only of unpaired spins on impurity sites communicating through conventional exchange (8,9). There is the class of strongly correlated electronic materials, including heavy-fermion metals, high-T_c and organic superconductors, and colossal magnetoresistive manganites, which exhibit many strange behaviors at the mesoscopic scale that have thus far defied description. Among these behaviors are dynamic magnetic domains (stripes) (10), and anomalous low-frequency spin fluctuations (11) in the cuprate superconductors, large low temperature-specific heats in the heavy electron systems (12), and extreme impurity sensitivity. These latter effects have not been conclusively identified as mesoscopic, but their failure to disappear as the sample quality improves is highly suggestive. Ideas about mesoscopic organization in correlated-electron materials are particularly relevant to the larger issue of measurement because they are so obviously prejudiced by the lack of mesoscopic eyes.

Conflicts of Principle

The existence or nonexistence of mesoscopic organizing principles has become an issue of deeply held belief, rarely discussed in public yet informing much of what we do. Whether this situation is the result of intrinsic limitations on measurement capability is perhaps debatable, but its effect on science is unmistakable. For example, our experience with macroscopic physics argues strongly for the fundamental impossibility of proceeding from sequence to structure to function in biology by means of computer modeling unless there are principles that protect the calculations and make them predictive. Thus this agenda of the computational biologist tacitly acknowledges the existence of principles, even at the same time that some of its adherents forcefully disavow the idea. Similarly our experience with macroscopic organization tells us that rules that are dreamt up without the benefit of physical insight are nearly always wrong, for correct rules are really natural phenomena and therefore must be discovered, not invented. The widely held view of bioinformatics as librarianship effectively proceeds from the assumption that there are no principles, for otherwise the ad hoc organizations of data would be seen as theories without physical basis and therefore meaningless. But the way forward in science begins with understanding what one doesn't understand—identifying which parts of one's world view are informed and which parts are prejudice. Are there organizing principles in mesoscopic systems? The truth is that we do not know one way or the other. The experimental record has not yet spoken. But it is clear that the question is sufficiently important that it cannot be evaded much longer. Whether we want to or not, we are now forced to take a stand.

In the world of biology, that at least some simple rules operate at the mesoscopic scale is demonstrated by the fact that some amino acid sequences fold and others do not. This distinction, which is quite sharp for large proteins, is arguably attributed to energy landscapes that funnel the molecule through a sequence of configurations that are virtually never metastable, so that the folded state can be reached by any one of a large number of paths (13, 14). Even more persuasive is the observation of the nonuniqueness of the sequence that folds into a protein with a particular structure, say that of myoglobin. This happens reliably for sequences that almost appear randomly related to each other, so it would appear that small perturbations of the underlying system still preserve myoglobiness, which could then be regarded as an emergent collective property. How this occurs is only partially understood.

There is also evidence that not only the final structure but also the average properties of the structures that form on the routes to the folded state are largely shared by members of a family of folds. Statistics of the partially folded state vary only weakly with sequence, but strongly depend on topology (15). This robustness of folding behavior makes the empirical case for some protected behavior of mesoscopic biological matter. Does there then exist a funnel protectorate?

Not only structure, but also some aspects of biomolecular function appear to be protected. This protection is most elegantly seen in the polymorphism of enzymes: in the same individual slightly different sequence versions of the same enzyme catalyze appropriate reactions (16). Single molecule experiments on enzymes show that biological catalysts sometimes have highly fluctuating rates from copy to copy (17). Yet the organism lives. This is a hint that protection in biology may arise from the evolutionary necessity of tolerating diversity. But is that the only cause?

Outside the biological world there is circumstantial evidence for protection at mesoscopic scales. Glasses often are thought of as just very slow liquids. Explaining their dynamics then would be just a question of getting the local molecular interactions right and studying the movement of the atoms on a computer. Arguing against this is the well-known correlation between transport properties and configurational entropy, known since the 1940s to occur across a wide range of substances (18). This correlation is sufficiently good that it can be used to engineer the properties of glassy polymers via addition of plasticizers. There are experimental hints from neutron scattering (19) and NMR (20) experiments that glassy dynamics involves motion on mesoscopic length scales. But we are truly stymied at getting more details at these length scales by the lack of better tools for ferreting out organization at this size range.

While the transition from liquid to glass lies in a regime where classical statistical mechanics probably holds sway, in the low-temperature quantum regime there is evidence for protected behavior related to structures we cannot see. All amorphous substances show a linear-specific heat, a result found experimentally and a shock to theorists brought up on Debye's continuum description of solids at low temperature. Although theorists cleverly resolved the problem by pointing out the existence of two level tunneling systems (21), it has later surprised them to find universal characteristics of the density and scattering properties of these two level systems in a wide range of chemically distinct substances (22). Despite recent progress (23, 24) no entirely convincing microscopic identification of what is actually tunneling has yet been made by experiment.

Struggling to Overcome Large and Small Prejudices

The success of the sciences of the small and large has been based on some simple general guidelines. One of these guidelines is the expectation that systems possess a unique favored state and that the important motions of the system can be described as combinations of excitations that involve structures in some sense close to that favored state (25). These excitations may scatter off each other, but primarily retain their integrity during their motions (26). Occasionally, a second state can emerge through a phase transition. In this case also, there is considerable understanding of how structures self similar on all length scales can emerge near a continuous phase transition. But these principles are no longer sufficient in the mesoscopic realm. The phenomena of nonexponential dynamics and aging suggest that many states, each potentially very long lived, can be found for systems with mesoscopic organization. In some situations no single one dominates. Not all motions can be simply described as fluctuations near one of these states. Transitions between states are also important (27).

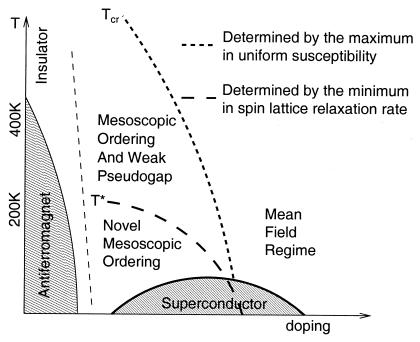
In one-component systems, either classical or quantum mechanical, a candidate principle for understanding the breakdown of the elementary excitation picture and the emergence of mesoscopic organization is nonlinear feedback. This is illustrated in one approach to strongly correlated electron systems in which the interaction between electrons plays the dominant role in determining system behavior. Feedback occurs because the interaction between charge carriers that can dramatically alter the nature of the excitations is itself determined by the excitations it alters (28). This feedback has, of course, been known since Debye's theory of electrolytes was pushed outside the dilute unit, but its quantum mechanical consequences are more subtle, because the speed at which an environmental disturbance disappears can determine the nature of an interaction. An example is the emergence of an effective dynamically attractive interaction between the essential repulsive helium atoms in 3He, an attraction that leads to Cooper pairs. Dynamical feedback often will just renormalize the excitations, which is clearly the case when the associated feedback is negative, in which case the system tends to stay in its existing state. If it is positive, however, it can give rise to a transition or crossover to another state, one that may possess organization on the mesoscopic scale. Such feedback is believed by many to be responsible for the remarkable behavior found in the normal state of the underdoped cuprate superconductors, where, as shown in Fig. 1, mesoscopic organization may be present in one or more of the three distinct phases of matter found as one lowers the temperature in the normal state before the system finally makes its transition to the superconducting state (29).

Figure 1.

Generic phase diagram of high temperature superconducting cuprates. The true thermodynamic phases (antiferromagnetic at low doping and superconducting at higher doping are depicted by the shaded regions. The remaining lines correspond to crossovers, visible in a variety of experiments.

Mesoscopic organization induced by feedback may not be confined to strongly correlated electron systems. The layered structure argued by theorists to exist at densities just below nuclear matter density in the neutron-rich crust of a neutron star (30) represents an additional example from the quantum domain. The well-known mode-mode coupling theory (31) for classical fluids also represents an attempt to use dynamical feedback to account for the nascent mesoscopic organization found in a system of strongly correlated atoms moving in a liquid. Dynamical feedback in liquids may be visualized as a cage effect. The slow motions of the neighbors of a given molecule allow them to provide a frictional cage on a central molecule's motion, slowing it. Because, in the democratic tradition, these neighbors would have their own cages, they must slow, too. These equations predict a transition to a nonergodic state in which molecules remain localized near their initial locations. Some of the predictions of this feedback theory are borne out in neutron scattering studies of liquids (19), but others are not. It now seems that this theory indicates a kind of stability limit for the usual picture of a liquid as merely a dense gas, all of whose motions occur on the natural microscopic time scale of intermolecular collisions. The predicted nonergodicity signals the need to describe more complex motions involving transitions between widely different configurations (32).

One concept to describe this complexity of classical liquids, glasses and proteins, is the energy landscape (33, 34). Energy landscapes try to capture the idea that, although any many body system has myriad microscopic states, these can be organized into a collection of basins. These basins are robust to small external perturbations. Motions within these basins can be described much as for the simpler systems and occur on the natural microscopic time scale. On the other hand, the experimental clues suggest that unlike the simpler systems, here there are a large number of structurally distinct basins. Many of these are distant from each other, but have comparable energies. The arrangements of these often are pictured as low dimensional plots. These caricatures of energy landscapes are meant to capture the idea of the diversity of the basins and the nature of the bottlenecks and energy barriers in configurations that prevent the system from rapidly moving from one state to another. The difficulty with these pictures is that the only fully accurate picture of an energy landscape would have an extremely high dimension. One can ascribe a coordinate system locally to any one basin and perhaps a few similar neighboring ones, but this does not apply throughout the configuration space. An analogous, but much simpler situation arises when making flat maps of the spherical Earth, where the topology of the sphere makes the position of the pole on a two-dimensional plot ambiguous. Quantitative treatments of thermodynamics and dynamics of energy landscapes currently try to use only statistical information about landscape topography.

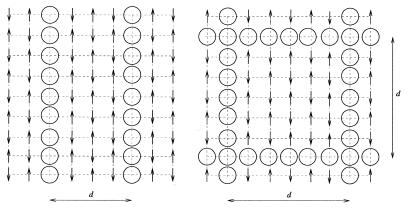
One prototype landscape is very rugged. On such a landscape, explicitly found for some statistical models, you can find configurations of comparable and rather low energies that are quite different in appearance. In Fig. 2 two different configurations of holes in simple model of a transition metal oxide are shown, along with their energies. Although these states can interconvert, they do so in a very complex way, involving large-scale rearrangements of structure and correspondingly large activation energies. A similar situation would be found most of the time for the energy landscape of a polymer of amino acids, if one chooses its sequence at random. The property of having such a set of low-energy states is connected with the idea of replica symmetry breaking (35–37): different copies of the same system may well fall into different long-lived states through accidents of detailed molecular motion.

Figure 2.

Stripe and grid configurations of holes (circles) in an antiferromagnetic background (arrows, indicating spin direction) at the same hole concentration level (d denotes the distance between stripe or grid lines). Note the change in sign of the local magnetization in the magnetic domains (π phase shift), which makes motion of the holes across line segments energetically inexpensive. Both configurations correspond to low energy states, with a large activation energy for a transition between them, caused by the Coulomb repulsion between holes.

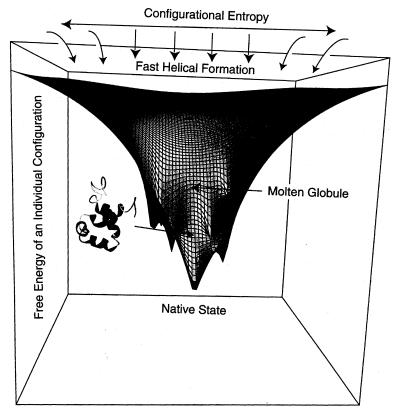
Another prototype landscape for mesoscopic systems is not so rugged but has one dominant basin of attraction. This so-called funnel landscape, shown in Fig. 3, is not typically found for most polymers of amino acids, but seems to describe the important special case of the proteins of nature that evolve to fold into a small set of related states. Out of all possible sequences, funnel landscapes are exponentially rare compared with rugged landscapes.

Figure 3.

Sketch of a funnel landscape found in certain protein structures.

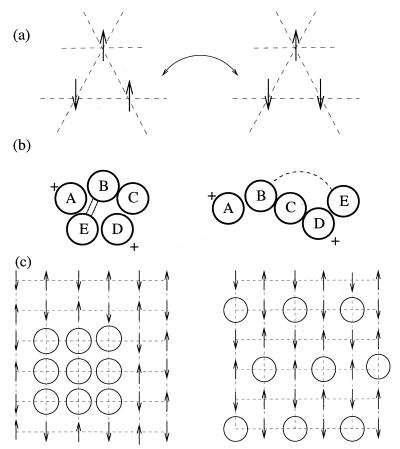
Although the complexity of the energy landscape is probably a fact of life at these mesoscopic scales, its origin often has been pictured as caused by frustration (38), examples of which are depicted in Fig. 4. Frustration is an anthropomorphic and therefore perhaps provisional candidate concept. To explain the concept, we imagine the energies governing the motions of the system can be partitioned into competing parts. Of course the system does not know how we divide its energy up. Sometimes, however, the division seems very natural to us. For example, in a magnetic alloy some impurity spins will be directly coupled in such a way to favor their becoming parallel to each other whereas others at different separations will be coupled so as to favor an antiparallel arrangement. The tendency of these individual parts of the energy to produce local order cannot be simultaneously satisfied in any given individual system configuration. This frustration suggests the possibility that quite different states can be stable and compete with each other, giving rise to the diversity of the landscape. The common frustration of the interactions between different pairs of amino acids is the cause of the random polypeptide's rugged energy landscape. The funnel landscape emerges only for those special sequences for which there is a structure in which nearly all the different interactions are simultaneously minimized; i.e., biological proteins are only minimally frustrated.

Figure 4.

Examples of frustration. (a) For antiferromagnetically (AF) coupled Ising spins on a triangular lattice one of the AF bonds is always broken. (b) Folding of heteropolymers can be frustrated by the competing, e.g., bonding (indicated by solid lines) and Coulomb interactions (indicated by +) between different constituents (A–E). (c) AF interactions in doped transition metal oxides energetically favor a phase-separated state, which is unfavorable for the Coulomb interaction, whereas the Coulomb interaction favors a Wigner crystal state that is unfavorable for the AF interactions; the result of the competition (frustration) yields formation of patterns, such as those shown in Fig. 2.

Both the amphiphile systems and the correlated electron systems also have been described by using the concept of frustration. In the case of amphiphiles the conflict arises between the tendency of the hydrophobic forces to separate lipid and water. The head group of the amphiphile has a tendency to remain in the water phase and the tail group in the lipid. Head and tail must remain connected, however. This example is rather analogous to the origin of frustration in the protein situation. Various views exist on the source of frustration in correlated electron systems. One idea is that positively charged vacancies, induced by chemical doping, inhibit any intrinsic magnetic order but cannot completely avoid magnetic regions. To do this they would have to group together, which in turn leads to a large Coulomb interaction between them. Thus magnetic order and electrostatic interactions frustrate each other and are in conflict, which is surprisingly similar to the amphiphile problem. In a sense the vacancies act like a surfactant.

Energy landscape pictures have a hard time indicating how distant parts of a system communicate with each other. It is thought that generally mesoscopic parts of the system with frustration will break up into domains or droplets. This idea started by McMillan has been extended to describe a large number of systems, including glasses and proteins (39–43). The interface energy between the droplets is scale dependent. Scale dependence of the interaction energy may be a more objective way of quantifying the concept of frustration. Droplet excitations for large systems with mesoscopic correlations may replace the concept of collective modes or quasiparticles relevant to simple systems with a single preferred state. One interesting question is whether the droplets should be thought of themselves as simple objects or have within them a complex energy landscape. Also the existence and nature of droplet configurations remains controversial because no mesoscopic probe has yet been devised to clearly visualize them.

Although the feedback idea has been applied to both quantum and classical systems, this rapid survey of candidate concepts largely borrowed from macroscopic systems for use in mesoscopically organized systems shows that the situation in quantum mechanics is much less developed than even for the classical systems. For example, frustration often is used to argue that a correlated electron system will not order. The resulting state then is often described as a resonance hybrid, but the properties of these quantum mechanical superpositions of different states are hard to deduce. What takes the place of energy landscapes? The dynamics and role of droplet excitations for highly quantum systems is still quite murky, which is unfortunate because attempts to build quantum computers will doubtless require this sort of understanding.

The Mesoscopic Frontier

To many people the world of mesoscale phenomena would seem to be intrinsically confined, but we do not believe this is so. First, the richness of experimental phenomena in the field shows that the subject is still in its infancy. In the short run even the basics have to be more firmly established. The nascent theoretical concepts are sketchy because they have been informed primarily by experiments on the wrong length scales. Indeed an argument can be made that the lack of appropriate probes for characterizing mesoscopic order is not the result of lack of scientific attention or inadequate funds but may represent intrinsic physical limitations. Our own ability to see is based on sensing the multiple correlations intrinsic in the complex shape of an object. The constraints of quantum mechanics limit the complexity of correlations that can be measured with light or particles when they have a wavelength sufficiently short to resolve an individual mesoscopic object. We may have to destroy an object if we want to study it.

Still, there is considerable hope for progress on the experimental side. Scanning tunneling microscopy and atomic force microscopy allow us to measure mesoscale phenomena, albeit only on the surface of complex objects. The time scale for such measurements also requires improvement. Other techniques probing small mesoscale regions in three dimensions are likely to be developed. For example, time-dependent x-ray spectroscopy and x-ray speckle dynamics (44) using synchrotron radiation will allow probes of structure and dynamics beyond the currently available simple static diffraction pattern. Nonlinear and fluctuation spectroscopies (45), including improved neutron scattering and single molecule techniques (46), also should help. The scientific community needs to support these efforts to establish the experimental basis for the development of scientific principles of mesoscopic organization. Clearly, experiment alone will not be enough and theorists will have to work hard to keep up with the onslaught of new information.

The discovery of physical principles at mesoscale will reinforce the attack by biologists on the mysteries of cellular function. But, beyond this, a framework for understanding mesoscopic organization will be an extraordinary help in the effort to create an entirely artificial system with the complex adaptive behavior characteristic of life. Such artificial systems should be capable of a variety of functions that present biological systems cannot perform.

In any event, the applicability of the science of mesoscale organization that we believe can be developed will not be limited to the world between angstroms and centimeters. Organization following similar principles may well be manifested in astrophysics. As we have noted, complex structures already have been proposed for the exotic matter expected in neutron stars, while ideas developed to explain mescoscopic organization on Earth may be useful in explaining the origin of large-scale structure in the universe.