Mechanistic role of movement and strain sensitivity in muscle contraction

Abstract

Tension generation can be studied by applying step perturbations to contracting muscle fibers and subdividing the mechanical response into exponential phases. The de novo tension-generating isomerization is associated with one of these phases. Earlier work has shown that a temperature jump perturbs the equilibrium constant directly to increase tension. Here, we show that a length jump functions quite differently. A step release (relative movement of thick and thin filaments) appears to release a steric constraint on an ensemble of noncompetent postphosphate release actomyosin cross-bridges, enabling them to generate tension, a concentration jump in effect. Structural studies [Taylor KA, et al. (1999) Tomographic 3D reconstruction of quick-frozen, Ca²⁺-activated contracting insect flight muscle. Cell 99:421–431] that map to these kinetics indicate that both catalytic and lever arm domains of noncompetent myosin heads change angle on actin, whereas lever arm movement alone mediates the power stroke. Together, these kinetic and structural observations show a 13-nm overall interaction distance of myosin with actin, including a final 4- to 6-nm power stroke when the catalytic domain is fixed on actin. Raising fiber temperature with both perturbation techniques accelerates the forward, but slows the reverse rate constant of tension generation, kinetics akin to the unfolding/folding of small proteins. Decreasing strain, however, causes both forward and reverse rate constants to increase. Despite these changes in rate, the equilibrium constant is strain-insensitive. Activation enthalpy and entropy data show this invariance to be the result of enthalpy–entropy compensation. Reaction amplitudes confirm a strain-invariant equilibrium constant and thus a strain-insensitive ratio of pretension- to tension-generating states as work is done.

The question of how the many asynchronously operating myosin motors generate tension and movement in muscle fibers is a critical issue in biology. Two different mechanisms have been proposed. In one, thermal fluctuations in position enable myosin heads (cross-bridges) to bind actin in a strained configuration to generate tension (1, 2). This rectification process can occur between detached and attached heads or by heads changing angle between subsites while attached to actin. For these thermal ratchet models to function at physiological rates, a sequence of multiple attached states is generally required, the stiffer the cross-bridge the larger the number of states. Heterogeneous mechanisms, some with sequential temperature-sensitive and -insensitive tension-generating transitions, have also been invoked (3–5). Power stroke mechanisms in which tension generation occurs as a single-step conformational change in attached cross-bridges offer an alternative mechanism e.g. (6–10). Other important aspects include the relationship between intermediate states of the ATPase cycle and tension generation. Defining the link between tension generation and the release of the products of hydrolysis and to the free energy change of P_i release, in particular, has proved demanding. Articles placing tension generation before (11–14), during (15, 16), or after (7, 17–20) P_i release reflect this issue. In contrast, there is general agreement that dissociation of ADP occurs last from low-strain cross-bridges at the end of the cycle. Aside from these issues, there is discussion over whether tension is the product of a state(s) or whether it is synchronous with a biochemical transition (16).

Our experiments are on single-muscle fibers in which multiple motors are set in a paracrystalline array of interdigitating myosin thick and actin thin filaments. This array increases signal over single-molecule experiments. The disadvantage of fibers is that mechanical linking of individual motors through thick and thin filaments significantly complicates interpretation (16, 21–23). Our approach is to select experimental conditions carefully to minimize this cooperativity. To this end, we found that with minimal movement (obtained by changing fiber temperature alone) and fast myosin fibers contracting in the presence of low concentrations of ATP hydrolysis products there is a “kinetic window” in which the contractile cycle can be modeled as a fast isomerization between pretension- and tension-generating states in a much slower background steady-state ATPase cycle (9). Under these conditions, the equilibrium constant for tension generation was obtained from the temperature dependence of fiber tension (8, 9), and the forward and reverse rate constants were obtained from laser temperature jump (T-jump) experiments (9). The unexpected finding was that raising temperature accelerates the rate of tension generation and slows its reversal, similar to the two-state fast unfolding/folding of small proteins. Thus, tension generation and unfolding show Arrhenius behavior (a normal, positive activation enthalpy) whereas reversal of tension generation and folding show non/anti-Arrhenius kinetics (an “apparent” negative activation enthalpy). The anomalous temperature dependence of protein folding, and by analogy the reversal of tension generation, is thought to arise from the expansion of the ensemble of denatured states as temperature increases to slow the multipathway search for the folded state. Accordingly, localized unfolding of cross-bridge tertiary and/or secondary structure (possibly SH1-helix melting, bending of the β-sheet core of the myosin head, and related structural changes) coupled to rigid-body movements described in structural studies (10, 24) was proposed as a plausible mechanism of contraction (9). Although these observations support a temperature-dependent power stroke mechanism, the possibility remains that temperature-insensitive steps could contribute to tension generation (3–5).

This progress encouraged us to test whether two-state analysis could be extended to tension generation triggered by movement. To do this, a small length jump (L-jump) is applied to a contracting muscle fiber held at both ends to prevent shortening. The resulting tension transients are complex because all actomyosin cross-bridge states that generate or bear tension (transiently or continuously) are affected. The 4-exponential L-jump response contrasts with the simpler, biexponential laser T-jump tension transients (7, 25). One exponential phase (phase 2_slow in the L-jump, τ₂ in the laser T-jump) appears associated with de novo tension generation. Phase 2_slow and phase 2_fast, a damped elasticity, comprise the classical Huxley–Simmons phase 2 (7, 19) or “rapid recovery of tension” associated with studies on tension generation in muscle for well on 3 decades (1).

Strain sensitivity is a signature property of the kinetics of tension generation (e.g., 26). In muscle, step releases lower strain, accelerating the reaction; step stretches increase strain, slowing the reaction (1). This has led to the general assumption of a strain-sensitive equilibrium constant(s) for tension generation. The hypothesis, however, has not been tested because the strain dependence of the intrinsic forward and reverse rate constants has been unavailable, only the strain sensitivity of the observed/apparent rate constant has been measured. Thus, there has been a widely held, but experimentally unverified, assumption that changes in strain alter the ratio of pretension-generating:tension-generating states. Here, we determine the strain dependence of the forward and reverse rate constants of tension generation. Strain dependences of the activation parameters for tension generation and its reversal are used to probe the compensatory mechanism involved. Reaction amplitudes show the L-jump mechanism to be more complex than the two-state sequence adequate to model T-jump amplitude data.

Results

L-Jump Tension Transients.

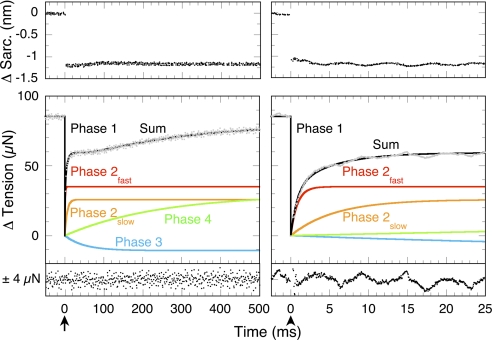
A typical tension transient after a small L-jump of a maximally Ca²⁺-activated fiber contracting under isometric conditions is illustrated in Fig. 1. The tension drop synchronous with the L-jump is termed phase 1 and measures instantaneous stiffness (1). A tension transient of four simultaneous and progressively slower exponential phases (2_fast, 2_slow, 3, 4) follows. The fastest [phase 2_fast (red)], is a component of the classical phase 2. Its rate is virtually temperature-insensitive, and its amplitude is proportional to phase 1 stiffness (19). Thus, phase 2_fast has the mechanical properties of a damped (slow-responding) entropic spring (27). Accordingly, phases 2_fast and 1 are absent (except as low-amplitude artifacts caused by fiber expansion) from laser T-jump tension transients (7). Phase 2_slow (orange), the other slower component of phase 2, has properties consistent with de novo tension generation (7). Its T-jump equivalent is phase τ₂ (7, 9, 18, 19, 25, 28). Phase 3 (blue) appears associated with the kinetics of P_i release (see Table 2 in ref. 19). Phase 4 (green), the slowest phase, mediates the asymptotic return to isometric tension. The entire tension transient is determined by nine numbers: a rate and amplitude each for phases 2_fast, 2_slow, 3, and 4 plus an amplitude for phase 1. The task here is to characterize phase 2_slow, the hypothesized tension-generating state.

Fig. 1.

Exponential phases of an L-jump tension transient. The response of a skinned, maximally Ca²⁺-activated, rabbit psoas fiber undergoing isometric contraction at 11 °C to a 160-μs L-jump of −1.5 nm per half sarcomere applied at the arrows is shown. Eight transients were averaged. Sarcomere length and tension records are shown on two different time bases. Resolved fits to phases 1, 2_fast, 2_slow, 3, and 4 are labeled, and the overall fit (the sum of their amplitudes) is drawn in black through gray raw data. Residuals are plotted below each panel.

Temperature and the Rate of Phase 2_slow.

An Arrhenius plot of the temperature dependence of the rate of phase 2_slow for a small −0.75-nm L-jump is illustrated in Fig. 2A. As with T-jump data (9), tension generation is modeled as a fast two-state isomerization in a much slower steady-state cycle

where A is the preforce-generating state, B is the force-generating state, and isometric tension is used as a measure of the concentration of B. For this, the simplest of mechanisms, the observed rate constant or reciprocal relaxation time is phase 2_slow = k₁ + k₋₁. Forward and reverse rate constants at a particular temperature can be readily calculated (9): k₋₁ = phase 2_slow/(K_T + 1) and k₁ = phase 2_slow − k₋₁. The equilibrium constant for tension generation K_T at temperature T is calculated by using the van't Hoff equation K_T = [B]/[A] = k₁/k₋₁ = exp[(−ΔH^o/R)(1/T − 1/T_m)] with a ΔH^o of 116.1 ± 13.6 kJ mol⁻¹ and a T_m (transition midpoint temperature) of 9.9 ± 0.6 °C obtained from isometric tension vs. temperature data (9). As in the T-jump, Arrhenius plots of the k₁ and k₋₁ values show normal Arrhenius behavior for tension generation (Fig. 2A, red) and anti-Arrhenius behavior for its reversal (Fig. 2A, blue). Above the ≈10 °C T_m, acceleration of k₁ with increasing temperature progressively dominates the kinetics of phase 2_slow (Fig. 2A, orange); below the T_m, the increase in k₋₁ with decreasing temperature progressively dominates the kinetics. This inversion or “dog's leg” at ≈10 °C in the phase 2_slow plot, commented on (7, 19), is now understood to arise from the positive and negative temperature dependences of k₁, and k₋₁ (9), the larger the step release the more apparent this feature (e.g., Fig. 4). Associated activation enthalpy (ΔH^‡) and entropy (ΔS^‡) values for k₁ and k₋₁ are listed in the legend.

Fig. 2.

Response of phase 2_slow rates and amplitudes to temperature. (A) Arrhenius plots of the forward and reverse rate constants of phase 2_slow show that k₁ (red) increases (Arrhenius behavior) whereas the rate of k₋₁ (blue) decreases (anti-Arrhenius behavior) with temperature. The continuous line drawn through the observed rate constant of phase 2_slow (orange) is the sum of fits to the forward and reverse rate constants. Phase 2_slow rate data were obtained from a −0.75 nm per half-sarcomere step releases. Activation parameters for k₁ are ΔH^‡ = 72.7 ± 11.2 kJ mol⁻¹, ΔS^‡ = 51.9 ± 38.0 J mol⁻¹ K⁻¹; for k₋₁ ΔH^‡ = −40.9 ± 5.8 kJ mol⁻¹, ΔS^‡ = −349.4 ± 21.1 J mol⁻¹ K⁻¹. (B) Dependence of L-jump phase 2_slow and laser T-jump phase τ₂ amplitudes on the temperature-induced increase in fiber isometric tension. A linear least-squares fit is applied to the phase 2_slow amplitudes at and above 5 °C (solid orange circles). The outlier at 1 °C is shown (hollow orange circle). A −1.5 nm per half-sarcomere step release was used. These data contrast with the quite different bell-shaped dependence of the amplitude of T-jump phase τ₂ (gray) on isometric tension (9). A maximum tension of 351.6 kN m⁻² is used as the x axis limit tension. Error bars are mean ± SE.

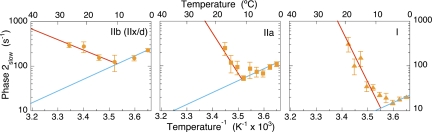
Fig. 4.

Phase 2_slow kinetics in different fiber types used to locate the tension-generating step in the cross-bridge cycle. Tangents drawn to the high (red) and low (blue) temperature dependences of the observed rate constant of phase 2_slow are used to approximate the forward and reverse rate constants of tension generation in rabbit psoas type II D/X (IIB old nomenclature), and mouse medium speed type IIA and type I slow fibers. The slope of the Arrhenius plot of the forward rate constant increases the slower the fiber type. The slope of the anti-Arrhenius plot of the reverse rate constant is fiber type-independent. Data are adapted with permission from Davis and Epstein (19). Error bars are mean ± SE. [Reproduced with permission from ref. 19 (Copyright 2003, Biophysical Society).]

Strain and the Kinetics of Phase 2_slow.

Arrhenius plots of k₁ and k₋₁ values from different-sized length-step experiments give insights into the strain sensitivity of tension generation. We show K_T for tension generation to be strain-insensitive even though the lower strain accelerates both k₁ and k₋₁. Rate and equilibrium constant data at 20 °C illustrate this. Tension generation at isometric strain [T-jump data (9)] has k₁, k₋₁, and K_20° values of 162 s⁻¹, 28.9 s⁻¹, and 5.6, respectively, lower strain (−0.75-nm per half-sarcomere) results in faster k₁ and k₋₁ values of 348 s⁻¹, 66.8 s⁻¹, but a similar K_20° of 5.2. Thus, rate constants change, but equilibrium constants are invariant. Changes in the activation parameters provide additional insights into mechanism. Table 1 lists ΔH^‡ and ΔS^‡ values for k₁ and k₋₁ obtained at isometric tension and with two different-sized step releases. Here, ΔH^‡_k1 and ΔS^‡_k1 values decrease, whereas ΔH^‡_k−1 and ΔS^‡_k−1 values increase with decreasing strain. Equations ΔH^o = ΔH^‡_k1 − ΔH^‡_k−1, ΔS^o = ΔS^‡_k1 − ΔS^‡_k−1, and ΔG^o = ΔH^o − TΔS relate the activation and thermodynamic parameters. Near-constant ΔH^o values of 115.0 ± 7.7, 113.6 ± 12.6, and, 119.6 ± 21.1 kJ mol⁻¹ and ΔS^o values of 406.6 ± 27.0, 401.3 ± 43.5, and 422.1 ± 76.3 J mol⁻¹ K⁻¹ result, respectively, at isometric strain, −0.75 and −1.5 nm per half-sarcomere step releases. It is evident that despite large changes in ΔH^‡ and ΔS^‡ values, enthalpy–entropy compensation results in a largely strain-independent ΔG^o and K_T for tension generation. Work done can be readily calculated from the displacement by assuming a linear spring as series compliance. A concern is that the use of K_T values, determined at isometric tension, could introduce error. To test this, we offset K_T to higher and lower values and fitted the kinetics. No systematic bias in quality of fit was detected. To summarize, the larger the step release, the faster phase 2_slow, k₁, and k₋₁, but large changes in ΔH^‡ and ΔS^‡ values for k₁ and k₋₁ compensate to render ΔG^o and K_T for tension generation close to invariant. This remarkable observation, related to the biophysics of protein conformational change, is confirmed by amplitude data treated next.

Table 1.

Comparison of activation enthalpy and entropy values for the forward and reverse rate constants of tension generation at different levels of strain

L-jump, nm/half-sarcomere	k1		k−1
	ΔH‡, kJ mol−1	ΔS‡, J mol−1K−1	ΔH‡, kJ mol−1	ΔS‡, J mol−1K−1
0	88.1 ± 3.9	98.1 ± 13.0	−26.9 ± 6.6	−308.5 ± 23.7
−0.75	72.7 ± 11.2	51.9 ± 38.0	−40.9 ± 5.8	−349.4 ± 21.1
−1.50	54.7 ± 11.4	−15.3 ± 38.6	−64.9 ± 17.7	−437.4 ± 65.8

Temperature and the Amplitude of Phase 2_slow.

The isomerization of Reaction 1 can be perturbed in two ways: (i) directly, with a step change in K_T, a bell-shaped dependence of amplitude vs. tension (B) results; and (ii) indirectly, via a step change in the concentration of A, in this case, a linear dependence of amplitude vs. tension results. Amplitude plots of phase 2_slow (orange) and τ₂ (gray) (9) vs. isometric tension in Fig. 2B typify these two modes of perturbation. Linearity of the phase 2_slow plot is indicative of indirect perturbation by a concentration jump, whereas the coplotted symmetrical bell-shaped curve of τ₂ amplitude data with midpoint at the T_m (half-maximum tension) signifies direct perturbation (9). Note, the maximum (limit) tension of 184 kN m⁻² (see Fig. 1 of ref. 9) requires scaling by ≈1.9 to yield the 351.6 kN m⁻² value we use here to match the systematically higher tensions of our fibers.

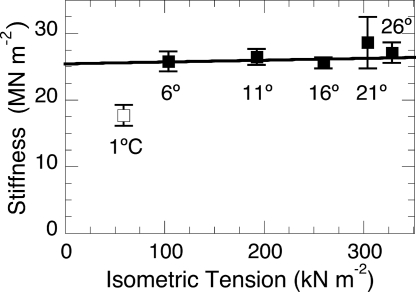
For two-state isomerizations, the sum of the reactant concentrations is always constant. In fibers, this translates into a requirement for the saturation of accessible binding sites on actin by myosin. This condition appears to hold at and above 5 °C (9). Usefully, fiber stiffness provides a second measure of changes in attached cross-bridge number, constant stiffness equates with constant occupancy. Myofilament compliance causes fiber stiffness to be a nonlinear measure of cross-bridge occupancy with elevated sensitivity at the low (≈25%) occupancy level of isometric fibers (29). Fig. 3 shows fiber stiffness to be virtually constant at and above 5 °C. [This corrects our earlier incorrect report (19) that stiffness is temperature-dependent and confirms rat fiber data (30).] At 1 °C where two-state amplitude analysis fails, stiffness drops, and the linear dependence of phase 2_slow and the bell-shaped form of T-jump amplitude data [τ₂ to a degree, τ₃ markedly (9)] are lost (see mechanism in ref. 9).

Fig. 3.

Dependence of instantaneous (phase 1) stiffness on the temperature-induced increase in fiber isometric tension. These data (filled squares) show fiber stiffness (Young's modulus) to be temperature/tension-independent at and above 6 °C. A weighted linear least-squares fit is applied to these data. Constant stiffness indicates thin filament saturation with myosin heads. The outlier at 1 °C (open square) indicates a loss of saturation. Loss of saturation is mirrored in the discontinuity of the L-jump amplitude data of Fig. 2B. Error bars are mean ± SE.

There is no indication of a mixed response and a convolution of bell-shaped and linear dependences in the L-jump amplitude data of Fig. 2B. This result is expected because, as seen, enthalpy–entropy compensation renders K_T virtually strain-independent/-insensitive. To accommodate the concentration jump mechanism, we propose that a fixed number of hitherto non-tension-generating (noncompetent) bridges X are instantaneously activated to competent cross-bridges by the L-jump

to produce a step increase in the concentration of the pretension-generating state A, while isometric tension-generating cross-bridges B are moved to low strain Y and dissociate rapidly. Activated cross-bridges then redistribute between preforce-generating (A) and force-generating (B) cross-bridge states with the kinetics of two-state tension generation and phase 2_slow. The larger the step release, the lower the average strain at which equilibration occurs. The scheme in Reaction 2 is related to intermediate states of the cross-bridge cycle presented in Discussion.

Location of the Phase 2_slow Transition in the Cross-Bridge Cycle.

Before discovery of the Arrhenius/anti-Arrhenius kinetics, we used comparative studies of phase 2_slow kinetics in fast, medium speed, and slow fibers to locate tension generation within the cross-bridge cycle (19). Arrhenius plots of these phase 2_slow rate data are replotted in Fig.4. Tangents in red and blue are drawn to the left and right arms, respectively, of the dog's leg to approximate the temperature dependencies of the forward and reverse rate constants for tension generation. The slope of the Arrhenius plot (red), and thus ΔH^‡ of the forward rate constant, increases the slower the fiber type. In contrast, the slope of the fit to the reverse rate constant (blue) remains constant and fiber-type independent. A model system with a fast reaction governed by k_fast coupled to a second slow reaction governed by k_slow serves to illustrate such asymmetric coupling mechanisms.

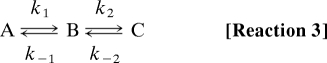With k₁ + k₋₁ ≫ k₂, k₋₂ the observed rate constants for steps 1 and 2 are k_fast = k₁ + k₋₁ and k_slow = [k₁/(k₁ + k₋₁)] k₂ + k₋₂, respectively (27). It is evident that the forward rate constant k₂ is modulated by the kinetics of the first step whereas the reverse rate constant k₋₂ is not. Thus, as observed experimentally in Fig. 4, for tension generation by phase 2_slow in medium speed and slow fibers, modification of the forward rate constant of tension generation but not the reverse indicates coupling to upstream (earlier) temperature-sensitive steps in the cross-bridge cycle.

Discussion

To date, there has been little reason to doubt that a step release would bias tension generation toward high-force state(s) and that a stretch step would do the reverse, behavior in accordance with Le Chatelier's principle. The results we describe here show that this is probably not the case. Temperature biases the equilibrium as expected for an endothermic isomerization, but L-jump-imposed changes in strain appear to leave the equilibrium distribution unaffected. We discuss the mechanistic consequences of these findings.

L-Jump Kinetics and the Cross-Bridge Cycle.

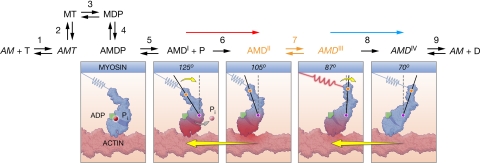
To give the proposed L-jump mechanism of Reaction 2 in context for discussion, we integrate it into the cross-bridge cycle illustrated in Fig. 5(8, 19). Intermediate states X, A, B, and Y map, respectively, to cycle states AMD^I, AMD^II, AMD^III, and AMD^IV. Thus, a step release causes sterically inhibited noncompetent AMD^I cross-bridges to be rendered tension-competent in step 6 by a relative sliding of the thick and thin filaments (Fig. 5, red arrow) whereas isometric cross-bridges moved to the low-strain AMD^IV state dissociate rapidly in step 2. Newly competent AMD^II cross-bridges subsequently redistribute between preforce AMD^II and force-generating AMD^III states at about step 7 with the kinetics of phase 2_slow in a ratio determined by K_T. Overall, the mechanism functions rapidly to buffer tension when movement occurs.

Fig. 5.

Mechanochemical cross-bridge cycle in fast fibers. The cycle illustrates indirect coupling of P_i release to two-state tension generation (step 7, orange). Before step 6, noncompetent AMD^I cross-bridges can bind phosphate but cannot generate tension. After step 6, competent cross-bridges cannot bind phosphate but can generate tension (18, 19). An open and a closed “back door” channel for P_i release (31) symbolizes these two states in the diagrams. Interconversion of the pretension AMD^II to tension-generating AMD^III states occurs at step 7. Discharge of tension through movement at step 8 creates the unloaded AMD^IV state. Diagrams illustrate the flow of free energy (rose shading) from phosphate, to cross-bridge, to work. A step release activates mobile low-stiffness AMD^I cross-bridges by movement (red arrow) while simultaneously discharging tension-generating AMD^II/AMD^III isometric cross-bridges (blue arrow). Diagrams based on 3D tomograms of contracting insect flight muscle (32, 33) show both axial and azimuthal catalytic and lever arm domain movement during step 6 activation. After activation, the lever arm domain alone appears to change angle during the power stroke (steps 7 and 8). In the scheme, M is myosin, A is actin, T is ATP, D is ADP, P is P_i, and italicized actomyosin AM states represent power and post-power stroke states. Step numbering corresponds to a published cycle (19).

Assignment of X to the AMD^I state and P_i release to step 5 are considered first. As mentioned in the Introduction, the relationship of the tension generation to the free-energy change of P_i release has proved a challenge. Comparative data on the kinetics of phase 2_slow are relevant here. These experiments (Fig. 4) showed that the forward rate constant of tension generation is coupled to earlier temperature-sensitive steps in medium speed and slow fibers, but not in fast fibers. This confirms an earlier study in detail (19). Usefully, this pattern of coupling mirrors the P_i sensitivity of phase 2_slow; P_i sensitivity is apparent in slow- (34) and medium-speed fibers (35), but not fast fibers (18, 36). This correlation locates P_i release before tension generation with step 6 reversible in all but fast fibers. Assignment of the noncompetent AMD^I state to X is confirmed by L-jump experiments in which P_i release was measured directly (37). In step releases, phases 1 and 2 showed no P_i release signal; only phases 3 and 4 exhibited a synchronous release of free P_i.

The existence of bridges that reversibly bind P_i but cannot generate tension was proposed over a decade ago to accommodate the uncoupling of tension generation from the kinetics of P_i release in fast rabbit psoas fibers (18). At the time, we likened the mechanism to the operation of a clock, with P_i release providing energy to tension the spring, and the irreversible step functioning as the escapement mechanism, which is followed in turn by tension generation as the movement of the hands. There was no appreciation then that noncompetent AMD^I cross-bridges were present at high concentration or that they could be rapidly switched by movement in step 6 to the competent AMD^II state. The contribution of AMD^I heads to fiber stiffness is a low 10–15% of the total (38, 39). Thus, the AMD^I state appears well tethered to prevent dissociation and development of a futile cycle, but it has minimal short-range stiffness, an unexpected property for a post-P_i-release cross-bridge. Apart from being noncompetent, the AMD^I state resembles the AM′.D state proposed by Sleep and Hutton to mediate exchange between medium P_i and ATP during the actomyosin ATPase cycle (40). As considered later, the noncompetent state probably exists in quantity because stereospecific docking of the catalytic domain on actin is prevented by filament lattice constraints, much like the clock escapement alluded to before.

Tension generation by phase 2_slow/τ₂ is assigned to step 7 in Fig. 5 as an isomerization between attached states with AMD^III as force generator. The temperature-sensitive equilibrium constant K_T governs the step 7 isomerization in both L- and T-jump experiments and the macroscopic property of isometric tension (8, 9). This direct correspondence between step 7 step and fiber properties suggests that cooperativity between cross-bridges is minimal. It is worth noting that at physiological temperatures in the rabbit, occupancy of the AMD^III state approaches 99% (K_40.3° = 124). How our observations under constrained conditions relate to experiments that show fiber tension to be a distributed property [spectroscopic studies that show minimal changes in cycle intermediate states as tension are modulated with P_i (16, 41)] is intriguing and needs to be explored.

The results obtained generally support tension generation by a single power stroke at step 7 rather than as a multistep reaction with either a series of like states (1, 2) or a heterogeneous sequence of L-jump-sensitive and T-jump-sensitive states (3, 4). Thus, a power stroke appears to be the canonical mechanism of de novo tension generation, confirming earlier results (6–9); minor substeps associated with changes in stiffness or head detachment (9) are not excluded. Of all kinetic studies, only Kawai's group routinely resolves all four L-jump exponential phases as we do. However, interpretations differ in that phase 3 (process B) and not phase 2_slow (process C) is assigned to de novo tension generation (11, 12). The signature negative amplitude of phase 3 (Fig. 1, blue) in L-jump and other experiments (see Discussion and Table 2 in ref. 19) makes this unlikely (18, 28). More importantly, to accommodate this scheme, phase 2_slow is assigned to the ATP-triggered detachment of myosin from actin (Fig. 5, step 2) (42), a mechanism incompatible with the isomerization kinetics we describe.

Isometric cross-bridges simultaneously moved to low-strain AMD^IV state by the L-jump dissociate upon displacement of ADP by ATP. Cross-bridge discharge is illustrated schematically in the mechanochemical cross-bridge cycle (Fig. 5, blue arrow). To avoid mechanical resistance, bridges moved to low strain by the L-jump in step 8 must dissociate rapidly in step 2. This is probably so in fast fibers because all L-jump phases are accounted for, and none has kinetics of cross-bridge dissociation (19). Also, the dissociation of unstrained AMD bridges in fast fibers by ATP occurs at >1,000 s⁻¹ (43), fast enough to ensure rapid dissociation and no mechanical signal. It is thus unlikely that AMD^IV, AM, or AMT bridges retard movement here.

Structural Identity of the Kinetic States.

Comprehensive mechanisms require a structural identity for their kinetic intermediates. Our kinetic scheme resembles mechanisms in which myosin heads are enabled by movement to generate tension after an L-jump, a class of model first proposed by Huxley and Kress in the mid 1980s (44). We find a compelling match between our kinetics and a structural mechanism based on 3D images of individual attached cross-bridges obtained from electron micrographs of flash-frozen contracting insect flight muscle (33). Here, lever arm domains of heads attached to thin filaments occupy a wide sweep of angles from an antirigor angle of 125° to a rigor-like end-of-stroke angle of 70°, an angular motion equivalent to an ≈13-nm swing of the lever arm, a sequence illustrated in the diagrams of Fig. 5. The key feature relevant to our kinetics is that this distribution of cross-bridge angles classifies into two structural classes (32, 33). In the first antirigor group, both the catalytic and lever arm domains assume different angles of attachment to actin. Attachment of the lower 50-kDa domain of the myosin head to actin provides a plausible tether for these cross-bridges (10). In group 2, the catalytic domain appears immobilized on actin, and the lever arm alone swings. The authors (32, 33) proposed a 13-nm interaction distance with a 4- to 6-nm power stroke, a match to our kinetics in which movement activates compliant noncompetent AMD^I cross-bridges to create stiff, competent AMD^II/AMD^III cross-bridges. Activation appears synchronous with a locking down of the catalytic domain, a reaction assigned to a disorder–order transition in probe experiments (45).

Mechanism of Tension Generation.

Having considered the placement of tension generation in the cross-bridge cycle (Fig. 5) and proposed a mechanism for the L-jump response, it is now appropriate to consider tension generation itself. From a kinetic perspective, increasing temperature accelerates the forward and slows the reverse rate constant of tension generation by phase 2_slow, similar to laser T-jump kinetics. Interpretation of these anomalous kinetics of tension generation in which Arrhenius behavior (positive enthalpy of activation) for tension generation and anti-Arrhenius behavior (an “apparent” negative enthalpy of activation) for its reversal has been aided by their similarity to the two-state unfolding/folding kinetics of small proteins (see ref. 9). A recent article in which the observed, forward and reverse rate constants obtained from various T-jump studies on the folding of a dozen proteins were collected, plotted similarly to our data (Fig. 2A), and assembled into one figure (Fig. 2 in ref. 46) highlights the resemblance. In general, negative activation enthalpies arise from an increase in the ensemble (population) of unfolded conformations as temperature rises compared with a relatively stable native state little affected by temperature. Tension generation differs from studies on protein folding in that it occurs under physiological conditions and does not involve the entire protein. Protein conformational changes usually show normal Arrhenius kinetics. An exception is the closed to open transition of a loop in the lactate dehydrogenase, NADH, and pyruvate ternary complex that appears associated with a negative activation enthalpy (47). Progress in understanding the mechanism of these outwardly simple (two-state behavior, exponential kinetics) protein-mediated reactions continues apace. The success of a combination macroscopic mass action and microscopic energy landscape model (Thruway Search Model) to fit the ultrafast folding kinetics proteins (46) reflects this.

The unexpected protein-related discovery presented here is the strain independence of K_T, the equilibrium constant for tension generation even though the lower strain accelerates forward, reverse, and observed rate constants. Of interest is the linear decrease in the contribution of ΔH^‡ to the transition state ΔG^‡ of tension generation (unfolding) as strain declines being matched by an equal increase in the contribution of ΔS^‡. Reversal of tension generation (folding) exhibits matching reciprocal changes. Such enthalpy–entropy compensation is often encountered in protein-mediated reactions and is characteristic of reactions in aqueous media. A plausible interpretation is that the structure of the tension-generating AMD^III states changes as strain changes: the tension-producing spring-like structure of the AMD^III state becomes progressively disordered (fewer bonds, greater disorder) as the strain is lowered, and the potential energy declines as mechanical work is done. A recent article in which enthalpy–entropy compensation in proteins is considered from a nanomotor perspective as a Carnot cycle in which microscopic phase transitions occur may prove relevant here (48).

Materials and Methods

Design of the L-jump, preparation of detergent-skinned muscle fibers, methods of activation, stabilization of the fiber sarcomere pattern, advantages of using fixed-end rather than length-clamped fibers in very small-perturbation experiments, and data analysis are detailed elsewhere (7, 19, 28, 49). On average, 18% of the L-jump is absorbed by fiber end compliance. Rabbits were killed under National Heart, Lung, and Blood Institute Animal Care and Use Protocol 2-MC-30(R). Relaxing, preactivating, and activating solutions were set to pH 7.1 and i = 0.2 M (7).

Respective activation energies (E_A) for the forward and reverse rate constants are determined from Arrhenius plots of the k₁ and k₋₁ rate constants where A is the preexponential factor, R is the gas constant and T is absolute temperature and k = Aexp(−E_A/RT). Reformulation of the Arrhenius equation by using transition state theory for a first-order isomerization (27) results in the following relationship: k = (k_BT/h) exp(ΔS^‡/R) exp(−ΔH^‡/RT), where k_B is Boltzmann's constant, h is Planck's constant, ΔS^‡ is the entropy of activation, and ΔH^‡ is the enthalpy of activation. Activation parameters were obtained by applying a weighted nonlinear least-squares fit with KaleidaGraph (Synergy Software) to rate data by using this equation.