Normalization of a spatially variant image reconstruction problem in electrical impedance tomography using system blurring properties

Abstract

The electrical impedance tomography (EIT) image reconstruction problem is ill posed and spatially variant. Because of the problem’s ill-posed nature, small amounts of measurement noise can corrupt reconstructed images. The problem must be regularized to reduce image artifacts. In this paper, we focus on the spatially variant characteristics of the problem. Correcting errors due to spatial variance should improve reconstruction accuracy. In this paper, we present methods to normalize the spatially variant image reconstruction problem by equalizing the point spread function (PSF). In order to equalize the PSF, we used the reconstruction blurring properties obtained from the sensitivity matrix. We compared three mathematical normalization schemes: pixel-wise scaling (PWS), weighted pseudo-inversion (WPI) and weighted minimum norm method (WMNM) to equalize images. The quantity index (QI), defined as the integral of pixel values of an EIT conductivity image, was considered in investigating spatial variance. The QI values along with reconstructed images are presented for cases of two-dimensional full array and hemiarray electrode topologies. We found that a spatially invariant QI could be obtained by applying normalization methods based on equalization of the PSF using conventional regularized reconstruction methods such as truncated singular value decomposition (TSVD) and WMNM. We found that WMNM normalization applied to WMNM regularized reconstruction was the best of the methods tested overall, for both hemiarray and full array electrode topologies.

1. Introduction

The human body is made of tissues that are well contrasted in electrical conductivity (Barber and Brown 1984). Therefore, an imaging modality such as electrical impedance tomography (EIT) that produces conductivity distribution information within the body may find useful clinical application. In EIT, a set of electrodes is positioned on the patient’s skin. Low-amplitude currents are applied through a pair of electrodes, and the resulting surface voltages are measured. This procedure is repeated until we obtain all the possible independent measurements. The measurements are a function of the body’s internal conductivity distribution. Therefore, cross-sectional conductivity images can be reconstructed from the measurements, given knowledge of the input current pattern and the patient’s body shape. Images of conductivity changes may provide information about changes in physiological states. Thus, EIT has potential clinical applications as a real-time bedside monitor.

Potential limitations in performance of the EIT systems include that input current travels nonlinearly within the body, and its trajectory cannot be predicted precisely, and that the available information about the object is limited by the total number of electrodes, yet using many electrodes may not be practical in clinical settings. Consequently, we must pay special attention to the ill-posed nature and spatial variability of the EIT image reconstruction problem, which are mathematical embodiments of the above limitations. Due to its ill-posed nature, small measurement errors can impair reconstructed images. In this case, the problem must be regularized to return reasonable images. Further, the image reconstruction problem is spatially variant, meaning that the same anomaly may produce different reconstruction signatures depending on its location within the image plane. In this case, regularization methods may still produce inaccurate reconstructions. Therefore, we diagnose spatial variability as a critical problem that needs resolution.

As a consequence of spatial variability, estimated quantities of conductive anomalies will also appear to vary according to their positions (Sadleir and Fox 1998). In EIT monitoring of lung air and liquid volume changes, Adler et al (1997) also reported quantification errors that depended on radial positions of anomalies. Spatial variance may not be a significant problem when the region of interest (ROI) is relatively small. For example, in Blott et al’s study (2000) of simulated two-dimensional intra-ventricular haemorrhage, quantitation errors due to spatial variance of reconstructions were likely negligible for that reason. However, in other applications such as detection of intra-peritoneal bleeding, determining an ROI is not straightforward, because bleeding may occur over a large fraction of the imaged domain. Therefore, reducing spatial variability is desired to improve accuracy in estimating anomaly quantities.

In this paper, we used reconstruction blur analysis in order to reduce errors caused by spatial variance. We demonstrate that normalizing the point spread function (PSF) by its integral can result in a spatially invariant quantity index (QI). We considered the PSF to be the reconstruction (or blurring) of single-element (pixel) anomalies. Cohen-Bacrie et al (1997) used variance of this PSF as penalty term in Tikhonov regularization. In this paper, we used the integral of PSF functions as normalizing terms. Three mathematical frameworks of normalization were compared: pixel-wise scaling (PWS), weighted pseudo-inversion (WPI) and weighted minimum norm method (WMNM) for two-dimensional eight-electrode ‘full array’ and ‘hemiarray’ reconstructions. Data were obtained from numerically simulated two-dimensional disk models (Comsol Multiphysics: Burlington, MA) containing simulated disk anomalies placed at various locations in the image plane and a cylindrical saline phantom containing blood-like anomalies in a less-conducting background.

2. Methods

2.1. Forward problem

Given an object Ω, input current is transmitted through the object boundary dΩ, which is assumed smooth. A corresponding electric potential Φ is generated following the Laplace equation (1a) with boundary conditions (1b) for conductivity σ, which is a function of position:

$$\nabla ·(\sigma \nabla \hspace{0.17em}\mathrm{\Phi })=0\text{in}\mathrm{\Omega },\text{subject}\text{to}$$ (1a)

$$\sigma (x,y,z)(\partial \mathrm{\Phi }/\partial n)=-J\text{on}\text{d}\mathrm{\Omega },$$ (1b)

where J is the current density prescribed on the object boundary, and n is a unit outward normal to the surface.

2.2. Full array and hemiarray topologies

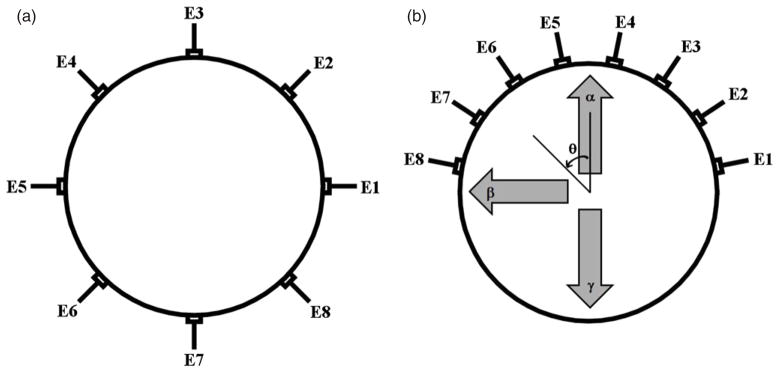
In a conventional EIT electrode topology, electrodes are spaced equidistantly around the entire object boundary. This ensures current projections are axially symmetric within the assumed object shape. We call this the full array (figure 1(a)). The novel hemiarray electrode layout (figure 1(b)) is motivated by clinical requirement to place electrodes only on the anterior surface of the body (Sadleir et al 2008). Although there are practical advantages over the full array, the hemiarray forms current projections that are highly asymmetric with respect to the image plane, worsening the spatial variability of reconstructions.

Figure 1.

Illustration of eight-electrode arrays applied to the boundary of a disk object. Electrodes are labeled by indices E1, E2, …, E8. (a) Full array electrode layout. (b) Hemiarray electrode layout. The variable θ represents clockwise angular displacement away from the north pole. Directions at θ values of 0, 90 and 180° were denoted as α, β and γ, respectively.

2.3. Adjacent electrode measurement

A standard adjacent electrode configuration was employed for both full array and hemiarray topologies. In the adjacent electrode configuration (Malmivuo and Plonsey 1995), a neighboring pair of electrodes is used to inject input currents. Other electrode pairs, excluding the current pair, are used to make adjacent boundary voltage measurements. The following adjacent pair of electrodes is chosen for the next current injection, and the next set of adjacent boundary voltage measurements is made. This procedure is repeated until all the possible adjacent pairs are tried. For n electrodes, adjacent electrode configuration produces n × (n − 3) measurements in total. Therefore, using eight electrodes produces 40 measurements in total. Among these, only 20 measurements are independent due to reciprocity (Malmivuo and Plonsey 1995).

2.4. Inverse problem

In EIT image reconstruction, the conductivity distribution within an object is estimated from measured boundary voltage, given input current patterns and an object shape. We used a linearized reconstruction problem given by (2), where the conductivity change Δσ (dimension N × 1, where N is the total number of pixels (elements) in the image plane) is to be estimated from a reference condition (Lionheart 2004):

$$\mathrm{\Delta }V=\mathbf{S}\mathrm{\Delta }\sigma .$$ (2)

Here, ΔV (M × 1, where M is the total number of measurements) is the change of voltage measurement from a reference measurement, and S (M × N) is the sensitivity matrix. Reference measurements were made on a disk model that contains a homogenous background medium (Meeson et al 1995). Each entry S_ij in S is the sensitivity (i.e. amount of voltage change expected) of measurement i to a unit conductivity change in element j (Lionheart 2004).

The image plane used throughout this paper had 344 elements. Excluding elements that lay on the boundary, all elements were square and had the same area. In table 1 the properties of S calculated for this plane are summarized for both eight-electrode full array and hemiarray cases. S was a rectangular matrix for our image plane, which made (2) an underdetermined problem. The large condition numbers indicate that equation (2) is an ill-posed inverse problem that must be regularized to obtain reasonable solutions. According to table 1, the hemiarray sensitivity matrix has a larger condition number than the full array for the same number (eight) of electrodes.

Table 1.

Properties of the sensitivity matrices S of eight-electrode full array and hemiarray topologies.

	Full array	Hemiarray
Dimensions	40 × 344	40 × 344
Rank	20	20
Condition number	2.21 × 1017	2.02 × 1018

2.5. Truncated singular value decomposition

In order to invert (2) and obtain Δσ, singular value decomposition (SVD) can be used to calculate the pseudo-inverse of the sensitivity matrix S⁺ as in (3):

$${\mathbf{S}}^{+}=\mathbf{V}{\mathbf{D}}^{+}{\mathbf{U}}^T.$$ (3)

Here, U and V are unitary matrices whose columns are the left and right singular vectors of S. D⁺ is a truncated inverse of the singular value matrix. Obtaining an estimated conductivity solution Δσ̂ of (2) using S⁺ as the reconstruction matrix is termed truncated SVD (TSVD) (4). TSVD was proposed for discrete ill-posed problems by Hansen (1987) to achieve smooth solutions:

$$\mathrm{\Delta }\widehat{\sigma }={\mathbf{S}}^{+}\mathrm{\Delta }V.$$ (4)

Once the reconstruction vector Δσ̂ is calculated, images can be made by simply assigning entries of Δσ̂ to their corresponding elements in the image plane. The estimated solution Δσ̂ can be expressed as the weighted sum of rank-1 matrices as in (5):

$$\mathrm{\Delta }\widehat{\sigma }=\sum _{i=1}^k\frac{u_i^T\mathrm{\Delta }V}{d_i}{v}_i,$$ (5)

where k is termed the regularization parameter (or truncation number in TSVD) and can be chosen based on the amount of noise in the measurement ΔV (Hansen 1987).

2.6. L-curve criterion

Determination of the regularization parameter is not straightforward, since the noise quantity is generally unknown. Hansen (1992) suggested the use of the l-curve in selecting adequate regularization parameters. In the l-curve, solution norm of the problem is plotted versus residual norm in the log–log scale. The resulting curve is usually L-shaped with a corner, hence its name. In this paper, we examined the l-curve for each reconstruction and chose the minimum k value (5) corresponding to the corner determined by visual inspection to reconstruct all data.

2.7. Weighted minimum norm method (WMNM)

WMNM has been implemented in EIT image reconstruction as a way to resolve the problems arising from low sensitivity (Clay and Ferree 2002). In WMNM, columns of the sensitivity matrix are equalized in terms of its power before pseudo-inversion and recovered by rescaling the pixels. The final form of WMNM is displayed in (6):

$$\mathrm{\Delta }\widehat{\sigma }=\mathbf{W}{(\mathbf{SW})}^{+}\mathrm{\Delta }V,$$ (6)

where the weighting matrix W (N × N) is a diagonal matrix whose terms (w_j) are defined as in (7):

$$w_j={\left(\sum _{i=1}^M{S}_{ij}^2\right)}^{-1/2},j=1,2,\dots ,N.$$ (7)

2.8. Quantity index (QI)

At an early stage of EIT’s development, Barber (1990) suggested that a volume integral of relative resistivity changes in reconstructed images may be a useful quantitative measure. Here, we propose integrals of EIT images as a useful measure to estimate changes of anomaly volume. The quantity defined in (8) is termed the QI. QI can be thought of as the average of the conductivity change Δσ multiplied by the number of elements N:

$$\text{QI}=\sum _{j=1}^N{A}_j·\mathrm{\Delta }{\sigma }_j.$$ (8)

For an element (or pixel) j, the conductivity change and element area are denoted as Δσ_j and A_j, respectively.

The relative QI (δQI) for a reference QI (where QI₀ is that calculated from the anomaly located at the domain center) is defined in (9):

$$\delta \text{QI}=\text{QI}/{\text{QI}}_0.$$ (9)

2.9. Point spread function (PSF) and blurring

In order to investigate blurring in EIT image reconstruction, we introduce the PSF. Consider a unit conductivity change in an element (pixel) j within the image. This unit change can be expressed in a vector form as an entry of 1 in the jth position and zeros elsewhere ([0 … 0 1 0 … 0]^T). The weighted sum of these vectors is a vector form of the ideal image. The change in boundary voltage measurements subject to this unit conductivity change is the jth column of the sensitivity matrix S. Ideally any measurement can be represented as a weighted sum of sensitivity matrix columns. Therefore, the column space of S can be termed the ideal measurement space. By reconstructing from the ideal measurements, a blurred version of the ideal element (pixel) image is obtained, which we term the PSF:

$${\delta }_j=\mathbf{B}{[\begin{array}{ccccccc}0& \dots & 0& 1& 0& \dots & 0\end{array}]}^T,$$ (10)

where B (N × N) is the blurring matrix and δ_j is the PSF vector for an anomaly in the jth element. The column space of B is a blurred version of the ideal images. The blur matrix B is defined as the product of the sensitivity matrix and the reconstruction matrix. Therefore, it can be easily obtained for reconstruction matrices that are expressed in algebraic form. In (11a) and (11b), definitions of the Bs are displayed in the context of TSVD and WMNM regularization, respectively. One can also easily obtain B for other regularization methods such as Tikhonov regularization:

$$\mathbf{B}={\mathbf{S}}^{+}\mathbf{S},$$ (11a)

$$\mathbf{B}=\mathbf{W}{(\mathbf{SW})}^{+}\mathbf{S}.$$ (11b)

We are interested in using the properties of B to normalize spatially variant image reconstruction problems. When normalizing such problems, the unit of the reconstructed quantity should be preserved after normalization (Barber 1990). Entries in B are dimensionless (10). Therefore, reconstruction quantities after normalization have the same units as quantities before normalization. In (12), the column sum of B is defined as q_j:

$$q_j=\left(\sum _{i=1}^N{\mathbf{B}}_{ij}\right),J=1,2,\dots ,N.$$ (12)

The normalization matrix used throughout this paper is defined as Q (N × N) in (13), which is a diagonal matrix whose entries are q_j’s:

$$\mathbf{Q}=\left[\begin{array}{cccc}{q}_1& 0& \cdots & 0\\ 0& q_2& 0& ⋮\\ ⋮& 0& \ddots & 0\\ 0& \cdots & 0& q_N\end{array}\right].$$ (13)

2.10. Eigenimages

Using SVD, we can estimate basis images that determine the system blurring B (eigenimages). It is clear from (14) that columns of the right singular matrix V can be seen as eigenimage vectors:

$$\mathbf{B}={\mathbf{S}}^{+}\mathbf{S}={(\mathbf{UD}{\mathbf{V}}^T)}^{+}(\mathbf{UD}{\mathbf{V}}^T)=\mathbf{V}{\mathbf{D}}^{+}\mathbf{D}{\mathbf{V}}^T=\mathbf{V}\left[\begin{array}{cc}{\mathbf{I}}_k& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]{\mathbf{V}}^T,$$ (14)

where I_k (k × k) is the identity matrix. It is also clear in (14) that the blurring depends on the truncation number k.

2.11. Pixel-wise scaling (PWS)

Thomas et al (1994) used a method that scaled log-resistivity images pixel-wise in order to reduce variation in quantity estimates. We can also apply PWS to our case in which conductivity change is to be reconstructed. In (15), PWS is presented in a matrix form:

$$\mathrm{\Delta }\widehat{\sigma }={\mathbf{Q}}^{-1}{\mathbf{S}}^{+}\mathrm{\Delta }V.$$ (15)

A more advanced method was proposed by Sadleir and Fox (1998), who demonstrated a post-reconstructive filtering method that combined PWS and conformal transformations. In their work, the maximum spatial error in quantitation from phantom experimental results decreased from 30% to 6%. However, a large region near the object boundary (normalized radius > 0.75) was excluded from quantification.

2.12. Weighted pseudo-inversion (WPI)

The normalization that we use here is WPI. The normalized reconstruction can be obtained by weighting columns of the sensitivity matrix by terms in Q prior to reconstruction as in (16):

$$\mathrm{\Delta }\widehat{\sigma }={(\mathbf{SQ})}^{+}\mathrm{\Delta }V.$$ (16)

If SQ is a full-rank matrix, (16) will become identical to (15). In this vein, we speculate that WPI should normalize the reconstruction in a similar way to PWS, with an additional advantage of using the truncated pseudo-inverse.

2.13. Normalization in the framework of WMNM

In the work of Oh and Sadleir (2007), a WPI method was shown to decrease spatial variance of the QI. However, the normalized reconstruction Δσ̂ in (16) did not produce reasonable images. To obtain meaningful images, one can borrow the mathematical framework of WMNM, which can be done by multiplying Q post-reconstructively. The final form is shown in (17):

$$\mathrm{\Delta }\widehat{\sigma }=\mathbf{Q}{(\mathbf{SQ})}^{+}\mathrm{\Delta }V.$$ (17)

It was also noticed that using the WMNM framework can introduce normalization effects in some cases. Sadleir et al (2008) used a combined method of WMNM regularization (11) and WMNM normalization (17) in the eight-electrode hemiarray case, which produced normalized QIs and images. The matrix equation of this normalized reconstruction method is shown in (18):

$$\mathrm{\Delta }\widehat{\sigma }=\mathbf{QW}{(\mathbf{SWQ})}^{+}\mathrm{\Delta }V.$$ (18)

2.14. Computer simulation

Two-dimensional forward models of a disk (r_d) containing a single internal anomaly (r_a) at various locations were designed and solved using Comsol Multiphysics (Burlington, MA) and Matlab. We tested two types of models with anomaly locations as shown in figure 1. The full array model had eight boundary electrodes placed equidistantly. The hemiarray model had eight electrodes placed on the anterior boundary only. All electrodes had the conductivity of copper (6 × 10⁷ [S m⁻¹]). The length of each electrode was 0.1 relative to the disk radius, subtending an angle of 5.7° on the disk perimeter. The models were discretized to 1374 second-order triangular finite elements, and then solved for boundary voltage values subject to adjacent input current patterns using the direct linear system solver UMFPACK (Unsymmetric MultiFrontal PACKage). The anomaly had a radius 0.1 × r_d and was centered at locations with relative radii (r_a/r_d) of 0, 0.2, 0.4, 0.6 and 0.8 from the origin. For hemiarray cases, the anomaly position was varied in angles (θ) from 0° to 180° with 5° increment. In full array cases, only θ = −90° was used. The model background conductivity was set to 1, and anomalies represented a unit conductivity increase from the background.

2.15. Phantom experiments

A cylindrical phantom (r_P = 14.0 cm) was filled with saline solution (5 L). Vertical bar electrodes (width 13.0 mm and length 101.5 mm) were attached equidistantly around the phantom boundary to create an approximately two-dimensional field pattern. An insulating plastic rod of radius 1.4 cm (0.1 × r_P) was used as an anomaly, and it was moved along the α, −β and γ axes (at θ = 0°, −90° and 180°), with the anomaly center placed successively at relative radial displacements (r_A/r_P) of 0 (center), 0.25, 0.5 and 0.75, ten locations in total. This procedure was repeated for different volumes (50, 100, 150, 200 and 250 mL) of anomaly having conductivity similar to that of blood (0.67 S m⁻¹) placed in the background of saline with a conductivity of 0.2 S m⁻¹. We used the ePack eight-channel EIT system (Tang et al 2006) to collect measurements. The device was operated at a 2 mA constant current and 62.5 kHz.

3. Results

Results of methods using (15)–(18) were compared in terms of spatial variability. For convenience, each normalization method was given an index as in table 2.

Table 2.

Index assignment for various normalization methods. The methods are represented by reconstruction matrices. The normalization matrices Q_t and Q_w were calculated using (11a) and (11b) respectively. Methods A1–A4 are based on TSVD reconstruction (9), and methods B1–B4 and C5 are based on WMNM reconstruction (11).

Index	Normalization method	Reconstruction matrix
A1	None	S+
A2	PWS	${\mathbf{Q}}_t^{-1}$ S+
A3	WPI	(SQt)+
A4	WMNM	Qt(SQt)+
B1	None	W(SW)+
B2	PWS	${\mathbf{Q}}_w^{-1}$ W(SW)+
B3	WPI	W(SWQw)+
B4	WMNM	Qw W(SWQw)+
C5	WMNM	QtW(SWQt)+

Normalization method C5 defined in the last row of table 2 is based on WMNM reconstruction and WMNM normalization as for B4. However, the normalization matrix Q_t was used instead of Q_w.

The pseudo-inverted part of the reconstruction matrix can be understood as pseudo-inversion of a matrix product of the normalization matrix (Q_t or Q_w) and the sensitivity matrix (S). Changes of the system matrix condition number owing to this matrix multiplication are presented in table 3. Table 3 shows that matrix conditions can improve depending on the choice of the normalization matrix. For a full array, W tended to decrease the condition number, while Q_t and Q_w did not. For the hemiarray, Q_t tended to decrease the condition number, while W and Q_w tended to increase them. Therefore, when noisy measurements are to be reconstructed, using a normalization matrix that decreases the condition number could be beneficial.

Table 3.

Condition numbers of the normalized system matrices

System matrix	Condition number (full array)	Condition number (hemiarray)
S	2.21 × 1017	2.02 × 1018
SW	2.00 × 1017	3.21 × 1018
SQt	6.37 × 1017	3.93 × 1017
SWQw	2.31 × 1017	2.51 × 1018
SWQt	2.05 × 1017	4.10 × 1017

3.1. Ideal measurement reconstructions

Ideal measurements were obtained by individually perturbing all elements by unit conductivity increase. They are effectively columns of the sensitivity matrix. Their corresponding QI values were calculated using (8) for all the measurements. We compared normalization methods in terms of relative STD (RSD: absolute value of variation expressed as standard deviation divided by the average) calculated using all QI values (19):

$$\text{RSD}(\text{QI})=\text{STD}(\text{QI})/\text{average}(\text{QI}).$$ (19)

According to the results in table 4, method A3 resulted in an RSD decrease in all cases, while C5 resulted in an overall decrease of RSD except along the hemiarray α axis.

Table 4.

RSD of QI (19) calculated from the ideal measurement reconstructions (at full rank, k = 20) of eight electrode cases

Normalization method	Full array (θ = 0 °)	Hemiarray (α: θ = 0°)	Hemiarray (β: θ = 90°)	Hemiarray (γ: θ = 180°)
A1	0.1478	0.1749	0.1734	0.9579
A2	0.3294	0.4000	0.2586	0.4829
A3	0.0628	0.1023	0.1019	0.9095
A4	0.0878	0.1053	0.1790	0.9846
B1	0.1124	0.5440	0.8739	0.1946
B2	1.1087	5.8956	2.9424	16.7774
B3	2.4142	0.8479	0.2373	0.5036
B4	0.2141	0.2729	0.0936	0.8172
C5	0.0672	0.3413	0.0184	0.6702

3.2. Simulated measurement

Simulated measurements were created from the computer models described as in section 2.15. We investigated relative QI (θQI) (9) with the central anomaly as the reference. Maximum deviation errors (ε) away from the central QI value (QI₀) were calculated as in (20) and displayed in table 5:

$$\epsilon =\text{Max}\{\mid \delta \text{QI}-1\mid \}.$$ (20)

Table 5.

Maximum deviation error (ε) of the relative QI, calculated from the simulated measurement reconstructions (k = 16) of eight electrode cases. Truncation number k was chosen based on the l-curve investigation

Normalization method	Full array (θ = 0°)	Hemiarray (α: θ = 0°)	Hemiarray (β: θ = 90°	Hemiarray (γ: θ = 180°)
A1	0.7239	0.3134	0.7409	0.9539
A2	2.7983	2.2928	0.5365	0.5759
A3	0.2437	0.0671	0.8284	0.9075
A4	0.4398	0.3078	0.8478	0.9574
B1	0.2740	3.9886	2.8486	0.7287
B2	1.0667	4.9794	5.2909	2.2658
B3	0.3379	6.2294	2.2075	0.9253
B4	0.9985	0.1382	0.5224	0.8945
C5	0.2239	0.5944	0.6117	0.7948

Method A3, which was shown to perform most stably in the case of ideal measurements, also reduced ε for simulated measurements. However, it failed to decrease ε for the hemiarray β axis. B4 showed overall decrease of ε for hemiarray cases, but its ε increased for the full array case. C5 produced results similar to the ideal measurement case. Its ε decreased in all cases except for the hemiarray α axis.

3.3. Phantom measurement

Phantom measurements were made as described in section 2.15. The investigation was executed in the same way as in section 3.2. In table 6, ε values are displayed for various volumes of the blood-like anomaly. The ε values were calculated from δQI values calculated from ten different anomaly positions.

Table 6.

Maximum deviation error of the relative QI (ε) calculated from phantom reconstructions of eight-electrode full array and hemiarray topologies. In the full array, the anomaly was placed on four different locations on the negative β axis with relative displacement from the domain center (r_A/r_P = 0, 0.25, 0.5 and 0.75). In the hemiarray, the anomaly was placed on ten different locations on the α, −β, and γ axes (r_A/r_P = 0, 0.25, 0.5 and 0.75). Truncation number k was chosen by investigation of the l-curve

	Full array
	Anomaly volume
Normalization method	50 mL (k = 16)	100 mL (k = 17)	150 mL (k = 17)	200 mL (k = 17)	250 mL (k = 17)
A1	0.3344	0.3799	0.3048	0.2631	0.2377
A2	0.8131	0.8741	0.6714	0.6055	0.5685
A3	0.1570	0.1634	0.1517	0.1173	0.1017
A4	0.2266	0.2588	0.2129	0.1760	0.1562
B1	0.1896	0.1918	0.1831	0.1492	0.1318
B2	1.6966	9.6980	17.6351	5.3715	3.5571
B3	0.1961	0.3818	0.1346	0.1869	0.1777
B4	0.4055	0.4456	0.3568	0.3126	0.2852
C5	0.1513	0.1582	0.1483	0.1138	0.0980
	Hemiarray
	Anomaly volume
Normalization method	50 mL (k = 15)	100 mL (k = 16)	150 mL (k = 16)	200 mL (k = 16)	250 mL (k = 17)
A1	0.5084	0.6845	0.4759	0.4213	0.4219
A2	0.5319	0.2658	0.1438	0.2028	0.2872
A3	0.6003	0.6216	0.5373	0.5155	0.5536
A4	0.5923	0.7090	0.5181	0.4819	0.4940
B1	0.6883	0.4502	0.2519	0.4558	0.3855
B2	3.0771	4.5643	8.2285	6.4299	1.3628
B3	0.7296	0.8014	0.7127	0.8695	0.9601
B4	0.4587	0.4695	0.3345	0.3314	0.4013
C5	0.3072	0.2578	0.2660	0.2253	0.2609

Our results in table 6 show that method A2 worked better for anomalies of larger volumes in the hemiarray case. B4 showed a decrease for the hemiarray case, and ε values tended to increase as the anomaly volume increased. This may have been due to our assumption of reconstructions being the weighted sum of system’s PSFs. Method C5 decreased ε values for anomalies of all volumes in both full array and hemiarray cases.

Cross-examination of tables 3–6 allows us make some findings. For the full array, the spatial variability (in terms of relative STD of QI or ε) decreased for A3, A4, B1 and C5. A3 and C5 seem to be the best candidates since they resulted in the most decrease in most cases.

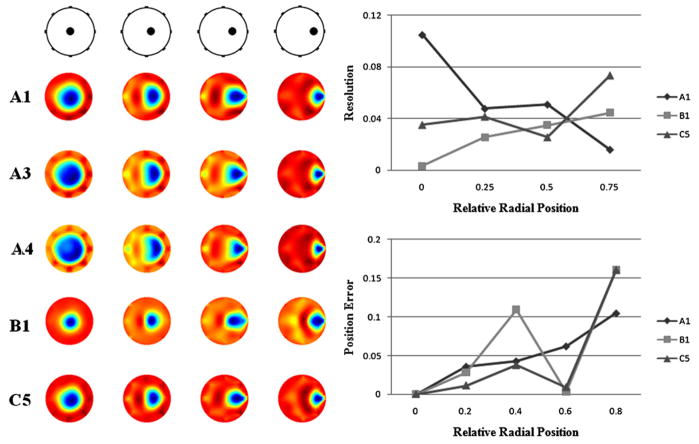
In figure 2 (left), methods A3 and A4, which successfully reduced spatial variability of QI, resulted in blurred reconstruction of a central anomaly compared to reconstructions using B1 and C5, which produced more compact central anomaly. It should be noted that B1 and C5 are methods that are based on WNMN regularization. Method B1 blurred images of the anomaly near the boundary. C5 did not produce a blurred reconstruction of this location. Thus, C5 appears to be the most reasonable method for the full array. In figure 2 (right), selected methods (A1, B1 and C5) were compared in terms of resolution and position error. In order to estimate resolution, we followed definition of the blur radius suggested by Adler and Guardo (1996). Elements that have values greater than half the maximum element value were chosen as the half amplitude (HA) set. Then, the resolution was calculated as a square root of the ratio between the area of the HA set (A_HA) and the domain area (A_o) (21):

$$\text{resolution}=\sqrt{\frac{A_{\text{HA}}}{A_o}}.$$ (21)

Figure 2.

Eight-electrode full array images (k = 17) reconstructed from phantom measurements made for a blood-like anomaly (100 mL) in four different locations on the negative β axis (r_A/r_P = 0, 0.25, 0.5 and 0.75). (Left) Images reconstructed using normalization methods A1, A3, A4, B1 and C5 are compared. (Right) Images reconstructed using A1, B1 and C5 were investigated in terms of the anomaly’s blur radius (resolution) and position error. Resolution was calculated as a square root of the ratio between area of the half amplitude set and the actual anomaly size. Position was estimated as a center of mass of the half amplitude set.

The position of an anomaly was located as the center of mass of the HA set in reconstruction images (22):

$$\text{position}=\frac{{\sum }_m{\sigma }_m·p_m}{{\sum }_m{\sigma }_m}.$$ (22)

Here, p_m is the position vector (x_m, y_m) within the domain.

Small and uniform resolution values are regarded to be desirable indicating less blurring. In figure 2, there are overall enhancement of resolution when using B1 and C5. In terms of position error, C5 shows great improvement except when the anomaly was close to the domain boundary.

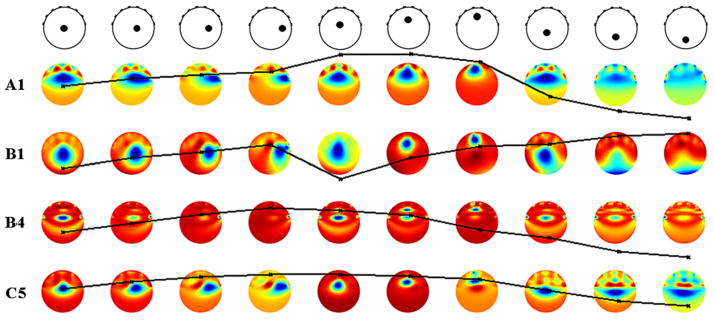
For the hemiarray case, normalization could be made particularly effective for anomalies on the γ axis. However, this was obtained at the expense of increasing variability along the α axis. Even though B4 and C5 were most effective for β and γ axes anomalies, they were not effective for α axis anomalies (tables 4 and 5). Investigation for various anomaly volumes (50, 100, 150, 200 and 250 mL) used in our phantom experiments (table 6) revealed that B4 and C5 consistently reduced spatial variability. In figure 3, methods that reduced variability are compared for 100 mL anomaly in ten locations. Anomaly images reconstructed using B1 were comparatively less blurry than A1, B4 and C5. In reconstruction of anomalies on the γ axis, B1 reduced the spatial variability. B4 performed well in terms of reducing spatial variability of QI but did not produce a good image quality, as shown in figure 3 (B4). C5 resulted in reduced variability producing images of improved qualities. However, images of anomalies on the γ axis were still unclear.

Figure 3.

Eight-electrode hemiarray images (k = 16) and relative QI curves reconstructed from a blood-like anomaly (100 mL) using methods A1, B1, B4 and C5. Relative QI values were calculated with the central anomaly (r_A/r_P = 0) as a reference and scaled to a value of 1. All relative QI plots have the same scale (0.5–2) and have been overlaid on top of corresponding reconstruction images. The anomalies were positioned at ten different locations on the β, α and γ axes (r_A/r_P = 0.25, 0.5 and 0.75).

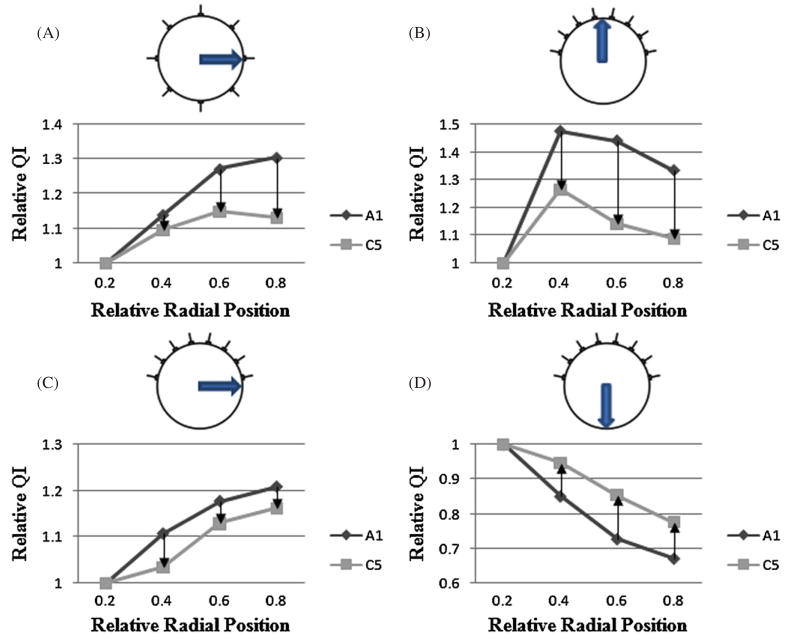
In figure 4, performance of our proposed method C5 was demonstrated for normalizing QI in the full array and hemiarray topology. The relative QI values were plotted versus the radial axis. The uniformity of the relative QI curves increased, when C5 was used. The improvement was consistent for all axes considered (α, β and γ).

Figure 4.

Radial curves of relative QI calculated using TSVD (A1) and normalization method (C5). The QI values are obtained from reconstructions for the full array (k = 17) and hemiarray (k = 16). The anomaly (100 mL) was positioned on various locations. The curves were plotted for the (A) full array −β, (B) hemiarray α, (C) hemiarray −β and (D) hemiarray γ axes.

4. Discussion

Image reconstruction in EIT is a nonlinear and ill-posed inverse problem. Uncertainties caused by these properties prevent EIT images from having the high resolution typically found in MRI and CT imaging. However, one may extract a unique property (electric conductivity) of an imaged object in EIT, which is potentially valuable in clinical monitoring. EIT image reconstruction is a spatially variant estimation problem. In this paper, we attempted to reduce spatial variance of QI. Spatial variance is hard to deal with because its properties also depend on the regularization method chosen. Therefore, we sought a general approach that can reduce spatial variance in this paper. We proposed methods that normalize full array and hemiarray EIT reconstructions using blurring properties calculated directly from the sensitivity matrix as a normalization term. This term is dimensionless, and units of reconstructed quantities were preserved after normalization. We found that the spatial variability observed was dependent on the regularization scheme rather than the inverse model. Additionally, we found that patterns of the spatial variability were similar for different forward models. We chose the model that had elements of similar areas in order to simplify QI calculations.

We implemented normalization of spatially variant EIT image reconstruction using three different methods: PWS, WPI and WMNM. We found in our comparison that PWS methods generally worked poorly in reducing spatial variance. Employing WPI methods (A3 and A4) worked well for the full array but not for the hemiarray. The WMNM-regularized reconstruction (B1) produced images of improved contrast in both full array and hemiarray cases. While B1 succeeded in reducing spatial variability for the full array, it did not reduce variability for hemiarray cases. By using the WMNM framework, but with a differently defined normalization matrix as in C5 (WQ_t) rather than B1 (W), Sadleir et al (2008) succeeded in decreasing spatial variability of QI. C5 also produced images that were generally superior to those produced using A1. In our investigation, we confirmed the results of Sadleir et al (2008) in terms of QI. Further, we demonstrated that C5 performed fairly well for the full array as well. The images in figure 3 (C5) were reconstructed from phantom measurements, while the images shown in Sadleir et al (2008) were reconstructed from noiseless simulated measurements. Our images did not match the images in Sadleir et al (2008) closely for anomalies in the γ axis. Even though the condition number of the system matrix of B1 (SW) was larger than that of C5 (SWQ_t) (table 3), anomaly images reconstructed by B1 appeared less diffuse than those by C5 over all regions including the γ axis.

We tested our methods for single anomalies located at various positions within the domain. We have yet to determine if our method works well for multiple anomaly cases. Our normalization scheme was based on 2D and we obtained the blurring matrix from the sensitivity matrix of a 2D inverse model. We applied the 2D normalization method successfully to cylindrical phantom data acquired using bar electrodes. The blur matrix can easily be obtained from a 3D sensitivity matrix, and there is restriction on implementing our normalization method in 3D.

Overall, we found that the best normalized QI values were obtained by applying a WMNM normalization method to WMNM regularization (C5) for both full array and hemiarray topologies. Our comparison showed that C5 was generally superior to other methods, even though there were test cases where it did not perform better than other candidates.

5. Conclusion

In this paper, we compared various normalization methods in terms of QI. We demonstrated that some of these methods successfully reduced spatial variability of QI for the measurements obtained in numerical simulations and phantom experiments. Our investigation included many different approaches to resolve a spatial variability problem in EIT image reconstruction. Although method C5 generally performed well, there was no single method that performed significantly better over both electrode topologies. However, we have showed that discrete use of this type of normalization method should result in increased quantitation stability in EIT reconstruction.

Further testing of these methods is necessary for more realistic geometries in 2D and 3D. Formulated in a straightforward manner, the methods should be simple to implement without great computational burden. Thus, they should be easily applicable to various image reconstruction problems that are spatially variant. We anticipate that this type of normalization method could also be used for highly asymmetric image reconstruction problems.