Waist-to-height ratio is correlated with height in US children and adolescents aged 2–18 years

Abstract

The waist-to-height ratio is an anthropometric measure of central adiposity that has emerged as a significant predictor of cardiovascular disease risk factors in children and adolescents. However, the simple waist-to-height ratio retains residual correlation with height, which could cause the measure to over- or under-adjust for the effect of height at certain ages. We investigated the dependence of waist-to-height ratio on height in the representative US National Health and Nutrition Examination Survey 1999–2004. We stratified 11 270 subjects aged 2–18 years by age and sex. There was considerable residual correlation between height and the waist-to-height ratio, ranging from −0.29 to 0.36. Thus, simply dividing waist circumference by height (WC/Ht¹) might not be appropriate to “adjust for height” during periods of growth. We fitted a log-log regression of waist circumference on height to determine which exponent for height ensures that the log of the ratio is uncorrelated with the log of height, which we call the optimal exponent for WC/Ht^p. This optimal power for height in the age- and sex-specific waist-to-height ratio varies from 0.5 to 2.0, with similar patterns for males and females. The value peaks at age 8, and is close to 1 at age 18. Future research should investigate how this affects relationships between central adiposity and cardiovascular disease risk factors across these ages, and how using a power other than 1 might reduce bias and improve precision.

Introduction

Central adiposity is a significant predictor of chronic disease risk factors in children and adolescents, including total cholesterol, high-density lipoprotein (HDL) cholesterol, low-density lipoprotein (LDL) cholesterol, triglycerides, glucose and insulin (1–5). Anthropometric measures of central adiposity are used in population-based studies and for screening purposes. The waist-to-height ratio is one such measure; dividing waist circumference (WC) by height (Ht) presumably provides an index of central adiposity that is independent of height (6). In some studies of children, the waist-to-height ratio emerges as a better predictor of health risk, compared with body mass index (BMI) or WC alone (7,8). However, it is possible that during periods of growth, the waist-to-height ratio (WC/Ht¹) retains residual correlation with height, causing the measure to over- or under-adjust for the effect of height at different ages. It might be necessary to raise height to a power other than 1 in order to construct an index of central adiposity that is independent of height.

Using a nationally-representative sample of US children and adolescents, we investigated whether the waist-to-height ratio was independent of height, by measuring the residual correlation with height. During the growth periods of childhood and adolescence, waist circumference and height increase at different rates within an individual. As a result of this allometric growth, the ratio of waist circumference to height changes during development. These rates of growth are likely to differ according to sex, age, and other factors like the onset of sexual maturation. Therefore, we hypothesized that the simple waist-to-height ratio is not independent of height, thus causing residual correlation with height within age-and sex-strata.

Methods

We analyzed data from the continuing National Health and Nutrition Examination Survey, 1999–2004, a multistage, stratified sample representative of the civilian, non-institutionalized US population. Data were extracted for all non-pregnant subjects aged 2–18 years. Subjects had their height, weight, and waist circumference measured in a mobile examination center, with CDC standardized methods and equipment. Weight was measured on a Toledo self-zeroing scale. Height was measured to the nearest millimeter, using a stadiometer. Waist circumference was measured to the nearest 0.1 cm, with subjects standing, at the high point of the iliac crest at minimal respiration, using a steel measurement tape.

We first stratified subjects by sex and age at last birthday. We then examined scatter plots of waist circumference versus height, and removed bivariate outliers (0.1% of sample). Within each age- and sex-specific group, we calculated the residual correlation of height and the waist-to-height ratio. Then, within each group, we fit a log-log regression of waist circumference on height. We considered the regression coefficient for height from the regression model to be the optimal exponent for height in the ratio WC/Ht^p. This is the power that ensures that the log of the ratio is uncorrelated with the log of height. To investigate the role of race/ethnicity, we further stratified subjects by non-Hispanic white, non-Hispanic black, and Mexican American; small sample size did not permit the use of NHANES categories “Other Hispanic” and “Other, including Multi-Racial.” All analyses were conducted using SAS v9.1 (SAS Institute, Cary, NC), using sample weights per NHANES analytic guidelines.

Results

Sample sizes ranged from 230 to 467 in each sex-and age-stratified group, with a total sample of 11 270 subjects (Table I). We observed considerable residual correlation between height and the simple waist-to-height ratio (WC/Ht¹). For males, the residual correlation with height ranged from −0.29 at age 4 to 0.32 at age 8. For females, the range was −0.17 to 0.36, at ages 3 and 8, respectively.

Table I.

Residual correlation between waist-to-height ratio and height in NHANES 1999–2004.

	Boys				Girls
Age (years)	n	Correlation: WC/Ht vs. Ht	Optimal★p, in WC/Htp	Standard Error of optimal p	n	Correlation: WC/Ht vs. Ht	Optimal p, in WC/Htp	Standard Error of optimal p
2	230	−0.25	0.67	0.11	344	−0.12	0.81	0.12
3	291	−0.05	0.91	0.10	240	−0.17	0.69	0.15
4	260	−0.29	0.52	0.12	284	0.06	1.07	0.17
5	247	0.12	1.21	0.20	266	0.17	1.24	0.22
6	253	0.05	1.07	0.15	256	0.02	1.00	0.20
7	267	0.21	1.44	0.19	270	0.30	1.67	0.13
8	278	0.32	1.84	0.23	272	0.36	1.84	0.23
9	262	0.16	1.51	0.23	260	0.26	1.72	0.16
10	263	0.14	1.40	0.29	248	0.14	1.37	0.20
11	251	0.22	1.68	0.22	285	0.14	1.39	0.19
12	441	0.16	1.43	0.19	444	0.00	1.00	0.21
13	439	0.18	1.48	0.11	464	0.05	1.17	0.25
14	408	0.01	1.00	0.23	467	−0.05	0.76	0.17
15	417	−0.04	0.89	0.20	379	−0.11	0.61	0.25
16	462	0.03	1.11	0.24	380	−0.09	0.62	0.22
17	462	0.01	1.02	0.23	393	−0.05	0.74	0.22
18	409	0.00	0.96	0.21	378	−0.01	0.93	0.26

^★We consider optimal to be the exponent that ensures that the log of the ratio is uncorrelated with the log of height.

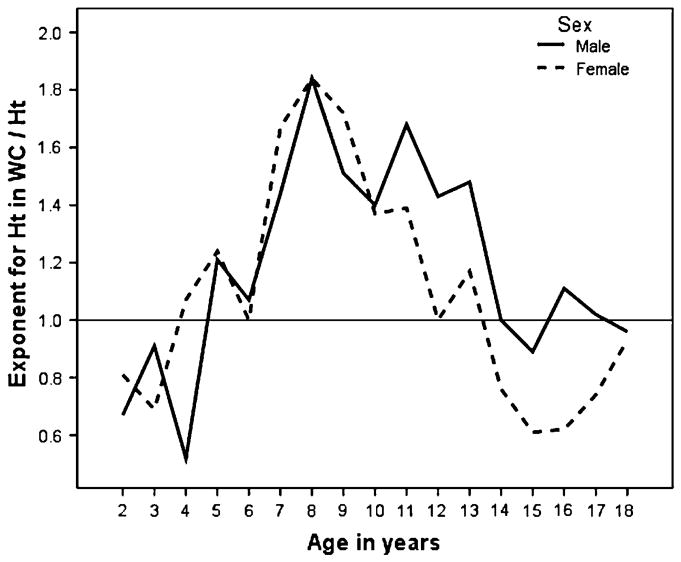
The optimal power for height in the age- and sex-specific waist-to-height index (WC/Ht^p) in these data increases from age 2 until age 8 (in boys, from 0.67 at age 2 to 1.84 at age 8; in girls, from 0.81 at age 2 to 1.84 at age 8), when it begins to decline and diverge by sex (Table I, Figure 1). At age 6, the value is near 1, indicating that simply dividing waist circumference by height is appropriate to adjust for height at that age. In very young children, the optimal power is smaller than 1, and therefore simply dividing waist circumference by height will over-adjust for the effect of height. In children aged 6–13 years, the optimal power is greater than 1, indicating that a simple waist-to-height ratio does not completely control for the effect of height. After age 13, patterns differ for boys and girls. In girls aged 14–17 years, waist/height^0.7 minimizes the residual correlation with height. In boys, the value of 1 (i.e., WC/Ht) is optimal from age 14 onward.

Figure 1.

In the waist-to-height ratio, the optimal exponent for height (in that it minimizes the residual correlation with height), differs by age and sex.

In further analyses, we determined what the optimal exponents would be if the intent were to minimize the residual correlation of the untransformed data. To do this, we modified the exponents from Table I in successive small increments, recalculating the ensuing residual correlation until the minimum correlation was reached for each age- and sex-strata. We found that the individual exponents changed only slightly (at the second decimal place), and that the overall pattern did not change (data not shown). Also, when data were stratified by race/ethnicity, the observed patterns were not appreciably altered (data not shown).

Discussion

A simple anthropometric measure that identifies children and adolescents at increased risk for cardiovascular risk factors could potentially improve screening and early intervention for chronic disease. The waist-to-height ratio has been suggested as a useful measure, with a proposed cut-off of 0.5 indicating excess risk (6). Our data suggest that simply dividing waist circumference by height might not adequately “adjust for height” during periods of growth. Our analyses also suggest that in order to minimize residual correlation with height, the exponent for height in a waist-to-height index would need to be sex- and age-specific. This might affect the validity of the proposed 0.5 cut-off for extra risk (6). If the simple waist-to-height ratio (WC/Ht¹) is used in very young children, it will over-adjust for the effect of height. In children aged 6–13 years, the simple waist-to-height ratio will under-adjust for the effect of height. And in girls aged 14+, the simple waist-to-height ratio will over-adjust for the effect of height. We observed that the optimal power for height in the waist-to-height ratio changes with age, with a peak at age 8 for both boys and girls. One explanation for the peak at this age is the mid-childhood growth spurt, which is seen in both sexes around this time (9). It is possible that during this growth spurt, the average increase in waist circumference for a given gain in height is larger than the corresponding average increase in early childhood. However, looking at published waist circumference references from US and UK children, it is not clear if there is a marked increase in waist circumference velocity at this age (10,11).

If the waist-to-height ratio were constructed with a power of 1 for height, instead of the optimal power, there would be effects in terms of both bias and precision. We attempted to quantify how differences in p would bias the estimate of relative waist circumference. Cole, in similar analyses investigating BMI as a measure of weight relative to height, showed that one interpretation of the exponent p is the percent increase in expected weight for each percent increase in height (12). Using Cole’s method (12), we can conceptualize how an individual’s expected waist circumference for height (WC_H) differs from that of the average child: a child’s expected waist circumference for height is the median waist circumference for his age group (WC_M), adjusted for his relative height (Ht/Ht_M) raised to the appropriate power: WC_H = WC_M (Ht/Ht_M)^P. From this equation, it is clear that subjects with a height equal to the median will not be affected by the value of p. However, those who are extremely tall or short for their age will have biased estimates of relative waist circumference if the optimal p is not used. In a parallel analysis to Cole’s, we looked at children at the 5^th or 95^th percentile for height, a departure of about 7.5% from the median in our data. For example, if a p of 1 were used for an 8 year old, instead of the optimal 1.8 (a difference of 0.8), there would be a percentage change of (0.8 × 7.5%)=6% in the waist-for-height ratio. Future research should examine the effects of this bias when waist circumference is used to predict health outcomes of interest. Similarly, it is warranted to investigate the effects of the imprecision that results from using a non-optimal power and the corresponding incomplete control for the effect of height.

Our estimates of the optimal exponents for height were generated in the NHANES 1999–2004 dataset, a representative sample of US children studied during a period of high obesity prevalence. If our analyses were repeated on other data, with a different prevalence of obesity, different estimates for the optimal formulation of the waist-to-height ratio might be observed. In our sample, within each age- and sex-specific group, overweight subjects (BMI z-score >85^th CDC percentile) tended to have the largest values for waist circumference and thus the largest influence on the steepness of the slope. We expect that similar patterns exist in contemporary populations with comparable levels of obesity.

In summary, the simple waist-to-height ratio (WC/Ht) maintains considerable and variable residual correlation with height over childhood and adolescence. This residual correlation may affect how this measure of central adiposity relates to risk factors of interest in this age group. Future research should investigate to what extent, if any, this residual correlation affects the ability of waist-to-height ratio to explain variability in cardiovascular disease risk factors in children and adolescents.