A comparative study of Gaussian geostatistical models and Gaussian Markov random field models

Abstract

Gaussian geostatistical models (GGMs) and Gaussian Markov random fields (GM-RFs) are two distinct approaches commonly used in spatial models for modeling point referenced and areal data, respectively. In this paper, the relations between GGMs and GMRFs are explored based on approximations of GMRFs by GGMs, and approximations of GGMs by GMRFs. Two new metrics of approximation are proposed: (i) the Kullback-Leibler discrepancy of spectral densities and (ii) the chi-squared distance between spectral densities. The distances between the spectral density functions of GGMs and GMRFs measured by these metrics are minimized to obtain the approximations of GGMs and GMRFs. The proposed methodologies are validated through several empirical studies. We compare the performance of our approach to other methods based on covariance functions, in terms of the average mean squared prediction error and also the computational time. A spatial analysis of a dataset on PM_2.5 collected in California is presented to illustrate the proposed method.

1 Introduction

In many applications in spatial and environmental epidemiology, data concerning a spatial process of interest are often observed at different spatial resolutions, and the overall problem of incompatible spatial data has been encountered very commonly when relating two spatial variables with different supports. For example, in studies of the association between air pollution exposure and adverse health effects, relevant health outcomes are usually available as areal data due to confidentiality while the pollution data are available as a point level (Best et al. 2000; Tolbert et al. 2000). To investigate the relationships between two variables with different spatial resolutions, the mismatch problem in the support of the two variables need to be resolved. One common solution to this spatial misaligment problem is to aggregate the point-referenced data to the area level, and create a common support for both variables. Once the point-referenced data are aggregated to the relevant level, the process representing the aggregated data is modeled using integrals of spatial continuous process (Journel & Huijbregts, 1978; Martin and Dwyer, 1994). Consider a continuous Gaussian process Y (s) with mean function µ(s) and covariance function c(s_i, s_j) for s_i, s_j ⊂ D∈R^d, where s_i is a location in a fixed domain D. The aggregated process over a region B, Y (B) = ∫_B Y (s)ds has a multivariate normal distribution with mean function µ(B) and covariance function Σ(B₁,B₂),

$$\begin{array}{c}\hfill \mu (B)=E(Y(B))=|B{|}^{-1}{\displaystyle {\int }_B\mu (s)ds}\hfill \\ \hfill \Sigma \left(B_1,B_2\right)=\mathit{cov}(Y(B_1),Y(B_2))=\left|B_1{|}^{-1}\right|B_2{|}^{-1}{\displaystyle {\int }_{B_1}{\displaystyle {\int }_{B_2}c}}(s_1,s_2)d{s}_{1}d{s}_2,\hfill \end{array}$$

where |B_i| denotes the area of a region B_i for i=1,2. Modeling aggregated data using these spatial integrals requires lots of computation. Hence, instead of using the aggregated models directly in modeling aggregated point-referenced data, it is becoming very common to use Gaussian Markov random fields.

The modeling of aggregated point-referenced data using GMRFs serves as one of our motivations to investigate the relations between GMRFs and GGMs. GGMs are used in modeling a process over a domain based upon a set of measurements taken at a finite number of sites in the domain. On the other hand, GMRFs are widely used for modeling areal data measured as averages of a quantity over subregions of a larger study region. There have been several attempts in the literature to explore the relationship between GGMs and GMRFs. Besag (1981) showed that covariance function of GMRFs could be approximately represented in terms of a modified Bessel function that decreases monotonically with distance, which suggested the possibility of approximations of GMRFs by GGMs. Griffith and Csillag (1993) investigated the approximation of GMRFs using several geostatistical models by minimizing the squared differences between the covariances of GMRFs and GGMs. Hrafnkelsson and Cressie (2003) explored a relationship between a specific class of GMRFs and a Matérn covariance model through an empirical parametrization of the relations between parameters of two models. On the other hand, Rue and Tjelmeland (2002) investigated approximations of GGMs by GMRFs using two approximation methods of GGMs by GMRFs, one using the Kulback-Leibler (KL) discrepancy between probability densities and the other one by matching the correlation functions of the models, showing that the matching correlation approach performed better than the KL method.

From these earlier studies, it appears that one of the key elements of this comparative study is the choice of the metric to measure the discrepancy between GGMs and GMRFs. Although various metrics are suggested in previous research, they are mainly based on covariance functions of models and, no evaluations have been conducted on suggested metrics. In this paper, we introduce two new metrics using spectral density functions to explore the relations between GGMs and GMRFs, and compare our metrics and covariance metrics based on the average mean squared prediction error and computation time. The aim of this study is to explore the relations betwen GGMs and GMRFs through a variety of empirical studies based on our suggested metrics. In Section 2, we present general overviews of GGMs and GMRFs. In Section 3, we propose new approximation metrics using spectral density functions. In Section 4, we compare the performance of our spectral method to the other covariance-based type of approaches, using as criteria the averaged mean squared prediction error and also taking into account the computational time. Section 5 presents an illustration of our methods using PM_2.5 data. Section 6 summarizes our findings and suggests possible extensions of this research.

2 Spatial models

In this section, we briefly review two general classes of spatial models, GGMs and GMRFs. The choice of models usually depends on the data types whether the data are collected as points in space or are observed as averages over regions. GGMs (e.g. Cressie, 1993) are usually used in modeling geostatistical data such as measurements on several attributes at point referenced spatial locations, s₁,…,s_n in a fixed region D where the measurement points vary continuously, while GMRFs (e.g. Besag, 1974) are used for modeling areal data which are collected over a certain region. These models specify the process in a different way. GGMs model spatial associations directly through the parametric covariance models while GMRFs specify spatial associations through the conditional specification of the precision matrix.

2.1 Gaussian geostatistical models (GGMs)

GGMs are used to model continous spatial Gaussian processes using a spatial covariance that is often just a function of distance and direction between locations. GGMs are generally based on two common assumptions which are second order stationarity and isotropy. Second order stationarity implies that the mean of a process is constant and the covariance function depends on the spatial vector distance between two locations. When the covariance function only depends on the Euclidean distance (no direction) between two locations, the process is called isotropic. The spatial covariance of a stationary and isotropic spatial process could be modeled using parametric functions of Euclidean distances. The Matérn covariance is one of the commonly used parametric covariance functions, which is defined as,

$$\begin{array}{c}\hfill \\ C(h)=\{\begin{array}{cc}{\sigma }^2\frac{1}{2^{v-1}\mathrm{\Gamma }(v)}{(\frac{2\sqrt{v}h}{\varphi })}^{v}2K_v(\frac{2\sqrt{v}h}{\varphi })\hfill & \text{if}h>0\hfill \\ {\tau }^2+{\sigma }^2\hfill & \text{if}h=0\hfill \end{array}\hfill \end{array}$$

where h denotes the Euclidean distance between two points, K_v is a modified Bessel function of the third kind (Arfken and Weber, 1995) of order v, τ², σ² and ϕ represent the nugget effect, partial sill and effective range of the covariance, respectively. The nugget effect is a discontinuity at the origin due to microscale variations and measurement errors. The sill parameter is the variance of the process, and the partial sill is the sill minus the nugget effect. The effective range is the distance where the correlation drops below 0.05. The order v > 0 of the K_v function controls the smoothness of the function. In particular, when v = 1/2, the Matérn covariance reduces to an exponential model and when v → ∞, it approaches to a Gaussian covariance model (e.g. Stein, 1999). Due to its flexibility, the Matérn covariance is widely used in a variety of spatial applications.

2.2 Gaussian Markov random models (GMRFs)

A GMRF is specified through full conditional based on the Markov property in space where the conditional distribution of data at a certain location given all of the other data depends only on the values in the neighborhood. Let Z_i denote a random variable observed at the site i. A GMRF is characterized by the following conditional distribution

$$Z_i|\left\{Z_j:j\ne i\right\}\sim N({\mu }_i+\alpha {\displaystyle \sum _{j=1}^n{b}_{ij}(z_i-{\mu }_j),{\tau }_i),}$$

where µ_i is the mean of Z_i, and τ_i is the conditional variance of Z_i given {Z_j : j ≠ i}. By Brook’s Lemma and Hammersley-Clifford Theorem (Besag 1974), the joint distribution of a GMRF Z = (Z₁,…,Z_n)^T is uniquely determined as,

$$\mathbf{Z}\sim N(\mathit{\mu },{(\mathbf{I}-\alpha \mathbf{B})}^{-1}\mathbf{M})$$

where µ is an n×1 vector of means with elements µ_i, and M is an n×n diagonal matrix with elements τ_i. The matrix B is an n×n neighborhood matrix with elements b_ij , which satisfy b_ii = 0, Σ_j b_ij = 1, b_ijτ_j = b_jiτ_i and b_ij = 0, unless i and j are neighbors. The parameter α is known as the spatial dependency parameter which somehow controls spatial dependence in the covariance. Specific choices of α lead to the covariance matrix being nonsingular. When α = 0, the model becomes independent, and when α = 1, the covariance matrix becomes singular and the joint distribution is improper. In particular, the model with α = 1 is called an intrinsic GMRF, (Besag et al. 1991; Besag and Kooperberg, 1995) which has been extensively used in spatial statistics as a prior for random effects in Bayesian hierarchical models (Sun et al. 1999; Carlin and Banerjee, 2003).

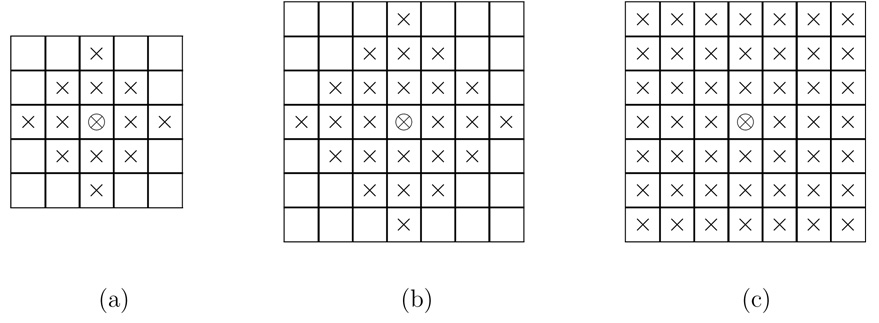
A GMRF introduces spatial associations in the model through the specification of neighborhoods based on the arrangement of the regions in the map. We impose a neighborhood structure on a site i, and assign weights to the neighboring values, which are prespecified according to some criterion. In the case of a regular lattice, some popular neighborhoods structures are defined as orders depending on the touching borders between grid cells. Some examples of neighborhoods with different orders are illustrated by Figure 2. For irregular lattices, two sites can be considered a neighbor if they are within some specified distance of one another or they share a common boundary. The weights assigned to each neighborhood are determined in several ways. Common weight functions are binary functions with value 1 if two sites are neighbors and 0 otherwise, and scaled weights which are standardized by the row sum.

Figure 2.

(a) neighborhood I, (b) neighborhood II, (c) neighborhood III

3 Spectral methods to measure discrepancy

Spectral densities and covariance functions are related through Fourier transforms, both of which are used to explore the second order properties of a spatial process. Although analyzing the variability of a process via the covariance function and the spectral density can be regarded as equivalent, they provide different ways of analyzing the process, and spectral analysis might offer some advantages compared to analysis based on the covariance function. For instance, since spectral densities of stationary processes evaluated at different frequencies are approximately independent, the inference made based on the spectral density is usually easier to derive than using the covariance function. In addition, the spectral density function can highlight subtle differences in the second order structure more easily than the covariance function (Stein, 1999). Considering these advantages of the spectral approaches, we introduce approximation methods using spectral densities. One limitation of this method is that spectral analysis generally requires gridded data.

3.1 Spectral densities of spatial processes

Consider Z(s) a stationary spatial process at location s, defined on D where D ⊂ R². The process Z(s) can be represented in terms of a spectral process X using a Fourier-Stieltjes integral,

$$Z(\mathbf{s})={\displaystyle {\int }_{R^2}\text{exp}}(i{\mathbf{w}}^T\mathbf{s})dX(\mathbf{w}),$$

where {X(w),w = (w₁,w₂) ∈ R²} is a process with zero mean and orthogonal increments, i.e.

$$\begin{array}{c}\hfill E(X(\mathbf{w}))=0\hfill \\ \hfill \mathit{Cov}(X({\mathbf{w}}_3)-X({\mathbf{w}}_2),X({\mathbf{w}}_1)-X({\mathbf{w}}_0))=0,\hfill \end{array}$$

for disjoint rectangles (w₃,w₂) and (w₁,w₀). The process X(·) is called the spectral process associated to the stationary process Z(·).

Using the spectral process X, we define a monotonically increasing function F(w) as

$$E(|dX(\mathbf{w}){|}^2)=dF(\mathbf{w}),$$

where $d\text{}X(\mathbf{w})={\text{lim}}_{\mathbf{h}\to 0}\frac{(X(\mathbf{w}+\mathbf{h})-X(\mathbf{w}))}{\mathbf{h}}\text{and}dF(\mathbf{w})={\text{lim}}_{\mathbf{h}\to 0}\frac{(F(\mathbf{w}+\mathbf{h})-F(\mathbf{w}))}{\mathbf{h}}$. The function F(w) represents the contribution to the total variance of the process by frequencies in the range (0,w). The derivative of F(w) denoted by f(w) (if it exists) is called the spectral density function of Z.

The covariance function C(h) of a weakly stationary process and the spectral density function f(w) form a Fourier transform pair,

$$\begin{array}{c}\hfill C(\mathbf{h})={\displaystyle {\int }_{R^2}\text{exp}}(i{\mathbf{w}}^T\mathbf{h})f(\mathbf{w})d\mathbf{w}\hfill \\ \hfill f(\mathbf{w})=\frac{1}{{(2\pi )}^2}{\displaystyle {\int }_{R^2}C(\mathbf{h})\text{exp}(-i{\mathbf{w}}^T\mathbf{h})d\mathbf{h},}\hfill \end{array}$$

where {h = ∥s₁ − s₂∥, s₁, s₂ ∈ D ⊂ R²} (Brillinger, 1981; Cramer and Leadbetter, 1967; Yaglom, 1962). If a stochastic process is defined on a lattice Λ, the integral in the expression of f(w) is replaced by a sum, and the frequency domain is restricted to the open square A = (−π,π]²,

$$\begin{array}{c}\hfill C(\mathbf{h})={\displaystyle {\int }_A\text{exp}}(i{\mathbf{w}}^T\mathbf{h})f(\mathbf{w})d\mathbf{w}\hfill \\ \hfill f(\mathbf{w})=\frac{1}{{(2\pi )}^2}{\displaystyle \sum _{\mathbf{h}}C(\mathbf{h})\text{exp}(-i{\mathbf{w}}^T\mathbf{h}).}\hfill \end{array}$$

When the underlying process is continuous, but observed only on a integer lattice Λ with an interval between neighboring observations δ, we can not distinguish between the frequency components w and $\mathbf{w}+\frac{2\pi \mathbf{l}}{\delta },\text{for}\mathbf{\text{l}}\subset \{(l_1,l_2);l{}_1,l_2=\pm 1,\pm 2,\cdots \}$. This phenomenon is known as the aliasing effect, and the frequencies $\mathbf{w}+\frac{2\pi \mathbf{l}}{\delta }$ are called the aliases of w for any w in ${(-\frac{\pi }{\delta },\frac{\pi }{\delta }]}^2.$ Due to the aliaing effects, the power in the sampled process from the set of frequencies $\mathbf{w}\in {(-\frac{\pi }{\delta },\frac{\pi }{\delta })}^2$ is the accumulation of power in the original process from all the sets of frequencies $\mathbf{w}+\frac{2\pi \mathbf{l}}{\delta }$. The spectral density of the sampled process is defined as follows,

$$f_{\delta }(\mathbf{w})={\displaystyle \sum _{l\in Z^2}f(\mathbf{w}+\frac{2\pi \mathbf{l}}{\delta }),}$$

where w ∈ (−π, π]² and δ > 0.

While the spectral density of a stationary process is represented by orthognal increments, the corresponding spectral process of a nonstationary process is no longer orthogonal, but correlated. The Fourier transform pairs of a process defined on a lattice Λ are,

$$\begin{array}{c}\hfill C({\mathbf{z}}_1,{\mathbf{z}}_2)={\displaystyle {\int }_{R^4}\exp (i({\mathbf{z}}_1{\mathbf{w}}_1-{\mathbf{z}}_2{\mathbf{w}}_2))f({\mathbf{w}}_1,{\mathbf{w}}_2)d{\mathbf{w}}_{1}d{\mathbf{w}}_2}\hfill \\ \hfill f({\mathbf{w}}_1,{\mathbf{w}}_2)=\frac{1}{{(2\pi )}^4}{\displaystyle \sum _{{\mathbf{z}}_1,{\mathbf{z}}_2}C({\mathbf{z}}_1,{\mathbf{z}}_2)\text{exp}(-i({\mathbf{z}}_1{\mathbf{w}}_1-{\mathbf{z}}_2{\mathbf{w}}_2)),}\hfill \end{array}$$

where z₁, z₂2 ∈ Λ and w₁,w₂ ∈ (−π, π]². The nonstationary spectral density can be represented as the stationary spectral density for the special case in which the spectral density is zero for all the elements except for the ones along the diagonal (w₁ = w₂),

3.2 Approximation methods using spectral densities

We consider a continuous stationary and isotropic Gaussian spatial process on a r × c finite lattice Λ, with an interval δ between neighboring points, and define a GGM and a GMRF on this lattice. The GGM represents a weakly stationary and isotropic process, and the corresponding GMRF would be a nonstationary process due to the finiteness of the lattice and the edge effect. Since we define a GGM on a discrete lattice Λ, we observe only a sampled GGM on a lattice Λ. The spectral density of the sampled GGM g_l is defined as,

$$gl(\mathbf{w})={\displaystyle \sum _{\mathbf{Q}\in Z^2}g}\left(\mathbf{w}+\frac{2\pi \mathbf{Q}}{l}\right)$$

$$\text{where}g(\mathbf{w})=\frac{1}{{(2\pi )}^2}{\displaystyle {\int }_{R^2}C(\mathbf{h})\text{exp}(-i{\mathbf{w}}^T\mathbf{h})dh}$$

for w ∈ (−π, π]² and Z={0,±1,±2,… }. Nonstationary processes corresponding to GMRFs defined on a lattice can not be represented as a function with orthogonal increments but require correlated increments. The spectral density of a nonstationary process is

$$f({\mathbf{w}}_1,{\mathbf{w}}_2)=\frac{1}{{(2\pi )}^4}{\displaystyle \sum _{{\mathbf{z}}_1,{\mathbf{z}}_2\subset \mathrm{\Lambda }}C({\mathbf{z}}_1,{\mathbf{z}}_2)\text{exp}(-i({\mathbf{z}}_1{\mathbf{w}}_1-{\mathbf{z}}_2{\mathbf{w}}_2)),}$$

where w₁,w₂ ∈ (π, π]².

Using spectral densities, we suggest two approximation criteria; the KL discrepancy between two spectral densities and the chi-squared distance (CSD) between two spectral densities. We use these criteria to approximate the spectral density of a geostatistical process with the spectral density of a GMRF or vice versa by minimizing the differences of the spectral densities of two processes. The KL discrepancy between two spectral densities is defined as,

$$KL(f,\tilde{f};\theta )={\displaystyle {\int }_{-\pi }^{\pi }f(\mathbf{w})\log \frac{f(\mathbf{w})}{\tilde{f}(\mathbf{w};\theta )}d\mathbf{w},}$$

where f(w) and f˜ (w;θ) are the spectral densities of the true and approximated model, respectively. Through the numerical minimization of the criterion, we estimate the parameters of the approximated model,

$$\widehat{\theta }={\text{argmin}}_{\theta }KL(f,\tilde{f};\theta ).$$

The CSD between two spectral densities is expressed as,

$$G(f,\tilde{f};\theta )={\displaystyle {\int }_{-\pi }^{\pi }\frac{{(f(\mathbf{w})-\tilde{f}(\mathbf{w};\theta ))}^2}{f(\mathbf{w})}d\mathbf{w},}$$

where f(w) and f˜ (w;θ) are the spectral densities of the true and approximated model, respectively. The best fitting model is obtained using the optimal parameters estimated by minimizing the CSD between the two spectral densities,

$$\widehat{\theta }={\text{argmin}}_{\theta }G(f,\tilde{f};\theta ).$$

3.3 Comparisons of spectral density approximation methods with covariance function approximation methods

We compare our approximation approaches using spectral densities in the frequency domain to the squared relative differences (SRD) between covariance functions in the spatial domain. The SRD approach in the spatial domain is to minimize the squared relative differences between the covariance functions of the two models,

$$\widehat{\theta }={\text{argmin}}_{\theta }{\displaystyle {\int }_{R^2}{\left(\frac{C({\mathbf{s}}_1,{\mathbf{s}}_2)-\tilde{C}({\mathbf{s}}_1,{\mathbf{s}}_2;\theta )}{C({\mathbf{s}}_1{\mathbf{s}}_2)}\right)}^{2}d{\mathbf{s}}_{1}d{\mathbf{s}}_2,}$$

where C(s₁, s₂) and C˜ (s₁, s₂;θ) are the true and approximated covariances at s₁,s₂ ∈ R². We compare the three approximation methods based on the mean squared prediction error (MSPE). The MSPE is the average squared difference between the actual and predicted values at different locations, defined as,

$$MSPE=\frac{1}{N}{\displaystyle \sum _i{(Z(s_i)-\widehat{Z}(s_i))}^2,}$$

where Z(s_i) and Z^ (s_i) are the observed and predicted values at site i, and N is the number of sites.

Instead of conducting simulations by generating data from a spatial process with known covariance models to calculate MSPE, we obtain the averaged mean squared prediction error (AMSPE), which can be expressed as a function of the known covariances of GGMs or GMRFs to compare various metrics. We consider a spatial process with mean zero and a known covariance which follows either a GGM or a GMRF. In the approximations of GGMs by GMRFs, the predicted value at site s_i given other values Ẑ_GGM(s_i) is expressed as

$${\widehat{Z}}_{GGM}({\mathbf{s}}_i)=-{\displaystyle \sum _{j=1,j\ne i}^N{Q}_{ij}{Q}_{ii}^{-1}Z({\mathbf{s}}_j)}$$

where Q_ij is the (i, j)th element of the precision matrix of the approximated GMRF. Then the AMSPE of a GGM is represented as

$$AMSP{E}_{GGM}=E(Z({\mathbf{s}}_i)-(-{\displaystyle \sum _{j=1,j\ne i}^N{Q}_{ij}{Q}_{ii}^{-1}Z({\mathbf{s}}_j)){)}^2=E{(\mathbf{C}\prime \mathbf{Z})}^2=\mathbf{C}\prime }{\sum }_{GGM}\mathbf{C},$$

where C is an N × 1 vector with c_i = 1 and $c_j=Q_{ij}{Q}_{ii}^{-1},\mathbf{Z}=(Z({\mathbf{s}}_1),\cdots ,Z({\mathbf{s}}_N))\prime \text{and}{\mathrm{\Sigma }}_{GGM}$ and Σ_GGM is the covariance matrix of a GGM. The expectation in the AMSPE of a GGM is taken with respect to the true underlying GGM. In the approximation of GMRFs by GGMs, the predicted value Z^_GMRF (s_i) is expressed as

$${\widehat{Z}}_{GMRF}({\mathbf{s}}_i)={\sigma }_{iJ}{\sigma }_{JJ}^{-1}{\mathbf{Z}}_{-i}$$

where σ_iJ is an 1 × (N − 1) matrix with the j th element,, σiJ(j) = cov(Z(s_i), Z(s_j)), σ_JJ is a (N − 1) × (N −1) matrix with the (j, k)th element, σ_JJ(jk) = cov(Z (s_j), Z(s_k)) where j, k = 1,… , i −1, i + 1,… ,N, and Z_−i = (Z(s₁),…,Z(s_i−1), Z(s_i+1),… , Z(s_N))′.The AMSPE of a GMRF is

$$AMSP{E}_{GMRF}=E{(Z({\mathbf{s}}_i)-{\sigma }_{iJ}{\sigma }_{JJ}^{-1}{\mathbf{Z}}_{-i})}^2=E{(\mathbf{D}\prime \mathbf{Z})}^2=\mathbf{D}\prime {\mathrm{\Sigma }}_{GMRF}\mathbf{D},$$

where D is an N × 1 vector with with d_i = 1, $d_j=-{({\sigma }_{iJ}{\sigma }_{JJ}^{-1})}_j\text{for}j<i,d_j=-({\sigma }_{iJ}{\sigma }_{jj}^{-1}{)}_{j-1}\text{for}j>i\text{and}{\mathrm{\Sigma }}_{GMRF}$ for j > i and Σ_GMRF is the covariance matrix of a GMRF. The expectation in the AMSPE of a GMRF is taken with respect to the true underlying GMRF. We also compare the AMSPE of the approximated model with the AMSPE of the original model (AOM) to check the performance of the criteria. The AMSPE of the original GGM is defined as,

$$AMSPE=E{(Z({\mathbf{s}}_i)-Z^{pred}({\mathbf{s}}_i))}^2=E{(Z({\mathbf{s}}_i)-{\sigma }_{iJ}{\sigma }_{JJ}^{-1}{\mathbf{Z}}_{-i})}^2=E{(\mathbf{D}\prime \mathbf{Z})}^2=\mathbf{D}\prime {\mathrm{\Sigma }}_{GGM}\mathbf{D},$$

and the AMSPE of the original GMRF is,

$$\begin{array}{c}\hfill AMSPE=E(Z({\mathbf{s}}_i)-Z_{GMRF}^{pred}({\mathbf{s}}_i){)}^2\hfill \\ \hfill =E(Z({\mathbf{s}}_i)-(-{\displaystyle \sum _{j=1,j\ne i}^N{Q}_{ij}{Q}_{ii}^{-1}Z({\mathbf{s}}_j)){)}^2=E{(\mathbf{C}\prime \mathbf{Z})}^2=\mathbf{C}\prime {\mathrm{\Sigma }}_{GMRF}\mathbf{C},}\hfill \end{array}$$

$\mathit{\text{where}}{Z}_{GGM}^{pred}({\mathbf{s}}_i)\text{and}{Z}_{GMRF}^{pred}({\mathbf{s}}_i)$ are the predicted values of the GGM and the GMRF at s_i, respectively.

4 An empirical study

In this Section, an empirical study is conducted to compare the spectral density approximation methods to the covariance approximation method in the approximations of GGMs and GMRFs. Let us define a Gaussian Geostatistical process (GGP) and a GMRF on a 30×30 lattice. To reduce the nonstationarity problem of the GMRF which arises due to the edge effect, we consider a buffer zone by extending the lattice to a 32×32 grid to cover a larger domain, and we use only the covariance of the original lattice within the covariance of the extended lattice for approximations. We consider a Matérn model with various smoothness parameters for the GGP and different neighborhood structures that are shown in Figure 2 with scaled weights for the GMRF.

The empirical study is composed of two steps, estimating parameters using each metric, and compare them in terms of the AMSPE. In the estimation step, we estimate the parameters of the approximated models by minimizing the criteria suggested in the previous section: CSDS (chi-squared differences between spectral densities), KLS (Kullback-Leibler discrepancy between spectral densities) and SRDC (squared relative differences between covariance functions). In the approximations of GMRFs by GGMs, we estimate the range (ϕ) and sill (σ²) parameters of the Matérn model,

$$C(h)=\frac{2{\sigma }^2}{\mathrm{\Gamma }(v)}{(\frac{h}{2\varphi })}^v{K}_v(\frac{h}{\varphi }),$$

where h denotes the Euclidean distance and v is a smoothness parameter. For the approximations of GGMs by GMRFs, we estimate the spatial dependency (α), scale (τ) parameters in the GMRF covariance function,

$${(\mathbf{I}-\alpha \mathbf{B})}^{-1}\mathbf{M}(\tau ),$$

where B is the neighborhood matrix and M(τ) is the diagonal matrix with elements τ. These parameters are estimated using the nlm function in the R software (http://www.rproject. org/). We perform various empirical studies to explore the relation between GGMs and GMRFs. Table 1 shows the estimated parameters of GGMs when approximating GMRFs with different values for α and the neighborhood III using GGMs. We obtain different estimated parameters depending on the matching criteria. When we use the covariance as an approximation criterion, the estimated sill and range vary severely over different values of α, while the estimated parameters are stable over different values of α is the case of using spectral density criteria. We compare our methods by the average mean squared prediction error (AMSPE). Table 2 shows that the AMSPEs obtained using the CSDS and the KLS criteria are smaller than those obtained using the SRDC, and they are close to the AOM. This suggest that the CSDS and KLS are good criteria for the approximations of GMRFs by GGMs.

Table 1.

Estimated parameters of GGMs in approximations of GMRFs with the neighborhood III and various values of α by GGMs with v=0.5

	α=0.9		α=0.95		α=0.98
method	σ2	ϕ	σ2	ϕ	σ2	ϕ
CSDS	0.43	0.14	0.43	0.15	0.43	0.15
KLS	0.43	0.13	0.43	0.14	0.43	0.15
SRDC	0.43	0.14	0.001	10.40	0.002	19.37

Table 2.

AMSPE in approximations of GMRFs with the neighborhood III and various values of α by GGMs with v=0.5

	AMSPE
method	α=0.9	α=0.95	α=0.98
CSDS	0.019	0.019	0.020
KLS	0.019	0.019	0.020
SRDC	0.024	0.023	0.023
AOM	0.018	0.018	0.018

In Table 3, we present the estimation results for GGMs in the approximation of GMRFs with α=0.95 and various neighborhood structures using GGMs. For the CSDS and the KLS, the estimated sill and range parameters tend to decrease as the neighborhood increases. However, the SRDC gives increasing estimated range parameters along with the increasing neighborhood. Table 4 shows the prediction results using the estimated parameters. As the neighborhood increases, the AMSPE decreases, and the SRDC gives the largest AMSPE for the II and III neighborhoods. Comparing with the AOM, the CSDS and KLS yield closer values of the AMSPE than the SRDC.

Table 3.

Estimated parameters of GGMs in approximations of GMRFs with α=0.95 and various neighborhood structures by GGMs with v=0.5

	I		II		III
method	σ2	ϕ	σ2	ϕ	σ2	ϕ
CSDS	2.35	0.42	0.90	0.21	0.43	0.15
KLS	2.31	0.28	0.90	0.18	0.43	0.14
SRDC	0.02	4.50	0.005	6.71	0.001	10.45

Table 4.

AMSPE in approximations of GMRFs with α=0.95 and various neighborhood structures by GGMs with v=0.5

	AMSPE
method	I	II	III
CSDS	0.103	0.043	0.019
KLS	0.109	0.043	0.019
SRDC	0.101	0.046	0.023
AOM	0.08	0.037	0.018

We approximate GMRFs using Matérn models with different smoothness parameters (v) to study the effect of the smoothness parameter on the approximations of GMRFs by Matérn models. Table 5 presents the estimated parameters of GGMs in the approximations of GMRFs with α=0.95 and neighborhood III using Matérn models with various values of v. The parameters estimated by the SRDC vary over the various values of v while those estimated by the CSDS and the KLS show a little change by the different values of v. Table 6 displays the AMSPE results, which show that AMSPEs obtained by the SRDC are larger than the other methods.

Table 5.

Estimated parameters of GGMs in approximations of GMRFs with α=0.95 and neighborhood III using Matérn models with various values of v

	v=0.1		v=0.5		v=1
method	σ2	ϕ	σ2	ϕ	σ2	ϕ
CSDS	0.66	0.15	0.43	0.15	0.42	0.15
KLS	0.68	0.12	0.43	0.14	0.42	0.15
SRDC	0.005	5.74	0.001	10.40	0.001	12.34

Table 6.

AMSPE in approximations of GMRFs with α=0.95 and neighborhood III using Matérn models with various values of v

	AMSPE
method	v=0.1	v=0.5	v=1
CSDS	0.019	0.019	0.019
KLS	0.020	0.019	0.019
SRDC	0.020	0.023	0.023
AOM	0.018	0.018	0.018

Table 7 shows the parameter estimates of GMRFs corresponding to GGMs with σ²=1 and various values ofϕ. We consider the three different cases, 1) when ϕ is smaller than the maximum distance within the neighborhood (MDN), 2) when ϕ is the same to the MDN and 3) when ϕ is larger than the MDN, and assign different values of ϕ for each case. The estimated α is close to one when ϕ is larger than the MDN. The AMSPE becomes smaller as ϕ increases, and we obtain values closer to the AOM by using the CSDS and the KLS criteria (Table 8).

Table 7.

Estimated parameters of GMRFs in approximations of GGMs with σ²=1, v=0.5 and various values of ϕ by GMRFs with the neighborhood II

	ϕ=2 (ϕ <MDN)		ϕ=3 (ϕ =MDN)		ϕ=5 (ϕ >MDN)
method	α	τ	α	τ	α	τ
CSDS	0.99	0.32	0.99	0.22	0.99	0.13
KLS	0.99	0.22	0.99	0.13	0.99	0.08
SRDC	0.63	101.52	0.79	166.42	0.91	140.61

Table 8.

AMSPE in approximations of GGMs with σ²=1, v=0.5, and various values of ϕ by GMRFs with neighborhood II

	AMSPE
method	ϕ=2	ϕ=3	ϕ=5
CSDS	0.70	0.54	0.36
KLS	0.70	0.54	0.36
SRDC	0.76	0.58	0.38
AOM	0.51	0.36	0.21

To study the effects of σ² values on the approximations of GGMs by GMRFs, we fit GGMs with various values of σ² to GMRFs. Table 9 presents the estimated parameters of GMRFs which approximate GGMs with ϕ=3 and various values of σ². As σ² increases, the estimated conditional variance increases for all criteria, which suggest a positive relation between the sill parameter in the GGM and the conditional variance in the GMRF. Table 10 presents the AMSPE results, showing that the CSDS and the KLS gives closer values of the AMSPE to the AOM than the SRDC.

Table 9.

Estimated parameters of GMRFs in approximations of GGMs with ϕ=3, v=0.5 and various values of σ² by GMRFs with the neighborhood II

	σ2=0.5		σ2=1		σ2=2
method	α	τ	α	τ	α	τ
CSDS	0.99	0.11	0.99	0.22	0.99	0.44
KLS	0.99	0.06	0.99	0.13	0.99	0.26
SRDC	0.79	83	0.79	166.42	0.82	332.53

Table 10.

AMSPE in approximations of GGMs with ϕ=3, v=0.5 and various values of σ² by GMRFs with the neighborhood II

	AMSPE
method	σ2=0.5	σ2=1	σ2=2
CSDS	0.27	0.54	1.09
KLS	0.27	0.54	1.09
SRDC	0.29	0.58	1.17
AOM	0.17	0.36	0.71

We investigate the effects of the Matern smoothness parameter (v) on approximations of Matern models by GMRFs. In the CSDS and the KLS, α is constant and τ decreases, while in the SRDC, α decreases and τ increases as v increases (Table 11). Comparing our methods using the AMSPE, the AMSPE decreases as v increases, and the CSDS and the KLS yield smaller AMSPEs than the SRDC (Table 12). Comparing our methods using the AOM, AMSPEs obtained using the CSDS and the KLS are closer to the AOM than those obtained using the SRDC criterion.

Table 11.

Estimated parameters of GMRFs in approximations of GGMs with ϕ=3, σ²=1and various values of v by GMRFs with the neighborhood II

	v=0.1		v=0.5		v=1
method	α	τ	α	τ	α	τ
CSDS	0.99	0.64	0.99	0.41	0.99	0.03
KLS	0.99	0.45	0.99	0.33	0.99	0.02
SRDC	0.93	37.23	0.85	90.06	0.67	250.92

Table 12.

AMSPE in approximations of GGMs with ϕ=3, σ²=1 and various values of v by GMRFs with the neighborhood II

	AMSPE
method	v=0.1	v=0.5	v=1
CSDS	0.80	0.49	0.44
KLS	0.80	0.49	0.44
SRDC	0.80	0.52	0.54
AOM	0.77	0.36	0.16

To study the potential impact of the weight function of GMRFs on the approximations of GGMs by GMRFs, we use a distance-based weight parameterized by γ, and estimate γ in addition to the α and τ,

$$b_{ij}=\frac{\mathit{\text{exp}}(-\frac{d_{ij}}{\gamma })}{{\sum }_{j=1}^N\mathit{\text{exp}}(-\frac{d_{ij}}{\gamma })},$$

where b_ij is the weight for sites i and j,γ is a scale parameter, and d_ij is a distance between sites i and j. We performed this study on 16 by 16 lattices. The estimated parameters are slightly different from those based on the scaled binary weights in GMRFs. However, we still obtain smaller AMSPEs using the CSDS and the KLS (Table 14).

Table 14.

AMSPE in approximations of GGMs with ϕ=3, σ²=1and various values of v by GMRFs with parameterized weights and the neighborhood II

	AMSPE
method	v=0.1	v=0.5	v=1
CSDS	0.79	0.38	0.19
KLS	0.77	0.37	0.19
SRDC	0.81	0.37	0.21
AOM	0.77	0.36	0.16

We also compare the suggested metrics taking into account the computational time. Table 15 and Table 16 display the computational time in approximations of GGMs by GMRFs, and approximations of GMRFs by GGMs. The unit of time is seconds, and these results are obtained using a Pentium PC with a 3.20 GHz CPU, showing that the approximation methods based on the spectral density faster than those based on covariance functions.

Table 15.

computation times in approximations of GGMs with σ²=1, ϕ=3 and v=0.5 by GMRFs with the neighborhood II

methods	computation times
CSDS	26698
KLS	226585
SRDC	347815

Table 16.

computational times in seconds in approximations of GMRFs with α = 0.95 and neighborhood III by GGMs with v=0.5

methods	computation times
CSDS	25238
KLS	31111
SRDC	54991

5 Applications

GGMs and GMRFs are two different models commonly used in modeling spatial data, and they have different characteristics in terms of modeling the spatial structure of an underlying process. GGMs are usually used for modeling point level data, and explain the spatial relation based on the distance between two points, while GMRFs have been developed for modeling areal level data, and the spatial structure is considered in the model based on the conditional location between two areas which is specified in the neighborhood structure. GMRFs have some advantages over GGMs in that they are more convenient to use in Bayesian hierarchical models to capture the spatial structure in the data due to the conditional form of GMRFs, and the computational benefits. Because of this, point level data are often aggregated to a certain areal level, and GMRFs are used to model aggregated point level data. The main objective of this paper is to investigate the possibility of the interchangeable use of GGMs and GMRFs by suggesting approximations of GGMs by GMRFs, and approximations of GMRFs by GGMs. For the approximations, we use the theoretical covariance of each model and approximate the models based on the different proposed criteria. One widely used criterion to approximate one covariance model with another model is to minimize the squared differences between the two covariance models. We suggest some new criteria based on the spectral density and our simulation study shows that our suggested criteria are more accurate in terms of the AMSPE and easier to compute than the previously suggested criterion.

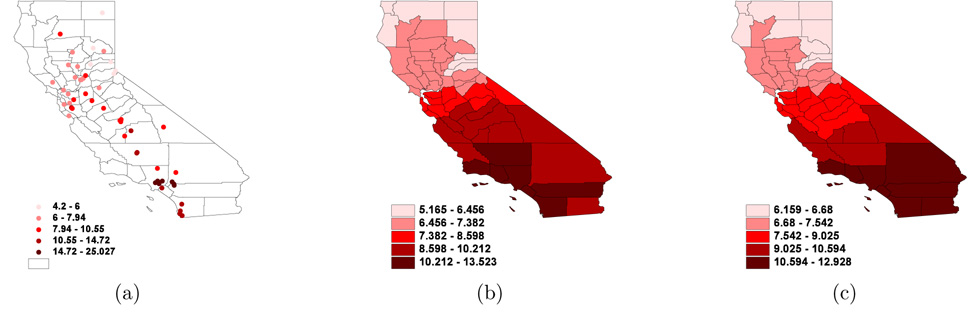
Particulate Matter (PM) is the general term used for a complex mixture of solid particles and liquid droplets suspended in the air, which incudes a broad class of chemically diverse particles whose range in size is from 0.005 µm to 100 µm in diameter. PM is usually sorted by its size because size is an important factor that determines the health effects of PM. In particular, PM_2.5, also known as fine PM, which includes the fine particles that are less than or equal to 2.5 µm in diameter, causes a variety of serious health disease such as respiratory and cardiovascular problems. PM_2.5 observations are typical point-referenced data collected at point monitoring stations. This type of data can be aggregated to a level of interest to associate spatial variables with different spatial resolutions. For example, in the study of associations between PM_2.5 and adverse health effects, since health outcomes are generally collected over geographic regions, point-referenced PM_2.5 values are commonly aggregated to the level of the health outcomes to solve the mismatch support problem. (Fuentes et al., 2005). In this application, we apply the approximation methods described in the previous sections to approximate the aggregated PM_2.5 data at the county level in California by GMRFs. The aggregated point data at each county are obtained by averaging the predicted values of PM_2.5 at 20 locations within each county based on the PM_2.5 observations. Since the underlying process is a point process, the aggregated PM_2.5 process is also based on a point process. However, we can also consider the aggregated PM_2.5 as areal level data and model them using a GMRF. To approximate the aggregated PM process by a GMRF, we obtain the empirical covariance of GGMs based on the aggregated PM process and approximate the empirical covariance of the aggregated PM process by a GMRF using the several criteria we suggested in the previous section. We also investigate the effects of the neighborhood of GMRFs in the approximations by considering the first and second order neighborhoods in GMRFs. After estimating the parameters of the GMRF, the performance of the different methods are evaluated through the MSPE. Figure 3 display the point and aggregated county level PM_2.5 values and the GMRF with the first order neighborhood estimated by the CSDS with the first order neighborhood. In the point level map, we see that the Southern California areas are highly polluted with PM_2.5, these patterns are also observed in the county level map and the predictied map using approximated GGMs. We can also notice that the high magnitude of PM_2.5 found in the Southern California areas is reduced after the aggregation.

Figure 3.

a) point level PM_2.5 values, b) county level averaged PM_2.5 values and c) predicted values using GMRFs estimated by the CSDS

Table 17 is the MSPE obtained from approximations of the aggregated PM_2.5 county values using a GMRF. In our example, the MSPE values are the same for the all methods with the first order neighborhood and the SRDC gives a little larger MSPE than the other methods for the second order neighborhood. Also we notice that the GMRF with the first order neighborhood performs better than the GMRF with the second order neighrborhood in that the first order neighborhood yields smaller MSPE than the second order neighborhood.

Table 17.

MSPE in the approximations of aggregated PM_2.5 using GMRFs with a first and second order neighborhood structures.

	MSPE
method	first order neighborhood	second order neighborhood
CSDS	0.68	1.12
KLS	0.68	1.12
SRDC	0.68	1.19

6 Conclusions

The major objective of this paper is to study relations between GMRFs and GGMs through approximations of GMRFs by GGMs, and vice versa. We approximate GMRFs by GGMs and GGMs by GMRFs using three approximation methods based on spectral density functions and covariance functions, which are evaluated in terms of the AMSPE and computation times. The approach presented here using spectral densities is easy and fast to compute compare to covariance-based criteria. Our approach reduces considerable the total computation time by the use of Fast Fourier transform algorithm and also yields smaller AMSPEs than the covariance criterion. One noticeable result is that there is positive relationships between range parameter and spatial dependancy parameter, and sill and conditional variance which might be expected since these parameters control the strength of the correlation of the data and variance in GMRFs and GGMs. Since we use different criteria in approximations of GGMs and GMRFs, the parameter estimates are different depending on the criteria used. However, the results in terms of prediction were not very different, and show some patterns as we change parameters of GGMs and GMRFs. In the approximations of GMRFs by GGMs, as the neighborhood order increases, the AMSPE becomes smaller, while the AMSPE decreases as the range increases and the conditional variance decreases in the approximations of GGMs by GMRFs. In our application, we approximated county-level averaged PM_2.5 using GMRFs. The smallest MSPE was obtained using the CSDS and the KLS criteria.

Further investigation is being conducted to study the effect of the level of aggregation on the approximations of averaged process using GMRFs. Also we plan to study the bias that might occur in estimated parameters when GMRFs are used in modeling aggregated data instead of averaged continuous spatial process.

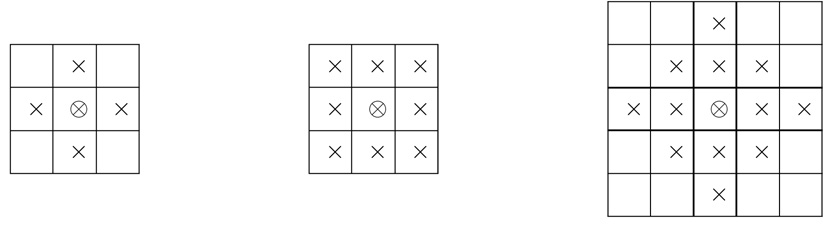
Figure 1.

(a) First order neighbors (b) Second order neighbors (c) Third order neighbors

Table 13.

Estimated parameters of GMRFs with parameterized weights in approximations of GGMs with ϕ=3, σ²=1and various values of v by GMRFs with the neighborhood II

	v=0.1			v=0.5			v=1
method	α	τ	θ	α	τ	θ	α	τ	θ
CSDS	0.99	1.65	2.59	0.99	0.018	0.35	0.99	0.0005	0.21
KLS	0.99	0.15	0.72	0.99	0.0006	0.20	0.99	0.0005	0.56
SRDC	0.97	0.02	0.24	0.94	0.015	0.17	0.92	0.002	0.13