Abstract
The authors investigated the relatively short-term and longer term effects of grade retention in 1st grade on the growth of mathematics and reading achievement over 4 years. The authors initially identified a large multiethnic sample (n = 784) of children who were below the median in literacy at school entrance. From this sample, the authors closely matched 1 retained with 1 promoted child (n = 97 pairs) on the basis of propensity scores constructed from 72 background variables and compared growth of retained and promoted children using Rasch-modeled W scores and grade standard scores, which facilitate age-based and grade-based comparisons, respectively. When using W scores, retained children experienced a slower increase in both mathematics and reading achievement in the short term but a faster increase in reading achievement in the longer term than did the promoted children. When using grade standard scores, retained children experienced a faster increase in the short term but a faster decrease in the longer term in both mathematics and reading achievement than did promoted children. Some of the retention effects were moderated by limited English language proficiency, home-school relationship, and children’s externalizing problems.
Keywords: grade retention, growth curve model, propensity score, optimal matching, achievement
Since the mid-1990s, “ending social promotion” has become a central component of the standards-based reform movement that emphasizes setting content-based standards for students and holding both schools and students accountable for meeting them. In his 1998 and 1999 State of the Union addresses, President Clinton urged an end to social promotion and stated that scores on standardized tests should be the basis for promotion. The No Child Left Behind federal legislation passed in 2001, championed by President George W. Bush, requires that assessments aligned with state standards be used to measure the achievement of all children at each grade level. States increasingly use performance on these tests to evaluate schools and to reach decisions about promotion of children to the next grade.
Texas, the location of the present study, has been a leader in the standards-based reform movement. In 1990, the Texas legislature enacted a policy requiring all schools to test students in Grades 3 and higher with a test aligned with statewide curricular standards. Schools are evaluated on the basis of performance on this test, currently the Texas Assessment of Knowledge and Skills; test results are widely publicized; and rewards and sanctions are allocated to schools on the basis of performance standards. In 1999, Texas enacted legislation that took effect in the 2002-2003 school year that requires students in Grades 3, 5, and 8 to pass the Texas Assessment of Knowledge and Skills in specified content areas to be promoted to the next grade, unless certain exceptional circumstances apply (e.g., documented learning disability). These policies were initiated by then-Governor George W. Bush and served as the model for the No Child Left Behind federal legislation.
Although the effectiveness of these educational accountability policies is hotly disputed (Evans, Baugh, & Sheffer, 2005; Hong & Raudenbush, 2005; Sipple, Killeen, & Monk, 2004; Warren & Edwards, 2005), there is little doubt that one consequence of the use of high-stakes testing is a decrease in the frequency of social promotion (defined as promoting to the next grade children who have not mastered curriculum content at their current grade) and an increase in grade retention (Gootman, 2005; Roderick, Bryk, Jacob, Easton, & Allensworth, 1999; Roderick & Nagaoka, 2005). In Texas, retention rates in Grades K-5 increased from 1994-1995 to 2003-2004, with the retention rate for Grade 3, the first promotional gate grade, up 100% over this time period (Texas Education Agency, 2005). The accountability movement likely affects retention policies even when performance on the curriculum-aligned test is not the sole or primary criterion for grade retention decisions. In Texas in 2003-2004, retention in first grade, the focal grade in this study, was 6.4%, compared with 5.8% in 1994-1995 (Texas Education Agency, 2005).
Previous Research on Retention Effects
When a student has failed to demonstrate grade-level competencies, one option is to retain the student in hopes that another year of maturity and exposure to the curriculum of the repeated grade will prepare the child to meet the academic and social demands of the next grade, thereby increasing the probability of academic and social success in future grades. Despite the intuitive appeal of the argument for grade retention as an intervention for poor achievement, the weight of available empirical evidence of varying methodological quality collected over 50 years suggests that grade retention either bestows no benefits on the retained student or has a negative impact on achievement and on social and emotional adjustment, self-confidence, and attachment to school (Dennebaum & Kulberg, 1994; Hong & Raudenbush, 2005; McCoy & Reynolds, 1999; Miesels & Liaw, 1993; Pagani, Tremblay, Vitaro, Boulerice, & McDuff, 2001; Reynolds & Bezruczko, 1993). Meta-analytic investigations of the published literature report overall negative effects of grade retention (Holmes, 1989; Holmes & Matthews, 1984; Jimerson, 2001). Grade retention has also been associated with a substantial increase in school withdrawal before high school completion (Jimerson, 1999; Roderick, 1994), even when retained students’ academic performance is similar to that of comparably low-achieving promoted peers (Alexander, Entwisle, & Dauber, 2003).
Because children are not randomly assigned to the retention intervention, some critics (e.g., Hong & Raudenbush, 2005; Reynolds, 1992) have argued that many of the available studies that compare the postretention performance of retained children with that of nonselected promoted children tell us little about the impact of grade retention. Since the 1980s, the majority of studies on the effect of grade retention have compared the performance of retained students with that of low-achieving promoted peers. These studies have used two types of comparisons: (a) same-grade comparisons and (b) same-age comparisons. Same-grade comparisons evaluate retained and promoted students when they are in the same school grade. Thus, the performance of retained children is compared with promoted students who are, on average, a year younger. Alternatively, a proxy for this direct same-grade comparison can be used in which retained and promoted students are compared with extensive norms based on children in the same school grade. In contrast, same-age comparisons compare retained and nonretained children directly on measures of performance. Thus, the performance of retained children is compared with that of promoted students who are the same age but who will be one grade ahead of the target children. Both types of comparisons are informative, but they clearly answer different questions.
Results of these studies have been mixed, with some studies finding positive effects for achievement (Alexander, Entwisle, & Dauber, 1994; Mantzicopoulos & Morrison, 1992) and others reporting no effects or negative effects (Miesels & Liaw, 1993; Pianta, Tietbohl, & Bennett, 1997; Reynolds, 1992). When positive effects are reported, they are typically short-term effects that diminish within 2 or more years after the repeat year (Pierson & Connell, 1992). Studies using same-age comparisons compare the outcomes of retained children with those of children deemed at risk for promotion who were, nevertheless, promoted to the next grade. Results of these studies are more consistent in documenting negative effects of grade retention (Dennebaum & Kulberg, 1994; Hong & Raudenbush, 2005; Jimerson, 1999).
Despite the large number of published studies investigating the effects of grade retention, methodological limitations of these studies provide a weak basis for reaching conclusions about the impact of grade retention. The basic problem is the challenge of making causal inferences in the absence of a randomized experimental design (West & Thoemmes, 2008). It is neither feasible nor ethically appropriate to randomly assign students to the “treatments” of retention and promotion. A large number of variables at the child, family, school, and district level are associated with the treatment selection (i.e., retention versus promotion) and with the measured outcomes (Reynolds, 1992; Willson & Hughes, 2006). Because of this potential selection bias, a finding that retained children experience more negative outcomes at some future point in their academic careers, compared with all promoted children, may often tell us little about the effect of retention on these outcomes. Whereas some researchers have made no attempt to control for preretention differences, in recent years researchers have attempted to deal with this confounder in one or both of two ways.
In the first approach, researchers compare the performance of retained students with that of a comparison group of students who were deemed as being at risk for being retained but who were promoted. The typical approach is to select students in the same grade as the retained students who scored below a specific score (e.g., below the 25th or 50th percentile) on a measure of achievement or cognitive ability during that year, but who were promoted to the next grade the subsequent year. Some studies using this approach document equivalent performance for retained and promoted students on preretention measures. Unfortunately, there is no guarantee with this approach that the promoted and retained groups are fully equivalent on the measured variable. In addition, potential differences between promoted and retained children on other important variables known to be related to school performance (e.g., child hyperactivity, parental education level, and peer acceptance) may exist. These sources of nonequivalence from selection bias confound the interpretation of the effects of retention on outcomes (Reichardt, 2006).
In the second approach, statistical adjustments are made for a limited number of preretention variables, using analysis of covariance or, equivalently, multiple regression (Cohen, Cohen, West, & Aiken, 2003; Huitema, 1980). These statistical adjustment procedures make three key assumptions. First, the limited number of covariates that can be included in the model adequately capture the important preexisting differences between the retained and promoted groups. Second, the relationship (typically linear) between each covariate and the outcome is correctly specified. Third, the regression lines for the retained and nonretained groups are parallel. Researchers have rarely reported checking these critical assumptions, nor have they used alternative procedures that relax one or more of them (see, e.g., Little, Hyonggin, Johanns, & Giordani, 2000). In addition, when groups are disparate at pretest, the application of statistical adjustment procedures often assumes that the effect of the treatment (retention) can be extrapolated beyond the region in which the baseline data for the two groups actually overlap, often a very risky procedure (Shadish, Cook, & Campbell, 2002; Shadish, Luellen, & Clark, 2006).
During the past 2 decades, a new method of equating groups, propensity score analysis (McCaffrey, Ridgeway, & Morral, 2004; Rosenbaum, 2002; Rosenbaum & Rubin, 1983; Shadish et al., 2006; West & Thoemmes, 2008), has been extensively developed in statistics. Propensity score analysis offers important benefits over previous equating approaches, and it has begun to be used in applied research on important social issues in which randomization is not possible. In this approach, participants are measured on a wide variety of baseline measures believed on the basis of prior substantive theory and research to be related to treatment selection, the outcome variable, or ideally both. To the extent that researchers have identified the important variables related to both treatment selection and outcome, it is possible to remove baseline differences between treatment groups and achieve unbiased estimates of treatment effects. A statistical model is used to estimate a single propensity score for each participant, the predicted probability that the participant will be in the treatment (retention) condition. Typically, logistic regression using all measured baseline variables as predictors is used for this step, although other, more complicated statistical models are occasionally needed.1 The propensity score is then used to equate the treatment and control groups using matching, blocking (creating strata), or analysis of covariance. Both statistical theory (Rosenbaum, 2002; Rosenbaum & Rubin, 1983) and empirical research (Shadish & Clark, 2006) have shown that the use of propensity scores substantially reduces or eliminates selection bias when properly used. Careful use of propensity scores achieves approximate balance on the baseline levels of each of a comprehensive set of measured variables. Hong and Raudenbush (2005) recently introduced propensity score methods as a device to equate retained and promoted children in studies of grade retention.
Study Purpose
The purpose of the current study was to combine three methods that help maximize the internal validity of nonrandomized studies to examine the effect of retention in first grade on children’s growth in reading and math over a 4-year period, beginning with the child’s 1st year in first grade. First, before any of the children were retained, we selected and comprehensively assessed a sample of children at risk for retention on the basis of their scores below the 50th percentile on school district tests of reading. Second, we used propensity score matching, which corrects for selection bias, using an extensive, carefully chosen set of variables measured at baseline. Third, we used growth curve modeling that permits estimation of each child’s trajectory of growth in mathematics and reading achievement. With four waves of data, we can examine the effects of retention on both short-term and longer term growth in math and reading achievement. Specifically, we used piecewise linear trajectory models (Singer & Willett, 2003) to investigate both immediate and longer term effects. We expected the slope for retention effects in the interval from Year 1 through Year 2 would differ from that in the interval from Year 2 though Year 4 for the retained children. Otherwise stated, we could compare the differences in the growth of the retained and promoted children in the short term, when retained children are repeating the first-grade curriculum, and in subsequent years, when retained and promoted children are exposed to novel curriculum at new grade levels.
We analyzed achievement results using both grade-level standard scores and W scores (a Rasch-type measure of ability) from the Woodcock-Johnson III (WJ-III), a well-researched, nationally standardized measure of reading and math achievement. Gradelevel standard scores compare students with grade-level norms based on the student’s current grade. W scores are a measure of actual growth in math and reading ability; comparisons between retained and promoted children using W scores are comparable to age norms, in that retained children’s rate of growth in the underlying, latent construct of math or reading is directly compared with that of promoted children for the same time interval. We expected that results would differ on the basis of whether grade standard scores or W scores were analyzed. Specifically, using grade standard scores, we expected retention would favor retained children during the short term but that the benefit would begin to dissipate when retained students were promoted to the second grade. Using W scores, we expected retention to favor promoted children in the short term, when promoted students are exposed to a new curriculum. We also hypothesized that the slopes representing the longer term growth for retained and promoted students would either be comparable (parallel) after the repeat year or, if the promise of retention were fulfilled, higher for retained students because of their stronger foundation in the content covered in the repeat grade.
Finally, we investigated whether several factors at various levels of analysis (i.e., child, family, and classroom) moderate the effects of grade retention. Consistent with developmental systems theory (Lerner, 1989), we expected that the impact of retention on a child’s achievement trajectory would differ on the basis of the interplay of the retention “treatment” and factors at multiple levels of analysis, including factors within and outside the child (Cicchetti & Posner, 2005; Sameroff, 1975, 1989). Previous investigations of moderator variables have been restricted to distal demographic variables such as gender, race, or family socioeconomic status, with inconsistent findings (Pagani et al., 2001; Reynolds, 1992). We investigated more proximal child and classroom variables that were expected to moderate the effects of retention. Specifically, we examined children’s behavioral regulation, as indexed by teacher, peer, and parent ratings of externalizing behaviors, child personality resilience, and teacher-student and home-school relationship quality. We expected that the relative benefit of promotion versus retention on children’s achievement trajectories would be stronger for children with better behavioral regulation, greater personality resilience (agreeable, conscientious, and persistent), and more supportive teacher-student and home-school relationships. We reasoned that such child assets would enable children who are promoted, relative to their propensity-matched retained children, to successfully meet the greater maturity and academic demands of higher grades. We also tested age as a moderator because parents and educators are more likely to retain younger children for age, relative to similar low-achieving students (Mantzicopoulos, 2003; Reynolds, 1992; Willson & Hughes, 2006). Thus, it is important to evaluate the wisdom of using age as a selection factor for the retention treatment.
This study extends a previous study (Wu, West, & Hughes, 2008) with this sample. Because only three waves, or years, of data were available in the Wu et al. (2008) study, short-term and longer term change could not be investigated. That study found negative effects for retention on math W scores but no effects for reading W scores. Finally, the short-term beneficial effects of promotion were stronger for children with good behavioral regulation and for children who were not classified as Limited English Proficient.
The current study analyzes both grade standard scores and W scores, whereas the previous study analyzed only W scores. The analysis of both W scores and grade standard scores permits us to answer two different questions. Specifically, because W scores are an interval-level measure of reading and math skills, their use permits a determination of the effect of grade retention on children’s growth in achievement. Because grade standard scores compare a student’s performance to grade-level norms for the same grade as that in which the student is enrolled, it permits a determination of the effect of grade retention on children’s performance relative to the student’s current grade placement. Both comparisons have merit (Alexander et al., 2003). By modeling both short-term and longer term effects and by analyzing both children’s performance relative to grademates and children’s actual growth in reading and math, we are able to render a more comprehensive picture of the impact of grade retention than has been possible in previous studies. Research by Miles and Stipek (2006) and Skinner, Zimmer-Gemback, and Connell (1998) has suggested that children’s relative (rank order) level of achievement becomes relatively stable after Grade 3. Although their research did not investigate children’s achievement trajectories, which is the focus of the present study, it does suggest that understanding the impact of early grade retention may potentially be important in the understanding of children’s long-term achievement outcomes.
Method
Participants
Participants were drawn from a larger sample of children participating in a longitudinal study examining the impact of grade retention on academic achievement. Participants were recruited from three school districts in Texas (one urban and two small cities) across two sequential cohorts in first grade during the fall of 2001 and 2002. Children were eligible to participate in the longitudinal study if they scored below the median score on a state-approved district-administered measure of literacy, spoke either English or Spanish, were not receiving special education services, and had not previously been retained in first grade. School records identified 1,374 children as eligible to participate. Because teachers distributed consent forms to parents via children’s weekly folders, the exact number of parents who received the consent forms cannot be determined. Incentives in the form of small gifts to children and the opportunity to win a larger prize in a random drawing were instrumental in obtaining 1,200 returned consent forms, of which 784 parents (65%) provided consent and 416 declined.
Analyses of a broad array of archival variables including performance on the district-administered test of literacy (standardized within district because of differences in the test used), age, gender, ethnicity, eligibility for free or reduced-price lunch, bilingual class placement, cohort, and school context variables (i.e., percentage ethnic or racial minority and percentage economically disadvantaged) did not indicate any differences between children with and without consent. The resulting sample of 784 participants (52.6% male) closely resembles the population from which they were drawn on demographic and literacy variables relevant to students’ educational performance. The ethnic composition of the achieved sample (N = 784) was 37% Hispanic (39% of whom were Spanish language dominant), 34% White Caucasian, 23% African American, and 6% other; 62% of the children qualified for free or reduced-price lunch. The mean full scale IQ based on the Universal Nonverbal Intelligence Test (Bracken & McCallum, 1998) for the sample was 92.91 (SD = 18.01), and the mean reading achievement score was 96.40 (SD = 14.28).
Participants for the growth curve analyses were those 196 children (58% male) who were successfully matched with respect to their propensity to be retained in first grade (see description of propensity-matching procedures below) and who had achievement test scores for at least one of the four assessment periods. The racial and ethnic composition of the sample was 33% Caucasian, 33% Hispanic, 31% African American, and 3% other. At entrance to first grade, children’s mean age was 6.46 (SD = 0.33) years. Of the 196 matched cases (98 pairs), the proportions of children who completed the WJ-III were 96%, 85%, 86%, and 85%, respectively, at each of the four measurement waves.
Design Overview
Demographic information including child age, gender, race or ethnicity, eligibility for free or reduced-price lunch, and status as Limited English Proficient were obtained from school district records. Teacher, parent, and peer data were collected in the spring of Year 1, when all participants were in first grade. Teachers and parents received $25.00 for completing and returning the questionnaires. Peers’ perceptions of the level of externalizing behaviors were obtained via individual interviews conducted between February and May of Year 1. Beginning in Year 1, annual measures of math and reading achievement were individually administered at school for 4 years, with the constraint that at least 8 months separated each annual assessment.
Measures
A complete list of the 72 baseline variables collected at measurement Wave 1 used in calculation of propensity scores is available from Jan N. Hughes. The baseline variables included demographic measures, cognitive and behavioral performance, social and emotional functioning, and classroom and school variables. The 72 variables were intended to be as comprehensive as possible, including variables that have been shown in prior research to be related to early retention versus promotion, early academic achievement, or ideally both. The measures of academic achievement served as the primary outcome measures for this study. Selected baseline measures were used to explore potential moderator variables that might affect the rate of growth of children in response to retention versus promotion. These measures and the achievement measures are described below.
Academic achievement
The WJ-III Tests of Achievement (Woodcock, McGrew, & Mather, 2001) are individually administered measures of academic achievement for individuals ages 2 to adulthood. We used the WJ-III Broad Reading (Letter-Word Identification, Reading Fluency, and Passage Comprehension subtests) and Broad Math (Calculations, Math Fluency, and Math Calculation Skills subtests) W scores and grade standard scores. The Reading and Math W scores are based on the Rasch measurement model, which ensures interval-level measurement of change on a single dimension.2 Grade standard scores compare children’s performance to grade-level national norms and only approximate an equal-interval measurement scale. Extensive research has documented the reliability and construct validity of the WJ-III and its predecessors (Woodcock & Johnson, 1989; Woodcock et al., 2001).
The Batería Woodcock-Muñoz: Pruebas de Aprovechamiento—Revisada (Batería-R; Woodcock & Muñoz-Sandoval, 1996) is the comparable Spanish version of the Woodcock-Johnson Tests of Achievement—Revised (WJ-R; Woodcock & Johnson, 1989), the precursor to the WJ-III. If children or their parents spoke any Spanish, children were administered the Woodcock-Muñoz Language Test (Woodcock & Muñoz-Sandoval, 1993) to determine the child’s language proficiency in English and Spanish. The test of achievement (WJ-III or the Batería-R) was chosen to match the language in which the child had greater proficiency. The Woodcock Compuscore (Woodcock & Muñoz-Sandoval, 2001) program yields W scores for the Batería-R that are comparable to W scores on the WJ-R. In the following, scores are referred to as WJ scores (W or grade standard scores), irrespective of which test the child took.
Teacher and parent report of conduct problems and hyperactivity
Teachers and parents completed the Strengths and Difficulties Questionnaire (Goodman, 1997), a brief (25-item) screening measure for psychopathology. Each item is rated on a scale ranging from 0 to 2 (i.e., not true, somewhat true, and certainly true). The Strengths and Difficulties Questionnaire yields five scales consisting of 5 items each. The Conduct Problems and the Hyperactivity scales assess externalizing behaviors. For our sample, coefficient alpha for Conduct Problems was .84 for teachers and .71 for parents. For Hyperactivity, coefficient alpha was .89 for teachers and .81 for parents. In a sample of children participating in this longitudinal study, teacher reports of Conduct Problems and of Hyperactivity were moderately to strongly correlated with both parent report (.47 and .30, for conduct problems and hyperactivity, respectively) and peer reports (.50 and .46, for conduct problems and hyperactivity, respectively; Hill & Hughes, 2007). Exploratory and confirmatory factor analyses support the construct validity of the teacher and parent versions of the Strengths and Difficulties Questionnaire (Dickey & Blumberg, 2004; Goodman, 2001; Hill & Hughes, 2007).
Peer nomination of externalizing problems
Peers’ perceptions of classmates’ hyperactivity and aggression were obtained following procedures widely recommended in the peer assessment literature (Cillessen & Bukowski, 2000). Scores of similar constructs obtained from similar peer nomination procedures have demonstrated good reliability and validity (Realmuto, August, Sieler, & Pessoa-Brandao, 1997). In individual interviews, children were presented a roster with the names of all classmates. The interviewer read each of the classmates’ names and asked the child whether he or she knew each child. Then the interviewer asked the child to nominate as few or as many classmates as he or she wished who fit each descriptor. Of interest to this study are the aggression item (“Some kids start fights, say mean things, or hit others”) and the hyperactivity item (“Some kids do strange things and make a lot of noise. They bother people who are trying to work”). Each class member received an aggression and hyperactivity score based on the number of nominations that child received. Sociometric scores were standardized within classrooms. Because the two scores were highly correlated (r = .74), we computed a composite peer-rated externalizing score as the mean standardized score on the aggression and hyperactivity items. Written parent consent was obtained for each child who participated in the sociometric interview. However, all children in a classroom were eligible to be rated or nominated. Terry (1999) reported that reliable and valid sociometric data can be collected using the unlimited nomination approach when as few as 40% of children in a classroom participate. We followed Terry’s guideline, computing sociometric scores only for those 602 (77%) children located in classrooms in which more than 40% of classmates participated in the sociometric assessment. The mean rate of classmate participation in the sociometric administrations was .65 (range = .40 to .95). Elementary school children’s peer nomination scores derived from procedures similar to those used in this study have been found to be stable over periods from 6 weeks to 4 years and to be associated with concurrent and future behavior and adjustment (for review, see Hughes, 1990).
Resilient personality
A confirmatory factor analysis (Kwok, Hughes, & Luo, 2007) on a sample of 445 first-grade children participating in the current longitudinal study supported a second-order measurement model of resilient personality defined by three first-order factors: Agreeableness (nine items), Conscientiousness (eight items), and Ego Resiliency (seven items). Agreeableness and Conscientiousness items were taken from the scales of the same name of the Big Five Inventory (John & Srivastava, 1999). Sample Agreeableness items include “is helpful and unselfish with others,” “likes to cooperate with others,” and “is sometimes rude to others” (reverse scored). Sample Conscientiousness items include “does a thorough job,” “is a reliable worker,” and “tends to be disorganized” (reverse scored). Coefficient alpha for each scale was .94. Ego Resiliency items were derived from items on the California Child Q-Sort (Caspi, Block, Block, & Klopp, 1992). Sample items include “resourceful in initiating necessary activities” and “falls to pieces under stress” (reverse scored). Teachers responded to each of the items using a 5-point scale. Coefficient alpha for our sample was .85. We computed a score for resilient personality as the mean of the standardized score for each scale.
Teacher-student relationship quality
The 22-item Teacher Student Relationship Inventory (Hughes, Cavell, & Willson, 2001) is based on the Network of Relationships Inventory (Buhrmester & Furman, 1987). Teachers indicated on a 5-point Likert-type scale their level of support (16 items, coefficient α = .94) or conflict (6 items, coefficient α = .92) in their relationships with individual students. Because the Support and Conflict scales were negatively correlated (-.57), we recoded the Conflict items in the opposite direction. The coefficient alpha of the 22 items after recoding the Conflict items was .95. A total relationship quality score was computed as the mean of the 22 item scores. In a longitudinal study of behaviorally at-risk elementary school students, the Teacher Student Relationship Inventory Support score predicted changes in behavioral adjustment and peer relationships (Meehan, Hughes, & Cavell, 2003). In the larger sample, the Teacher Student Relationship Inventory predicted cross-year changes in children’s achievement (Hughes & Kwok, 2006).
Home-school relationship
The Teacher Report of Parent Involvement Scale (Wong & Hughes, 2006) consists of 20 items assessing teachers’ perceptions of the parent-teacher alliance (e.g., “I respect this parent” and “Communication between us is difficult”; reverse scored) and of the frequency of parents’ engagement of various involvement activities (e.g., volunteering at school and calling the teacher). Coefficient alpha for the current sample was .87.
Propensity Score Estimation
Propensity scores, the predicted probability of being retained in first grade, were estimated for the 768 children for whom retention information was available, using 72 background variables collected at the initial testing, including child demographic variables and child, peer, teacher, and parent data covering the areas of academic aptitude (e.g., the Universal Nonverbal Intelligence Test), academic achievement (WJ-III or the Spanish-language Batería-R broad math and reading), personality (e.g., agreeableness and effortful control), behavioral and social adjustment, peer relations, and family adversity. Methods based on logistic regression (Rosenbaum, 2002; Rosenbaum & Rubin, 1983) were used to estimate propensity scores. The larger the propensity score, the larger the predicted probability that the child would be retained in the first grade. For the 768 cases, the propensity score ranged from .0003 to .989 with a mean of .215 (SD = .215). The children who were subsequently promoted had substantially lower propensity scores (n = 603, M = .114, SD = .166) than those who were subsequently retained (n = 165, M = .583, SD = .309), t(190.6) = -18.769, Cohen’s d = -1.890. Although not the primary criterion in evaluating the success of the propensity model (see Rosenbaum 2002; Shadish et al., 2006), the logistic regression equation led to relatively good prediction of the decision to retain or promote each child with a Nagelkerke pseudo-R2 index of .552 (see Cohen et al., 2003, p. 503).
Despite identifying an at-risk sample of children who were below the median on literacy at entrance to first grade, substantial differences existed between the retained and the promoted groups. These results indicated that an adjustment procedure would be needed to equate the retained and the promoted groups. Following the recommendations of West and Thoemmes (2008; see also Rosenbaum, 2002), we chose a procedure that produces optimal matches on propensity scores.
Matching Procedure
We matched 1 retained child with 1 promoted child on the basis of their propensity scores using SAS 8.0 PROC ASSIGN (Ming & Rosenbaum, 2001). PROC ASSIGN matches retained children with promoted children so that the sum of distance between the propensity scores within each of the matched pairs was minimized for the whole sample. To avoid matching two children with propensity scores far away from each other, we imposed a caliper distance of .025, the maximum distance in propensity scores allowed for a match to take place. That is, any pair of retained and promoted children who differed in their propensity scores by more than .025 could not be matched with each other. We chose a very small caliper distance to obtain high-quality matching. Using this method, a total of 98 pairs (196 children) were successfully matched. For the 98 matched pairs, the propensity score ranged from .003 to .918 (M = .367, SD = .225). The mean within-pair distance in propensity score was .007 (SD = .008). Following the optimal matching process, the two groups were closely equated on their propensity scores: For the promoted group, N = 98 (M = .366, SD = .225), and for the retained group, N = 98 (M = .367, SD = .226), t(194) = -0.044, ns, Cohen’s d = -0.006. This outcome contrasts sharply with the substantial mean differences in the propensity scores between the promoted and retained groups in the full sample (Npromoted = 603; Nretained = 165). Table 1 reports descriptive information for the 98 pairs.
Table 1. Descriptive Statistics of Selected Time 1 Measures.
| Retained (n = 98) |
Promoted (n = 98) |
Effect size |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time 1 measure | M | SD | n | % | M | SD | n | % | d | h |
| WJ-III math W score | 461.85 | 12.54 | 460.85 | 15.77 | 0.07 | |||||
| WJ-II reading W score | 423.13 | 26.19 | 423.52 | 21.79 | -0.02 | |||||
| WJ-III math grade score | 98.92 | 13.76 | 100.27 | 15.36 | -0.09 | |||||
| WJ-III reading grade score | 89.43 | 17.32 | 92.95 | 12.83 | -0.23 | |||||
| Age at eligibility determination | 6.45 | 0.29 | 6.46 | 0.36 | -0.03 | |||||
| Parent-rated conduct problems | 0.54 | 0.50 | 0.48 | 0.44 | 0.13 | |||||
| Parent-rated hyperactivity | 1.25 | 0.57 | 1.09 | 0.48 | 0.30 | |||||
| Teacher-rated conduct problems | 0.40 | 0.50 | 0.52 | 0.57 | -0.22 | |||||
| Teacher-rated hyperactivity | 0.95 | 0.63 | 1.06 | 0.61 | -0.18 | |||||
| Peer-rated externalizing problems | 0.30 | 0.99 | 0.25 | 0.97 | 0.05 | |||||
| Teacher-student relationship quality | 3.99 | 0.75 | 3.92 | 0.83 | 0.09 | |||||
| Home-school relationship | 3.45 | 0.53 | 3.28 | 0.46 | 0.34 | |||||
| Resilient personality | -0.12 | 0.84 | -0.29 | 0.87 | 0.20 | |||||
| Economically disadvantaged | 65 | 66 | 63 | 66 | .00 | |||||
| Ethnicity | ||||||||||
| African American | 33 | 34 | 27 | 28 | .06 | |||||
| Hispanic | 30 | 31 | 34 | 35 | .04 | |||||
| Caucasian | 32 | 33 | 35 | 36 | .03 | |||||
| Others | 1 | 1 | 2 | 2 | .10 | |||||
note. d is reported as a measure of the standardized effect size for the difference between two means and h is reported as the standardized effect size for the difference between two proportions (Cohen, 1977). For both measures, Cohen suggested 0.2, 0.5, and 0.8 represented small, medium, and large effects, respectively. WJ-III = Woodcock-Johnson III.
Data Analysis
To investigate the relatively short-term and longer term effects of retention on the growth rate of WJ scores, we split the time span into two pieces at the point at which the measurement wave was 2 (the 2nd year of the study). The first piece included the measurements on Waves 1 and 2, which covers the change in WJ scores from roughly 0.5 year before retention to 0.5 year after retention. The second piece included the measurements on Waves 2, 3 and 4, which covers the change in WJ scores from roughly 0.5 year after retention to 2.5 years after retention. Then we fit a linear growth curve on each piece for the four WJ scores separately using SAS 8.0 PROC Mixed. Such growth curve models are called two-piece linear growth curve models (Singer & Willett, 2003). Given the existence of missing data, we used full information maximum likelihood estimation to estimate the growth curve models. Full information maximum likelihood estimation uses all of the observations available for each case to compute the likelihood function (Enders & Bandalos, 2001). It provides unbiased estimates with minimal standard errors when data are missing at random (Schafer & Graham, 2002). Otherwise stated, full information maximum likelihood estimation provides estimates that are appropriately corrected for all measured variables included in the analysis.
The specification of the two-piece linear growth curve model for any one of the WJ scores is shown in Equations 1 to 3, which includes three levels. Level 1 (within individual, Equation 1) captures the two-piece linear growth trajectory for each individual over the 4 years of the study. At Level 1, two time variables (T1tip and T2tip), corresponding to the two pieces, were created to predict the WJ scores. To simplify the presentation, two coding schemes were adopted to create T1tip and T2tip as follows.
Coding Scheme 1.
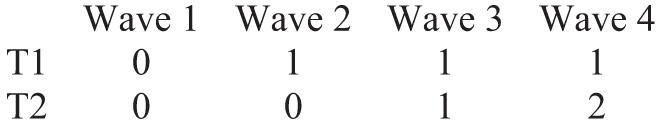
Coding Scheme 2.
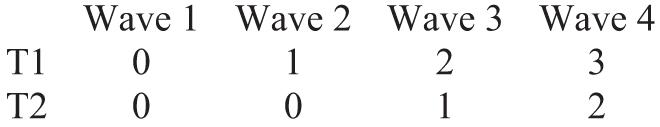
Following guidelines in Cohen et al. (2003, chap. 8), we used two coding schemes in the study even though their results are algebraically related and produce identical results for overall model fit and predicted values at each measurement wave. The use of the two schemes permitted us to conduct a significance test of each of the parameters of interest and to present the simplest possible interpretation of the results. Coding Scheme 1 allowed us to test the slope separately for each piece and furthermore to test whether the slopes in each piece differ between retained and promoted groups. However, Coding Scheme 1 does not permit us to test the significance of the difference in the change in slope between the short and longer term. That is one reason why we used Coding Scheme 2, which provides both this significance test and a test of whether the pattern of change in slope differs between the retained and the promoted groups. We centered time at Wave 1 (the point at which both T1tip and T2tip were coded 0); thus, the intercept represents the student’s predicted level of WJ scores on the first wave of measurement (initial status in first grade before retention or promotion).
Level 2 (between individual, Equation 2) captures the variation in individual intercepts and slopes across individuals. At Level 2, we used grade retention status after first grade (coded 1 = retained, 0 = promoted) to predict the individual intercepts, individual slopes for the short term (Slope 1), and individual slopes for the longer term (Slope 2). Because matching produces dependency in the data, Level 3 (between pairs, Equation 3) was added to take into account the within-pair correlation for individual intercepts (clustering). This procedure adjusts for biased estimates of the standard errors caused by the dependency, thus leading to more accurate significance tests for the parameter estimates. The effects of retention on Slope 1 (short-term effect, λ110) and Slope 2 (longer term effect, λ210) are our primary interest. The equations for the three-level model are presented below.
| (1) |
| (2) |
| (3) |
Here the subscript t indicates time point (Wave 1, 2, 3, or 4), i indicates individual, and p indicates pair. γ000 and γ100 represent, respectively, the grand mean of the intercept and Slope 1 for the promoted group. Under Coding Scheme 1, γ200 represents the grand mean of Slope 2 for the promoted group. Under Coding Scheme 2, γ200 represents the average slope difference between the two pieces (Slope 2 - Slope 1) for the promoted group. γ010 and γ110 represent the estimated effects of grade retention in first grade on the intercept and Slope 1, respectively. Under Coding Scheme 1, γ210 represents the effect of grade retention on Slope 2, whereas under Coding Scheme 2, γ210 represents the effect of retention on the slope difference between the two pieces. etip represents the Level 1 residual for the ith individual within the pth pair at Wave t, which was assumed to follow a normal distribution with mean (μ) = 0 and homogeneous variance (σ2) across 4 years. σ2 is the within-individual variance in WJ scores that cannot be accounted for by time. r0ip represents Level 2 residual in intercept for the ith individual within the pth pair, which was assumed to follow a normal distribution with μ= 0 and variance =τπ00. τπ00 is the between-individual variance in intercept that cannot be accounted for by grade retention. u00p represents the deviation of the mean intercept of the pth pair from the grand meanintercept for promoted children, which was also assumed to follow a normal distribution with μ= 0 and variance =τβ00. τβ00 is the between-pair variance in intercepts. Given that only four measurement waves were available to estimate a complex model, we assumed that there is neither between-individual residual variance nor between-pair variance in Slope 1 and Slope 2.
Next, the potential moderator variables were added into Level 2 of the growth model one at a time as shown in Equation 4. The moderating effects of these variables were captured by the coefficients associated with their interaction with grade retention (γ130 for Slope 1 and γ230 for Slope 2 with Coding Scheme 1). The moderating effects are assumed to be constant across matched groups (see Equation 5). We only used Coding Scheme 1 in the moderator analyses for ease of presentation because we could interpret the moderating effects on Slope 1 and Slope 2 separately.
| (4) |
| (5) |
Here γ000, γ100, and γ200 represent the estimated mean intercept, Slope 1, and Slope 2 for the promoted group with 0 value on moderator, respectively; γ010, γ110, and γ210 represent the main effects of grade retention on the intercept and slope, respectively; γ020, γ120, and γ220 represent the main effects of moderator on the intercept, Slope 1, and Slope 2, respectively; and γ030, γ130, and γ230 represent the interaction effects of moderator and retention on the intercept, Slope 1, and Slope 2, respectively. The interpretations of Level 1 and Level 2 residuals are similar with the model without moderator included. u00p represents Level 3 deviations of pair mean intercepts from the grand mean intercept for promoted children with a value of 0 on the moderator.
Results
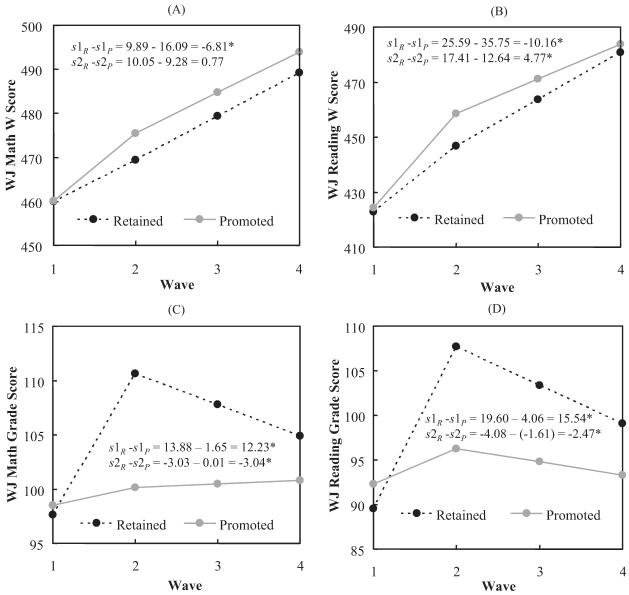
Table 2 presents the estimates for parameters of theoretical interest obtained from the two-piece linear growth models (see Equations 1 to 3). The first two sets of results examine the effects of retention using WJ W scores for math and reading, which implicitly compare the children’s performance to that of agemates. The second two sets of results examine the WJ grade standard scores for math and reading, which compare the children’s performance to that of grademates. For ease of presentation, in the following we use s1P and s2P to represent Slope 1 (short term) and Slope 2 (longer term) for promoted children and s1R and s2R to represent Slope 1 and Slope 2 for retained children.
Table 2. Selected Parameter Estimates for the Two-Piece Linear Growth Curve Model Without Moderators.
| Parameter | WJ-III math W score | WJ-III reading W score | WJ-III math grade score | WJ-III reading grade score |
|---|---|---|---|---|
| Intercept for promoted | 459.37* (1.24) | 424.70* (2.17) | 98.53* (1.40) | 92.33* (1.56) |
| Slope 1 for promoted | 16.09* (0.97) | 35.75* (1.66) | 1.65 (1.12) | 4.06* (1.21) |
| Slope 2 for promoted | 9.28* (0.51) | 12.64* (0.87) | 0.01 (0.59) | -1.61* (0.64) |
| (Slope 2 - Slope 1) for promoted | -6.81* (1.31) | -23.11* (2.25) | -1.64 (1.52) | -5.67* (1.64) |
| Effect of retention on intercept | 0.31 (1.73) | -1.18 (2.94) | -1.68 (1.97) | -4.01 (2.13) |
| Effect of retention on Slope 1 | -6.20* (1.41) | -10.16* (2.40) | 12.23* (1.63) | 15.54* (1.75) |
| Effect of retention on Slope 2 | 0.77 (0.74) | 4.77* (1.26) | -3.04* (0.86) | -2.47* (0.93) |
| Effect of retention on (Slope 2 - Slope 1) | 6.97* (1.90) | 14.93* (3.25) | -15.27* (2.20) | -18.02* (2.37) |
Note. Standard errors are in parentheses. WJ-III = Woodcock-Johnson III.
p < .05.
WJ W Scores
WJ math W score
As shown in Table 2, both Slope 1 and Slope 2 were positive for promoted children (s1P = 16.09, Wald z = 16.67, p < .001; s2P = 9.28, Wald z = 18.20, p < .001), indicating that there was an increase on WJ math W score in both pieces for promoted children, but that the increase for promoted children in the longer term was slower than the increase in the short term. Subsequent grade retention was not associated with the initial status in first grade (Wald z = 0.18, ns), indicating that matching on propensity scores achieved initial equivalence of the promoted and retained groups on WJ math W score. Grade retention had a negative effect on Slope 1 (s1R - s1P = -6.20, Wald z = -4.83, p < .001), indicating that in the short term, the retained children had a lower annual rate of gain of 6.20 points on the WJ math W score than did the promoted children. To put this gain in context, the normative annual gain on the WJ math W score is 9.17 for children ages 8-9. In contrast, grade retention had no significant effect on Slope 2 (Wald z = 1.04, ns), indicating that the annual rate of gain on the WJ math W score in the longer term did not differ significantly between the retained and promoted groups.
Coding Scheme 2 focuses on slope differences between the two pieces. Grade retention had a positive effect on the slope difference between the two pieces ([s2R - s1R] - [s2P - s1P] = 6.97, Wald z = 3.67, p < .001). Slope 1 and Slope 2 differed by -6.81 for promoted children (s2P - s1P = -6.81, Wald z = -5.20, p < .001), whereas the rate of growth did not change across the short and longer term for retained children (s2R - s1R = 0.16, ns). These results are illustrated in Figure 1A, which portrays the estimated two-piece linear growth lines for the overall retained and promoted groups.
Figure 1.
Estimated two-piece linear growth curves of the four WJ scores. s1P and s2P represent the slopes in the short and longer terms for promoted children, and s1R and s2R represent the slopes in the short and longer terms for retained children. WJ = Woodcock-Johnson III. * p < .05.
WJ reading W score
Similar to the WJ math W score, there was an increase on WJ reading W score in both the short and the longer term for promoted children (s1P = 35.75, Wald z = 21.54, p < .001; s2P = 12.64, Wald z = 14.53, p < .001). Subsequent grade retention was not associated with initial status in first grade (Wald z = -0.69, ns) of the WJ reading W score. This provides further evidence of the success of the propensity score-matching procedure. Grade retention had a negative effect on Slope 1 (s1R - s1P = -10.16, Wald z = 4.23, p < .001), whereas it had a positive effect on Slope 2 (s2R - s2P = 4.77, Wald z = 3.79, p < .001), indicating that in the short term, the average annual rate gain on WJ reading W score for retained children was 10.16 points lower than that for promoted children, whereas in the longer term, retained children had an annual rate gain of 4.77 points higher on WJ reading W score than did promoted children (see Figure 1B). To put this gain in context, the normative annual gain on the WJ reading W score is 14.32 for children ages 8-9. Combining the two results using Coding Scheme 2, grade retention was found to have a positive effect on the slope difference between the two pieces ([s2R - s1R] - [s2P - s1P] = 14.93, Wald z = 4.59, p < .001). Slope 1 and Slope 2 differ by -23.11 (s2P - s1P = -23.11, Wald z = -10.27, p < .001) for promoted children, whereas they only differed by -8.18 (s2R - s1R = -8.18) for retained children. These results indicate that compared with promoted children, retained children showed a smaller reduction in slope from the short term to the longer term for WJ reading W score.
WJ Grade Standard Scores
WJ math grade score
For promoted children, neither Slope 1 nor Slope 2 was significantly different from 0 (s1P = 1.65, Wald z = 1.47, ns; s2P = 0.01, Wald z = .02, ns). Promoted children showed nearly no change in WJ math grade standard score across 4 years. Once again, subsequent grade retention was not associated with initial status of WJ math grade score (Wald z = 0.85, ns). Grade retention showed a positive effect on Slope 1 (s1R - s1P = 12.23, Wald z = 7.50, p < .001), but a negative effect on Slope 2 (s2R - s2P = -3.04, Wald z = -3.53, p < .001). This finding indicates that rather than keeping a constant rate of growth relative to grademates on WJ math, as did promoted children, retained children showed a dramatic increase in the short term (the repeat year) and decreased markedly on WJ math relative to their grademates in the longer term as they encountered new material (see Figure 1C). Combining these results using Coding Scheme 2, grade retention had a negative effect on the slope difference between two pieces ([s2R - s1R] - [s2P - s1P] = -15.27, Wald z = -6.94, p < .001). Slope 1 and Slope 2 did not differ for promoted children (s2P - s1P = -1.64, Wald z = -1.08, ns). However, Slope 2 was significantly lower than Slope 1 for retained children (s2R - s1R = -16.91).
WJ reading grade score
For promoted children, Slope 1 was positive (s1P = 4.06, Wald z = 3.36, p < .001), whereas Slope 2 was negative (s2P = -1.61, Wald z = -2.52, p = .01). This result indicates that for promoted children, there was an increase on WJ reading grade score in the short term followed by a slight yearly decrease on WJ reading grade score in the longer term. Again, subsequent grade retention was not associated with a significant effect on the initial status for WJ reading grade score in first grade (Wald z = 1.88, ns). Grade retention showed similar effects on Slope 1 and Slope 2 for WJ reading grade score as for the WJ math grade score. The effect of grade retention on Slope 1 was positive (s1R - s1P = 15.54, Wald z = 8.88, p < .001), which indicates that retained children showed an average higher annual rate gain of 15.54 points on WJ reading grade score in the short term (see Figure 1D). In contrast, the effect of grade retention on Slope 2 was negative (s2R - s2P = -2.47, Wald z = -2.66, p = .01).
Focusing now on slope differences between the two pieces using Coding Scheme 2, we found that grade retention had a negative effect on the slope difference between the two pieces ([s2R - s1R] - [s2P - s1P] = -18.02, Wald z = -7.60, p < .001). For promoted children, Slope 2 was 5.67 points smaller than Slope 1 (s2P - s1P = -5.67, Wald z = -3.46, p < .001). In contrast, for retained children Slope 2 was 23.69 points smaller than Slope 1 for retained children (s2R - s1R = -23.69). These results show that for WJ reading grade score, retained children showed more reduction in slope from the short term to the longer term than did promoted children (see Figure 1D).
In the matched sample, there were children in the promoted group (n = 19) who were subsequently retained in second or third grade; none of the children in the retained group were retained a second time. These results highlight the relatively high likelihood of subsequent retention for socially promoted children before the end of Grade 3 when state-mandated testing occurs. To minimize the possible influence of retention at a later time on the effect of retention in first grade on the growth of WJ scores, we ran the same growth curve analyses with 19 pairs deleted that included the children retained after second grade. The obtained results were very similar to those reported above, and the inferences were identical on the basis of both sets of results.
Moderating Effects
The moderating effects of the potential moderators on Slope 1 and Slope 2 for WJ W and grade scores are summarized in Table 3. For ease of presentation, we used only Coding Scheme 1. A significant moderating effect indicates that the effect of retention on Slope 1 and Slope 2 varied across different levels on a moderator. Only two of the nine moderator variables interacted with retention to affect Slope 1 for WJ reading W score and WJ math and reading grade scores. None of the moderators showed a significant moderating effect for Slope 2 for any of the WJ scores. The interaction between peer-rated externalizing problems and grade retention had a positive effect on Slope 1 for WJ reading W score (γ130 = 5.60, Wald z = 2.08, p = .02), indicating that in the short term, the benefit of promotion relative to retention on the WJ reading W score was higher for the children with lower levels of externalizing problems than for those with higher levels of externalizing problems (see Figure 2). The interaction between teacher-rated home-school relationship and grade retention had a negative effect on Slope 1 for WJ grade standard scores for math (γ130 = -8.19, Wald z = 2.05, p = .02) and for reading (γ130 = -8.37, Wald z = 2.04, p = .02), indicating that in the first piece, the relative benefit of retention versus promotion on grade scores was greater for children with less positive home-school relationships. Figure 3 displays the moderating effect of home-school relationship for WJ math grade score, which is very similar to that for WJ reading grade score.
Table 3. Moderating Effects on Slope 1 and Slope 2 for Each of the Four WJ-III Scores.
| Math W score |
Reading W score |
Math grade score |
Reading grade score |
|||||
|---|---|---|---|---|---|---|---|---|
| Moderator | Slope 1 (γ130) | Slope 2 (γ230) | Slope 1 (γ130) | Slope 2 (γ230) | Slope 1 (γ130) | Slope 2 (γ230) | Slope 1 (γ130) | Slope 2 (γ230) |
| Age at eligibility determination | -3.97 (4.46) | 2.93 (2.26) | 11.96 (7.53) | -2.94 (3.80) | -8.87 (5.18) | 3.67 (2.62) | 5.86 (5.52) | -0.32 (2.79) |
| Parent-rated conduct problems | 0.63 (3.27) | 1.89 (1.75) | 10.46 (5.60) | 5.18 (3.02) | -0.24 (3.73) | -0.42 (2.00) | 6.99 (3.91) | 1.25 (2.11) |
| Parent-rated hyperactivity | 0.22 (2.90) | 0.47 (1.52) | -2.25 (5.01) | 0.53 (2.65) | -0.78 (3.32) | -0.37 (1.74) | -3.30 (3.51) | -0.83 (1.84) |
| Teacher-rated conduct problems | 2.27 (2.79) | 1.19 (1.50) | 3.98 (4.54) | 2.54 (2.42) | 0.08 (3.40) | 1.39 (1.82) | 0.85 (3.42) | 2.19 (1.83) |
| Teacher-rated hyperactivity | 1.42 (2.47) | 0.75 (1.31) | 2.49 (4.04) | 3.05 (2.14) | 2.11 (3.00) | -0.59 (1.60) | 2.38 (3.04) | 1.17 (1.61) |
| Peer-rated externalizing problems | 2.26 (1.67) | 0.82 (.88) | 5.60* (2.69) | -0.97 (1.43) | -0.38 (1.91) | 0.90 (1.01) | 1.82 (2.00) | 0.09 (1.06) |
| Teacher-student relationship | 0.96 (1.96) | -0.90 (1.19) | -3.68 (3.28) | 0.36 (1.97) | 4.10 (2.23) | -1.72 (1.37) | 0.43 (2.46) | -.28 (1.46) |
| Home-school relationship | -3.49 (3.28) | 1.70 (1.73) | -8.35 (5.37) | 3.00 (2.81) | -8.19* (4.00) | 4.05 (2.12) | -8.37* (4.10) | 3.78 (2.15) |
| Resilient personality | -0.15 (1.75) | -1.05 (.95) | -5.17 (2.88) | -0.49 (1.55) | 1.63 (2.00) | -0.18 (1.08) | -2.48 (2.15) | 0.36 (1.16) |
Figure 2.
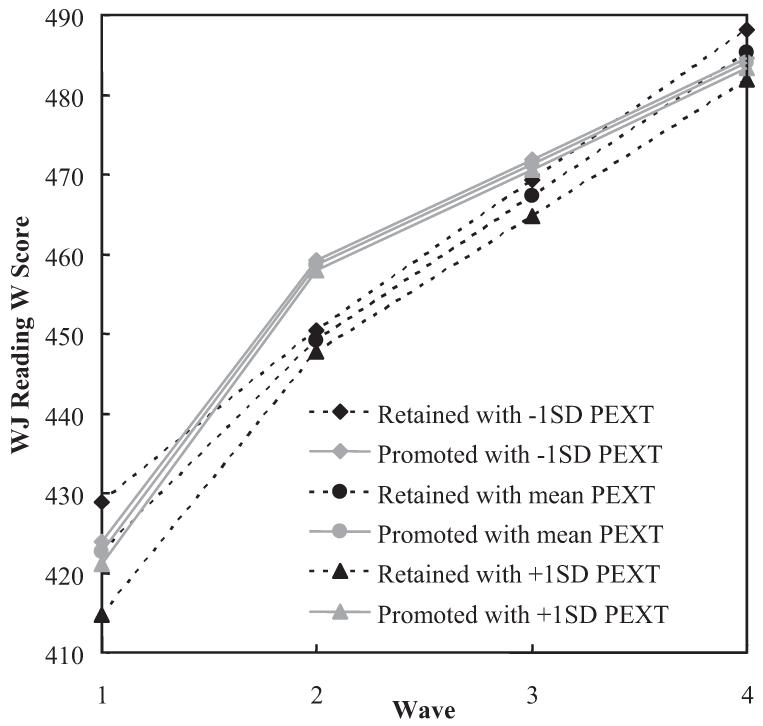
Estimated two-piece linear growth curves of WJ reading W score for retained and promoted children with different levels of peer-rated externalizing problems (PEXT). WJ = Woodcock-Johnson III.
Figure 3.
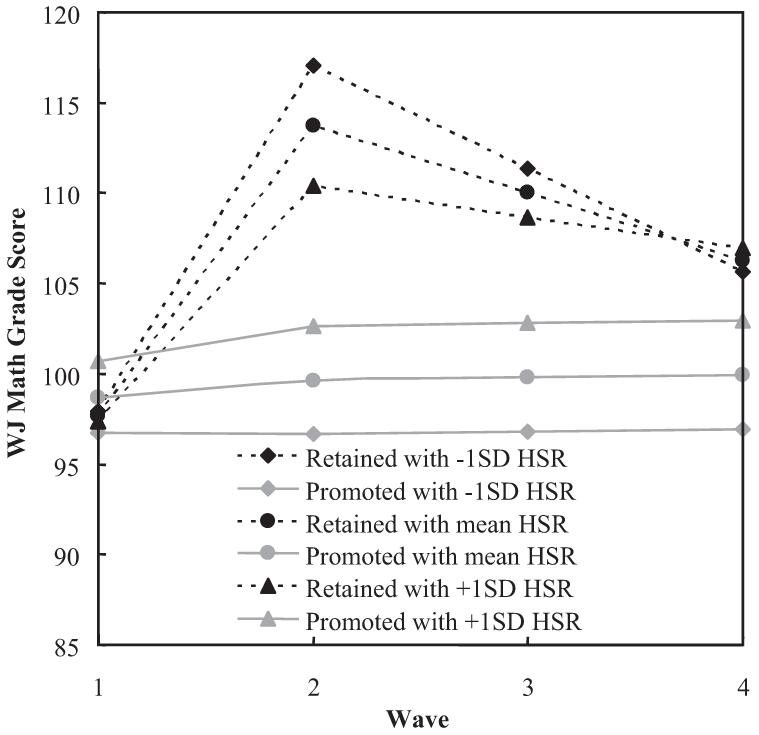
Estimated two-piece linear growth curves of WJ math grade score for retained and promoted children with different levels of home-school relationship (HSR). WJ = Woodcock-Johnson III.
Discussion
In this study, we used two-piece linear growth curve models to examine the short-term and longer term effects of grade retention on the change of WJ math and reading W and grade scores across 4 years. Analyses were conducted with retained and promoted children who were closely matched using modern propensity-matching procedures. One indicator of success of the propensity-matching procedure is the lack of initial differences in achievement between the retained and promoted children (see also Table 1).
W Scores
For W scores, grade retention decreased the growth rate in the first piece (short term), but had either no significant effect on the growth rate (math) or increased the growth rate (reading) in the second piece (longer term). Thus, retained children grew more slowly in reading in the repeat year than did matched promoted children but “caught up” to the promoted children in the longer term. In the longer term, they grew in reading at a faster rate than did their matched promoted peers such that by Time 4 (when retained children were in third grade and most promoted children were in fourth grade), retained and promoted children did not differ significantly in reading ability.3 Although it is tempting to extrapolate the linear growth for Slope 2 beyond Time 4, such extrapolation would be risky for related statistical and substantive reasons. Statistically, given the limited number of measurement waves collected so far in the present study, we were not able to fit nonlinear models of longer term growth. It is likely that longer term change will approach an asymptote over time so that linear growth only provides an approximation of the true form of growth over the 4-year period that was studied. Extrapolation beyond the range of the data from models that are only approximate is risky (Cook, 1993; MacCallum, 2003). Substantively, there is a rather abrupt change in the nature of reading and reading instruction that occurs between Grades 3 and 4 (Chall, 1996; Duke & Pearson, 2002). As retained children make this transition, their growth may slow. For math, the faster growth for promoted children in the short term disappears in the longer term when retained and promoted children’s rate of growth is equivalent. However, the early disadvantage of retention on math growth is not compensated by more rapid growth in the longer term.
Grade Standard Scores
In contrast to results for W scores, grade retention increased the growth rates of both the WJ math and reading grade standard scores in the short term but decreased growth rate of both scores in the longer term. Whereas promoted children showed only a slight decrease in their rate of growth in math and a somewhat larger decrease in their rate of growth in reading, retained children showed large drops in their growth rate from the first piece to the second piece for both the math and the reading grade standard scores. Thus, children did benefit from grade retention in the short term in terms of their performance relative to national grade norms. Previously published research on this sample at the end of Measurement Wave 2 found that retained students were rated by their classroom teacher as achieving more in the classroom than did their low-achieving promoted peers (Gleason, Kwok, & Hughes, 2007). The current findings suggest that this benefit erodes as retained students encounter an unfamiliar and more challenging curriculum. Again, additional waves of data are needed to determine whether the short-term benefits of retention on grade standard scores evaporate or reverse with additional years postretention.4 Of particular concern is the impact of the sequence of failure, success, and failure that retained children appear to experience in their first 4 years of formal schooling on their academic self-efficacy and beliefs regarding the degree to which they can control academic outcomes. In future studies, we will investigate whether the documented association between grade retention and school withdrawal is mediated, in part, by the effect of grade retention on such academic-related beliefs.
Moderators
We investigated nine potential moderators in a total of 72 tests (9 moderators × 4 achievement outcomes × 2 pieces). By chance alone, 3.6 tests would be expected to be statistically significant at an alpha of less than .05. Thus, the three significant results obtained should be interpreted as preliminary and requiring replication. As expected, the relative short-term benefit of promotion versus retention on growth in reading ability was greater for children with lower levels of peer-rated externalizing problems. This finding is consistent with the view that children with few behavioral problems (and greater prosocial skills) may be better prepared to meet the challenges of a more challenging curriculum. Similarly, the relative short-term benefit of retention versus promotion on growth in grade standard scores is greater for children who do not have strong parent involvement in their education. The limited number of significant interactions between retention and the moderator variables obtained in this study does suggest that the effects of retention are robust across a range of individual differences. An alternative explanation, of course, is that we failed to select the most appropriate variables for our tests of moderation.
Strengths and Limitations of the Present Study
In contrast to many of the previous investigations of grade retention, this investigation drew on several recent advances in the design and analysis of observational studies that can greatly strengthen causal inferences (see West & Thoemmes, 2008, for a review). First, we selected a large sample of children at risk for retention before the retention decision. This feature was expected to reduce, but not eliminate, baseline differences between retained and promoted children. It maximized the overlap between the promoted and the retained groups, eliminating the need to use statistical adjustment methods that may involve extrapolation. Second, we used an extensive battery of 72 pretest measures that were expected to be related to retention, math and reading achievement scores, or both. These measures were used to create propensity scores that were used to optimally match the retained and nonretained children before retention. Rosenbaum and Rubin (1983; see also Rosenbaum, 2002) showed analytically that propensity score methods provide a device that properly equates groups in observational studies if all of the important variables have been measured and balance on the variables is achieved between the treatment and control groups. Our selection of 72 baseline variables based on current theory and research represented a thorough attempt to measure all important baseline variables. As shown in Table 1, remaining differences between the groups after matching on propensity scores were minimal and nonsignificant. Third, we conducted growth curve modeling of the WJ achievement scores that are scaled by means of the Rasch model. Rasch model scaling yields interval-level measurements on a single dimension. The use of the WJ measures that are not part of school district or state education assessments prevents teachers from “teaching to the test.” Growth modeling permitted comparison of the slopes of the retained and promoted groups, both in the short term and in the longer term. This method represents an alternative strategy of comparing the groups. The combination of the use of two distinct methods, propensity scores and growth modeling, gave us two chances to get the adjustment for preexisting group differences right, giving us far greater confidence although not certainty in the causal interpretation of the effects of grade retention in the present study.
The primary limitations of the present study result are associated with the collection of only four waves of data to date. First, the number of waves of data restricts the forms of growth that could be investigated. We were able to investigate both short- and longer term growth in both WJ W scores and WJ grade standard scores. However, with only four waves of observation, our modeling was limited to the examination of linear effects. Other possible nonlinear models, such as the effects of grade retention increasing or decreasing over time to an asymptote, could not be investigated. We are currently collecting additional waves of data that will permit examination of such nonlinear effects. Second, additional waves of data collection will also permit a direct comparison between matched retained and promoted children when they are in the same grade. Same-grade comparisons involve examining the mean achievement of retained and promoted students when they are in the same grade, but not in the same year. Thus, the measurement of achievement for the retained children typically lags 1 year behind that for the promoted peers. Such direct grade comparisons are important because educators and parents may be more concerned with how retained students perform relative to their current classmates and grade expectations than to their former classmates, who are in a different grade (Lorence, 2006).
In summary, the picture is complicated. Results differ on the basis of the scale used (age or grade), time elapsed since retention year, and achievement domain (reading vs. math). These results suggest that the question “What is the effect of grade retention on achievement?” is inappropriate. The more appropriate question is “What is the effect of grade retention, for whom, on what academic competencies, in reference to what standard (age or grade), at what point in time postretention?” With additional waves of data, we hope to provide a more complete picture of the effects of retention on achievement over time.
Acknowledgments
This research was supported in part by National Institute of Child Health and Development Grant 5 R01 HD39367-02 to Jan N. Hughes.
Footnotes
Logistic regression is the most commonly used method of estimating propensity scores, although other approaches such as regression tree methods can also be used (see McCaffrey et al., 2004, and West & Thommes, 2008, for a discussion of the major estimation methods).
In contrast, measures of reliability within classical test theory do not ensure that a single dimension has been measured or that interval-level measurement has been achieved.
Difference = -1.50, Wald z = -0.51, p = .31.
This study makes comparisons across grades on the basis of extensive normative data underlying the Woodcock-Johnson III grade standard scores. At this point in the longitudinal study, direct comparison of the trajectories of the retained and promoted groups (same-grade comparison) is not possible in the two-piece growth model that we used. Such a comparison would require discarding the measurement taken in the repeated year for the retained participants. Such a procedure would leave us with only two waves of postretention measurement (second grade and third grade) on which to compare the two groups. At least three postretention measurements are required to estimate the two-piece model of growth.
References
- Alexander KL, Entwisle DR, Dauber SL. On the success of failure: A reassessment of the effects of retention in the primary grades. Cambridge University Press; Cambridge, England: 1994. [Google Scholar]
- Alexander KL, Entwisle DR, Dauber SL. On the success of failure: A reassessment of the effects of retention in the primary grades. 2nd ed. Cambridge University Press; Cambridge, England: 2003. [Google Scholar]
- Bracken BA, McCallum RS. Universal Nonverbal Intelligence Test: Examiner’s manual. Riverside; Itasca, IL: 1998. [Google Scholar]
- Buhrmester D, Furman W. The development of companionship and intimacy. Child Development. 1987;54:1386–1399. doi: 10.1111/j.1467-8624.1987.tb01444.x. [DOI] [PubMed] [Google Scholar]
- Caspi A, Block J, Block JH, Klopp B. A “common-language” version of the California Child Q-set for personality assessment. Psychological Assessment. 1992;4:512–523. [Google Scholar]
- Chall JS. Stages of reading development. 2nd ed. Harcourt Brace; Fort Worth, TX: 1996. [Google Scholar]
- Cicchetti D, Posner MI. Cognitive and affective neuroscience and developmental psychopathology. Development and Psychopathology. 2005;17:569–575. doi: 10.1017/S0954579405050273. [DOI] [PubMed] [Google Scholar]
- Cillessen AHN, Bukowski WM. Recent advances in the measurement of acceptance and rejection in the peer system. Jossey-Bass; San Francisco: 2000. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. Rev. ed. Academic Press; New York: 1977. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Erlbaum; Mahwah, NJ: 2003. [Google Scholar]
- Cook TD. A quasi-sampling theory of the generalization of causal relationships. In: Sechrest LB, Scott AG, editors. New directions for program evaluation. 57. Jossey-Bass; San Francisco: 1993. pp. 39–81. [Google Scholar]
- Dennebaum JM, Kulberg JM. Kindergarten retention and transition classrooms: Their relationship to achievement. Psychology in the Schools. 1994;31:5–12. [Google Scholar]
- Dickey WC, Blumberg SJ. Journal of the American Academy of Child & Adolescent Psychiatry. Vol. 43. 2004. Revisiting the factor structure of the Strengths and Difficulties Questionnaire: United States, 2001; pp. 1159–1167. [DOI] [PubMed] [Google Scholar]
- Duke NK, Pearson PD. Effective practices for developing reading comprehension. In: Farstrup AE, Samuels SJ, editors. What research has to say about reading instruction. 3rd ed. International Reading Association; Newark, DE: 2002. pp. 205–242. [Google Scholar]
- Enders CK, Bandalos DL. The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Structural Equation Modeling. 2001;8:430–457. [PubMed] [Google Scholar]
- Evans W, Baugh C, Sheffer J. A study of the sustained effects of comprehensive school reform programs in Pennsylvania. School Community Journal. 2005;15:15–28. [Google Scholar]
- Gleason KA, Kwok O, Hughes JN. The short-term effect of grade retention on peer relations and academic performance of at-risk first graders. Elementary School Journal. 2007;107:327–340. doi: 10.1086/516667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman R. The Strengths and Difficulties Questionnaire: A research note. Journal of Child Psychology and Psychiatry. 1997;38:581–586. doi: 10.1111/j.1469-7610.1997.tb01545.x. [DOI] [PubMed] [Google Scholar]
- Goodman R. Psychometric properties of the Strengths and Difficulties Questionnaire. Journal of Child Psychology and Psychiatry. 2001;40:791–799. [PubMed] [Google Scholar]
- Gootman E. One in 3 city 4th graders may not advance to 5th. New York Times. 2005 March 19;:5. Section B. [Google Scholar]
- Hill CR, Hughes JN. An examination of the convergent and discriminant validity of the Strengths and Difficulties Questionnaire. School Psychology Quarterly. 2007;22:380–406. doi: 10.1037/1045-3830.22.3.380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes CT. Grade-level retention effects: A meta-analysis of research studies. In: Shepard LA, Smith ML, editors. Flunking grades: Research and policies on retention. Falmer Press; London: 1989. pp. 16–33. [Google Scholar]
- Holmes CT, Matthews KM. The effects of nonpromotion on elementary and junior high school pupils: A meta-analysis. Review of Educational Research. 1984;54:225–236. [Google Scholar]
- Hong G, Raudenbush SW. Effects of kindergarten retention policy on children’s cognitive growth in reading and mathematics. Educational Evaluation and Policy Analysis. 2005;27:205–224. [Google Scholar]
- Hughes J. Assessment of children’s social competence. In: Reynolds CR, Kamphaus R, editors. Handbook of psychological and educational assessment of children. Guilford Press; New York: 1990. pp. 423–444. [Google Scholar]
- Hughes JN, Cavell TA, Willson V. Further evidence of the developmental significance of the teacher-student relationship. Journal of School Psychology. 2001;39:289–302. [Google Scholar]
- Hughes JN, Kwok O. Classroom engagement mediates the effect of teacher-student support on elementary students’ peer acceptance: A prospective analysis. Journal of School Psychology. 2006;43:465–480. doi: 10.1016/j.jsp.2005.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huitema BE. The analysis of covariance and alternatives. Wiley; New York: 1980. [Google Scholar]
- Jimerson SR. On the failure of failure: Examining the association between early grade retention and education and employment outcomes during late adolescence. Journal of School Psychology. 1999;37:243–272. [Google Scholar]
- Jimerson SR. Meta-analysis of grade retention research: Implications for practice in the 21st century. School Psychology Review. 2001;30:420–437. [Google Scholar]
- John OP, Srivastava S. The Big Five trait taxonomy: History, measurement, and theoretical perspectives. In: Pervin LA, John OP, editors. Handbook of personality: Theory and research. 2nd ed. Guilford Press; New York: 1999. pp. 102–138. [Google Scholar]
- Kwok O, Hughes JN, Luo W. The role of personality resilience on lower achieving first grade students’ current and future achievement. Journal of School Psychology. 2007;45:61–82. doi: 10.1016/j.jsp.2006.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerner RM. Developmental contextualism and the life-span view of person-context interaction. In: Bornstein MH, Bruner JS, editors. Interaction in human development. Crosscurrents in contemporary psychology. Erlbaum; Hillsdale, NJ: 1989. pp. 217–239. [Google Scholar]
- Little RJ, Hyonggin J, Johanns J, Giordani B. A comparison of subset selection and analysis of covariance for the adjustment of confounders. Psychological Methods. 2000;5:459–476. doi: 10.1037/1082-989x.5.4.459. [DOI] [PubMed] [Google Scholar]
- Lorence J. Retention and academic achievement research revisited from a United States perspective. International Education Journal. 2006;7:731–777. [Google Scholar]
- MacCallum RC. Working with imperfect models. Multivariate Behavioral Research. 2003;38:113. doi: 10.1207/S15327906MBR3801_5. [DOI] [PubMed] [Google Scholar]
- Mantzicopoulos P. Flunking kindergarten after head start: An inquiry into the contribution of contextual and individual variables. Journal of Educational Psychology. 2003;95:268–278. [Google Scholar]
- Mantzicopoulos P, Morrison D. Kindergarten retention: Academic and behavioral outcomes through the end of the second grade. American Educational Research Journal. 1992;29:182–198. [Google Scholar]
- McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- McCoy AR, Reynolds AJ. Grade retention and school performance: An extended investigation. Journal of School Psychology. 1999;37:273–298. [Google Scholar]
- Meehan BT, Hughes JN, Cavell TA. Teacher-student relationships as compensatory resources for aggressive children. Child Development. 2003;74:1145–1157. doi: 10.1111/1467-8624.00598. [DOI] [PubMed] [Google Scholar]
- Miesels SJ, Liaw FR. Failure in grade: Do retained students catch up? Journal of Educational Research. 1993;8:69–77. [Google Scholar]
- Miles SB, Stipek D. Contemporaneous and longitudinal associations between social behavior and literacy achievement in a sample of low-income elementary school children. Child Development. 2006;77:103–117. doi: 10.1111/j.1467-8624.2006.00859.x. [DOI] [PubMed] [Google Scholar]
- Ming K, Rosenbaum PA. A note on optimal matching with variable controls using the assignment algorithm. Journal of Computational and Graphical Statistics. 2001;10:455–463. [Google Scholar]
- No Child Left Behind Act of 2001, P. L. 107-110. (2001).
- Pagani L, Tremblay RE, Vitaro F, Boulerice B, McDuff P. Effect of grade retention on academic performance and behavioral development. Development and Psychopathology. 2001;13:297–315. doi: 10.1017/s0954579401002061. [DOI] [PubMed] [Google Scholar]
- Pianta RC, Tietbohl PJ, Bennett EM. Differences in social adjustment and classroom behavior between children retained in kindergarten and groups of age and grade matched peers. Early Education and Development. 1997;8:137–152. [Google Scholar]
- Pierson LH, Connell JP. Effects of grade retention on self-system processes, school engagement, and academic performance. Journal of Educational Psychology. 1992;84:300–307. [Google Scholar]
- Realmuto GM, August GJ, Sieler JD, Pessoa-Brandao L. Peer assessment of social reputation in community samples of disruptive and nondisruptive children: Utility of the Revised Class Play Method. Journal of Clinical Child Psychology. 1997;26:67–76. doi: 10.1207/s15374424jccp2601_7. [DOI] [PubMed] [Google Scholar]
- Reichardt CS. The principle of parallelism in the design of studies to estimate treatment effects. Psychological Methods. 2006;11:1–18. doi: 10.1037/1082-989X.11.1.1. [DOI] [PubMed] [Google Scholar]
- Reynolds AJ. Grade retention and school adjustment: An explanatory analysis. Education Evaluation and Policy Analysis. 1992;14:101–121. [Google Scholar]
- Reynolds AJ, Bezruczko N. School adjustment of children at risk through fourth grade. Merrill-Palmer Quarterly. 1993;39:457–480. [Google Scholar]
- Roderick M. Grade retention and school dropout: Investigating the association. American Educational Research Journal. 1994;31:729–759. [Google Scholar]
- Roderick M, Bryk AS, Jacob BA, Easton JQ, Allensworth E. Ending social promotion: Results from the first two years. Consortium on Chicago School Research; Chicago: 1999. Retrieved August 9, 2002, from www.consortium-chicago.org/publications/p0g04.html. [Google Scholar]
- Roderick M, Nagaoka J. Retention under Chicago’s high stakes testing program: Helpful, harmful, or harmless? Educational Evaluation and Policy Analysis. 2005;27:309–340. [Google Scholar]
- Rosenbaum PA. Observational studies. 2nd ed. Springer; New York: 2002. [Google Scholar]
- Rosenbaum PA, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Sameroff AJ. Transactional models in early social relations. Human Development. 1975;18:65–79. [Google Scholar]
- Sameroff AJ. Principles of development and psychopathology. In: Sameroff A, Emde R, editors. Relationship disturbances in early childhood. Basic Books; New York: 1989. pp. 17–32. [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Shadish WR, Clark MH. A randomized experiment comparing random to nonrandom assignment; Paper presented at the Symposium on Causality 2006; Jena, Germany. 2006, July; Retrieved March 11, 2007, from http://www.metheval.uni-jena.de/projekte/symposium2006/contributions.php. [Google Scholar]
- Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference. Houghton-Mifflin; Boston: 2002. [Google Scholar]
- Shadish WR, Luellen JK, Clark MH. Propensity scores and quasi-experiments: A testimony to the practical side of Lee Sechrest. In: Bootzin RR, McKnight PE, editors. Strengthening research methodology: Psychological measurement and evaluation. American Psychological Association; Washington, DC: 2006. pp. 143–157. [Google Scholar]
- Singer JD, Willett JB. Applied longitudinal data analysis: Modeling change and event occurrence. Oxford University Press; New York: 2003. [Google Scholar]
- Sipple JW, Killeen K, Monk DH. Adoption and adaptation: School district responses to state imposed learning and graduation requirements. Educational Evaluation and Policy Analysis. 2004;26:143–168. [Google Scholar]
- Skinner EA, Zimmer-Gembeck MJ, Connell JP. Individual differences and the development of perceived control. Monographs of the Society for Research in Child Development. 1998;63(23) Serial No. 254. [PubMed] [Google Scholar]
- Terry R. Measurement and scaling issues in sociometry: A latent trait approach; Paper presented at the biennial meeting of the Society for Research in Child Development; Albuquerque, New Mexico. 1999, April. [Google Scholar]
- Texas Education Agency . Grade-level retention in Texas public schools. Author; Austin, TX: 2005. 2003-04 (Document No. GE06 601 01) [Google Scholar]
- Warren JR, Edwards MR. High school exit examinations and high school completion: Evidence from the early 1990s. Educational Evaluation and Policy Analysis. 2005;27:53–74. [Google Scholar]
- West SG, Thoemmes F. Equating groups. In: Alasuutari P, Bickman L, Brannon J, editors. Handbook of social research methods. Sage; London: 2008. pp. 414–430. [Google Scholar]
- Willson V, Hughes JN. Retention of Hispanic/Latino students in first grade: Child, parent, teacher, school, and peer predictors. Journal of School Psychology. 2006;44:31–49. doi: 10.1016/j.jsp.2005.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong SW, Hughes JN. Ethnicity and language contributions to dimensions of parent involvement. School Psychology Review. 2006;35:645–662. [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock-Johnson tests of achievement: Standard and supplemental batteries. DLM Teaching Resources; Allen, TX: 1989. [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. WJ-III Tests of Achievement. Riverside; Itasca, IL: 2001. [Google Scholar]
- Woodcock RW, Muñoz-Sandoval AF. Woodcock-Muñoz Language Survey. Riverside; Chicago: 1993. [Google Scholar]
- Woodcock RW, Muñoz-Sandoval AF. Batería Woodcock-Muñoz Pruebas de Aprovechamiento—Revisada. Riverside; Itasca, IL: 1996. [Google Scholar]
- Woodcock RW, Muñoz-Sandoval AF. Comprehensive manual: Woodcock-Muñoz Language Survey Normative Update. Riverside; Itasca, IL: 2001. [Google Scholar]
- Wu W, West SG, Hughes JN. Short-term effects of grade retention on growth rate of Woodcock-Johnson III broad math and reading scores. Journal of School Psychology. 2008;46:85–105. doi: 10.1016/j.jsp.2007.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]