Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure

Abstract

Single chicken erythrocyte chromatin fibers were stretched and released at room temperature with force-measuring laser tweezers. In low ionic strength, the stretch-release curves reveal a process of continuous deformation with little or no internucleosomal attraction. A persistence length of 30 nm and a stretch modulus of ≈5 pN is determined for the fibers. At forces of 20 pN and higher, the fibers are modified irreversibly, probably through the mechanical removal of the histone cores from native chromatin. In 40–150 mM NaCl, a distinctive condensation-decondensation transition appears between 5 and 6 pN, corresponding to an internucleosomal attraction energy of ≈2.0 kcal/mol per nucleosome. Thus, in physiological ionic strength the fibers possess a dynamic structure in which the fiber locally interconverting between “open” and “closed” states because of thermal fluctuations.

The DNA of all eukaryotic cells is organized in the form of chromatin and its structure has been the subject of intense research during the last 25 years. These studies have shown that the basic structural unit of chromatin is the nucleosome comprising the core particle and linker DNA. The core particle contains two of each of four core histones H2A, H2B, H3, and H4, and 146 bp of DNA wrapped around this core. The chromatosome (1, 2) includes the core particle and an additional 20 bp of linker DNA associated to a linker histone (H1 or H5). Although there is still some controversy about the position of the linker histone (3, 4) and the location of H3 and H4 histone tails in the chromatosome, many details have been revealed by the crystal structure of the nucleosome core particle (5–7).

Much less is known about the next level of chromatin structure, i.e., the spatial organization of chromatosomes interspersed by linker DNA (8, 9). Many models involving the regular, three-dimensional organization of nucleosomes into chromatin fibers have been proposed (10). Recently, new methods of direct visualization such as scanning force microscopy (11–13) and cryo-electron microscopy (14–16), as well as reinterpretation of older data, indicate that, at low ionic strength at least, nucleosomes in the so-called 30-nm fiber are organized in an irregular three-dimensional zigzag.

Chromatin undergoes a process of condensation and decondensation during the cell cycle in vivo. Higher-order structures occur in transcriptionally inactive regions, whereas regions of decondensed nucleosomal arrays often are associated with active chromatin (10). Because in most cell types only a small percentage of the total chromatin content is active at any given time, dynamic changes in the folding state of local chromatin domains must occur to modify the accessibility of the transcription machinery to these domains. These structural transitions may involve H1 removal, histone modifications (acetylation, phosphorylation, or methylation), and changes in the nonhistone protein complement (10, 17). Despite the role played by changes in fiber compaction in the regulation of gene expression, little is known about the magnitude and the origin of the forces that maintain and stabilize these variously compacted forms of the fiber or how these forces are modified during the cell cycle. A simple way to address these questions is to grab a single chromatin fiber by its ends and pull it to determine its mechanical behavior. The response of the fiber to a range of forces thus can provide insights into the nature, range, and magnitude of the interactions holding together its three-dimensional structure. In vitro, chromatin fibers also can become compacted or extended in high and low ionic strength, respectively. By carrying out the experiments in different ionic strengths, it may be possible to determine how these conditions selectively modulate the strength of some interactions over others to bring about the condensation-decondensation transition of the fiber.

Single molecule manipulation methods recently have been used to investigate the mechanical responses of DNA and proteins. In particular, the entropic elasticity of double-stranded DNA (dsDNA) has been studied with magnetic beads (18), laser tweezers (19), and hydrodynamic drag (20). The response of DNA to torsional force also has been characterized (21). Single molecules of the muscle protein titin (22–24) and tenascin (25) have been mechanically unfolded. In the present study, single, intact fibers of chicken erythrocyte chromatin are extended between two polystyrene beads by using a force-measuring, dual-beam, laser tweezers apparatus (Fig. 1) under various ionic strength conditions.

Figure 1.

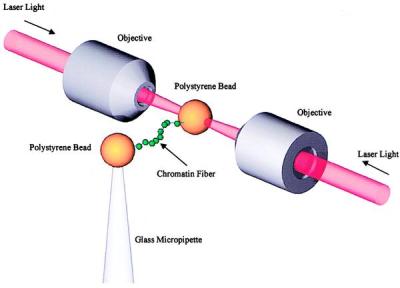
Schematic drawing of a chromatin fiber pulled between two beads by laser tweezers (19) formed by two laser beams counter-propagating through the objectives with a common focus, not to scale. The stiffness of the trap is ≈28 pN/μm. The Brownian noise in the force ≈0.34 pN, which is also close to the thermal drift.

Materials and Methods

Nuclei.

Fresh adult chicken blood mixed with equal volume of 25 mM EDTA, 75 mM NaCl (EDTA saline) was purchased from Lampire Biological Laboratory, Pipersville, PA. All operations were carried out at 4°C unless stated otherwise. Red blood cells were washed three times in EDTA saline at 4,000 × g and resuspended in 10 mM MgCl₂, 250 mM sucrose, 0.2 mM PMSF (nuclei washing buffer) back to the original volume of blood. Then, 1% Triton X-100 was added slowly, and the solution was stirred for 1 hr before the nuclei were spun at 5,000 × g for 1 hr. Nuclei then were washed repeatedly in nuclei washing buffer until clean at 4,000 × g for 20 min each time and stored at −80°C.

Chromatin.

Nuclei were thawed at 37°C and washed twice in 10 mM Tris, pH 8.0/1 mM CaCl₂/0.2 mM PMSF/250 mM sucrose (isolation buffer) at 800 × g for 10 min each time and resuspended in the same buffer. At A₂₆₀ = 50, nuclei were digested with 0.014 unit/ml micrococcal nuclease (Sigma) for 6 min at 34°C, and the digestion was stopped by adding 2 mM EGTA, pH 8.0. Nuclei were spun at 3,000 × g for 10 min, and the pellet was resuspended and dialyzed against 10 mM Tris, pH 8.0/0.5 mM EGTA/0.2 mM PMSF (dialysis buffer) overnight at 4°C. Nuclear debris was removed by spinning at 8,000 × g for 15 min, and the chromatin solution was stored on ice.

All fibers used in this study were previously fractionated by sucrose gradients. About 2 ml of chromatin solution was carefully loaded on top of a linear 10–40% sucrose gradient in dialysis buffer (≈34 ml), and the gradient was centrifuged in a Beckman LM-8 μltracentrifuge by using a SW28 rotor at 27,000 rpm for 6 hr. Fractions of about 1.8 ml each were collected. The DNA lengths of different fractions were determined by pulse-field gel electrophoresis. Samples were incubated in 1% SDS at 37°C for 30 min before being loaded on 1% Fastlane agarose (FMC) gel. Fractions that contained the longest fibers were selected for biotinylation.

Chromatin was washed once in Centricon Plus 100 (Amicon) with 10 mM Tris, 0.1 mM EDTA, pH 7.5, then in 25 mM Na phosphate, 0.5 mM MgCl₂, pH 7.5. Three units of T4 DNA polymerase (NEB, Beverly, MA) was added to about 30 μg of DNA at 37°C for 8 min to create 3′ single-stranded overhangs. Six micromolar each of biotin-14-dATP, biotin-14-dCTP, dGTP, and dTTP (GIBCO/BRL) were added, and the reaction was incubated for another 15 min before being stopped by adding 10 mM EDTA, pH 8.0. The chromatin then was washed repeatedly in 10 mM Tris, 2 mM EDTA, pH 7.5 through a Centricon Plus 100 filter to remove free biotinylated nucleotides and stored at 4°C. The ratio of linker histones to core histones of the modified fibers is not changed by the labeling process judged by SDS/PAGE.

Fiber Assembly.

A single biotinylated chromatin fiber was connected by its ends between two avidin-coated polystyrene beads (2.54 μm in diameter, Bangs Laboratory, Carmel, IN) inside a flow chamber. One bead was held in a force-measuring dual beam laser tweezers (19); the other was held on top of a movable glass micropipette (Fig. 1). A diluted chromatin solution was passed through the two beads to prevent multiple fiber connections. The tethering of a single fiber also can be confirmed by stripping the fiber of histones by using SDS, and recording the elastic behavior of the DNA, at the end of the experiments. After the connection was made, a saturated solution of calf thymus nucleosomes (Worthington) was passed through the chamber to prevent nonspecific interactions. Throughout this process, care was exercised to prevent permanent mechanical damage to the fiber.

Force-Extension Curves.

During one stretch/release cycle, the fiber was first stretched by moving the glass micropipette with steps of ≈0.05 μm and increasing the distance between the beads until a predetermined force was reached. The end-to-end distance of the fiber (extension) was determined from the distance between the centers of the two beads, by using video microscopy. The force was measured directly from the change in momentum of the light in the trap as described (19). The extension and the corresponding force were averaged typically over a period of 0.25 s. The fiber then was relaxed by gradually decreasing the distance. The normal rate of data acquisition was 2 points/s. The experiments were done at room temperature, in buffers ranging from 5 to 150 mM NaCl with 2 mg/ml BSA to prevent nonspecific interactions.

Results

The stretch/release curves of chromatin fibers display more variability than those observed for DNA (18, 19). This finding is expected given the greater heterogeneity and complexity of the chromatin samples. Some variability may have been introduced by the interaction of the fibers with the bead or with the glass micropipette during the assembly of the fibers (such as nonspecific binding and mechanical damage to the fiber). A few very long fibers with force-extension characteristics similar to that of naked dsDNA (19) sometimes were encountered. These fibers, presumably to have lost either part or most of their linker histones and/or histone octamers, were segregated in a different class. Only curves corresponding to intact fibers are presented here. In general, these fibers displayed more consistent, less variable force-extension curves. The examples illustrated are typical of this class of fibers.

Fiber Elasticity in 5 mM NaCl.

At low ionic strengths (5 mM NaCl), three distinct force regimes can be recognized in the elastic response of native chromatin fibers. Between 0 and 7 pN, the stretch-relaxation cycles yield reversible force-extension curves (Fig. 2A), i.e., the curve obtained during relaxation coincides with that obtained during stretching, indicating that the process is reversible and the fiber is at equilibrium throughout the cycle. In this force regime, the curves are also repeatable, namely, the same fiber can be cycled over and over, yielding each time the same force-extension curves. More significantly, the force-extension curves are monotonic and display a slightly positive curvature.

Figure 2.

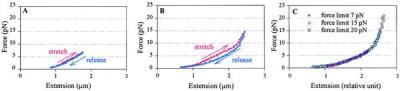
Force-extension curves of chicken erythrocyte chromatin fibers at low and intermediate force regimes in 5 mM NaCl, 10 mM Tris (pH 7.5), 2 mM EDTA, 2 mg/ml BSA. (A) In the low force regime, below 6 pN, the stretch release curves are repeatable and reversible with a positive curvature. (B) Between 6 and 20 pN the stretch and release curves no longer coincide and hysteresis is evident in the cycle. (C) Shown are the relaxation curves, adjusted to the same length by a constant factor, corresponding to a fiber stretched in three cycles with different maximum forces.

In the intermediate force regime (7–20 pN), the relaxation curve no longer coincides with the stretching curve (hysteresis) and rejoins it only below 2 pN (Fig. 2B). But the stretch and relaxation halves of the cycle are still repeatable during successive cycles. Another feature is observed between cycles that reach different maximum stretching force. The stretch curves of a fiber extended by different amounts in successive cycles will approximately coincide in the shared force interval, whereas the release curves differ each time only by a constant length factor (Fig. 2C), indicating that fibers subjected to successively higher forces become proportionately longer without changing their elastic properties. If a cycle is repeated with the same force limit the stretch and release curves also repeat.

The hysteresis observed above 7 pN indicates that the rate at which the fiber is stretched or released exceeds the rate of extension and contraction of the fiber at equilibrium at that extension. Chromatin fibers pulled 4–6 times slower than those showed in Fig. 2 (data not shown) did not display a reduced hysteresis.

Above 20 pN, the force-extension curves are neither reversible nor repeatable, i.e., hysteresis appears between each stretch and release curve, and for each successive stretch it takes less force to obtain an equivalent extension (Fig. 3). Once the fiber has been pulled above 20 pN, successive stretch/release curves of this fiber in the low force regime no longer reproduce the curves of fibers never exposed to high force. Between 20 and 35 pN, a transition appears in the stretching curve the first time the fiber is subjected to these forces (Fig. 3, green curve, between the vertical arrows). In successive stretching curves the transition becomes less evident, occurring at higher forces (Fig. 3, red curve, between the vertical arrows) until it finally disappears altogether (Fig. 3, blue curve). The relaxation curves are repeatable, as long as they start from the same fiber extension. If the maximum force applied to the fiber is the same between successive cycles, the fiber gets longer with each cycle. The change experienced by the fiber appears to be permanent, as the fibers never regain their initial properties regardless of the waiting time elapsed between cycles. These observations suggest that extension beyond 20 pN is accompanied each time by an irreversible change in the fiber, possibly involving the loss of linker histones and histone octamers to the histone-free surrounding buffer. When the tension reaches ≈65 pN, the overstretching transition characteristic of dsDNA is observed (19) (Fig. 3 horizontal arrow). These observations taken together are consistent with the interpretation that forces beyond 20 pN lead to the mechanical detachment of the histone octamers from the DNA, a process that may continue at higher forces. Not all the histone octamers are eliminated when the fiber is stretched to 65 pN, as revealed by analysis of the low force region of irreversibly modified fibers. The persistence length of these fibers treated as inextensible worm-like chains (estimated from many low force data points) is significantly smaller than that of dsDNA (53 nm; ref. 26). This reduced persistence length is most likely caused by the residual histones still present on the DNA that bend and thus decrease its apparent persistence length (27, 28). The reduced persistence length also may have resulted from the highly positively charged tails of the residual histones, which decrease the net negative charge of the phosphate backbone. Only after the fiber is washed by SDS does its elastic response become indistinguishable from that of naked dsDNA (data not shown).

Figure 3.

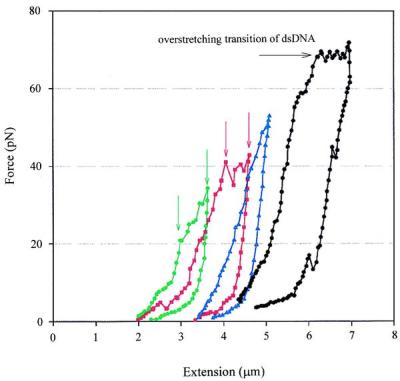
Force-induced irreversible changes in chromatin fibers successively extended to increasing forces well above 20 pN in 5 mM NaCl, 10 mM Tris (pH 7.5), 2 mM EDTA, 2 mg/ml BSA. Hysteresis between the stretch and release part of the curve is evident in all curves. During the first stretch-release cycle (green) the fiber undergoes a transition that appears between 20 and 35 pN (between the green vertical arrows). In the successive cycles this transition occurs at higher forces (red curve and red vertical arrows) and eventually become less noticeable (blue curve). When the fiber is stretched up to ≈65 pN, a plateau corresponding to the overstretching of dsDNA can be seen (black curve and horizontal arrow).

Fiber Elasticity in 40 and 150 mM NaCl.

To determine the effect of ionic strength on the elastic response of chromatin, individual fibers were stretched in 40 and 150 mM NaCl buffer. Force-extension curves of chromatin fibers obtained in these conditions show features not present at the low ionic strengths. At high ionic strength, it takes higher forces to arrive at the same extension during the stretching half of the cycle than at low ionic strength, consistent with the fiber being more condensed in high salt (2, 8, 29). At very low force (0–4 pN), the stretch and release curves of fibers pulled in 40 mM NaCl are both repeatable and reversible, as observed in low salt, but their curvature is negative (Fig. 4A). Between 4 and 6 pN, the fiber starts to get longer with little increase in tension and give rise to a plateau in the force-extension curve (Fig. 4, horizontal arrow). Once the fiber has been stretched beyond the plateau at 6 pN, the relaxation curves are repeatable but no longer coincide with the stretching curves, as they regain the positive curvature characteristic of curves obtained in 5 mM NaCl in the same force regime.

Figure 4.

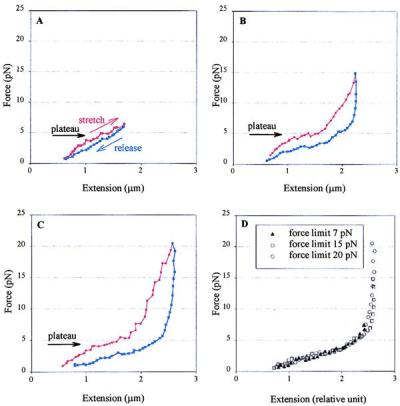
Force-extension curves for chicken erythrocyte chromatin fibers pulled below 20 pN in 40 mM NaCl, 10 mM Tris (pH 7.5), 2 mM EDTA, 2 mg/ml BSA. (A) In low force regime, the stretch and release halves of the cycle nearly coincide. (B and C) Intermediate force regime. The stretch and release curves no longer coincide and the process displays hysteresis. The plateau corresponding to the condensation-decondensation transition is indicated by the horizontal arrows. (D) Three relaxation curves, adjusted to the same length by using a constant factor, corresponding to a fiber stretched successively to different maximum forces. The negative curvature and the plateau although less obvious, are still present.

If the fiber is stretched between 10 and 20 pN, the stretching curves behave again as curves obtained in 5 mM NaCl but with higher slope and the stretch/release cycle displays larger hysteresis (Fig. 4C). The stretch and release curves are not reversible but repeatable, and the stretching curve still shows the plateau each time between 4 and 6 pN, an indication that, even after being stretched up to 20 pN, the fiber still can attain its condensed state. As in 5 mM NaCl, no histone dissociation occurred in this force regime, because the curves within 20 pN are repeatable in the histone-free buffer. As in the previous regime, chromatin fibers are more compact than in low salt, judged by the consistently higher forces that are needed to stretch the fibers to the same extension. The relaxation curves display similar characteristics as those obtained in this force regime at low ionic strength. In particular, fibers extended to higher forces yield curves that are related to those of fibers extended to lower forces by a constant length factor. However, a region of negative curvature also appears below 5 pN (Fig. 4D). Above 20 pN, the stretch/release curves are indistinguishable from those in low-salt buffer. In this high force regime the fiber again is modified irreversibly by the force. Curves corresponding to fibers stretched in 150 mM NaCl show similar characteristics to those observed in 40 mM (data not shown).

Discussion

Hysteresis.

The mechanical force applied to the fiber should act mainly on the entry and exit angle of the DNA around the core particle, fixed by the interaction of the linker histones H1 and H5 with the DNA. The hysteresis observed in the intermediate force regime (7–20 pN) thus may reflect the mechanically induced modification of these interactions. Such modification could involve the detachment of the linker histone from binding sites on the DNA and the core particle, and even its partial denaturation, but not its release into the solution. During the stretch half of the cycle, the force increases until it is high enough to break these interactions. Therefore, to extend the fiber at the experimental pulling rate, the force must increase above its equilibrium value. During the release part of the cycle, the tension in the fiber may prevent the immediate reformation of the linker histone-DNA contacts. The force then must be lowered below its equilibrium value for the contacts to be re-established, giving rise to the observed hysteresis. This scenario could account for the apparent “lengthening” of the fiber seen in the release curves: removal of the angle constraint imposed on the DNA at its entry and exit point around the core particle would lead to additional extension of the fiber. However, this model will not easily explain the invariance of the elastic property of the fiber as they get longer (Figs. 2C and 4D).

Such invariance suggests a different type of hysteresis model. Here it is required that distant, nonadjacent nucleosomes along the fiber interact with each other at low force. During the stretch half of the cycle, the force increases until it breaks those interactions. During the release part of the cycle, the tension in the fiber aligns the nucleosomes and prevents them from making the nonadjacent contacts. The force then must be lowered below its equilibrium value for the contacts and the loops to be reformed. In this model, the apparent “lengthening” of the fiber occurs as the sections of chromatin delimited by the broken interactions become incorporated in the extendable length of the fiber. Different relaxation curves thus are obtained when the fiber is extended to different maximum forces, but these curves can be related to one another each time by a constant length factor. Consistent with this interpretation is the observation that hysteresis is reduced if the fiber is repeatedly extended and released in the range between 5 and 20 pN, presumably because in these conditions the force is never low enough to permit the full reformation of re-entrant structures. That the extension and release curves are still repeatable in this regime indicates that the changes involved in the extension of the fiber can be reversed at low tensions. It is not clear what the nature of these interactions would be. They do not appear to be electrostatic, because they persist over 2 orders of magnitude variation in ionic strength. One possibility is nucleosomal interactions via H3 and H4 tails, another is that the nucleosomes in the zigzag become re-entrant (tangled) so, as the fiber is stretched, the nucleosomes may become hooked on each other forming local loops (30). Here, the tension effectively tightens the tangles at the re-entrant points. This process continues until the tension deforms the fiber, allowing one nucleosome to slip pass the other to unhook the tangle. At present, it is not possible to discriminate between any of these models.

Force Extension in Low Salt.

The positive curvature of the force-extension curves at forces between 0 and 20 pN suggests that, in this regime of ionic strength and forces, the extension of the fiber corresponds to a continuous deformation process. The elasticity presumably is dominated by the alignment and local straightening of the fiber, possibly through the deformation of the intrinsically straight linker DNA whose entry-exit angle appears to be maintained by steric (14, 31, 32) (globular domain of the linker histones H1 and H5) and electrostatic (linker repulsion) interactions (Fig. 5). Thus, a continuous, extensible worm-like chain model (33) can be used to attempt a first-order description of the release half of the force-extension cycle of chromatin fibers in low ionic strength buffer and between 0 and 20 pN. The release part of the cycle is used for the model, because the stretch part is more likely to be dominated by the nonequilibrium processes responsible for the observed hysteresis (see previous section). These processes, which involve the disruption of the nonlocal, nonadjacent contacts formed in the fiber at low or zero force, lead to the overestimation of the forces in the stretching part of the cycle. In contrast, during release, particularly between 20 pN and 5 pN (see above), no re-entrant interactions are expected to reform and the elastic behavior of the fiber mainly is controlled by the nature of its local interactions, such as the entry-exit angle of the DNA around the nucleosome maintained by the linker histones. In this regime, the release curves can be reasonably well described by an equilibrium model.

Figure 5.

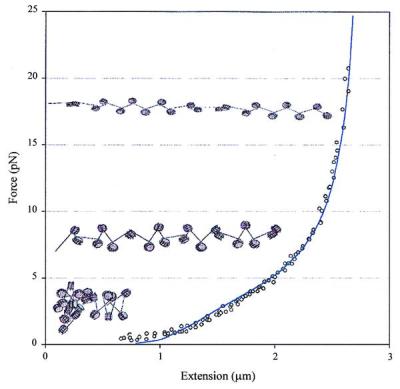
Fit of the release part of the force-extension curve of a chromatin fiber at low ionic strength by using an extensible worm-like chain model. Fitting of the data gives a persistence length of 30 nm, a stretch modulus of 5 pN, and a maximum length of 3.05 times the original fiber length, estimated to be 1 μm based on the x-intercept of the linear part of the curve. The fiber attains its maximum length when the linkers become completely aligned in the direction of the applied force. For reference, the chromatin models, schematic drawing depicting qualitatively the continuous deformation of the chromatin fiber as it is subjected to increasing tension at low ionic strengths, have been superimposed to the relaxation curve of a fiber pulled under those conditions.

The effective energy of an extensible worm-like chain can be expressed as (33):

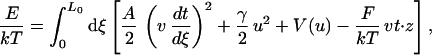1

where L₀ is the contour length of the chain in the absence of thermal fluctuations, ξ is the chemical distance along the chain. The axial strain u is defined as u = v − 1, where dr/dx = vt, and r is the position of point ξ along the chain, and t is the tangent to the chain at that point. The first term in this equation describes the bending energy of an inextensible worm-like chain, where A is the persistence length. The second term describes the energy associated with the stretching of the chain, where γ is the stretch modulus. The third term is the potential energy that defines the maximum extension of the chain, and the last term describes the free energy of the chain under a force F acting in z direction. The model assumes that the fiber can rotate freely between its points of attachment and no torsional energy is stored in the fiber as it is being extended. The equilibrium extension is calculated from the conformation of the chain that minimizes the effective energy at any given force. In this model, the mechanical properties of the fiber are determined by its persistence length, its stretch modulus (defined here as the force at which the fiber doubles its contour length at zero force), and its maximum extension. When using this model for a chromatin fiber, the stretch modulus is obtained directly from the measurements, whereas the persistence length and the maximum fiber extension are treated as fitting parameters. The fit of the data to this model (Fig. 5) reveals some of the unique mechanical properties of the chromatin fiber at low ionic strengths, i.e., a bending rigidity comparable to that of dsDNA and an extremely low stretch modulus. The low value of the stretch modulus of chromatin compared with dsDNA (≈1,000 pN; ref. 19) probably reflects the tertiary nature of the interactions disrupted during the mechanical extension of the fiber at low ionic strength, such as the straightening of the linker zigzags during stretching. A more elaborate model of the force-extension characteristics of chromatin at low ionic strength will be presented elsewhere (30).

Mechanical Dissociation of the Histone Core Particle.

A force of 20 pN or higher appears to be required to induce the mechanical removal of the core particles from native chromatin in these experiments. This value is ≈10 times larger than recently predicted (34) by using an equilibrium model in which the DNA-core binding energy (20 kT) was dissipated over the complete DNA length (146 bp). However, in our experiments the dissociation process between histone octamer and DNA does not occur at equilibrium because (i) pulling is too rapid and (ii) once detached, the histone core can never rebind the DNA because it is washed away in the histone-free buffer. Further, the equilibrium model is equivalent to peeling the DNA off the core, but tension in a chromatin fiber actually may wrap the DNA tighter around the particle, rather than peeling it off. Could such tightening deform the protein core and extrude it out the ends of the DNA helix? An estimate of the pressure generated on the core particle by pulling the linker with 20 pN yields a pressure of ≈2 × 10⁶ Pa, which is ≈1,000 times less than the Young's modulus of a typical protein, effectively ruling out the core-extrusion hypothesis. In fact, the external force probably induces core dissociation by twisting the core particle so that the force acquires a component perpendicular to the plane in which the DNA wraps around the histones. Then the force can act to peel the DNA wraps off the ends of the two-turn helix.

Assume some sizable twist, say 45°, is necessary on the core particle before the 2 pN peeling force (34) can act. Further assume fiber tension acts through the torque generated on a 4-nm offset at the entry and exit points of the DNA to bend the linker DNA and enable twist. Then a fiber tension of ≈6 pN is required to achieve such a twist. If greater twist angle is required for peeling, or if the bending rigidity of linker DNA is increased by its interaction with histone tails, then this force estimate will increase and may account for the observed value (20 pN).

Internucleosomal Interaction.

Electron microscopy and scanning force microscopy images of chromatin in high ionic strength (≥ 40 mM NaCl) reveal chromatin fibers condensed into compact rod-like structures with a reduced average distance between nucleosomes (29) and smaller entry-exit angles (2). This structure may be stabilized by the additional neutralization of the linker DNA charge (effectively reducing the entry-exit angle of the linker DNA and bringing the nucleosomes closer to each other), and by an increased internucleosomal attraction that may be mediated by the N-terminal tails of the core histones (31). Correspondingly, the stretch/release curves obtained in high ionic strength show a distinct, mechanically induced transition between 5 and 6 pN in which the fiber becomes longer within a relatively small force range. This transition is identified here with the disruption of nucleosomal-nucleosomal attraction. The negative curvature observed in this force regime and leading to the plateau in Fig. 4, is, in fact, the signature of a continuous transition between two distinct forms of the fiber characterized by different end-to-end extensions. According to this interpretation, the short form corresponds to the condensed structure in which nucleosomes interact with each other through an attractive potential, whereas the long form corresponds to the extended structure with little or no residual internucleosomal interactions (30). Throughout this range, the fiber thus can be thought of possessing bistability and displaying the coexistence of two phases corresponding to condensed and decondensed structures. At high ionic strength and below 6 pN, the fiber is in its condensed state and the force extension curve simply corresponds to the energy required to orient and straighten the condensed fiber against thermal fluctuations. At some critical tension (5–6 pN), however, it becomes energetically more favorable to decondense the fiber, resulting in the observed transition (34).

The average energy required to pull apart the nucleosomes in high ionic strength can be estimated directly from the stretch/release curves at low forces, assuming that the plateau observed at low force (5–6 pN) corresponds to the interaction of the fiber between condensed and decondensed states. An equilibrium calculation is justified in this case, because at high ionic strength the curves in the regime between 0 and 6 pN (Fig. 4A) are very nearly equilibrium curves, with minimal hysteresis, which is not the case for forces above this range (Fig. 4 B and C). However, the low force/low extension regime is of interest here as in this region the short-ranged internucleosomal interactions are likely to play a role in the elasticity of the fiber. The total length of DNA in the fiber shown in Fig. 4C is about 20 μm, as estimated from fibers treated with SDS at the end of the experiments. Using 210 bp per nucleosome for chicken erythrocyte chromatin, this length corresponds to ≈280 nucleosomes. A force of 5 pN acting over a distance of 0.6 μm (the extent of the plateau) during the decondensation (Fig. 4C) yields a binding energy of ≈2.6 kT per nucleosome. However, because of the re-entrant nature of the fiber, only ≈78% of the fiber participates in the extension in the low force regime comparing the extensions of the fiber in the stretch and release parts of the curve at ≈6 pN. Taking this figure into account, a binding energy per nucleosome of ≈3.4 kT is obtained.

The force-extension curve of a condensed fiber in high ionic strength also can be fitted to a simplified two-state model (34) (Fig. 6). In this model, the fiber can interconvert between a short (condensed) and a long (decondensed) states. For simplicity, both states are assumed to behave as inextensible worm-like chains. The transition occurs when the work done by the external force equals the difference of the chemical potential between these two states. This model reproduces the magnitude and the main features of the transition region reasonably well, when the internucleosomal attractive energy is set to be 3.8 kT, a figure comparable to that estimated from the experiment directly. The critical force required to convert the short into the long state is given by the ratio of the free energy difference to the difference in end-to-end distance between the two states at that force (34). A critical force of 5 pN gives the change in length upon decondensation of 3 nm, which is two times the contour length of the condensed form in 40 mM NaCl. The distance between the projections of two adjacent nucleosomes on the polymer axis of the decondensed chromatin in 40 mM NaCl therefore is estimated to be 4.5 nm. This value yields, in turn, an entry-exit angle of linker DNA of ≈40°, consistent with the value estimated at these ionic strengths from cryo-electron microscopy studies. Notice that, as expected, the model is good only up to ≈6 pN.

Figure 6.

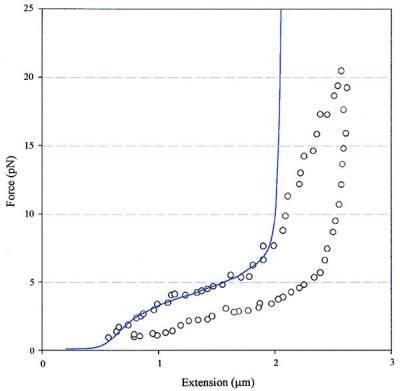
Fit of chromatin decondensation data by a two-state model. A persistence length of 30 nm is assumed for both before and after the transition (either side of the plateau). A contour length of 0.7 μm was used for the condensed fiber (short form), whereas the contour length for the decondensed fiber (long form) is assumed to be two times longer. The energy to convert the short form to long form is found to be 3.8 kT from the fit. The divergence between the experimental values (○) and the calculated values (solid line) at high forces results from the inextensible nature of the model.

The value of the internucleosomal attractive energy estimated here from the force-extension curves at physiological ionic strength (≈3.4 kT) indicates that the compact, inactive form of the fiber is a dynamic structure that can locally interconvert between an “open” and a “closed” state through thermal fluctuations. This interaction energy indicates that, on the average, two adjacent nucleosomes should be found in the open state about 4% of the time. The local dynamics of the fiber structure thus may play an essential role in the regulation of gene expression by providing local access to trans-acting factors such as acetyltransferases, deacetylases, and phosphorylases (17, 35), that can modify the fiber to stabilize its active or inactive conformations.

Abbreviation

dsDNA

double-stranded DNA