Mechanisms of the ultrasonic modulation of fluorescence in turbid media

Abstract

To understand the modulation mechanisms of fluorescence emission induced by ultrasonic waves in turbid media, a mathematical model is proposed and compared with the recent experimental observations of Kobayashi et al. [Appl. Phys. Lett. 89, 181102 (2006)]. Modulation of fluorophore concentration is considered as the source of the oscillation of fluorescence signals when fluorophore concentration is low enough so that quenching effects can be ignored. By solving the rate equation and photon diffusion equation, quantitative solutions are given to quantify the modulation strength. Our calculations predict that the modulation depth (the ratio of the modulated signal strength to the unmodulated signal strength) can reach 10⁻⁴ when ultrasonic pressure with the order of magnitude of megapascals is applied in the ultrasound focal zone. Our model explains the relationship between the modulation strength and the average fluorophore concentration and also predicts a method to measure or image fluorescence lifetime in the turbid medium. When fluorophore concentration is high enough so that fluorescence quenching occurs, the fluorescence modulation is attributed to the modulation of quenching efficiency. Quenching caused by fluorescence resonance energy transfer can lead to a nonlinear relationship between the modulation fluorescence strength and the applied ultrasound strength.

INTRODUCTION

Ultrasound-modulated fluorescence tomography (UMFT) has been proposed and feasibility demonstrations have been reported recently.^{1, 2, 3, 4, 5} In UMFT, a focused ultrasound beam is used to modulate an illuminated fluorescent turbid medium. In the focal zone of the beam, the fluorescence emission intensity is modulated by the radio frequency (rf) ultrasonic pressure oscillation. By scanning the ultrasonic beam and measuring the modulated fluorescence signal, a map of fluorophore concentration in the turbid medium can be acquired.^{1, 2, 4, 5} This technique offers ultrasound resolution even within a highly scattering optically turbid medium and thus is well suited for high-resolution and high-contrast imaging of biological tissue.^{1, 2, 3, 4, 5}

The underlying fluorescence modulation mechanism, however, has still not been completely understood. The modulation of the displacements of scatters and the refractive index of the medium caused by ultrasonic wave (eventually resulting in a change in the phase of the electrical field of a scattered photon) is usually used to explain the coherent light modulation.^{6, 7, 8, 9, 10, 11, 12, 13} However, this mechanism cannot explain fluorescence modulation because fluorescence radiation in a turbid medium should be considered as incoherent light (see Sec. 2 for detailed discussions).^{3, 6, 9, 10, 13} Krishnan et al.³ proposed a model to explain the modulation of fluorescence based on an acoustic lens assumption. In this model, the refractive index variation in the turbid medium within the ultrasound focal zone was assumed to change the propagation characteristics of the diffuse fluorescence photons. This model predicted that the maximum modulation strength of fluorescence signals occurs when the modulation region (ultrasound focal zone) is close to the fluorescent molecules or to the detector.³ However, the experimentally measured results reported by Kobayashi et al.^{1, 2} indicated that the modulation fluorescence signals were only dependent on local fluorophore concentration in the ultrasound focal zone. It was shown that if there were no fluorescent molecules around the detector the modulation signal was weak even when the modulation region was very close to the detector.^{1, 2} To address this conflict and understand the mechanisms of ultrasonic modulation fluorescence, we propose two mechanisms based on the experimental results of Kobayashi et al.^{1, 2} Because the fluorescence modulation strength is found to be related to local fluorophore concentration, it is reasonable to assume that the oscillation of ultrasonic pressure can modulate the density of microsphere and fluorophore concentrations in the turbid medium. Based on this assumption, a rate equation with a two-energy-level model is used to derive an expression for the modulation of fluorescence signal in a turbid medium without consideration of quenching effects. When the concentrations of microspheres and fluorophore are high or quenchers are adopted in a microsphere-fluorophore system, we propose a second mechanism in which the quenching efficiency is modulated as a result of the oscillation of the microsphere volume caused by ultrasonic field. Also, a method to image fluorescence lifetime is proposed.

ANALYSIS OF EXISTING ULTRASOUND-MODULATION MODELS

Before introducing mechanisms for fluorescence modulation, some discussion about the applicability of well-known ultrasound-modulated optical tomography (UMOT, nonfluorescent case) is necessary. In UMOT, the dominant mechanisms are believed to be the coherent modulation of the phases of the electric fields of diffused photons, which are generated from the modulation of the displacements of the scatters or the refractive index of the medium caused by ultrasonic wave.^{6, 7, 8, 9, 10, 11, 12, 13} The interference between the modulated and unmodulated lights converts the phase modulation to intensity modulation of the laser speckle. By detecting the modulated laser speckle, the optical properties of the medium can be extracted.^{6, 7, 8, 9, 10, 11, 12, 13} When considering the ultrasonic fluorescence modulation, the most intuitive consideration is that the modulated fluorescence might result from the modulation of the excitation light inside the medium. Currently, all theories in UMOT assume that interference that contributes to the final signal comes only outside the sample (at the detector).¹⁴ A lack of knowledge about the interference inside the turbid medium makes it difficult to provide a quantitative or even a qualitative analysis. However, to enable a general analysis, here we conceptually assume that modulated speckles of excitation light due to the phase modulation caused by the ultrasonic wave could also be formed inside the fluorescent target, and we will demonstrate that the fluorescence modulation cannot be explained by this mechanism.

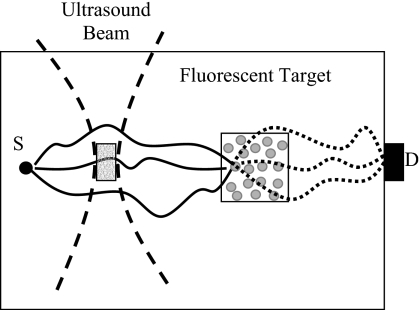
Figure 1 shows the experimental setup adopted by Kobayashi et al.^{1, 2} When the ultrasound is focused outside the fluorescent target, the modulated “speckles” from the excitation light are indicated by the gray dots inside the fluorescent target. These speckles should be able to excite the local fluorophore to emit fluorescence at the ultrasonic frequency if they do exist. However, this was not observed in the experiments of Kobayashi et al.,^{1, 2} where the modulated fluorescence signals were found only when the ultrasonic wave was focused inside the fluorescent target. The modulated fluorescence seems to be directly related to fluorophore in the focal zone of ultrasonic wave.^{1, 2} Two possible reasons can explain this conflict: (1) the excitation speckles do not exist; (2) so many speckles are formed inside the fluorescent target that the averaging among the uncorrelated speckles results in a very low averaged modulation depth at the detector.¹⁵ Note that a typical size of a laser speckle outside the medium in a typical experimental setup is in the order of 1 μm².^{9, 16} The volume of a three-dimensional speckle, which has been defined in holography, is also in the order of μm³ although it is dependent on the laser wavelength and the experimental setup.¹⁷ The volume of the fluorescent target used by Kobayashi et al.^{1, 2} was ∼3.5×10¹⁰ μm³. If we assume that these data can be used for conceptually imagining the number of speckles inside the medium, the averaged modulation depth at the detector in the experiments of Kobayashi et al.^{1, 2} would be almost zero. This is because the modulated signal at the detector is contributed from all the uncorrelated speckles by intensity superposition with random initial modulation phases. Consequently, whether modulated excitation speckles exist within the fluorescent region or not, the modulated fluorescence signal observed by Kobayashi et al.^{1, 2} should not be considered from the phase modulation of the excitation light but from an incoherent mechanism.

Figure 1.

Schematic of an experimental setup similar to that in the experiment of Kobayashi et al. (Ref. ¹). S and D represent the excitation light source and the detector. The solid curves indicate the diffused excitation photon paths and the dotted curves represent the emitted fluorescence photon paths generated from one excitation speckle. The two dashed curves represent the focused ultrasound beam

The experimental results of Kobayashi et al.^{1, 2} imply that the observed modulated fluorescence should originate from the physical interaction between the ultrasonic wave and the fluorophore in the focal zone. This implication stimulates us to reconsider the ultrasonic modulation of the scattering particles (fluorescent microspheres in the experiment of Kobayashi et al.^{1, 2}). For UMOT, Mahan et al.⁹ established a relationship between the modulations of the density and the scattering coefficient of the medium based on Brillouin scattering and quantum mechanics. Furthermore, authors believed that the variation in the scattering coefficient causes modulation of the excitation laser beam in the medium and gave an expression for the modulation efficiency in terms of the Boltzmann transport equation. For the fluorescence modulation, this mechanism will result in the modulation of the excitation light in the focal zone, which in turn excites the fluorophore to emit modulated fluorescence signals. Although this mechanism does not require the use of coherent light,¹⁰ the modulation efficiency is much lower compared with the coherent phase modulation mechanisms in UMOT.^{10, 16} How much this mechanism contributes to the modulated fluorescence signals in the experiments of Kobayashi et al.^{1, 2} remains unknown. However, we think the contribution from this mechanism may be less than the contribution from the first mechanism that will be proposed in this study, modulation of fluorophore concentration, although they essentially have the same modulation principle (density modulation). This may be because the modulation of fluorophore concentration can be directly converted into fluorescence intensity modulation. In contrast, several intermediate steps may be needed for converting the modulation of the excitation light to the modulation of the fluorescence intensity.⁹ In addition, the differences in phase of the modulation across the ultrasound focal volume may further cause cancellation of this mechanism.

MODELING

Modulation of fluorophore concentration

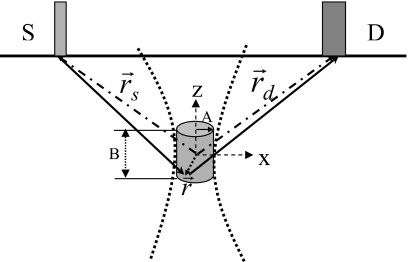
Figure 2 shows a schematic for a typical experimental setup using a reflection geometry for a semi-infinite medium. We discuss our theoretical model based on this configuration. S and D indicate the source and detector fibers, respectively, and are placed on the surface of the medium. The gray cylinder represents the focal zone of the ultrasound beam with a radius of A in the x or y directions and a length B in the z direction. The origin of the coordinate system is chosen as the center of the focal zone. We only consider the modulation of fluorophore molecules in the focal zone because the acoustic pressure in this volume is much stronger than those outside the focal zone. Following Kobayashi et al.,^{1, 2} a continuous sinusoidal voltage signal of 1 MHz frequency is assumed to drive an ultrasound transducer and generate a pressure wave in the medium. Because fluorescent microspheres were used in the experiments of Kobayashi et al.,^{1, 2} we focus our discussion on the modulation of microsphere concentration first and then convert the microsphere concentration to fluorophore concentration using a scaling factor.

Figure 2.

A schematic for theoretical analysis. The gray cylinder represents the focal zone of the ultrasonic beam. The ultrasonic beam is indicated by two bold dotted lines. The fluorophores in the focal zone interact strongly with ultrasound wave only within the focal zone. The radius of the focal zone in x-y plane is indicated as A and the length as B in z direction. $\vec{r}$ represents an arbitrary vector within the focal zone originating from origin of the coordinate system (the center of the focal zone). The two dash dotted lines with arrows indicate the positions of the light source and the detector. The two solid lines with arrows show the excitation light propagating from the source to the arbitrary position $\vec{r}$ inside the focal zone and the emitted fluorescence propagating from the position $\vec{r}$ to the detector.

The motion of microspheres in an acoustic field has been intensively investigated and three types of motions have been proposed.^{18, 19, 20, 21, 22, 23, 24} The first type of motion is position oscillation of the microsphere in response to the ultrasonic pressure variation with the ultrasonic wave frequency.¹⁸ The second type is the motion that is caused by radiation force, which has a much lower dynamic response speed relative to the rf motion and is considered as second order in magnitude relative to the first type of motion.^{19, 20, 21, 22, 23} Usually, the motion caused by the radiation force in a standing acoustic field is much stronger than in a progressive field.^{18, 19, 20, 21, 22, 23, 24} This fact explains the observed spatial pattern of the modulated fluorescence signal in the experiments of Kobayashi et al.¹ The third type of motion, common for a gas-filled microbubble, is the oscillation of microsphere radius induced by the ultrasonic field.²⁴ The frequency of this type of motion is dominated by the ultrasound frequency but, depending on the strength of ultrasonic pressure, vibration with harmonic and subharmonic frequencies may occur.²⁴

The second type of motion should not be considered for rf modulated fluorescence signals because of the low response speed. The first and the third types of motion are possible contributors to the modulated signals. When microsphere concentration and fluorophore load in each microsphere are low so that self-quenching effects (such as energy transfer from fluorescent molecules to nonfluorescent dimers) can be ignored, the rf modulation of fluorescence signal may be considered resulting from the first type of motion. As we discuss in a later section, the third type of motion does not contribute to the oscillation of macroscopic concentration if the fluorophore concentration in each microsphere is constant. However, modulation due to self-quenching may occur as the result of increased microsphere concentration (if fluorophore is labeled on the outer surface of the sphere) or fluorophore load in each microsphere (see Sec. 5 and the corresponding references). Therefore, both the first (if fluorophore is labeled on the outer surface of the microsphere) and the third types of motions are potential sources of the modulated fluorescence signals based on quenching modulation mechanism. Therefore, in Secs. 3, 4, we discuss the first modulation mechanism in which the macroscopic concentration is low, quenching effects are ignored, and the modulation of fluorescence is due to the modulation of the macroscopic concentration caused by ultrasonic pressure vibration. The detailed derivation of concentration modulation is provided in the Appendix0. In Sec. 5, we discuss the second modulation mechanism in which the quenching effects are considered as the major contributors.

According to the discussion in the Appendix0, the oscillation of microsphere concentration as a result of responding to the variation in ultrasonic pressure [see Eqs. A8, A12, A14] can be expressed as

$$n\left(r,t\right)=n_0+n_1\text{exp}i\left(kr-{\omega }_{s}t+{\varphi }_{\text{con}}\right)+\text{c}\text{.c}\text{.,}$$ (1)

where n₀ is the average microsphere concentration in the medium, n₁ is the modulation amplitude of the microsphere concentration, k and ω_s are the wave vector and angular frequency of the ultrasound wave, respectively, ϕ_con is the initial phase, and c.c. represents the complex conjugate. The oscillation of microsphere concentration further leads to the oscillation of fluorescent molecule concentration in the focal zone of the ultrasound, which can be expressed as

$$N\left(r,t\right)=N_0+N_1\left(r\right)\text{exp}\left(-i{\omega }_{s}t\right)+N_1^{\ast }\left(r\right)\text{exp}\left(i{\omega }_{s}t\right),$$ (2)

where N(r,t) is the fluorophore concentration at the time t and the position r in the focal zone. N₀ is the average fluorophore concentration in the focal zone, which is time invariant and can be viewed as the direct current (dc) component of the fluorophore distribution. N₁(r) is the complex amplitude [or alternating current (ac) component] of fluorophore concentration at position r. The modulation amplitude of fluorophore concentration N₁(r) can be expressed as a linear function of the amplitude of ultrasonic pressure P₁ [see Eqs. A14, A15 in Appendix0],

$$N_1\left(r\right)=K^{\prime }{N}_0{P}_1\text{exp}\left(ikr\right),$$ (3)

where K^′ is the factor in the curled parentheses of Eq. A14 and P₁ is the amplitude of acoustic pressure [see Eq. A3]. To convert the microsphere concentration to fluorescent molecule concentration, a scaling factor M is introduced. M is defined as the number of fluorescent molecules per microsphere; therefore N=nM. If M is considered as a constant (for example, the fluorophore does not leak outside the microsphere), macroscopic concentration oscillation [N(r,t)] is correlated with the oscillation of the number density of the microsphere. This result implies that the concentration oscillation is mainly attributed to the first type of motion.

Modulation of excitation light

As in frequency-domain diffuse optical tomography,^{25, 26, 27} we assume that a point excitation light source located at position r_s is modulated as a sinusoidal wave in intensity and the excitation photon fluence rate can be written as

$$U^{\text{ex}}\left(r_s,r,t\right)=U_0^{\text{ex}}\left(r_s,r\right)+U_1^{\text{ex}}\left(r_s,r\right)\text{exp}\left(-i{\omega }_{l}t\right)+U_1^{{\text{ex}}^{\ast }}\left(r_s,r\right)\text{exp}\left(i{\omega }_{l}t\right),$$ (4)

where U^ex(r_s,r,t) is the excitation photon fluence rate at position r and time t generated by a point source at position r_s [photons∕(s m²)]. $U_0^{\mathrm{ex}}\left(r_s,r\right)$ is the average fluence rate of the excitation light at the position r, which is time invariant and can be viewed as the dc component of the excitation light at the position r. $U_1^{\mathrm{ex}}\left(r_s,r\right)$ is the amplitude (or ac component) of the modulated excitation fluence rate at the position r. It is independent of time and is a complex value whose complex conjugate is denoted as $U_1^{{\mathrm{ex}}^{\ast }}\left(r_s,r\right)$. ω_l is the modulation angular frequency of the excitation light. According to diffusion theory,^{26, 27} we have

$$U_0^{\text{ex}}\left(r_s,r\right)=\frac{S_{\text{dc}}}{D_{\text{ex}}}{G}_0^{\text{ex}}\left(r_s,r\right),$$ (5)

$$U_1^{\text{ex}}\left(r_s,r\right)=\frac{S_{\text{ac}}}{D_{\text{ex}}}{G}_1^{\text{ex}}\left(r_s,r\right),$$ (6)

where $D_{\mathrm{ex}}=1∕\left(3{\mu }_{s\_\mathrm{ex}}^{\prime }\right)$ is diffusion coefficient at the excitation wavelength and ${\mu }_{s\_\mathrm{ex}}^{\prime }$ is the reduced scattering coefficient of the medium. S_dc and S_ac are the dc and ac strengths (or powers) of the modulated light source (photons∕s), respectively. $G_0^{\mathrm{ex}}$ and $G_1^{\mathrm{ex}}$ are Green’s functions for the dc and ac components, respectively. Two Green’s functions describe the photon propagation in the turbid medium and are determined by the specific boundary conditions.^{26, 27} For an infinite geometry, $G_0^{\mathrm{ex}}\left(r_s,r\right)=\exp \left(-k_0^{\mathrm{ex}}\mid r_s-r\mid \right)∕4\pi \mid r_s-r\mid$ and $G_1^{\mathrm{ex}}\left(r_s,r,{\omega }_l\right)=\exp \left(i{k}^{\mathrm{ex}}\mid r_s-r\mid \right)∕4\pi \mid r_s-r\mid$, where $k_0^{\mathrm{ex}}=\sqrt{3u_{\alpha \_\mathrm{ex}}{\mu }_{s\_\mathrm{ex}}^{\prime }}$ and $k^{\mathrm{ex}}=\sqrt{\left(-{\mu }_{\alpha \_\mathrm{ex}}+i{\omega }_l∕\tilde{c}\right)∕D_{\mathrm{ex}}}$, respectively. μ_{α_ex} and $\tilde{c}$ are the absorption coefficient at the excitation wavelength and the light speed in the medium, respectively.

Modulation of emission light

When the modulated excitation light reaches the focal zone where fluorophore concentration is oscillated by the ultrasound wave, the fluorescence emission source at the position r in the focal zone can be expressed as^{26, 28}

$$S^{\text{fl}}\left(r_s,r,t\right)=\varphi \Gamma N_e\left(r,t\right),$$ (7)

where S^fl(r_s,r,t) is the emission strength by fluorophores at position r and time t [photons∕(s m³)]. ϕ is the quantum efficiency of the fluorophore. Γ is the total decay rate from excited state to ground state including radiative and nonradiative decay rates. The lifetime of the fluorophore is defined as the inverse of Γ (τ=1∕Γ). N_e(r,t) is the number of the excited fluorophores at position r and time t. For simplicity, a rate equation with a two-energy-level model is adopted to solve for N_e(r,t),^{26, 28}

$$\frac{\partial N_e\left(r,t\right)}{\partial t}=-\Gamma N_e\left(r,t\right)+\epsilon U^{\text{ex}}\left(r_s,r,t\right)\left[N\left(r,t\right)-N_e\left(r,t\right)\right],$$ (8)

where ε is absorption cross section of the dye at the excitation wavelength. Generally, the number of the excited fluorescent molecules is much lower than the number of fluorescent molecules in the ground state, which indicates that we can neglect the second term, N_e(r,t), in the square bracket.²⁶ It is clear that Eq. 8 is a nonlinear equation because both U^ex(r_s,r,t) and N(r,t) are time variant. Therefore, we expect additional components with frequencies different from both the modulation frequencies of light (ω_l) and ultrasound (ω_s) occur. Inserting Eqs. 2, 4 into Eq. 8 and equating the coefficients of zero-order, first-order, and second-order terms at the two sides of the equation, we obtain the solution of N_e(r,t). Substituting the solution of N_e(r,t) into Eq. 7, we obtain

$$S^{\text{fl}}\left(r_s,r,t\right)=\epsilon \varphi U_0^{\text{ex}}\left(r_s,r\right)N_0+\frac{\epsilon \varphi U_1^{\text{ex}}\left(r_s,r\right)N_0}{1-i{\omega }_l\tau }\text{exp}\left(-i{\omega }_{l}t\right)+\text{c}\text{.c}\text{.}+\frac{\epsilon \varphi U_0^{\text{ex}}\left(r_s,r\right)N_1\left(r\right)}{1-i{\omega }_s\tau }\text{exp}\left(-i{\omega }_{s}t\right)+\text{c}\text{.c}\text{.}+\frac{\epsilon \varphi U_1^{\text{ex}}\left(r_s,r\right)N_1\left(r\right)}{1-i\left({\omega }_l+{\omega }_s\right)\tau }\text{exp}\left[-i\left({\omega }_l+{\omega }_s\right)t\right]+\text{c}\text{.c}\text{.}+\frac{\epsilon \varphi U_1^{\text{ex}}\left(r_s,r\right)N_1^{\ast }\left(r\right)}{1-i\left({\omega }_l-{\omega }_s\right)\tau }\text{exp}\left[-i\left({\omega }_l-{\omega }_s\right)t\right]+\text{c}\text{.c}\text{.}$$ (9)

Considering the propagation of the emitted light from the position r to the detector position D in Fig. 2,^{26, 27} we obtain

$$U^{\text{fl}}\left(r_s,r_d,{\omega }_i,t\right)={\int }_{\Omega }\frac{S^{\text{fl}}\left(r_s,r,{\omega }_i,t\right)}{D_{\text{fl}}}{G}^{\text{fl}}\left(r,r_d,{\omega }_i\right)d{r}^3,$$ (10)

where U^fl(r_s,r_d,ω_i,t) is the fluorescence fluence rate at the detector position r_d and time t [photons∕(s m²)] with the modulation frequency ω_i. The modulation frequency ω_i represents any frequency component in Eq. 9. $D_{\mathrm{fl}}=1∕\left(3{\mu }_{s\_\mathrm{fl}}^{\prime }\right)$ is the diffusion coefficient at the emission wavelength and ${\mu }_{s\_\mathrm{fl}}^{\prime }$ is the reduced scattering coefficient of the medium at the emission wavelength. G^fl is the Green’s function describing the propagation of the emission light in the turbid medium and it depends on the boundary condition.^{26, 27} For an infinite geometry, G^fl(r,r_d,ω_i)=exp(ik_fl∣r_d−r∣)∕4π∣r_d−r∣, where $k^{\mathrm{fl}}=\sqrt{\left(-{\mu }_{\alpha \_\mathrm{fl}}+i{\omega }_i∕\tilde{c}\right)∕D_{\mathrm{fl}}}$, μ_{α_fl} is the absorption coefficient of the medium at the emission wavelength. Ω is the integral volume, which is identical to the volume of the focal zone for the third, fourth, and fifth terms and to the volume of the fluorescent target for the first and second terms that are not modulated by the ultrasound signal. Because Eq. 10 is a linear equation with respect to time, one can separately insert each term in Eq. 9 into Eq. 10 and calculate the corresponding components of the fluorescent fluence rates.

ANALYSIS AND DISCUSSION

The first term on the right-hand side of Eq. 9 represents the dc fluorescence signal and the second term describes the fluorescence signal oscillating with the modulation frequency of the light (ω_l). These two signals do not relate to the ultrasonic modulation, so they cannot be differentiated from the signals with the same frequency but generated from the volume outside the focal zone. Therefore, these two components should be filtered out experimentally. The remaining three components include the ultrasound information, which means they can be generated only from the focal zone and each of them can be used to extract the information about the fluorescent molecules in the focal zone.

Extracting fluorophore concentration and lifetime distributions is particularly interesting because they are usually related to some physiological states and biological environments of tissue.²⁸ The third term in Eq. 9 represents the modulated fluorescence signal with ultrasound frequency ω_s, and the fourth and the fifth terms describe the modulated signals with the sum frequency (ω_l+ω_s) and the difference frequency (ω_l−ω_s) between the light modulation frequency ω_l and the ultrasound frequency ω_s. Inserting the third, the fourth, and the fifth terms of Eqs. 3, 9 into Eq. 10, we obtain

$$U^{\text{fl}}\left(r_s,r_d,{\omega }_s,t\right)=\frac{\epsilon \varphi S_{\text{dc}}}{D_{\text{ex}}{D}_{\text{fl}}\left[1-i{\omega }_s\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_0^{\text{ex}}\left(r_s,r\right)\text{exp}\left(i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_s\right)dr\right]\text{exp}\left(-i{\omega }_{s}t\right),$$ (11)

$$U^{\text{fl}}\left(r_s,r_d,{\omega }_l+{\omega }_s,t\right)=\frac{\epsilon \varphi S_{\text{ac}}}{D_{\text{ex}}{D}_{\text{fl}}\left[1-i\left({\omega }_l+{\omega }_s\right)\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l+{\omega }_s\right)dr\right]\text{exp}\left[-i\left({\omega }_l+{\omega }_s\right)t\right],$$ (12)

$$U^{\text{fl}}\left(r_s,r_d,{\omega }_l-{\omega }_s,t\right)=\frac{\epsilon \varphi S_{\text{ac}}}{D_{\text{ex}}{D}_{\text{fl}}\left[1-i\left({\omega }_l-{\omega }_s\right)\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(-i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l-{\omega }_s\right)dr\right]\text{exp}\left[-\left(i{\omega }_l-{\omega }_s\right)t\right].$$ (13)

As pointed out by Haskell et al.,²⁹ the measured signal by an optical fiber placed at the surface of the semi-infinite medium can be expressed as

$${\text{signal}}^{\text{fl}}\left(r_s,r_d,\omega \right)=\Theta \int {\int }_{A\text{fiber}}dA\int {\int }_{\Omega \text{fiber}}d\Omega \frac{1}{4\pi }\left(U^{\text{fl}}\left(r_s,r_d,\omega \right)+3D_{\text{fl}}\frac{\partial U^{\text{fl}}\left(r_s,r_d,\omega \right)}{\partial z}\text{cos}\theta \right)\text{cos}\theta ,$$ (14)

where Θ is the gain of the optical filter that is used to collect the fluorescent emission (reject excitation light) and is dimensionless, Afiber represents the effective detecting area of the fiber, and Ωfiber is the collection solid angle of the fiber depending on the numerical aperture of the fiber. The unit of the measured fluorescence signal is photons∕s. As an example, if a detector with 180° acceptance angle and an effective collection area of α is used and the air∕tissue refractive index mismatch is 1∕1.4, Eq. 14 becomes^{30, 31}

$${\text{signal}}^{\text{fl}}\left(r_s,r_d,\omega \right)=0.165\Theta \alpha U^{\text{fl}}\left(r_s,r_d,\omega \right).$$ (15)

In the derivation of Eq. 15, an extrapolated boundary condition is adopted,^{29, 30, 31} and the U^fl(r_s,r_d) is assumed to uniformly distributed over the effective collection area α if α is small. From Eqs. 11, 12, 13, 14, 15, three dimensionless quantities can be defined as follows to describe the relative modulation strengths of fluorescence signals:

$$\frac{{\text{signal}}^{\text{fl}}\left(r_s,r_d,{\omega }_s\right)}{S_{\text{dc}}}=\frac{0.165\Theta \alpha \epsilon \varphi }{D_{\text{ex}}{D}_{\text{fl}}\left[1-i{\omega }_s\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_0^{\text{ex}}\left(r_s,r\right)\text{exp}\left(i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_s\right)dr\right]\text{exp}\left(-i{\omega }_{s}t\right),$$ (16)

$$\frac{{\text{signal}}^{\text{fl}}\left(r_s,r_d,{\omega }_l+{\omega }_s,t\right)}{S_{\text{ac}}}=\frac{0.165\Theta \alpha \epsilon \varphi }{D_{\text{ex}}{D}_{\text{fl}}\left[1-i\left({\omega }_l+{\omega }_s\right)\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l+{\omega }_s\right)dr\right]\text{exp}\left[-i\left({\omega }_l+{\omega }_s\right)t\right],$$ (17)

$$\frac{{\text{signal}}^{\text{fl}}\left(r_s,r_d,{\omega }_l-{\omega }_s,t\right)}{S_{\text{ac}}}=\frac{0.165\Theta \alpha \epsilon \varphi }{D_{\text{ex}}{D}_{\text{fl}}\left[1-i\left({\omega }_l-{\omega }_s\right)\tau \right]}\left(K^{\prime }{P}_1{N}_0\right)\left[{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(-i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l-{\omega }_s\right)dr\right]\text{exp}\left[-i\left({\omega }_l-{\omega }_s\right)t\right].$$ (18)

Equations 16, 17, 18 describe the modulation strengths of fluorescence signals relative to the power of the original incident light (excitation light) at the three different frequencies and have similar structures. Four factors are present on the right-hand side expression of each equation. The first factor, 0.165Θαεϕ∕D_exD_fl[1−iω_sτ] [in Eq. 16], 0.165Θαεϕ∕D_exD_fl[1−i(ω_l+ω_s)τ] [in Eq. 17], and 0.165Θαεϕ∕D_exD_fl[1−i(ω_l−ω_s)τ] (in Eq. 18), has units of m² and depends on the optical properties of the medium, the fluorescent dye, and the measurement system. The second factor, (K^′P₁N₀), is same for all the three equations and represents the strength of the ultrasonic wave, ultrasonic properties of the medium, and the fluorophore concentration with units of m⁻³. The third factors (the integral terms) describe excitation and emission photon propagation in the turbid medium, which are determined by the geometry of light source and detector and the ultrasonic focal zone and possess units of meter. The last factors are dimensionless complex harmonic functions that indicate the oscillations of fluorescence signals relative to time with different frequencies. For a fluorophore with lifetime less than 10 ns, an excitation light source with 140 MHz modulation frequency and ultrasound with 1 MHz frequency, the following relationships hold: ∣1−iω_sτ∣≈1 and 1<∣1−i(ω_l+ω_s)τ∣≈∣1−i(ω_l−ω_s)τ∣<10. Therefore, the amplitude of the modulated signal with frequency (ω_l+ω_s) has similar magnitude to the signal with frequency (ω_l−ω_s), and both of them are weaker than the modulated signal with the frequency ω_s if the S_dc is close to the S_ac. In the experiments of Kobayashi et al.,^{1, 2} the excitation light is a continuous light source, which means S_ac=0 and ω_l=0. Consequently, only the signal described by Eq. 16 exists.

Modulation strength

Quantification of the modulation strength is important for understanding the modulation mechanism. From Eq. 16, one can see that the modulated fluorescence signal with the frequency ω_s is proportional to the local average fluorophore concentration N₀, which is in agreement with the experimental measurements,^{1, 2} and also proportional to the amplitude of the ultrasound pressure P₁. The model of Krishnan et al.³ predicts the same linear relationship between the modulation strength and the pressure amplitude P₁.³ However, the measurements of Kobayashi et al.^{1, 2} showed a quadratic relation between the modulation strength and the pressure P₁. This discrepancy implies that multiple modulation mechanisms may exist as will be discussed in Sec. 5. While N₀ and P₁ can be controlled by experiments, K^′, another key quantity to determine the modulated signal strength, is a parameter that is determined by the medium and the micro-sphere system [K^′ is the factor in the curled parentheses of Eq. A14], which can be quantified based on the parameters listed in both Tables 1, 2. The integral term in Eq. 16 is related to specific experimental setup and boundary condition. In this study a semi-infinite geometry with an extrapolated boundary condition is adopted,^{26, 27, 29} which is a typical setup for biomedical imaging applications (see Fig. 2). The specific parameters for the integral are given in Table 2. As an example, we locate the center of the focal zone midway between the source and detector and set the depth of the focal zone as 0.4 cm. According to the parameters given in Tables 1, 2, the ratio on the left-hand side of Eq. 16 (the ratio of modulated fluorescence signal to the amplitude of dc component of the excitation light S_dc) is on the order of 10⁻⁶–10⁻⁸ depending on the pressure intensity with assumptions of α=0.65 cm² and Θ=1. With a 60 mW excitation light as adopted in the experiments of Kobayashi et al.,¹ a 0.6–60 nW modulated fluorescence signal is predicted based on our calculations. Optical signal with this intensity range is readily detectable using highly sensitive photodetectors (such as photomultiplier tubes) after filtering of the strong excitation light. The experimental challenge is separation of the effect of the unmodulated fluorescence signal on the modulated fluorescence signal because it cannot be filtered out using an optical filter in front of the photodetector. The unmodulated fluorescence signal is described by the first term on the right-hand side of Eq. 9. Inserting it into Eq. 10 and following the same steps to analyze the intensity of unmodulated light, we can calculate the ratio of the unmodulated fluorescence intensity to the intensity of the excitation light (S_dc) and it is on the order of 10⁻². Therefore, the ratio of the modulated fluorescence intensity to the unmodulatedfluorescence intensity falls in the range of 10⁻⁴–10⁻⁶. However, this ratio will be further reduced if the unmodulated signals contributed from fluorophore outside the focal zone are considered. To detect the relatively weak modulated fluorescence signal, shot noise (usually with wide bandwidth) generated by the strong unmodulated fluorescence signal should be reduced through signal averaging or narrow electronic filters such as employed in spectrum analyzers.

Table 1.

Parameters of the microsphere inclusion and the turbid medium. (a) ρ_p and ρ₀ are the density of microspheres and the turbid medium, respectively (Ref. ³²). (b) a is the radius of the microsphere (Ref. ³²). (c) N₀ is the average fluorophore concentration which is equal to the average microsphere concentration multiplied by the number of fluorophores per microsphere (Ref. ³²). (d) ε and ϕ are the absorption cross section and quantum efficiency of fluorescent, respectively (Ref. ³³). (e) γ and β are the kinematic viscosity and compressibility of the turbid medium, respectively (Refs. ²³, ³⁴). (f) P₁ and c are the amplitude of pressure and the speed of the ultrasound wave (Refs. ¹, ³⁵).

ρ=ρp∕ρ0	a (μm)	γ (cm2/s)	β (m2/N)	N0 (1/m3)	ε (cm2)	ϕ	P1 (Pa)	(m/s)
1.05/1.0	0.1	0.05	4.5×10−10	3.6×1022	3×10−16	0.99	5×104–5×106	1550

Table 2.

Optical parameters of the turbid medium and the ultrasound beam. The refractive index of the medium is considered as 1.33. The subscripts of “ex” and “fl” represent the values at excitation wavelength and fluorescence (emission) wavelength, respectively. The ultrasound focal zone is modeled as a cylinder of radius “A” and of length “B”.

Medium parameters(1/cm)				Ultrasound focus size(cm)		Distance between source and detector(cm)
μα_ex	${\mu }_{s\_\text{ex}}^{\prime }$	μα_fl	${\mu }_{s\_\text{fl}}^{\prime }$	Radius (A)	Length (B)
0.04	6.5	0.03	7.0	0.15	1.0	1.0

Fluorescence lifetime

As mentioned above, the fluorophore concentration and lifetime are the most important parameters in fluorescence imaging. From Eqs. 17, 18 we realize that the fluorophore lifetime within the focal zone can be extracted by the ratio of Eqs. 17, 18. The ratio and its first-order derivative with respect to lifetime can be expressed as

$$R=\mid \frac{{\text{signal}}^{\text{fl}}\left(r_s,r_d,{\omega }_l+{\omega }_s,t\right)}{{\text{signal}}^{\text{fl}}\left(r_s,r_d,{\omega }_l-{\omega }_s,t\right)}\mid =\sqrt{\frac{1+{\left({\omega }_l-{\omega }_s\right)}^2{\tau }^2}{1+{\left({\omega }_l+{\omega }_s\right)}^2{\tau }^2}}\mid \frac{{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l+{\omega }_s\right)dr}{{\int }_{\Omega }{G}_1^{\text{ex}}\left(r_s,r,{\omega }_l\right)\text{exp}\left(-i{k}_{s}r\right)G^{\text{fl}}\left(r,r_d,{\omega }_l-{\omega }_s\right)dr}\mid ,$$ (19)

$$\frac{dR}{d\tau }=\frac{1}{2}\sqrt{\frac{1+{\left({\omega }_l+{\omega }_s\right)}^2{\tau }^2}{1+{\left({\omega }_l-{\omega }_s\right)}^2{\tau }^2}}\left[\frac{2\tau {\left({\omega }_l-{\omega }_s\right)}^2\left[1+{\left({\omega }_l+{\omega }_s\right)}^2{\tau }^2\right]-2\tau {\left({\omega }_l+{\omega }_s\right)}^2\left[1+{\left({\omega }_l-{\omega }_s\right)}^2{\tau }^2\right]}{{\left[1+{\left({\omega }_l+{\omega }_s\right)}^2{\tau }^2\right]}^2}\right]I\left(r_s,r,r_d,{\omega }_l,{\omega }_s\right).$$ (20)

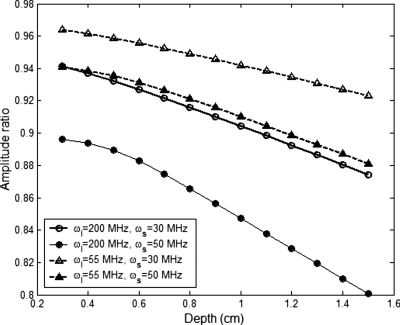
A structural factor, I(r_s,r,r_d,ω_l,ω_s), is defined in Eq. 20, which is the amplitude of the ratio between the two integrals in Eq. 19. This structural factor is weakly related to the distance between the light source and the ultrasound focal zone and the distance from the focal zone to the detector. Also it is weakly dependent on the modulation frequency of light and the ultrasound frequency. Figure 3 provides a numerical result for I(r_s,r,r_d,ω_l,ω_s) as a function of the focal zone depth. Generally, the structural factor is close to 1 and slightly decreases with the increase in the focal zone depth. When increasing the light modulation frequency or the ultrasound frequency, the structural factor decreases. We also found that the ratio approaches to 1 either when the ultrasound frequency is low or when the light modulation frequency is low (see the following discussion). When I(r_s,r,r_d,ω_l,ω_s) is close to 1, it may be ignored for convenience. Equation 19 implies that R can be used to measure the lifetime of fluorescent molecules in the ultrasound focal zone. Therefore, one can expect to map the distribution of the fluorophore lifetime of a sample by scanning the system in the area of interest.

Figure 3.

The amplitude of the ratio between the two integrals in Eq. 19 as a function of the depth of ultrasound focal zone.

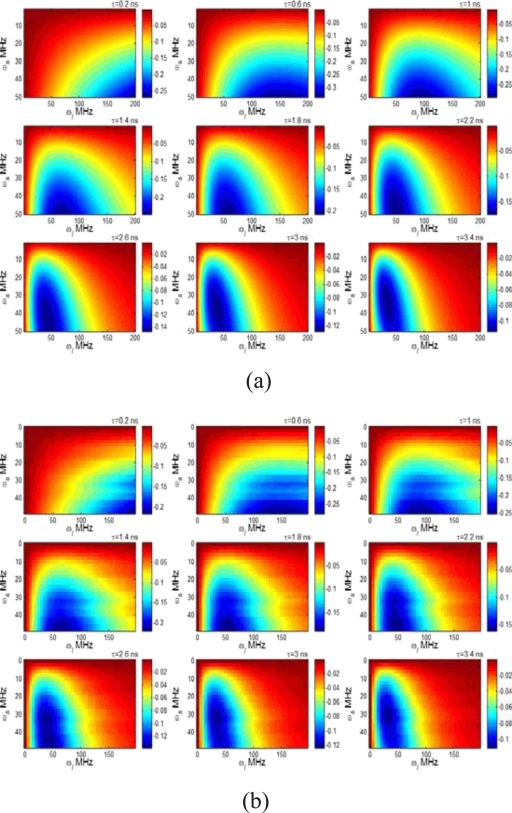
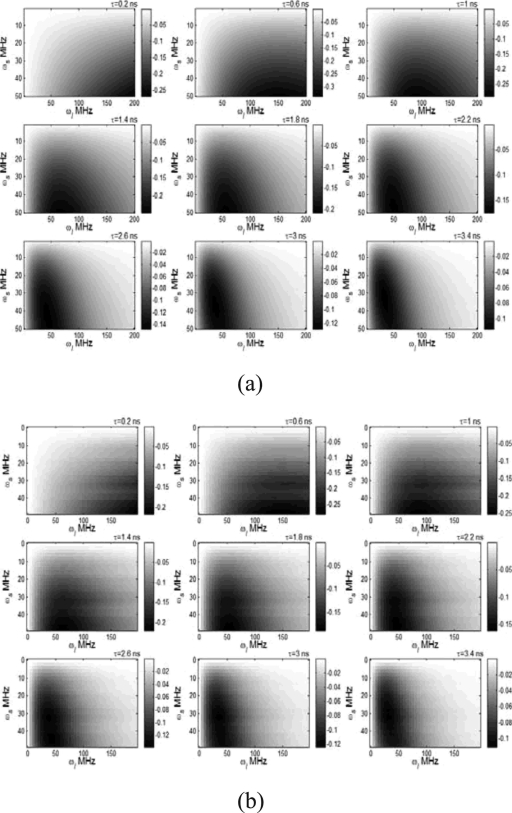
In order to investigate the sensitivity of R to lifetime τ, we swept the ultrasound frequency ω_s from 0.1 to 50 MHz and the light modulation frequency ω_l from 0.1 to 200 MHz and calculated the first-order derivative of R with respect to lifetime in terms of Eq. 20 for different lifetimes. Figures 4a, 4b show the results when ignoring and including the structural factor in the calculation, respectively. The depth of the ultrasound focal zone is 1 cm in Fig. 4b. The horizontal and vertical axes represent the light modulation frequency and the ultrasound frequency, respectively. The color indicates the value of dR∕dτ with unit of 1/ns, which represents how much R changes when the lifetime increases 1 ns. Negative value of dR∕dτ means the increase in lifetime causes the decrease in R. Figure 4a indicates that the most sensitive area (the most negative area) is around the line of ω_l=ω_s. However, light with high modulation frequency is more sensitive to the short lifetime. In practice ω_l and ω_s cannot be chosen to be equal. Otherwise, the difference frequency will be zero so that the signal reduces to dc signal that cannot be differentiated from the background fluorescence signals. In comparison with Fig. 4a, Fig. 4b shows slightly lower value for dR∕dτ, which is caused by the structural factor. The distribution of dR∕dτ in ω_l-ω_s plane was distorted; however, the most sensitive area was similar with that in Fig. 4a. In the calculation in Fig. 4b, low frequency resolutions were adopted for effective computation and ∣ω_l-ω_s∣ was used in Green’s function, G^fl(r,r_d,ω_i), to avoid negative frequency. In practice, ω_s may be limited lower than ω_l.

Figure 4.

The first-order derivative of R with respect to lifetime as a function of ultrasound frequency and light modulation frequency at different lifetimes: (a) the structural factor was ignored in the calculation and (b) the structural factor was included in the calculation (the depth of ultrasound focal zone is 1.0 cm). The lifetime value is shown on the upper-right corner of each image. The value of dR∕dτ is mapped to the color with unit of 1∕ns.

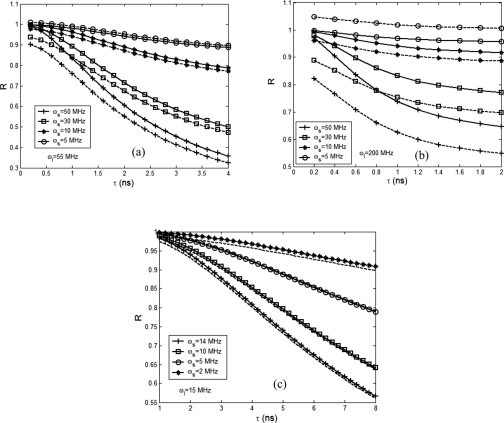
On the other hand, we calculated R as a function of lifetime τ and showed in Fig. 5. Figures 5a, 5b correspond to ω_l=55 MHz and ω_l=200 MHz, respectively, while the values for ω_s are same for both figures. The depth of the ultrasound focal zone is 1.0 cm. All the solid lines in Figs. 5a, 5b, 5c were calculated by ignoring the structural factor I(r_s,r,r_d,ω_l,ω_s) and the dashed lines show the corresponding results without neglecting the structural factor. Figure 5b indicates that the structural factor may not be ignored when the light modulation frequency is high. In contrast, Fig. 5c implies the factor may be ignored for convenience when the light frequency is low. Figure 5a shows that when the ultrasound frequency is close to the light modulation frequency, the structural factor needs to be considered. When ω_s=50 MHz, Fig. 5a provides a linear dynamic range from ∼0.6 to 2 ns while Fig. 5b shows a linear dynamic range when τ<0.8 ns. This result indicates that high modulation frequency is suitable for detecting short fluorescence lifetime. Also, both figures show that the sensitivity of R to lifetime is increasingly improved when ω_s approaches to ω_l. To study the sensitivity and linearity of R to lifetime at low ultrasonic frequencies, we varied ω_s from 2 to 14 MHz and maintained ω_l as a constant of 15 MHz. The results are shown in Fig. 5c. When the lifetime is greater than ∼2 ns, a linear relationship between R and lifetime exists. In comparison with Figs. 5a, 5b, Fig. 5c shows a lower sensitivity of R to lifetime.

Figure 5.

R as a function of lifetime when the ultrasound beam is focused at a depth of 1.0 cm: (a) ω_l=55 MHz, (b) ω_l=200 MHz, and (c) ω_l=15 MHz. All the solid lines are calculated by ignoring the structural factor and the dashed lines with the structural factor.

QUENCHING MODULATION MECHANISMS

Quenching can occur when quenchers are adopted^{36, 37} or when microsphere concentration and∕or fluorophore concentration loaded in each microsphere are relatively high.^{38, 39} Depending on the specific microsphere-fluorophore system, the quenching can be self-quenching or quenching caused by the quenchers. Quenching mechanisms may involve dynamic collisional quenching and∕or fluorescence resonance energy transfer (FRET).^{28, 36, 37, 38, 39} Quenching can occur on the outer surfaces^{36, 37, 38} or the inner³⁹ volume of microspheres depending on the fluorophore labeling locations. By ultrasonically modulating quencher concentration or the distance between the fluorophore and its quencher and hence the quenching efficiency, the fluorescence intensity can be modulated.

Collisional quenching

It has been found that polystyrene microspheres in tissue-simulating phantoms can collisionally quench fluorophores that are mixed with microspheres and the quenching efficiency is correlated with the concentration of microspheres.^{40, 41} Based on these results, we infer that the position vibration of the microsphere induced by the ultrasonic field [the first type particle motion (see Sec. 3A)] can lead to the modulation of quenching efficiency via the modulation of macroscopic microsphere concentration if fluorophores are labeled on the outside surface of the microsphere.³⁸ Consequently, Eq. 7 can be rewritten as

$$S^{\text{fl}}\left(r_s,r,t\right)=\frac{\varphi \Gamma N_e\left(r,t\right)}{\left(1+k_q\tau \left[Q\right]\right)},$$ (21)

where k_q is the bimolecular quenching constant, τ is the lifetime of the fluorophore in the absence of quencher, and [Q] is the quencher concentration. Note that ϕ, Γ, and N_e should be considered as the quantities in the absence of quenching. The modulation of [Q] can be similarly described by Eqs. 2, 3 as discussed in Sec. 3A.

FRET quenching

It has been reported that self-quenching occurs when fluorophores are labeled on a resin bead surface and the quenching efficiency is related to the surface concentration of fluorophores.³⁸ Also, when fluorophores (such as fluorescent) are encapsulated in liposomes, energy transfer to nonfluorescent dimers occurs and the quenching efficiency is highly dependent on fluorophore concentration.³⁹ These results imply that for those microspheres loaded with high concentrations of fluorophore and oscillated in radius induced by ultrasound pressure (the third type of motion) the fluorescence modulation may originate from the modulation of quenching efficiency if quenchers exist or nonfluorescent dimers can be formed. Considering FRET quenching, Eq. 21 can be modified as

$$S^{\text{fl}}\left(r_s,r,t\right)=\varphi \Gamma N_e\left(r,t\right)\left(1-\frac{1}{1+{\left(r∕{\tilde{R}}_0\right)}^6}\right).$$ (22)

Note that ϕ, Γ, and N_e should be considered as the quantities in the absence of quenching. r is the distance between the fluorescent molecule and its quencher. ${\tilde{R}}_0$ is the the Förster distance corresponding to the distance at which the lifetime is reduced to 50% relative to the natural lifetime.⁴² The distance r between two molecules (or between the fluorophore and its quencher) is modulated by ultrasonic pressure via the oscillation of the radius of the microsphere and can be expressed as

$$r=C{R}_0\left(1+\frac{\Delta R}{R_0}\right).$$ (23)

R₀ is the equilibrium radius of the microsphere and ΔR is the change in radius of microsphere induced by ultrasonic pressure. When there is no ultrasound applied, ΔR=0 and the equilibrium distance between two molecules is indicated as r₀=CR₀. C is a constant and equals to $\sqrt{4\pi ∕M}$ when fluorophores and quenchers are labeled on the outer surface and equals to 2∕M^1∕3 when fluorophores and quenchers are loaded in the microsphere. M is the total number of fluorophore and quenchers labeled on or loaded in each microsphere. Two assumptions are adopted in the derivation of C: fluorophore and quenchers are considered as spheres and they are homogenously and equally distributed on or in the microsphere.

For a hollow polymeric microsphere insolated with low power ultrasonic wave, the relationship between the radius change and the amplitude of ultrasonic pressure P₁ may be expressed as⁴³

$$\Delta R=C^{\prime }{P}_1\text{sin}\left({\omega }_{s}t+{\varphi }_c\right),$$ (24)

where C^′ and ϕ_c are constants and can be found in Eq. 13 of Ref. 43. Inserting Eqs. 23, 24 into Eq. 22, the modulation of fluorescence may be expressed as a power function of ultrasonic pressure amplitude P₁,

$$S^{\text{fl}}\left(r_s,r,t\right)=\varphi \Gamma N_e\left(r,t\right)\left(1-\frac{1}{1+{\left\{\left[C{R}_0+C{C}^{\prime }{P}_1\text{sin}\left({\omega }_{s}t+{\varphi }_c\right)\right]∕{\tilde{R}}_0\right\}}^6}\right).$$ (25)

Numerical simulation indicates that the power depends strongly on the equilibrium distance r₀. When $r_0={\tilde{R}}_0$, the modulated fluorescence strength changes as a function of the pressure amplitude P₁ with a power 3. When $r_0>{\tilde{R}}_0$, the power is less than 3, and when $r_0<{\tilde{R}}_0$, the power is between 3 and 6. Because r₀ is directly determined by M, the number of fluorophore and quenchers labeled on or loaded in each microsphere, the specific relationship between the modulated fluorescence and applied ultrasound intensity may be highly dependent on experimental conditions. This result may partially explain the quadratic relationship measured by Kobayashi et al.^{1, 2} Further experiments with well-controlled experimental parameters are needed to validate this mechanism.

CONCLUSION

We proposed two mechanisms to explain the ultrasonically modulated fluorescence signal in turbid media. The modulation of fluorophore concentration caused by the ultrasonic pressure is considered as the source of the modulated fluorescence signal at low fluorophore concentrations. By solving the rate equation and the photon diffusion equation, a quantitative solution to the modulation strength of the fluorescence signal generated from the ultrasound focal zone was derived. The model indicates that the modulated fluorescence signal is proportional to the average fluorophore concentration in the ultrasound focal zone. To quantify the modulated signal strength, calculations based on the parameters provided in literature were performed and the results indicate that the modulation depth (the ratio of the modulated signal to the unmodulated signal) can reach 10⁻⁴–10⁻⁶ when the ultrasound pressure is in the order of 10⁶–10⁴ Pa (based on the parameters used in this study). Such a signal level is detectable if appropriate detecting systems are adopted.

When fluorophore concentration is high so that fluorescence quenching occurs or when quenchers are adopted, a fluorescence contribution due to the modulation of quenching efficiency caused by the oscillation of the microsphere radius can occur. Collisional quenching and FRET quenching were presented as possible mechanisms responsible for the fluorescence modulation. A nonlinear relationship between the modulation strength and the applied ultrasound amplitude was found when FRET is considered as the major quenching mechanism.

Recently, microbubbles were proposed to replace the polystyrene microspheres to increase the compressibility under ultrasonic field.^{36, 37} It has been reported that a microbubble with a lipid shell has much higher compressibility than the hollow polymeric microbubble.^{24, 43} This result indicates that the fluorescence modulation efficiency may be significantly improved when using microbubbles. A detailed study on this topic will be performed in the future.

APPENDIX

Based on fundamentals of acoustic wave propagation in a fluid, the acoustic pressure can be expressed as follows:³⁵

$${\nabla }^{2}P=\frac{1}{c^2}\frac{{\partial }^{2}P}{\partial t^2},$$ (A1)

where P is acoustic pressure and c is the speed of pressure wave. The relationship between fluid velocity and pressure can be express as

$${\rho }_0\frac{\partial \vec{u}}{\partial t}=-\nabla P,$$ (A2)

where ρ₀ is the average density of fluid and $\vec{u}$ s the fluid velocity. For simplicity, we limit the pressure solution of Eq. A1 to a plane wave, which can be written as

$$P=P_0+P_1\text{exp}i\left(kr-{\omega }_{s}t\right)+\text{c}\text{.c}\text{.,}$$ (A3)

where c.c. represents complex conjugate, P₀ and P₁ are average pressure and the amplitude of the pressure oscillation, and k and ω_s are the wave vector and the angular frequency of the pressure wave, respectively. Based on the linear relationship between the pressure and fluid velocity, which is expressed as

$$u_1=\frac{P_1}{{\rho }_{0}c},$$ (A4)

the fluid velocity can be written as

$$\vec{u}={\vec{u}}_0+{\vec{u}}_1\text{exp}i\left(kr-{\omega }_{s}t\right)+\text{c}\text{.c}\text{.}$$ (A5)

Based on Mei’s theory,⁸ for the first type of motion, the velocity of the motion of the microsphere in the fluid caused by the ultrasonic field exhibits a low pass characteristic, which can be expressed as

$$\vec{v}=\frac{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{2}{3}{\tilde{\epsilon }}^2\right]}{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{4}{9}\left(\rho +1∕2\right){\tilde{\epsilon }}^2\right]}\vec{u},$$ (A6)

where $\tilde{\epsilon }=\sqrt{{\omega }_s{a}^2∕2\gamma }$, a is the radius of the microsphere, γ is fluid kinematic viscosity, and ρ=ρ_p∕ρ₀ is the ratio between the density of the microsphere and the average density of the fluid. The concentration of the microsphere n can be related to microsphere velocity $\vec{v}$ by the following continuity equation²⁰:

$$\frac{\partial n}{\partial t}+\nabla \cdot \left(n\vec{v}\right)=0,$$ (A7)

Following the same linearization rule, the concentration of the microsphere is written as

$$n=n_0+n_1\text{exp}i\left(kr-{\omega }_{s}t+{\varphi }_{\text{con}}\right)+\text{c}\text{.c}\text{.}$$ (A8)

Inserting Eqs. A6, A8 into Eq. A7, the amplitude of the concentration oscillation n₁ can be expressed as

$$n_1=\frac{k{n}_0}{k{v}_0-\omega }{v}_1,$$ (A9)

where k is the ultrasound wave vector and v₀ and v₁ are the average velocity of the microsphere and the oscillation amplitude of the microsphere velocity, respectively. Based on Eqs. A6, A4, v₀ and v₁ can be written as

$$v_0=u_0=\frac{P_0}{{\rho }_{0}c},$$ (A10)

$$v_1=\frac{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{2}{3}{\tilde{\epsilon }}^2\right]}{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{4}{9}\left(\rho +1∕2\right){\tilde{\epsilon }}^2\right]}{u}_1.$$ (A11)

Inserting Eq. A11 into Eq. A9, the amplitude of the concentration oscillation n₁ can be written as

$$n_1=\frac{k{n}_0}{k{v}_0-{\omega }_s}\cdot \frac{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{2}{3}{\tilde{\epsilon }}^2\right]}{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{4}{9}\left(\rho +1∕2\right){\tilde{\epsilon }}^2\right]}\frac{P_1}{{\rho }_{0}c}.$$ (A12)

From this equation, a linear relationship between n₁ and P₁ (the amplitude of pressure oscillation) is established. Further, if the fluid is compressible, an additional concentration change caused by the volume change in the fluid can be included based on the following discussion:

$$n_1^{\prime }=n-n_0=\frac{N_0^{\prime }+\Delta N^{\prime }}{V_0-\Delta V}-\frac{N_0^{\prime }}{V_0}=\frac{\Delta N^{\prime }{V}_0+N_0^{\prime }\Delta V}{\left(V_0-\Delta V\right)V_0}=\frac{\Delta N^{\prime }}{\left(V_0-\Delta V\right)}+n_0\frac{\Delta V}{\left(V_0-\Delta V\right)}\approx \frac{\Delta N^{\prime }}{V_0}+n_0\beta P_1=n_1+n_0\beta P_1,$$ (A13)

where $n_1^{\prime }$ is the total oscillation amplitude of the microsphere concentration caused by both microsphere oscillation and volume changes in the fluid, $N_0^{\prime }$ is the average microsphere number in volume V₀, ΔN^′ is the change in the number of microspheres in the volume V₀, ΔV is the volume change caused by acoustic pressure, and β is the compressibility of the fluid. Inserting Eq. A12 into Eq. A13, the oscillation amplitude of the microsphere concentration relative to the average microsphere concentration is written as

$$n_1^{\prime }=\left\{\frac{k}{{\rho }_{0}c\left(k{v}_0-{\omega }_s\right)}\cdot \frac{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{2}{3}{\tilde{\epsilon }}^2\right]}{1+\tilde{\epsilon }-i\left[\tilde{\epsilon }+\frac{4}{9}\left(\rho +1∕2\right){\tilde{\epsilon }}^2\right]}+\beta \right\}{n}_0{P}_1.$$ (A14)

To convert the microsphere concentration to fluorescent molecule concentration, a scaling factor M is introduced and defined as the number of fluorescent molecules in one microsphere. Therefore,

$$N_1\left(r\right)=M{n}_1^{\prime }=K^{\prime }{N}_0{P}_1,$$ (A15)

where N₁(r) is the complex amplitude of the modulated fluorophore concentration [see Eq. 1], K^′ is the factor in the curled parentheses of Eq. A14, and N₀ is the average fluorophore concentration and equals n₀M.