Landmark-referenced Voxel-based Analysis of Diffusion Tensor Images of the Brainstem White Matter Tracts. Application in Patients with Middle Cerebral Artery Stroke

Abstract

Although DTI can provide detailed information about white matter anatomy, it is not yet straightforward enough to quantify the anatomical information it visualizes. In this study, we developed and tested a new tool to perform brain normalization and voxel-based analysis of DTI data. For the normalization part, manually placed landmarks ensured that the visualized white matter tracts were well-registered among the populations. A standard landmark set in ICBM-152 space and an interface to remap them to subject data were integrated in the procedure. After landmark placement, highly elastic non-linear Large Deformation Diffeomorphic Metric Mapping (LDDMM) was driven by the landmarks to normalize the brainstem anatomy of normal subjects. The approach was then applied to delineate brainstem tract abnormalities in patients with left chronic Middle Cerebral Artery (MCA) stroke. The voxel-based comparison between control and patient groups identified abnormalities in the ipsilesional corticospinal tract and contralesional cerebellar peduncles. We believe that this tool is useful for regional brain normalization of patients with severe anatomical alterations, such as stroke, brain tumor, and lobectomy, for whom standard automated normalization tools may not work properly.

Introduction

Diffusion tensor imaging (DTI) can reveal detailed anatomy of the brain white matter (Basser et al., 1994; Catani et al., 2002; Makris et al., 1997; Mori et al., 2005; Pajevic and Pierpaoli, 1999; Wakana et al., 2004) by visualizing various white matter tracts that cannot be identified by conventional MRI. This, in theory, would enable one to evaluate the anatomy of specific white matter tracts. For example, before and after brain damage, such as that caused by stroke, trauma and/or neurosurgery, it is often important to know the status of functionally important tracts (e.g., those responsible for motor, visual, and speech functions) (Luft et al., 2005). Until the advent of DTI technology, this type of tract-specific analysis was difficult to perform on a daily clinical basis.

The orientation of individual tracts in DTI images can be visualized through a color-coded orientation map (Makris et al., 1997; Pajevic and Pierpaoli, 1999). Once a tract of interest is identified, important clinical information could be derived from a quantitative analysis of the tract properties, such as shape and size, and MR parameters such as diffusion anisotropy, average diffusion constant, and relaxation parameters (Glenn et al., 2003; Pagani et al., 2005; Partridge et al., 2004; Stieltjes et al., 2001; Virta et al., 1999; Wilson et al., 2003; Xue et al., 1999). The most straightforward approach is to manually delineate each specific tract directly on color-coded maps. Alternatively, pixels that belong to a specific tract system can be semi-automatically grouped using a region-growing tool, such as tractography (Basser et al., 2000; Conturo et al., 1999; Mori et al., 1999; Parker et al., 2002; Poupon et al., 2000). These types of manual or semiautomated methods for tract delineation are currently widely used, and are often denoted as “tract-specific MR quantification” (Pagani et al., 2005; Xue et al., 1999).

An alternative to tract-specific approaches is voxel-based analysis, in which brains are normalized to a template brain and compared in a voxel-by-voxel manner (Ashburner and Friston, 2000; Wright et al., 1995). This is a very effective approach to evaluate a large amount of data in a systematic manner without a hypothesis about which tracts might be affected. The application of this approach to DTI data is, however, not straightforward. Similar to other methods, the first issue is the quality of the normalization. Corresponding anatomical locations between the template and the subject need to be well-aligned in the template space after the normalization, which is not always guaranteed because of substantial anatomic differences between subjects. One of the advantages of DTI is that it can reveal very convoluted white matter anatomy. However, unless the normalization quality is high enough to align these white matter structures, the rich anatomic information provided by DTI cannot be fully appreciated. A second issue is related to the fact that the anatomic DTI information is stored as a tensor field, not a scalar field. Thus, algorithms are needed to judge the quality of image alignment based on tensor properties (Cao et al., 2005; Zhang et al., 2006). In addition, transformation of the brain shape must be accompanied by re-orientation of the tensor. Algorithms for the automated normalization of tensor fields have been postulated, but are not widely available (Alexander et al., 2001; Xu et al., 2002). In this study, we introduce a landmark-based tool for normalization of DTI data. In this approach, corresponding structures revealed by DTI are manually identified by placing landmarks and a highly elastic non-linear transformation was driven by the landmarks using a Large Deformation Diffeomorphic Metric (LDDMM) (Miller et al., 2002).

As a first application, we investigated tract anatomy in the brainstem of a group of middle cerebral artery stroke patients. Even though primary lesion sites in these patients can be readily delineated by hyperintensities in conventional T2-weighted images, it is generally not straightforward to predict the functional outcomes. Development of image-based markers of functional outcome or predictors of rehabilitation response would have a significant impact on patient care. The hypothesis of this study is that the detailed analysis of white matter anatomy enhances our ability to predict functional outcome in stroke patients. We are especially interested in brainstem anatomy because all important motor and sensory pathways penetrate this area and can be clearly delineated by DTI. Secondary lesions in the corticospinal tract and the medial lemniscus may accurately reflect the motor and sensory functional status of the patient, respectively. Toward this long-term goal, we first need to establish a tool for group-based anatomical analyses of DTI, which is the main goal of this paper. As an initial feasibility study, quantitative assessment of secondary lesions in the brainstem of a small group of stroke patients was performed.

Materials and Methods

Subjects

The study was approved by the Institutional Review Board and written, informed consent, including a HIPAA-compliant data sharing agreement, was obtained from all subjects. Twelve healthy adults, who were free of current and past medical or neurological disorders, participated in the study as controls (mean age, 32 +/− 10.54 years; seven males, five females). For stroke studies, six patients (mean age, 55.23 +/−12.86 years; three males, three females) with chronic infarction in the territory of the left middle cerebral artery (MCA) participated.

Image acquisiton

A 1.5T MR unit (Gyroscan NT, Philips Medical Systems) was used. DTI data were acquired using a single-shot, echo-planar imaging (EPI) sequence with sensitivity encoding (SENSE, parallel-imaging factor of 2.5 (Pruessmann et al., 1999)). The imaging matrix was 96 × 96 with a field-of-view of 240 × 240 mm (nominal resolution, 2.5 mm), zero-filled to 256 × 256 pixels. Transverse sections of 2.5 mm thickness were acquired parallel to the anterior commissure-posterior commissure line. A total of 50–55 sections covered the entire brain and brainstem without gaps. Diffusion weighting was encoded along 30 independent orientations (Jones et al., 1999), and the b-value was 700 s/mm². Five additional images with minimal diffusion weighting (b ≈ 33 s/mm²) were also acquired. The scanning time per dataset was approximately six minutes. To enhance the signal-to-noise ratio, imaging was repeated three times.

Data processing

The DTI datasets were transferred to a personal computer running a Windows platform, and were processed using DtiStudio (www.MriStudio.org or mri.kennedykrieger.org) (Jiang et al., 2006). Images were first realigned with Automatic Image Registration (Woods et al., 1998) using the minimally diffusion-weighted image as a template to remove any potential small bulk motion that may have occurred during the scans. The six elements of the diffusion tensor were calculated for each voxel using multivariant linear fitting. After diagonalization, three eigenvalues and eigenvectors were obtained. For the anisotropy map, fractional anisotropy (FA) was used (Pierpaoli and Basser, 1996). The eigenvector associated with the largest eigenvalue was used as an indicator of the fiber orientation. We also created an averaged diffusion-weighted image (aDWI) by adding all of the diffusion-weighted (b = 700 s/mm²) images. This image was used to drive the initial affine image registration for all subjects in this study.

Normalization and landmark sets

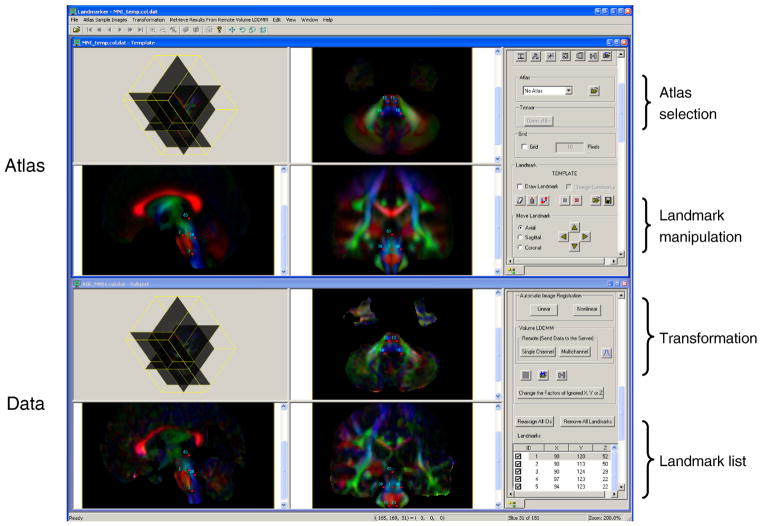
The entire registration process was performed using our in-house software called Landmarker (Xin Li, Hangyi Jiang, and Susumu Mori, www.mristudio.org or mri.kennedykrieger.org). The interface of the Landmarker is shown in Fig. 1. For the anatomical template, the JHU-DTI atlas (lbam.med.jhmi.edu) was used, which was created by linearly normalizing DTI data from 28 healthy subjects to the ICBM-152 template. In this study, we first normalized our subject DTI data (both controls and patients) into this template using the 12-mode affine transformation. This initial alignment was performed using the aDWI images for the entire brain, which brought the brainstem close to that of the template. The subsequent landmark placement was performed using color-coded orientation maps. We defined a “standard landmark set” in the color-coded orientation map of the JHU-DTI atlas. This set consisted of 53 landmarks strategically defined on easy-to-define structures (the MNI coordinates and an anatomical description of these landmarks can be downloaded from our website, www.mristudio.org/wiki/installation). The initial affine transformation was based on Automated Image Registration (AIR) (Woods et al., 1998) using_[S1] the ratio image uniformity (RIU) cost function (Woods et al., 1998). Then the normalized color-coded map from each subject was loaded to Landmarker, where the standard landmark set is displayed in the atlas, which provides visual guidance for landmark placement (upper images in Fig. 1). The same landmarks are copied for each subject and moved to the corresponding structures (bottom images in Fig. 1). In principle, landmarks are defined using imaging planes perpendicular to the tracts being identified. In the brainstem, there are only a small number of tracts running along the right-left axis, which are defined using the mid-sagittal plane. The majority of the tracts run along the inferior-superior axis and, thus, axial planes are used. Any mismatch between the standard landmarks and subject anatomy can be immediately appreciated (Fig. 2 inset C,D). Landmarker allows fine adjustment of the landmarks to the corresponding structures, which typically takes about 15 min. If an ith landmark defined on the template, L_i^T, is moved to a new location, L_i^S, in the subject brain, the difference vector can be defined by $\overline{D_i}={L^S}_i-{L^T}_i$. From the 53 $\overline{D_i}$, a deformation field was calculated and the subject image (tensor field) was transformed to the template space using landmarked-based LDDMM (Miller et al., 2002).

Fig. 1.

Interface for the brain normalization tool for DTI. The software has built-in atlases as a target, to which each subject data is normalized. It allows AIR-based linear and non-linear transformation as an initial normalization method. The software has a control panel to allow adjustment of the locations of the landmarks.

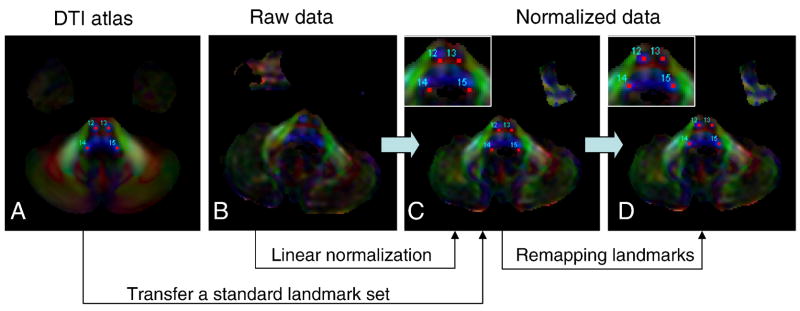
Fig. 2.

An example of the landmark-based brainstem normalization. First, a standard landmark set was established on the JHU-DTI atlas in the ICBM-152 coordinates (A), which consisted of 53 landmarks placed on easy-to-identify white matter structures in the brainstem. Subject DTI data (B) were linearly normalized to the template (C) and the standard landmarks were superimposed. The residual anatomical difference after the linear normalization can be appreciated as a mismatch between the linearly normalized subject data and the standard landmarks (C). An operator then manually adjusts these landmarks to their designated anatomical locations in the subject data (D). With the adjusted landmarks and standard landmarks, the software performs a non-linear transformation between the subject data and the atlas. The insets in (C) and (D) show the magnified inset views of the medulla. In these images, landmarks #12-#15 of 53 landmarks (see Appendix) are shown.

The LDDMM algorithm computes a transformation φ:Ω → Ω between two image spaces, where Ω ⊆ R³ is the 3D cube on which the data is defined. The transformation computed by LDDMM is generated as the end point φ = ϕ₁ of the flow of smooth time-dependent vector fields v_t with the ordinary differential equation ϕ̇_t = v_t ○ ϕ_t, t ∈ [0,1] where ϕ₀ (x) = x, x ∈ Ω.

The smoothness of the vector fields v_t is required to ensure that the computed transformation is a diffeomorphism. This is enforced with a regularization term based on constraints induced by a suitable Sobolev norm, denoted ||v||_V. This leads to the following generic inexact matching problem

$$\widehat{\varphi }=\underset{\varphi ={\phi }_1:{\stackrel{.}{\phi }}_t=v_t\circ {\phi }_t,t\in [0,1]}{argmin}{\int }_0^1\parallel v_t\mid {\mid }_V^{2}dt+D(\varphi )$$

whereD(φ) is a matching term between the transformed source and target data.

The goal of this algorithm is to interpolate a given landmark correspondence x_k → y_k, k = 1,…, N into a dense relation defined on the image space. The matching term in this case is

$$D(\varphi )=\frac{1}{{\sigma }^2}\sum _{k=1}^N\mid \varphi (x_k)-y_k{\mid }^2.$$

In our study, σ was set to 1, meaning all landmarks received the same weighting.

The problem can be reduced to a finite dimensional matching problem, and solved with a shooting algorithm that solves the associated Euler-Lagrange equation (Allassonnière et al., 2005). In this finite dimensional reduction, the velocity is expressed as a linear combination of the form $v_t(x)={\displaystyle \sum _{k=1}^n}{\lambda }_k(t)\mathit{Exp}(-\sqrt{\alpha }\mid x-x_k(t)\mid )$. The kernel $\mathit{Exp}(-{\sqrt{\alpha }}^{\ast }\mid x_k-x\mid )$ defines the influence of the landmark on the deformation of the whole space, with a parameter, α. In this study, the α was set to 0.002. This means the effect of each landmark is reduced to 50% over 22 pixels (mm). The 53 landmarks in this study covered brainstem volumes of approximately 35,000 mm³. Each landmark covers anatomical regions with a 7 mm sphere, on average, and is separated from others by approximately 14 mm. Therefore, transformation of each pixel is influenced by the weighted sum of 3–4 nearby landmarks. This also means that any brain regions further than 22 mm from the brainstem are not registered. Based on the approximate size of the brainstem (approximately 3×3×4 cm), landmark density, and the registration parameter, our study is designed to normalize the overall shapes, sizes, and orientations of the brainstem, but not the fine anatomical features significantly smaller than a 10 mm scale. As discussed further in the Discussion section, any anatomical differences smaller than this size would remain in the transformed image and be detected by voxel-based analysis. These parameters (landmark density and kernel), of course, can be adjusted, depending on the biological questions being asked in each application study.

After the LDDMM-based image transformation, the transformation matrix was applied to the tensor field using the method postulated by Xu et al. (Xu et al., 2003) and Zhang et al. (Zhang et al., 2006). The entire normalization procedure is also incorporated in Landmarker. The transformation takes about 15 minutes using a 2.66 MHz Intel processor.

Statistics_[S2] for voxel-based analysis

Group comparison between normal population (n = 12) and the six patients with a stroke of the left MCA were performed using voxel by voxel nonparametric Wilcoxon rank sum test (Matlab, The Mathworks, Inc., Natick, MA, USA) without_[S3] applying a smoothing filter. To avoid type one error in multiple comparison, we set the false discovery rate (FDR) at 0.05 (Genovese et al., 2002). The threshold for p value (FDR = 0.05) was 0.0082.

Measurements of intra and inter-rater variability of landmark placement

The 53 landmarks used in this study were placed three times on one of the normal_[S4] subjects by two experienced (W. Z. and S.M.) and one inexperienced rater to measure the intra and inter-rater variability of landmark placement. The inter-rater variability was measured from the distances between the multiple placements; (dist (L₁, L₂)+dist(L₁, L₃)+dist (L₂, L₃))/3, in which L_1–3 are landmark locations after three trials. The same equation was also used for the inter-rater variability among three raters. This measurement was repeated using data from three subjects and the averaged results are reported.

Results

The intra-rater variability was 0.82 ± 0.71 mm with no significant difference between the experienced and inexperienced raters. The inter-rater variability was 0.89 ± 0.76 mm.

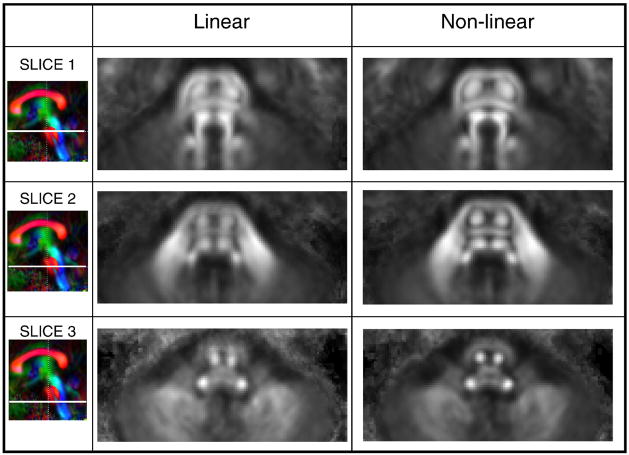
Fig. 3 shows averaged maps at three different axial brainstem levels created from the 12 normal subjects after linear (affine) and non-linear (landmark-based LDDMM) registration to the JHU-DTI template. Each averaged map after the non-linear registration is noticeably crisper, defining individual brainstem structures more clearly than the one produced by the linear registration.

Fig. 3.

Comparison of the linear (affine) and non-linear (LDDMM) transformation methods for cross-subject registration of the brainstem. Averaged FA maps from 12 normal subjects after the transformation are shown at three different slices at the pons (upper, middle, and lower pons).

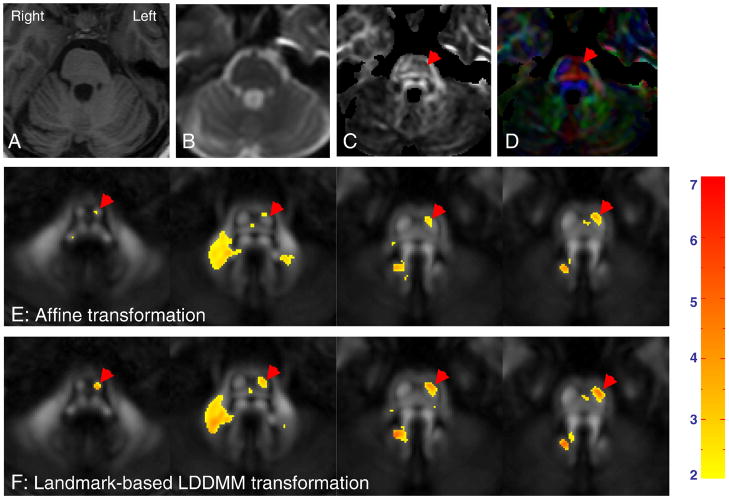
The images from the six left-MCA stroke patients were normalized to the JHU-DTI template using the same method as that used for the control subjects. In Fig. 4A–4D, T1, T2 (b0 image), FA, and color-coded orientation maps of a stroke patient with a left MCA infarct are compared at the same slice levels for demonstration purposes. Although atrophy of the pons is apparent in the T1-weighted image at the left side of the brainstem, detailed assignment of the origin of the neuroanatomical deficit to the pons can only be appreciated by the anisotropy-based images (Fig. 4C and 4D), where reduced size and loss of FA in the CST (indicated by red arrowheads) can be visually appreciated. These images exemplify the efficacy of DTI for detection of abnormalities in specific white matter tracts. Fig. 4E and 4F compare the results of the linear and non-linear approaches for voxel-based analysis, in which data from one of the six patients was normalized and, at each pixel, the FA value from the patient was compared to the average FA value obtained from the 12 normal subjects. In these figures, pixels with FA differences (a patient vs 12 controls) of more than two standard deviations are color-coded and overlaid without a geometrical filter. The better registration of intra-white matter structures by the non-linear transformation leads to delineation of the entire CST with substantially lower FA values.

Fig. 4.

Detection of regions with abnormally low FA using a pixel-by-pixel comparison between a stroke patient (A – D) and normal population data (E and F). Images in (A – D) show a T1-weighted image (A), a T2-weighted image (b0-image) (B), an FA map (C), and a color-coded orientation map (D) from a stroke patient. After linear (E) or non-linear (F) transformation, the transformed FA maps were compared to the population data and pixels with lower-than-average FA values (beyond twice the standard deviations of FA in the normal population) are indicated by a color scale (the extent of FA difference in terms of the standard deviation). The red arrows indicate the stroke-damaged corticospinal tract and middle cerebellar peduncle with lower than average FA values.

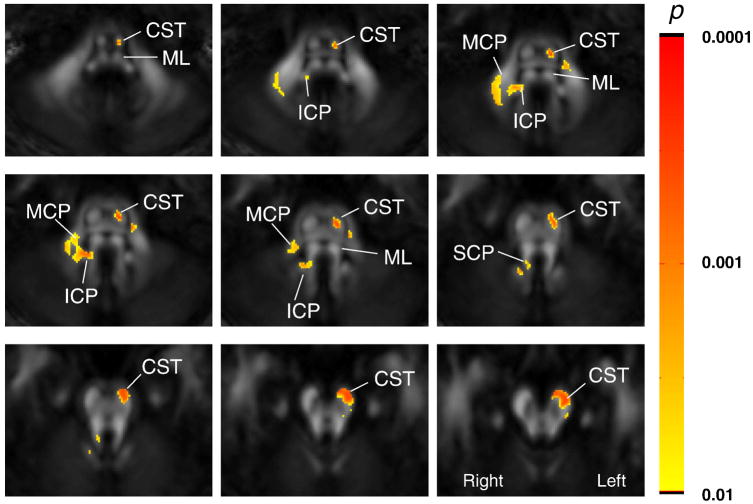
Fig. 5 shows the result of a non-parametric Wilcoxon Rank Sum Test for a group analysis between the normal population (n = 12) and the six patients with a stroke of the left MCA. The group results are consistent with the single-subject data shown in Fig. 4; FA of the ipsilateral CST and the contralateral MCP and ICP are significantly affected by the left MCA stroke. To confirm these results we also manually delineated the CST at the mid-pons level in each subject and measured the sizes (the number of pixels) and FA values (Table 1). The manually delineated results clearly indicate that the ipsilesional (left side) CST is smaller and has a lower FA than that in the control subjects.

Fig. 5.

Results of a pixel-by-pixel analysis of FA values between healthy volunteers (n = 12) and left chronic MCA stroke patients (n = 6). Images from nine slices are shown. The color scale represents p values from a Wilcoxon Rank-Sum Test for pixels with p<0.0082, which corresponds to p<0.05 after multiple-comparison corrections. The abbreviations are: MCP: middle cerebellar peduncle; SCP: superior cerebellar peduncle, CST: corticospinal tract; PCT: pontine crossing tract; ICP: inferior cerebellar peduncle; and ML: medial lemniscus.

Table 1.

Results of manual ROI-based analysis of the corticospinal tracts of the normal subjects (Ctrl, n = 12) and patients (Pt, n = 6)

	Size (mm2)				FA
	Ctrl-R	Ctrl-L	Pt-R	Pt-L	Ctrl-R	Ctrl-L	Pt-R	Pt-L
Average	63.6	61.3	61.1	17.6*	0.45	0.46	0.44	0.31*
Stdev	11.9	10.2	11.0	6.3	0.07	0.07	0.03	0.08

^*: Significantly different from the normal subjects (p < 0.0001 for the size and p = 0.0036 for the FA).

Discussion

DTI provides unique information about white matter anatomy and can delineate the degeneration of specific distal white matter tracts in stroke patients, as shown in Fig. 4C and 4D. The decrease of diffusion anisotropy of the corticospinal tract after stroke, due to Wallerian degeneration and correlation with motor functions, has been reported in the past (Khong et al., 2004; Moller et al., 2007; Mukherjee, 2005; Pierpaoli et al., 2001; Thomalla et al., 2004; Werring et al., 2000). This is an exciting quantitative advantage of this MR technique, because the availability of such an unbiased sensitive marker of anatomical change may provide us with a better understanding of the impact of infarctions on brain anatomy and functions. To further elaborate on this type of anatomic/function correlation study, group-based analyses are the essential next step. One of the widely used quantification tools for MRI is manual ROI placement. While it is a valid approach, it has significant limitations. The ROI placement is inherently subjective and time-consuming. Reproducibility of the size and locations could also be an issue, depending on the structures of interest. In addition, the ROI-based approach is usually hypothesis-driven and focused on pre-determined brain areas. This approach also leaves many brain regions unexamined.

To assist the ROI-based analyses, voxel-based template-referenced analyses are powerful methods. Although these approaches have been used widely for T1 and T2-weighted images, application to DTI poses a unique challenge. DTI data consists of tensor fields (as opposed to scalar fields for conventional MRI) and white matter tracts revealed by the tensor field need to be well-registered after normalization to fully exploit the delineated anatomical information. After simple linear normalization, this condition is not guaranteed. This can be clearly seen in Fig. 2C, where landmarks placed at specific white matter tracts of an atlas image (Fig. 2A) are not aligned to the corresponding structures in the linearly-normalized subject image (Fig. 2C). This leads to blurred structures in population-averaged images after linear normalization (Fig. 3) and reduced sensitivity to detect lesions in patients (Fig. 5).

The improved registration quality provided by a nonlinear method, compared to linear registration, is an expected result. Recently, automated non-linear registration tools for DTI have been actively developed, including the widely used, tract-based spatial statistics (TBSS) method (Chiang et al., 2008; Smith et al., 2006; Verma et al., 2005; Yushkevich et al., 2008; Zhang et al., 2006). This may invoke the question of the usefulness of the time-consuming, landmark-based method. In the past, it has been shown that careful manual-based approaches can improve registration quality, compared to fully automated methods (see, e.g., (Kirwan et al., 2007)). Nonetheless, it is important to carefully evaluate the cost-benefit relationship of manual landmark-based methods for each specific application. If both methods lead to comparable accuracy, there is no reason to use the landmark-based method. As a general guideline, the landmark-based method excels in applications in which: 1) the region of interest is localized, because dense landmarks can be flexibly targeted to such regions; and 2) there are severe anatomical and/or intensity differences among subjects, because such differences could mislead non-linear automated algorithms. These applications include stroke, brain tumor, or lobectomy. Other examples include studies of brain development (both human and animal) in the early neonatal stages during which there is a large amount of contrast and structural change and automated non-linear registration methods are not expected to work properly. Even in such cases, landmarks could be placed at easy-to-identify structures throughout the development stages, and could quantitatively characterize brain shape changes (Zhang et al., 2003). In the present study, we tested non-linear normalization of the brainstem (regional normalization) in stroke patients. The group analysis results for the stroke patients clearly indicate abnormalities in the ipsilesional corticospinal tract and contralesional cerebellar peduncles. These abnormalities in the contralesional cerebellar pathways are fully expected because they cross the midline (decussate) at the pons level. This tool can be applied to other regions of the brain, as well as the entire brain, but a landmark set must be created and tested to determine the reproducibility of each set. Our brainstem landmark set (53 landmarks), with anatomical descriptions, can be downloaded from our website (www.mristudio.org/wiki/installation) for testing.

To facilitate this time- and labor-consuming process, we developed software and established a “standard landmark” set for the brainstem studies. The software provides an interface that allows remapping of the 53 standard landmarks within approximately 15 min by an experienced operator. In our current tool (Landmarker), there is room for several improvements. First, there is the issue of landmark-placement reproducibility. The intra- and inter-rater variability in landmark placement would lead to lower sensitivity to detect differences between groups. It is, therefore, important to measure test-retest reproducibility of landmark placement. In this study, the intra and inter-rater reproducibility was approximately 1 mm. This high reproducibility is due to the small size of the tracts used as anatomical landmarks. If this approach is used in the cerebral hemisphere which has less density of distinctive anatomical features, the reproducibility would be worse. Although, in theory, the placement errors could be measured once for the given standard landmark set and incorporated in image normalization and statistical procedures, our current tool does not incorporate such features. Please note that the sparse anatomical features and difficulty of reproducible structure identification could also influence the accuracy of automated approaches. Another important issue that is not addressed in this paper is the difficulty of identifying corresponding points along tubular-shaped tracts. In such cases, landmark placements must rely on nearby anatomical clues to identify corresponding locations in the tract. Anisotropic cost functions, which have fewer penalties for a mismatch tangential to the structure, may be necessary to further improve the registration quality.

The quality of the normalization results also depends on the number and locations of the landmarks. The volume of the brainstem that is covered by the 53 landmarks is approximately 350 mm³, meaning each landmark represents an area of 7 mm³ of tissue, on average. The landmark-based method cannot capture and correct morphological differences smaller than the landmark density. This means that anatomical differences may remain after the landmark-based transformation. If a pixel-by-pixel statistic such as that shown in Figs. 5 and 6 finds pixels with abnormal values, it could be attributable to differences in image intensity (in this paper, it is FA) and/or due to morphological differences (see (Ashburner and Friston, 2000) and (Smith et al., 2006) for discussions related to this issue). Therefore, the interpretation of the results requires a subsequent, more detailed analysis, such as a manual ROI-based method. For example, the manual ROI-based analysis (Table 1) suggests that both size and FA value were decreased in patients. The proposed method could, therefore, serve as a screening method to characterize abnormal regions.

In summary, we developed an interface for landmark placement in the brainstem, followed by LDDMM-based non-linear transformation. The software was tested on the brainstem anatomy of a group of MCA stroke patients to test for Wallerian degeneration. We first devised a standard landmark set consisting of 53 landmarks placed on our JHU-DTI atlas in the MNI coordinates. Compared to linear transformation, a clear improvement was observed in registration quality. A pixel-by-pixel comparison between the control and stroke patient groups identified abnormalities in the ipsilateral corticospinal tract and in the contralateral cerebellar peduncles. The software and the anatomical templates are available for downloading at www.mristudio.org and lbam.med.jhmi.edu.