Evaluation of dosimetric margins in prostate IMRT treatment plans

Abstract

This work introduces a new concept—the dosimetric margin distribution (DMD)—and uses it to explain the sensitivity of a group of prostate IMRT treatment plans to patient setup errors. Prior work simulated the effect of setup errors on 27 prostate IMRT treatment plans and found the plans could tolerate larger setup errors than predicted by the van Herk margin formula. The conjectured reason for this disagreement was a breakdown in van Herk's assumption that the planned dose distribution conforms perfectly to target structures. To resolve the disagreement, this work employed the same 27 plans to evaluate the actual margin distributions that exist between: (i) the clinical target volume (CTV) and planning target volume (PTV) and (ii) the CTV and PTV minimum dose isodose surface. These distributions were evaluated for both prostate and nodal targets. Distribution (ii) is the DMD. The dosimetric margin in a given direction determines the probability that the CTV will be underdosed due to setup errors in that direction. Averaging over 4π sr gives the overall probability of CTV coverage. Minimum doses for prostate and nodal PTVs were obtained from dose volume histograms. Corresponding isodose surfaces were created and converted to regions of interest (ROIs). CTV, PTV, and isodose ROIs were saved as mesh files and then imported into a computational geometry application which calculated distances between meshes (i.e., margins) in 614 discrete directions covering 4π sr in 10 deg increments. Measured prostate CTV-to-PTV margins were close to the nominal value of 0.5 cm specified in the treatment planning protocol. However, depending on direction, prostate dosimetric margins ranged from 0.5 to 3 cm, reflecting the imperfect conformance of the planned dose distribution to the prostate PTV. For the nodal CTV, the nominal CTV-to-PTV margin employed in treatment planning was again 0.5 cm. However, due to the planning protocol, the nodal PTV follows the surface of the nodal CTV in several places, ensuring that there is no room for rigid body motion of the nodal CTV inside the nodal PTV. Measured nodal CTV-to-PTV margins were therefore zero, while nodal dosimetric margins ranged from 0.2 to 2.8 cm. Prostate and nodal target coverage were found to be well correlated with the measured DMDs, thereby resolving the apparent disagreement with our prior results. The principal conclusion is that target coverage in the presence of setup errors should be evaluated using the DMD, rather than the CTV-to-PTV margin distribution. The DMD is a useful planning metric, which generalizes the ICRU conformity index. DMDs could vary with number of beams, beam arrangements, TPS, and treatment site.

I. INTRODUCTION

The purpose of this work is to introduce a new concept, termed the dosimetric margin distribution, and use it to explain the sensitivity of a group of prostate IMRT treatment plans to patient setup errors. To accommodate inter- and intrafraction patient setup uncertainties and organ motion, the ICRU recommends expanding the clinical target volume (CTV) by a margin to obtain the planning target volume (PTV).^1,2 The ICRU further defines the treated volume (TV) as the “volume enclosed by an isodose surface, selected, and specified by the radiation oncologist as being appropriate to achieve the purpose of the treatment,”¹ and the conformity index (CI) as the ratio of TV to PTV volume.²

The dosimetric margin distribution (DMD), which is the margin distribution that is achieved between the CTV and TV for a given plan, is a generalization of the ICRU CI. Importantly, sensitivity of the CTV dose to setup errors is a function of the TV (or DMD), not the PTV (or CTV-to-PTV margin distribution). By assuming tight conformance of the dose distribution to the PTV, the van Herk margin formula³(VHMF) identifies the TV with the PTV. In general, the TV is larger than the PTV, resulting in a mismatch between the theory and application of the VHMF.

This work considers only interfraction patient setup errors. (Note, however, that the analysis readily generalizes to other types of geometric errors.) These are categorized as random or systematic. Systematic (preparation) errors⁴ are those which, over a course of treatment, result in an average offset from the intended isocenter. They include, for instance, setup errors at the time of initial patient imaging which carry through the whole of the patient's treatment. Random (execution) errors are the deviations from the mean within each treatment fraction. Both types of error are typically assumed to be normally distributed.^4,5 Here the standard deviations (SDs) of systematic and random errors, assumed common to all axes, are denoted by Σ and σ. Under these conditions, the VHMF gives the required margin as: M = 2.5Σ+0.7σ.³ According to the van Herk model, this formula ensures that 90% of patients experience a CTV minimum dose (after setup errors) which is greater than or equal to the planned PTV minimum dose.

[Note that the full version of the van Herk margin formula is: M = 2.5Σ + 1.64(σ′-σ_P), where ${\sigma }^{\prime }=\sqrt{{\sigma }^2+{\sigma }_P^2}$ and σ_P is the standard deviation characterizing the dose penumbra. For an assumed value σ_P = 3.2 mm, van Herk et al. linearized this equation to: M = 2.5Σ + 0.7σ.³]

The VHMF is based on several assumptions or approximations: (a) homogeneous tissue, (b) a number of fractions that is sufficiently large for the sum of fraction doses to be well-approximated by a convolution (convolution method), (c) a spherical target that is large in comparison to setup errors, (d) a normal beam penumbra of width ~0.5 cm (used to derive the linearized version of the VHMF), and (e) perfect conformance of the dose distribution to the target (i.e., an isodose surface exactly conforms to the PTV, so that any movement of the CTV outside the PTV reduces the minimum CTV dose below the planned minimum PTV dose).

Approximations (a)-(d) have been analyzed in the literature. For instance, Gordon et al.⁶ showed that tissue inhomogeneities have little effect on prostate margins. Other authors who have studied this issue include Cho et al.,⁷ who looked at a lung treatment and concluded the effect of heterogeneities is minimal, and Craig et al.,⁸ who looked at phantom and clinical (prostate, lung, sinus, breast) cases, reaching the same conclusion, provided errors caused by dose discontinuities at the patient surface are corrected for.

The issue of finite fractions is addressed by van Herk et al.,⁹ Gordon and Siebers,¹⁰ and others.^11-14 The VHMF is based on the convolution method (CM), which approximates the cumulative fluence resulting from N fractions by the convolution of the planned fluence with the random setup error distribution. For IMRT delivered with typical fractionation schemes (N≈30), it appears that the CM is accurate. However, it could become inaccurate in the case of hypofractionated or adaptive therapy.¹⁰

The VHMF is based on the assumption that the dose distribution falls away at its edge like a normal cumulative distribution function (CDF). McKenzie et al.¹⁵ rederived the margin formula for more realistic scenarios, where the dose distribution was produced by 1-6 coplanar beams. The effect of more beams is to “spread out” the exit dose around the target, resulting in a smaller σ coefficient than in the original VHMF. This effect is non-negligible and should be taken into account in margin estimates. (See also, Witte et al.¹⁶)

Of the approximations (a)-(e) underlying the VHMF, the only one that has not been quantitatively analyzed in the literature is (e), the assumption that the dose distribution conforms perfectly to the PTV. Van Herk et al.³ qualitatively discussed the issue and suggested using a weighted sum of dose-population histograms from different levels of conformation and setup errors to obtain an overall dose-population histogram. Siebers et al.¹⁷ simulated setup errors for head and neck IMRT plans, concluding that margin formulas overestimate the required CTV-to-PTV margins. In a similar study, Gordon et al.⁶ simulated the effect of normally distributed setup errors on 27 simultaneous integrated boost (SIB) IMRT plans. The key finding of that study was that 0.5 cm margins could absorb setup errors having Σ=σ = 0.3 cm. According to the VHMF, 0.5 cm margins can absorb only errors having SDs Σ=σ≤0.16 cm. The conjectured reason for this disagreement was a breakdown in van Herk's assumption of perfect conformance. The present work resolves the disagreement by using the same 27 prostate plans to evaluate the CTV-to-PTV and dosimetric margin distributions. Dosimetric margins are shown to extend beyond CTV-to-PTV margins and target coverage is shown to be well correlated with the DMD, rather than the CTV-to-PTV margin distribution.

In this work, all dose calculations are performed using the superposition convolution algorithm in Pinnacle 7.9 on a 2 mm dose grid. We use PTVMinDose to denote the prostate PTV minimum dose isodose surface and PTVNodesMinDose to denote the nodal PTV minimum dose isodose surface. Similarly, the CTV-to-PTVMinDose margin is referred to as the prostate dosimetric margin and the CTVNodes-to-PTVNodesMinDose margin as the nodal dosimetric margin.

II. MATERIALS AND METHODS

II.A. Prostate plans and prior simulations

In prior work Gordon et al.⁶ simulated the effect of normally distributed setup errors on 27 SIB IMRT plans generated using the Pinnacle treatment planning system (Philips Medical Systems, Fitchburg, WI) interfaced to an in-house IMRT optimization algorithm. These plans, which are utilized again in the present study, were derived from Virginia Commonwealth University (VCU) patients, but were recontoured and replanned by a single physician using the VCU prostate IMRT protocol.

The plans include two clinical target volumes—the prostate CTV (CTV) and nodal CTV (CTVNodes)—delineation of which is described in Gordon et al.⁶ The prostate PTV is derived by expanding the CTV 0.5 cm in all directions. PTVNodes is obtained by expanding CTVNodes 0.5 cm in all directions, excluding the PTV. In addition to the two target structures, the plans include OAR which are described in detail in Gordon et al.⁶ Prescribed doses were 65 Gy to 98% of the PTV and 50.4 Gy to 95% of PTVNodes, delivered in 28 fractions. (Note that before radiation therapy, all patients had received an initial 9 Gy of high dose rate brachytherapy.) Plan optimization was based on dose volume histogram criteria.

In Gordon et al.,⁶ the effect of random setup errors was simulated by fluence convolution,¹⁸ while the effect of systematic setup errors was simulated for each patient by sampling 50 different errors from a normal distribution and recalculating dose for each error. The resulting 27×50 = 1350 plans were used to generate dose population histograms (DPHs). (See van Herk et al.³ for an explanation of dose population histograms.) Because the margins in these plans were fixed at 0.5 cm, the standard deviations Σ and σ of systematic and random errors were varied in order to determine the magnitude of rigid setup errors that could be absorbed by a 0.5 cm margin. Specifically, setup errors having Σ=σ = 0.15, 0.3, 0.5, and 1.0 cm were simulated by moving the isocenter and recomputing the dose.

From the simulations, Gordon et al.⁶ generated DPHs for a number of target and OAR dose metrics. For example, DPHs were generated for the CTV D₉₈ and CTVNodes D₉₅ because these metrics feature in the dose prescription. (D_p denotes the dose delivered to p% of the structure, e.g., D₉₈ denotes the dose delivered to 98% of the CTV.) However, DPHs were also generated for the CTV and CTVNodes minimum dose (D_MIN), equivalent uniform dose (EUD), and tumor control probability (TCP), as well as for various OAR dose metrics. The key finding of the study was that 0.5 cm margins could absorb setup errors having Σ=σ = 0.3 cm. This conclusion was consistent across all target metrics: DPHs for D₉₈, D_MIN, TCP, etc., all showed that a 0.5 cm margin could absorb 0.3 cm errors.

II.B. Dosimetric margin distribution

In general the dosimetric margin M_D(ϕ,θ) associated with a CTV is defined to be the distance that the CTV can move in direction (ϕ,θ)—where ϕ is elevation and θ azimuth—before it intersects a specified isodose surface. In this work, the treated volume is defined to be the volume enclosed by the planned PTV minimum dose isodose surface. That is, the isodose surfaces of interest are the prostate and nodal PTV minimum dose isodose surfaces. Consequently, in this work the dosimetric margin is the distance from the CTV (CTVNodes) to the PTVMinDose (PTVNodesMinDose) isodose surface. However, other dosimetric margins might be of interest in other contexts. For example, although not considered here, the relevant dosimetric margin for a serial critical structure such as the cord would be the margin to the maximum dose isodose surface. This quantity would be relevant if one were to generalize this work to the case of margins around critical structures.

[The term “dosimetric margin” appears to be used in brachytherapy with the same meaning as adopted here: it denotes the distance from a structure to an isodose surface; see, e.g., Merrick et al.,¹⁹ Eshleman et al.,²⁰ and Butler.²¹ The term has been used in a different sense by van Herk et al.,³ to refer to the part of the CTV-to-PTV margin that accounts for dose penumbra plus random setup errors. It has also been used by Killoran et al.,²² apparently to refer to the part of the CTV-to-PTV margin that accounts for dose penumbra, though the term is not explicitly defined in that paper. These alternate usages are noted here to avoid confusion.]

In this work, coverage Q is defined to be the percent of patient plans for which the CTV minimum dose is greater than or equal to the PTV minimum dose. That is, following the original derivation of the VHMF,³ coverage is defined in terms of minimum dose. Note that coverage could alternatively be defined in terms of other dose metrics, such as EUD or TCP—see, e.g., van Herk et al.,²³ Song and Dunscombe,²⁴ and Gordon et al.⁶ Here, for clarity, we focus solely on minimum dose. For this case, the VHMF margin is designed to give coverage equal to 90%. That is, the VHMF is intended to ensure that 90% of patients receive a CTV minimum dose (after setup errors) that is greater than or equal to the planned PTV minimum dose.

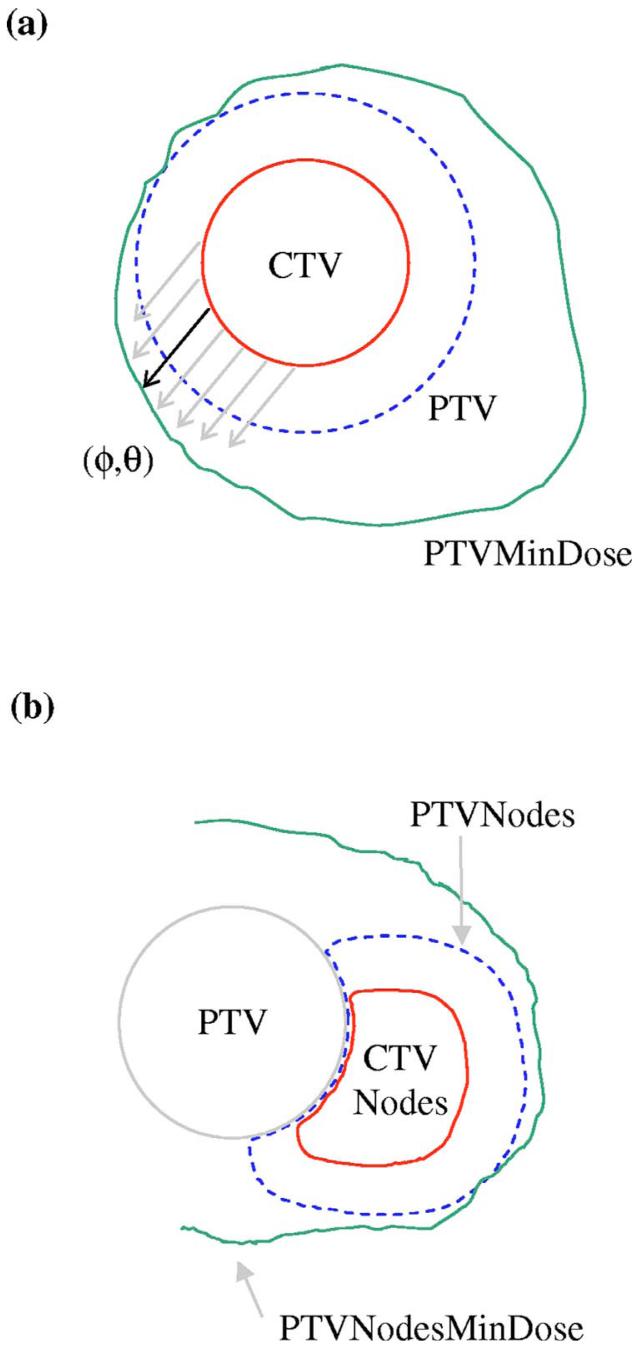
The dosimetric margin in one direction is illustrated in Fig. 1(a), which shows a uniform CTV-to-PTV margin around a spherical CTV. Each direction can potentially have a different dosimetric margin. The DMD is the distribution of margins over all directions. Naively, if one were to set the CTV-to-PTV margin equal to the VHMF value, one would expect 90% of patients to achieve a CTV minimum dose at least as high as the planned PTV minimum dose. However, due to the beam arrangement and the constraints imposed by OAR, the PTVMinDose contour typically extends beyond the PTV in some directions. In those directions, the CTV can move outside the PTV and still achieve a minimum dose greater than or equal to PTVMinDose. When averaged over many possible patient alignment deviations and all directions (ϕ,θ), the existence of dosimetric margins can result in an apparent disagreement with the VHMF. In practice, patients may be observed to tolerate larger values of Σ and σ than the VHMF would predict. Conversely, they could utilize smaller CTV-to-PTV margins than given by the VHMF and still achieve the desired level of target coverage. (As noted in the conclusion section, the degree to which CTV-to-PTV margins can be reduced could depend on the patient anatomy, treatment site, treatment technique, and planning system. Software tools for evaluating the DMD during the treatment planning process are therefore desirable. See also Killoran et al.²² and van Herk et al.²³ for additional methods of evaluating the effects of setup errors.)

FIG. 1.

Illustration of margin calculations. (a) CTV-to-PTVMinDose margin M_D (ϕ,θ). The solid arrow indicates the margin (minimum separation) in the direction (ϕ,θ). (b) Right nodal volumes. Because they are adjacent to the prostate PTV, CTVNodes and PTVNodes share a common surface. Because the high dose region is centered on the PTV, the PTVNodesMinDose surface extends around both the PTV and right/left nodal volumes.

II.C. Margin calculation

This sections describes how CTV-to-PTV and dosimetric margin distributions were calculated in this study. CTV-to-PTV and dosimetric margin distributions were obtained by first exporting the relevant structures—prostate and nodal CTV, PTV, and isodose surface—from the TPS in the form of triangular meshes, then using a computational geometry algorithm to calculate collision distances between the meshes in multiple directions. (The computational geometry algorithm was implemented using the Computational Geometry Algorithm Library, see Ref. 25) This is something of a brute force method and it is possible that more elegant (and faster) methods, e.g., based on ray tracing, could be developed.

For each of the 27 prostate plans analyzed here, four margins were determined: CTV-to-PTV, CTV-to-PTVMinDose, CTVNodes-to-PTVNodes, and CTVNodes-to-PTVNodesMinDose. (Nodal margins were calculated for right and left sides and the minimum was taken.) In each case, the margin was calculated for 10 deg increments of ϕ from -90° to 90° and 10 deg increments of θ from -180° to +180°. Allowing for degeneracy of θ at ϕ=-90° and ϕ=+90°, this gave margins in 614 evenly spaced directions covering 4π sr. These 614 measurements constituted the DMD.

The algorithm for calculating the margin in the direction (ϕ,θ) defined an initial step size and iteratively moved the inner mesh away from its initial position by a distance of step size in direction (ϕ,θ). At each iteration, the algorithm checked whether the interior mesh surface had intersected the exterior mesh surface. If it had, the interior mesh had been moved too far. In this case it was returned to its former position and the step size was halved. If there was no intersection, the interior mesh remained in the new position. This loop continued until the step size fell below the required accuracy (0.005 cm).

The above method of calculating margins relies on exported triangular meshes to function as accurate models of Pinnacle regions of interest (ROIs). However, testing found that Pinnacle's meshes deviated slightly from the source ROI surfaces. Specifically, meshes exhibited small surface deviations on the order of 0.5 mm or less. The result of these surface deviations was to produce a slight underestimate of actual margins—essentially, collision distances between meshes were slightly smaller than the distances between the source ROIs. The size of this effect was quantified for artificial ROIs and isodose contours. The end result was that measured ROI-to-ROI margins were increased by 0.05 cm and measured ROI-to-isodose margins were increased by 0.1 cm to account for the measurement bias due to mesh surface deviations. Margins quoted below include this correction.

II.D. Target coverage calculation

Recall that coverage Q is the percent of patients for which the CTV minimum dose is greater than or equal to the PTV minimum dose. This section shows how coverage may be calculated from a margin distribution. The resulting coverage value can then be used to assess whether the margin (distribution) is meeting, exceeding, or falling short of the van Herk 90% coverage criterion.

In the VHMF, the effect of random errors is to blur the dose distribution. This is modeled via the convolution method. The effect of systematic errors is to displace the dose distribution. Systematic displacements d occur isotropically, with the following three-dimensional normal CDF having the standard deviation Σ:

$$\mathrm{Pr}[d\le r]=\mathrm{normcdf}3D(r,\Sigma )=\mathrm{erf}(r∕\sqrt{2}\Sigma )-(2∕\sqrt{\pi })\cdot (r∕\sqrt{2}\Sigma )\cdot \exp (-r^2∕2{\Sigma }^2),$$ (1)

where erf() is the error function. In the van Herk formulation, the total margin M = M_R+M_S consists of a random component M_R that compensates for blurring and a systematic component M_S that compensates for displacement. The systematic component is given by

$$\begin{array}{cc}\hfill M_S& =\mathrm{norminv}3D(0.90,\Sigma )\hfill \\ \hfill & =\mathrm{norminv}3D(0.90,1)\ast \Sigma \approx 2.5\ast \Sigma ,\hfill \end{array}$$ (2)

where norminv3D(p,κ) is the inverse CDF for normcdf3D(r,κ). The reader is referred to van Herk et al.³ for the derivation of this formula. Suppose one knows the random margin M_R that exactly compensates for blurring. Then, in the case of a uniform total margin M, M - M_R is the balance of the margin that is available for absorbing systematic errors. Since M_R is assumed to exactly compensate for blurring, coverage Q is consequently the percent of patients whose systematic error is absorbed by margin M-M_R,

$$Q=\mathrm{normcdf}3D(M-M_R,\Sigma ).$$ (3)

Self-consistency of the VHMF can be checked by substituting Eq. (2) for M-M_R in Eq. (3), and verifying that Q = 90%, which is the van Herk population criterion.³ In the more general case where the dose distribution does not conform perfectly to the PTV, the above isotropic margin M must be replaced with the direction-dependent dosimetric margin M_D (ϕ,θ). In this case, the coverage Q becomes

$$Q=\iint d\varphi d\theta \mathrm{normcdf}3D(M_D(\varphi ,\theta )-M_R,\Sigma ).$$ (4)

If one knows the margin M_R that exactly compensates for blurring, this equation allows one to calculate the percentage of patient plans that receive acceptable target coverage. For a given value of Σ, if Q is below 0.90, then the overall margin needs to be increased. If Q is above 0.90, then the overall margin can be decreased.

Equation (4) is used below to estimate the degree of target coverage provided by the measured CTV-to-PTV and dosimetric margin distributions in the 27 prostate IMRT plans. In order to use Eq. (4), it is necessary to make a reasonable assumption regarding the value of M_R. We use the value of M_R given by the original van Herk model, corrected for the wider penumbra associated with multibeam dose distributions, as in McKenzie et al.¹⁵ (In IMRT there are overlapping beams which have the cumulative effect of changing the edge of the dose penumbra via the exit dose. In this situation, the required value of M_R is reduced, as described by McKenzie et al.¹⁵)

The prostate treatments considered here utilized seven coplanar beams. McKenzie et al.¹⁵ provided corrected σ coefficients in the VHMF for up to six coplanar beams. We adopt their six-beam result, as it should differ only slightly from the seven-beam value. It scales the σ coefficient by a factor of 0.52/1.64. Consequently, in the subsequent analysis we use the following value for M_R in Eq. (4):

$$M_R=(0.52∕1.64)\cdot [\mathrm{norminv}(0.95,0,\sqrt{{\sigma }_P^2+{\sigma }^2})-\mathrm{norminv}(0.95,0,{\sigma }_P)],$$ (5)

where norminv(p, μ, κ) is the inverse of the normal CDF having the mean μ and SD κ, and σ_P is the SD of the normal dose penumbra. For the detailed derivation of Eq. (5), the reader is referred to van Herk et al.³ and McKenzie et al.¹⁵

III. RESULTS

III.A. Prostate margins

Table I gives statistics for the prostate CTV-to-PTV margin (column 2) and dosimetric margin (column 3). These were obtained from 26 of the 27 prostate IMRT plans. In one of the plans, the Pinnacle-generated mesh for the PTVMin-Dose structure was malformed and was consequently omitted from the analysis.

Table I.

Corrected margins in centimeters (cm). Prostate margins were obtained for 26 of the 27 patients, nodal margins for 21 of the 27 patients. Excluded patients had mesh import problems. ROI-ROI margins were increased by 0.05 cm and ROI-isodose margins by 0.1 cm, to correct for measurement bias (see text).

	CTV to PTV	CTV to PTVMinDose	CTVNodes to PTVNodesMinDose
Margin μ ± σ	0.57 ± 0.07	1.04 ± 0.27	0.89 ± 0.27
Margin range	0.22:0.73	0.55:3.03	0.16:2.81

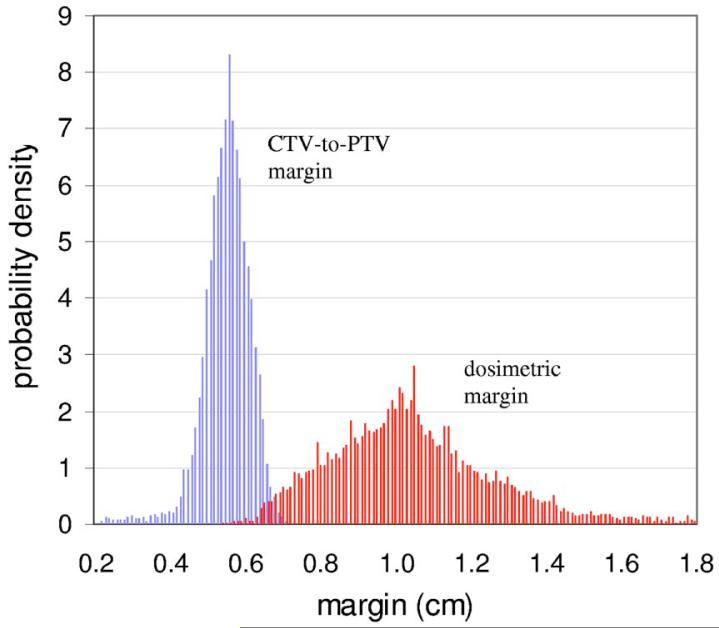
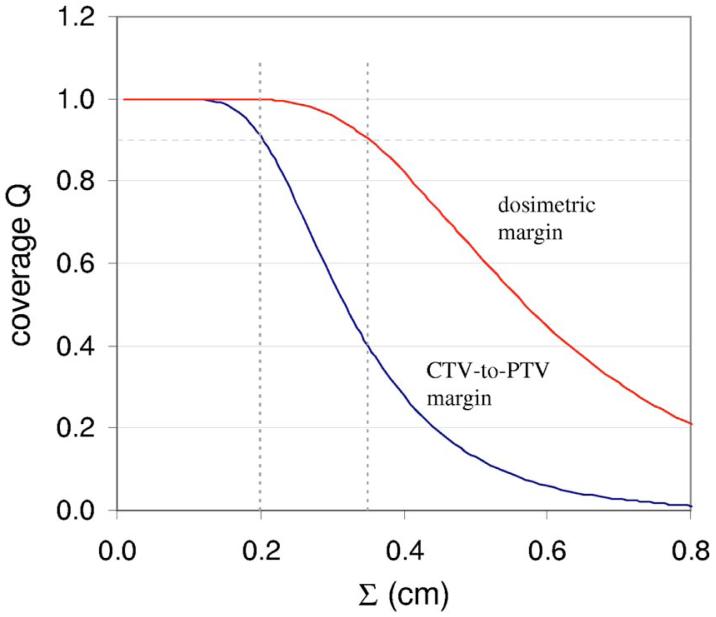
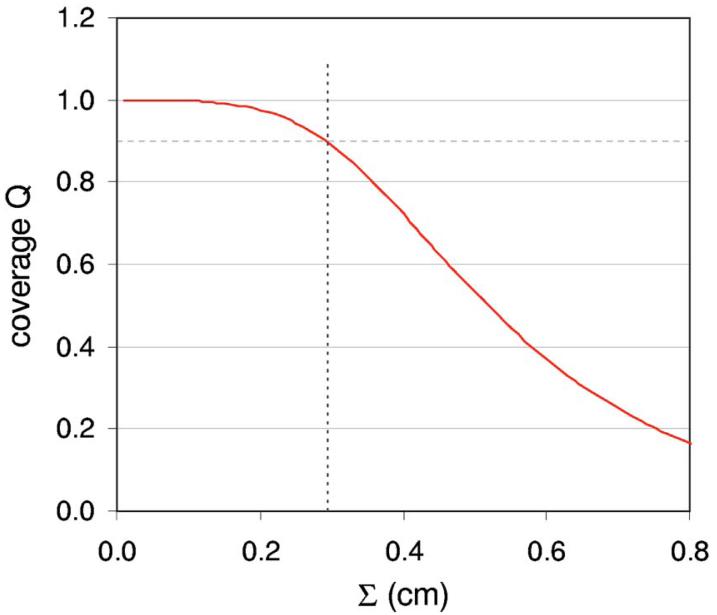
Figure 2 plots the distributions of prostate CTV-to-PTV and dosimetric margins for 26 of the 27 plans. The DMD extends well beyond the CTV-to-PTV margin in most directions. Figure 3 shows the coverage Q provided by the two margins—i.e., margin distributions obtained from 26 plans—as a function of the SD Σ of systematic setup errors. Note that coverage is calculated using Eqs. (4) and (5), with σ set equal to Σ in Eq. (5). (This parallels the simulations in Gordon et al.,⁶ where setup errors having various values of σ=Σ were simulated.) Figure 3 shows that the CTV-to-PTV margin distribution can tolerate values of σ=Σ up to 0.2 cm before Q falls below 0.9. In contrast, the dosimetric margin distribution can tolerate values of σ=Σ up to 0.35 cm.

FIG. 2.

Distributions of the prostate CTV-to-PTV margin and the prostate dosimetric (CTV-to-PTVMinDose) margins.

FIG. 3.

Target coverage Q as a function of the standard deviation Σ of systematic patient setup errors, for prostate CTV-to-PTV and dosimetric margins. Coverage is calculated using Eqs. (4) and (5). The nominal CTV-to-PTV margin was 5 mm.

This resolves the apparent disagreement between the van Herk margin formula and the findings of Gordon et al.⁶ The VHMF is conventionally applied to the CTV-to-PTV margin. Figure 3 shows that if patients' tolerance to setup errors was determined by the CTV-to-PTV margin distribution, then the VHMF would be accurate: for σ=Σ = 0.2 cm, the VHMF requires a margin M = 0.64 cm, which is close to the measured average CTV-to-PTV margin of 0.57 cm in Table I.

However, patients' tolerance to setup errors is in reality determined by the DMD, i.e., by the CTV-to-TV margin distribution. Figure 3 shows that the VHMF—or, more specifically, the coverage formula (4) on which the VHMF is based—can accurately predict target coverage, provided it is applied to the DMD. The finding that the measured DMD can tolerate setup errors with σ=Σ up to 0.35 cm is consistent with Gordon et al.,⁶ which showed via direct simulation that the 27 IMRT plans could tolerate errors up to σ=Σ ≈0.3 cm.

(Gordon et al.⁶ simulated setup errors with SDs σ=Σ = 0.15, 0.3, 0.5, and 1.0 cm. That study found that the IMRT plans could tolerate prostate setup errors with σ=Σ = 0.3 cm, but could not tolerate errors with σ=Σ = 0.5 cm. Based on dose population histograms, the maximum tolerated setup errors were for σ=Σ a little larger than 0.3 cm. The findings are therefore consistent with a value σ=Σ = 0.35 cm.)

III.B. Nodal CTV margins

Table I gives statistics for the nodal dosimetric margin (column 4). These were obtained from 21 of the 27 prostate IMRT plans. Six plans experienced problems importing Pinnacle generated meshes into the computational geometry application and were therefore omitted from the analysis.

Note that Table I does not give statistics for the nodal CTV-to-PTV margin. The reason is that this margin was found to be zero. The nodal PTV is obtained by expanding the nodal CTV by 0.5 cm. However, after this step the nodal PTV is modified: the prostate PTV is excluded [as in Fig. 1(b)] and the vicinity of the patient's skin is excluded. Because of this, the nodal PTV is collapsed onto the nodal CTV in several locations: close to the prostate PTV and where the nodal CTV approaches the skin. This ensures that the nodal CTV has no room for rigid body motion inside the nodal PTV, and margins are therefore identically zero.

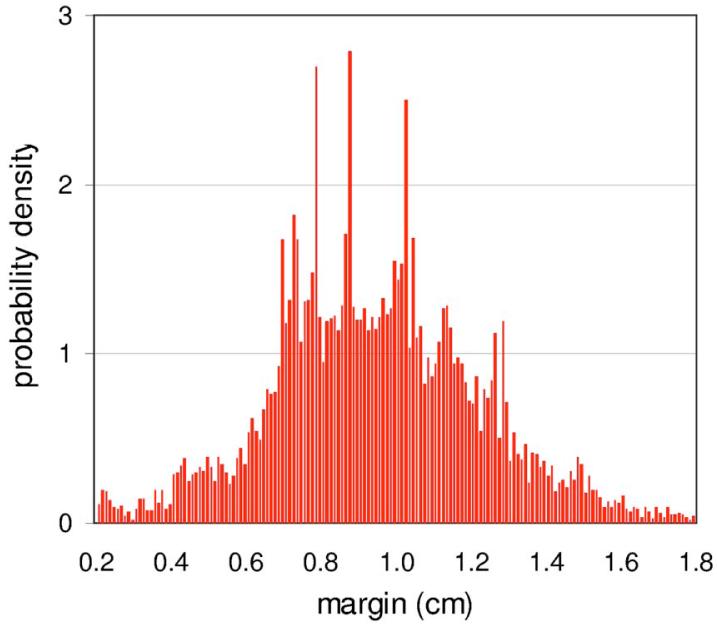
Figure 4 plots the distribution of nodal dosimetric margins for 21 of the 27 plans. In this case the DMD extends below 0.5 cm, but also extends well above it. Figure 5 shows the coverage Q provided by the dosimetric margin, as a function of the SD Σ of systematic setup errors. As before, coverage is calculated using Eqs. (4) and (5), with σ set equal to Σ in Eq. (5).

FIG. 4.

Distribution of the nodal dosimetric (CTVNodes-to-PTVNodesMinDose) margin.

FIG. 5.

Target coverage Q as a function of the standard deviation Σ of systematic patient setup errors, for the nodal dosimetric margin. Coverage is calculated using Eqs. (4) and (5).

Figure 5 shows that the dosimetric margin distribution can tolerate values of σ=Σ up to 0.30 cm before Q falls below 0.9. This finding is again consistent with Gordon et al.⁶ That study found that the IMRT plans could tolerate nodal setup errors with σ=Σ = 0.3 cm, which matches the value of 0.30 cm obtained from Fig. 5.

IV. DISCUSSION AND CONCLUSIONS

This work introduces a new concept—DMD—and successfully uses it to explain the sensitivity of a group of prostate IMRT treatment plans to patient setup errors. Margin formulas, including the van Herk margin formula considered here, are conventionally applied to the CTV-to-PTV margin, in the expectation that this will enable treatment plans to tolerate a specified level of patient setup errors (or other geometric errors). This practice is based on the assumption that it is the CTV-to-PTV margin that determines sensitivity to setup errors.

However, patients' sensitivity to setup errors is in reality determined by the dosimetric margin distribution, i.e., the distribution of margins from the CTV to the treated volume. In general, dosimetric margins extend beyond the CTV-to-PTV margin. As a consequence, if a margin formula derived from a specific target coverage criterion is applied to the CTV-to-PTV margin, it can overcompensate for setup errors and will achieve a level of target coverage that is higher than the specified value. Conversely, the resulting plans will tolerate larger setup errors than one would naively expect.

The starting point for this work was an apparent disagreement between the van Herk margin formula and the results of setup error simulations on 27 IMRT plans created with an in-house IMRT algorithm. The conclusion is not that the VHMF is wrong, but rather that is being misapplied to the CTV-to-PTV margin. This work shows that it should in fact be applied—or used in conjunction with—the dosimetric margin distribution.

As noted, the dosimetric margin distribution developed here is a generalization of the ICRU conformity index. In conjunction with an appropriate model of setup errors, it provides a measure of plans' robustness to setup errors. More generally, the dosimetric margin distribution has the potential to be a useful tool in both assessing the effects of setup errors on treatment plans and in modifying plans so that they are more robust with respect to errors. Image guided radiation therapy and adaptive radiation therapy are reducing geometric uncertainties and are therefore driving toward smaller PTV margins. In this environment, evaluation of the DMD will be a valuable tool in defining appropriate margins.

In this work, the treated volume was defined to be the volume enclosed by the planned PTV minimum dose isodose surface. However, alternative definitions that are consistent with the ICRU framework could also be used. For example, the TV could be defined with respect to the PTV D₉₈ or D₉₅, rather than D_min. This would differ from van Herk's original margin model, which was formulated in terms of D_min. However, it could have advantages in terms of producing more stable treated volumes, i.e., TVs that are less variable due to small dose variations at the fringe of the PTV.

It is worth noting that for the same nominal CTV-to-PTV margin size, the dosimetric margin distribution is likely to vary with the type of treatment (3DCRT, IMRT, etc.), the treatment site, the particular patient geometry, the beam arrangement, and the treatment planning system. One would expect IMRT plans to be more conformal to the PTV than traditional plans. Conformality is also likely to vary with the treatment site and patient, due to the differing position of the target with respect to surrounding critical structures. Finally, the DMD may vary between treatment planning systems, due to their differing approaches to inverse planning.