An energy transfer method for 4D Monte Carlo dose calculation

Abstract

This article presents a new method for four-dimensional Monte Carlo dose calculations which properly addresses dose mapping for deforming anatomy. The method, called the energy transfer method (ETM), separates the particle transport and particle scoring geometries: Particle transport takes place in the typical rectilinear coordinate system of the source image, while energy deposition scoring takes place in a desired reference image via use of deformable image registration. Dose is the energy deposited per unit mass in the reference image. ETM has been implemented into DOSXYZnrc and compared with a conventional dose interpolation method (DIM) on deformable phantoms. For voxels whose contents merge in the deforming phantom, the doses calculated by ETM are exactly the same as an analytical solution, contrasting to the DIM which has an average 1.1% dose discrepancy in the beam direction with a maximum error of 24.9% found in the penumbra of a 6 MV beam. The DIM error observed persists even if voxel subdivision is used. The ETM is computationally efficient and will be useful for 4D dose addition and benchmarking alternative 4D dose addition algorithms.

INTRODUCTION

During radiation therapy delivery, the underlying patient geometry can change on a fraction-by-fraction basis, or, during a fraction via intrafraction motion, such as that caused by respiratory motion. These changes result in a time-dependent delivered dose distribution. The introduction of image-guided techniques such as in-room computed tomography (CT) imaging, four-dimensional (4D) CT, and real-time tumor tracking coupled with deformable image registration techniques has enabled the ability to track patient geometry changes throughout the course of radiation therapy treatment. The expected cumulative response (e.g. TCP, NTCP, …) of a time dependent dose delivery can be determined by accumulating the response effect estimates on the changing patient geometry, or, for responses that are proportional to dose, by mapping the time dependent dose distributions to a common time point (on a common geometry) and then performing the response analysis. This latter method must use some form of deformable dose mapping or deformable dose addition (DDA) to determine the cumulative dose. DDA allows delivered-dose-based treatment adaptations and potentially, a more accurate assessment of the patient dose-response relationship.

Several groups have studied and used various DDA processes.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} In DDA, dose delivered to a floating source image (I_S) is mapped to its physical location on a fixed reference image (I_R) via the use of a displacement vector field (DVF) which relates the locations of points in I_S to those in I_R. [Our terminology differs slightly from DIR literature where the terms “moving” (floating, source) and “fixed” (target, reference) are found. Deformable image registration (DIR) image labels refer to the DVF direction: moving image points are moved to the fixed target image. For dose mapping, the DVF direction required (hence, DIR labels of moving and fixed images) depends upon the dose mapping algorithm. In this article, I_S refers to the image where radiation is delivered and I_R refers to the image that dose is being mapped to.] The DVF is typically obtained by performing DIR. As will be observed below, the direction of the DVF (from I_R to I_S or from I_S to I_R) depends on the algorithm used in the dose mapping. The most common dose mapping method is to compute the dose delivered from a radiation fluence incident on I_S, then map that dose to I_R in a dose-calculation post processing step. For each voxel in I_R, the DVF is used to identify the location in I_S which corresponds with the I_R voxel’s center, and the dose at I_R’s voxel center is assigned to be equal to the dose at the corresponding point in I_S.

A weakness of this method is that a true one-to-one correspondence between image or dose voxels in I_S and I_R is unlikely to exist; in reality, the tissue contents contained within I_S’s voxels are rearranged (split or merged) in I_R’s voxels. Consequently, some compensation mechanism must be provided in the DDA process to account for the rearrangement of the energy deposited per unit mass, particularly in dose gradient regions. For a 4D-lung case, Flampouri et al.⁷ employed the above approach, termed the center of mass (COM) approach, to move the dose in each voxel for one breathing phase I_S to its corresponding location in a reference breathing phase I_R. Rosu et al.⁶ observed that reducing the dose grid point spacing, subdividing I_R voxels into octants, and interpolating the dose within I_S prior to dose mapping reduced differences between deformed dose estimates in dose gradient regions when a trilinear interpolation method was used to evaluate the dose at the point in I_R. However, although Rosu et al. showed reduced differences between the methods, they were not able to demonstrate that the method converged to the correct dose estimate since they did not have a gold standard.

For Monte Carlo (MC) dose calculations, Paganettiet al.^{5, 11} used GEANT4 with simulated 4D organ motion, computing the dose mapping from multiple breathing phases (I_S’s) to a single I_R in a single simulation. Similar to the previous works, DVF-based voxel displacement maps were used to map dose deposition per voxel to I_R, effectively utilizing a COM dose mapping.

In the above approaches, the information mapped is dose, and thereby they can be regarded as dose interpolation methods (DIMs). Due to the fact that both energy deposition by the radiation source can be nonuniform and mass redistribution by the organ deformation can be nonuniform, each I_S voxel in a dose mapping process can contribute a different amount of energy deposited to the dose interpreted on I_R. An interpolation of the dose distribution without weighing the source voxel contributions is not sufficient to guarantee accurate deformable dose calculation (see Sec. 2A).

To circumvent errors introduced by mapping dose distributions computed on a regular rectilinear grid via application of the DVF, Heath et al.⁹ developed the MC code defDOSXYZnrc, which used a DVF to directly warp the dose grid established on I_R onto I_S. We call their method the voxel warping method (VWM). The VWM results in an irregular dose grid on I_S composed of irregular dodecahedron voxels whose tissue contents are then the same as in I_R. While the dodecahedron voxel is only an approximation of its physically deformed geometry, it generally circumvents the effects of voxel material variations that impair traditional DDA implementations (after a scaling procedure characterized by the DIR mapping is used to account for voxel mass density variation between I_S and I_R). This Monte Carlo specific calculation using deformed voxels was implemented by modifying the DOSXYZnrc Monte Carlo dose calculation algorithm.⁹ Although not reported, one can estimate that the deformed-voxel approach will take ∼2–6 times longer than a standard DOSXYZnrc dose computation due to the number of irregular boundaries that must be checked at each particle step. In addition, to prevent collapsing or merging of the dodecahedral voxels on I_S due to DIR errors, the VWM voxel size must be much larger than the image registration errors.

To avoid the voxel merging related issues suffered by VWM and allow accurate high-resolution deformable dose mapping, this article presents a new method for mapping of Monte Carlo computed dose distributions. We call this the energy transfer method (ETM). In the ETM, the particle transport takes place in a typical rectilinear grid in the source image I_S, however, the energy deposition events are mapped using the DVF to the reference image I_R. Note, this DVF has the opposite sense of the DVF used for the DIM methods. The dose in each voxel in I_R is simply defined as the ratio of the deposited energy (mapped into the voxel in the reference image from possibly various different I_S’s images and image locations) and the mass of the voxel in the reference image. Conceptually, ETM’s separation of the radiation transport and energy deposition grids is similar to the Peregrine concept of using “dosels” to score the energy deposition,¹² the MCNP5∕MCNPX mesh tally concept,^{13, 14} and the use of nonvoxelized geometries in DOSXYZnrc.¹⁵ The ETM method is free of the excessive computational burden in VWM and the dose transfer inaccuracy of DIM.

The goal of this article is to describe the implementation and testing of the ETM. The testing is performed on simple digital phantoms with invertible DVFs that are manually generated. For these test cases, the true dose mapping solution can be directly determined. The digital phantoms are specifically selected to demonstrate specific instances which may exist within a deformed image. By using digital phantoms, we demonstrate potential errors in DIM, and that the ETM agrees with the true dose. This article does not perform any clinical 4D dose calculations since doing so would require use of a DIR algorithm to generate the DVF maps between I_S and I_R, and the dose mapping would be dependent upon the accuracy of the DVFs. Clinical application of ETM and the evaluation of the clinical significance of DVF induced dose mapping errors are saved for future work. As developed, ETM will be useful by itself as a fast, MC specific dose mapping method as well as for a general voxel-based dose mapping QA tool.

MATERIAL AND METHODS

Begin with two (or more) presentations of the patient anatomy with I_R being the fixed reference image set to which information from (multiple) source image(s) I_Si=I_i will be mapped. Let x be a three-dimensional (3D) position in I_R and x^′ the corresponding location of x in I_i. The DVF mapping φ_i→R(x^′) maps the coordinates of a tissue element contained at x^′ in I_i to its location x in I_R. Similarly, φ_R→i(x) maps the coordinates x from the reference image I_R to x^′ in the source image I_i. We use ϕ_i→R to denote φ_i→R(x^′)∀x^′. Denote the radiation dose at x^′ computed on I_i as d(x^′∣I_i,Ξ_i)=d_i(x^′), where Ξ_i represents the radiation source used to deliver the radiation. For DDA or dose mapping, d_i(x^′) needs to be interpreted at the reference image set as d_i→R(x)=d_i[φ_i→R(x^′)]=d_i→R[x^′,∣I_i,Ξ_i,φ_i→R(x^′)], where the subscript i→R is retained on the dose to indicate that it is a reinterpretation of the dose received on anatomy I_i (from source Ξ_i) mapped to anatomy I_R. The detailed representation of d_i→R(x) depends on different dose interpretation strategies used and will be discussed in the next section. Deformable dose addition involves determining the cumulative patient dose D_R(x) by adding the dose over all presentations of the patient’s anatomy, i.e., D_R(x)=∑_id_i→R(x)=∑_id_i[φ_i→R(x^′)].

Without loss of generality, in this work a single source image set is considered, therefore, i=1, and S can be substituted into the expressions to yield D_R(x)=d_S→R(x)=d_S[φ_S→R(x^′)]. In this case, deformable dose addition is simplified to deformable dose mapping.

Analysis of dose mapping

Recall that dose is energy deposited per unit mass. In Monte Carlo simulations, dose is typically evaluated over some volume V. Physiologically, V can change without appreciable changes in mass, such as during breathing. Likewise, physical changes can result in changes in mass, including mass elements in which dose is deposited, such as in expelling the bladder or rectal contents. In this work, it is assumed that the mass in which energy depositions occurs is preserved during the image deformation process, however, if φ properly keeps track of mass changes, the ETM described below will hold.

Dose interpolation methods

Suppose a volume is deformed from I_S to I_R, and suppose material loss or gain during the deformation is negligible. When the dose calculated from energy deposited within the volume at the I_S is warped to I_R, directly mapping the dose d^′=d_S or its spatial interpolation to the I_R can be inadequate.

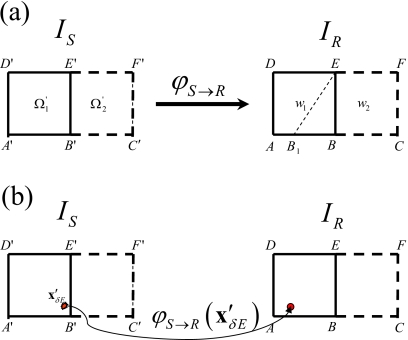
Consider the following example: Let v₁ and v₂ be two adjacent voxels from I_S which, as a result of tissue deformation, are merged into a single voxel w₁ on I_R (see Fig. 1). A clinical example of this could result in the lung, with I_S being an inhale image and I_R being an exhale image. The dose interpolation method assigns dose delivered on I_S to I_R as

$$d^{\mathrm{DIM}}\left(w_1\right)=d_{S\to R}^{\mathrm{DIM}}\left(w_1\right)=\frac{d^{\prime }\left(v_1\right)+d^{\prime }\left(v_2\right)}{2}=\frac{E\left(v_1\right)∕M\left(v_1\right)+E\left(v_2\right)∕M\left(v_2\right)}{2},$$ (1)

where E(v_x) and M(v_x) are the energy deposited and the mass in voxel v_x, respectively. However, the correct interpretation of the dose d^T(w₁) is

$$d^T\left(w_1\right)=\frac{E\left(v_1\right)+E\left(v_2\right)}{M\left(v_1\right)+M\left(v_2\right)}=\frac{d^{\prime }\left(v_1\right)+d^{\prime }\left(v_2\right)\gamma }{1+\gamma },$$ (2)

$$\gamma =\frac{M\left(v_2\right)}{M\left(v_1\right)}.$$

It follows that the dose interpolation error is

$$\epsilon \left[d^{\mathrm{DIM}}\left(w_1\right)\right]=\mid d^{\mathrm{DIM}}\left(w_1\right)-d^T\left(w_1\right)\mid =\frac{\mid [d\left(v_2\right)-d\left(v_1\right)](1-\gamma )\mid }{2(1+\gamma )}.$$ (3)

If the material is homogenous, then γ=1, and ε[d^DIM(w₁)]=0. However, for heterogeneous regions, such as lung, if M(v₁) is ICRU tissue (ρ=0.302–1.101 g∕cm³) and M(v₂) is ICRU lung (ρ=0.044–0.302 g∕cm³),^{16, 17} γ could be large (>20), resulting in large dose mapping errors for the DIM, especially in the region with steep dose gradients [i.e., ∣d(v₂)−d(v₁)∣⪢0].

Figure 1.

An example deformation which demonstrates a failure of the DIM. In this deformation, voxel v₀ is directly mapped to voxel w₀, voxels v₁ and v₂ are merged into voxel w₁, and voxel v₃ is directly mapped to voxel w₂.

As an example, let the voxel masses M(v₀)=M(v₁)=2 and M(v₂)=M(v₃)=1 and the energy deposited in the voxels E(v₀)=E(v₁)=E(v₂)=E(v₃)=2 for the I_S indicated in Fig. 1. This results in the dose d^′(v₀)=d^′(v₁)=1 and d^′(v₂)=d^′(v₃)=2. The voxel merging that occurs in the transformation to I_R results in M(w₀)=2, M(w₁)=3, M(w₂)=1; E(w₀)=E(w₂)=2, E(w₁)=4; yielding doses of d^T(w₀)=1, d^T(w₁)=1.33, and d^T(w₂)=2. However, DIM yields d^DIM(w₁)=1.5 with ε[d^DIM(w₁)]=0.17. Furthermore, it is easy to show that subdividing voxel w₁ into any number of equal subdivisions (such as octant subdivisions for 3D voxels by Rosu et al.⁶) and averaging these subdivisions results in d^DIM(w₁)=1.5. Therefore, DIM has an inherent dose interpolation error for merging voxels which cannot be corrected by voxel subdivision.

Energy transfer method

The ETM directly maps each particle energy deposition occurring in I_S to I_R. To demonstrate, consider a deformation of two adjacent voxels from the simplified two-dimensional images given in Fig. 2. Voxel ${\Omega }_1^{\prime }=\left(A^{\prime }{B}^{\prime }{E}^{\prime }{D}^{\prime }\right)$, $({\Omega }_1^{\prime }\subset I_S)$, is mapped to ${\phi }_{S\to R}\left({\Omega }_1^{\prime }\right)=\left(A{B}_{1}ED\right)$, $[{\varphi }_{S\to R}\left({\Omega }_1^{\prime }\right)\subset I_R]$ which is different from the regular voxel w₁=(ABED), (w₁⊂I_R). Actually $w_1={\phi }_{S\to R}\left({\Omega }_1^{\prime }\right)\cup \left(B_{1}BE\right)$ with the domain (B₁BE) warped from some part of ${\Omega }_2^{\prime }$. To calculate the dose at w₁ with the ETM, the particle energy deposition events (δE) occurring at point ${\mathbf{x}}_{\delta E}^{\prime }$ within ${\Omega }_1^{\prime }$ and ${\Omega }_2^{\prime }$ are mapped to w₁ and w₂ using ${\phi }_{S\to R}\left({\mathbf{x}}_{\delta E}^{\prime }\right)$.

Figure 2.

(a) Example voxels from source and reference images used to explain the ETM. (b) In the ETM, energy depositions occurring in I_S at ${\mathbf{x}}_{\delta E}^{\prime }$ are mapped to I_R using the deformation vector field ${\phi }_{S\to R}\left({\mathbf{x}}_{\delta E}^{\prime }\right)$ without requiring detection of the deformed boundary B₁E.

After particle transport is completed for all particles, the dose in w₁ is set equal to the sum of all energy depositions in w₁ divided by the mass of w₁.

ETM is implemented by modifying the DOSXYZnrc MC code.¹⁸ We call the modified code etmDOSXYZnrc. As input, in addition to the incident radiation source, etmDOSXYZnrc requires voxel boundary locations and materials for both I_S and I_R, as well as the DVF φ_S→R to describe the coordinate deformations. Voxelized material maps m(S) and m(R), created using the CTCREATE code, are required: m(S) is utilized in the EGSnrc particle transport routine for determining cross sections during particle tracking, while m(R) is used for energy scoring and dose determination at the completion of particle transport.

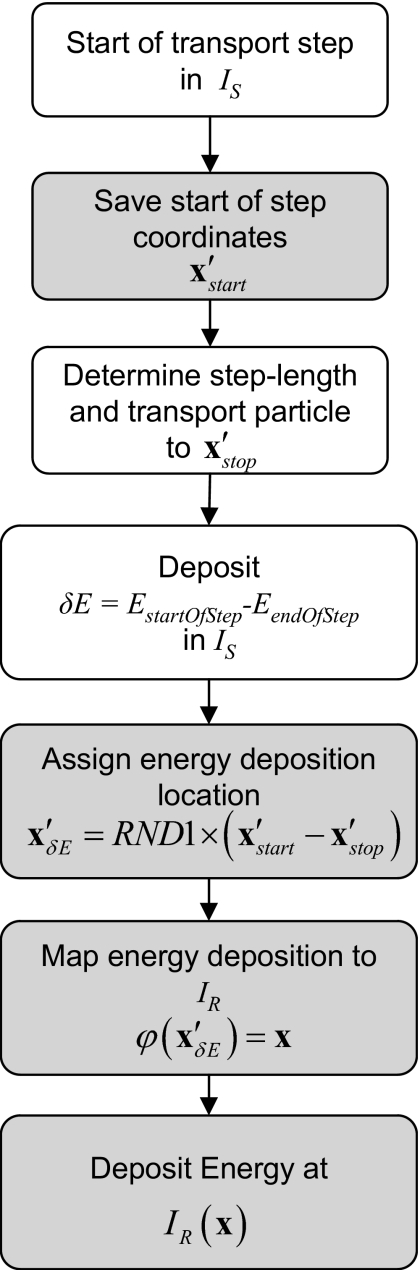
The schematic flow for a particle step in ETM is given in Fig. 3.

Figure 3.

Schematic flow of a particle transport step for the ETM as implemented in etmDOSXYZnrc. Boxes in gray are additional steps required by the ETM. The RND1 function selects a pseudorandom number on the interval (0,1].

To accomplish dose mapping in etmDOSXYZnrc, energy deposition at each particle step in I_S is directly mapped to I_R and accumulated in I_R’s voxel space. As a result of the DVF mapping, a particle step path that is wholly contained in a single voxel in I_S can span over two or more voxels in I_R. Since mapping the energy deposition at either end of each transport step will result in a systematic misaccounting of the scoring locations, a random scoring location between the starting and ending points is selected. Alternatively, one could select multiple locations along the step and distribute a fraction of the energy at each substep location, however, this would have required more computations.

In these simulations that follow, the EXACT boundary crossing algorithm is used, thus, single elastic scattering is used to cross the boundaries. This selection has no impact on the comparative results, as validated by test simulations performed (not shown).

The simulations are performed to a nominal statistical uncertainty of ∼2% of the maximum dose. However, this statistical uncertainty is not relevant to the comparison between the DIM and ETM since, for the test cases presented, the dose in I_S and the energy deposited in I_R are scored in a single simulation. Thus, the doses in I_S and I_R are fully correlated. The dose in merged and split voxels can be solved for analytically and deviations with respect to the analytic solution for each method can be attributed to errors inherent to the method.

VALIDATION PROCESSES AND RESULTS

The validation of etmDOSXYZnrc is performed first on a homogeneous phantom for two cases, one with a rigid shift and the other with a one-dimensional deformation. It is then evaluated with a heterogeneous material phantom for a beam parallel to the deformation direction and a beam perpendicular to the deformation direction. In this latter case, the deformation region is located within the beam penumbra. The outputs are compared with the DIM results as well as with analytic solutions. All the tests are performed using previously commissioned phase space files for 6 MV x rays from a Varian Cl2100 machine as input to the Monte Carlo simulation.^{19, 20, 21} BEAMnrc is used to transport the particles through the beam-defining jaws.

Validation with rigid translation

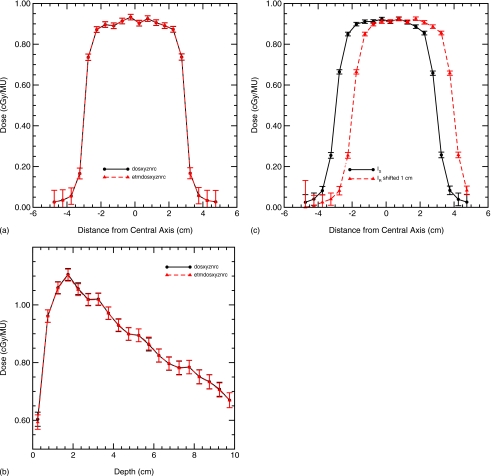
The purpose of this test is to show that the energy deposition warping operations are correct in general. A 10×10×10 cm³ digital phantom with 0.5×0.5×0.5 cm³ voxels is created. The density of each voxel is set equal to 1.0 g∕cm³, corresponding with the material water. The phantom, which is converted to a material density table, serves both as the reference image and as source image. The DVF is set to zero for all voxels to be consistent to the two identical images. The output dose distribution from etmDOSXYZnrc is the same as that from DOSXYZnrc [Figs. 4a, 4b]. In all the figures, doses are indicated at the center of voxels and lines are drawn only to guide the eye.

Figure 4.

Validation of the etmDOSXYZnrc implementation in a homogeneous phantom. (a) The dose lateral profiles at depth=5 cm agree; (b) the central axis depth-dose profiles agree; and (c) a DVF resulting in a 1 cm lateral shift is also correctly computed with etmDOSXYZnrc.

To validate the directions of the implemented energy deposition mapping, a DVF mimicking a 1 cm rigid shift is performed along each axis. The results verified that the warping direction and deformation amplitude are correct and its dose distribution is the same as that from the original DOSXYZnrc except for the expected shift [Fig. 4c].

Validation with a deformable homogeneous phantom

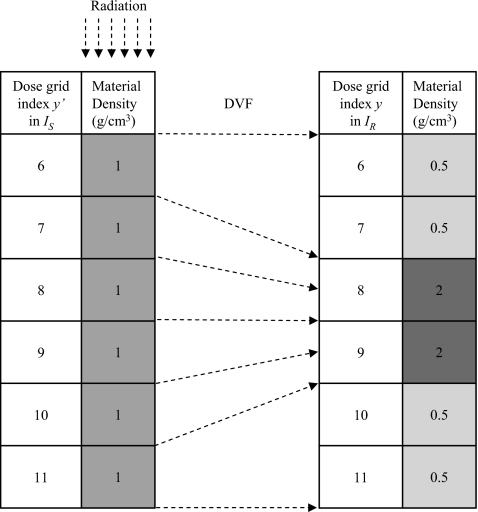
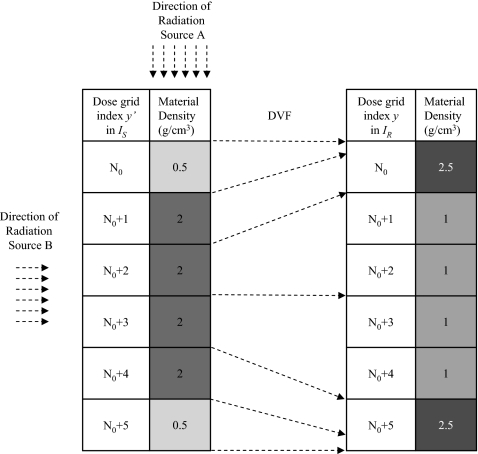
As indicated by Eq. 3, when the transport geometry material is homogeneous (γ=1), the dose discrepancy of the DIM in an exactly merged voxel should be zero. This fact is used to validate the implementation of etmDOSXYZnrc for a deforming geometry. The transport geometry is set to be equivalent to the geometry from the previous test case, a 10×10×10 cm³ digital homogeneous water phantom subdivided into 0.5×0.5×0.5 cm³ voxels. The scoring geometry, however, incorporates splitting and merging of the transport geometry voxels via manual generation of the appropriate DVF. For the sake of simplicity, a one-dimensional deformation in the vertical direction (y axis), which corresponds to the beam direction for this test case, is considered. Let the primed coordinate system (^′) denote the voxel coordinate in I_S and the unprimed system the coordinate in I_R. Figure 5 shows the deformation modeled: voxels y^′(7) and y^′(8) from I_S are merged to voxel y(8) in I_R, while voxel y^′(6) is split to voxels y(6) and y(7). Similarly, y^′(9) and y^′(10) are merged to y(9), and y^′(11) is split to y(10) and y(11).

Figure 5.

A simple test phantom with a homogeneous particle transport geometry (I_S) but heterogeneous particle scoring geometry (I_R). The phantom is 10×10×10 cm³ subdivided into 0.5×0.5×0.5 cm³ voxels. Laterally, all voxels with a given y or y^′ index have the same density. The vectors show the displacement vector field of the voxel edges. Upstream voxels (1–5) and downstream voxels (12–20) have a density 1.0 g∕cm³ in both I_S and I_R.

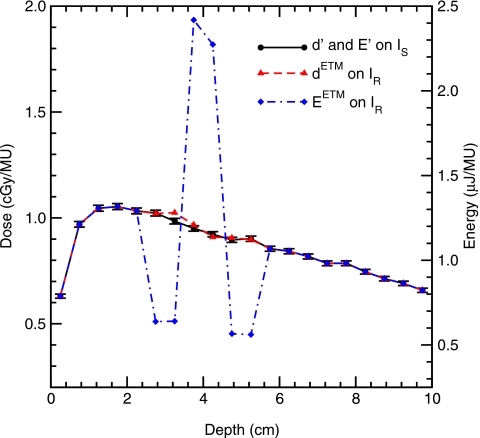
Recall, with the ETM, particle transport is simulated within I_S but energy deposition is scored at a deformed position in I_R. Figure 6 illustrates the deposited energy warped by the mapping given in Fig. 5. The mapped energy is doubled at y(8) and y(9), but halved at y(6), y(7) and y(10), y(11). The resultant dose, being energy per unit mass, does not experience the extreme undulations and is much smoother as indicated in Fig. 6.

Figure 6.

Central axis depth profile of the dose and energy deposited for the phantom indicated by Fig. 5. For clarity, statistical error bars are only plotted for the dose computed on I_S. Error bars on the other quantities are of similar size.

The principle of energy conservation can be simply applied to check the ETM for the merged voxels:

$$E^{\mathrm{ETM}}\left(8\right)=E^{\prime }\left(7\right)+E^{\prime }\left(8\right),E^{\mathrm{ETM}}\left(9\right)=E^{\prime }\left(9\right)+E^{\prime }\left(10\right).$$ (4)

Similarly, since y^′(6) and y^′(11) are split,

$$E^{\prime }\left(6\right)=E^{\mathrm{ETM}}\left(6\right)+E^{\mathrm{ETM}}\left(7\right),\text{and}$$ (5)

$$E^{\prime }\left(11\right)=E^{\mathrm{ETM}}\left(10\right)+E^{\mathrm{ETM}}\left(11\right).$$

In Table 1, the energy E^′ and dose d^′ are calculated in I_S, and E^ETM and d^ETM are calculated in I_R using etmDOSXYZnrc. The results have validated the energy conservation principle described by Eqs. 4, 5. [Deviations in the least significant digit in these tables, e.g., for E^′(11)=E^ETM(10)+E^ETM(11) is due to round-off error of the values given in the table. Actual values agree to within the least significant bit of the precision used in the calculation, fortran double precision].

Table 1.

Energies and doses deposited in the voxels as calculated in I_S (E^′ and d^′) and I_R (E^ETM and d^ETM) using etmDOSXYZnrc for irradiation of the homogeneous phantom that undergoes the non-rigid deformation indicated in Fig. 5.

Dose grid index y or y′:	6	7	8	9	10	11
E′ in IS (μJ∕MU)	1.278	1.230	1.187	1.153	1.120	1.127
EETM in IR (μJ∕MU)	0.638	0.640	2.417	2.273	0.566	0.562
d′ in IS (cGy/MU)	1.023	0.984	0.950	0.923	0.896	0.901
dETM in IR (cGy/MU)	1.021	1.025	0.967	0.909	0.906	0.898

For this test, the exact analytical evaluation of the dose in the merged voxels can be obtained from Eq. 2. Since the source phantom is homogeneous water, γ=1, it follows that the true dose, d^T(8)=[d^′(7)+d^′(8)]∕2=0.967, and d^T(9)=[d^′(9)+d^′(10)]∕2=0.909, exactly equal to the d^ETM values in Table 1, indicating that the ETM and the DIM based dose mapping agree for homogenous material as expected.

Heterogeneous deforming phantom I

When the phantom is heterogeneous, as indicated by Eq. 3, the DIM and ETMs are expected to differ. To test this, a phantom geometry similar to before is configured: A 10×10×10 cm³ digital phantom subdivided into 0.5×0.5×0.5 cm³ voxels with heterogeneous densities in the beam direction for both I_S and I_R as indicated in Fig. 7. The tissue deformation simulated is confined to the region with the y index of the dose grid being between N₀=8 and N₀+5=13.

Figure 7.

A test phantom with particle transport (I_S) and particle scoring geometries (I_R). The arrows show the displacement vector field of the source voxel boundaries. The density of the voxels out of the heterogeneous region, y=y^′<N₀ and y=y^′>N₀+5, in I_S and in I_R is 1.0 g∕cm³. Radiation source A, used for the test given in Table 2, has N₀=8 and the source particles are nearly parallel to the deformation direction of the heterogeneous region, while source B has N₀=12 and the source particle direction nearly perpendicular to the deformation of the heterogeneous region.

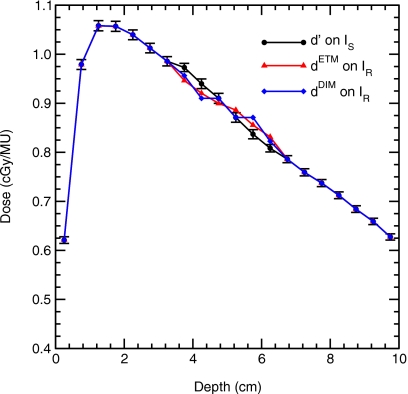
Figure 8 compares the depth-dose results and Table 2 summarizes the results for energy deposition and dose in this geometry for radiation source A, where the source particles are parallel to the direction of the deformation. The ETM results can be directly confirmed. Consider the voxels that merge: y^′(8)+y^′(9)→y(8) with γ=4 and y^′(12)+y^′(13)→y(13) with γ=0.25. Analytic solutions using Eq. 2 yield d^T(8)=[d^′(8)+d^′(9)γ]∕(1+γ)=0.946 and d^T(13)=0.831, exactly equal to d^ETM(8) and d^ETM(13), respectively. Also given in Table 2 are the doses calculated by the DIM as well as the relative error in the DIM, calculated via μ^DIM(y)=(∣d^DIM(y)−d^ETM(y)∣)∕d^ETM(y).

Figure 8.

Central axis depth-dose profiles computed in the geometry indicated in Fig. 7 with source A. The deformation was confined to voxels whose centers are located at depths of 3.75–6.25 cm. One standard deviation statistical error bars are shown on the d^′ only, statistical errors in d^ETM and d^DIM are of the same size. However, deviations between the d^ETM and d^DIM are not statistical due to the correlated method of scoring the data.

Table 2.

Energies and doses deposited in the voxels indicated as calculated in I_S by DOSXYZnrc (E^′ and d^′) and etmDOSXYZnrc (E^ETM and d^ETM) for irradiation of the heterogeneous phantom that undergoes the nonrigid deformation indicated in Fig. 7 with source A. Also shown is the dose computed by the DIM and the relative DIM error (μ^DIM).

Dose grid index y	8	9	10	11	12	13
E′(y′) in IS (μJ∕MU)	0.608	2.349	2.275	2.178	2.092	0.505
EETM(y) in IR (μJ∕MU)	2.958	1.150	1.125	1.108	1.070	2.598
d′(y′) in IS (cGy/MU)	0.973	0.940	0.910	0.871	0.837	0.808
dETM(y) in IR (cGy/MU)	0.946	0.920	0.900	0.886	0.856	0.831
dDIM(y) in IR (cGy/MU)	0.956	0.910	0.910	0.871	0.871	0.823
μDIM(y) (%)	1.05	1.12	1.15	1.71	1.80	1.05

The DIM dose error ranges from 1.0% to 1.8% in the deformation region for this simple test case.

Note, the randomly selection of the scoring location along the particle step has no impact on the deviations presented in these results. For the merged voxels, the DVFs are aligned to match voxel boundaries in I_S and I_R and particle steps in DOSXYZnrc are contained within an I_S voxel. Thus, selection of any point along the particle step result in the energy deposition occurring in the same I_R voxel. For I_S voxels which split in I_R, the randomization along the particle step will result in typical MC statistical variations, however, due to our correlated scoring in I_S and I_R, the comparisons with respect to the true dose deposited is unaffected. Also note, the randomization of energy deposition along a particle step will be important for cases where the DVF is not aligned to match voxel boundaries, as would occur for clinical DVFs.

Heterogeneous deforming phantom II

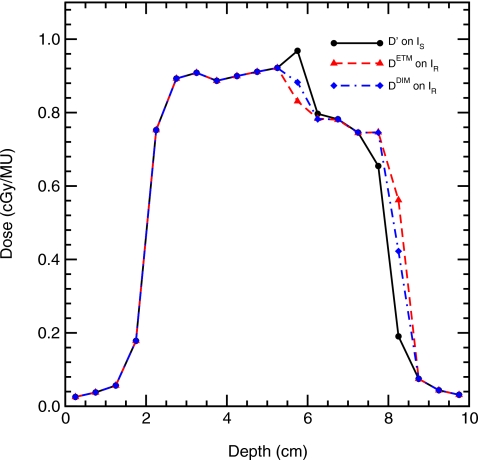
Equation 3 indicates that regions with steep dose gradients are susceptible to errors when the DIM is used, a fact observed by Rosu et al.⁶ and Heath et al.⁹ To quantify the DIM dose error in a dose gradient region, source B is applied to the deformation schematically presented in Fig. 7, therefore the direction of the incident beam is nearly perpendicular to the direction of the phantom deformation. For this test N₀=12 with a 6×6 cm² field size. The interface between voxel y^′=10 and y^′=11 is at the center of the beam while y^′=N₀+4=16 and y^′=N₀+5=17 are at the beam penumbra. These two voxels merge into voxel y=N₀+5=17 in I_R.

Results for this test case at a depth of 5 cm in the phantom are shown in Fig. 9. Substantial differences between the dose in the I_S and I_R geometries are observed for voxels that are deformed, indicating the need for performing dose warping. Furthermore, DIM errors are evident in this geometry. Specific values of the energy deposited and dose computed with each method are listed in Table 3. For the merged voxel y^′(16)+y^′(17)→y(17), γ=0.25, and the correct dose generated from Eq. 2 is d^T(17)=[d^′(16)+d^′(17)γ]∕(1+γ)=0.562, exactly equal to d^ETM(17), but the result of the dose interpolation is d^DIM(17)=0.422, resulting in μ^DIM(17)=24.9%. Similarly, y(12) is a merged voxel consisting of heterogeneous materials, and d^ETM(12)=0.831, the same as that calculated by Eq. 2. These tests have validated etmDOSXYZnrc’s correctness for dose mapping with merged voxels.

Figure 9.

Dose profile results at a depth of 5 cm for irradiation of the deformation indicated in Fig. 7 by source B, where the deformation is nearly perpendicular to the source particle directions. Monte Carlo statistical errors are not included on this plot since the correlated scoring method results in the fact that differences with respect to the DIM error are not statistical in nature.

Table 3.

Energies and doses deposited in the voxels indicated as calculated in I_S (E^′ and d^′) and (E^ETM and d^ETM) using etmDOSXYZnrc for irradiation of the heterogeneous phantom that undergoes the nonrigid deformation indicated in Fig. 7 with N₀=12 and source B. Also shown is the dose computed by the DIM, and percentage DIM error (μ^DIM).

Dose grid y or y′	12	13	14	15	16	17
E′ in IS (μJ∕MU)	0.605	1.991	1.956	1.865	1.637	0.119
EETM in IR (μJ∕MU)	2.596	0.980	0.975	0.931	0.933	1.756
d′ in IS (cGy/MU)	0.968	0.797	0.782	0.746	0.655	0.190
dETM in IR (cGy/MU)	0.831	0.784	0.780	0.744	0.747	0.562
dDIM in IR (cGy/MU)	0.882	0.782	0.782	0.746	0.746	0.422
μDIM (%)	6.2	0.18	0.27	0.19	0.10	24.9

Note in I_S image, the material density at the voxel y^′=12 is 0.5 g∕cm³, less than its neighboring voxels at y^′=11 and y^′=13 with densities of 1.0 and 2.0 g∕cm³, respectively. On I_S, the dose at voxel y^′=12 is elevated due to photons streaming from the source down the low density region. The dose interpolation error at this point is μ^DIM(12)=5.7%, even though this point is not in a steep dose gradient or beam penumbra region. Similar to the above case, Heath et al.⁹ compared a trilinear DIM to their VWM for a 0.5 cm voxel under 50% compression and found DIM had an average of 8% dose error in non-penumbra regions.

DISCUSSION

The ETM presented in this article functions by separating the radiation transport and energy scoring grids for a Monte Carlo dose computation. ETM treats the energy deposited in each voxel as a pseudocontinuous distribution instead of the dose accumulated at the voxel center of mass as in the center of mass or subdivisions thereof, such as octants for Rosu’s trilinear method.⁶ The infinitesimal particle-based energy deposition mapping provides a natural and accurate way to map dose.

For the merged voxels shown in Fig. 7, the outputs of ETM exactly match their analytic solutions, while DIM demonstrated errors as high as 24.9% errors for a deformed voxel within the beam penumbra. In these tests, the material heterogeneity ratio of two adjacent voxels is 4, which is not as large as what could be observed clinically, where adjacent voxels in lung could have a density ratio of up to 20. As illustrated in Eq. 3, the high contrast in two adjacent voxels’ densities in a deforming region could result in a large discrepancy.

In the test cases presented, the registration error is zero via the use of manually generated hypothetical DVFs. As a result, each dose voxel is exactly recovered from voxels in the source image. This results in the warped source image identical to the reference image. Consequently, for the test cases presented, the difference between DIM and ETM is due entirely to DIM’s equal weighting of the dose deposition to the reference volume elements instead of the variable energy deposition weighting that naturally occurs with ETM.

As is the case for DIM, use of ETM for clinical cases will require use of DIR algorithms to determine the DVF mappings between I_S and I_R. Both DIM and ETM will propagate errors in the DVFs, however, they may propagate the errors differently. This analysis is left to future work. For ETM, evaluation is required to see if mass of the reference (target) image, mass of the deformed source image (with or without density corrections^{9, 10}), or some other method should be used to determine the mass that the mapped energy should be divided by to get the dose.

By using simple known DVFs that match on voxel boundaries, this study also avoided inaccuracies inherent to three-dimensional interpolation.²²

The GEANT4 4D MC implemented by Paganetti, which allows the ability for pseudocontinuous geometry changes^{5, 11} currently maps particle dose using a COM method.⁷ Therefore, one would expect that it would be susceptible to the DIM errors demonstrated here.

The ETM and VWM of Heath et al.⁹ differ in the information they map and in the particle transport. The VWM maps the dose at an irregularly shaped voxel in the warped source image to a regularly shaped voxel in the reference image. As a result, the irregular boundaries of the dodecahedral voxels must be detected for each particle transport step. The ETM simulates the particle transport within the source image, but scores the energy deposition at its warped location in the reference image. Therefore, no irregular boundary detection is required, and the dodecahedral approximation is unnecessary. For the test cases presented here, we would expect the VWM to give identical results to the ETM method. In general cases, we would expect the ETM to be faster and possibly more accurate since ETM does not require the (arbitrary) selection of which voxel corners are coplanar in the generation of planes to create the dodecahedral voxels. ETM’s separation of the particle transport and the energy deposition grids allows the dose scoring or reference grids to be higher resolution (e.g., the same as its image resolution) than the VWM allows if an appropriate image registration can be made. Recall, the VWM method used fairly coarse voxel sizes to prevent merging of adjacent voxels (due to DIR errors) when creating the dodecahedral voxels.

Compared with the VWM, the ETM handles the case of voxel merging in a natural way, and consequently it is computationally efficient. As implemented, the ETM increases DOSXYZnrc’s computation time by ∼10% (from 250.7 to 275.6 s for a sample test case), but allows an accurate dose addition on any deformable anatomies. The etmDOSXYZnrc implementation was not optimized for speed. Furthermore, it should be noted that for the ETM test cases, the incident particles in each voxel are warped with the same displacement field; hence, no interpolation of the DVF is required. In clinical cases, interpolation of the DVF for each energy deposition may be required unless the DVF is saved with sufficiently high resolution to merit errors introduced by assigning the DVF from a nearest neighbor voxel as negligible. If repeated DVF interpolation is required, it will degrade the efficiency of the ETM.

In ETM, since the energy transport and energy scoring grids are separate, it is immediately apparent that the ETM method is applicable to MC implementations which merge neighboring voxels or use nonvoxelized geometries for code speed up.¹⁵ For ETM, there is no requirement that the transport and scoring grids be of the same resolution or of the same shape.

Although implemented in DOSXYZnrc in which charged particle steps are contained within a given voxel, the ETM approach is general and could be applied to MC codes in which charged particle steps span over several voxels. For algorithms that have large electron steps which span multiple voxels, it may be more efficient to deposit a fraction of the step energy deposition at multiple random locations along the particle step than to use a single random location as is done in this study.

With the ETM it would be possible to map energy depositions from multiple different source anatomies to multiple different “reference” anatomies simultaneously. An example where this could be useful is in 4D IMRT optimization for 4D lung cases. In this case, beam intensities are simultaneously optimized on multiple breathing phases, thus, accurate dose evaluation is desired not only at a reference phase, but also at each phase of the breathing cycle. The alternative, mapping dose to a common reference phase then remapping that dose using a DIM, could introduce dose evaluation errors.

While MC dose algorithms are “volumetric” dose computations, integrating the energy deposition over the volume of the voxels, non-MC dose algorithms are typically point-based computations, with the point separation indicated by the voxel coordinates and spacing. Errors in the DIM method shown in this work suggest that the proper way to do 4D dose addition or 4D dose mapping for non-MC dose algorithms is not by interpolating dose at points, but instead by mapping the energy deposited and voxel mass. If this method were applied to the test case of Fig. 1, integrating the energy deposited within the bounds of voxel w₁ mapped from image I_S would have resulted in correct mapping of the dose. In realistic cases, where voxel boundaries do not exactly match on I_S and I_R, the integration can be complex. In this case, it may be beneficial to compute the dose at each point in I_S with the point-based dose computation instead of interpolating the dose and to use multiple points in the integration. These issues will be studied further in future studies.

CONCLUSION

Deformable dose calculation may provide an accurate evaluation of the delivered dose on a deforming anatomy for adaptive treatment planning and for treatment outcomes analysis. In this article, a new Monte Carlo dose calculation scheme is implemented and validated with different tissue deformation cases. Its separate treatment of particle transport and energy deposition within the dose mapping process eliminates the inaccuracy inherent to dose interpolation methods as illustrated in Eq. 3. The ETM method is computationally efficient. In general, given a correct DVF, the MC-based ETM could achieve better accuracy than a voxel-based dose interpolation approach for heterogeneous geometries. While dose interpolation methods are applicable to arbitrary dose calculation algorithms, accuracy would be improved by integrating the mapped energy deposited and mass.

Compared with VWM, the ETM does not require the dodecahedral voxel approximation and is time efficient. ETM increases DOSXYZnrc’s computation time by about 10%. Additionally, it allows for arbitrary image registration resolution while avoiding voxel merging issues. However, like other methods, the ETM accuracy will be degraded by inaccuracies in image registration, which requires further investigation.