Ultra-low Output Impedance RF Power Amplifier for Parallel Excitation

Abstract

Inductive coupling between coil elements of a transmit array is one of the key challenges that parallel RF transmission faces. An ultra-low output impedance RF power amplifier concept was introduced to address this challenge. In an example implementation, an output-matching network was designed to transform the drain-source impedance of the MOSFET into a very low value for suppressing inter-element coupling effect, and meanwhile, to match the input impedance of the coil to the optimum load of the MOSFET for maximizing the available output power. Two prototype amplifiers with 500W output rating were developed accordingly, and were further evaluated with a transmit array in phantom experiments. Compared to the conventional 50Ω sources, the new approach exhibited considerable effectiveness suppressing the effects of inter-element coupling. The experiments further indicated that the isolation performance was comparable to that achieved by optimized overlap decoupling. The new approach, benefiting from a distinctive current-source characteristic, also exhibited a superior robustness against load variation. Feasibility of the new approach in high field MR was demonstrated on a 3T clinical scanner.

INTRODUCTION

Parallel RF transmission with multiple transmit elements promises to advance high field MR and benefit various applications. In high field MR B₁ inhomogeneity caused by wave propagation and dielectric resonance effects in particular may be reduced by optimizing the amplitude and phase of the driving currents when conducting multi-port excitation on birdcage coils (1,2) or transmit arrays consisted of individual coil elements (3-5). It is possible to further reduce B₁ inhomogeneity effect by independently controlling the waveform of individual transmit channels (6-8), which leverages the capacity of full-fledged parallel RF transmission in accelerating multi-dimensional excitation (9,10) and managing RF power deposition (10,11).

Recent hardware development has provided support for direct validations of full-fledged parallel RF transmission principles (12-15). There remain significant challenges however, which include the development of efficient parallel transmit coil arrays. Unlike the well-established preamplifier decoupling approach for parallel receive (16), for parallel transmit, typical RF amplifiers’ 50Ω impedance seen by the coils in effect rules out the possibility of practicing an analogous scheme. Coupling between transmit coil elements still remains one of the key challenges to transmit coil array construction and use. Many decoupling methods have been proposed to address the inter-coil coupling problem. One category of methods introduces partial geometric overlap of coils to annul the mutual inductance between them (16, 17). Such methods are effective for nearest neighbor elements only, and tend to impose stringent constraints on the geometry and placement of the individual coils. Another category of methods employs a capacitive or inductive decoupling bridge or a multi-port network (18-21), at the cost of increased RF loss and increased complexity of the decoupling circuits and tuning efforts. A third category of methods suppresses the coupling-induced currents with high source impedance, by, for example, integrating RF power MOSFET’s with the rungs of a TEM coil (22, 23) or driving nonresonant loop-shaped coils directly (24). In these examples, a MOSFET is configured to function approximately as a current source, and thus to yield high impedance at the driving ports. However, the series resonant element in this method also acts as a severely mismatched load to the MOSFET, which may significantly degrades its maximum available output power. A fourth category of methods applies active decoupling. Such methods calibrate coupling between element coils first and then introduce proper correlations, realized either by analog circuits (25) or a digital vector modulation array (26, 27), between the driving voltages of each element to cancel the coupling components in the currents.

In this work, inspired by the approach of using ultra-low input impedance preamplifiers for receive coil arrays (16), we explore the possibility of accomplishing inter-element isolation for parallel transmit through ultra-low output impedance power amplifiers. Our goal is to develop RF power amplifiers that effectively support parallel transmit applications and a decoupling method that facilitates transmit performance optimization (11) by eliminating constraints on array geometry. A theoretical analysis was carried out, then a practical circuit was proposed. Two prototype amplifiers were accordingly developed. Experimental studies were conducted to verify the new concept, to evaluate the prototype amplifier designs, and to investigate the decoupling performance.

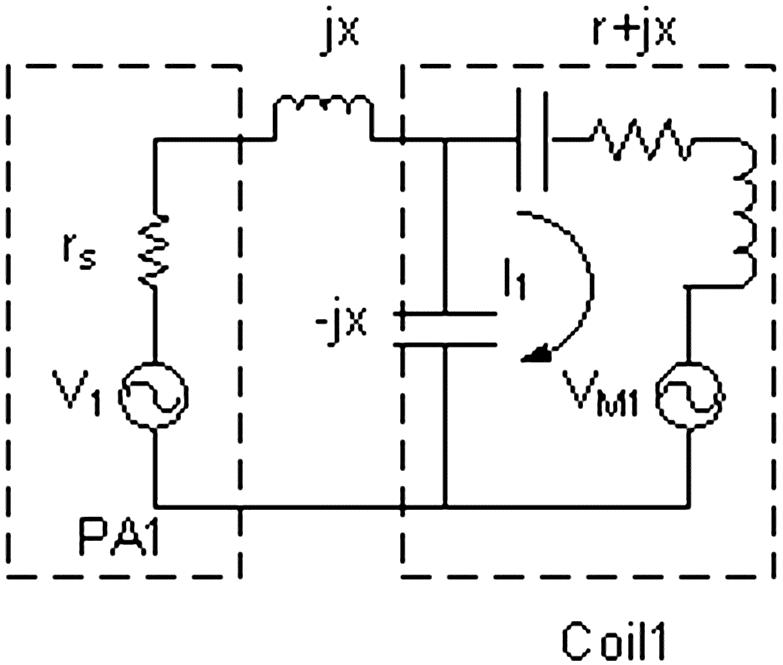
THEORY

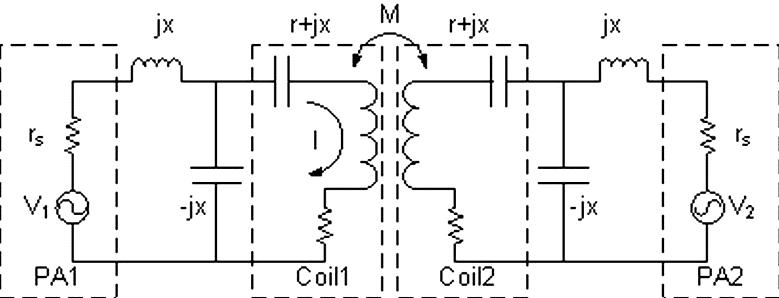
Multiple transmit chains are employed in parallel RF transmission for setting up the currents in an array of transmit coils in a coordinated way. The currents in turn induce transmit B₁ field in the subject. However the current in each of the element coils is typically subject to corruption due to inter-coil coupling. The coupling-induced corruptive components are much influenced by the source impedance seen by the element coils. Consider an example where two identical transmit coils are driven by two independent RF power amplifiers. Fig. 1 shows an equivalent circuit model. In this case each power amplifier is modeled as a voltage source with a source resistance r_s. The impedance of each coil without the matching components is r+jx, and the inductive coupling between these two coils is captured by mutual inductance M. Representing a common configuration, the L-shaped matching network on each coil, which is consisted of a capacitor and an inductor, not only transforms the low impedance of the series resonant coil into a desired value (normally 50Ω), but also scales the input current by a factor of x/r. When both coils are driven by their corresponding amplifiers, the current I running in coil 1 is consisted of two components, the desired one I^(S) that is due to the controlling voltage V₁ and the undesired (corruptive) one I^(M) that is due to V₂ (see Appendix):

$$\{\begin{array}{c}{I}^{\left(S\right)}=\frac{-jx{V}_1}{r{r}_S+{\omega }^2{M}^2{r}_S^2∕(r{r}_S+x^2)+x^2}\hfill \\ I^{\left(M\right)}=\frac{-jx{V}_2}{r{r}_S+{\omega }^2{M}^2{r}_S^2∕(r{r}_S+x^2)+x^2}\cdot \frac{j\omega M}{r+x^2∕r_s}\hfill \end{array}\phantom{\}},$$ [1]

where ω is the Larmor frequency. The severity of current corruption caused by the coupling effect could be represented by the ratio of I^(M) to I^(S):

$$\frac{\mid I^{\left(M\right)}\mid }{\mid I^{\left(S\right)}\mid }=\frac{\omega M}{r+x^2∕r_s}\frac{\mid V_2\mid }{\mid V_1\mid }.$$ [2]

For given r, x, M and ω, the minimum of the first term on the right hand side is achieved by minimizing r_s, which suggests minimization of source impedance as a method for improving isolation. This is analogous to the preamplifier decoupling approach for phased array receive (16), where a low input-impedance preamplifier makes a coil’s input-matching network an effective parallel resonant circuit presenting a large impedance to coupling-induced current.

FIG. 1.

Equivalent circuit model of coupled transmit coils

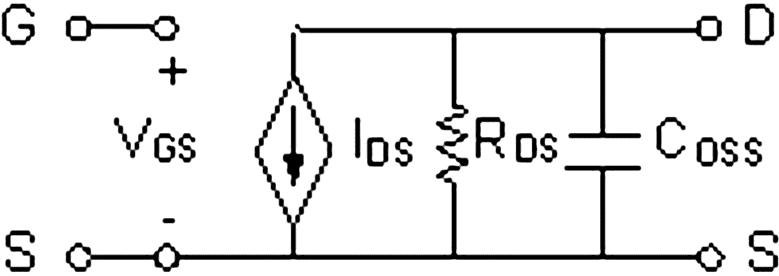
In practical solid-state RF power amplifiers, metallic oxide semiconductor field effect transistors (MOSFET) are commonly used to drive the RF power to a desired level. When a MOSFET operates in the saturation region of its DC characteristic, it behaves approximately as a voltage-controlled current source. Fig. 2 illustrates an equivalent circuit model in this case (28), in which the drain-source resistance R_DS is typically a very high value. When a MOSFET operates in a linear mode (Class A or AB) with a fixed DC drain-source voltage, its maximum output power without distortion critically depends on its load impedance. The maximum rated power can only be achieved when the load impedance equals an optimum value, which is normally provided by the manufacturer.

FIG. 2.

Equivalent circuit model of a MOSFET

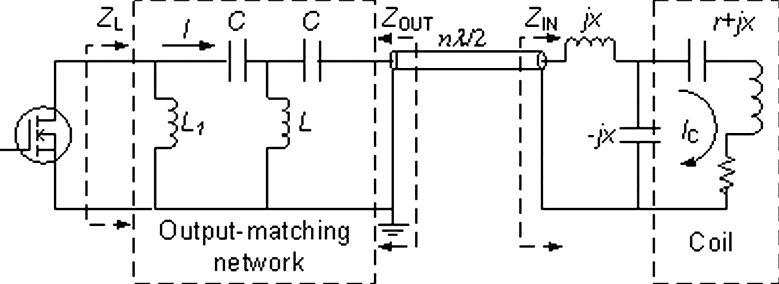
To maximize inter-element isolation by taking advantage of the low source-impedance idea above and to simultaneously maximize the available output power, a new amplifier output stage design has been developed (Fig. 3). In the new design an output-matching network for the MOSFET is introduced. The matching network applies an inductor L₁ in parallel to the output of the MOSFET to resonate its drain-source capacitance C_OSS. Then a T-shaped network consisted of two capacitors C and an inductor L, which are chosen to be series resonant at the working frequency, further transforms the drain-source resistance R_DS into

$$Z_{\text{OUT}}=\frac{j\omega L(\frac{-j}{\omega C}+R_{DS})}{j\omega L+\frac{-j}{\omega C}+R_{DS}}-\frac{j}{\omega C}=\frac{\frac{1}{{\omega }^2{C}^2}+j\omega L{R}_{DS}}{R_{DS}}-\frac{j}{\omega C}=\frac{1}{{\omega }^2{C}^2{R}_{DS}}.$$ [3]

Because of the high resistance presented by R_DS, the output impedance Z_OUT can thus be made very low as it is primarily determined by the series resonant circuit, which is nearly a short circuit at the resonant frequency. When Z_OUT is close to zero, the input-matching network at the coil side acts as a parallel resonant circuit, and the corruptive current component due to inter-coil coupling sees a large impedance and is thereby substantially suppressed. In the meanwhile, the same output-matching network for the MOSFET transforms the input impedance of the coil, normally matched to 50 Ω, into

$$Z_L=\frac{1}{1∕\left(\frac{j\omega L(\frac{-j}{\omega C}+50)}{j\omega L+\frac{-j}{\omega C}+50}-\frac{j}{\omega C}\right)+\frac{1}{j\omega L_1}}=\frac{1}{50{\omega }^2{C}^2-\frac{j}{\omega L_1}}.$$ [4]

FIG. 3.

The output-matching network in the ultra-low output impedance RF power amplifier

Generally, the optimum load can be expressed as

$$Z_{OL}=\frac{1}{\frac{1}{R_{OL}}-j\omega C_{OSS}},$$ [5]

in which R_OL represents the load resistance that enables the MOSFET to output highest power. By setting L and C to satisfy

$$R_{OL}=\frac{1}{50{\omega }^2{C}^2}=50{\omega }^2{L}^2,$$ [6]

and resonating C_OSS with L₁, the load impedance Z_L is matched to the optimum value specified for the MOSFET, and thus ensures that highest output power can be achieved. This design allows flexible placement of the RF power amplifier’s power stage. For off-coil placement, a coax cable with nλ/2 length may be used to connect a coil with its corresponding amplifier that is some distance away. Because of the current transformation effect at the matching network on each coil, the current in the cable can be much lower than that in the coil, which facilitates management of cable loss.

The configuration shown in Fig. 3 in effect represents a way to realize current source. The output-matching network of the MOSFET scales its input current I by a factor of 1/(ωCZ_IN). The network’s output current becomes the input current of the coil, which is further scaled by a factor of x/r by the input-matching network on the coil. The current running in the coil can therefore be expressed as:

$$I_C=\frac{x}{r}\frac{1}{\omega C{Z}_{IN}}I=\frac{x}{r}\frac{1}{\omega C\left(\frac{-jx(r+jx)}{r+jx-jx}+jx\right)}I=\frac{x}{r}\frac{1}{\omega C\frac{x^2}{r}}I=\frac{1}{\omega Cx}I.$$ [7]

Eqn. 7 indicates that r, the load of the coil, has no impact on the current in the coil, as the current I is only controlled by the gate voltage of the MOSFET. In addition to this current source property, Eqn. 7 also shows that the circuit shown in Fig. 3 is able to drive the current in the coil beyond the current rating of the MOSFET.

METHODS

Ultra-low Output Impedance Amplifiers

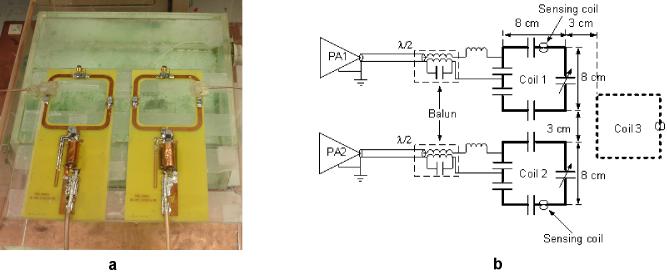
Two ultra-low output impedance RF power amplifier prototypes were developed to work at 128 MHz (Fig. 4). Each amplifier was consisted of three amplification stages, and the final stage was built with a high power MOSFET (ARF475FL, Advanced Power Technology, USA) based on the design shown in Fig. 3. Based on power efficiency and linearity considerations, the device was set to operate in Class AB and the bias current was set to 200 mA. The bias voltage was applied in pulse mode, as triggered by an external gating signal. The drain voltage was set to 150V and the R_OL of the MOSFET at this voltage is about 25 Ω. According to Eqn. 6, C was selected to be 35 pF and L was adjusted to resonate with it at 128 MHz. With a 50-Ω load connected and a 3ms hard pulse at 1% duty cycle as input, the gain of the final stage was measured to be 17 dB as the amplifier was driven to output 500W power, while the 3rd output harmonic was measured to be -27 dBc.

FIG. 4.

a: Two ultra-low output impedance amplifier prototypes. b: Each amplifier is consisted of three amplification stages

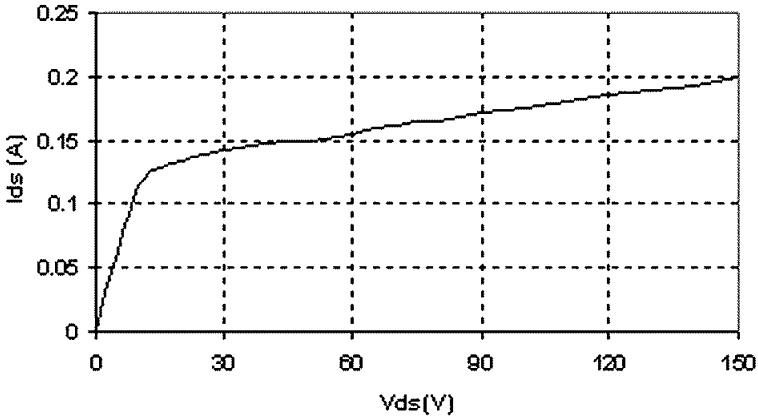
The equivalent R_DS of ARF475FL was evaluated by measuring the differential of the drain source voltage V_DS to current I_DS in the saturation region of the MOSFET’s DC characteristics, with the gate voltage fixed to a value that could bias the I_DS to 200 mA at 150V V_DS. The results are shown in Fig. 5 and the R_DS was accordingly calculated to be about 2 kΩ. Ignoring matching network loss, an analysis based on Eqn. 3 then predicts 1.25Ω as the output impedance of the amplifier.

FIG. 5.

The DC output characteristics of ARF475FL

Transmit Coil Array and Phantom

Experimental evaluation of the decoupling performance of the two prototype amplifiers employed primarily a setup involving two 8×8 cm² surface coils in a phased array configuration. The array was placed above a saline phantom (1.33g/L NaCl, 0.66g/L CuSO4) that is 30 cm by 20 cm by 20 cm, as shown in Fig. 6a. The separation between element coils 1 and 2 and the distance from each of them to phantom was adjustable. Fig. 6b illustrates the experiment setup. Initially both element coils were placed 2 cm above the phantom and with a 3 cm inter-element separation. Half-wavelength cables were used to connect the prototype amplifiers PA1 and PA2 to element coils 1 and 2 respectively. High power rating MR-compatible baluns were used on each cable to block common mode currents.

FIG. 6.

a: A phased array consisting of two 8×8 cm² surface coils was placed above a saline phantom b: Illustration of the experiment setup in its initial configuration. The location and size of a third coil that was introduced in a further configuration is also shown (dotted line).

I₁ and I₂, the current running in element coils 1 and 2 respectively, were monitored through two sensing coils. The sensing coil for element 1 employed a butterfly structure, which has two 1 cm diameter loops placed across a segment of the element’s conductor that was farthest away from element 2. With this configuration the electromotive forces (EMF) induced in the two loops of the sensing coil by I₁ were in-phase and thus enhanced, while those by I₂ were approximately anti-phase and thus neutralized. Consequently, compared to that of element 1, the contribution of element 2 to this sensing coil was reduced to a negligible level. Similarly, another sensing coil was constructed to detect I₂. With the local sensitivity the sensing coils provided a means for tracking I₁ and I₂, which, within a constant offset as determined by the sensing coils’ sensitivity, further allows quantification of the ratio of I₂/I₁ in dB.

To gauge the performance trend as the number of coils and the length of the cables increase, in a sub set of the experiments a third coil was additionally installed and longer cables were used. The construction of coil 3 is the same as that of coils 1 and 2, and its placement (Fig. 6b) was intentionally set to introduce strong mutual coupling between any pair of coils within the three.

Tuning Strategies

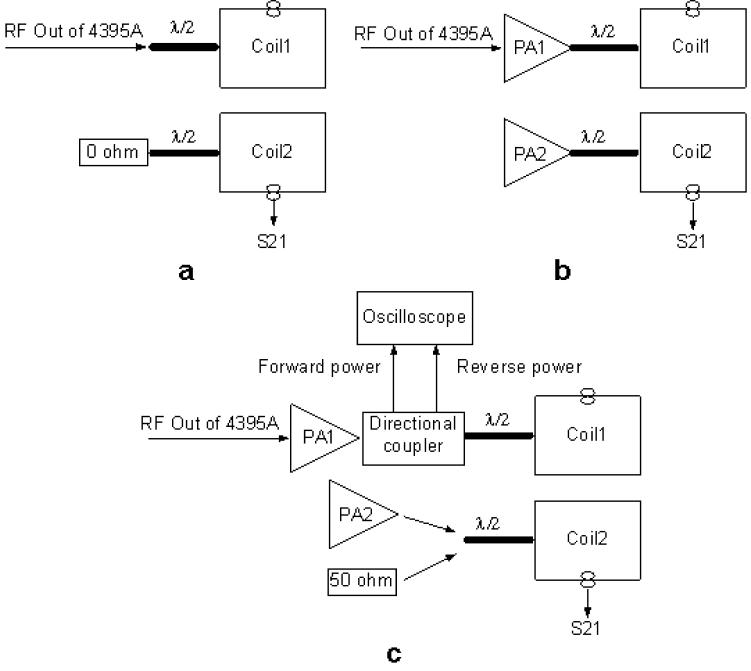
The inductor in the L-type matching network and the inductor L₁ significantly impact the source impedance seen by coils. The following tuning process was carried out to determine their values. At the initial configuration of the array-phantom placement, the two element coils with half wavelength cables were first tuned and matched to 50 Ω independently. Then a setup was used where coil 1 was driven by a network analyzer (4395A, Agilent, USA) while coil 2 was connected to a short terminator. The current induced in coil 2 was gauged through the S21 measurement of its sensing coil (Fig. 7a), and the inductor in the input-matching network on coil 2 was adjusted until the induced current was the lowest. To determine the value of L₁ that compensates the output capacitance of ARF475FL, a further setup was used where each element coil was driven by its corresponding amplifier (Fig. 7b). Both amplifiers were simultaneously gated on with 3ms pulses and 1% duty circle, and PA1 was driven by 4395A to output 1W power. The L₁ of PA2 was tuned to minimize the induced current in coil 2. Similar strategies were applied to tune coil 1 and PA1. The L₁ optimized for each amplifier through this process were kept unchanged in all the other experiments of this work. When coil 3 was introduced, a similar tuning strategy was applied to determine the inductor in coil 3’s L-type matching network while coil 2 was kept open.

FIG. 7.

Measurement setup. a: Coil 1 was driven by 4395A, and coil 2 was connected to a short terminator. b: Coils 1 and 2 were fed by PA1 and PA2 respectively. c: Coil 1 was driven by PA1, and the output power was calculated by the difference of the forward and reflected power, measured with the directional coupler. Coil 2 was first fed by PA2 and then by a 50Ω terminator.

MR Imaging Experiments

To assess the feasibility of the present approach in an MR environment, imaging experiments using the new amplifiers on a 3T clinical scanner (GE HealthCare, Milwaukee, WI) were conducted. As the approach supports relatively flexible placement of the RF power amplifier’s power stage, the amplifiers were placed in the same equipment room as the stock amplifier was, with coax cables each of about 8.5 meters long connecting the amplifiers with their corresponding coils. This averted the need to make the amplifiers fully MR-compatible in the present investigation.

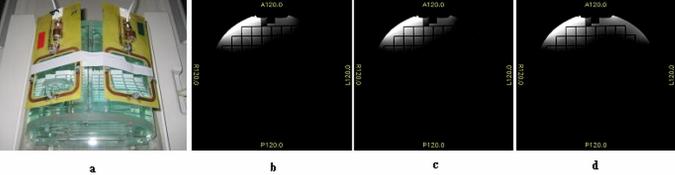
In one set of imaging experiments a coil array consisting of two 8×8 cm² surface coils was placed above a cylindrical phantom (Fig. 10a), and was configured to perform parallel transmit and parallel receive. Each of the element coils in the array was connected to its corresponding RF power amplifier and RF signal receiver via a dedicated T/R switch.

FIG. 10.

3T imaging results. a: A coil array consisting of two 8cm × 8cm surface coils was placed above a cylindrical phantom, and was configured to perform parallel transmit and parallel receive. Each of the element coils in the array was connected to its corresponding RF power amplifier and signal receiver via a dedicated T/R switch. For parallel receive image reconstruction, phased array sum of squares combination was used. MR images correspond to cases where element coil 2 (on the right) was connected, through a T/R switch and a 8.5m-long coax cable, with a short terminator (b), an active new amplifier with zero input (c), and an active conventional amplifier with zero input (d).

MR images were acquired using a spoiled gradient echo sequence, with TE = 4.8 ms, TR = 34 ms, flip angle = 20 °, matrix size = 256 × 160 and FOV = 24 cm × 24 cm. During transmit both amplifiers were gated on, where amplifier 1 had as input a 3ms RF pulse synthesized by the scanner system and output a peak power of up to 100W, and amplifier 2 had zero-amplitude pulse as input. In this case effects of coupling-induced corruptive currents on imaging mainly manifest in significant flip of spins that are located near element 2 but distant from element 1, in spite of zero input to the amplifier that drives element 2. Imaging results obtained with the use of two new amplifiers were compared to that obtained with the use of two conventional amplifiers. For parallel receive image reconstruction, phased array sum of squares combination was used.

RESULTS

Input Impedance Curves

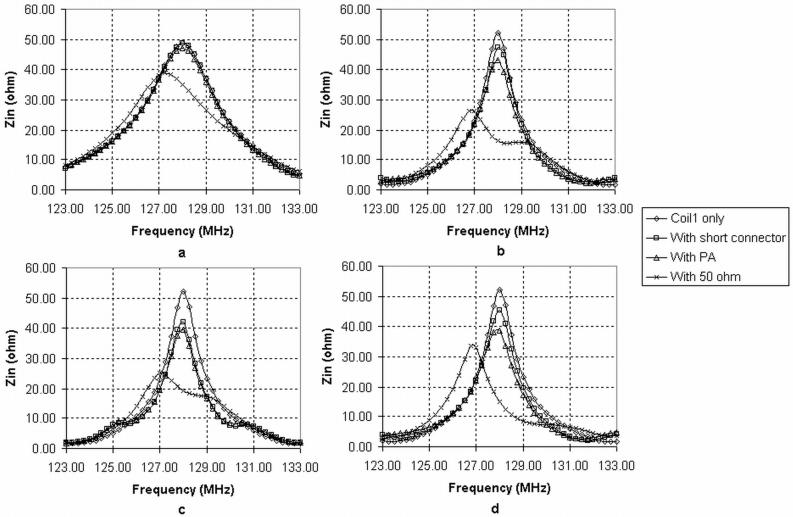
To study the characteristics of multi-coil operation as supported by the new prototype amplifiers, we evaluated the impact of source impedance to the input characteristics of element coils in experiments. In a first experiment, with the initial placement of the transmit array, the input impedance curves of coil 1 were measured with 4395A in cases where coil 2 was connected to respectively a short terminator, a 50Ω terminator (emulating the output impedance of a conventional RF power amplifier) and PA2. These results were compared with that when coil 2 was disabled. Note that in the case where coil 2 was connected to PA2, direct impedance curve measurement under the condition that PA2 was gated on was avoided, due to concerns over possible damage to 4395A caused by potential oscillation of PA2 and strong coupling between coils. Instead, the MOSFET and L₁ in PA2 were removed and the remaining of the output-matching network was used to terminate coil 2, which represents a more accurate emulation of an active PA2 than that of just a simple short terminator. The results are summarized in Fig. 8a. Compared with that of coil 1 alone, the impedance of coil 1 in a 10MHz sweeping range was almost not affected when coil 2 was connected to the short terminator or PA2, while in the 50Ω termination case there was a shift in the impedance curve and the input impedance at 128MHz was decreased from 48.7Ω to 35.2Ω.

FIG. 8.

Coil 1 input impedance curve measurements. a: The distance from the 2-coil transmit array to phantom was 2 cm and the cable length was λ/2. b: The distance from the 2-coil transmit array to phantom was 5 cm and the cable length was λ/2. c: The distance from the 2-coil transmit array to phantom was 5 cm and the cable length was 7λ/2. d: The distance from the 3-coil transmit array to phantom was 5 cm and the cable length was λ/2.

Next, under a light load condition, the first experiment was repeated. To set up the light load condition the distance between the transmit array and the phantom was increased to 5 cm. Coils 1 and 2 were individually retuned and matched to 50 Ω to accommodate the load alteration. The impedance measurement results are summarized in Fig. 8b. The impedance curve of coil 1 alone reached its peak value of 52.1 Ω at 128 MHz, as shown in Fig. 8b. When coil 2 was present but was connected to the short terminator the curve changed slightly with an impedance value of 47.5 Ω at 128 MHz. The impedance value decreased drastically to 16.2 Ω and the curve split into two peaks in the 50Ω termination case. As a result of additional loss associated with the inductor and capacitors in the output-matching network, the curve measured when coil 2 was connected to PA2 indicated more coupling effect compared to that of the ideal short case, with an impedance value of 43.1 Ω at 128 MHz.

To evaluate the impact of cable length on decoupling performance, a third experiment used the setup of the second experiment, but with the cable length of coil 2 increased to 7λ/2 (∼ 4.7m). In this case, as shown in Fig. 8c, the impedance at 128 MHz when PA2 was connected dropped a bit further to 39.6 Ω, but was still significantly higher than that when 50Ω terminator was used. Furthermore, the curve was very close to that when coil 2 was connected with a short terminator. This was expected as the source impedance seen by coil 2 started to be dominated by the loss of the cable, which measured at an insertion loss of 0.52 dB. As a reference, actual MR scanner systems commonly use low-loss cables with an insertion loss of 0.03 dB/m or better.

A fourth experiment used the 3-coil setup illustrated in Fig. 6b to assess the performance trend as the transmit coil array increases in complexity. The cable length was set to λ/2. The placement of the coils gave rise to significant mutual coupling amongst all three coils, representing a non-trivial coil array configuration. The input impedance curves of coil 1 were measured when both of coil 2 and 3 were connected to, respectively, short terminators, 50Ω terminators, PA2 and PA1. Compared to that measured in the second experiment, the curves shown in Fig. 8d indicated that more coupling effects resulted due to the introduction of the third coil. The impedance at 128 MHz when PA2 and PA1 were connected was 38.7 Ω. However the overall shape of the curve obtained with the use of PA2 and PA1 remained intact, indicating a much improved robustness than that of the 50Ω case.

Comparison with 50Ω Sources

In a second study, we compared the isolation associated with the use of the new prototype amplifiers to that of the 50Ω sources. We again used the initial setup, where coils 1 and 2 with a 3cm separation in-between were placed 2cm above the top surface of the phantom, and the coils were individually matched to 50 Ω. Coil 1 was driven by PA1, whose input was connected to 4395A’s output port and whose output was connected to a directional coupler (C2310, Werlatone, USA) for power measurement (Fig. 7c). Coil 2 was first connected with PA2, which had zero input but was gated on simultaneously with PA1. The source current I₁ in coil 1 and the induced current I₂ in coil 2 were measured versus the output power of PA1. The isolation improvements, quantified each time by normalizing I₂/I₁ with the corresponding one that was obtained with coil 2 connected to a 50Ω terminator instead of PA2, are summarized in Table 1. For a range of output power levels that were between 1W and 430W the data indicate that the isolation was improved by at least -14 dB compared to that of the 50Ω case.

Table 1.

Isolation improvement compared to 50Ω source

Output power (W)	1	10	47	110	250	430
Isolation improvement (dB)	-14.5	-14.5	-14.5	-14.5	-14.4	-14.4

Comparison with Overlap Decoupling

A third study was conducted to compare the isolation performance of the proposed new approach with that of an overlap decoupling approach. With the latter approach element coils were decoupled by partial geometrical overlap and were driven with conventional 50Ω sources. In this study coil 2 was placed 1 cm farther to phantom than coil 1 was to allow easy adjustment of horizontal overlap or separation between the two coils, as shown in Fig. 6a. Experiments were carried out with the distance between the coil array and the phantom set at various values. In each experiment, the two coils were tuned and matched to 50Ω separately. In evaluating the overlap decoupling approach, with the aid of the conventional S21 measurement the overlap between the two coils were finely adjusted to minimize the mutual inductance. Coil 1 was driven by PA1 at 10W output power, while coil 2 was terminated with 50Ω. The S21 response of each sensing coil was measured, and the difference between them, Δ_S21, was used to quantify the isolation (Δ_S21 = c + 20log(I₂/I₁), where c is a constant determined by the sensing coils’ sensitivity). In evaluating the low output-impedance approach, the same measurement was carried out except that instead of optimal overlap the horizontal separation between the two element coils were fixed at 3 cm. This underlap geometry caused substantial inter-element mutual inductance - the burden of decoupling the two element coils in this case was entirely on the new power amplifiers.

The results are summarized in Table 2, in which the second column captures, in terms of conventional S21 response, the level of residual coupling with the overlap approach. The third and fourth columns show the ratio of the coupled current to source current with, respectively, the overlap approach and the new amplifier-based approach. As the distance between the array and the phantom decreased, the isolation performance of the overlap approach got worse. This was mainly caused by an increase in the coupling mediated by the phantom, which could not be eliminated through annulling the mutual inductance. In comparison, the isolation performance of the new amplifier approach showed an upward trend as the load became heavier, and the performance was better than that of the overlap approach when the distance was less than 6 cm. This is in agreement with Eqn. 2, which indicates that load increase also helps to reduce the induced current.

Table 2.

Isolation performance comparison between the overlap approach and the new approach

Distance between coil 1 and the phantom (cm)	S21 (dB)	ΔS21 with overlapping (dB)	ΔS21 with PA2 (dB)
7	-12.2	-8.9	-6.6
6	-11.6	-8.3	-8.5
5	-10.7	-7.2	-10.6
4	-10.5	-7.0	-12.5
3	-10.3	-6.5	-14.1
2	-10.3	-6.2	-15.6

Sensitivity to Load Change

The loading of RF coils in clinical practice tends to vary significantly with different patients and/or patient positioning. The fourth set of experiments in this work was performed to study the effect of load variation on isolation performance achieved by, respectively, the overlap approach and the new amplifier-based approach. The experiment configuration and measurement were similar to that described above, which were set up to compare the isolation performance of the two decoupling approaches, except that the tuning and matching of the two coils were only performed once for the case in which the array was placed 4 cm above the top surface of the phantom, and they were not changed for the other cases. To address the impact of the cable length, the measurements were also repeated when 7λ/2 cables were used. The results summarized in Table 3 suggest that, as the distance between the array and the phantom decreased from 7 cm to 2 cm and the input impedance of coil1 Z_in correspondingly varied from 89.3+j27.4 Ω to 25.4-j6.3 Ω, the isolation represented by the ratio I₂/I₁ deteriorated from -11.3 dB to -3.9 dB with the overlap approach. In the amplifier decoupling approach, the isolation was consistently around -12 dB when λ/2 cables were employed, and -9 dB when the length was increased to 7λ/2. In both cases the new approach exhibited significantly more robust decoupling behavior.

Table 3.

Isolation performance as a function of loading

Distance between coil 1 and the phantom (cm)	ZIN (Ω)	ΔS21 with overlapping, λ/2 cable (dB)	ΔS21 with PA2, λ/2 cable (dB)	ΔS21 with PA2, 7λ/2 cable (dB)
7	89.3+j27.4	-11.3	-12.4	-9.0
6	80.5+j18.4	-10.3	-12.1	-9.1
5	61.5+j6.0	-7.9	-11.6	-8.7
4	50.4+j0.5	-7.0	-12.5	-9.2
3	36.3-j5.8	-5.3	-11.9	-9.0
2	25.4-j6.3	-3.9	-11.3	-8.9

Feasibility in High Field MR

Imaging study conducted on the 3T clinical scanner evaluated the feasibility of the new approach in high field MR. Placement of the amplifiers in the equipment room (as opposed to near the imaging volume) in the present study relaxed the compatibility requirements on power electronics and facilitated system integration.

Fig. 10c shows an image that was acquired with the two element coils driven by two corresponding new amplifiers. The amplifier for element 1 (on the left) had a 3ms RF pulse as input and the amplifier for element 2 (on the right) had a zero-amplitude pulse as input. Fig. 10d shows an image that was acquired in the same way except that two conventional amplifiers were used in place of the two new amplifiers. A comparison of the two images suggests that use of the new amplifiers realized a significant reduction of coupling-induced current in element 2. The image intensity in the region that was near element 2 but distant from element 1 was reduced approximately by a factor of four with the use of the new amplifiers, in agreement with current measurements independently obtained in bench tests. The result shown in Fig. 10c was comparable to a reference result shown in Fig. 10b. The latter was obtained in the same way as the former was except that element coil 2 was connected, through a T/R switch and a 8.5m-long coax cable, with a short terminator, mimicking an extreme of the new amplifier optimization. Further improved results were obtained by reducing the coax cable length and moving the short closer to the input port of element 2. This was as expected as a reduction in cable loss would make the resonance circuitry at the input port more effective suppressing coupling-induced current in element 2.

DISCUSSION AND CONCLUSIONS

Equivalent circuit model analysis of inductively coupled coils driven by independent amplifiers suggests that the isolation between transmit coil elements could be significantly improved with a new approach that employs unique matching networks and minimized source impedances. A properly designed output-matching network in particular could be applied at the output stage of an amplifier to implement this new approach, which is referred to as ultra-low output impedance amplifier. The output-matching network transforms the output impedance of a given MOSFET into a low value, and simultaneously maximizes the available output power by establishing an optimal load for the MOSFET. With the aid of the L-type input-matching network on coil, this new amplifier acts as a current source, and the current variation due to coupling and load change is much suppressed. Two accordingly developed amplifiers in our prototyping work were able to deliver 500W peak power without distortion, which represents a significant support for approaches employing distributed transmit coil elements, e.g., parallel RF transmit.

The first experimental study investigated the input impedance characteristics of a transmit array under various array configuration, cable length and sample load conditions. The study verified that coil isolation benefits from a decrease in source impedance, especially under moderate to light sample-load conditions. The study also indicated that the loss of coaxial cables and passive components in the output-matching network impact the minimum output impedance of the amplifier and need to be better managed for best isolation performance.

In the second experimental study, a comparison with 50Ω source cases suggested that the new type of amplifiers has significant advantage in term of suppressing coupling-induced currents in a transmit coil array within the full output power range of the investigation. Note that for typical RF power amplifiers used in practice, their output impedance is not always matched to 50Ω - for those exhibiting higher-than-50Ω source impedance, their replacement with the amplifiers proposed is expected to be even more desirable from a coil isolation improvement point of view (Eqn. 2).

Data from the third experimental study suggest that the decoupling performance accompanied with the use of the prototype amplifiers, under various sample-load conditions, are comparable to those obtained with optimized overlap decoupling, and may even outperform overlap decoupling under moderate-to-heavy sample-load conditions. Furthermore, data from similar experiments in the fourth study indicated that the isolation achieved by the prototype amplifiers is robust against the change of sample load, while a substantial variation was observed when overlap decoupling was employed. These results indicate that the new approach promises to relax coil geometry or field pattern constraints that are often imposed by conventional decoupling approaches, and thereby facilitate transmit coil array optimization.

The imaging study conducted on a 3T clinical scanner demonstrated the feasibility of the new approach in high field MR. The approach’s support for positioning the amplifiers some distance away from the coils allowed placement of the amplifiers in the equipment room next to the 3T scanner. Compared to the use of conventional amplifiers, the new approach achieved significant improvements in suppressing coupling effects associated with the use of a parallel transmit coil array. There were clear indications that further improvements were possible by reducing the length of the coax cables that connect the amplifiers to the coils, consistent with the analysis and bench results on the effect of cable/component loss. One plan for continuing work is to place the amplifiers within a meter or two from the coils (and inside the scanner room). A resulting reduction in cable loss could lead to a significant performance gain while the moderate distance from the imaging volume could facilitate the task of making the amplifiers fully compatible with the environment.

APPENDIX

Coil 1 in Fig. 1 can be equivalently modeled as in Fig. 9, in which V_M1 represents the electromotive force induced by the current in coil 2. The current in coil 1 can thus be expressed as:

$$I_1=\frac{V_1}{r_S+x^2∕r}\cdot \frac{-jx}{r}-\frac{V_{M1}}{r+x^2∕r_S}$$ [8]

V_M1 is related to the current in coil 2 by V_M1 = jωMI₂, which allows rewriting Eqn. 8 as:

$$I_1=\frac{V_1}{r_S+x^2∕r}\cdot \frac{-jx}{r}-\frac{j\omega M{I}_2}{r+x^2∕r_S}$$ [9]

Similarly, I₂ can be expressed as:

$$I_2=\frac{V_2}{r_S+x^2∕r}\cdot \frac{-jx}{r}-\frac{j\omega M{I}_1}{r+x^2∕r_S}$$ [10]

Substituting I₂ in Eqn. 9 with Eqn. 10, one obtains the following:

$$I_1=\frac{V_1}{r_S+x^2∕r}\cdot \frac{-jx}{r}-\frac{j\omega M}{r+x^2∕r_S}\left[\frac{V_2}{r_S+x^2∕r}\cdot \frac{-jx}{r}-\frac{j\omega M{I}_1}{r+x^2∕r_S}\right]$$ [11]

Solving Eqn. 11 then gives rise to the following expression for I₁:

$$I_1=\frac{-jx{V}_1}{r{r}_S+{\omega }^2{M}^2{r}_S^2∕(r{r}_S+x^2)+x^2}+\frac{-jx{V}_2}{r{r}_S+{\omega }^2{M}^2{r}_S^2∕(r{r}_S+x^2)+x^2}\cdot \frac{j\omega M}{r+x^2∕r_S}$$ [12]

FIG. 9.

Equivalent circuit model of coil 1.