Abstract
Valgus moments on the knee joint during single-leg landing have been suggested as a risk factor for anterior cruciate ligament (ACL) injury. The purpose of this study was to test the influence of isolated valgus moment on ACL strain during single-leg landing. Physiologic levels of valgus moments from an in vivo study of single-leg landing were applied to a three-dimensional dynamic knee model, previously developed and tested for ACL strain measurement during simulated landing. The ACL strain, knee valgus angle, tibial rotation, and medial collateral ligament (MCL) strain were calculated and analyzed. The study shows that the peak ACL strain increased nonlinearly with increasing peak valgus moment. Subjects with naturally high valgus moments showed greater sensitivity for increased ACL strain with increased valgus moment, but ACL strain plateaus below reported ACL failure levels when the applied isolated valgus moment rises above the maximum values observed during normal cutting activities. In addition, the tibia was observed to rotate externally as the peak valgus moment increased due to bony and soft-tissue constraints. In conclusion, knee valgus moment increases peak ACL strain during single-leg landing. However, valgus moment alone may not be sufficient to induce an isolated ACL tear without concomitant damage to the MCL, because coupled tibial external rotation and increasing strain in the MCL prevent proportional increases in ACL strain at higher levels of valgus moment. Training that reduces the external valgus moment, however, can reduce the ACL strain and thus may help athletes reduce their overall ACL injury risk.
Keywords: valgus moment, ACL injury, ACL strain, knee model, single-leg landing
1. Introduction
Injuries to the anterior cruciate ligament (ACL) frequently occur during the deceleration phase of landing or in preparation for a change of direction (Boden et al., 2000; Griffin et al., 2000). Females who participate in sports that include jumping and cutting often suffer from ACL injuries significantly higher than males (Agel et al., 2005; Gwinn et al., 2000). Recent studies have suggested that the gender difference in dynamic frontal-plane motion during landing may be associated with higher ACL injury rates in females: women often land with more valgus frontal-plane alignment than men and this valgus alignment caused larger valgus moments to the knee joint (Chaudhari et al., 2003; Kernozek et al., 2005; McLean et al., 2005). A prospective study has shown that female athletes who subsequently ruptured the ACL performed jump landing tasks with significantly higher valgus moments than athletes who did not rupture their ACL (Hewett et al., 2005). However, it remains unknown how much these observed gender differences in dynamic valgus alignment and valgus moments increase ACL strain during landing.
Several studies have shown that valgus loading at the knee joint can increase ACL force (Fukuda et al., 2003; Hollis et al., 1991; Markolf et al., 1995). In contrast, some other studies have not observed significant ACL strain under valgus loading (Bendjaballah et al. 1997; Fleming et al., 2001). Another study observed no significant ACL strain until the MCL was torn by valgus loading (Mazzocca et al., 2003). However, these previous studies were often performed while constraining other degrees of freedom (DOF’s) or by applying valgus loading without shear forces that occur during landing. Further, cadaver studies which predict static characteristics of the knee joint under low levels of loading may not predict ACL rupture under the large loading magnitudes and loading rates experienced during sports activities. In vivo studies of ACL strain during injury-causing events are not feasible for human subjects, either. Dynamic three-dimensional simulation studies offer an attractive alternative, because they can include more joint complexity, allow unconstrained motion, and permit physiologic loads to be applied. However, predictions of ACL strain during dynamic landing have not been previously studied using a model validated for the estimation of ACL strain. The purpose of this study was to test the influence of isolated valgus moment on ACL strain during single-leg landing using a dynamic three-dimensional simulation model driven by in vivo human loading data.
2. Methods
We developed a three-dimensional dynamic specimen-specific force-driven knee model, tested for ACL strain measurement against previous cadaveric experiment. In addition to vertical dynamic impact load which simulates loads caused by landing, physiologic levels of valgus moments from a previous in vivo study were scaled and applied to this knee model to investigate the influence of valgus moments on the ACL.
The development and validation test of this knee model to predict ACL strain during landing under a vertical impact force (without additional externally applied torques) has been described in detail by Shin et al. (2007), thus a brief description is given here. The knee model was constructed from sagittal MRI (GE 3D-Spoiled-Gradient-Recalled-Echo, 1.5T, 140×140mm, 256×256, thickness 1.5mm) of a cadaveric knee (Figure 1). MR images were segmented and imported into dynamic rigid-body motion simulation software (MSC.ADAMS, MSC.Software, Santa Ana, CA). This knee model includes ligament bundles (the ACL, PCL, MCL, LCL, posterior capsules, and patellar ligament) formulated as non-linear elastic springs (Shin et al. 2007) with properties adapted from published data (Abdel-Rahman and Hefzy, 1998; Cooper et al., 1993; Noyes et al., 1984; Shelburne and Pandy, 1997; Woo et al., 1991; Yu et al., 2001). The origins and insertions of the ACL/PCL were determined based on segmented MRI. Two functional bundles of the ACL/PCL were identified as previously quantified (Harner et al., 1999), and the centroids of each region were estimated to be the insertion points. The MCL, LCL, and posterior capsule were placed over the appropriate bony landmarks (Garg and Walker 1990; Reicher 1993) using the same method and bundle orientation as described by Yu et al. (2001). The patellar ligament was modeled by medial/lateral bundles and placed based between the patellar apex and tibial tuberosity. The contact forces at the tibiofemoral and patellofemoral articulation were defined using a penalty regulation of normal contact force constraints (Lötstedt, 1982) with previously reported properties (Nam et al., 2004; Oni and Morrison, 1998). The passive characteristics of the knee model were tested under various conditions, including valgus rotational stiffness and passive flexion movement to ensure proper tibiofemoral behavior. The femoral rollback and screw-home motion were properly simulated with the model (Shin, 2006; Shin et al., 2007).
Figure 1.
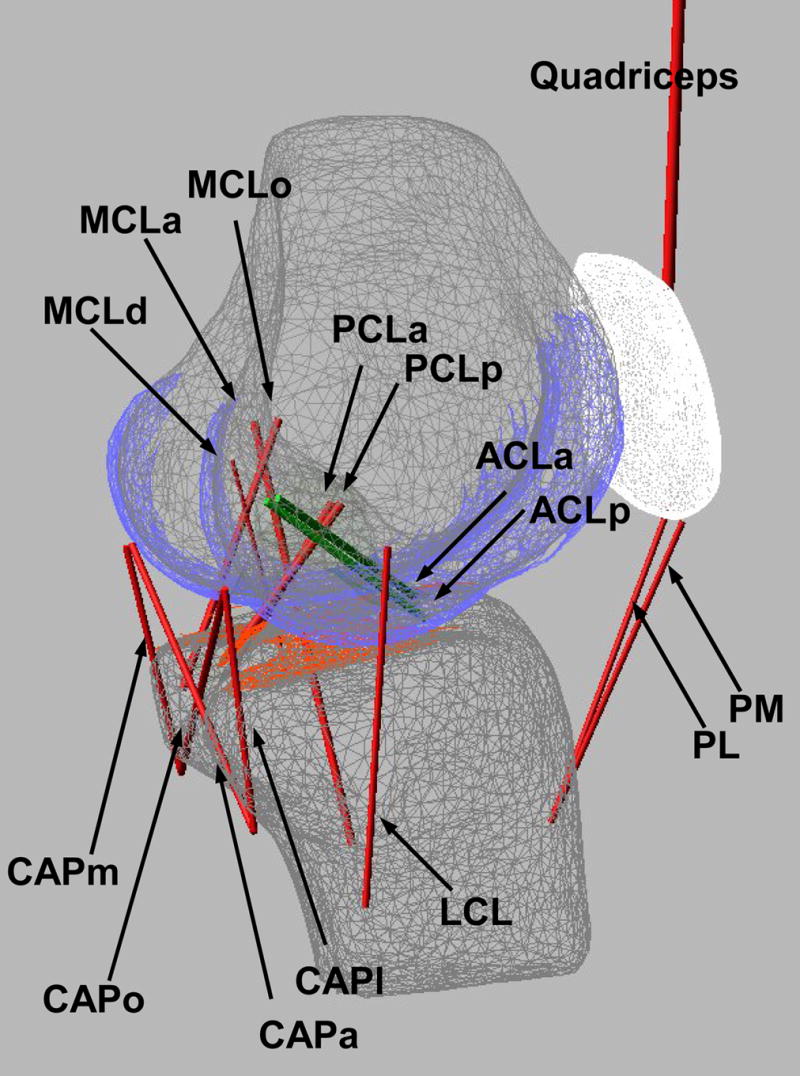
Schematic of the knee model showing the locations and numbers of bundles of the modeled ligaments: the anterior and posterior bundle of the anterior cruciate ligament (ACLa and ACLp, green); the anterior and posterior bundle of the posterior cruciate ligament (PCLa and PCLp); the lateral collateral ligament; the anterior, oblique and deep bundle of the medial collateral ligament (MCLa, MCLo, and MCLd); the medial, lateral, oblique popliteal and arcuate popliteal bundle of the posterior capsules (CAPm, CAPl, CAPo, and CAPa); and the medial and lateral patellar ligament (PM and PL).
To simulate the motion of a single-leg landing, a simulated landing apparatus was created with the same geometric configuration using the same cadaver knee specimen (Figure 2) as in a previously-described cadaver experiment (Withrow et al., 2006). Three musculotendinous groups (the quadriceps, medial/lateral hamstrings, and medial/lateral gastrocnemius) were modeled as linear tension-springs with the same pretension and stiffness used in the experiment to provide the appropriate tension to hold the initial knee flexion angle at 25° before impact load and to simulate eccentric contraction in the quadriceps as done in the physical experiment (Withrow et al., 2006). The proximal femur was connected to the mounting apparatus through a spherical joint and linear slide, allowing free rotation analogous to a hip joint and vertical motion. The distal tibia was connected to a spherical joint, functioning like an ankle joint. This complete model + apparatus were previously tested to validate the model for predicting ACL strain during landing (without additional external valgus loading) against the physical experiment, in which a DVRT was attached to the ACL to measure anteromedial bundle strain (Shin et al., 2007). The comparison between simulation and experiment showed good correspondence in ACL strain, validating the use of the simulation to predict changes in ACL strain under different loading conditions but not validating its use to accurately predict absolute ACL strains.
Figure 2.
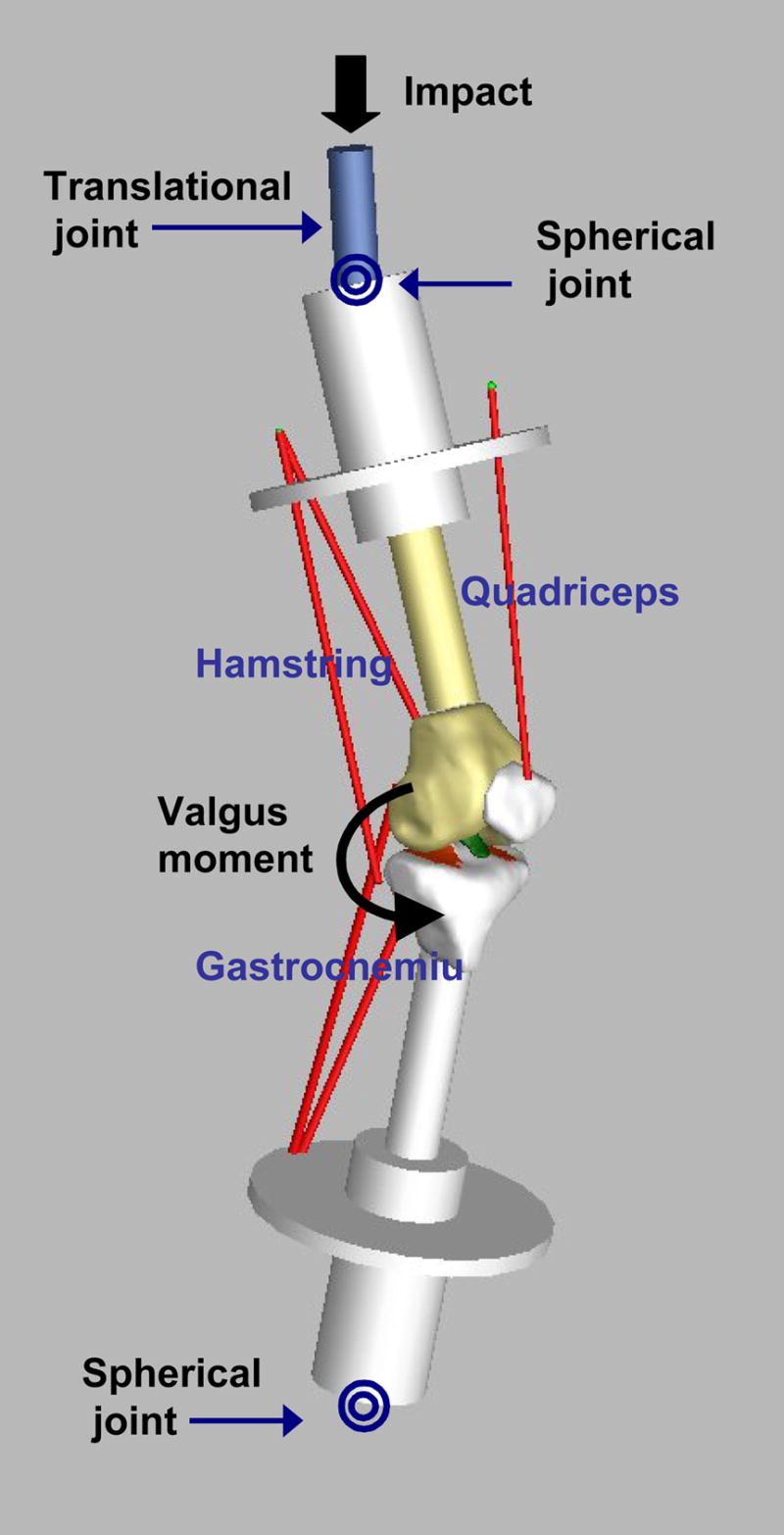
An illustration of the knee model with the simulated dynamic landing apparatus showing five musculotendinous bundles (the quadriceps, the hamstrings, and the gastrocnemius). The segmented ACL is shown in green. The tibial cartilage is shown in orange. The femoral cartilage is not shown to enhance the inside view of the tibiofemoral joint. Before external loading is applied, the muscles of the knee joint are pretensioned to hold 25° of flexion. The impact force was applied at the top of the femoral axis of the upper limb and the valgus moment was applied at the tibiofemoral knee joint
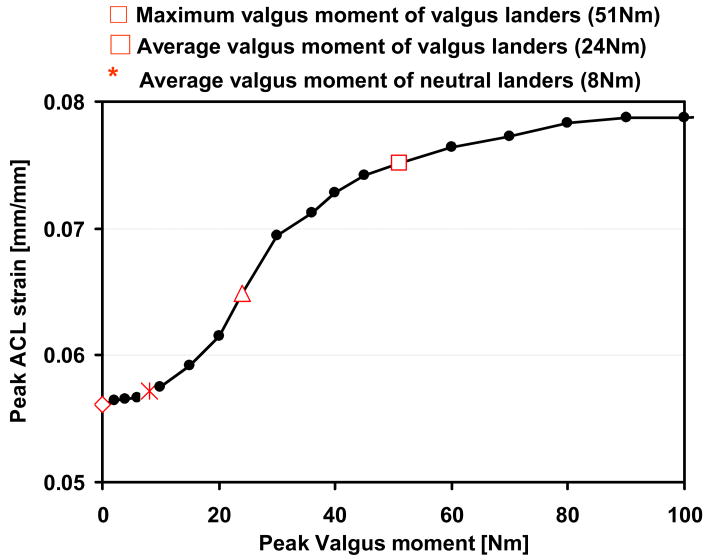
Four physiologic levels of peak valgus moment were selected to simulate the normal range of in vivo valgus loading (Table 1). The dynamic profile and magnitude of valgus moment were adopted from an in vivo run-to-cut landing (Chaudhari et al., 2003). Peak valgus moments were normalized to an average-size person (height=1.75m, body mass = 76.5 kg). Neutral-lander, valgus-lander, and varus-lander group were classified based on the apparent coronal angle between the shank and the thigh during weight acceptance, the interval between initial contact and maximum knee flexion. The maximum valgus moment observed in our data of 51 Nm for a 76.5 kg individual was consistent with previous reports of maximum valgus moments in at-risk individuals (45.3 Nm: Hewett et al., 2005 and 91.8 Nm: Sigward et al., 2007). In addition, other values between 0 and 100 Nm were added to fully characterize the entire reported range of valgus moments (Sigward et al., 2007).
Table 1.
Physiologic levels of valgus torque applied to the simulation model (Adopted from an in vivo study of a 90° lateral sidestep run-to-cut maneuver; Chaudhari et al., 2003). Among 21 subjects, most of the female participants (67%) showed valgus dynamic alignment while most of men (78%) showed neutral or varus alignment. Thus, four physiologic levels of valgus moment were determined as follows:
| Type | Peak valgus moment [Nm] |
|---|---|
| Minimum valgus moment of neutral landers | 0 |
| Average valgus moment of neutral landers | 8 |
| Average valgus moment of valgus landers | 24 |
| Maximum valgus moment of valgus landers | 51 |
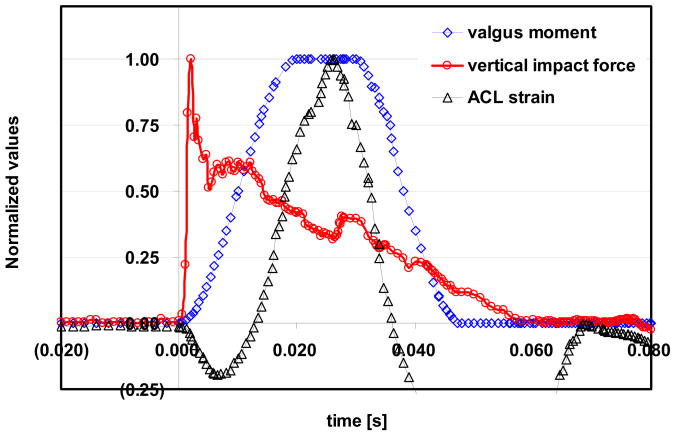
Two types of loading were simultaneously applied with an initial knee flexion of 25° (Figure 2). A dynamic vertical impact force (peak value: 1300N) was applied at the top of the femoral axis of the upper limb to simulate landing. This value was chosen to match the experimental study (Withrow et al., 2006) and is approximately equal to 2 body weights. This value was within the range observed in the in vivo study. In addition to impact force, several levels of valgus moment were applied at the knee joint. The dynamic simulations were conducted with simulation steps ≤1ms using an implicit method (GSTIFF integrator; Gear 1971) built in MSC.ADAMS solver. In response to the applied loading, the model calculated knee kinematics and ACL strain during each simulation (Figure 3). It should be noted that only a vertical force and a valgus moment were applied, but since the knee was unconstrained motions in all six DOF’s were possible. In addition to the peak strain in the ACL, peak valgus angle, peak tibial rotation, and peak strains in the anterior and deep bundles of the MCL are presented.
Figure 3.
The temporal profile of the applied impact force (N), sample applied valgus moment (Nm) and sample output of ACL strain (mm/mm). Values were normalized to their peak values and their initial values (i.e. impact force: 0 to 1300N; valgus moment: 0 to 51Nm; ACL strain: 0.020 to 0.076 for this figure).
3. Results
Increasing the applied peak valgus moment increased the peak ACL strain nonlinearly (Figure 4). The peak ACL strain increased from 0.056 without valgus moment to 0.076 with the maximum valgus moment observed in vivo. The ACL strain generated for the average valgus-landers(0.065) was higher than average neutral-landers(0.057). The peak ACL strain increased at a more rapid rate near the average of the valgus-landers, as shown by the steeper slope of the curve near 24Nm (Figure 4). At lower levels of valgus loading (0 to 10Nm) or higher levels of valgus loading (over 40Nm), the ACL strain increased at a 75% less rapid rate than in the middle region.
Figure 4.
Peak strain in the anteromedial bundle of the ACL during the first 50ms after impact. Peak ACL strain during landing nonlinearly increased when the applied peak valgus moment increased.
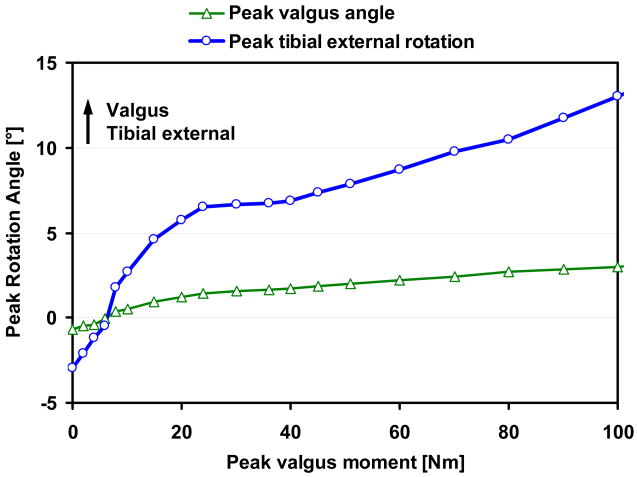
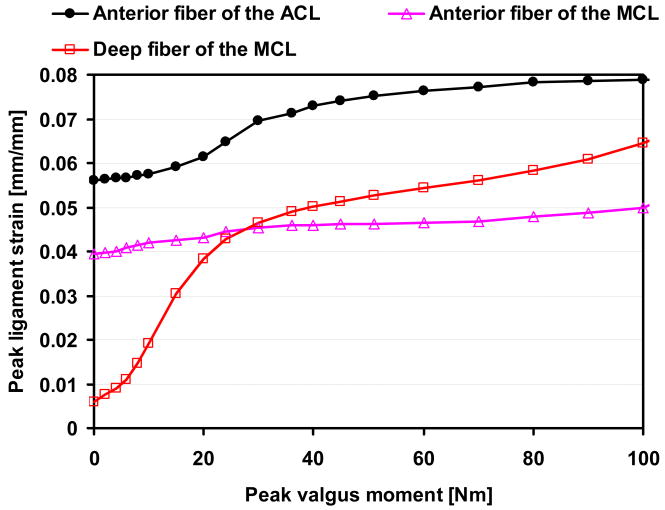
Increasing the applied peak valgus moment increased both the peak valgus rotation and peak tibial external rotation (Figure 5). Peak tibial external rotation increased more rapidly as peak valgus moment increased above 40Nm. Peak strain in the anterior bundle of the MCL gradually increased but peak strain in the deep bundle increased more nonlinearly (Figure 6).
Figure 5.
Peak valgus angle[°] and peak tibial external rotation[°] during the first 50ms after impact. Both peak valgus angle and tibial external rotation angle increased with increasing peak valgus moment applied.
Figure 6.
Peak strain in the anterior bundle and the deep bundle of MCL during the first 50ms after impact. The peak MCL strain increased when the applied peak valgus moment increased. .
4. Discussion
This study showed that the peak ACL strain increases nonlinearly with the magnitude of external valgus moments that typically occurs during in vivo run-to-cut landing maneuvers. Peak ACL strain increased by 35% at maximum valgus moments(51 Nm) observed in the in vivo study (Chaudhari et al. 2003), when compared to no valgus moment applied. This predicted peak ACL strain of 0.076 at maximum valgus moment is consistent with the fact that subjects were asked to perform the activity at a comfortable, sub-maximum speed. Therefore, the predicted ACL strain, 0.076, should be below the failure levels, 0.09–0.15 (Butler et al., 1992; Momersteeg et al., 1995). However, the ACL strain associated with the maximum valgus moment may be a more relevant quantity than the average value for estimating the risk of injury, since additional perturbations during landing could increase the ACL strain further. Peak valgus moments could be twice during unanticipated maneuvers as compared to preplanned maneuvers (Besier et al., 2001).
Our results indicate that peak ACL strain is insensitive to an increase in valgus moment for subjects who land with neutral alignment. The peak ACL strain increased only 0.001 as valgus moments increased from 0Nm to 8Nm (slope= 0.00013/Nm, Figure 4), which is the average valgus moment that neutral-landers experience during landing. However, for valgus moments between 10Nm and 40Nm, the ACL strain increases more rapidly (slope= 0.00050/Nm, Figure 4). These results imply that valgus-landers may be at higher risk of injury because the loading in their knees is within the steeper region, where ACL strain is more sensitive to variations in valgus moment.
The ACL strain appears to plateau when the valgus moment rises above 50 Nm (Figure 4). This result suggests that isolated valgus moment alone may not tear the ACL during single-leg landing, which is consistent with the conclusions made in previous studies (Bendjaballah et al. 1997; Mazzocca et al., 2003). When a large valgus moment was applied, the tibia was observed to rotate externally with valgus rotation (Figure 5). This coupled tibial external rotation may reduce the influence of valgus moment on ACL strain, since the addition of external tibial torque to a knee loaded by either anterior tibial force or valgus moment is known to decrease ACL force (Markolf et al., 1995). A previous simulation study suggested that a valgus torque of 94Nm could cause ACL injury (McLean et al., 2003). However, exclusion of tibial axial rotation in their model may over-estimate ACL force, since constraining tibial external rotation is equivalent to applying an additional internal rotation moment to an unconstrained knee joint. Our results suggest that additional externally-applied loading such as internal tibial rotation moment or anterior shear force may increase ACL strains further as suggested by cadaver experiments (Kanamori et al., 2000; Markolf et al., 1995). The combined effect of dynamic valgus and internal tibial rotation moments on ACL strain during landing deserves future study, since previous cadaver studies used low quasi-static loading, which do not represent the dynamic conditions during ACL injury events.
The results also showed that valgus loading is resisted by both the MCL and ACL (Figure 6). The contribution by the MCL to resisting larger valgus loads seems to be another reason that peak ACL strain becomes less sensitive to valgus moment at higher levels of valgus load. As a high valgus moment is applied (i.e. >50Nm), the MCL becomes more sensitive to the valgus loading than the ACL. Since the MCL prevents valgus instability by stopping medial opening (Matsumoto et al., 2001), the MCL may resist valgus loading effectively only after some degree of medial opening occurs. In addition, it is interesting that peak MCL strain of the deep fiber exceeds that of the anterior fiber. This finding agrees with previous reports that the deeper fibers undergo greater strains than do the superficial fibers (the anterior fiber of the MCL in this study) for the same bone-to-bone separation (Amis 1985). This high sensitivity of the deep fiber of the MCL at higher valgus loading may allow the deep fiber of the MCL to be damaged earlier than the ACL. This increasing contribution of the MCL to the total resistance to valgus moment also suggests that valgus moment alone may not be sufficient to tear the ACL without concomitant damage to the MCL during landing.
One major advantage of this model is that it allows unconstrained kinematics at the knee joint. Previous studies often constrained flexion/extension or tibial axial rotation (DeMorat et al., 2004; Fleming et al., 2001; Markolf et al., 1976; Mazzocca et al., 2003; McLean et al., 2003). It has been reported that kinematics of the knee and the relative contributions of the ACL to resisting motion vary depending upon the constraints applied by the testing apparatus (Woo et al., 2006). Constraining tibial axial rotation would have altered the natural motion of the knee under applied valgus moment. Thus, the unconstrained knee joint seems to be the most appropriate for predicting ACL strain. The ACL strain increase with valgus loading observed in this study was much higher than previous studies with constrained axial rotation knees (Fleming et al. 2001, Mazzocca et al., 2003). However, other studies have shown that ACL force significantly increases in response to a valgus loading when axial rotation is unconstrained (Markolf et al., 1995, Fukuda et al., 2003), which agrees with our findings in general. The discrepancies between our results and other studies are likely due to different DOF’s allowed, different methods to support specimens, different simulated motions (landing for this study), or error in simulated results. These many factors make it difficult to compare results readily from different studies.
The results from this study should be considered in light of the fact that the specific relationship between valgus loading and ACL strain during landing has not been validated for this model. In the previous study (Shin et al., 2007) the model was tested to validate the ACL strain, knee flexion, and quadriceps force in response to vertical impact loading during landing. Only a rigorous comparison of the ACL strain response to an applied valgus moment between the simulation and the physical apparatus could definitively determine the exact accuracy of the simulation in predicting ACL strain under applied valgus moments. However, the knee model was developed based on previous efforts to build a standalone knee model to ensure proper tibiofemoral behavior. Thus, we assumed that the knee model should predict kinematic landing motion correctly. Moreover, our validation comparisons showed good correspondence in ACL strain. Therefore, the model should predict changes in ACL strain with the application of additional valgus loading correctly.
One limitation of this study is that in real sport activities the total combined loading applied to the knee joint may include other loadings, such as tibial rotation moment or medial-lateral forces. However, the purpose of this study was to evaluate the isolated influence of the valgus moment on ACL strain during landing, because females experience more valgus alignment and higher valgus moments than males. Thus, understanding the isolated influence of valgus moment on the ACL strain may provide valuable insights into ACL injury. In addition, the interpretation that coupled tibial external rotation reduces ACL strain should be considered with care because this knee model does not account for ACL impingement. Fung et al. (2007) reported that the combination of 8° of valgus rotation, and 13° of tibial external rotation resulted in impingement of the ACL against the lateral wall of the intercondylar notch, and resulted in ACL strain increase by 0.01. In this study, peak values for valgus rotation of 3° and external rotation of 13° were observed with the applied valgus moment of 100Nm.
Since the knee model was created using the anatomy of one knee specimen, one must take care in over-applying its results generally to all knees. In this study we did not separately calculate an individual’s ACL strain based on his/her specific in vivo kinematics and kinetics, but we used the average in vivo data from a group of subjects as input into our force-driven model. To calculate an individual’s ACL strain accurately, it would be necessary to generate different subject-specific geometries with their tissues properties, and to apply subject-specific forces. However, the model was created using the anatomy of an average-sized male based on the bicondylar width (Shelbourne et al., 1998) and inspected for mal-alignment or radiographic deformity. The height-of-patella ratio of this knee represents normal patellofemoral movement (Shin et al. 2007). Thus, the results from this study should be generally applicable to the normal movement of an average-sized knee joint. Although some differences in anatomy and motions between individuals may exist, the general finding of the study should be preserved.
Additionally, in this study, musculotendinous forces were modeled as passive linear springs which may not be consistent with concentric muscle forces during in vivo tasks. This formulation of musculotendinous forces was chosen both because subject specific properties were not known and to best replicate the apparatus used in the cadaver experiment. A complete discussion of the limitations and assumptions of this computational model and the cadaver experiments has been previously presented (Shin et al., 2007; Withrow et al., 2006).
In conclusion, this study has shown that increasing the peak valgus moment during single-leg landing increases the peak ACL strain nonlinearly. However, isolated valgus moment alone within physiologic levels may not be sufficient to induce an isolated tear of the ACL without concomitant damage to the MCL during landing, because coupled tibial external rotation and increasing strain in the MCL reduce the sensitivity of ACL strain to valgus moment at higher levels of valgus moment. Training that reduces these external valgus moments, however, can reduce the ACL strain and thus may help athletes reduce their overall ACL injury risk.
Acknowledgments
The authors acknowledge partial funding from NIH Grant #R01-AR39421.
Footnotes
Conflict of interest statement
No conflict of interest with respect to any material in the manuscript
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amis AA. Biomechanics of ligaments. In: Jenkins DHR, editor. Ligament Injuries and their Treatment. Chapman Hall; London: 1985. pp. 3–28. [Google Scholar]
- Abdel-Rahman EM, Hefzy MS. Three-dimensional dynamic behaviour of the human knee joint under impact loading. Med Eng Phys. 1998;204:276–290. doi: 10.1016/s1350-4533(98)00010-1. [DOI] [PubMed] [Google Scholar]
- Agel J, Arendt EA, Bershadsky B. Anterior cruciate ligament injury in national collegiate athletic association basketball and soccer: a 13-year review. American Journal of Sports Medicine. 2005;33:524–530. doi: 10.1177/0363546504269937. [DOI] [PubMed] [Google Scholar]
- Bendjaballah MZ, Shirazi-Adl A, Zukor DJ. Finite element analysis of human knee joint in varus-valgus. Clinical Biomechanics. 1997;12:139–148. doi: 10.1016/s0268-0033(97)00072-7. [DOI] [PubMed] [Google Scholar]
- Besier TF, Lloyd DG, Ackland TR, Cochrane JL. Anticipatory effects on knee joint loading during running and cutting maneuvers. Medicine and Science in Sports and Exercise. 2001;33:1176–1181. doi: 10.1097/00005768-200107000-00015. [DOI] [PubMed] [Google Scholar]
- Boden BP, Dean GS, Feagin JA, Jr, Garrett WE., Jr Mechanisms of anterior cruciate ligament injury. Orthopedics. 2000;23:573–578. doi: 10.3928/0147-7447-20000601-15. [DOI] [PubMed] [Google Scholar]
- Butler DL, Guan Y, Kay MD, Cummings JF, Feder SM, Levy MS. Location-dependent variations in the material properties of the anterior cruciate ligament. Journal of Biomechanics. 1992;25:511–518. doi: 10.1016/0021-9290(92)90091-e. [DOI] [PubMed] [Google Scholar]
- Chaudhari AM, Hearn BK, Leveille LA, Johnson ER, Andriacchi TP. The effects of dynamic limb alignment on knee moments during single limb landing: Implications for the analysis of the non-contact injury to the anterior cruciate ligament. ASME Summer Bioengineering Conference; Key Biscayne, FL. 2003. pp. 395–396. [Google Scholar]
- Chaudhari AM, Andriacchi TP. The mechanical consequences of dynamic frontal plane limb alignment for non-contact ACL injury. Journal of Biomechanics. 2006;39:330–338. doi: 10.1016/j.jbiomech.2004.11.013. [DOI] [PubMed] [Google Scholar]
- Cooper DE, Deng XH, Burstein AL, Warren RF. The strength of the central third patellar tendon graft. A biomechanical study. American Journal of Sports Medicine. 1993;21:818–23. doi: 10.1177/036354659302100610. discussion 823–4. [DOI] [PubMed] [Google Scholar]
- DeMorat G, Weinhold P, Blackburn T, Chudik S, Garrett W. Aggressive quadriceps loading can induce noncontact anterior cruciate ligament injury. American Journal of Sports Medicine. 2004;32:477–483. doi: 10.1177/0363546503258928. [DOI] [PubMed] [Google Scholar]
- Fleming BC, Renstrom PA, Beynnon BD, Engstrom B, Peura GD, Badger GJ, Johnson RJ. The effect of weightbearing and external loading on anterior cruciate ligament strain. Journal of Biomechanics. 2001;34:163–170. doi: 10.1016/s0021-9290(00)00154-8. [DOI] [PubMed] [Google Scholar]
- Fukuda Y, Woo SL, Loh JC, Tsuda E, Tang P, McMahon PJ, Debski RE. A quantitative analysis of valgus torque on the ACL: a human cadaveric study. Journal of Orthopaedic Research. 2003;21:1107–1112. doi: 10.1016/S0736-0266(03)00084-6. [DOI] [PubMed] [Google Scholar]
- Fung DT, Hendrix RW, Koh JL, Zhang LQ. ACL Impingement Prediction Based on MRI Scans of Individual Knees. Clinical Orthopaedics and Related Research. 2007;46:210–218. doi: 10.1097/BLO.0b013e31804d2339. [DOI] [PubMed] [Google Scholar]
- Garg A, Walker PS. Prediction of total knee motion using a three-dimensional computer-graphics model. Journal of Biomechanics. 1990;23:45–58. doi: 10.1016/0021-9290(90)90368-d. [DOI] [PubMed] [Google Scholar]
- Graf BK, Cook DA, De Smet AA, Keene JS. “Bone bruises” on magnetic resonance imaging evaluation of anterior cruciate ligament injuries. American Journal of Sports Medicine. 1993;21:220–223. doi: 10.1177/036354659302100210. [DOI] [PubMed] [Google Scholar]
- Griffin LY, Agel J, Albohm MJ, Arendt EA, Dick RW, Garrett WE, Garrick JG, Hewett TE, Huston L, Ireland ML, Johnson RJ, Kibler WB, Lephart S, Lewis JL, Lindenfeld TN, Mandelbaum BR, Marchak P, Teitz CC, Wojtys EM. Noncontact anterior cruciate ligament injuries: risk factors and prevention strategies. The Journal of the American Academy of Orthopaedic Surgeons. 2000;8:141–150. doi: 10.5435/00124635-200005000-00001. [DOI] [PubMed] [Google Scholar]
- Gwinn DE, Wilckens JH, McDevitt ER, Ross G, Kao TC. The relative incidence of anterior cruciate ligament injury in men and women at the United States Naval Academy. American Journal of Sports Medicine. 2000;28:98–102. doi: 10.1177/03635465000280012901. [DOI] [PubMed] [Google Scholar]
- Harner CD, Baek GH, Vogrin TM, Carlin GJ, Kashiwaguchi S, Woo SL. Quantitative analysis of human cruciate ligament insertions. Arthroscopy. 1999;15:741–749. doi: 10.1016/s0749-8063(99)70006-x. [DOI] [PubMed] [Google Scholar]
- Hewett TE, Myer GD, Ford KR, Heidt RS, Jr, Colosimo AJ, McLean SG, van den Bogert AJ, Paterno MV, Succop P. Biomechanical measures of neuromuscular control and valgus loading of the knee predict anterior cruciate ligament injury risk in female athletes: a prospective study. American Journal of Sports Medicine. 2005;33:492–501. doi: 10.1177/0363546504269591. [DOI] [PubMed] [Google Scholar]
- Hollis JM, Takai S, Adams DJ, Horibe S, Woo SL. The effects of knee motion and external loading on the length of the anterior cruciate ligament (ACL): a kinematic study. Journal Biomechanical Engineering. 1991;113:208–214. doi: 10.1115/1.2891236. [DOI] [PubMed] [Google Scholar]
- Kanamori A, Woo SL, Ma CB, Zeminski J, Rudy TW, Li G, Livesay GA. The forces in the anterior cruciate ligament and knee kinematics during a simulated pivot shift test: A human cadaveric study using robotic technology. Arthroscopy. 2000;16:633–639. doi: 10.1053/jars.2000.7682. [DOI] [PubMed] [Google Scholar]
- Kernozek TW, Torry MR, VAN Hoof H, Cowley H, Tanner S. Gender differences in frontal and sagittal plane biomechanics during drop landings. Medicine and Science in Sports and Exercise. 2005;37:1003–12. discussion 1013. [PubMed] [Google Scholar]
- Lötstedt P. Mechanical systems of rigid bodies subject to unilateral constraints. SIAM Journal of Applied Mathematics. 1982;42:281–296. [Google Scholar]
- Lloyd DG, Buchanan TS. Strategies of muscular support of varus and valgus isometric loads at the human knee. Journal of Biomechanics. 2001;34:1257–1267. doi: 10.1016/s0021-9290(01)00095-1. [DOI] [PubMed] [Google Scholar]
- Markolf KL, Burchfield DM, Shapiro MM, Shepard MF, Finerman GA, Slauterbeck JL. Combined knee loading states that generate high anterior cruciate ligament forces. Journal of Orthopaedic Research. 1995;13:930–935. doi: 10.1002/jor.1100130618. [DOI] [PubMed] [Google Scholar]
- Markolf KL, Mensch JS, Amstutz HC. Stiffness and laxity of the knee – the contributions of the supporting structures. A quantitative in vitro study. The Journal of Bone and Joint Surgery. American Volume. 1976;58:583–594. [PubMed] [Google Scholar]
- Matsumoto H, Suda Y, Otani T, Niki Y, Seedhom BB, Fujikawa K. Roles of the anterior cruciate ligament and the medial collateral ligament in preventing valgus instability. Journal of Orthopaedic Science. 2001;6:28–32. doi: 10.1007/s007760170021. [DOI] [PubMed] [Google Scholar]
- Mazzocca AD, Nissen CW, Geary M, Adams DJ. Valgus medial collateral ligament rupture causes concomitant loading and damage of the anterior cruciate ligament. The Journal of Knee Surgery. 2003;16:148–51. [PubMed] [Google Scholar]
- McLean SG, Su A, van den Bogert AJ. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. Journal of Biomechanical Engineering. 2003;125:864–874. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- McLean SG, Walker KB, van den Bogert AJ. Effect of gender on lower extremity kinematics during rapid direction changes: an integrated analysis of three sports movements. Journal of Science and Medicine in Sport. 2005;8:411–422. doi: 10.1016/s1440-2440(05)80056-8. [DOI] [PubMed] [Google Scholar]
- Momersteeg TJ, Blankevoort L, Huiskes R, Kooloos JG, Kauer JM, Hendriks JC. The effect of variable relative insertion orientation of human knee bone-ligament-bone complexes on the tensile stiffness. Journal of Biomechanics. 1995;28:745–752. doi: 10.1016/0021-9290(94)00121-j. [DOI] [PubMed] [Google Scholar]
- Nam EK, Makhsous M, Koh J, Bowen M, Nuber G, Zhang LQ. Biomechanical and histological evaluation of osteochondral transplantation in a rabbit model. American Journal of Sports Medicine. 2004;32:308–316. doi: 10.1177/0363546503259616. [DOI] [PubMed] [Google Scholar]
- Noyes FR, Butler DL, Grood ES, Zernicke RF, Hefzy MS. Biomechanical analysis of human ligament grafts used in knee-ligament repairs and reconstructions. The Journal of Bone and Joint Surgery. American Volume. 1984;66:344–352. [PubMed] [Google Scholar]
- Olsen OE, Myklebust G, Engebretsen L, Bahr R. Injury mechanisms for anterior cruciate ligament injuries in team handball: a systematic video analysis. American Journal of Sports Medicine. 2004;32:1002–1012. doi: 10.1177/0363546503261724. [DOI] [PubMed] [Google Scholar]
- Oni OO, Morrison CJ. The mechanical ‘quality’ of osteophytes. Injury. 1998;29:31–33. doi: 10.1016/s0020-1383(97)00122-8. [DOI] [PubMed] [Google Scholar]
- Reicher MA. An atlas of normal multiplanar anatomy of the knee joint. In: Mink JH, Reicher MA, Crues JV, Deutsch AL, editors. Magnetic Resonance Imaging of the Knee. Raven Press; New York: 1993. pp. 51–90. [Google Scholar]
- Shelbourne KD, Davis TJ, Klootwyk TE. The relationship between intercondylar notch width of the femur and the incidence of anterior cruciate ligament tears. A prospective study. American Journal of Sports Medicine. 1998;26:402–408. doi: 10.1177/03635465980260031001. [DOI] [PubMed] [Google Scholar]
- Shelburne KB, Pandy MG. A musculoskeletal model of the knee for evaluating ligament forces during isometric contractions. Journal of Biomechanics. 1997;30:163–176. doi: 10.1016/s0021-9290(96)00119-4. [DOI] [PubMed] [Google Scholar]
- Shin CS. PhD Thesis. Stanford University Press; Stanford: 2006. The development, validation, and applications of a three-dimensional dynamic specimen-specific knee model to study ACL strain. [Google Scholar]
- Shin CS, Chaudhari AM, Andriacchi TP. The influence of deceleration forces on ACL strain during single-leg landing: A simulation study. Journal of Biomechanics. 2007;40:1145–1152. doi: 10.1016/j.jbiomech.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Sigward SM, Powers CM. Loading characteristics of females exhibiting excessive valgus moments during cutting. Clinical Biomechanics (Bristol, Avon) 2007;22:827–833. doi: 10.1016/j.clinbiomech.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Speer KP, Spritzer CE, Bassett FH, 3rd, Feagin JA, Jr, Garrett WE., Jr Osseous injury associated with acute tears of the anterior cruciate ligament. American Journal of Sports Medicine. 1992;20:382–389. doi: 10.1177/036354659202000403. [DOI] [PubMed] [Google Scholar]
- Withrow TJ, Huston LJ, Wojtys EM, Ashton-Miller JA. The relationship between quadriceps muscle force, knee flexion, and anterior cruciate ligament strain in an in vitro simulated jump landing. American Journal of Sports Medicine. 2006;34:269–274. doi: 10.1177/0363546505280906. [DOI] [PubMed] [Google Scholar]
- Woo SL, Abramowitch SD, Kilger R, Liang R. Biomechanics of knee ligaments: injury, healing, and repair. Journal of Biomechanics. 2006;39:1–20. doi: 10.1016/j.jbiomech.2004.10.025. [DOI] [PubMed] [Google Scholar]
- Woo SL, Hollis JM, Adams DJ, Lyon RM, Takai S. Tensile properties of the human femur-anterior cruciate ligament-tibia complex. The effects of specimen age and orientation. American Journal of Sports Medicine. 1991;19:217–225. doi: 10.1177/036354659101900303. [DOI] [PubMed] [Google Scholar]
- Yu CH, Walker PS, Dewar ME. The effect of design variables of condylar total knees on the joint forces in step climbing based on a computer model. Journal of Biomechanics. 2001;34:1011–1021. doi: 10.1016/s0021-9290(01)00060-4. [DOI] [PubMed] [Google Scholar]