Biologically Closed Electrical Circuits in Venus Flytrap

Abstract

The Venus flytrap (Dionaea muscipula Ellis) is a marvel of plant electrical, mechanical, and biochemical engineering. The rapid closure of the Venus flytrap upper leaf in about 0.1 s is one of the fastest movements in the plant kingdom. We found earlier that the electrical stimulus between a midrib and a lobe closes the Venus flytrap upper leaf without mechanical stimulation of trigger hairs. The Venus flytrap can accumulate small subthreshold charges and, when the threshold value is reached, the trap closes. Here, we investigated the electrical properties of the upper leaf of the Venus flytrap and proposed the equivalent electrical circuit in agreement with the experimental data.

Electrical processes associated with rapid closure of the carnivorous plant Venus flytrap (Dionaea muscipula Ellis) have been attracting the attention of researchers and, as a result, its mechanism has been widely investigated (Burdon-Sanderson, 1874; Lloyd, 1942; Hodick and Sievers, 1989; Fagerberg and Allain, 1991; Volkov et al., 2007, 2008a, 2008b, 2008c; Markin et al., 2008). When an insect touches the trigger hairs, these mechanosensors trigger a receptor potential (Jacobson, 1965; DiPalma et al., 1966; Benolken and Jacobson, 1970; Williams and Mozingo, 1971), which generates an electrical signal that acts as an action potential (Hodick and Sievers, 1988; Volkov et al., 2007). Two stimuli generate two action potentials, which activate the trap closing at room temperature in a fraction of a second (Volkov et al., 2007). Propagation of action potentials and the trap closing can be blocked by uncouplers, inhibitors of voltage-gated channels and aquaporins (Volkov et al., 2007, 2008c).

The inducement of nonexcitability after excitation (refractory period) and the summation of subthreshold irritations were developed in the vegetative and animal kingdoms in protoplasmic structures prior to morphological differentiation of nervous tissues. These protoplasmic structures merged into the organs of a nervous system providing the interfacing of the organism with the environment. Some neuromotoric components include acetylcholine neurotransmitters (Roshchina, 2001), cellular messenger calmodulin, cellular motors actin and myosin, voltage-gated channels, and sensors for touch, light, gravity, and temperature (Volkov, 2006a; Lang and Volkov, 2008). Although this nerve-like cellular equipment has not reached the same level of great complexity as in animal nerves, a simple neural network has been formed within the plasma membrane of a phloem or plasmodesmata enabling it to communicate efficiently over long distances (Volkov and Brown, 2006a, 2006b). The reason why plants have developed pathways for electrical signal transmission most probably lies in the necessity to respond rapidly to environmental stress factors (Volkov and Haack, 1995). Different environmental stimuli evoke specific responses in living cells, which have the capacity to transmit a signal to the responding region (Ksenzhek and Volkov, 1998). In contrast to chemical signals such as hormones, electrical signals are able to transmit information rapidly over long distances (Volkov, 2000). Electrical potentials have been measured at the tissue and whole-plant levels (Volkov, 2006a, 2006b).

We found that Venus flytrap has a short-term electrical memory (Volkov et al., 2008a, 2008b). Using the charge injection method (Volkov et al., 2008a), it was evident that the application of an electrical stimulus between the midrib (positive potential) and a lobe (negative potential) causes Venus flytrap to close the trap without any mechanical stimulation. The average stimulation pulse voltage sufficient for rapid closure of the Venus flytrap was 1.5 V (+ in the midrib; − in a lobe).

Application of a single 14-μC electrical charge from a capacitor causes trap closure and induces an electrical signal propagating between the lobes and the midrib (Volkov et al., 2008a, 2008b). The Venus flytrap can accumulate and sum small charges and, when the threshold value is reached, the trap closes. A summation of stimuli is demonstrated through the repetitive application of smaller charges (Volkov et al., 2008a). The capacitor discharges exponentially with time, so, although a 14-μC charge was applied, not all of this charge was accumulated to assist in closing the trap. As soon as a 9.01-μC charge is transmitted between a lobe and midrib from the capacitor, the trap begins to close at room temperature. It was shown that voltage-gated ion channels have a time-dependent molecular memory phenomenon with profound implications on the biophysical properties of voltage-gated ion channels (Nayak and Sikdar, 2007).

Biologically closed electrical circuits operate over large distances in biological tissues (Nordestrom, 1983; Volkov et al., 1998). The activation of such a circuit can lead to various physiological and biophysical responses (Lang and Volkov, 2008).

In this article, we investigated the biologically closed electrical circuits in the upper leaf of the Venus flytrap and proposed the equivalent electrical circuit of the trap. It is often convenient to represent the real electrical and electrochemical properties of biointerfaces with idealized equivalent electrical circuit models consisting of discrete electrical components.

RESULTS AND DISCUSSION

Electrical Discharge in the Venus Flytrap and Electrical Memory

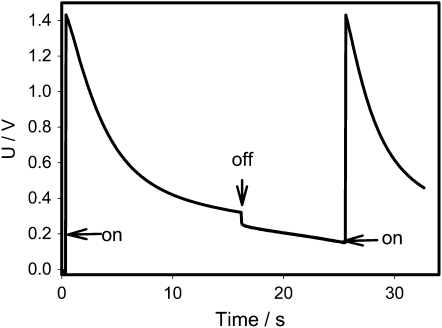
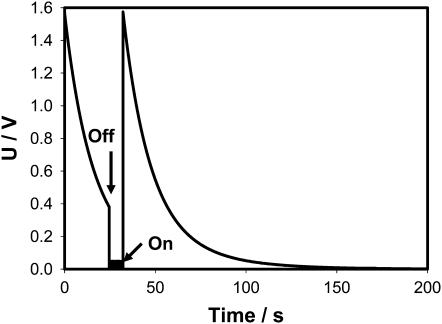
A charge can be delivered from a charged capacitor by small portions and, as soon as the threshold value will be accumulated, the trap will start to close. Figure 1 shows that this closing charge can be delivered from a charged capacitor by two subsequent electrical discharges and the Venus flytrap memorizes the first charge. It is interesting to mention that, after disconnection of a charged capacitor from the Venus flytrap to recharge the capacitor (Fig. 1), the potential difference on Ag/AgCl electrodes (+ in the midrib; − in a lobe) decreases very slowly with time.

Figure 1.

Electrical discharge in the Venus flytrap between electrodes located in a lobe (−) and a midrib (+) connected to a charged 4.7-μC capacitor and a NI-PXI-4071 digital multimeter. The length of the midrib was 2 cm. These results were reproduced 23 times on different Venus flytrap plants. The capacitor was disconnected (off), recharged, and connected again (on). U is the capacitor voltage in volts.

Biologically Closed Electrical Circuits

If a capacitor of capacitance C is discharged through a resistor R (Fig. 2A), the capacitor voltage U is then

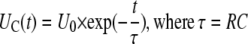(1)

and

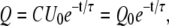(2)

where Q₀ = CU₀ is the initial charge on the capacitor. The capacitive time constant RC governs the discharging process. At t = τ = RC the capacitor charge is reduced to CU₀e⁻¹, which is about 37% of its initial charge. For R in ohms and C in farads, the time constant RC is in seconds. The voltage across the capacitor decreases exponentially with the same time constant τ from the initial value U₀ to zero.

Figure 2.

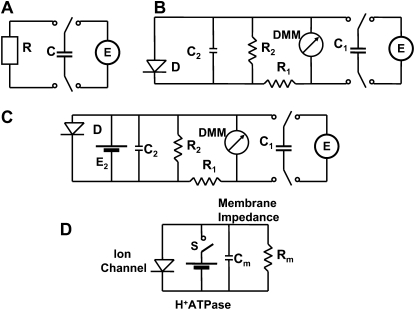
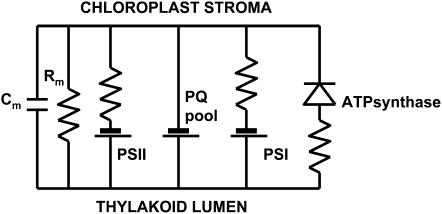
Equivalent electrical circuits. E, Battery; C₁, external charged capacitor; C₂, C_m, membrane capacitance; R₁, resistance in a lobe; R₂, R_m, membrane resistance; D, diode as a model of a voltage-gated ion channel; DMM, digital multimeter; S, electrical charge or voltage sensor and switch.

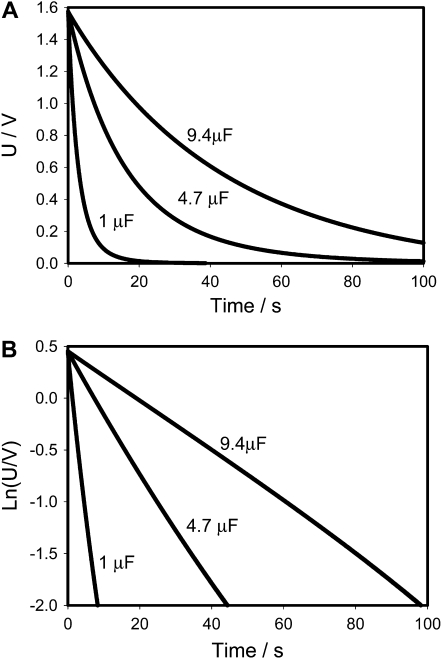
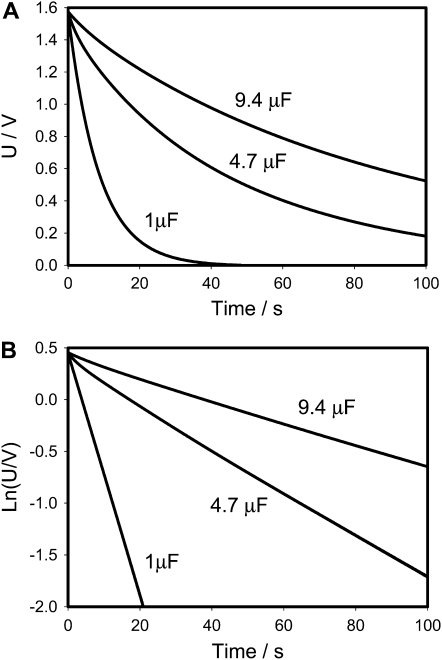
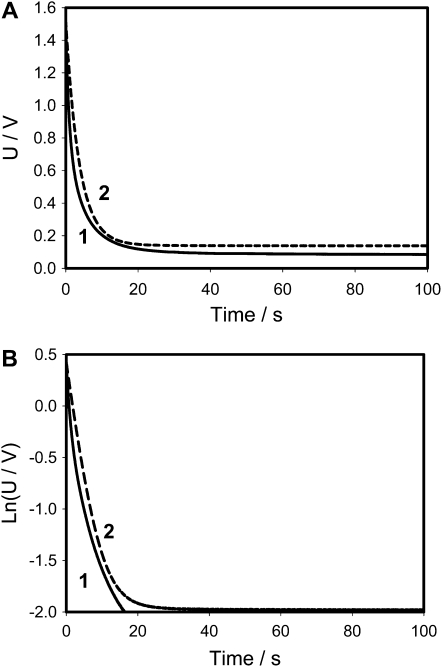
Figures 3 and 4 show that the experimental dependencies look like they are predicted by Equations 1 and 2 when capacitors were charged by a 1.53 V battery, but more detailed consideration on Figure 3B shows deviations from Equation 1 because the equivalent electrical circuit of the Venus flytrap is more complicated than just a resistor (Fig. 2A). The equivalent electrical circuit should include the capacitance C₂ and resistance R₂ of the plasma membrane (Fig. 2B). Figures 3 and 4 also show the dependence of capacitor discharge kinetics on the polarity of the applied voltage. When a positive electrode is located in the midrib, the discharge of the capacitor is much faster (Fig. 3) than when a negative electrode is in the midrib (Fig. 4). The equivalent electrical circuit should include additional elements sensitive to electrical polarity, such as a diode (Fig. 2B).

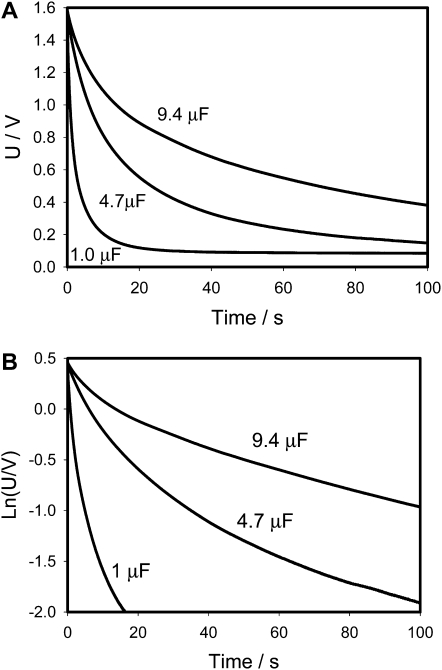
Figure 3.

Electrical discharge in the Venus flytrap between electrodes located in a lobe (−) and a midrib (+) connected to charged capacitor and NI-PXI-4071 digital multimeter. The length of the midrib was 2 cm. These results were reproduced 34 times on different Venus flytrap plants. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

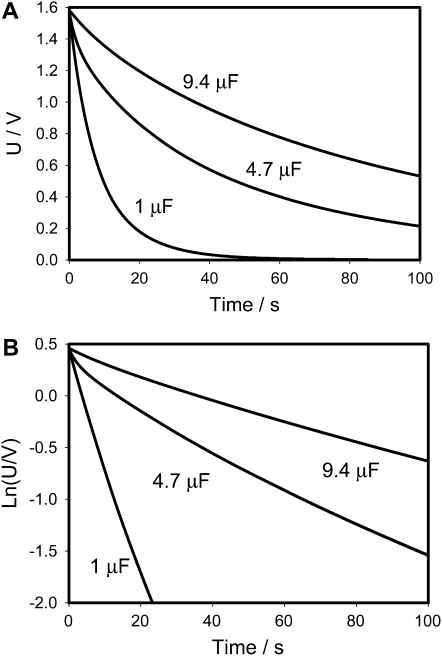
Figure 4.

Time dependence of voltage on a capacitor during a discharge between electrodes located in a lobe (+) and a midrib (−) connected to charged capacitor and NI-PXI-4071 digital multimeter in the Venus flytrap on time. These results were reproduced 27 times on different Venus flytrap plants. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

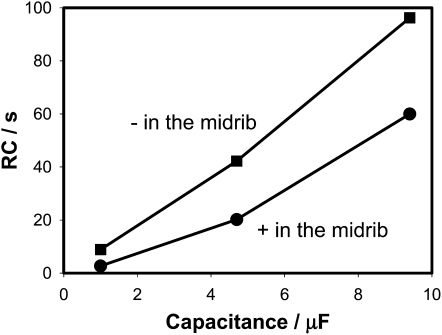
Figure 5 shows dependencies of τ = RC on capacitance estimated according to Equation 1. These dependencies are functions of the polarity of the applied voltage (Fig. 5). According to the mechanism of the trap closing, which we recently proposed, the voltage-gated ion channel plays an important role in the trap-closing process. Uncouplers and blockers of K⁺ voltage-gated channels inhibit the trap closing. As soon as H⁺ or K⁺ channels open and transport of ions starts, the water flow through aquaporins increases the pressure in the outer layer of lobes closing the trap. We used a silicon rectifier Schotky diode NTE583 as a model of a voltage-gated ion channel (Fig. 2B). Figures 6 and 7 show that the equivalent electrical circuit in Figure 2B gives good correlation between our results in vivo on the Venus flytrap (Figs. 3 and 4) and on the electrical circuit shown in Figure 2B.

Figure 5.

Dependence of τ = RC in the Venus flytrap according to the equivalent circuit shown in Figure 2A.

Figure 6.

Time dependence of voltage on a capacitor during a discharge between electrodes in the circuit shown in Figure 2B. R₁ = 3.7 MΩ, R₂ = 5.32 MΩ, diode D is NTE583, C₂ = 11 nF, E = 1.53 V (− on a diode cathode), and C₁ as shown in the figure. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

Figure 7.

Time dependence of voltage on a capacitor during a discharge between electrodes in the circuit shown in Figure 2B. R₁ = 3.7 MΩ, R₂ = 5.32 MΩ, diode D is NTE583, C₂ = 11 nF, E = 1.53 V (+ on the diode cathode), and C₁ as shown in the figure. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

There are two important differences between Figures 3 and 6. There is a deviation from linear dependence in Figure 3B, and such deviation does not exist in our electronic model shown in Figure 6B. Figure 3A shows that electrical potential does not drop to zero during the 100 s; the Venus flytrap remembers an electrical potential of about 0.1 V for a short period of time.

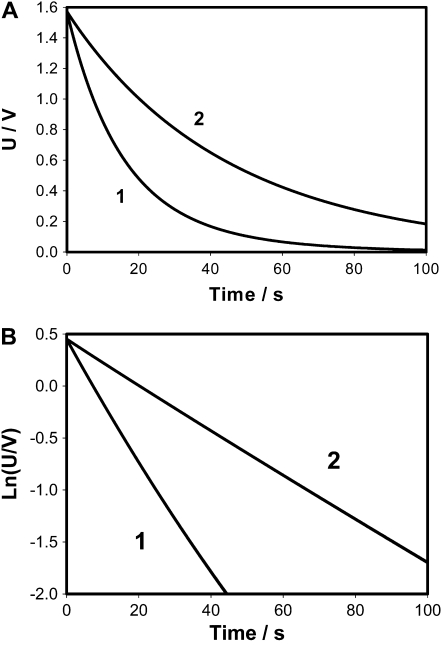
Introducing a diode D into the electronic circuit (Fig. 2B) as a model of a voltage-gated ion channel gives a good answer (Fig. 8) on the difference in kinetics of the capacitor discharge shown in Figures 3 and 4. When a positive electrode is located in the midrib, it stimulates the opening of ion channels and the capacitor discharge is much faster than in the case with reverse polarity.

Figure 8.

Time dependence of voltage on a capacitor during a discharge between electrodes in the circuit shown in Figure 2B. C₁ = 4.7 μF, R₁ = 3.7 MΩ, R₂ = 5.32 MΩ, diode D is NTE583, C₂ = 11 nF, E = 1.53 V. 1, − on the diode cathode; 2, + on the diode cathode. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

There is a significant difference between the model shown in Figure 2B and the Venus flytrap. After switching off the charged capacitor, electrical potential drops to zero (Fig. 9) in the electronic model shown in Figure 2B. In the Venus flytrap, after disconnecting the charged capacitor (Fig. 1; line between switch off and on), the voltage drops to about 0.1 V (Fig. 3A), which is approximately constant during a time period of 200 s. The equivalent electrical circuit should have the additional element responsible for this small electrical voltage in the Venus flytrap after discharging the capacitor C₁ (Fig. 2C). It means that there is an additional electromotive force in the leaf. This could be a proton pump existing in the leaf (Williams and Bennet, 1982; Rea, 1983). The process of the trap closing requires ATP hydrolysis in the midrib (Jaffe, 1973; Williams and Bennet, 1982). We modeled the proton motive force of ATPase as a small electrical battery E₂ in Figure 2C. Figure 10 shows that the equivalent electrical circuit in Figure 2C describes very well the experimental data on the kinetics of electrical discharge in the Venus flytrap in vivo.

Figure 9.

Time dependence of voltage on a capacitor during a discharge between electrodes in the circuit shown in Figure 2B. C₁ = 4.7 μF, R₁ = 3.7 MΩ, R₂ = 5.32 MΩ, diode D is NTE583, C₂ = 11 nF, E = 1.53 V. U is the capacitor voltage in volts.

Figure 10.

Time dependence of voltage on a 1-μF capacitor during a discharge between electrodes in the circuit shown in Figure 2C (2) and between electrodes located in a lobe (−) and a midrib (+) in the Venus flytrap (1) connected to NI-PXI-4071 digital multimeter. The length of the midrib was 2 cm. 2, C₁ = 4.7 μF, R₁= 3.7 MΩ, R₂ = 5.32 MΩ, diode D is NTE583, C₂ = 11 nF, E = 1.53 V, E₂ = 0.14 V. U is the capacitor voltage in volts. Ln(U/V) is the natural logarithm of capacitor voltage.

Figure 2D shows the equivalent electrical circuit of the osmotic motor responsible for fast osmotic flow of water through aquaporins to the outer layer of lobes after electrical stimulation. To analyze the consecutive stages of the Venus flytrap closing and to interpret the processes that govern these stages, we employed the recently developed hydroelastic curvature model. This model is based on the assumption that the trap possesses curvature elasticity and consists of outer and inner hydraulic layers where a difference of hydrostatic pressures can build up (Markin et al., 2008). The open state of the trap contains high elastic energy due to the hydrostatic pressure difference between the outer and inner layers of the lobe. Stimuli induce water flow from one hydraulic layer to another and the trap relaxes to the equilibrium configuration corresponding to the closed state. Water transport leads to extension of the cells on the exterior surface of the leaf and to a change in the natural curvature of the leaf, which is likely to drive the closure process.

Our data suggest that elastic energy does play an important role, but closing the trap also involves another process that determines the transformation from an open to a closed state. So the hydroelastic model includes bending elasticity, turgor pressure, and water jets. The closure of the Venus flytrap represents the nonmuscular movement based on hydraulics and mechanical elasticity. The nastic movements in various plants involve a large internal pressure (turgor) actively regulated by plants.

In the open state, the pressure in the upper layer is higher than in the lower layer, maintaining the convex shape of the leaf. The trigger signal induces fluid rushes from one layer to another. The leaf relaxes to its equilibrium state corresponding to the closed configuration.

Biologically Closed Photosynthetic Electrical Circuit

There are many different biologically closed electrical circuits in plants: photophosphorylation electrical circuit (Fig. 11), plasma membrane electrical circuits responsible for action and resting potentials, and others. During the light-dependent reaction, protons are pumped across the thylakoid membrane into the lumen making it acidic. PSI utilizes light energy to reduce NADP⁺ to NADPH and is active in both noncyclic and cyclic electron transport. PSII uses light energy to oxidize water molecules, producing electrons, protons, and molecular oxygen. These protons are basically linked with the membrane and can be used for a condensation reaction, such as the synthesis of ATP via ATP synthase (Volkov et al., 1998). Plastoquinone (PQ) is a quinone molecule involved in the electron transport chain in the light-dependent reactions of photosynthesis. PQ is reduced from the stromal matrix of the chloroplast, coupled to two electrons from PSII, forming plastoquinol. It transports the protons to the lumen of thylakoid discs, while the electrons continue through the electron transport chain into the cytochrome b₆f protein complex.

Figure 11.

The equivalent electrical circuit of thylakoid membrane. C_m, Membrane capacitance; R_m, membrane resistance; cF₁, coupling factor; cF₀, proton channel; PQ pool, plastoquinone pool.

The vectorial transport of electrons in the thylakoid membrane leads to the translocation of protons and to ATP synthesis. Significant amounts of ATP are hydrolyzed in the midrib of the Venus flytrap during the trap closing (Jaffe, 1973; Williams and Bennet, 1982).

MATERIALS AND METHODS

Electrodes

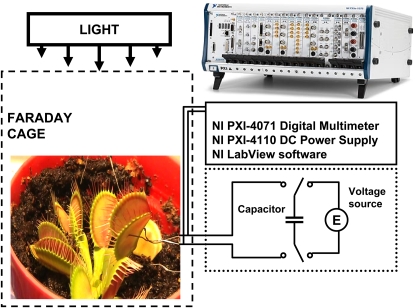
All measurements were conducted in the laboratory at 21°C inside a Faraday cage mounted on a vibration-stabilized table. Ag/AgCl electrodes were prepared from Teflon-coated silver wires. Following insertion of the electrodes into lobes and the midrib, the traps closed. We allowed plants to rest until the traps were completely open.

Data Acquisition

NI-PXI-4071 digital multimeter (National Instruments) interfaced to 0.1-mm-thick nonpolarizable reversible Ag/AgCl electrodes were used to record the digital data (Fig. 12). Measuring signals were recorded as ASCII files using LabView (National Instruments) software. The NI-PXI-4071 high-resolution digital multimeter delivers fast voltage measurements from 10 nV to 1,000 V, current measurements from 1 pA to 3 A, and resistance measurements from 10 μΩ to 5 GΩ.

Figure 12.

Experimental setup.

The same results were obtained using digital multimeters Keithley 2000 and Keithley 6514.

Plant Electrostimulation

The charge-injection method (Volkov et al., 2008a) has been used to precisely estimate the amount of electrical charge. The National Instruments PXI-4110 is a programmable, triple-output precision DC power supply in a single-slot, 3-unit PXI module. The PXI-4110 has 16-bit resolution for programming the voltage set point and current limit and for using the voltage and current read-back/measurement functionality.

Plants

Three hundred bulbs of Venus flytrap (Dionaea muscipula Ellis) were purchased for this experimental work from Fly-Trap Farm (Supply, North Carolina) and grown in well-drained peat moss in plastic pots at 21°C with a 12-h light/12-h dark photoperiod. The peat moss was treated with distilled water. Humidity averaged 45% to 50%. Irradiance was 77 μE/m²s. All experiments were performed on healthy adult specimens.