Computer Simulation of the Dynamic Behavior of the Glutathione-Ascorbate Redox Cycle in Chloroplasts^,

Abstract

The glutathione-ascorbate redox pathway in chloroplasts is a complex network of spontaneous, photochemical, and enzymatic reactions for detoxifying hydrogen peroxide. This article presents a comprehensive sensitivity analysis of the system. A model has been constructed to simulate oxidative stress conditions, enabling steady-state concentrations of the metabolites involved in the pathway and photochemical and enzymatic fluxes to be calculated. The model includes an electron source whose flux is distributed among three competitive routes (photogeneration of 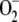, photoreduction of NADP⁺ to NADPH, and photoreduction of monodehydroascorbate to ascorbate) and that allows the simulation of variations in NADPH concentration with time. Each enzyme considered is introduced in the model, taking into account its particular catalytic mechanism, including the inactivation of ascorbate peroxidase in the presence of low-ascorbate concentrations. Computer simulations pointed to the great sensitivity of the system to the ratio among fluxes corresponding to ascorbate and NADPH photoproduction and NADPH consumption by the Calvin cycle. Under oxidative stress conditions, the model shows a sequential depletion of antioxidant power in chloroplasts in the order NADPH, glutathione, ascorbate and their recovery in the reverse order. Decreasing levels of glutathione reductase, ascorbate peroxidase, and superoxide dismutase led to the irreversible photoinactivation of ascorbate peroxidase and the subsequent increase in hydrogen peroxide concentration, preceded by a maximum in dehydroascorbate reductase activity.

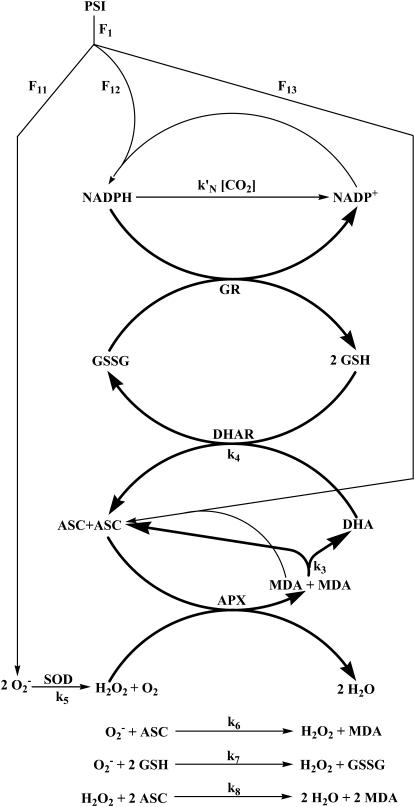
In plants, the main generation sites of reactive oxygen species (ROS) are the reaction centers of PSI and PSII in chloroplast thylakoids. Under steady-state conditions, the intracellular level of ROS is tightly buffered and controlled by detoxifying antioxidant systems formed of a network of enzymatic and nonenzymatic components (Noctor and Foyer, 1998; Mittler, 2002). Superoxide dismutase (superoxide:superoxide oxidoreductase [SOD]; EC 1.15.1.1) acts as the first line of defense against ROS by dismutating 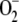to hydrogen peroxide (H₂O₂) and O₂. In chloroplasts, the H₂O₂ thus generated is reduced to water by ascorbate (ASC) catalyzed with l-ascorbate peroxidase (l-ascorbate:hydrogen peroxide oxidoreductase [APX]; EC 1.11.1.11). This is the first step of the so-called glutathione-ascorbate (GSH-ASC) cycle, also named the water-water cycle (Asada, 1999, 2006). Dehydroascorbate reductase (glutathione:dehydroascorbate oxidoreductase [DHAR]; EC 1.8.5.1), monodehydroascorbate reductase (NADH:monodehydroascorbate oxidoreductase [MDAR]; EC 1.6.5.4), and glutathione reductase (glutathione:NADP⁺ oxidoreductase [GR]; EC 1.8.1.7) also participate in the pathway (Fig. 1), which uses ASC, GSH, and NADPH as electron donors (for an extensive review of the pathway, see Asada, 1999).

Figure 1.

Schematic representation of the model to simulate the dynamic behavior of the GSH-ASC pathway in chloroplasts. k_i values (i = 3–8) are apparent bimolecular rate constants for the spontaneous steps included in the model.

Numerous studies have been performed on the GSH-ASC cycle, and it is still a matter of intensive research (Noctor and Foyer, 1998; Asada, 1999, 2006). The computer modeling of metabolic systems is an increasingly used tool that has enhanced our understanding of the behavior of metabolic pathways. It was introduced to analyze pathways in chloroplasts in the early 1980s (Laisk and Walker, 1986; Hahn, 1987), and more recently, a very interesting paper has analyzed the network of redox reactions of the GSH-ASC cycle (Polle, 2001). The model was successfully used to simulate the functioning of the redox cycle in chloroplasts, making it possible to calculate steady-state concentrations of species and fluxes of steps involved in the reaction scheme proposed. However, the model has some limitations, such as the assumption of a constant NADPH concentration during the simulation time, the nonreduction of the NADP⁺ formed (leading to the erroneous accumulation of NADP⁺ in the chloroplast), and a constant 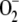production rate during the simulation time. Furthermore, the fact that the kinetic behavior of the enzymes involved in the pathway was introduced with an identical equation, that corresponding to a ping-pong bi bi reaction mechanism (except SOD, which was treated as a bimolecular reaction), means that the model should be modified.

The aim of this article was to extend the above approach in several aspects in an attempt to improve the model and to bring it closer to what occurs in reality. In this way, the model will allow a better scientific understanding of the spontaneous and enzymatic reactions involved in the pathway and may contribute to the prediction of results in the design of experiments. (1) The electron flux from PSI has been considered as being distributed among three competitive routes involving the photogeneration of 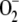from O₂, the photoreduction of NADP⁺ to NADPH, and the photoreduction of monodehydroascorbate radicals (MDA) to ASC. In this way, NADP⁺ is recycled to NADPH and the electron flux related to the production of 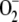is changeable and dependent on the availability of NADPH and MDA, making the model much more flexible, since the three fluxes must be adapted to each other to respond to stress conditions. (2) Each enzymatic activity involved in the cycle has been introduced in the model, taking into account the particular catalytic mechanism of each enzyme. In addition, an inactivation step for APX in the presence of H₂O₂ (Miyake et al., 2006) has been included along with a route for the de novo synthesis of the protein. This last step represents one of the main defense mechanisms of plants to mitigate oxidative stress, so the recovery of APX inactivated by an excess of H₂O₂ can be simulated. (3) An additional step representing NADPH consumption in the Calvin cycle has been added, so that the competition between the NADPH consumed by the ROS-detoxifying pathway and the NADPH consumed by the Calvin cycle is included. (4) The model has been constructed based on the ordinary differential equations (ODE) system corresponding to the network of spontaneous and enzymatic steps involved in the cycle. Computer simulations have been performed by numerical integration of this set of ODE using the easily accessible software MATLAB. This software has several ODE solver routines for nonstiff and stiff (as in the present case) problems, so users can choose the best option for their specific problem.

DESCRIPTION OF THE MODEL

The system being studied is depicted in Figure 1. There is a constant electron source in the model, PSI, whose flux is divided among three competitive routes: (1) the photoproduction of 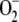; (2) the photoreduction of NADP⁺; and (3) the photoreduction of MDA. The last two processess are ferredoxin (Fd) dependent, although Fd has not been introduced as a variable in the present model, and only electron fluxes have been considered. The same holds for the electron donor species involved in the photogeneration of 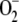(in the same way, [O₂] and [CO₂] have also been considered constants). For the notation and definitions used for the fluxes, see Table I. F₁₃ has been considered as directly proportional to [MDA], k₁₃ being the proportionality constant. Factor 2 in F₁₂ indicates the fact that the reduction of NADP⁺ to NADPH is a two-electron process. F₁₁ is the remaining flux from PSI. In this way F₁₁, F₁₂, and F₁₃ are variable and dependent on the [NADP⁺] and [MDA] present in chloroplasts. This imparts great flexibility to the model and a greater ability to study stress conditions in chloroplasts.

Table I.

Notation and definitions of fluxes used in the present model

Notation	Definition	Mathematical Expression
F1	Electron flow from PSI	F1 = F11 + F12 + F13
F11	Electron flow related to the one-electron photoreduction of	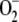F1 − 2k12[NADP+] − k13[MDA]
F12	Electron flow related to the two-electron photoreduction of NADP+ to NADPH	2k12[NADP+]
F13	Electron flow related to the one-electron reduction of MDA to ASC	k13[MDA]
FN	NADPH flow related to the Calvin cycle	k′N[CO2][NADPH]
F5	Rate of de novo synthesis of APX	k5APX([APX]0 − [APX] − [CoI] − [CoII])

Enzymes Involved in the Model

SOD

The 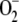photogenerated directly by the PSI complex is mainly disproportionated to H₂O₂ and O₂ catalyzed by SOD. This reaction has a 10,000-fold faster rate than spontaneous dismutation (Bowler et al., 1992). In almost all plants, chloroplasts contain CuZn-SOD as the major isoform of the enzyme (Asada, 1999). These enzymes are known as superefficient 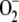scavengers with pseudo first-order (k_cat/K_m) catalytic rates as high as 2 × 10⁹ m⁻¹ s⁻¹ in water and 2 × 10⁸ m⁻¹ s⁻¹ in the stroma, owing to its high viscosity (Ogawa et al., 1995). Taking this into account and the fact that [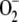] inside chloroplasts is on the order of micromolar, first-order kinetics can be assumed for the rate of SOD with respect to [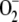]. So the following rate equation was used in our model:

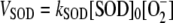(1)

APX

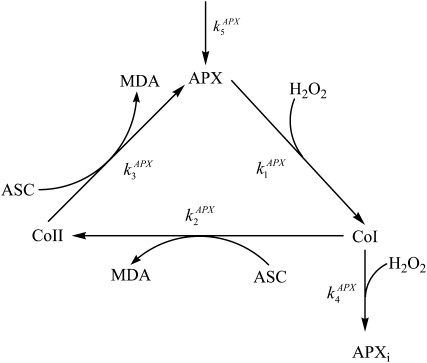
The H₂O₂ produced via the SOD-catalyzed disproportionation of is reduced to water by ASC, catalyzed with APX. This enzyme is a class I heme peroxidase (Welinder, 1992) whose catalytic mechanism is reminiscent of that observed in other peroxidases and involves the formation of an oxidized compound I (CoI) intermediate, which is subsequently reduced by substrate in two sequential, single-electron-transfer steps (Fig. 2). A characteristic property of APX, especially of the chloroplastic isoform, is its lability in the absence of its electron donor ASC (Miyake et al., 2006), since it is inactivated by the interaction of CoI with H₂O₂. To account for this fact, the step has been included in the catalytic cycle of the enzyme, along with a step corresponding to the de novo synthesis of APX. This last step must be included in the mechanism for the APX activity to attain the steady-state rate under nonstress conditions. The rate of the biosynthetic route (F₅) is considered directly proportional to the amount of initial enzyme present in a nonactive form (Table I). So, at t = 0, [APX] = [APX]₀, [CoI] = [CoII] = [APX_i] = 0, and then F₅ becomes F₅ = k₅^APX (0) = 0 (i.e. the biosynthetic route does not work at t = 0 since there is no inactive enzyme present). The more APX in the inactive form, the higher the term ([APX]₀ − [APX] − [CoI] − [CoII]), so the rate of the biosynthetic route increases as the amount of active enzyme decreases. It is evident that the de novo synthesis in vivo is largely controlled by many factors other than APX, but we have chosen a simplified formula, since it is not possible to take into account all of these factors in the computer simulation. However, this fact does not change the general concept of our model. Taking into account the complexity of the APX mechanism and the great interest in simulating its kinetic behavior at the physiological level, it has been included in full in the model (Supplemental Equations S9–S12).

Figure 2.

APX mechanism introduced in the model, including the inactivation of the enzyme by reaction of CoI with H₂O₂ and a continuous input of APX into the system by the de novo synthesis of the protein. APX_i is the inactive enzyme.

MDA is the primary product of the APX-catalyzed reduction of H₂O₂ by ASC, whose recovery is essential for maintaining the activity of the ROS-scavenging system. MDA spontaneously disproportionates to dehydroascorbate (DHA) and ASC in a pH-dependent way (Bielski et al., 1971). It is also directly reduced to ASC by photoreduced ferredoxin (redFd) in thylakoids (Miyake and Asada, 1994). The redFd competes between MDA and NADP⁺, but the reduction rate of MDA is 34-fold higher than that of NADP⁺ (Miyake and Asada, 1994; Asada, 1999). Thus, redFd is preferably used to reduce MDA rather than NADP⁺, suggesting that MDA is mainly photoreduced via Fd but not via NAD(P)H with MDAR, at least in the thylakoidal scavenging system. Taking this into account, MDAR is not included in the present model, which does not change the general concept of our model.

DHAR

This enzyme catalyzes the reduction of DHA to ASC, with GSH as the electron donor, in a ter bi reaction. The regeneration of ASC from DHA by GSH also occurs spontaneously, but the rate is too slow to account for the observed photoreduction of DHA in chloroplasts (Asada, 1999). Kinetic analysis of the enzymatic reaction (Shimaoka et al., 2003) suggested that the reaction proceeds by means of a bi uni uni uni ping-pong mechanism (Segel, 1975), in which the binding of DHA to the free, reduced form of the enzyme was followed by the binding of GSH. Solving the ODE system corresponding to this mechanism for the forward reaction leads to the following rate equation under steady-state conditions, which has been used in our model:

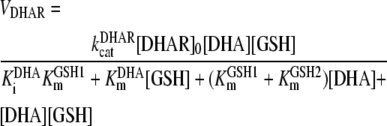(2)

This equation contains an independent term in the denominator, K_i^DHAK_m^GSH1, which we have grouped as K. The first expression, K_i^DHA, is the equilibrium constant between DHA, DHAR, and the enzyme-substrate DHAR-DHA complex. K_m^GSH1 and K_m^GSH2 are the values of K_m for the first-binding and the second-binding molecules of GSH, respectively. The sum K_m^GSH1 + K_m^GSH2 has also been grouped as K_m^GSH in our model, since it has not been possible to calculate these values separately in kinetic assays (Shimaoka et al., 2003).

Note that Equation 2 can be simplified to the following expression:

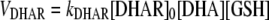(3)

when the following condition is fulfilled:

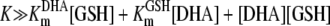(4)

being:

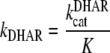(5)

GR

The supply of GSH is regenerated in an NADPH-dependent reaction catalyzed by GR. Kinetic studies performed with this enzyme have revealed a bi ter ping-pong mechanism (Vanoni et al., 1990). The rate equation corresponding to this mechanism under steady-state conditions for the forward reaction is the following, used in our model:

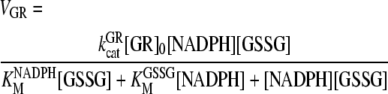(6)

Other Steps Involved in the Model

An additional route of NADPH consumption by the Calvin cycle (and other electron-consuming reactions) has also been added to the model, although in a simplified way, as a flux with an apparent rate constant, k_N = k′_N[CO₂]. Other nonenzymatic reactions participating in the cycle and included in our model are indicated in Figure 1.

The ODE system that describes the mechanism shown in Figure 1 is shown in the supplemental data. The values for the kinetic constants and the initial conditions used to run the model are listed in Tables II and III, respectively. The rate constants corresponding to spontaneous steps are apparent bimolecular rate constants. Values for the kinetic parameters involved in the model have been taken from Asada (1999), Polle (2001), or from references describing kinetic studies of the target reaction. Other numerical values used were arbitrary but chosen to furnish reasonable data.

Table II.

Kinetic constants used to run the present model

Kinetic Constant	Value	Unit	Reference
F1	640	μm s−1	Polle (2001)
kcatGR	595	s−1	Polle (2001)
kcatDHAR	142	s−1	Polle (2001)
kSOD	200	μm−1 s−1	Asada (1999)
k1APX	12	μm−1 s−1	Asada (1999)
k2APX	50	μm−1 s−1	Asada (1999)
k3APX	2.1	μm−1 s−1	Asada (1999)
k4APX	0.7	μm−1 s−1	Asada (1999)
k5APX	0.01	s−1	–
k3	0.5 (pH 7.0)	μm−1 s−1	Bielski et al. (1971)
k4	0.1	μm−1 s−1	Hausladen and Kunert (1990)
k5	0.2 (pH 7.0)	μm−1 s−1	Fridovich (1998)
k6	0.2	μm−1 s−1	Asada and Takahashi (1987)
k7	0.7	μm−1 s−1	Asada and Takahashi (1987)
k8	2.0 × 10−6	μm−1 s−1	Polle and Junkermann (1996)
k12	1.3	s−1	–
k13	42.5	s−1	–
kN = k′N[CO2]	0.5	s−1	–
KmNADPH	3	μm	Polle (2001)
KmGSSG	2.0 × 102	μm	Polle (2001)
KmDHA	70	μm	Polle (2001)
KmGSH	2.5 × 103	μm	Polle (2001)
K	5.0 × 105	μm2	–

Table III.

Initial concentrations used to run the model

These values were chosen to be similar to those used by Polle (2001), although we have preferred the system to synthesize 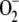and H₂O₂ by itself at the beginning of the reaction as a function of the initial conditions. The initial concentrations of 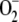, H₂O₂, and other species, therefore, were set to zero.

Species	Initial Concentration
	μm
GR	1.4
DHAR	1.7
SOD	50
APX	70
NADPH	150
GSH	4,000
ASC	10,000

RESULTS

Kinetic Behavior of the GSH-ASC Cycle as a Substrate Cycle

At the enzymatic level (i.e. without considering any spontaneous steps involved in the cycle or the electron source from PSI, except for the spontaneous dismutation of the MDA necessary for DHAR), the GSH-ASC cycle can be seen as two coupled substrate cycles involving the participation of APX, DHAR, and GR (Fig. 1, boldface steps). Substrate cycles are powerful metabolic tools involving two enzymes acting in opposite directions, whereby a target metabolite is reversibly interconverted into another chemical species without being consumed (Newsholme et al., 1984; Valero and García-Carmona, 1996; Valero et al., 2000). This is accompanied by the concomitant accumulation of other noncycling products at each turn of the cycle. The physiological explanation proposed for this wasteful cycling is that it is mainly a way of amplifying a metabolic response to a change in a metabolic concentration, thus greatly improving the sensitivity of metabolic regulation.

One of the main advantages of computer simulation is that it allows the dynamic behavior of a metabolic pathway to be studied by introducing the desired steps in the model until it is understood. The great amplification capacity of the GSH-ASC cycle can be checked by computer simulation of the boldface steps in Figure 1. The results obtained showed that an initial concentration of H₂O₂ as high as 10 μm, which has been reported to inhibit photosynthesis by 50% (Kaiser, 1979), was rapidly removed by the cyclic system in less than 0.02 s (half-time = 0.83 ms) at the expense of the equivalent consumption of NADPH.

When the spontaneous steps shown in Figure 1 were added to the model, the results obtained were very similar (data not shown), the most noteworthy differences being the lower accumulation of DHA in the first instants of the reaction, the shorter recovery time of the reducing species (GSH and ASC), an increased V_GR, and a decreased V_DHAR. In contrast, if [GR]₀, [DHAR]₀, and [APX]₀ are made equal to zero and only spontaneous steps are operative in the system, the data obtained point to the slower removal of H₂O₂ (half-time = 34.65 s) and low ASC recovery. GSH cannot recover simply by means of these spontaneous reactions.

Kinetic Behavior of the System in Unstressed Chloroplasts

In the chloroplast, the cycle is not metabolically isolated; so now that we know how the cycle functions, we can introduce its immediate environment. Photoreduction of molecular oxygen in the PSI of chloroplasts generates 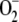continuously in daylight, which means that the H₂O₂ must be continuously removed by the GSH-ASC cycle, for which the level of NADPH must recover. This process occurs in the photochemical phase of photosynthesis in PSI, although it is also important to take into account the consumption of NADPH in the Calvin cycle in the presence of CO₂. All of these steps, as well as the photoreduction of MDA, have been included in our model.

Unstressed chloroplasts generally show low, stationary levels of ROS and high ratios for the reduced form/oxidized form of the redox pairs involved in the cycle. The conditions indicated in Tables II and III have been chosen to mimic the behavior of the GSH-ASC cycle in unstressed chloroplasts. Under these conditions, a steady state was rapidly achieved by the system, in which metabolite concentrations and fluxes remained constant. The steady-state concentrations thus obtained were as follows: [NADPH]_ss = 84.95 μm, [GSH]_ss = 3.98 mm, [ASC]_ss = 9.99 mm, [DHA]_ss = 42.9 nm, [MDA]_ss = 5.85 μm, 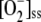= 8.9 nm, and [H₂O₂]_ss = 0.16 μm. These values are close to the ranges estimated for healthy tissues (Asada, 1994). The [MDA]_ss is a little high, perhaps because MDAR is not included in our model. However [DHA]_ss is very low in comparison with the levels usually found in plants (Polle, 1997; Kwon et al., 2003). Any inactivation of APX during integration time was negligible under these conditions, since ASC levels remained high throughout the reaction.

An 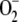steady-state production rate of 222.2 μm s⁻¹ was obtained, which is within the range previously mentioned by other authors (Asada, 1999; Polle, 2001), while the conversion rate of MDA into ASC (248.7 μm s⁻¹) was slightly higher and the photochemical recycling of NADPH (169.1 μm s⁻¹) was slightly slower, reflecting the preference of redFd to reduce MDA rather than NADP⁺. The most active enzymes were APX and SOD followed by GR and DHAR, since the low glutathione oxidized concentration ([GSSG]) and [DHA] in these conditions limits their velocity. A maximum in V_SOD and V_APX was appreciated at the start of the reaction, since the enzymes must work hard to lower the accumulation of 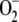and H₂O₂, respectively, in the initial phase (Supplemental Fig. S1).

Kinetic Behavior of the System in Stressed Chloroplasts

Oxidative stress is characterized by the disruption of cellular homeostasis, leading to the enhanced production of ROS and changes in the redox state of chloroplasts. Many environmental perturbations, including intense light, temperature stress, air pollutants, and herbicides, affect the efficiency of photosynthetic electron transport. To study the dynamic behavior of the system under these conditions, F₁ was increased to 2,450 μm s⁻¹. NADPH levels fell very rapidly in the first instants of the reaction, followed by GSH. ASC levels remained high as long as NADPH and GSH were present in the chloroplasts, although afterward they decreased sharply to reach limiting concentrations. The disappearance of ASC was followed by the rapid inactivation of APX, reflecting what occurs in reality (Miyake and Asada, 1996), accompanied by a sharp increase in [APX_i]. Once APX has been inactivated, H₂O₂ is accumulated in the chloroplast at a very high rate, since it is continuously produced from 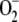, spontaneously and enzymatically catalyzed by SOD. A minimum in [MDA] and in F₁₃ could also be observed, after which [MDA] recovered by spontaneous steps. Consequently, a maximum in F₁₁ and hence in [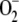] and V_SOD appeared. The increase in [ASC] once APX has been inactivated is due to the spontaneous redox steps involved in the model. However, it must be taken into account that all of these recoveries observed after APX inactivation are produced as a result of [H₂O₂] increasing above a life-compatible level, so they have no physical meaning. F₁₂ and V_GR reached a steady state, which was not affected by APX inactivation. F_N sharply decreased near the start of the reaction as a consequence of NADPH depletion in the chloroplast (Supplemental Fig. S2).

Kinetic Response of the System against an Increasing Electron Flux

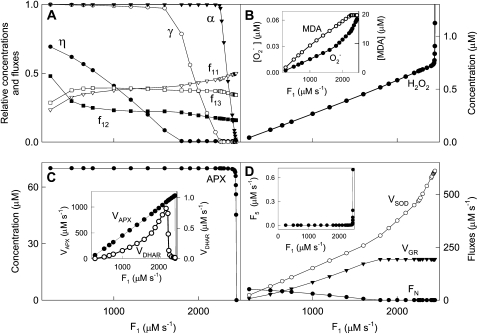
Intense light exposure causes oxidative stress in plants, but a high electron flux through the water-water cycle provides a way to dissipate excess light energy (Asada, 1999). To address the response of the system under study to this increasing oxidative stress, F₁ was varied from 250 to 2,450 μm s⁻¹ (i.e. until APX underwent photoinactivation by excess of H₂O₂). Steady-state concentrations of metabolites involved in the mechanism under study and the fluxes thus obtained are shown in Figure 3. The model shows a progressive decrease in the steady-state levels of antioxidants as F₁ increases, NADPH being the first to be depleted in the chloroplast, followed by GSH and ASC. The [MDA]_ss, 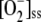, and [H₂O₂]_ss increased linearly as long as F₁ was low. At higher F₁, [MDA]_ss remained constant, the accumulation of 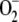was more pronounced (steeper slope of the plot), and [H₂O₂]_ss sharply increased owing to the induced photoinactivation of APX. APX falls in a very narrow range of F₁ (Fig. 3C) when its inactivation exceeds its de novo synthesis, although its enzymatic activity continues increasing almost until the end, with the aim of eliminating as much H₂O₂ as possible. The rate of de novo synthesis of APX (F₅; Fig. 3D, inset) sharply increased with the inactivation of APX, which represents a defense against ROS.

Figure 3.

Dependence of steady-state concentrations and fluxes on F₁ variations. The values of the rate constants and initial conditions used were those shown in Tables II and III, except that F₁ was varied between 250 and 2,450 μm s⁻¹. Relative concentrations and fluxes are defined in “Materials and Methods.”

The relative distribution of F₁ among the three routes considered under these conditions is also shown in Figure 3A. It can be seen that at high F₁, only the 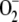production rate increased. F_N decreased owing to the lower availability of NADPH (Fig. 3D), although V_GR increased steadily to reach a constant value because of increasing levels of GSSG in the chloroplast. V_SOD increased in a parallel way with 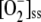, and V_DHAR showed a maximum, after which it abruptly fell, pointing to the next photoinactivation of APX.

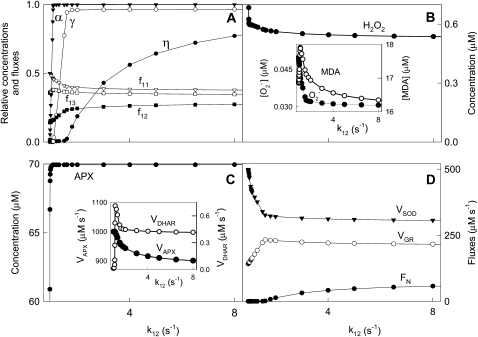
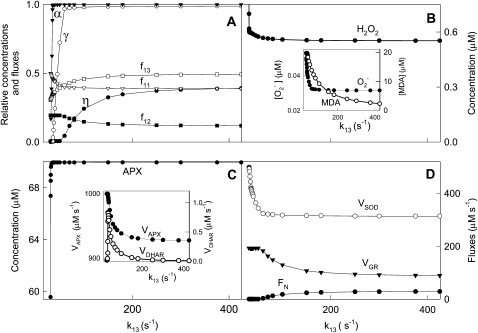
Effects on the System of Varying k₁₂ and k₁₃

The detoxifying efficiency of the mechanism under study is probably best evaluated by the relative distribution of F₁ among the three competitive routes through the system. To do this, we have introduced a constant value of F₁ = 2,000 μm s⁻¹, and computer simulations were performed by varying k₁₂ and k₁₃. The system is extremely sensitive to low values of k₁₂ and k₁₃ when the photochemical recovery of NADPH and ASC is inoperative and the photoproduction rate of 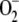is higher (Figs. 4 and 5). For this reason, antioxidants were rapidly depleted and APX suffered inactivation in a very low range of k₁₂ and k₁₃. Therefore, sharp increases in [NADP⁺]_ss, [GSSG]_ss, [DHA]_ss, 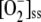, and [H₂O₂]_ss and increasing V_SOD and V_APX values are observed at low k₁₂ and k₁₃. The MDA plot, however, shows a maximum at low k₁₂, which is related to APX photoinactivation when ASC concentration is limiting. This maximum in [MDA]_ss is not seen at low k₁₃, since the electron flux deviated by the F₁₃ branch for the photorecycling of ASC continuously increases to reach a nearly constant value.

Figure 4.

Dependence of steady-state concentrations and fluxes on k₁₂ variation. The values of the rate constants and initial conditions used were those shown in Tables II and III, except that F₁ = 2,000 μm s⁻¹ and k₁₂ was varied between 0.95 and 250 s⁻¹.

Figure 5.

Dependence of steady-state concentrations and fluxes on k₁₃ variation. The values of the rate constants and initial conditions used were those shown in Tables II and III, except that F₁ = 2,000 μm s⁻¹ and k₁₃ was varied between 31.1 and 500 s⁻¹.

It is also possible to observe in Figure 4A an increase in F₁₂ when k₁₂ increased at low values, essentially at the expense of F₁₁. In contrast, F₁₂ remained constant when k₁₃ was increased at low values (Fig. 5A). In this last plot, F₁₃ increased basically at the expense of F₁₁; once F₁₁ attained a nearly constant value, F₁₃ continued increasing at the expense of F₁₂. Note that at higher k₁₂ and k₁₃ values, the distribution of the electron flux from PSI became almost constant (i.e. the system was saturated). Figures 4D and 5D show a similar dependence of F_N as k₁₂ and k₁₃ were increased, in agreement with the greater availability of NADPH. NADPH almost completely recovered at relatively high values of k₁₂, but not by increasing k₁₃ under the conditions used here. The dependence of V_GR on k₁₂ and k₁₃ was parallel to its respective F₁₂ plot, and a maximum in V_DHAR was also obtained in both cases at low k₁₂ and k₁₃, again pointing to the next photoinactivation of APX.

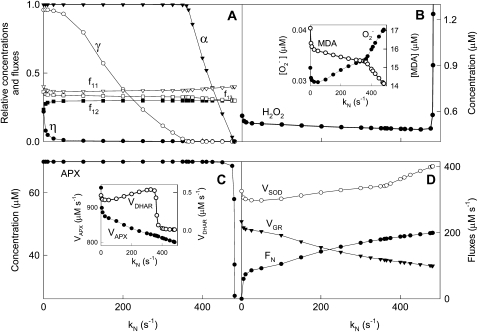
Effects on the System of Varying k_N

We have introduced the photoproduction of NADPH and its consumption during the CO₂ fixation in a simplified way through the F_N flux step. Thus, k_N is a kinetic parameter related to the Calvin cycle and other electron-consuming reactions under conditions of constant [CO₂]. Computer simulations pointed to the great sensitivity of the model to the k₁₂/k_N ratio. Figure 6 shows the results obtained when varying k_N for a fixed value of k₁₂ = 2 s⁻¹. Minimums in 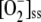, V_SOD, and F₁₁ can be seen at low k_N, meaning variations in k_N can lead to the system adapting to light intensity, giving rise to minimal ROS levels. Therefore, an appropriate Calvin cycle rate (e.g. by means of an adequate level of CO₂) might provide protection against ROS.

Figure 6.

Dependence of steady-state concentrations and fluxes on k_N variation. The values of the rate constants and initial conditions used were those shown in Tables II and III, except that F₁ = 2,000 μm s⁻¹, k₁₂ = 2 s⁻¹, and k_N was varied between 0 and 487 s⁻¹.

As k_N was increased, the antioxidant concentration in the chloroplast gradually decreased, in the order NADPH, GSH, ASC, so that their respective oxidized species concentrations increased, although [MDA]_ss decreased due to the lower availability of ASC to spontaneously react with 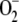to produce it. [H₂O₂]_ss showed a gradual decrease in spite of the increase in 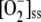once NADPH was nearly depleted, which was probably related to spontaneous steps since [APX]_ss, and its activity also decreased. Once ASC became limiting, APX was inactivated, so that [H₂O₂] increased abruptly.

With regard to the electron fluxes, F₁₂ increased as long as NADPH was left in the chloroplast but remained nearly constant when NADPH was nearly depleted. F₁₁ and F₁₃ decreased at low k_N and after F₁₁ increased at the expense of F₁₃. A maximum in V_DHAR prior to the photoinactivation of APX could be seen again. V_GR decreased with increasing k_N as a consequence of the lower availability of NADPH, whereas F_N evidently increased.

Effects on the System of Varying Antioxidant Enzyme Concentrations

Antioxidant enzymes are critical components in preventing oxidative stress in plants. Manipulation of the expression of these enzymes by gene transfer technology has provided new insight into their role in chloroplasts by allowing direct investigation of their functions and interactions (Foyer et al., 1994; Allen et al., 1997). Mathematical modeling is also a powerful tool that can be used to predict the response of the system to changes in the activities and concentrations of the enzymes involved in the pathway. Therefore, computer simulations were performed here at different initial concentrations of the four enzymes considered in our model.

Decreasing levels of [GR]₀ (data not shown) led to the irreversible photoinactivation of APX, again announced by a maximum in V_DHAR, resulting in considerable increases in [GSSG]_ss, [DHA]_ss, [H₂O₂]_ss, and 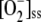, accompanied by increases in F₁₁, V_SOD, and V_APX. However, NADPH consumption was lower at low [GR]₀, and an increase in F_N was observed.

It has been reported that plants overexpressing GR are more tolerant of ROS-inducing herbicides such as methyl viologen, since they are able to maintain the reduction state of their ascorbate pools more effectively than control plants (Aono et al., 1991; Foyer et al., 1991). The numerical data obtained here agree with these results. Increasing levels of [GR]₀ led to the recovery of ASC and APX and the partial recovery of GSH, although NADPH decreased due to its greater consumption by GR. In the same way, [GSSG]_ss, [DHA]_ss, [H₂O₂]_ss, and 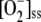decreased to reach nearly constant values. [MDA]_ss showed a maximum at low [GR]₀, and also reached a nearly constant value when [GR]₀ increased. F₁₂ and F₁₃ increased at low [GR]₀ as a consequence of the decrease in F₁₁, while V_GR only increased at low [GR]₀, also reaching a nearly constant value.

Unlike changes in [GR]₀, variations in [DHAR]₀ in our model had no noticeable effect on the steady-state concentrations of metabolites or on the fluxes through the GSH-ASC pathway (data not shown), even when [DHAR]₀ = 0. Only a very slight decrease in [DHA]_ss accompanied by a slight increase in [ASC]_ss could be observed as [DHAR]₀ increased, with a subsequent decrease in the rate of the spontaneous reaction between GSH and DHA. This means that this spontaneous step could be sufficient to cope with DHA removal, as suggested by Polle (2001). However, these results must be interpreted in the context of the present model, and they do not mean that DHAR is a dispensable enzyme in reality, in agreement with data reported by Chen and Gallie (2006). When computer simulations were performed in the absence of spontaneous DHA reduction (k₄ = 0), a threshold [DHAR]₀ was necessary if ASC levels were to recover and to prevent APX inactivation. It was also observed that under these conditions, V_DHAR was higher than usually observed when k₄ ≠ 0.

When [APX]₀ was increased, a threshold value of [APX]₀ of 3.37 μm was found to be necessary for the system to reach a steady state. Below this value, APX was irreversibly inactivated, since insufficient protein was supplied by de novo synthesis, and consequently, [H₂O₂] increased to toxic amounts. However, no appreciable effects on the steady state of the antioxidant pools, [MDA]_ss, and 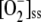or on the fluxes and velocities of the other enzymes involved in the system were observed, even when [APX]₀ = 0 (data not shown). These results indicate that high [H₂O₂] might coexist with high [GSH] and [ASC], although they should be treated with caution, since other possible pernicious effects of H₂O₂ in the cell have not been included in the model. Above the previously mentioned threshold value of [APX]₀, the plots remained constant and parallel to the abscissa axis, the only changes observed being a decrease in [H₂O₂]_ss, an increase in [APX]_ss, and a rapid increase in V_APX until it reached a constant value.

When k₅^APX (the apparent rate constant for the de novo synthesis of APX) was increased from 0.01 to 1 s⁻¹, the system showed greater tolerance against oxidative stress conditions and the inactivation of the peroxidase enzyme was less abrupt (data not shown). This result agrees with the experimentally observed increased tolerance to methyl viologen damage reported in tobacco (Nicotiana tabacum) plants overexpressing cytosolic APX (Pitcher et al., 1994), although it is in apparent contradiction with data obtained by the same authors (Torsethaugen et al., 1997), indicating that overproduction of APX in tobacco chloroplasts does not provide protection against O₃-induced stress. This may be due to the above-mentioned fact that V_APX remained nearly constant above a certain value (about 10 μm under the conditions used here) even when the [APX] was increased.

Finally, [SOD]₀ was varied from 9 nm to 1 mm (Fig. 7). A value of less than 9 nm led to depletion of antioxidants, the inactivation of APX, and an excessive accumulation of H₂O₂ even if [SOD]₀ = 0. However 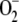was not accumulated, since most of the 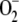photogenerated in the chloroplast disappeared through spontaneous dismutation and reaction with ASC and GSH, yielding H₂O₂.

Figure 7.

Dependence of steady-state concentrations and fluxes on [SOD]₀. The values of the rate constants and initial conditions used were those shown in Tables II and III, except that F₁ = 2,000 μm s⁻¹ and [SOD]₀ was varied between 9 nm and 1 mm.

Computer simulations performed at low values of [SOD]₀ yielded increased levels of NADP⁺, GSSG, DHA, MDA, H₂O₂, and 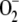, indicating that a certain level of SOD is necessary for the plant to maintain its reduction potential against oxidative stress. These responses of the system disappeared when [SOD]₀ was increased, since GSH levels began to recover and ASC was almost totally recovered. The inactivation of APX was negligible under these conditions, and [MDA]_ss, 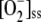, [H₂O₂]_ss, and V_APX decreased as a consequence of the lower amount of H₂O₂ accumulated. Again, a maximum in V_DHAR appeared. The increase in F₁₁ was accompanied by an increase in V_SOD. This illustrates the balance between 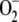production and elimination in the metabolism. That is, when the chloroplast has insufficient 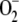because of an excess of SOD (or for any other reason), part of the electron flux from PSI is directed to the production of more , so that ASC and NADPH photochemical recovery fall.

These data demonstrate that SOD is a critical component of the ROS-scavenging system of chloroplasts and indicate that overexpression of this enzyme in transgenic plants may improve plant stress tolerance. Transgenic plants with high levels of the three types of SOD have been developed and characterized by several research groups. The results obtained showed that, in many cases, high levels of SOD in a variety of cellular compartments lead to detectable increases in cellular protection from oxidative stress (Allen et al., 1997), in agreement with the theoretical data obtained here.

DISCUSSION

A new mathematical model has been developed for the kinetic study of the complex network of redox reactions involved in the GSH-ASC pathway for detoxifying ROS in chloroplasts. The model is based on another one reported previously by Polle (2001), although we have included several modifications that considerably improve it, bringing the results obtained nearer to reality.

We have introduced into the model the ODE corresponding to NADPH and NADP⁺, taking into account the balance between the photochemical recovery of NADPH, its consumption by the Calvin cycle, and the GR-catalyzed reaction. Polle's model (2001) could not contemplate this important subject from a physiological point of view because of excessive run times in the computer, so the corresponding equations were simplified. The consequence was that NADPH could not be recovered (it was assumed as a constant value), leading to the continuous accumulation of NADP⁺ in the chloroplast. However, as shown here, H₂O₂ is detoxified at the expense of the reducing power of NADPH. In its evolution since the appearance of oxygen in the atmosphere, the cell has developed a very efficient defense tool against oxygen toxicity, based on two coupled substrate cycles, although it needs a supply of NADPH. The waste of NADPH can be understood as the cost that chloroplasts must pay to swiftly detoxify H₂O₂. The present model is able to simulate this.

The pathway under study is very interesting, since the same daylight that gives rise to the synthesis of 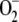toxic radicals also generates NADPH and ASC to detoxify the H₂O₂ arising from 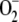dismutation. Therefore, it is very important to know the relative weight of each route in the growth conditions of the plant. This is taken into account in the present model by introducing a constant electron flux from PSI distributed among three competitive branches: the photoproduction of 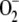, the photoreduction of NADP⁺, and the photoreduction of MDA. Electron fluxes through these routes must adjust to each other as a function of the growth conditions of the plant. The fit between the three branches is a better way to understand the kinetic behavior of the pathway and the physiological response of chloroplasts in the face of a given stimulus, as has been shown by means of the computer simulations performed here.

Each enzyme involved in our model has been introduced into the ODE, taking into account its particular catalytic mechanism. This is especially important in the case of APX, since it is the most H₂O₂ sensitive. SOD, DHAR, and GR are also inactivated, but only after long illumination in the presence of paraquat (Iturbe-Ormaetxe et al., 1998). Polle's model (2001) did not take into account the photoinactivation of APX, so a steady state was always attained. Instead, in our model, a steady state is only attained under nonstress conditions, when reducing power in the chloroplast is high and APX is not inactivated. The introduction of a step corresponding to the de novo synthesis of APX plays a double role in the model: on the one hand, it is necessary so that the system can reach a steady state under nonstress conditions; on the other hand, the results obtained are more realistic, since this is one of the main defense mechanisms of plants to mitigate oxidative stress. The present model is able to predict the rapid biosynthesis of the protein in response to harsh oxidative stress conditions.

The electron flux in the thylakoids also supplies NADPH for the Calvin cycle, so we included this in our model. There is a competition between the NADPH consumed by the ROS-detoxifying pathway and the NADPH consumed by the Calvin cycle. The results obtained here illustrate the importance of the fine regulation of the cycle, since the plots show a minimum of ROS production at low values of the apparent rate constant for the Calvin cycle (k_N; Fig. 6B, inset). It is known that plants can regulate temporary mechanisms of stomatal closure in response to abiotic stress, thus limiting the entrance of CO₂ into chloroplasts and decreasing the amount of NADPH consumed by the Calvin cycle (Fig. 6D). The model developed here is able to simulate, to our knowledge for the first time, this interesting physiological response of plants and therefore should contribute to its better understanding.

CONCLUSION

In conclusion, the mathematical model developed here is a very powerful tool for improving our theoretical understanding of the kinetic behavior of the ROS-detoxifying pathway in chloroplasts. The model, besides including new physiologically important aspects, such as the balance between the photogeneration and consumption of NADPH and APX inactivation, can easily be expanded to include new steps, such as regulatory devices for enzymes, dark-light interactions, the peroxiredoxin system (Dietz, 2003; Dietz et al., 2006), etc. It may also allow the guidance of future experimental work to evaluate those parameters involved in the cycle that have not been evaluated yet. In this way, the approach offers a new strategy for studying plant defense mechanisms against oxidative stress and can be used to predict the response of the plant to different stress conditions and where the limits of resistance can be expected.

MATERIALS AND METHODS

Simulated progress curves were obtained by numerical solution of the nonlinear set of differential equations corresponding to the mechanism shown in Figure 1 (Supplemental Equations S1–S13). Numerical integration was performed using the ode15s function from MATLAB software version 7.0 (http://www.mathworks.com). This is a variable-order solver based on numerical differentiation formulas and is a multistep solver recommended for stiff problems (Shampine and Reichelt, 1997). The file including the ODE and the kinetic constant values used is available to interested readers on request. Fluxes and enzymatic activities were calculated from data thus obtained by a computer program made by us using the Transform tool in the SigmaPlot scientific graphing system for Windows version 8.02 (http://www.spss.com), which is also available to interested readers on request. Data thus obtained were plotted using the same software. Steady-state values for metabolite concentrations and fluxes plotted in Figures 3 to 7 were obtained from the linear portion of progress curves given by the computer. The points represent theoretical data obtained in the computer, and the solid lines are straight lines linking them. Relative concentrations of antioxidants were defined as follows: α = [ASC]/[ASC]₀, γ = [GSH]/[GSH]₀, and η = [NADPH]/[NADPH]₀. Relative fluxes were defined as follows: f₁₁ = F₁₁/F₁, f₁₂ = F₁₂/F₁, and f₁₃ = F₁₃/F₁.

These programs were run on a PC-compatible computer based on a Pentium IV 2-GHz processor with 512 MB of RAM. The time consumed by this computer to obtain each particular numerical solution was on the order of a few seconds or even less in those cases in which a steady state was reached.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Simulated progress curves corresponding to the species involved in the mechanism shown in Figure 1, in unstressed chloroplasts.

• Supplemental Figure S2. Simulated progress curves corresponding to the species involved in the mechanism shown in Figure 1, in stressed chloroplasts.

• Supplemental Equations S1 to S13. Differential equations system corresponding to the mechanism shown in Figure 1.