Spectral integration under conditions of comodulation masking release

Abstract

Detection of a pure tone signal in a narrowband noise masker can be improved by the introduction of coherently amplitude modulated masker bands in neighboring frequency regions, an effect called comodulation masking release (CMR). Experiment 1 tested the hypothesis that detection of a spectrally complex signal in a comodulated masker critically depends on the signal∕masker interaction, with best sensitivity in conditions where the signal introduces across-frequency stimulus envelope differences. Consistent with this hypothesis, thresholds for a multi-frequency signal differed by approximately 10 dB depending on the relative patterns of signal∕masker interaction across frequency. In comodulated maskers, there was no improvement in threshold relative to the single-frequency signal threshold even in cases where the multi-frequency signal introduced across-frequency envelope differences. Experiment 2 tested conditions that have previously been associated with large spectral integration in comodulated but not random maskers. Results depended on the masker configuration used as the reference condition, with comparable integration for random and comodulated noise in some cases. The results suggest that CMR obtained with a pure tone signal can differ greatly from that obtained with a complex signal, and that spectral integration is inversely related to the amount of CMR under some conditions.

INTRODUCTION

Comodulation masking release (CMR) is the detection advantage associated with coherence in the patterns of masker amplitude modulation across frequency. This effect is typically demonstrated with a single pure tone signal, presented either in maskers of increasing bandwidth or in one of a family of narrowband noise maskers. While some of the masking release demonstrated with these stimuli may be due to within-channel cues (Schooneveldt and Moore, 1987; Berg, 1996; Verhey et al., 1999), such as envelope beats, it is often argued that CMR in the strictest definition is due to across-channel comparisons (Schooneveldt and Moore, 1987; Carlyon et al., 1989). Psychoacoustic models of across-channel cues underlying “true” across-channel CMR tend to be based on the change in envelope statistics across frequency (Buus, 1985; Cohen and Schubert, 1987; Piechowiak et al., 2007), such as a reduction in envelope correlation or “listening in the dips.” Naturally occurring sounds tend to be coherently modulated across frequency (Hall et al., 1984; Nelken et al., 1999), so the CMR paradigm could reflect a general auditory adaptation to the processing of natural sounds.

While most studies in the CMR literature have used spectrally simple signals, such as a pure tone presented for several hundred milliseconds, naturally occurring signals are usually spectrally complex. Several studies have demonstrated CMR for spectrally complex signals, such as speech (Grose and Hall, 1992; Festen, 1993; Kwon and Turner, 2001) or tonal complexes (Hall et al., 1988; Grose et al., 2005). Hall et al. (1988), for example, showed that the presence of a signal-free flanking band was not a prerequisite for obtaining masking release. In that study there were three maskers, all 30-Hz wide and centered on the fourth to sixth harmonics of 100, and the signal to be detected was a pure tone at one or more of those frequencies; all signals were presented at equal amplitude and with random starting phase. Thresholds in that study were lower for comodulated as compared to random maskers even when there was a signal present at all three masker frequencies.

Spectral integration for detection is defined as the advantage conferred by presenting multiple signal components in different frequency regions. Buus et al. (1986) showed that detection of relatively long pure tone signals in wideband noise improved by $10\log \left(\sqrt{n}\right)$ for tones presented to spectrally independent auditory channels (referred to hereafter as the n rule). This model assumes that d^′ increases linearly with signal intensity. The n rule is also consistent with detection of pure tone signals in narrowbands of Gaussian noise and with detection of intensity increments in bands of noise (Grose and Hall, 1997). The form of spectral integration for tones presented in coherently amplitude modulated masker bands is less clear. One reason to expect less than a n reduction in threshold is that coherent masker modulation reduces the statistical independence of information distributed across frequency; another reason is that the inclusion of multiple signals is likely to change the across-channel cues available for detection, such that detectability of each tone individually could be reduced in the context of multiple tones. Some psychoacoustic studies report that integration in a comodulated masker is comparable to that observed in random noise (Grose et al., 2005), while others report less integration (Hall et al., 1988; van den Brink et al., 1992) or substantially more integration in coherently modulated as compared to random bands (Bacon et al., 2002). The differences in integration across studies are related in part to the choice of single-component signal condition used as baseline. For example, Grose et al. (2005) defined integration relative to threshold for a single pure tone in the presence of four comodulated noise bands, whereas Bacon et al. (2002) defined it relative to pure tone detection threshold in a single band of noise. The implication of this difference will be revisited in the results and discussion of experiment 2.

Data on detection of multi-frequency signals have been interpreted as discriminating between potential cues in CMR. For example, Hall et al. (1988) argued that the CMR obtained with multi-frequency signals is difficult to reconcile with models based on envelope decorrelation or cued listening. van den Brink et al. (1992) asserted that CMR models based on either dip listening or envelope decorrelation predict no CMR for a multi-component signal in cases where the interactions between signals and masker produce compound output envelopes that are identical across frequency. If this is true for the auditory system, then thresholds for multi-component signals should be quite poor under conditions where the signal∕masker interactions are identical across frequency, a result which would be associated with reduced estimates of spectral integration. The first experiment tested this hypothesis by controlling the regularity of signal∕masker interactions via manipulation of signal amplitude and phase, with the prediction that masking release would be absent for conditions in which the signal∕masker interactions produce identical envelope cues across frequency. The second experiment assessed spectral integration in a family of Gaussian noise bands, a stimulus for which Bacon et al. (2002) reported elevated levels of spectral integration when the masker bands were coherently sinusoidally amplitude modulated (SAM) as compared to random noise conditions.

EXPERIMENT 1

The manipulation of signal∕masker interaction in this experiment can be understood in terms of the beating that occurs between pairs of tones. The inherent modulation of a narrowband noise is due to beating between components making up that band and is dependent on the phase and relative frequency of those components. Transposing those components uniformly up or down in frequency produces a comodulated band, whereas adjusting the phase or amplitude of one or more components can modify the pattern of inherent envelope fluctuation. Similarly, adding a pure tone signal to a narrowband masker can change the beating pattern of the summed stimulus. In the case of a multi-component signal, if each signal tone sums with the corresponding masker band in the same way—with the same amplitude and phase, and at the same relative frequency within the masker complex—then the associated envelope change is identical across frequency, whereas deviating from this configuration (e.g., randomizing signal phase) introduces potential envelope differences across frequency. The perceptual consequences of these differences for detecting a multi-component signal in comodulated maskers are the focus of the present experiment.

If the signal detection benefit associated with coherent masker modulation is based in part on the differences in stimulus envelope across frequency, then multi-signal configurations that reduce or eliminate those differences should likewise reduce the detection benefit. In the experiment that follows, the signal∕masker phase and amplitude relationships across frequency are manipulated. It is hypothesized that signal parameters minimizing across-frequency envelope differences will likewise reduce any detection benefit associated with masker modulation coherence, with greater benefit under conditions of greater across-frequency envelope differences associated with addition of the signal. This effect will be quantified in terms of the threshold difference for detection of a tone as compared to a tonal complex, a quantity defined as spectral integration.

Methods

Observers

Observers were six adults, from 23 to 51 years old (mean of 34 years). All had thresholds of 20 dB HL or less at octave frequencies of 250–8000 Hz (ANSI, 1996), and none reported a history of chronic ear disease. All observers were practiced in psychoacoustical tasks at the outset of the experiment, having participated in at least one prior experiment.

Stimuli

Maskers were 15-Hz wide bands of Gaussian noise presented at 50 dB SPL per band, and there were either one or five bands. Band center frequencies were separated by a factor of ∼1.9 and included 276, 525, 1000, 1904, and 3624 Hz. There were three types of maskers—on-signal (one single band for each of five frequencies), all-coherent, and all-random. The maskers were generated in the frequency domain at the outset of each threshold estimation track. A band of noise was generated based on random Gaussian draws defining the real and imaginary components contained within the masker passband. In the all-coherent conditions the same set of random draws was used to generate all five masker bands. In the all-random conditions each band was generated based on independent random draws. The stimulus generation array was 2¹⁷ points in length; when converted to the time domain and played at a sampling rate of 12 207 Hz, this produced a 10.7-s stimulus that repeated seamlessly and played continuously over the course of a threshold estimation track.

The signal was a pure tone or a set of five pure tones, with frequencies corresponding exactly to the center frequencies of the masker bands. There were five single-frequency signal conditions, with a single pure tone serving as the signal, and either a single masker band (on-signal) or a family of five masker bands present (all-coherent or all-random). For the all-coherent and all-random masker types there were four additional multi-frequency signal conditions, defined in terms of the relative level of tones (equal or normalized) and the starting phase of the signal tones (fixed-ϕ or random-ϕ). The normalized level tones were individually adjusted in amplitude based on detection threshold in the associated single-frequency conditions, with either all-coherent or all-random maskers. As such, each tone was presented at equal level in dB SL, estimated independently for each observer and for each masker type. The starting phases of signal tones in the multi-signal conditions were either based on a single random draw or five independent draws from a uniform distribution (0–2π). This difference has consequences for the all-coherent condition. In the all-coherent random-ϕ condition each signal tone had a different effect on the envelope of the band to which it was added. In contrast, signals in the fixed-ϕ condition had a similar effect on envelopes across frequency in the normalized level condition and identical effects in the equal level condition. Signals were generated in the frequency domain using similar methods as those used to generate the maskers in order to maintain precise control of the signal∕masker relationship.

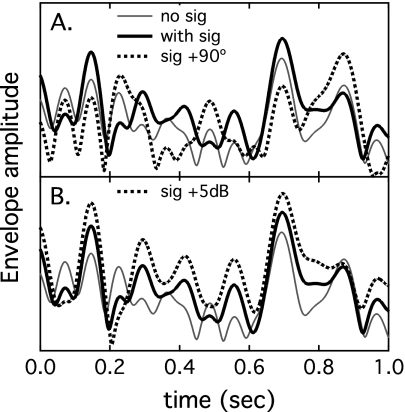
Figure 1 shows envelopes of example stimuli, illustrating the effects of signal phase and level manipulations. The Hilbert envelope associated with a 15-Hz wide band of noise is plotted as a function of time, shown with the thin gray lines in both panels. This 50-dB SPL masker sample was summed with a 45-dB pure tone signal at the masker center frequency, and the envelope of the result is plotted with the thick black line in each panel. The dotted lines in each panel indicate the different envelope effects obtained by incrementing the signal starting phase by 90° [panel (A)] or the signal amplitude by 5 dB [panel (B)]. On average adjusting starting phase of the signal does not affect the overall stimulus level, but it does have a marked effect on the envelope pattern; for a signal at −5 dB signal-to-noise ratio (SNR), randomizing signal starting phase reduces the envelope correlation across bands to a median of approximately r=0.75. Fixing starting phase and comparing signals at −5 and 0 dB SNRs, the overall level is incremented by a median of 1.8 dB and the envelope correlation across bands is relatively unchanged, with a median of r=0.96. In both cases, mismatches in signal parameters lead to differences in the envelope across bands. A signal level of 45-dB SPL was chosen for illustration purposes because observer thresholds in the single-signal, all-coherent masker condition were on the order of 45 dB. Likewise, a level mismatch of 5 dB was chosen because that was the median range of single-signal, all-coherent masker thresholds across frequency for an individual observer; as such, signal level adjustments in the normalized condition were on the order of 5 dB.

Figure 1.

Hilbert envelopes of example stimuli are plotted as a function of time. The masker, indicated with thin gray lines in both panels, was a 15-Hz wide band of noise scaled to 50 dB SPL. The thick black lines in both panels show the envelope of that same masker sample summed with a 45-dB SPL pure tone signal at the masker center frequency. The dotted lines in each panel indicate the different envelope effects obtained by incrementing the signal starting phase by 90° [panel (A)] or incrementing the signal amplitude by 5 dB [panel (B)].

The arrays defining masker and signal stimuli were loaded into an RPvds circuit (TDT), and signal gating was applied with 50-ms raised-cosine ramps implemented in software. All signal tones present in a given interval were ramped on and off synchronously, with a total duration of 400 ms including ramps.

Procedures

Stimuli were presented in a three-alternative forced-choice paradigm, with the signal equally likely to be present in each interval. Those intervals were marked visually and separated by 250 ms. Feedback was provided after each observer response. Signal level was adaptively varied following a three-down, one-up rule estimating 79% correct (Levitt, 1971). Level was initially adjusted in steps of 4 dB, and reduced to 2 dB after the second track reversal. The track continued for a total of eight reversals, and the associated threshold estimate was computed as the average signal level at the last six track reversals.

Single-frequency thresholds were collected first. For each observer the five signal frequencies were assigned a random order, and thresholds were collected in blocks by signal condition. Three threshold estimates were collected in each condition, with a fourth estimate collected if the first three spanned a range of 3 dB or more; all estimates were averaged to generate a final threshold estimate. After completing the single-frequency conditions the multi-frequency conditions were likewise run in random order. In the normalized multi-signal conditions thresholds are reported in decibels relative to the lowest-level tone (i.e., the level of the tone at the frequency associated with the lowest single-frequency threshold).

Results

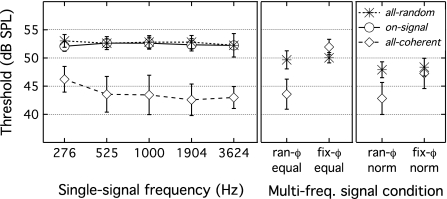
Results from all six observers were similar, so the mean threshold across observers is reported. Figure 2 shows thresholds as a function of signal condition, with error bars indicating ±1 standard deviation. Symbols reflect masker types, as indicated in the key above the figure. The left panel shows results for the single-frequency signal conditions, and those to the right show results for multi-signal conditions.

Figure 2.

Mean thresholds are plotted in dB SPL as a function of condition, with error bars showing ±1 standard deviation. Symbols reflect the masker type, either all-random (stars), on-signal (circles), or all-coherent (diamonds). The left panel shows single-frequency signal conditions, with frequency in hertz indicated on the abscissa. The middle panel shows multi-frequency signal conditions in which all signal tones were of equal amplitude. The panel on the right shows multi-frequency signal conditions in which the signal tones were presented at equal dB SL, determined separately for each observer and masker.

Single-frequency signals

The single-frequency signal conditions will be considered first. Thresholds in the on-signal and all-random masker conditions appear quite similar and consistent across frequency, with mean thresholds ranging from 52.1 to 53 dB across conditions. In contrast, thresholds in the all-coherent masker are on average 8.9 dB lower than those in the other two conditions. This CMR appears relatively constant across frequency, with the exception of the lowest frequency, where the all-coherent threshold is elevated by approximately 3 dB.

These observations were confirmed with a repeated-measures analysis of variance (ANOVA), with three levels of MASKER (on-signal, all-random, and all-coherent) and five levels of FREQ (276, 525, 1000, 1904, and 3624 Hz). There was a main effect of MASKER (F_2,10=90.33, p<0.0001), a main effect of FREQ (F_4,20=3.11, p<0.05), and a significant interaction (F_8,40=3.09, p<0.01). Preplanned comparisons indicated that the on-signal and all-random masker conditions did not differ (p=0.45), but both were significantly different from the all-coherent masker conditions (p<0.0001). Computing CMR as the difference between mean threshold in the all-random and all-coherent masker conditions, masking release ranged from 6.5 to 10.1 dB, with the smallest CMR occurring for a signal added to the lowest frequency band. A paired t-test indicated that the masking release differed significantly between the 276- and 525-Hz signal frequencies (t₅=5.09, p<0.005 two-tailed). No other paired comparison for adjacent bands approached significance (p>=0.25).

Multi-frequency signals

Data for the multi-frequency signals appear in the right two panels of Fig. 2. Thresholds in the all-random masker, multi-signal conditions spanned 47.9–50 dB SPL for the four signal conditions. Relative to the best single-frequency condition for each observer, this represents a threshold reduction of 1.2–3.3 dB.

In contrast, thresholds in the multi-frequency signal, all-coherent masker conditions spanned a range of about 9 dB across the four signal conditions (42.8–52.0 dB). A mean threshold of 43.6 dB was obtained in the random-ϕ, equal signal condition, where each signal tone had equal amplitude and had a random starting phase. Thresholds in this condition were not significantly different from those of the single-frequency condition with the lowest threshold (1904 Hz; t₅=0.79, p=0.46). Similarly, thresholds in the random-ϕ, normalized signal condition were not significantly different from those for the single-frequency, 1904-Hz signal (t₅=0.24, p=0.82), with an average of 42.8 dB. Whereas thresholds for the multi-signal, random-ϕ signal conditions were not different from those in the comparable single-frequency conditions, thresholds in both of the fixed-ϕ signal, all-coherent masker conditions were significantly elevated relative to the comparable single-frequency signal conditions; these trends held for both the equal and normalized level conditions. Relative to the 1904-Hz single-frequency condition, thresholds in the fixed-ϕ, equal signal condition were elevated by 9.4 dB (t₅=10.62, p<0.0001) and those in the fixed-ϕ, normalized signal condition were elevated by 4.7 dB (t₅=4.99, p<0.005).

For both the equal and normalized signal conditions, thresholds with random-ϕ signal were lower for the all-coherent than the all-random maskers (p<0.05), consistent with a significant CMR. No such CMR was observed for the fixed-ϕ signal conditions.

Discussion

Results of the single-frequency conditions are similar to those reported previously in literature. Thresholds in the on-signal masker conditions were quite consistent as a function of frequency, with a mean of 52–53 dB SPL. This result is in line with those of Bos and de Boer (1966) under comparable conditions. Thresholds in the all-random and on-signal masker conditions were statistically indistinguishable, suggesting that the bands were sufficiently separated in frequency to preclude energetic masking effects with random flanking bands. Mean thresholds in the comodulated masker conditions were more variable as a function of signal frequency, spanning about 3 dB. The poorest thresholds were obtained at the 256-Hz signal frequency. An analogous frequency effect was reported by Hall et al. (1988), where the smallest CMR was obtained for a signal added to the lowest masker band.

The most interesting aspect of the present results is the spectral integration observed in multi-frequency signal conditions. Table 1 reports the mean improvement in threshold for a multi-component signal relative to the lowest of the five associated single-frequency thresholds as measured in the associated all-coherent or all-random masker condition and computed separately for each of the six observers. The standard error of the mean (sem) is noted below each estimate of integration. For a five-component signal, the n rule predicts a 3.5 dB threshold improvement. For the all-random masker, spectral integration in both equal signal conditions is more than two sems below that prediction, but integration is within one sem of that target for both conditions utilizing the normalized amplitude signal. This result is consistent with the interpretation that individual differences in thresholds across frequency in the all-random masker conditions were reliable, such that across-frequency adjustments characterizing the normalized signal condition achieved equal signal audibility across frequency.

Table 1.

Estimates of spectral integration were computed as the lowest single-frequency signal threshold minus the associated multi-frequency signal threshold. The sem is indicated in parentheses. Assuming d^′ is proportional to signal intensity, integration of five independent cues is predicted to be 3.5 dB.

Masker condition	Signal condition (phase∕amplitude)
	Random-ϕ, equal	Fixed-ϕ, equal	Random-ϕ, normalized	Fixed-ϕ, normalized
All-random	1.55	1.19	3.30	2.87
	(0.51)	(0.60)	(0.62)	(0.49)
All-coherent	−2.07	−10.45	−1.31	−5.76
	(0.89)	(0.83)	(0.69)	(0.82)

In contrast to spectral integration computed for the all-random masker conditions, integration in the all-coherent masker conditions was uniformly negative. That is, best performance in a single-frequency condition was superior to that for a multi-component signal. This effect was most striking for the fixed-ϕ, equal signal condition, where thresholds rose to 10.45 dB with inclusion of all five signal tones. Thresholds in this condition were on average 51.9 dB, comparable to those in the single-frequency, all-random and the on-signal masker conditions. This threshold was also slightly poorer than the 50.0-dB threshold in the all-random masker, fixed-ϕ, equal signal condition (t₅=3.19, p<0.05). These comparisons suggest that fixing signal phase and level across frequency eliminates CMR and may elevate threshold above that obtained with a multi-frequency signal presented in random noise. One reason why thresholds for a fixed-ϕ, equal signal might be poorer in the all-coherent as compared to all-random masker conditions has to do with the redundancy of information across frequency in the all-coherent masker. If integration in the all-random masker is based in part on the benefits associated with having independent samples of signal-plus-masker available across frequency, then the fact that envelope patterns are identical across frequency in the all-coherent masker condition would reduce the available cues and increase threshold.

While integration is negative for all of the all-coherent masker, multi-frequency signal conditions, the magnitude of that effect is reduced for signal conditions associated with different signal∕masker interactions across frequency. Performance was worst for the fixed-ϕ, equal signal condition, but normalizing signal tone level relative to single-frequency threshold improved performance by 4.7 dB, and randomizing signal tone starting phase improved thresholds by 8.4 dB, with a combined effect of 9.1 dB. These results are consistent with the hypothesis that spectral integration in the presence of coherently amplitude modulated maskers depends strongly on the signal∕masker interaction and the resulting pattern of temporal envelopes across frequency.

One unpredicted result of the present study is the finding of negative integration for the random-ϕ, normalized signal condition with the all-coherent masker type. Mean thresholds in this condition rose by an average of 1.31 dB relative to thresholds in the best single-frequency condition. While this estimate of spectral integration is not significantly different from zero (t₅=1.91, p=0.11), the 95% confidence interval extends only up to 0.45 dB, well shy of the 3.5 dB predicted from a n rule. This outcome was not predicted at the outset of the experiment and suggests that integration in the presence of coherently modulated maskers may be less than that in random noise even in conditions where the signal∕masker interaction is non-uniform across frequency. This finding is not without precedent. In one set of conditions, Hall et al. (1988) measured detection thresholds in a family of three continuous 30-Hz wide bands of noise, each with the same pattern of inherent modulation. That study reported results in terms of CMR, computed as the threshold in the multi-signal condition, with random signal starting phase, minus the mean single-frequency thresholds obtained with a single (on-signal) masker band; these values can be used to compute thresholds and CMR (Table I; Hall et al., 1988). Thresholds for a single-frequency signal were lower in the presence of three coherently modulated masker bands relative to the on-signal threshold, an effect of 5.1 dB at 400 Hz, 9.9 dB at 500 Hz, and 8 dB at 600 Hz. Threshold for the three-tone signal, with tones at equal amplitude, was also reduced relative to the on-signal threshold, an effect of 6.3 dB. That is, the tone at 500 Hz was 3.6 dB more intense at threshold in the multi-signal condition as compared to the single-signal condition. When analyzed like the present data, this would be characterized as a −3.6 dB spectral integration.

In summary, the results of experiment 1 show that detection of a spectrally complex signal in a set of coherently modulated maskers is highly sensitive to the across-frequency envelope differences resulting from addition of a signal. There was no evidence of spectral integration in the all-coherent masker type even under conditions of robust across frequency cues. These results are also consistent with the hypothesis of van den Brink et al. (1992) that there should be no CMR for a multi-component signal in cases where the interactions between signals and masker produce compound output envelopes that are identical across frequency.

EXPERIMENT 2

The finding of reduced spectral integration in the context of coherently modulated masker bands stands in stark contrast to the conclusions of Bacon et al. (2002), where it was argued that spectral integration in the presence of coherently modulated bands can be substantially larger than that observed with random noise bands. In that study maskers were 100-Hz wide bands of Gaussian noise or noise that was sinusoidally modulated at a rate of 8 Hz. In one set of conditions thresholds were measured for a tonal signal at 500, 1000, or 2000 Hz, or a combination of all three frequencies. In each case there was a masker centered on each signal tone, but no “signal-free” maskers. Integration in Gaussian noise or incoherently modulated noise was close to 2.4 dB, as expected by the n rule. In coherently modulated noise integration was on the order of 5.5 dB, a result which could not be explained in terms of psychometric function slope, but was interpreted instead as evidence that spectral integration and CMR effects are additive.

In contrast to the paradigm of experiment 1 in the present study, Bacon et al. (2002) did not measure single-frequency thresholds in the three-masker complex; integration was computed instead based on single-frequency thresholds measured in the presence of a single masker band. The purpose of experiment 2 was therefore to replicate and extend the findings of Bacon et al. (2002) to include thresholds for individual signal tones in the three-masker complex. It was hypothesized that integration would be not be “greater than expected” when computed relative to single-frequency thresholds measured in a multi-masker complex. Another motivation for experiment 2 was to determine whether integration with coherent masker modulation is greater for SAM noise bands than for conditions where inherent masker modulation determines envelope coherence, as in experiment 1. Results of experiment 2 were therefore expected to provide insight into the stimulus features that drive the amount of spectral integration for comodulated maskers.

Methods

Observers

Observers were eight adults, from 21 to 53 years old (mean of 32 years). All had thresholds of 20 dB HL or less at octave frequencies of 250–8000 Hz (ANSI, 1996), and none reported a history of chronic ear disease. All observers were practiced in psychoacoustical tasks at the outset of the experiment, having participated in at least one prior experiment. One observer had previously participated in experiment 1.

Stimuli

Maskers were 100-Hz wide bands of noise, presented at 55 dB SPL per band. There was either a single band (on-signal) or a family of three bands (complex), with band center frequencies of 500, 1000, and 2000 Hz. Masker bands were either Gaussian noise or noise that was SAM at 8 Hz. Each band of noise was generated in the frequency domain based on Gaussian random draws defining the real and imaginary components contained within the masker passband, with an array size of 2¹⁷ points. When converted to the time domain and played at a sampling rate of 12 207 Hz, this stimulus was 10.7 s in duration.

The signal was a pure tone or a set of three pure tones, with frequencies corresponding to the center frequencies of the masker bands. Single-frequency signal thresholds were measured in two conditions: once in the presence of an on-signal masker alone and once in the presence of the complex masker including all three masker bands. Signal level in the multi-frequency signal conditions was defined in terms of these single-frequency thresholds, comparable to the normalized signal conditions of experiment 1. The starting phase of the signal tones was always coherent across frequency; because the maskers were based on independent Gaussian noise samples across frequency, the starting phase of the signal was assumed to be of no special significance.

As in experiment 1, the arrays describing masker and signal stimuli were loaded into an RPvds circuit (TDT) and stimulus gating was applied with software ramps. The masker and signal tone(s) present in a given interval were ramped on and off synchronously with 50-ms raised-cosine ramps and a 300-ms steady state. Masker amplitude modulation, when present, was synchronized to the listening interval, such that the modulation in each 400-ms listening interval began in sine phase.

Procedures

As in experiment 1, stimuli were presented in a three-alternative forced-choice paradigm, with the signal equally likely to be present in each interval. Listening intervals were marked visually and separated by 350 ms. Feedback was provided after each observer response. Signal level was adaptively varied following a three-down, one-up rule estimating 79% correct (Levitt, 1971). Level was initially adjusted in steps of 4 dB, reduced to 2 dB after the second track reversal. The track continued for a total of eight reversals, and threshold was estimated as the average signal level at the last six track reversals.

Single-frequency thresholds were collected first and in random order blocked by frequency. After completing the single-frequency conditions the multi-frequency conditions were likewise run in random order. In multi-frequency conditions signal level at threshold is reported in decibels relative to the highest-level tone (i.e., the level of the tone at the frequency associated with the highest single-frequency threshold). This convention is different from that adopted in experiment 1, where the lowest-level tone was the reference; the highest-level reference was used here to facilitate comparison with the data of Bacon et al. (2002). At completion of the experiment thresholds were examined for stability. Data were replaced if thresholds across the three or four estimates spanned a range of 8 dB or more. In cases where single-frequency thresholds were replaced the associated multi-frequency conditions were likewise replaced using the new estimates of threshold to normalize signal tone level.

Results

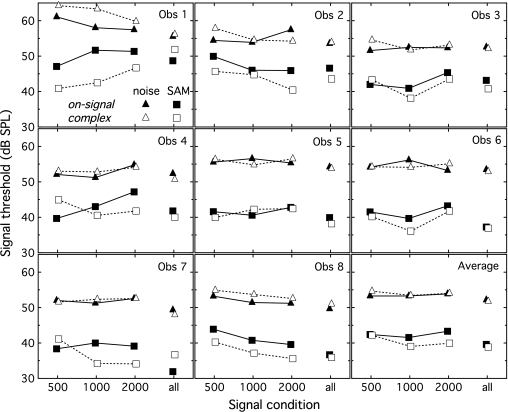
Mean thresholds for each observer are plotted in Fig. 3 as a function of signal condition, with symbols reflecting the masker condition. Triangles show thresholds in Gaussian noise conditions, and squares show those in SAM noise; filled symbols correspond to thresholds obtained in an on-signal masker alone and open symbols correspond to those obtained in a complex of three masker bands. Observer number, which appears in the top right of each panel, was assigned based on rank order of thresholds for the multi-frequency signal, with signal level normalization based on complex masker data; this condition may be viewed as a rough indicator of sensitivity to multi-frequency signals. Despite the individual differences evident in the figure, threshold estimates were relatively stable within observer (with a median standard deviation of 1.3 dB), and several trends in the data are evident.

Figure 3.

Mean thresholds for individual observers are shown in each panel, as well as the mean across Obs 2–8. Thresholds are plotted in dB SPL as a function of signal condition, with thresholds in the multi-frequency signal conditions plotted relative to the most intense of the three tones normalized to single-frequency signal thresholds. Symbols indicate the masker condition, either noise (triangle) or SAM noise (square). Filled symbols indicate threshold for a pure tone in a single masker band or a complex signal where relative tone levels are normalized based on results obtained with on-signal maskers. Open symbols indicate pure tone thresholds obtained in the presence of three masker bands, as well as the associated complex signal thresholds.

Data were replaced due to excessive variability in seven instances. In the original data of Obs 1, thresholds for the complex signal in SAM noise were quite variable, with two estimates near 40 dB SPL and two near 50 dB SPL. When these data were replaced all estimates were near 50 dB SPL. This threshold was 10 dB greater than the mean across observers and 8.3 dB greater than the next poorest threshold, suggesting that this observer’s multi-frequency signal thresholds should be viewed caution. For that reason all statistical tests reported below were performed omitting data from Obs 1. While this omission affected the level of significance reported for each test, repeating these statistical tests with those data included did not change the conclusions reached below.

Single-frequency signals

The single-frequency signal data will be considered first. As indicated by the connected triangles in Fig. 3, thresholds in the random noise masker tended to be similar for the on-signal and complex maskers, with mean thresholds spanning from 53.3 to 54.6 dB across frequency and noise masker condition. A repeated-measures ANOVA was performed with three levels of FREQ (500 Hz, 1 kHz, and 2 kHz) and two levels of MASKER (on-signal and complex). There was no effect of MASKER (F_1,6=5.35; p=0.06), no effect of FREQ (F_2,12=1.27; p=0.32), and no interaction (F_2,12=1.00; p=0.40). Though the effect of masker did not reach significance, there was a trend (p<0.1) for higher thresholds in the complex than on-signal noise masker, consistent with the possibility of more masking for a tone presented in a three-masker complex.

Thresholds in the on-signal SAM noise masker conditions (filled squares) appear to be unaffected or inconsistently affected by signal frequency, with mean thresholds of 41.6 to 43.3 dB. There was some evidence of an improvement with increasing frequency for the complex SAM noise masker (open squares) in some observer’s data (e.g., Obs 4, 7, and 8), but there were also striking counterexamples to this trend (Obs 1). A repeated-measures ANOVA was performed with three levels of FREQ (500 Hz, 1 kHz, and 2 kHz) and two levels of MASKER (on-signal and complex). There was a main effect of MASKER (F_1,6=14.60; p<0.01), no effect of FREQ (F_2,12=2.15; p=0.16), and no interaction (F_2,12=2.33; p=0.14). The main effect of MASKER reflects the fact that thresholds are on average 2.0 dB lower in the complex than on-signal SAM noise masker. Interpretation of these results is tempered by marked individual differences.

Multi-frequency signals

Attention now turns to the multi-frequency signal conditions indicated at the right-hand side of Fig. 3, denoted “all” on the abscissa. In these conditions there were three masker bands present, each with a signal tone, and symbol shading indicates the single-signal conditions used to normalize the relative levels of the three signal tones, either the on-signal masker (filled symbols) or complex masker (open symbols) conditions. As previously, symbol shape reflects masker type, either noise (triangles) or SAM noise (squares). In contrast to experiment 1, thresholds in these conditions are plotted relative to the level of the tone associated with the poorest (highest) single-frequency threshold. In general multi-signal thresholds in the complex masker conditions fall 2 dB or more below the highest associated signal-signal thresholds, with only two exceptions. For Obs 1 the multi-signal threshold in the complex SAM condition was 5.2 dB higher than the highest associated single-signal condition. For Obs 3, the multi-signal threshold in the on-signal noise condition was 0.11 dB higher than the highest associated single-signal condition.

Table 2 shows the mean spectral integration across individual observers. When signal tone level was normalized based on thresholds from the on-signal, single-frequency conditions, the estimates of spectral integration differed for noise and SAM noise conditions. There was 2.4 dB more integration in the SAM noise, a difference that was statistically significant (t₆=3.42, p<0.01 one-tailed). Thresholds were similar for noise and SAM noise when thresholds were normalized using thresholds from the complex, single-frequency conditions (t₆=1.18, p=0.28 two-tailed). One unexpected finding is that estimates of spectral integration based on single-frequency thresholds in the complex masker are significantly greater than the expected 2.4 dB (p<0.05) for both the noise and SAM noise conditions.

Table 2.

Estimates of spectral integration were computed as the maximum single-frequency signal threshold minus the associated multi-frequency signal threshold. The sem is indicated in parentheses. Assuming d^′ is proportional to signal intensity, integration of three independent cues is predicted to be 2.4 dB.

Relative levels based on	Signal condition
	On-signal	Complex
Noise	2.59	3.32
	(0.50)	(0.33)
SAM noise	5.01	3.95
	(0.86)	(0.41)

Discussion

The stimuli used here were roughly based on those used by Bacon et al. (2002). That study used a slightly higher presentation level (57 compared to 55 dB per band) and longer duration (500 ms compared to 400 ms), and masker bands were “frozen” noise generated as the sum of equal amplitude tones with 2 Hz spacing rather than Gaussian noise. Despite these differences, results are consistent across analogous conditions of the two studies. In the study of Bacon et al. (2002) integration was computed as the difference in threshold for the multi-frequency signal in a complex masker relative to single-frequency signals in the associated on-signal maskers; that is, there were no signal-free bands in the single-frequency conditions. For the masker composed of bands at 500, 1000, and 2000 Hz mean integration was approximately 2.4 dB for the noise masker and 5.5 dB for the SAM noise masker. Analogous estimates from the present study were 2.6 and 5.0 dB, replicating the original finding of a significant difference. Estimates of integration based instead on single-frequency thresholds in a complex masker, the method used in experiment 1, resulted in comparable estimates of integration for noise and SAM noise. This finding suggests that the large value of integration reported by Bacon et al. (2002) for the SAM noise as compared to the Gaussian noise conditions can be attributed to the choice of reference condition: Estimates based on the on-signal band alone reference result in greater estimates of integration in comodulated bands than those based on the complex masker as the reference condition, likely due to the masking release associated with inclusion of flanking masker bands.

It is unclear how to account for the integration of approximately 3.5 dB in both noise and SAM noise computed relative to the complex masker reference, a value which is 1.2 dB greater than the expected 2.4-dB effect size. Grose and Hall (1997) reported that spectral integration for a family of pure tone signals in random narrowband noise followed the n rule. In that experiment, however, there was a masker at each signal frequency and no signal-free maskers. Hall et al. (1988) measured thresholds for one or more signal tones presented in a family of three continuous narrowband random noise maskers and reported less than expected integration (1.1 dB as compared to 2.4 dB). Using gated masker presentation, Grose et al. (2005) reported approximately 3 dB of integration for both random and coherently modulated noise, the integration expected for the four-frequency signal used in that study. This range of results suggests that integration for bandpass noise maskers could depend on the stimulus details, such as gated versus continuous presentation. The finding of comparable integration in noise and SAM noise in the present paradigm, however, suggests that these effects exist independent of masking release based on coherent modulation.

One factor that could affect estimates of spectral integration is the degree to which channel independence can be assumed. In the present paradigm thresholds for a 500-Hz signal measured in the random noise conditions were on average 1.3 dB greater in the complex than in the on-signal masker, suggesting that some of the improvement observed could be due to a release from across-channel masking (Moore et al., 1990a).

GENERAL DISCUSSION AND CONCLUSIONS

Experiment 1 provided support for the hypothesis that spectral integration in the presence of a coherently amplitude modulated masker depends on the signal∕masker interaction differing across frequency. In cases where that interaction was consistent across frequency there was no evidence of integration, and, in fact, thresholds were elevated by more than 10 dB relative to threshold for a single-signal tone. Thresholds improved under signal conditions associated with different patterns of signal∕masker interaction. The best thresholds for a multi-frequency signal failed to show a positive spectral integration, however. One possible explanation for the lack of spectral integration in the context of coherently modulated masker bands has to do with the factors limiting performance. Langhans and Kohlrausch (1992) argued that detection of a brief tone in a frozen noise is limited by internal rather than external noise; this hypothesis was supported by the finding of better performance in diotic than monotic listening conditions, a result that would be expected if internal noise is independent across ears. Langhans and Kohlrausch (1992) noted that a similar diotic advantage is obtained with running comodulated noise (Cohen and Schubert, 1987; Schooneveldt and Moore, 1989), leading to the hypothesis that the auditory system can make use of the coherent envelope across frequency to reduce the effective variability of the external noise, leaving internal noise as the limit to performance. If accurate information about masker fluctuation allows observers to work at the limits of internal noise, then any benefits associated with spectral integration might be offset by corruption of the signal-free masker template.

Experiment 2 tested the hypothesis that the increased spectral integration for tones presented in amplitude modulated noise reported by Bacon et al. (2002) can be reconciled with previous literature by redefining integration referenced to the complex masker thresholds. Data were mostly consistent with that hypothesis. Defining integration relative to on-signal masker thresholds produced estimates of integration consistent with those reported by Bacon et al. (2002), whereas estimates based on the complex masker produced similar estimates for noise and SAM noise.

Results of experiment 1 provide no evidence of spectral integration in comodulated noise bands, but experiment 2 showed comparable integration for noise and SAM noise maskers. The differences in outcome between the experiments may well arise because of stimulus differences. A supplemental experiment described in the Appendix0 considered and rejected the possibility that differences in psychometric function slope could be responsible for these effects. Another possibility that we will consider briefly is that performance in the comodulated conditions was limited by internal noise for the stimuli used in experiment 1 but not for the stimuli used in experiment 2. In experiment 1 envelope coherence was manipulated via inherent modulation of each narrowband of noise; as a result, masker envelopes were identical across frequency prior to transduction by the auditory system. In experiment 2 the maskers were bands of independent Gaussian noise that had been sinusoidally amplitude modulated; as a result of random inherent modulation of these bands, envelopes across frequency were not perfectly correlated. If accurate representation of the masker alone envelope is necessary to effectively remove the masking associated with stimulus variability, then results of experiment 2 could be more strongly influenced by external noise than those of experiment 1. This reasoning is consistent with estimates of masking release. In experiment 1 inclusion of coherently modulated flanking masker bands improved threshold over that in the on-signal masker condition by 6.5–10.1 dB (mean of 8.9 dB). In experiment 2 thresholds in the three-band SAM noise improved by 0.2–3.4 dB (mean 2.0 dB) relative to the on-signal SAM masker threshold, suggesting that flanking masker bands were less beneficial to pure tone signal detection in the second experiment.

This interpretation suggests that spectral integration may be inversely related to the magnitude of CMR. The two studies on spectral integration in CMR previously reported from our laboratory are generally consistent with this idea. Comparing detection threshold for a pure tone signal in a single 30-Hz wide on-signal masker versus threshold in a three-band masker, Hall et al. (1988) reported a mean CMR of 9.9 dB: As in experiment 1, there was no evidence of spectral integration for a multi-frequency signal. Computing CMR in a similar way, the results of Grose et al. (2005) are consistent with a 3.8 dB CMR; as in experiment 2, there was robust spectral integration. Another difference between paradigms showing robust integration versus little benefit of additional signal components is continuous masker presentation in the former and gated masker presentations in the latter paradigms. Since CMR tends to be greater for continuous than gated stimuli (Fantini et al., 1993; Hatch et al., 1995), it could be difficult to tease apart effects associated with gating as compared to those related to the magnitude of CMR.

The most novel aspect of the present results is the demonstration that spectral integration under conditions associated with CMR depends critically on the details of signal∕masker interaction. It is likely that integration may also depend on baseline performance with a single signal, with greater integration under conditions of poorer performance.

APPENDIX

Four observers from experiment 2 subsequently participated in a supplemental experiment designed to determine whether psychometric function slope could be responsible for the differences in spectral integration observed for coherently amplitude modulated maskers in experiments 1 and 2. There were four stimulus conditions in total, each with a single pure tone signal at 1 kHz. Two conditions used stimuli identical to those described above for experiment 1; in these conditions the masker was a family of five 15-Hz wide masker bands, with modulation patterns being either all-coherent or all-random. The remaining two conditions used stimuli described above for experiment 2; in these conditions the masker was a set of three 100-Hz wide bands of noise, with either 8-Hz SAM or no modulation. In all cases the masker played continuously, and the signal was presented in one of three listening intervals.

Psychometric functions were estimated in two stages of testing. In the first stage, a tracking procedure was used to estimate the 71% correct using a two-down, one-up tracking rule. Four estimates based on four reversals each were collected for each observer. The mean (m) and standard deviation (sd) of these four estimates were used to select five signal levels for each observer: m-2sd, m-sd, m, m+sd, and m+2sd. Percent correct was then estimated for these five signal levels. Data were collected in ten blocks, each with eight repetitions of each signal level presented in random order.

Resulting estimates of percent correct were fitted with a logit function of the form

$$p\left(x\right)=\frac{1}{n}+\left(1-\frac{1}{n}\right)\frac{1}{1+e^{-\left(x-\mu \right)∕k}},$$ (A1)

where n is the number of listening intervals (in this case 3), x is the signal level in decibels, μ is the mean of the function, and k is the slope. These fits were quite accurate, with a median of 96.6% of the variance accounted for. Slopes for all observers appear in Table 3.

Table 3.

Estimates of psychometric function slope (k) for a subset of stimulus conditions from experiments 1 and 2.

	Exp. 1		Exp. 2
	All-coherent	All-random	Complex SAM	Complex noise
Obs 1	2.70	2.92	2.52	2.06
Obs 2	2.30	2.24	2.11	2.76
Obs 3	2.33	2.55	2.05	2.97
Obs 4	3.38	2.86	2.13	2.65
Mean	2.68	2.64	2.20	2.61

In general, integration is inversely related to the steepness of the psychometric function, with little integration in cases of steep psychometric functions. For the logit fitted here, steep functions are reflected by small values of k. Slopes are comparable for random noise for stimuli from the two experiments, with mean values near 2.6 in both cases. There are substantial individual differences, however, with estimates spanning 2.1–2.9. For comodulated maskers the mean values of k are larger (i.e., slopes are shallower) for stimuli from experiment 1 as compared to those from experiment 2. This trend is opposite from the predicted slope difference based on the integration reported above. This finding supports the conclusion that the negative values of spectral integration observed in experiment 1 may be affected by a change in cue quality with inclusion of multiple signal tones, such as a reduction in across-channel masking.

The finding of comparable or shallower slopes for comodulated as compared to random masker conditions is in contrast to the reports of Moore et al. (1990b). That study estimated function slope in a family of multiplied noise bands and reported steeper psychometric functions for coherently modulated than random bands.