Achieving Energy Conservation in Poisson-Boltzmann Molecular Dynamics: Accuracy and Precision with Finite-Difference Algorithms

Abstract

Violation of energy conservation in Poisson-Boltzmann molecular dynamics, due to the limited accuracy and precision of numerical methods, is a major bottleneck preventing its wide adoption in biomolecular simulations. We explored the ideas of enforcing interface conditions by the immerse interface method and of removing charge singularity to improve the finite-difference methods. Our analysis of these ideas on an analytical test system shows significant improvement in both energies and forces. Our analysis further indicates the need for more accurate force calculation, especially the boundary force calculation.

Introduction

Biomolecules are highly complex molecular machines with thousands to millions of atoms. What further complicates the picture is the need to realistically treat the interactions between biomolecules and their surrounding water molecules that are ubiquitous and paramount important for their structures, dynamics, and functions. Efficient molecular dynamics simulation in a realistic aqueous environment is still one of the few remaining challenges in molecular biophysics.

Since most particles in molecular dynamics are to represent water molecules solvating the target biomolecules, treating these water molecules implicitly allows the simulation efficiency to be increased greatly. Indeed, implicit solvation treatments, or implicit solvents, offer a unique opportunity for more efficient simulations without the loss of atomic-level resolution for biomolecules. The simplified implicit solvation treatments propose to model water molecules and any dissolved ions as a structureless and continuous medium. In contrast biomolecules, i.e. the solutes, are still represented in atomic detail. One of the most successful implicit solvents, the Poisson-Boltzmann (PB) implicit solvent has become a gold standard in implicit solvation treatments of biomolecules after years of basic research and development.

The earliest attempts to use PB implicit solvents in molecular dynamics date back to as early as the 1990s when Davis et al.[1], Zauhar[2], Sharp[3], Luty et al.[4], and Gilson et al.[5,6] contributed to adopting numerical PB solvents for dynamic simulations. Recently there has been renewed interest in finding ways to apply numerical PB solvents in dynamic simulations[7-15]. Efforts have also been reported to achieve higher-level accuracy in the finite-difference approach and thus to help the application of PB in dynamic simulations[16-19]. More interestingly, there are proposals to couple electrostatic and nonelectrostatic interactions within the implicit solvation treatment and to use level set to help the definition of solvent and solute interface[20-22].

Even with constant community-wide efforts to improve the efficiency and accuracy of numerical PB solvents, mathematical and computational challenges still remain in the adoption of the numerical PB solvents to molecular dynamics simulations, i.e. the PB molecular dynamics method. One of the issues is the observed violation of energy conservation in PB molecular dynamics, in part due to its limited numerical precision and accuracy in widely used finite-difference methods. This combined with other reported limitations or difficulties in the continuum treatment solute and solvent, such as efficient update of dielectric interface[12], lack of adaptive responses to molecular structural and energetic fluctuations[23], and the lack of asymmetric responses to positive and negative atom charges[24], prompt the researchers to develop next generation PB molecular dynamics that is more physical and more accurate in simulations of biomolecules.

In this study we investigate a higher-accuracy numerical scheme, the immersed interface method (IIM), which was proposed to solve the elliptic Partial Differential Equations with interface conditions on a rectangular finite-difference grid[25]. The key point of IIM is to enforce the interface conditions into the discretization, e.g., the finite-difference schemes, at grid points near the interface. The main advantages of IIM are: (1) the method is based on the finite-difference scheme on a simple rectangular grid that does not need to be aligned with the interface; (2) the scheme can achieve uniform high-order accuracy even near the interface; and (3) the finite-difference scheme on the rectangular grid can have a regular structure for certain jump conditions and hence efficient solvers can be applied to solve the linear system after discretization.

In this study we have analyzed the overall accuracy of IIM in reproducing reaction field energies and forces and dielectric boundary forces for a well studied test system of single dielectric sphere. We have also investigated the role of charge singularity in the numerical accuracy of energy and forces, especially dielectric interface forces within the finite-difference numerical scheme.

Methods

Finite-difference/finite-volume method

Without loss of generality, we focus on the Poisson’s equation in this study since the Boltzmann term is nonzero only outside the Stern layer, which is typically set 2 Å away from the dielectric interface where the dielectric constant is smooth. The partial differential equation

$$\nabla \cdot \epsilon \nabla \varphi =-4\pi \rho$$ (1)

establishes a relation between charge density (ρ) and electrostatic potential (ϕ) given a predefined dielectric distribution function (ε) for a solvated molecule.

A commonly used numerical method to solve the Poisson’s equation is to use a uniform Cartesian grid to discretize a finite rectangle box containing the molecule. The grid points are numbered as (i, j, k) , i=1,…,xm, j=1,…,ym, k=1,…,zm, where xm , ym , and zm are the numbers of points along the x, y, and z axes, respectively. The spacing between neighbor points is uniformly set to be h. With the finite-volume discretization, Equation (1) can be written as

$$\begin{array}{l}\epsilon (i-\frac{1}{2},j,k)[\varphi (i-1,j,k)-\varphi (i,j,k)]\\ +\epsilon (i+\frac{1}{2},j,k)[\varphi (i+1,j,k)-\varphi (i,j,k)]\\ +\epsilon (i,j-\frac{1}{2},k)[\varphi (i,j-1,k)-\varphi (i,j,k)]\\ +\epsilon (i,j+\frac{1}{2},k)[\varphi (i,j+1,k)-\varphi (i,j,k)].\\ +\epsilon (i,j,k-\frac{1}{2})[\varphi (i,j,k-1)-\varphi (i,j,k)]\\ +\epsilon (i,j,k+\frac{1}{2})[\varphi (i,j,k+1)-\varphi (i,j,k)]=\\ -4\pi q(i,j,k)/h\end{array}$$ (2)

Use of Equation (2) requires dielectric constant ε to be defined at the mid-points between any two neighbor grid points. It also requires mapping point charges onto the grid points. A commonly used method is the trilinear mapping method[26]. More detailed implementation information can be found in our recent works[11,12].

Interface treatment: Harmonic average

In biomolecular calculations the dielectric distribution often adopts a piece-wise constant model. In such a model, the dielectric constant at a midpoint apparently should be assigned to the dielectric constant in this region where the two neighbor grid points belong. However, when the two neighbor grid points belong to different dielectric regions, its dielectric constant is nontrivial to assign, because the dielectric constant is discontinuous across the interface. One simple treatment is the use of harmonic average (HA) of the two dielectric constants at the interface midpoints[27]. For example, if (i−1, j, k) and (i, j, k) belong to different dielectric regions, there must be an interface point on the grid edge between (i−1, j, k) and (i, j, k) . In HA $\epsilon (i-\frac{1}{2},j,k)$is defined as

$$\epsilon (i-\frac{1}{2},j,k)=\frac{h}{\frac{a}{\epsilon (i-1,j,k)}+\frac{b}{\epsilon (i,j,k)}}$$ (3)

Where a is the distance from the interface point to grid point (i−1, j, k) , b is the distance from the same interface point to grid point (i, j, k) . This strategy has been shown to improve the convergence of reaction field energies respect to the grid spacing[27].

Interface treatment: Immersed interface method

A more accurate method for interface treatment is IIM[25]. In IIM the interface is represent by a zero level set function φ(x,y,z)

$$\begin{array}{l}\varphi (x,y,z)<0\mathit{if}(x,y,z)\in {\mathrm{\Omega }}^{-}\\ \varphi (x,y,z)=0\mathit{if}(x,y,z)\in \mathrm{\Gamma }\\ \varphi (x,y,z)>0\mathit{if}(x,y,z)\in {\mathrm{\Omega }}^{+}\end{array}$$ (4)

where Ω⁻and Ω⁺ are the different regions and Γ is the interface. After defining

$$\begin{array}{c}{\varphi }_{\mathit{ijk}}^{\mathit{min}}=\min \{\varphi (i\pm 1,j,k),\varphi (i,j\pm 1,k),\varphi (i,j,k\pm 1)\}\\ {\varphi }_{\mathit{ijk}}^{\mathit{max}}=\max \{\varphi (i\pm 1,j,k),\varphi (i,j\pm 1,k),\varphi (i,j,k\pm 1)\}\end{array},$$ (5)

a grid point can be classified irregular if ${\varphi }_{\mathit{ijk}}^{\mathit{min}}{\varphi }_{\mathit{ijk}}^{\mathit{max}}<0$, and regular if otherwise. Given our interface problem as

$$\nabla \cdot \epsilon \nabla \varphi =f,$$ (6)

where f is used to denote the point charge term, and two jump conditions at interface Γ as

$$\begin{array}{l}{[\varphi ]}_{\mathrm{\Gamma }}=w\\ {[\epsilon {\varphi }_n]}_{\mathrm{\Gamma }}=v\end{array},$$ (7)

IIM propose new equations involving 27 points instead of the original 7-point finite-difference equations at irregular points.

The new equation at irregular point (i, j, k) can be written as

$$\sum _m^{n_s}{\gamma }_m\varphi (i+i_m,j+j_m,k+k_m)=f(i,j,k)+C(i,j,k),$$ (8)

where n_s is the number of grid points, γ_m are the undetermined coefficients, and C(i, j,k) is the undetermined correction term. The basic idea of IIM is to determine γ_m in Equation (8) for the irregular points so that the second-order global accuracy is obtained as in an interface-free problem with the finite-difference/finite-volume discretization scheme. Since only grid points nearby the interface are involved, it is sufficient to have an O(h) local truncation error at those points to reach the goal[25,28].

To compute the local truncation error T(i, j,k) at grid point (i, j, k)

$$T(i,j,k)=\sum _m^{n_s}{\gamma }_m\varphi (i+i_m,j+j_m,k+k_m)-f(i,j,k)-C(i,j,k),$$ (9)

we expand ϕ(i+i_m,j+j_m,k+k_m) in the local coordinate with a Taylor series about the grid point (i, j, k) ’s projection point (X*) on the interface. The following interface relations are used in the Taylor expansion

$$\begin{array}{lll}{\varphi }^{+}& =& {\varphi }^{-}+w\\ {\varphi }_{\xi }^{+}& =& \frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\xi }^{-}+\frac{v}{{\epsilon }^{+}}\\ {\varphi }_{\eta }^{+}& =& {\varphi }_{\eta }^{-}+w_{\eta }\\ {\varphi }_{\tau }^{+}& =& {\varphi }_{\tau }^{-}+w_{\tau }\\ {\varphi }_{\eta \tau }^{+}& =& {\varphi }_{\eta \tau }^{-}+({\varphi }_{\xi }^{-}-{\varphi }_{\xi }^{+}){\chi }_{\eta \tau }+w_{\eta \tau }\\ {\varphi }_{\eta \eta }^{+}& =& {\varphi }_{\eta \eta }^{-}+({\varphi }_{\xi }^{-}-{\varphi }_{\xi }^{+}){\chi }_{\eta \eta }+w_{\eta \eta }\\ {\varphi }_{\tau \tau }^{+}& =& {\varphi }_{\tau \tau }^{-}+({\varphi }_{\xi }^{-}-{\varphi }_{\xi }^{+}){\chi }_{\tau \tau }+w_{\tau \tau }\\ {\varphi }_{\xi \eta }^{+}& =& \frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\xi \eta }^{-}+({\varphi }_{\eta }^{+}-\frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\eta }^{-}){\chi }_{\eta \eta }+({\varphi }_{\tau }^{+}-\frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\tau }^{-}){\chi }_{\eta \tau }+\frac{v_{\eta }}{{\epsilon }^{+}}\\ {\varphi }_{\xi \tau }^{+}& =& \frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\xi \tau }^{-}+({\varphi }_{\eta }^{+}-\frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\eta }^{-}){\chi }_{\eta \tau }+({\varphi }_{\tau }^{+}-\frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\tau }^{-}){\chi }_{\tau \tau }+\frac{v_{\tau }}{{\epsilon }^{+}}\\ {\varphi }_{\xi \xi }^{+}& =& \frac{{\epsilon }^{-}}{{\epsilon }^{+}}{\varphi }_{\xi \xi }^{-}+(\frac{{\epsilon }^{-}}{{\epsilon }^{+}}-1){\varphi }_{\eta \eta }^{-}+(\frac{{\epsilon }^{-}}{{\epsilon }^{+}}-1){\varphi }_{\tau \tau }^{-}+{\varphi }_{\xi }^{+}({\chi }_{\eta \eta }+{\chi }_{\tau \tau })-{\varphi }_{\xi }^{-}({\chi }_{\eta \eta }+{\chi }_{\tau \tau })-w_{\eta \eta }-w_{\tau \tau }\end{array}$$ (10)

where the superscript denotes different sides of the interface, ξ is the normal direction, η and τ are two orthogonal tangential directions, and ξ=χ(η,τ) is the expression of the interface in the local coordinate system[28].

Thus the local truncation error can be written as

$$\begin{array}{ll}T(i,j,k)=& a_1{\varphi }^{-}+a_2{\varphi }_{\xi }^{-}+a_3{\varphi }_{\eta }^{-}+a_4{\varphi }_{\tau }^{-}+a_5{\varphi }_{\eta \tau }^{-}\\ & +a_6{\varphi }_{\eta \eta }^{-}+a_7{\varphi }_{\tau \tau }^{-}+a_8{\varphi }_{\xi \eta }^{-}+a_9{\varphi }_{\xi \tau }^{-}+a_{10}{\varphi }_{\xi \xi }^{-}\\ & +(\widehat{T}(i,j,k)-C(i,j,k))+O(h+\underset{m}{\max }\{\mid {\gamma }_m\mid \}{h}^3)\end{array}$$ (11)

where a_i,i =1,…,10, are in the linear combination of γ_m, T̂(i, j,k) is a linear combination of jump conditions and their surface derivatives from the interface relations[25,28]. To minimize T(i, j,k), all ten a_i should be set to zero. This leads to a linear system denoted as Bγ=b below[25,28]. To solve Bγ = b with 27 unknowns, a minimization problem is constructed:

$$\underset{{\gamma }_m}{\min }\frac{1}{2}\sum _m({\gamma }_m-d_m)$$

subject to

$$\begin{array}{l}\mathbf{B\gamma }=\mathbf{b}\\ {\gamma }_m<0,\mathrm{if}(i_m,j_m,k_m)=(0,0,0)\\ {\gamma }_m\ge 0,\mathrm{if}(i_m,j_m,k_m)\ne (0,0,0)\end{array}$$

where

$$\begin{array}{l}{d}_m=\frac{{\epsilon }_{i+i_m/2,j+j_m/2,k+k_m/2}}{h^2},\mathrm{if}{i}_m^2+j_m^2+k_m^2=1\\ d_m=0,\mathrm{otherwise}\\ d_0=-\frac{1}{h^2}\sum _{m,m\ne 0}{\epsilon }_{i+i_m/2,j+j_m/2,k+k_m/2}\end{array}$$

After obtaining γ_m, C(i, j,k) is calculated to cancel T̂(i, j,k) to construct the new equations at irregular points[25,28].

Charge singularity: Finite-volume treatment

Point charge models are widely used in molecular dynamics of biomolecules. The representation of point charges by delta functions apparently introduces singularity to the PB equation. The finite-volume discretization scheme overcomes this problem by resorting to the integral form of the PB equation. Thus the total charge, instead of the singular charge density, appears in the discretized form (Equation (2)). However, such a treatment does distort the otherwise singular Coulombic potential especially when it is close to a grid charge[4].

Charge singularity: Regulation treatment

Several strategies are available to remove the charge singularity[29-32]. Here we adopted an efficient strategy recently developed by us[33]. In our method two separate equations for two different potentials in two different regions are solved simultaneously, i.e., the reaction field potential in the solute region and the total potential in the solvent region, different from published decomposition schemes that require solution of separate set of equations[29-32].

Briefly we solve for the reaction field potential (ϕ_RF) in the solute region (Ω̅⁻) and solve for the total potential (ϕ =ϕ_RF+ϕ_C) in the solvent region (Ω⁺). Here ϕ_C is the Coulombic potential, satisfying ${\epsilon }_{-}{\nabla }^2{\varphi }_C=-4\pi \rho$[33]. The respective equations for ϕ_RF and ϕ are

$$\{\begin{array}{l}\nabla \cdot \epsilon \nabla {\varphi }_{RF}=0,\mathit{in}{\mathrm{\Omega }}^{-}\\ \nabla \cdot \epsilon \nabla \varphi -N(\varphi )=0,\mathit{in}{\mathrm{\Omega }}^{+}\end{array},$$ (12)

where N(ϕ) represents the Boltzmann term and is set to zero in the current study[33]. The corresponding jump condition across Γ are

$$\{\begin{array}{l}\varphi ={\varphi }_C+{\varphi }_{\mathit{RF}}\\ \left[\epsilon \frac{\partial {\varphi }_{\mathit{RF}}}{\partial n}\right]=-\left[\epsilon \frac{\partial {\varphi }_C}{\partial n}\right].\end{array}$$ (13)

Thus the Coulombic potential is needed on the interface in Equation (13)[33].

Electrostatic energy and force

Potential and electrostatic field

After solving the finite-difference equations, only potential at grid points are known. To obtain potential or electrostatic field at any position (x₀, y₀, z₀), we utilize the one-side least-square interpolation method[28]. Briefly a function of the form

$$\begin{array}{ll}f(x,y,z)=a_0& +a_1(x-x_0)+a_2(y-y_0)+a_3(z-z_0)\\ & +a_4{(x-x_0)}^2+a_5{(y-y_0)}^2+a_6{(z-z_0)}^2\\ & +a_7(x-x_0)(y-y_0)+a_8(y-y_0)(z-z_0)+a_9(x-x_0)(z-z_0)\end{array}$$ (14)

is fitted using the potentials of N_m(≥19) nearest grid points in the same region. The coefficients a_i, i =1, …, 10 are determined to minimize

$$d=\sum _m^{N_m}{\left[\varphi (x_m,y_m,z_m)-f(x_m,y_m,z_m)\right]}^2$$ (15)

so that the potential and gradient of potential at position (x₀,y₀,z₀) is given by the following relation:

$$\begin{array}{l}\varphi (x_0,y_0,z_0)\approx f(x_0,y_0,z_0)=a_0\\ {\varphi }_x(x_0,y_0,z_0)\approx f_x(x_0,y_0,z_0)=a_1\\ {\varphi }_y(x_0,y_0,z_0)\approx f_y(x_0,y_0,z_0)=a_2\\ {\varphi }_z(x_0,y_0,z_0)\approx f_z(x_0,y_0,z_0)=a_3\end{array}$$ (16)

Reaction field energy and force

The reaction field energy (ΔG) is calculated as

$$\mathrm{\Delta }G=\frac{1}{2}\sum _{i=1}^{N_q}{q}_i(\varphi -{\varphi }_C).$$ (17)

If the charge singularity is removed, it can be calculated as

$$\mathrm{\Delta }G=\frac{1}{2}\sum _{i=1}^{N_q}{q}_i{\varphi }_{\mathit{RF}}.$$ (18)

The reaction field force (qE) is readily obtained as

$${\mathbf{F}}_{\mathit{qE}}=\sum _{i=1}^{N_q}{q}_i{\mathbf{E}}_{\mathit{RF}}$$ (19)

with electric field computed in Equation (16).

Dielectric boundary force

The dielectric boundary (db) force can be written as

$${\mathbf{F}}_{\mathit{db}}=\underset{\mathrm{\Gamma }}{∯}p.\mathbf{n}d\mathrm{\Gamma }=\underset{\mathrm{\Gamma }}{∯}\frac{1}{8\pi }({\epsilon }^{+}-{\epsilon }^{-})({\mathbf{E}}^{\text{+}}.{\mathbf{E}}^{\text{−}})\mathbf{n}d\mathrm{\Gamma }$$ (20)

where p is the Maxwell stress tensor and n is the normal unit vector of the interface element[2]. The field E^– in Equation (20) is obtained by the one-side least-square interpolation, and E⁺ is calculated from E^– based on the jump condition. The surface integration is numerically implemented with a certain number of evenly-distributed elements on the surface, generated by the spiral method[34]. The number of surface elements is chosen to be large enough to secure 6-digit accuracy in the dielectric boundary force when analytical electrostatic field is used at the interface. This turns out to be 51.2 million elements for the worse case scenario, i.e. when the point charge is closest to the surface.

Test cases

To quantify the accuracy and precision of tested methods, we used a well-studied testing system, a single dielectric sphere imbedded with point charges (Fig. 1). The analytic potential and gradient is

Figure 1.

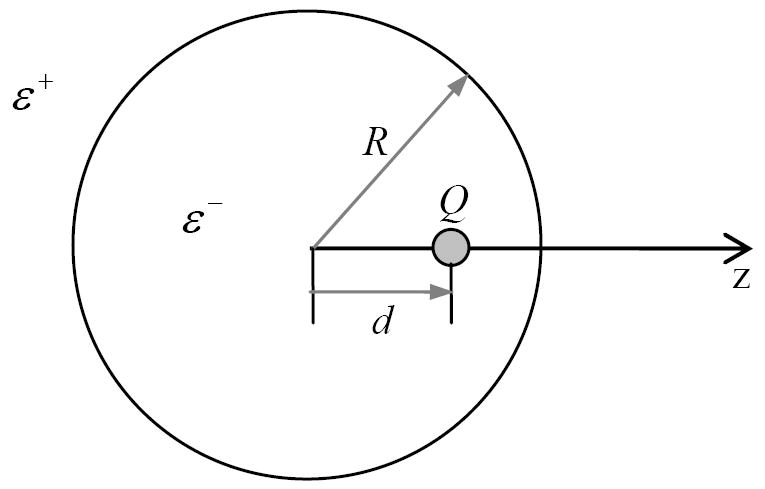
A single dielectric sphere with radius R=2Å. The inside dielectric is ε⁻ and outside dielectric is ε⁺ . A single point charge (Q=+e) is positioned d away from the center.

$$\begin{array}{ll}{\varphi }_{\mathit{RF}}^{-}(r,\theta ,\varphi )=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{2l+1}\frac{1}{R^{2l+1}}\frac{(l+1)({\epsilon }^{-}-{\epsilon }^{+})}{{\epsilon }^{-}(l{\epsilon }^{-}+(l+1){\epsilon }^{+})}{Q}_{\mathit{lm}}{r}^l{Y}_{\mathit{lm}}(\theta ,\varphi )\\ \frac{\partial {\varphi }_{\mathit{RF}}^{-}(r,\theta ,\varphi )}{\partial r}=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{2l+1}\frac{l}{R^{2l+1}}\frac{(l+1)({\epsilon }^{-}-{\epsilon }^{+})}{{\epsilon }^{-}(l{\epsilon }^{-}+(l+1){\epsilon }^{+})}{Q}_{\mathit{lm}}{r}^{l-1}{Y}_{\mathit{lm}}(\theta ,\varphi )\\ \frac{\partial {\varphi }_{\mathit{RF}}^{-}(r,\theta ,\varphi )}{\partial \theta }=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{2l+1}\frac{1}{R^{2l+1}}\frac{(l+1)({\epsilon }^{-}-{\epsilon }^{+})}{{\epsilon }^{-}(l{\epsilon }^{-}+(l+1){\epsilon }^{+})}{Q}_{\mathit{lm}}{r}^l\frac{\partial Y_{lm}(\theta ,\varphi )}{\partial \theta }\\ \frac{\partial {\varphi }_{\mathit{RF}}^{-}(r,\theta ,\varphi )}{\partial \varphi }=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{2l+1}\frac{1}{R^{2l+1}}\frac{(l+1)({\epsilon }^{-}-{\epsilon }^{+})}{{\epsilon }^{-}(l{\epsilon }^{-}+(l+1){\epsilon }^{+})}{Q}_{lm}{r}^l\frac{\partial Y_{lm}(\theta ,\varphi )}{\partial \varphi }\\ {\varphi }^{+}(r,\theta ,\varphi )=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{l{\epsilon }^{-}+(l+1){\epsilon }^{+}}{Q}_{\mathit{lm}}\frac{1}{r^{l+1}}{Y}_{\mathit{lm}}(\theta ,\varphi )\\ \frac{\partial {\varphi }^{+}(r,\theta ,\varphi )}{\partial r}=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{-4\pi (l+1)}{l{\epsilon }^{-}+(l+1){\epsilon }^{+}}{Q}_{\mathit{lm}}\frac{1}{r^{l+2}}{Y}_{\mathit{lm}}(\theta ,\varphi )\\ \frac{\partial {\varphi }^{+}(r,\theta ,\varphi )}{\partial \theta }=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{l{\epsilon }^{-}+(l+1){\epsilon }^{+}}{Q}_{\mathit{lm}}\frac{1}{r^{l+1}}\frac{\partial Y_{\mathit{lm}}(\theta ,\varphi )}{\partial \theta }\\ \frac{\partial {\varphi }^{+}(r,\theta ,\varphi )}{\partial \varphi }=& \sum _{l=0}^{\infty }\sum _{m=-l}^l\frac{4\pi }{l{\epsilon }^{-}+(l+1){\epsilon }^{+}}{Q}_{\mathit{lm}}\frac{1}{r^{l+1}}\frac{\partial Y_{\mathit{lm}}(\theta ,\varphi )}{\partial \varphi }\end{array},$$

with

$$Q_{\mathit{lm}}=\sum _{K=1}^{N_q}{q}_k{r}_k^l{Y}_{\mathit{lm}}^{\ast }({\theta }_k,{\varphi }_k).$$

Here N_q is the number of charges (set to be 1 in this study) and q_k is the kth charge located at (r_k,θ_k,φ_k). ε⁺ and ε⁻ are the dielectric constant outside and inside, respectively. R is the radius of the sphere.Y_lm is spherical harmonics.

The radius of the sphere R is 2.0Å, about the size of a united carbon atom. The charge is located 0.25Å to 1.50Å from the center. Q is set as +e . The dielectric constant outside ε⁻ is 1.0, The dielectric constant outside ε⁺ is set at 80.0. The grid spacing ranges from 1/4Å to 1/16Å. A total of 27 different finite-difference grid origins were used to analyze the precision the methods, i.e. the effect of relative location of finite-difference grids with respect to the interface and charge distribution.

Results and Discussion

In the following we focus on the influences of enforcing the interface conditions with IIM and removing charge singularity upon the accuracy and precision of reaction field energies and forces, and dielectric boundary forces. Here the accuracy is represented as the maximum error of numerical results, and the precision is represented with the standard deviation of numerical results for each test condition. Three methods were compared in reproducing analytical energies and forces. In the first method, IIM was used and charge singularity was removed, termed as “IIM−Singularity”. In the second method, HA was used and charge singularity was removed, termed as “HA−Singularity”. The third method is the original method in finite difference PB, HA was used and charge singularity was retained, termed as “HA+Singularity”.

Accuracy and precision of reaction field energies

The accuracy and precision of reaction field energies were investigated with three typical situations: (a) the charge is positioned close (0.25Å) to the spherical center, (b) the charge is 1.0Å away from the interface, and (c) the charge is only 0.50Å away from the interface. Reaction field energies by IIM−Singularity, HA−Singularity, and HA+Singularity were analyzed and shown in Table 1. Since the computation of reaction field energies naturally implies removal of the singular Coulombic component, HA−Singularity and HA+Singularity are equivalent in this analysis.

Table 1.

Accuracy and precision of reaction field energies (in ½e²/Å) with respect to dielectric interface treatments.

d	1/h	$q{\varphi }_{\mathit{RF}}^0$	IIM−Singularity			HA ±Singularity
			${\overline{\mathit{q\varphi }}}_{\mathit{RF}}$	σ	δMax	${\overline{\mathit{q\varphi }}}_{\mathit{RF}}$	σ	δMax
0.25	4	-0.501538	-0.501524	0.000002	0.000019	-0.502002	0.000016	0.000505
0.25	8	-0.501538	-0.501534	0.000000	0.000005	-0.501648	0.000003	0.000115
0.25	16	-0.501538	-0.501537	0.000000	0.000001	-0.501565	0.000001	0.000028
1.00	4	-0.657214	-0.657671	0.000070	0.000568	-0.658584	0.000585	0.002726
1.00	8	-0.657214	-0.657327	0.000009	0.000126	-0.657495	0.000132	0.000551
1.00	16	-0.657214	-0.657240	0.000001	0.000028	-0.657269	0.000033	0.000120
1.50	4	-1.123576	-1.131290	0.004526	0.013964	-1.142030	0.012984	0.055262
1.50	8	-1.123576	-1.125428	0.000708	0.002626	-1.126337	0.001823	0.006765
1.50	16	-1.123576	-1.124041	0.000089	0.000581	-1.124105	0.000417	0.001373

Clearly IIM−Singularity delivers the best accuracy in all three test cases regardless of h. Its numerical accuracy is the most impressive when the charge is far away from the interface, with the maximum error about 22-28 times smaller than that of HA ± Singularity. In the more challenging cases of charge placed 1.0Å and 0.5Å away from the interface, the accuracy advantage of IIM−Singularity over HA ±Singularity is reduced to a factor of 2 to 5, depending on h.

An issue important for stable dynamics simulation is the standard deviation of reaction field energies when the finite-difference grid is randomly positioned. Sensitivity of grid positions respect to the solute molecule has been a particularly annoying limitation in current finite-difference PB methods. We observed impressively reduced standard deviations for all three test cases, with reduction factors ranging from 8 to over 33 when the charge is at least 1.0Å away from the interface. The reduction factors in standard deviations for the most challenging case, nevertheless, are reduced to 2 to 5.

Accuracy and precision of qE forces

The accuracy and precision of reaction field forces by IIM−Singularity and HA ±Singularity were analyzed similarly and shown in Table 2. Consistent with the analysis of reaction field energies, IIM−Singularity delivers the most impressive advantage over HA ±Singularity when the charge is far away from the interface, with maximum errors up to 25 times smaller than that of HA ±Singularity. In the more challenging cases of the charge placed 1.0Å and 0.5Å away from the interface, the accuracy advantage of IIM−Singularity over HA ±Singularity is reduced to a factor of 1 to 4, indicating the high curvature of the reaction field close to the interface which cannot be improved dramatically without reducing h.

Table 2.

Accuracy and precision of reaction field forces (in e²/Ų) with respect to dielectric interface treatments.

d	1/h	$F_{\mathit{qE}}^0$	IIM−Singularity			HA ± Singularity
			F̅qE	σ	δMax	F̅qE	σ	δMax
0.25	4	0.031647	0.031641	0.000003	0.000012	0.031729	0.000107	0.000297
0.25	8	0.031647	0.031645	0.000001	0.000003	0.031664	0.000029	0.000067
0.25	16	0.031647	0.031646	0.000000	0.000001	0.031650	0.000007	0.000017
1.00	4	0.217841	0.217682	0.000570	0.001182	0.219196	0.001289	0.003601
1.00	8	0.217841	0.217801	0.000145	0.000314	0.218105	0.000301	0.000802
1.00	16	0.217841	0.217829	0.000037	0.000082	0.217880	0.000076	0.000173
1.50	4	0.958693	0.952007	0.022030	0.040824	0.986900	0.031927	0.087923
1.50	8	0.958693	0.958037	0.004630	0.009183	0.965090	0.004157	0.013047
1.50	16	0.958693	0.958677	0.001084	0.002296	0.960002	0.000860	0.002876

Standard deviations of IIM−Singularity over HA ±Singularity are reduced by a pronounced factor over 35 when the charge is far away from the interface. Unfortunately, the benefit of IIM−Singularity over HA ±Singularity is reduced to a factor of 1 to 3 in the more challenging cases of the charge placed 1.0Å and 0.5Å away from the interface, similar to the case of the accuracy analysis.

Accuracy and precision of db forces

The accuracy and the precision of db forces were also investigated. One difference here is the distinction between HA−Singularity and HA+Singularity, which turns out to be the most important improvement in the case of db forces as shown in Table 3.

Table 3.

Accuracy and precision of dielectric boundary forces (in e²/Ų) with respect to dielectric interface and charge singularity treatments.

d	1/h	$F_{\mathit{db}}^0$	IIM−Singularity			HA−Singularity			HA+Singularity
			F̅db	σ	δMax	F̅db	σ	δMax	F̅db	σ	δMax
0.25	4	0.031647	0.031647	0.000003	0.000005	0.031611	0.000107	0.000287	0.026089	0.000889	0.007136
0.25	8	0.031647	0.031646	0.000000	0.000002	0.031547	0.000018	0.000137	0.028474	0.000134	0.003402
0.25	16	0.031647	0.031647	0.000000	0.000000	0.031590	0.000004	0.000064	0.030832	0.000019	0.000845
1.00	4	0.217841	0.219628	0.001753	0.004458	0.217838	0.002136	0.004006	1.058431	0.404564	1.572224
1.00	8	0.217841	0.217474	0.000388	0.000940	0.217140	0.000361	0.001264	0.201324	0.001977	0.019043
1.00	16	0.217841	0.217694	0.000051	0.000223	0.217524	0.000034	0.000376	0.209472	0.000609	0.009309
1.50	4	0.958693	1.711778	0.135506	0.916579	1.595851	0.298070	1.148297	27.639244	18.097379	59.290638
1.50	8	0.958693	1.026442	0.022939	0.100221	0.997134	0.036111	0.096707	3.437920	2.275903	6.433441
1.50	16	0.958693	0.956963	0.005673	0.009313	0.954495	0.004549	0.010432	0.893824	0.008999	0.075564

First we focus on the effect of charge singularity by comparing HA−Singularity and HA+Singularity. Different from previous analyses, the advantage of HA−Singularity over HA+Singularity depends on grid spacing. Its advantage is highest with coarsest h: the maximum errors are 25 to 400 smaller and the standard deviations are 8 to 202 times smaller, especially at the two challenging cases. The factors of reductions are changed to 2 to 13 at the finest h as expected since the finite-difference Coulombic field is the most accurate.

Second we focus on the effect of jump conditions at sub-grid resolution by comparing IIM−Singularity and HA−Singularity. Similar to the tests of qE forces, IIM−Singularity delivers the most impressive advantage over HA−Singularity when the charge is far away from the interface, with maximum errors up to 50 times smaller than those of HA−Singularity. In the more challenging cases of the charge placed 1.0Å and 0.5Å away from the interface, the accuracy advantage of IIM−Singularity over HA−Singularity is unclear, though the average values are often better with IIM−Singularity, indicating a smaller systematic error. Similarly in the precision analysis, the advantage of IIM−Singularity over HA−Singularity is a pronounced factor over 35 when the charge is away from the interface, but it is unclear when the charge is placed 1.0Å and 0.5Å away from the interface.

Error analysis of numerical db forces

The calculation of the db forces is far more involving than that of the reaction field forces. First, we need to interpolate the electrostatic field on the interface. The extra step in principle introduces interpolation error. Second we need to perform numerical surface integration of the Maxwell stress tensor on the interface. The second step in principle introduces integration error. Thus the final error in db forces is dependent on the solver, the interpolation procedure, and the integration procedure.

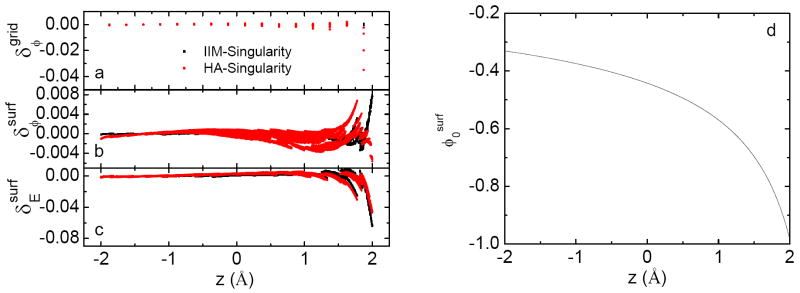
To understand the marginal improvement of IIM−Singularity over HA−Singularity in calculation of db forces, we conducted more detailed analysis at each numerical step. Fig. 2 shows the errors of the potential at the inside grid points nearby the interface, the potential at sample points on the interface, and the field at sample points on the interface from both IIM−Singularity and HA−Singularity. Fig. 2a clearly shows that the errors in IIM−Singularity are smaller than those in HA−Singularity at grid points. It is worth noting that the maximum errors from HA−Singularity are 100 times larger than those from IIM−Singularity and these occur at grid points nearby the interface with large z values, i.e. close to the charge (see Fig. 1). Least square fitting of potential certainly brings down the accuracy of IIM−Singularity. However the errors in least-square-fitted potentials from HA−Singularity are surprisingly reduced with maximum errors 10 times smaller than those at the grid points. The end result is comparable errors in least-square-fitted potentials and fields from IIM−Singularity and HA−Singularity (Fig. 2b&c). This abnormity can be understood from the potential distribution on the interface, as shown in Fig. 2d. The curvature of the potential on the interface makes the least-square-fitted potential systematically more positive due to extrapolation since no or few grids are on the interface. This systematic positive error happens to balance out the negative errors from HA−Singularity at grids nearby the interface, causing the fortuitous enhancement in fitted potentials and fields from HA−Singularity, which may not be possible in more complicated interfacial geometries. Nevertheless, our analysis shows the need for more robust interpolation scheme for high quality db force calculation.

Figure 2.

Comparison of errors of potential and electric field on inside grid points near the interface and those of interpolated potential and field on the interface (left). Analytical potential on the interface is shown on the right.

The numerical integration quality may also play a role here and can be analyzed by studying the convergence behavior of db forces versus the number of interface elements, as shown in Fig. 3. Note that when the number of interface elements increases, the numerical db forces converge, but not to the analytic value. There are systematic errors between the numerical values and the analytic value. This analysis also shows that about 0.1 million elements, instead of 51.2 million elements (obtained using analytical surface electric field, thus free of the systematic errors) are sufficient to calculate the db forces due to the existence of the systematic errors from the grid potentials. Nevertheless, the use of extra surface elements clearly rules out the cause of integration error in the final quality of db forces in this study.

Figure 3.

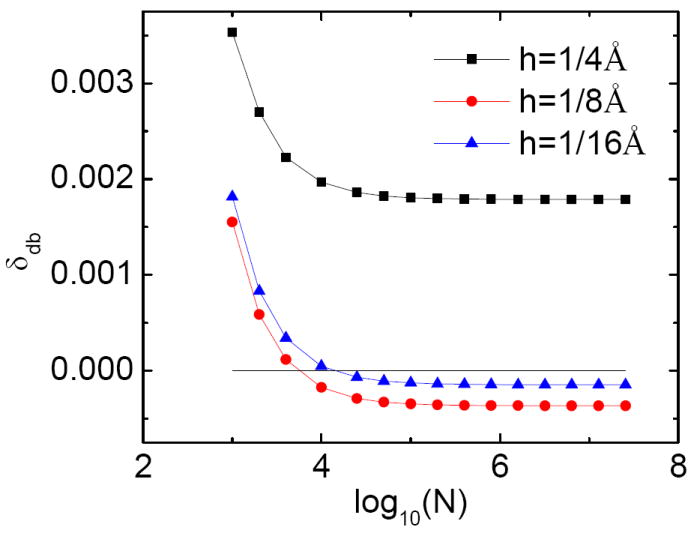
Convergence of numerical db forces with respect to the number of numerical surface elements (N) for the charge placed at d=1.0 Å.

Convergence of energies and forces versus grid spacing

Finally we studied the convergence of reaction field energies and forces and dielectric boundary forces with respect to grid spacing in IIM−Singularity (Fig. 4). Here the same three representative test cases are shown. It is apparent that the convergence trends of both standard deviations and maximum errors approximately follow the O(h²) global truncation errors for finite-difference algorithms. It is also interesting to ask, given the smallest atomic cavity radius to be set as 1.0Å, for example, what grid spacing can we use to achieve a reasonable energy conservation and stability in molecular dynamics? Let us assume, quite arbitrarily, this corresponds to the standard deviation in energies to be ≤10⁻⁴ and the standard deviations in forces to be 10≤⁻³ [35]. We can achieve this requirement at the grid spacing of 1/8Å with IIM−Singularity. If we relax the standard deviations in forces by a factor of two, we can also use the grid spacing of 1/4Å.

Figure 4.

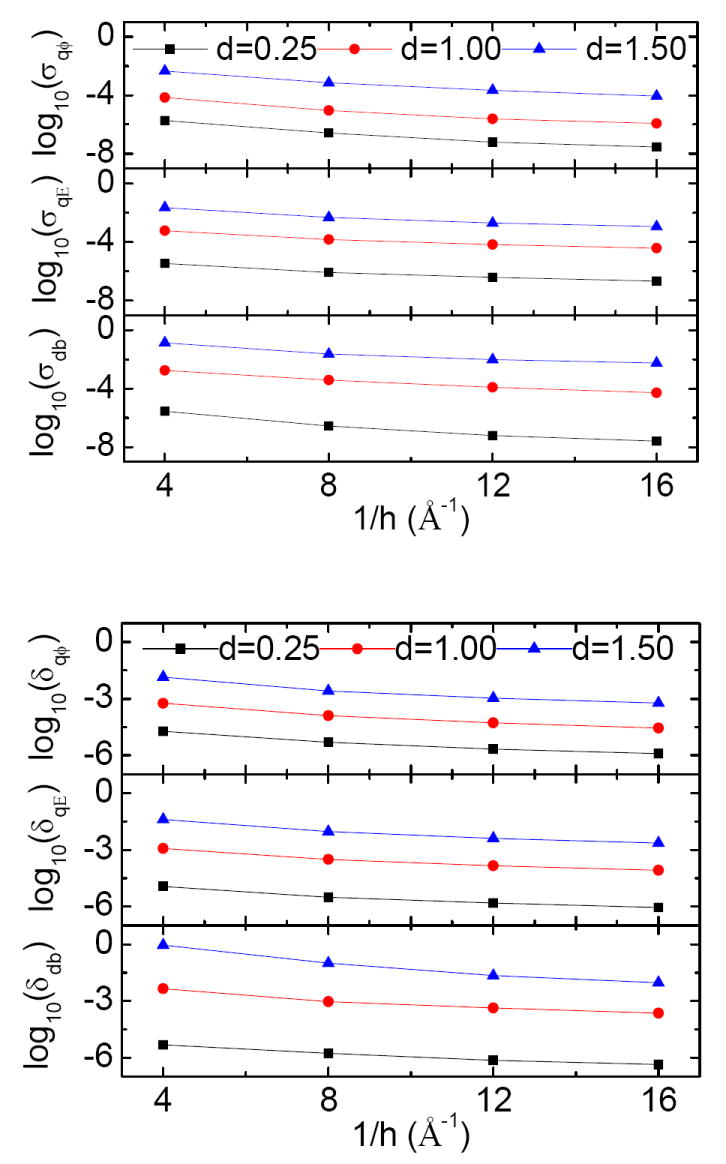
Standard deviations (upper) and maximum errors (lower) of reaction field energies, qE forces, and db forces versus decreasing h.