Tuning parameter selectors for the smoothly clipped absolute deviation method

Summary

The penalised least squares approach with smoothly clipped absolute deviation penalty has been consistently demonstrated to be an attractive regression shrinkage and selection method. It not only automatically and consistently selects the important variables, but also produces estimators which are as efficient as the oracle estimator. However, these attractive features depend on appropriately choosing the tuning parameter. We show that the commonly used the generalised crossvalidation cannot select the tuning parameter satisfactorily, with a nonignorable overfitting effect in the resulting model. In addition, we propose a bic tuning parameter selector, which is shown to be able to identify the true model consistently. Simulation studies are presented to support theoretical findings, and an empirical example is given to illustrate its use in the Female Labor Supply data.

1. Introduction

In regression analysis, an underfitted model can lead to severely biased estimation and prediction. In contrast, an overfitted model can seriously degrade the efficiency of the resulting parameter estimates and predictions. Hence, obtaining a sparsely parsimonious and effectively predictive model is essential.

Traditional model selection criteria, such as aic (Akaike, 1973) and bic (Schwarz, 1978), suffer from a number of limitations. Their major drawback arises because parameter estimation and model selection are two different processes, which can result in instability (Breiman, 1996) and complicated stochastic properties (Fan & Li, 2001). Moreover, the total number of candidate models increases exponentially as the number of covariates increases.

To overcome the deficiency of traditional methods, Fan & Li (2001) proposed the smoothly clipped absolute deviation or SCAD method, which estimates parameters while simultaneously selecting important variables. As compared with another popular regression shrinkage and selection method, the least absolute shrinkage and selection operator or Lasso of Tibshirani (1996), the smoothly clipped absolute deviation method not only selects important variables consistently, but also produces parameter estimators as efficient as if the true model were known, i.e., the oracle estimator, a property not enjoyed by the Lasso. The above features of the smoothly clipped absolute deviation method rely on the proper choice of tuning parameter, or regularisation parameter, which is usually selected by generalised crossvalidation (Craven & Wahba, 1979).

We show that the optimal tuning parameter selected by generalised crossvalidation has a nonignorable overfitting effect even as the sample size goes to infinity. Moreover, we propose a bic-based tuning parameter selector for the smoothly clipped absolute deviation method, and prove that the proposed procedure identifies the true model consistently.

2. The Smoothly Clipped Absolute Deviation Method

Consider the linear regression model,

$$y_i=x_i^{\prime }\beta +{∊}_i,$$ (2.1)

where y_i is the response from the ith subject, x_i = (x_i1, ⋯ , x_id)′ is the associated d-dimensional explanatory covariate, β = (β₁, ⋯ , β_d)′, and ∊_i is the random error with mean 0 and variance ${\sigma }_{∊}^2$. Let (x_i, y_i), i = 1, ⋯ , n, be a random sample from (2.1). To select simultaneously variables and estimate parameters, the smoothly clipped absolute deviation method of Fan & Li (2001) estimates β by minimising the penalised least squares function

$$\frac{1}{2n}\parallel Y-X\beta {\parallel }^2+\underset{j=1}{\overset{d}{\Sigma }}p\lambda \left(\left|{\beta }_j\right|\right),$$ (2.2)

where Y = (y₁, ⋯ , y_n)′, X = (x₁, ⋯ , x_n)′, ∥ · ∥ stands for the Euclidean norm, and p_λ(·) is the smoothly clipped absolute deviation penalty with a tuning parameter λ to be selected by a data-driven method. The penalty p_λ(·) satisfies p_λ(0) = 0, and its first-order derivative is

$$p_{\lambda }^{\prime }\left(\theta \right)=\lambda \left\{I(\theta \le \lambda )+\frac{{(a\lambda -\theta )}_{+}}{(a-1)\lambda }I(\theta >\lambda )\right\},$$

where a is some constant usually taken to be a = 3.7 (Fan & Li, 2001), and (t)₊ = tI{t > 0} is the hinge loss function. For a given tuning parameter, we denote the estimator obtained by minimising (2.2) by β̂_λ = (β̂_λ1, ⋯ , β̂_λd)′.

Fan & Li (2001) showed that if λ → 0 and $\sqrt{n}\lambda \to \infty$ as n → ∞, the method consistently identifies irrelevant variables by producing zero solutions for their associated regression coefficients. In addition, the method estimates the coefficients of the relevant variables with the same efficiency as if the true model were known, which is referred to as the oracle property (Fan & Li, 2001). Hence, the choice of λ is critical. In practice, λ is usually selected by minimising the generalised crossvalidation criterion

$${\mathrm{GCV}}_{\lambda }=\frac{{\parallel Y-X{\widehat{\beta }}_{\lambda }\parallel }^2}{n{(1-{\mathrm{DF}}_{\lambda }∕n)}^2}=\frac{{\widehat{\sigma }}_{\lambda }^2}{{(1-{\mathrm{DF}}_{\lambda }∕n)}^2,}$$ (2.3)

where ${\widehat{\sigma }}_{\lambda }^2=n^{-1}\Vert Y-X{\widehat{\beta }}_{\lambda }{\Vert }^2$, df_λ is the generalised degrees of freedom (Fan & Li, 2001) given by

$${\mathrm{DF}}_{\lambda }=\mathrm{tr}\left\{X{\left(X^{\prime }X+n{\Sigma }_{\lambda }\right)}^{-1}{X}^{\prime }\right\},$$

and ${\Sigma }_{\lambda }=\mathrm{diag}\{p_{\lambda }^{\prime }\left(\right|{\widehat{\beta }}_{\lambda 1}\left|\right)∕|{\widehat{\beta }}_{\lambda 1}|,\cdots ,p_{\lambda }^{\prime }\left(\right|{\widehat{\beta }}_{\lambda d}\left|\right)∕|{\widehat{\beta }}_{\lambda d}\left|\right\}$. The diagonal elements of Σ_λ are coefficients of quadratic terms in the local quadratic approximation to the smoothly clipped absolute deviation penalty function p_λ(·) (Fan & Li, 2001). Since some coefficients of the estimator of β are exactly equal to zero, df_λ is calculated by replacing X with its submatrix corresponding to the selected covariates, and by replacing Σ_λ with its corresponding submatrix. The resulting optimal tuning parameter is λ̂_gcv = argmin_λgcv_λ.

The log-transformation of gcv_λ can be approximated by

$$\log {\mathrm{GCV}}_{\lambda }=\log {\widehat{\sigma }}_{\lambda }^2-2\log (1-{\mathrm{DF}}_{\lambda }∕n)\bumpeq \log {\widehat{\sigma }}_{\lambda }^2+2{\mathrm{DF}}_{\lambda }∕n\triangleq {\mathrm{AIC}}_{\lambda }.$$

Hence, log gcv_λ is very similar to the traditional model selection criterion aic, which is an efficient selection criterion in that it selects the best finite-dimensional candidate model in terms of prediction accuracy when the true model is of infinite dimension. However, aic is not a consistent selection criterion, since it does not select the correct model with probability approaching 1 in large samples when the true model is of finite dimension. For further discussion of efficiency and consistency in model selection, see Shao (1997), McQuarrie & Tsai (1998) and Yang (2005). Consequently, the model selected by λ̂_gcv may not identify the finite-dimensional true model consistently. This motivated us to employ a variable selection criterion known to be consistent, bic (Schwarz, 1978), as the tuning parameter selector. We select the optimal λ by minimising

$${\mathrm{BIC}}_{\lambda }=\log {\widehat{\sigma }}_{\lambda }^2+{\mathrm{DF}}_{\lambda }\log \left(n\right)∕n.$$ (2.4)

The resulting optimal regularisation parameter is denoted by λ̂_bic.

3. Theoretical Results

3.1. Notation and conditions

Suppose that there is an integer 0 ≤ d₀ ≤ d, such that β_jk ≠ 0 for 1 ≤ k ≤ d₀, with the other β_j's equal to 0. Thus, the true model only contains the j₁th, ⋯ , j_d0th covariates as significant variables. Furthermore, in order to define the underfitted and overfitted models, we denote by 𝒮_F = {1, ⋯ , d} and 𝒮_T = {j₁, ⋯ , j_d0} the full and true parsimonious submodels, respectively. Then any candidate model 𝒮 ⊅ 𝒮_T, is referred to as an underfitted model in the sense that it misses at least one important variable. In contrast, any 𝒮 ⊃ 𝒮_T other than 𝒮_T itself, is referred to as an overfitted model in the sense that it contains all significant variables, but also at least one insignificant variable.

For an arbitrary model 𝒮 = {j₁, ⋯ , j_d*} ⊂ 𝒮_F, we denote its associated covariate matrix by X_𝒮, which is an n × d* matrix with the ith row given by (x_ij1, ⋯ , x_ijd*). After fitting the data with model 𝒮 by least squares, we denote the resulting ordinary least squares estimator, the residual sum of squares, the variance estimator and the generalised crossvalidation value by

$${\widehat{\beta }}_{𝒮}={\left(X_{𝒮}^{\prime }{X}_{𝒮}\right)}^{-1}\left(X_{𝒮}^{\prime }Y\right),$$ (3.1)

$${\mathrm{SSE}}_{𝒮}={\parallel Y-X_{𝒮}{\widehat{\beta }}_{𝒮}\parallel }^2,$$ (3.2)

$${\widehat{\sigma }}_{𝒮}^2={\mathrm{SSE}}_{𝒮}∕n,$$ (3.3)

$${\mathrm{GCV}}_{𝒮}=n^{-1}{\mathrm{SSE}}_{𝒮}∕{(1-d^{\ast }∕n)}^2,$$ (3.4)

respectively. The smoothly clipped absolute deviation estimator β̂_λ, obtained by minimising the objective function in (2.2), naturally identifies the model 𝒮_λ = {j : β̂_λj ≠ 0}, for which the ordinary least squares estimator is β̂_𝒮λ. By the definition of the ordinary least squares estimator, we have

$${\mathrm{SSE}}_{\lambda }={\parallel Y-X{\widehat{\beta }}_{\lambda }\parallel }^2\ge {\parallel Y-X_{𝒮\lambda }{\widehat{\beta }}_{𝒮\lambda }\parallel }^2={\mathrm{SSE}}_{{𝒮}_{\lambda }}.$$ (3.5)

Furthermore, the ${\widehat{\sigma }}_{\lambda }^2$ defined in (2.3) can be simply expressed as ${\widehat{\sigma }}_{\lambda }^2={\mathrm{SSE}}_{\lambda }∕n$. If λ = 0, then the penalty term in (2.2) is 0, and β̂₀, is exactly the same as the full-model's ordinary least squares estimator, β̂_𝒮F. Moreover, sse₀ = sse_𝒮F, ${\widehat{\sigma }}_0^2={\widehat{\sigma }}_{{𝒮}_F}^2$ and gcv₀ = gcv_𝒮F.

In practice, however, λ is unknown, and it is necessary to search for the optimal λ from the positive real line ℛ⁺, or, within the bounded interval Ω = [0, λ_max], for some upper limit λ_max. We now present the technical conditions that are needed for studying the theoretical properties of the tuning parameter selectors.

• Condition 1. For any 𝒮 ⊂ 𝒮_F, there is a ${\sigma }_{𝒮}^2>0$ such that ${\widehat{\sigma }}_{𝒮}^2\to {\sigma }_{𝒮}^2$ in probability.

• Condition 2. For any 𝒮 ⊅ 𝒮_T, we have ${\sigma }_{𝒮}^2>{\sigma }_{{𝒮}_T}^2$, where ${\sigma }_{{𝒮}_T}^2$ is a positive value such that ${\widehat{\sigma }}_{{𝒮}_T}^2\to {\sigma }_{{𝒮}_T}^2$, in probability.

• Condition 3. The ∊_i's are independent and identically distributed as $N(0,{\sigma }_{∊}^2)$.

• Condition 4. The upper limit λ_max → 0 as n → ∞.

• Condition 5. The matrix cov(x_i) = Σ_x is finite and positive definite.

Condition 1 facilitates the proof of the asymptotic results, while Condition 2 elucidates the underfitting effect. Both conditions are satisfied if (x_i, ∊_i) are jointly non-degenerate multivariate normal distribution. Similar conditions can be found in Shi & Tsai (2002, 2004) and Huang & Yang (2004). Condition 3 is needed only for evaluating generalised crossvalildation's overfitting effect in §3.2, and is not necessary for establishing the consistency of the proposed bic criterion. Condition 4 implies that the search region for λ shrinks towards 0 as the sample size goes to infinity. This condition is used to simplify the proof of the consistency of bic in §3.3. Note that the rate at which λ_max converges to 0 is not specified. Finally, Condition 5 ensures the root-n consistency of an unpenalised estimator.

3.2. The overfitting effect of generalised crossvalidation

We define Ω₋ = {λ ∈ Ω : 𝒮_λ ⊅ 𝒮_T}, Ω₀ = {λ ∈ Ω : 𝒮_λ = 𝒮_T}, and Ω₊ = {λ ∈ Ω : 𝒮_λ ⊃ 𝒮_T and 𝒮_λ ≠ 𝒮_T}. In other words, Ω₀, Ω₋ and Ω₊ are three subsets of Ω, in which the true, under, and overfitted models can be produced. We first show that the smoothly clipped absolute deviation method with generalised crossvalidation is conservative in the sense that it does not miss any important variables as long as the sample size is sufficiently large.

Lemma 1

Under Conditions 1 and 2, we have

$$\mathrm{pr}\left(\underset{\lambda ∊\Omega \_}{\inf }{\mathrm{GCV}}_{\lambda }>{\mathrm{GCV}}_{{𝒮}_F}={\mathrm{GCV}}_0\right)\to 1.$$

All proofs are given in the Appendix. According to this lemma, the generalised crossvalidation evaluated at the tuning parameter which produces the underfitted model, is consistently larger than ggv_𝒮F = gcv₀. As a result, the optimal model selected by minimising the generalised crossvalidation values, i.e., 𝒮_λ̂gcv, must contain all significant variables with probability tending to one. However, this does not necessarily imply that 𝒮_λ̂gcv is the true model 𝒮_T. In the next lemma, we show that the optimal model selected by generalised crossvalidation overfits the true model with a positive probability.

Lemma 2

Under Conditions 1—3 there exists a nonzero probability α > 0 such that lim inf_n pr(inf_λ∈Ω0 gcv_λ > gcv_𝒮F = gcv₀) ≥ α.

According to this lemma, there is a nonzero probability that the smallest value of generalised crossvalidation associated with the true model is larger than that of the full-model. Hence, there is a positive probability that any λ associated with the true model cannot be selected by generalised crossvalidation as the optimal tuning parameter. Combining the results from Lemmas 1 and 2, we obtain the following theorem.

Theorem 1

If Conditions 1—3 hold, there is a nonzero probability α > 0 such that pr(𝒮_λ̂gcv ⊃ 𝒮_T) → 1 and

$$\underset{n}{\mathrm{liminf}}\mathrm{pr}({𝒮}_{{\widehat{\lambda }}_{\mathrm{GCV}}}\supset {𝒮}_T\mathit{and}{𝒮}_{{\widehat{\lambda }}_{\mathrm{GCV}}}\ne {𝒮}_T)>\alpha .$$

Theorem 1 indicates that, with probability tending to 1, the model 𝒮_λ̂gcv contains all significant variables, but with nonzero probability includes superfluous variables, thereby leading to overfitting.

3.3. Consistency of bic

To establish the consistency of bic, we first construct a sequence of reference tuning parameters, ${\lambda }_n=\log \left(n\right)∕\sqrt{n}$. Thus, λ_n → 0 and $\sqrt{n}{\lambda }_n\to \infty$. According to Theorem 2 of Fan & Li (2001), pr(𝒮_λn = 𝒮_T) → 1 under appropriate regularity conditions. This implies that the model identified by the reference tuning parameter converges to the true model as the sample size gets large.

Lemma 3

Under Condition 5, pr(bic_λn = bic_𝒮T) → 1.

According to this lemma, with probability tending to 1,

$${\mathrm{BIC}}_{{\lambda }_n}={\mathrm{BIC}}_{{𝒮}_T}=\log {\widehat{\sigma }}_{{𝒮}_T}^2+d_0\log \left(n\right)∕n.$$

Applying this result, we finally show that, for any λ which cannot identify the true model, the bic value is consistently larger than bic_λn.

Lemma 4

Under Conditions 1, 2, 4 and 5,

$$\mathrm{pr}\left(\underset{\lambda ∊\Omega \_\cup {\Omega }_{+}}{\inf }{\mathrm{BIC}}_{\lambda }>{\mathrm{BIC}}_{{\lambda }_n}\right)\to 1.$$

Note that this lemma does not necessarily imply that λ_n = λ̂_bic. However, it does indicate that those λ's which fail to identify the true model cannot be selected by bic asymptotically, because at least the true model identified by λ_n is a better choice. As a result, the optimal value λ̂_bic can only be one of those λ's whose smoothly clipped absolute deviation estimator yields the true model, i.e., λ ∈ Ω₀. Hence, the subsequent theorem follows immediately.

Theorem 2

If Conditions 1, 2, 4, and 5 hold, pr(𝒮_λ̂bic = 𝒮_T) → 1.

In addition to generalised crossvalidation and bic, other selection criteria, such as aic and ric (Shi & Tsai, 2002) can be used to select the tuning parameter for the smoothly clipped absolute deviation method. Techniques similar to those used above show that aic performs like generalised crossvalidation, with a potential for overfitting, while ric consistently identifies the true model.

4. Partially Linear Model

In the context of partially linear models, Bunea (2004) and Bunea & Wegkamp (2004) proposed an information-type criterion and established a consistency property. Fan & Li (2004) extended their nonconvex penalised least squares method to partially linear models with longitudinal data, and showed that the resulting estimator performs as well as the oracle estimator. However, Fan & Li (2004) employed generalised crossvalidation for selecting the tuning parameter. In this section, we demonstrate that this results in overfitting. We further propose a bic approach and show that it can identify the true model consistently.

Consider the partially linear model

$$y_i=\alpha \left(u_i\right)+x_i^{\prime }\beta +{∊}_i,$$ (4.1)

where u_i is a covariate, α(u_i) is nonparametric smooth function of u_i, and the remainder of the notation is the same as that for model (2.1). Various estimation procedures have been proposed in the literature (Engle et al., 1986; Heckman, 1986; Robinson, 1988; Speckman, 1988), and a comprehensive survey for the partially linear model is given by Härdle et al. (2000).

Similar to (2.2), we propose

$$\frac{1}{2n}{\parallel Y-ϴ-X\beta \parallel }^2+\underset{j=1}{\overset{d}{\Sigma }}{p}_{\lambda }\left(\left|{\beta }_j\right|\right)$$ (4.2)

as a penalised least squares function for the partially linear model, where

$$ϴ={(\alpha \left(u_1\right),\cdots ,\alpha \left(u_n\right))}^{\prime },$$

the penalty function p_λ(|β_j|) is defined as in (2.2), and α(·) is a nonparametric smoothing function. To obtain the penalised least squares estimator, we first adopt Fan & Li's (2004) profile least squares technique to eliminate the nuisance parameter Θ for a given β. As a result, we have

$$y_i^{\ast }=\alpha \left(u_i\right)+{∊}_i,$$ (4.3)

where $y_i^{\ast }=y_i-x_i^{\prime }\beta$. We then use Fan & Gijbel's (1996) local linear regression approach to estimate α(·). For u in a neighbourhood of u_i, we find (α̂₀, α̂₁) by minimising

$$\underset{i=1}{\overset{n}{\Sigma }}{\{y_i^{\ast }-{\alpha }_0-\alpha (u_i-u)\}}^2{K}_h(u_i-u),$$

where K(·) is a kernel function, h is a bandwidth and K_h(·) = h⁻¹K(·/h). The local linear estimator at u is simply α̂(u; β) = α̂₀.

Since the local linear estimator is a linear smoother, Θ̂ has the closed-form expression

$$\widehat{ϴ}=S_h(Y-Y\beta ),$$ (4.4)

where S_h is the smoothing matrix corresponding to the local linear regression and depends only on u_i and K_h(·). Substituting Θ in (4.2) with Θ̂, we obtain the penalised profile least squares function

$$\frac{1}{2n}{\parallel (I-S_h)Y-(I-S_h)X\beta \parallel }^2+\underset{j=1}{\overset{d}{\Sigma }}{p}_{\lambda }\left(\left|{\beta }_j\right|\right),$$ (4.5)

where I is an n × n identity matrix. Under certain regularity conditions, Fan & Li (2004) established the oracle property for the penalised profile least squares estimator. Note that the profile least squares estimator of β is closely related to Speckman's (1988) partial residual estimator, which is obtained by minimising the first term of equation (4.5). In addition, Speckman (1988) used the kernel smoothing approach to estimate α, while we employed the local linear smoothing approach.

Based on (4.5), we define gcv_λ for the penalised profile least squares problem by substituting X and Y in (2.3) with X_h = (I − S_h)X and Y_h = (I − S_h)Y, respectively. Analogously, we define bic_λ by replacing X and Y in the calculation of ${\sigma }_{\lambda }^2$ in (2.4) with X_h and Y_h, respectively. Applying the selector gcv_λ or bic_λ, we are finally able to compute the SCAD estimator of β.

As shown in Fan & Li (2004), the penalised profile least squares estimator β̂_λ is root-n consistent provided that λ → 0 and $\sqrt{n}\lambda \to \infty$ as n → ∞. Under regularity conditions given in the Appendix, the asymptotic bias and variance of α̂(u) are of order O_p(h²) and O_p(1/nh), respectively, since the parametric convergence rate of β̂ is faster than the nonparametric convergence rate of α̂(u). Furthermore, it can be shown that

$$\underset{u\in \mathcal{U}}{\sup }|\widehat{\alpha }\left(u\right)-\alpha \left(u\right)|=O_P\left(n^{-1∕4}\right)$$

by using results in Mack & Silverman (1982), where 𝒰 is the support of u; see Fan & Huang (2005) for details. Thus, Conditions 1 and 2 are reasonable assumptions in the proofs of asymptotic properties of gcv and bic in partially linear models.

Applying Theorem 3.1 of Fan & Huang (2005), we have

$$n\left\{\frac{{\mathrm{SSE}}_{{𝒮}_T}-{\mathrm{SSE}}_{{𝒮}_F}}{{\mathrm{SSE}}_{{𝒮}_F}}\right\}\to {\chi }_{d-d_0}^2,$$

in distribution. This, together with the arguments used in the proofs of Lemmas 1 and 2, implies that Theorem 1 holds for penalised profile least squares with the smoothly clipped absolute deviation penalty. Theorem 3.1 of Fan & Huang (2005) also implies that

$${\mathrm{SSE}}_{S_T}-{\mathrm{SSE}}_{S_{\lambda }}\to {\chi }_{d_{\lambda }-d_0}^2$$

in distribution for any overfitted model 𝒮_λ(⊃ 𝒮_T) including d_λ variables. As a result, equation (A7) is valid for profile least squares estimators. Applying this result, in conjunction with the same arguments as those employed in the proofs of Lemmas 3 and 4, shows that Theorem 2 is true for penalised profile least squares with the smoothly clipped absolute deviation penalty.

Remark

To facilitate choosing the bandwidth h and the tuning parameter λ, we consider the β̂ to be a root-n consistent estimator of β. Thus, its convergence rate is faster than the nonparametric convergence rate of α̂(u). This motivates us to substitute β in the expression of $y_i^{\ast }$ with its root-n consistent estimator. By following the approach of Fan & Li (2004), we can show that the leading terms in the asymptotic bias and variance of the resulting local linear estimator α̂(u) are the same as those obtained by replacing β with its true value. This indicates that we are able to choose the bandwidth and tuning parameter separately, which expedites the computation of h and λ. To be specific, we adapt the approach of Fan & Li (2004) to obtain the difference-based estimator of β for the full-model, which is a root-n consistent estimator (Yatchew, 1997). Subsequently, we replace β in $y_i^{\ast }$ with the difference-based estimator so that (4.3) becomes a one-dimensional smoothing problem, and we use a smoothing selector to choose the bandwidth. Here, we use the plug-in method proposed by Ruppert et al. (1995) to choose the bandwidth, but this does not exclude the use of other known bandwidth selectors, such as generalised crossvalidation. Finally, we apply gcv_λ or bic_λ to choose λ.

5. Numerical Studies

5.1. Preliminaries

We examine the finite sample performance of the bic and generalised crossvalidation tuning parameter selectors in terms of both model error, i.e., lack-of-fit, and model complexity. However, we do not compare the smoothly clipped absolute deviation method with the best-subset variable selection bic since Fan & Li (2001, 2004) have compared them by Monte Carlo. To facilitate the computational process, we directly applied the local quadratic approximation algorithm to search the smoothly clipped absolute deviation solution. We set the threshold for shrinking β̂_j to zero at 10⁻⁶, which is much smaller than half of the standard error of the unpenalised least squares estimator, the threshold used in Fan & Li (2001). Thus, the average number of zeros using the generalised crossvalidation tuning parameter selector is expected to be slightly smaller than that in Fan & Li (2001). All simulations were conducted using Matlab code, which is available from the authors.

5.2. Simulation studies

We first consider Fan & Li's (2001) model error measure. Let (u,x,y) be a new observation from a regression model with E(y|u,x) = μ(u,x), and let μ̂ (·,·) be an estimate of the regression function based on data {(u_i,x_i,y_i), i = 1,…, n}. Then model error is defined to be E{μ̂(u,x) − μ(u,x)}², where the expectation is the conditional expectation given the data used in caluclating μ̂(·,·). For a partially linear model, μ(u,x) = α(u) + x′β, the model error is

$$E{\{\widehat{\alpha }\left(u\right)-\alpha \left(u\right)\}}^2+E{(x^{\prime }\widehat{\beta }-x^{\prime }\beta )}^2+2E\{\widehat{\alpha }\left(u\right)-\alpha \left(u\right)\}(x^{\prime }\widehat{\beta }-x^{\prime }\beta ),$$ (5.1)

The first term in (5.1) measures the nonparametric component fit, while the second term assesses the parametric component fit. To investigate the performance of the smoothly clipped absolute deviation method on the just parametric regression component, we chose the simulation setting so that the cross-product term in (5.1) equals 0. Note that for the linear regression model (2.1), the model error exactly equals E(x′β̂ − x′β)². To compare the generalised crossvalidation and bic approaches, we define the model error as

$$\mathrm{ME}\left(\widehat{\beta }\right)=E{(x^{\prime }\widehat{\beta }-x^{\prime }\beta )}^2={(\widehat{\beta }-\beta )}^{\prime }E\left({\mathit{xx}}^{\prime }\right)(\widehat{\beta }-\beta ),$$

and define the relative model error as RME = ME/ME_SF, where ME_SF is the model error obtained by fitting the data with the full-model S_F in conjunction with the unpenalised least squares estimator, β̂_𝒮F.

In addition to model error, we also calculate the percentages of models correctly fitted, underfitted and overfitted by generalised crossvalidation and bic, and the average number of zero coefficients produced by the smoothly clipped absolute deviation method.

Example 1

We simulated 1000 datasets, each consisting of a random sample of size n, from the linear regression model

$$y=x^{\prime }\beta +{\sigma }_{∊}∊,$$

where β = (3,1.5,0,0,2,0,0,0)′, ∊ ∼ N(0,1) and the 8 × 1 vector x ∼ N₈(0, Σ_x), in which (Σ_x)ij = ρ^|i–j| for all i and j. Values chosen were σ_∊ = 3 and 1, n = 50, 100 and 200, and ρ = 0.75, 0.5 and 0.25.

As a benchmark, we compute the oracle estimator, which is the least squares estimator, of the true submodel, y = β₁x1 + β₂x₂ + β₅x₅ + ∊. Since the pattern of the results is the same for all three correlations, we only present the results for ρ= 0.5. Table 1 indicates that median of RME over 1000 realisations of the bic approach rapidly approaches that of the oracle estimator as the sample size increases or the noise level decreases, whereas the value for the generalised crossvalidation method remains at almost the same level across different noise levels and sample sizes. Hence, the bic approach outperforms the generalised crossvalidation approach in terms of model error measure.

Table 1.

Example 1. Simulation results for the linear regression model

σε	n	Method	Underfitted(%)	Correctly fitted(%)	Overfitted(%)			No. of Zeros		MRME (%)
					1	2	≥ 3	I	C
3	50	λ̂gcv	6.4	16.9	23.0	31.6	22.1	0.064	3.279	64.17
		λ̂bic	10.1	30.0	31.1	20.5	8.3	0.101	3.899	62.30
		Oracle	0	100	0	0	0	0	5	30.63
	100	λ̂gcv	0.2	24.0	20.4	29.8	25.6	0 02	3.369	57.72
		λ̂bic	1.0	52.5	27.0	14.6	4.9	0.100	4.275	50.43
		Oracle	0	100	0	0	0	0	5	33.05
	200	λ̂gcv	0	25.4	35.8	25.4	13.4	0	3.300	55.18
		λ̂bic	0	72.7	21.9	4.5	0.9	0	4.528	42.12
		Oracle	0	100	0	0	0	0	5	34.45
1	50	λ̂gcv	0	17.1	24.5	33.2	25.2	0	3.272	55.64
		λ̂bic	0	45.6	23.9	21.1	9.4	0	4.042	40.97
		Oracle	0	100	0	0	0	0	5	30.62
	100	λ̂gcv	0	19.0	24.5	31.8	24.7	0	3.324	55.91
		λ̂bic	0	54.9	23.6	16.9	4.6	0	4.277	40.53
		Oracle	0	100	0	0	0	0	5	33.05
	200	λ̂gcv	0	48.1	37.5	11.7	2.7	0	3.302	55.00
		λ̂bic	0	81.8	16.4	1.3	0.5	0	4.405	38.36
		Oracle	0	100	0	0	0	0	5	34.42

I, the average number of the three truly nonzero coefficients incorrectly set to zero; C, the average number of the five true zero coefficients that were correctly set to zero; MRME, median of relative model error.

The column labelled ‘C’ in Table 1 denotes the average number of the five true zero coefficients that were correctly set to zero, and the column labeled ‘I’ denotes the average number of the three truly nonzero coefficients incorrectly set to zero. Table 1 also reports the proportions of models underfitted, correctly fitted and overfitted. In the case of overfitting, the columns labelled ‘1’, ‘2’ and ‘≥3’ are the proportions of models including 1, 2 and more than 2 irrelevant covariates, respectively. It shows that the bic method has a much better rate of correctly identifying the true submodel than does the generalised crossvalidation method. Furthermore, among the overfitted models, the bic method is likely to include just one irrelevant variable, whereas the generalised crossvalidation approach often includes two or more. Not surprisingly, both methods improve as the signal gets stronger, i.e., σ_∊ decreases from 3 to 1. However, the generalised crossvalidation method still seriously overfits even if σ_∊ = 1 and n = 200. In contrast, the bic method overfits less often. These results corroborate the theoretical findings.

Example 2

In this example, we considered the partially linear model,

$$y=\alpha \left(u\right)+x^{\prime }\beta +{\sigma }_{∊}∊,$$

where u ∼ Un(0,1), and α(u) = exp{2sin(2πu)}. The rest of the simulation settings are the same as in Example 1. As mentioned in the remark of §4, in each simulation, we replace β in $y_i^{\ast }$ with the difference-based estimator, and then use the plug-in method proposed by Ruppert et al. (1995) to choose a bandwidth. Table 2 presents the simulation results for ρ = 0.5, and shows that once more, the bic method out-performs the generalised crossvalidation method in both identifying the true model and in reducing the model error and complexity.

Table 2.

Example 2. Simulation results for the partially linear regression model

σε	n	Method	Underfitted(%)	Correctly fitted(%)	Overfitted(%)			No. of Zeros		MRME (%)
					1	2	≥ 3	I	C
3	50	λ̂gcv	10.9	15.9	24.6	25.8	22.8	0.112	3.263	66.78
		λ̂bic	15.5	29.3	29.3	18.4	7.5	0.160	3.929	67.04
		Oracle	0	100	0	0	0	0	5	29.29
	100	λ̂gcv	0.8	23.1	22.6	29.7	23.8	0 08	3.368	58.15
		λ̂bic	1.9	51.8	29.4	13.1	3.8	0 19	4.301	52.10
	100	Oracle	0	100	0	0	0	0	5	33.58
	200	λ̂gcv	0	22.9	21.5	30.5	25.1	0	3.352	54.47
		λ̂bic	0	70.0	16.7	10.9	2.4	0	4.540	43.34
		Oracle	0	100	0	0	0	0	5	34.50
1	50	λ̂gcv	0	26.0	25.7	31.0	17.3	0	3.567	51.93
		λ̂bic	0.1	60.3	20.6	13.9	5.1	0 01	4.356	38.31
		Oracle	0	100	0	0	0	0	5	29.30
	100	λ̂gcv	0	26.3	27.5	27.5	18.7	0	3.567	50.90
		λ̂bic	0	67.9	18.9	9.9	3.3	0	4.509	39.10
		Oracle	0	100	0	0	0	0	5	33.42
	200	λ̂gcv	0	26.5	26.9	28.9	17.7	0	3.582	49.24
		λ̂bic	0	75.7	15.7	7.2	1.4	0	4.656	39.01
		Oracle	0	100	0	0	0	0	5	34.77

I, the average number of the three truly nonzero coefficients incorrectly set to zero; C, the average number of the five true zero coefficients that were correctly set to zero; MRME, median of relative model error.

5.3. Real data examples

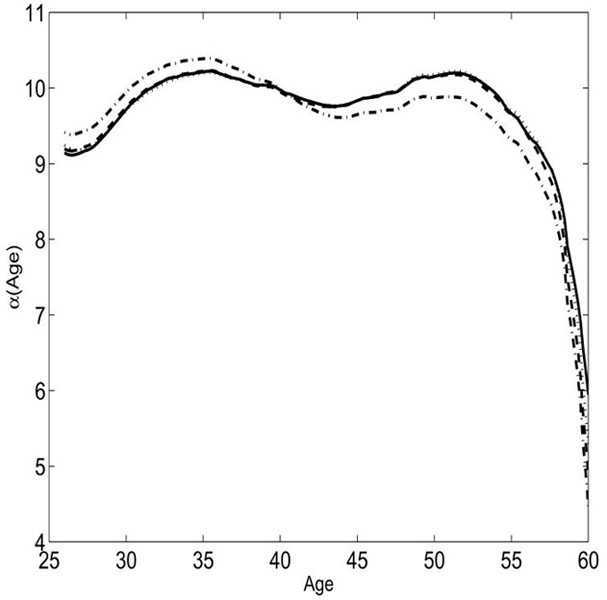
Example 3

We consider the Female Labour Supply data collected in East Germany in about 1994. The dataset consists of 607 observations and has been analysed by Fan et al. (1998) using additive models. Here we take the response variable y to be the ‘wage per hour’. The u-variable in the partially linear model is the ‘woman's age’; this is because the relationship between y and u cannot be characterised by a simple functional form; see Fig. 1. There are seven explanatory variables: x₁ is the weekly number of working hours; x₂ is the ‘Treiman prestige index’ of the woman's job; x₃ is the monthly net income of the woman's husband; x₄ = 1 if the years of the woman's education is between 13 and 16, and x₄ = 0 otherwise; x₅ = 1 if the years of the woman's education is not less than 17, and x₅ = 0 otherwise; x₆ = 1 if the woman has children less than 16-years-old, and x₆ = 0 otherwise; and x₇ is the unemployment rate in the place where she lives. After some preliminary analysis, we consider the following partially linear model with seven linear main effects and some first-order interaction effects among x₁, x₂ and x₃:

$$y=\alpha \left(u\right)+\underset{j=1}{\overset{7}{\Sigma }}{\beta }_j{x}_j+\underset{k=1}{\overset{3}{\Sigma }}\underset{l=k}{\overset{3}{\Sigma }}{\beta }_{\mathit{kl}}{x}_k{x}_l+∊.$$

Here the x-variables have been standardised.

Fig. 1.

Female Labour Study data. The plot of α̂(u). The solid curve is α̂(·) based on the penalised profile least squares with λ̂_bic, the dashed curve is α̂(·) based on the penalised profile least squares with λ̂_gcv, the dotted curve is α̂(·) obtained by smoothing partial residuals with the bic best-subset selection, over u_i, and the dash-dotted curve is α̂(·) based on the unpenalised full-model profile least squares estimate.

Following Fan & Li's (2004) approach, we first calculate the difference-based estimator for β, and then apply the plug-in method to select 4.6249 as a bandwidth for α̂(·). With this bandwidth, we next choose the tuning parameters by minimising the generalised crossvalidation and bic scores, resulting in λ̂_gcv = 0.0896 and λ̂_bic = 0.2655. Subsequently, we obtain the unpenalised profile least squares estimate (Fan & Li, 2004) and the smoothly clipped absolute deviation estimate based on generalised crossvalidation and bic, together with their standard errors (Table 3). We also consider the model selected by the unpenalised full-model profile least squares method, i.e., equation (4.5) without the penalty term, and the best-subset variable selection criterion, $\mathrm{BIC}=\log {\widehat{\sigma }}_h^2+d^{\ast }\log \left(n\right)∕n$, where ${\widehat{\sigma }}_h^2={\mathrm{SSE}}_{\mathit{hs}}∕n$, sse_hs is the sum of squares of the errors by fitting Y_h versus X_hs = (I – S_h)X_𝒮, and d* is the dimension of X_𝒮. The first four columns of Table 3 clearly show that the unpenalised full-model profile least squares approach fits spurious variables, while the smoothly clipped absolute deviation method based on gcv tends to include variables with small, insignificant effects. In contrast, all variables selected by the smoothly clipped absolute deviation method based on bic are significant at level 0.05. Fig. 1 shows that the four estimates of α(·) are fairly similar, but that the estimate from the unpenalised full-model profile least squares approach is slightly different from the others. Moreover, the resulting intercept function changes with age with no particular functional form.

Table 3.

Female Labour Supply data. Estimated coefficients and their standard errors.

Variable	Profile LSE	SCAD λ̂gcv	SCAD λ̂bic	Best-subset BIC	Best-subset BIC(n=602)
x1	1.244(0.637)	1.281(0.636)	1.872(0.562)	1.343(0.496)	0
$x_1^2$	−1.451(0.563)	−1.446(0.559)	−1.841(0.517)	−2.192(0.497)	−0.853(0.119)
x2	1.520(0.721)	1.602(0.704)	1.357(0.681)	0	0
$x_2^2$	1.162(0.617)	1.281(0.599)	1.341(0.601)	1.433(0.136)	1.410(0.137)
x3	−1.229(0.692)	−1.063(0.549)	0	0	0
$x_3^2$	−0.011(0.276)	0	0	0	0
x1x2	−1.781(0.702)	−1.885(0.684)	−1.493(0.653)	0	0
x1x3	0.922(0.559)	0.995(0.549)	0	0	0
x2x3	0.313(0.485)	0	0	0	0
x4	0.609(0.130)	0.593(0.130)	0.249(0.055)	0.605(0.129)	0.590(0.129)
x5	1.194(0.140)	1.183(0.140)	1.030(0.131)	1.168(0.138)	1.172(0.139)
x6	−0.290(0.189)	−0.028(0.019)	0	0	0
x7	0.118(0.117)	0.005(0.006)	0	0	0

LSE, least squares estimate

SCAD, smoothly clipped absolute deviation

The fourth column of Table 3 shows that the best-subset variable selection with the bic criterion yields a simpler model than that from the smoothly clipped absolute deviation method based on bic. However, Breiman (1996) found that the best-subset method suffers from a lack of stability. To demonstrate this point, we exclude the last 5 observations, so leaving a dataset with n = 602. The last column of Table 3 shows that the best-subset variable selection with bic criterion yields a different model from that with n = 607, which corroborates Breiman's finding. The model based on the smoothly clipped absolute deviation method with bic turns out to be unchanged, although details are not given.

We conclude that the best model in this study is that selected by the smoothly clipped absolute deviation method with bic:

$$\widehat{y}=\widehat{\alpha }\left(u\right)+{\widehat{\beta }}_1{x}_1+{\widehat{\beta }}_2{x}_2+{\widehat{\beta }}_{11}{x}_1^2+{\widehat{\beta }}_{12}{x}_1{x}_2+{\widehat{\beta }}_{22}{x}_2^2+{\widehat{\beta }}_4{x}_4+{\widehat{\beta }}_5{x}_5.$$

Hence, the hourly wage of a woman depends primarily on working hours, job prestige and years of education, while the husband's income, the local unemployment rate and the indicator of whether or not the woman has a young child seem not to affect the hourly wage significantly. Fig. 1 indicates that the hourly wage is almost constant before the age of 50, but decreases rapidly thereafter.

6. Discussion

One could extend the current work by adapting Fan & Li's (2001) approach to define the penalised likelihood function for the generalised linear model by replacing the first term of equation (2.2) with twice the negative of the corresponding loglikelihood function. Subsequently, one could explore the overfitting effect of generalised crossvalidation and the consistency of bic. It is also of interest to compare the generalised crossvalidation approach to the bic method for semiparametric models and single-index models. Research along these lines is currently under investigation.

Appendix

Proofs

Proof of Lemma 1

When λ = 0, we have df₀ = d and gcv₀ = gcv_𝒮F in (2.3). Then, applying Condition 1 together with 2log(1 – d/n) = O(n⁻ⁿ), we obtain

$$\log {\mathrm{GCV}}_{{𝒮}_F}=\log \left(\frac{{\mathrm{SSE}}_{{𝒮}_F}}{n}\right)-2\log \left(1-\frac{d}{n}\right)=\log {\widehat{\sigma }}_{{𝒮}_F}^2+O\left(n^{-1}\right).$$ (A1)

According to (3.5), sseλ ≥ sse_𝒮λ, which leads to

$$\log {\mathrm{GCV}}_{\lambda }\ge \log \left(\frac{1}{n}{\mathrm{SSE}}_{\lambda }\right)\ge \log \left(\frac{1}{n}{\mathrm{SSE}}_{{𝒮}_{\lambda }}\right)=\log {\widehat{\sigma }}_{{𝒮}_{\lambda }}^2.$$

As a result,

$$\underset{\lambda ∊\Omega \_}{\inf }\log {\mathrm{GCV}}_{\lambda }\ge \underset{𝒮\not\supset {𝒮}_T}{\min }\log {\stackrel{-}{\sigma }}_{𝒮}^2.$$ (A2)

In addition, Condition 2 implies that ${\sigma }_{𝒮}^2>{\sigma }_{{𝒮}_F}^2={\sigma }_{∊}^2$ for 𝒮 ⊅ 𝒮_T. Hence, ${\min }_{𝒮\not\supset {𝒮}_T}\log {\sigma }_{𝒮}^2>\log {\sigma }_{{𝒮}_F}^2$. This result, in conjunction with Conditions 1 and 2 and equations (A1), and (A2), yields

$$\mathrm{pr}\left(\underset{\lambda ∊\Omega \_}{\inf }\log {\mathrm{GCV}}_{\lambda }>\log {\mathrm{GCV}}_{{𝒮}_F}\right)\to 1$$

as n → ∞, and the proof is complete.

Proof of Lemma 2

For any λ ∈ Ω₀, we have 𝒮_λ = 𝒮_T. Hence, gcv_λ > (1/n)sse_𝒮λ = (1/n)sse_𝒮TT. This, together with the fact (1 − d/n)⁻² = 1 + 2d/n + O(n⁻²), leads to

$$\begin{array}{cc}\hfill \mathrm{pr}\left(\underset{\lambda ∊{\Omega }_0}{\inf }{\mathrm{GCV}}_{\lambda }>{\mathrm{GCV}}_{{𝒮}_F}\right)& \ge \mathrm{pr}\left\{\frac{{\mathrm{SSE}}_{{𝒮}_T}}{n}>\frac{{\mathrm{SSE}}_{{𝒮}_F}}{n{(1-d∕n)}^2}\right\}\hfill \\ \hfill & =\mathrm{pr}\left\{\frac{{\mathrm{SSE}}_{{𝒮}_T}-{\mathrm{SSE}}_{{𝒮}_F}}{{\widehat{\sigma }}_{{𝒮}_F}^2}>2d+O\left(n^{-1}\right)\right\}\hfill \end{array}$$ (A3)

since ${\widehat{\sigma }}_{{𝒮}_F}^2={\mathrm{SSE}}_{{𝒮}_F}∕n$. According to Conditions 1 and 2, we have that ${\widehat{\sigma }}_{{𝒮}_F}^2\to {\sigma }_{{𝒮}_F}^2={\sigma }_{∊}^2$ in probability. Furthermore, under Condition 3, $({\mathrm{SSE}}_{{𝒮}_T}-{\mathrm{SSE}}_{{𝒮}_F})∕{\sigma }_{∊}^2$ follows a ${\chi }_{d-d_0}^2$ distribution. As a result,

$$\begin{array}{cc}\hfill \mathrm{pr}\left(\underset{\lambda ∊{\Omega }_0}{\inf }{\mathrm{GCV}}_{\lambda }>{\mathrm{GCV}}_{{𝒮}_F}\right)& \ge \mathrm{pr}\left[{\chi }_{d-d_0}^2\{1+o_p\left(1\right)\}>+O\left(n^{-1}\right)\right]\hfill \\ \hfill & \to \mathrm{pr}({\chi }_{d-d_0}^2>2d)\triangleq \alpha .\hfill \end{array}$$

This completes the proof.

Proof of Lemma 3

Let β_𝒮 = (β_j1, ⋯ , β_jd0)′ be the vector of relevant coefficients, and let β_N consist of irrelevant coefficients. Without loss of generality, we assume that β_𝒮 = (β₁, ⋯ , β_d0)′, and β_N = (β_d0+1, ⋯ , β_d)′. In addition, let β̂_λn = (β̂′_Sλn, β̂′_Nλn)′, where β̂′_Sλn and β̂′_Nλn are the smoothly clipped absolute deviation estimators of β′_S and β′_N, respectively. Under Condition 5, we apply Theorem 2 of Fan & Li (2001) to obtain that, with probability tending to 1, β̂_Sλn satisfies

$$\frac{1}{n}{X}_{{𝒮}_T}^{\prime }(Y-X_{{𝒮}_T}{\widehat{\beta }}_{S{\lambda }_n})+b_n\left({\widehat{\beta }}_{S{\lambda }_n}\right)=0,$$ (A3)

where b_n(β_S) = (p′_λn(|β₁|)sign(β₁), ⋯ ,p′_λn(|β_d0|)sign(β_d0))′. According to Theorem 1 of Fan & Li (2001), β̂_Sλn → β_S ≠ 0 in probability. In addition, because ${\lambda }_n=\log \left(n\right)∕\sqrt{n}$, we have aλ_n → 0. As a result, pr(|β̂_Sλn| > aλ_n) → 1, which implies that pr{b_n(β̂_Sλn) = 0} → 1. This, together with (A4), implies that, with probability tending to 1, the normal equation (A4) is exactly the same as

$$\frac{1}{n}{X}_{{𝒮}_T}^{\prime }(Y-X_{{𝒮}_T}{\widehat{\beta }}_{S{\lambda }_n})=0,$$

which is the normal equation for the ordinary least squares estimator based on the true model. As a result, with probability tending to 1, the smoothly clipped absolute deviation estimator β̂_Sλn is exactly the same as β̂_𝒮T = (X′_𝒮TX_𝒮T)⁻¹ (X_𝒮TY), the first d₀ elements of the oracle estimator. It follows immediately that pr(sse_λn = sse_𝒮T) → 1, since, with probability tending to one, β̂_Nλn = 0 by the sparsity in Theorem 2 of Fan & Li (2001). Using similar arguments, we can show that, with probability tending to one, the non-vanished diagonal elements of Σ_λn converge to zero, which implies that pr(df_λn = d₀) → 1. As a result, with probability tending to one, we have bic_λ = bic_𝒮T. This completes the proof.

Proof of Lemma 4

For 𝒮_λ ≠ 𝒮_T, i.e., λ ∈ Ω_ U Ω₊, we can identify two different cases, i.e. underfitting or overfitting. In each case, we show that Lemma 4 holds as given below.

Case 1: Underfitted model, i.e. 𝒮_λ ⊅ 𝒮_T

Applying Lemma 3 and Condition 1, we first have that

$${\mathrm{BIC}}_{{\lambda }_n}=\log {\widehat{\sigma }}_{{𝒮}_T}^2+d_0\log \left(n\right)∕n\to \log \left({\sigma }_{{𝒮}_T}^2\right)=\log \left({\sigma }_{∊}^2\right),$$ (A5)

in probability. It follows by the fact of 𝒮_λ ⊅ 𝒮_T and Conditions 1 and 2 that

$$\begin{array}{cc}\hfill {\mathrm{BIC}}_{\lambda }=\log \left(\frac{1}{n}{\mathrm{SSE}}_{\lambda }\right)& +{\mathrm{DF}}_{\lambda }\frac{\log \left(n\right)}{n}\ge \log \left\{\frac{1}{n}{\mathrm{SSE}}_{{𝒮}_{\lambda }}\right\}\hfill \\ \hfill \ge \underset{\{𝒮:𝒮\not\supset {𝒮}_T\}}{\min }\log {\widehat{\sigma }}_{𝒮}^2& \to \underset{\{𝒮:𝒮\not\supset {𝒮}_T\}}{\min }\log {\widehat{\sigma }}_{𝒮}^2>\log {\sigma }_{∊}^2,\hfill \end{array}$$ (A6)

in probability. Finally, (A5) and (A6) imply that pr{inf_{λ∈Ω_} bicλ > bic_λn} → 1.

Case 2: Overfitted model, i.e. 𝒮_λ ⊃ 𝒮_T, but 𝒮_λ ≠ 𝒮_T

According to Condition 1, ${\widehat{\sigma }}_{{𝒮}_T}^2{\to }_p{\sigma }_{{𝒮}_T}^2={\sigma }_{∊}^2>0$. Next, let d_λ be the number of variables included in the model 𝒮_λ. Then, for the overfitted model, d_λ > d₀. Moreover, using the theory of the sum of squares decomposition, we can easily show that $({\mathrm{SSE}}_{{𝒮}_T}-{\mathrm{SSE}}_{{𝒮}_{\lambda }})∕{\sigma }_{∊}^2\to {\chi }_{d_{\lambda }-d_0}^2$ in distribution as n → ∞. Under the normality assumption, Condition 3, this is also true for a finite sample. Thus, for any overfitted model 𝒮,

$${\mathrm{SSE}}_{{𝒮}_T}-{\mathrm{SSE}}_{𝒮}=O_p\left(1\right).$$ (A7)

This, together with Lemma 3 and the definition of bic_λ, implies that, with probability tending to 1,

$$\begin{array}{cc}\hfill n\left({\mathrm{BIC}}_{\lambda }-{\mathrm{BIC}}_{{\lambda }_n}\right)& \ge n\log \left(\frac{{\mathrm{SSE}}_{{𝒮}_{\lambda }}}{{\mathrm{SSE}}_{{𝒮}_T}}\right)+({\mathrm{DF}}_{\lambda }-d_0)\log n\hfill \\ \hfill & =\{{\widehat{\sigma }}_{{𝒮}_T}^{-2}({\mathrm{SSE}}_{{𝒮}_{\lambda }}-{\mathrm{SSE}}_{{𝒮}_T})+O_p\left(1\right)\}+\{d_{\lambda }+O_p\left(\lambda \right)-d_0\}\log n,\hfill \end{array}$$

where the last equality follows because df_λ = d_λ + o_p(λ) by Conditions 4 and 5. Thus,

$$\underset{\lambda \in {\Omega }_{+}}{\inf }n\left({\mathrm{BIC}}_{\lambda }-{\mathrm{BIC}}_{{\lambda }_n}\right)\ge {\widehat{\sigma }}_{{𝒮}_T}^2\underset{\{𝒮\supset {𝒮}_T\}}{\min }\left({\mathrm{SSE}}_{𝒮}-{\mathrm{SSE}}_{{𝒮}_T}\right)+\left\{1+O_p\left(\lambda \right)\right\}\log n+O_p\left(1\right).$$ (A8)

It follows from (A7) that

$$\underset{\{𝒮:𝒮\supset {𝒮}_T\}}{\min }\left({\mathrm{SSE}}_{𝒮}-{\mathrm{SSE}}_{{𝒮}_T}\right)=O_p\left(1\right).$$

This, together with the fact ${\widehat{\sigma }}_{{𝒮}_T}^2\to {\sigma }_{{𝒮}_T}^2$ in probability, the right-hand side of (A8) diverges to +∞ as n → ∞, which implies that

$$\mathrm{pr}\left\{\underset{\lambda \in {\Omega }_{+}}{\inf }n\left({\mathrm{BIC}}_{\lambda }-{\mathrm{BIC}}_{{\lambda }_n}\right)>0\right\}=\mathrm{pr}\left(\underset{\lambda \in {\Omega }_{+}}{\inf }{\mathrm{BIC}}_{\lambda }>{\mathrm{BIC}}_{{\lambda }_n}\right)\to 1.$$

The results of Cases 1 and 2 complete the proof.

Regularity Conditions for Partially Linear Model

Suppose that {(u_i, x_i, y_i), i = 1, ⋯ , n}, is a random sample from (4.1). The following regularity conditions are imposed to facilitate the technical proofs:

• (i) the kernel function is a symmetric density function with compact support;

• (ii) the random variable u₁ has a bounded support 𝒰, and its density function f(·) is Lipschitz continuous and bounded away from 0 on its support;

• (iii) the function α(·) has a continuous second-order derivative for u ∈ 𝒰;

• (iv) the conditional expectation E(x₁|u₁ = u) is Lipschitz continuous for u ∈ 𝒰;

• (v) there is an s > 1 such that E∥x₁∥^2s < ∞ and for some η < 2 − s^-1 such that n^2η−1h → ∞;

• (vi) the bandwidth h = O_P(n^−1/5).