Protein folding, protein collapse and Tanford’s transfer model: Lessons from single-molecule FRET

Abstract

The essential and non-trivial role of the denatured state of proteins in their folding reaction is being increasingly scrutinized in recent years. Single molecule FRET (smFRET) experiments show that the denatured state undergoes a continuous collapse (or coil-to-globule) transition as the concentration of a chemical denaturant is decreased, suggesting that conformational entropy of the denatured state is an important part of the free energy of folding. Such observations question the validity of the classical Tanford transfer model, which suggests that the folding free energy can be understood solely based on the difference in amino acid solvation between the folded state and a fixed unfolded state. An alternative to the transfer model is obtained here from a polymer theoretical analysis of a series of published smFRET data. The analysis shows that the free energy of denatured-state collapse has a linear dependence on denaturant concentration, an outcome of the interplay between enthalpic and entropic contributions. Surprisingly, the slope of the free energy of collapse agrees very well with the respective slope of the free energy of folding. This conformity of values obtained from two very different measurements shows that it is the collapse transition in the denatured state which mediates the effect of denaturants on folding. The energetics of folding are thus governed by the competition of solvation and conformational entropy in the denatured state.

Ever since the seminal work of Anfinsen ¹, it is known that protein molecules can spontaneously fold into their native form. Thus, under native conditions, the folded state (N) is thermodynamically favored over the denatured (or unfolded) state (U), i.e. the free energy of folding ( $\mathrm{\Delta }{G}_{U\to N}^0$) is negative. For typical proteins $\mathrm{\Delta }{G}_{U\to N}^0$ is about 5–15 kcal/mol ². This marginal stability seems to be important for enzymatic catalysis ³, as well as other biological processes such as protein degradation ⁴. It also affects the probability for misfolding and aggregation ⁵, which are the cause of amyloidal diseases such as Alzheimer and Creutzfeldt-Jakob disease. It is therefore of great interest to understand the properties of proteins affecting their stability under various biologically relevant conditions, and to get a measure, even if indirect, of $\mathrm{\Delta }{G}_{U\to N}^0$.

Chemical denaturants such as urea or guanidinium chloride (GdmCl) have been traditionally used to study protein stability and denaturation. They disrupt the native structure of proteins, although the microscopic mechanism by which this is achieved remains a matter of some controversy ^6–12. By gradually increasing the concentration of a denaturant while observing a spectroscopic signature such as tryptophan fluorescence or circular dichroism, one can follow the complete process of protein denaturation. For small proteins (typically less than 100 amino acids) the ensuing "denaturation curve" is fitted well with a model having only two states ¹³. The free energy of folding between two denaturant concentrations D and D′ can be extracted from this analysis, and is often found to depend linearly on the molar concentration of denaturant ^14,15:

$$\mathrm{\Delta }{G}_{U\to N}-\mathrm{\Delta }{G}_{U^{\prime }\to N^{\prime }}=-m·(D^{\prime }-D)$$ [1]

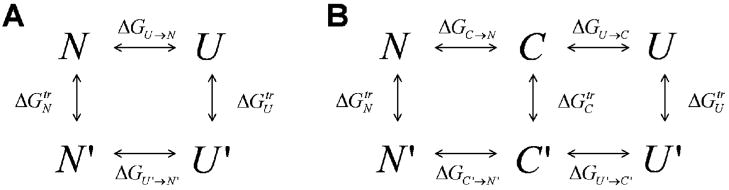
where m is the slope of this linear relation, and primes denote quantities at D′. Extrapolating Equation 1 to D = 0, one obtains a measure for the protein stability $\mathrm{\Delta }{G}_{U\to N}^0$. The m-value is related to the steepness or cooperativity of the folding transition. Despite its obvious importance in many aspects of protein chemistry, the physical interpretation of this m-value is not entirely clear. The well-known transfer model (TM), suggested originally by Tanford ^14,16 almost 50 years ago, relates the change in ΔG_U→N to the transfer free energy of the native and unfolded states ( $\mathrm{\Delta }{G}_N^{tr}$ and $\mathrm{\Delta }{G}_U^{tr}$, respectively), using the thermodynamic cycle in scheme 1A. Tanford’s TM model, which assumes that the transfer free energy involves only changes in solvation of amino acid residues, can be written approximately as:

$$\mathrm{\Delta }{G}_{U\to N}-\mathrm{\Delta }{G}_{U^{\prime }\to N^{\prime }}=\mathrm{\Delta }{G}_N^{tr}-\mathrm{\Delta }{G}_U^{tr}=n\overline{\delta \alpha }\overline{\delta g}(D^{\prime }-D)$$ [2]

Scheme 1.

Thermodynamic cycles for unfolding. A. The well-known thermodynamic cycle relating two states, native (N) and unfolded (U), at two denaturant concentrations D (top) and D′ (bottom). We use the notation U and U′ for the unfolded state at the two concentrations, to stress that in fact a different ensemble of conformations is sampled in each. Thus, the transfer energy $\mathrm{\Delta }{G}_U^{tr}$ is composed of the enthalpy of transfer and the change in the conformational entropy of the unfolded state ensemble. B. For the calculation of the free energy of collapse, we introduce a new reference state, which is designated the maximally compact denatured state (C). Notice that in general this state does not equal the unfolded state at zero D.

Equation 2 relates the transfer free energy of folding to the average transfer free energy of the amino acid residues of the protein from water to 1M denaturant solution ( $\overline{\delta g}$), and the average change in (fractional) solvent accessible surface area (SASA) between the folded state and the unfolded state ( $\overline{\delta \alpha }$). n is the number of amino acids in the protein. This equation provided a route for obtaining a theoretical estimate for the m-value of a protein, which has been exploited by several authors over the years. The calculation of SASA for the folded state is straight forward from available crystal structures. On the other hand, it is not trivial to decide what SASA should be used to represent the ensemble of conformations we refer to as the unfolded state. Myers et al. assumed an extended β-conformation for the unfolded state ¹⁷, while Auton et al. used the mean SASA of two conformations for the unfolded state – an extended conformation and a more “compact” conformation calculated from excised peptide fragments of folded structures ¹⁸. Since denaturation experiments show that the m-value is a constant, $\overline{\delta \alpha }$ must be a constant too and therefore the unfolded state SASA cannot depend on D. in other words, changes in the conformational entropy of the chain with denaturant concentration are ignored. One premise of this paper, based on the analysis of single-molecule fluorescence resonance energy transfer (smFRET) experiments, is to show that this assertion is incorrect.

It has been realized for some time that the folding transition may be preceded by a fast collapse into a compact structure ^19–21. A comprehensive discussion of the theoretical foundation and experimental evidence for denatured-state collapse can be found in a recent Perspective ²². Unlike the folding reaction, the collapse of denatured proteins has been barely studied by equilibrium methods, perhaps due to the inability to separate the denatured-state population from the folded state population under solution conditions where the two states co-exist. smFRET experiments are beginning to change this situation. In smFRET experiments individual protein molecules labeled with two fluorophores (typically close to their termini) are studied one by one as they diffuse in and out of a focused laser beam. It was shown that for most proteins studied with this method, the average FRET efficiency (Ē) of the denatured state (inversely related to the overall dimensions of the denatured protein) decreases monotonically as D increases, signifying that the denaturant causes the unfolded state to expand ^23–32. Clearly, then, both the SASA and $\overline{\delta \alpha }$ change with D. How can the m-value be constant?

In this paper we propose a solution to this conundrum. We analyze experimental smFRET data of several different proteins using a theory originally developed to explain the coil-to-globule (CG) transition in homopolymers. It is found that in essentially all of the smFRET experiments analyzed here the free energy of collapse is linear over the whole range of D, due to a subtle balance of enthalpy and conformational entropy terms; the latter is completely neglected in the TM. The denaturant dependence of the free energy of collapse is the same as the denaturant dependence of the free energy of folding, which implies that denaturants affects ΔG_U→N by modulating the energetics of the denatured state. Using a high D approximation to our model we propose an alternative model for the m-value.

Analysis and Results

Extracting thermodynamics from single-molecule FRET experiments

The CG transition in polymers has been extensively studied experimentally and theoretically for over 50 years ³³. Most of the theories of CG transition are either applicable only in one of the two phases (i.e. the expanded state or the collapsed states), or have too many parameters to be useful for analyzing experimental data. The mean-field Sanchez theory ³⁴, on the other hand, quantitatively describes the chain expansion throughout the CG transition and has just one free parameter. We modify this theory here to analyze the CG transition in denatured proteins. The theory models the probability distribution function of the radius of gyration S as:

$$P(S)=P_0(S)exp(-n·g(\phi ,\epsilon )/k_{B}T)$$ [3]

Here $P_0(S)\sim S^{6}exp\left(-\frac{7}{2}{S}^2/{\langle S^2\rangle }_0\right)$ is the Flory-Fisk empirical distribution for the radius of gyration of an ideal chain of n monomers (i.e. amino acid residues) ³⁵, and g(φ,ε), the excess free energy per monomer with respect to the ideal chain, is given by:

$$g(\phi ,\epsilon )=-\frac{1}{2}\phi \epsilon +k_{B}T\frac{1-\phi }{\phi }ln(1-\phi )$$ [4]

where φ is the volume fraction occupied by the chain, and ε is the difference in mean-field solvation energy between a residue within the maximally-collapsed chain and in free solution. Inter-residue interactions can be of varied origins (e.g. hydrobophic, electrostatic and even backbone-mediated ³⁶), and in principle ε includes all of these in an average way The first term in Equation 4 describes how attraction between residues (ε >0) favors compaction of the chain, while the second term is the entropy arising from excluded volume interactions, which favors expansion. The volume fraction is related to the radius of gyration through φ = S_N³/S³, where S_N is the radius of the gyration of the fully-compact native state (with φ_N = 1 by definition). One necessary parameter is the radius of gyration of the ideal chain, ${\langle S^2\rangle }_0^{1/2}$. This parameter is fixed by requiring that ${\phi }_0\equiv {S_N}^3/{\langle S^2\rangle }_0^{3/2}=\sqrt{19/27}{N}^{-1/2}$, which was derived using Landau’s theory of phase transitions ³⁴.

Recent experiments ^37–39 suggest that the end-to-end distance dynamics for a small denatured protein are on the microsecond (or even nanosecond) time scale, while smFRET data are averaged over millisecond fluorescence bursts. Under such circumstances the shape of the denatured-state FRET distribution (due mainly to photon shot-noise) does not contain useful information. Ē of the denatured-state distribution can, however, be ascribed to the following average over the end-to-end distance distribution, P(R_ee):

$$\overline{E}=\int P(R_{ee})/(1+{R_{ee}}^6/R_0^6)d{R}_{ee}$$ [5]

Here R₀ is the Förster radius for energy transfer and $1/(1+{R_{ee}}^6/R_0^6)$ is the FRET efficiency at an end-to-end distance R_ee. In the past either the P(R_ee) of a Gaussian chain or of a worm-like chain were used to fit smFRET experiments ^24,26,30. However, these probability distribution functions do not explicitly include information about the CG transition and its energetics. A model for P(R_ee) based on equation 3 corrects this deficiency. Formally, the end-to-end distance distribution P(R_ee) may be related to the distribution P(S) through the relation P(R_ee) = ∫ P(R_ee|S)P(S)dS, for which the conditional probability P(R_ee|S) needs to be specified. Here we adopt a simple model for this conditional probability, in the spirit of the mean-field approximation inherent in Sanchez’s theory, namely that P(R_ee|S) is given by the probability to find the two chain ends within a sphere with radius g · S. A single value of the constant g is used for all proteins (g ≡ 2.3), and it is selected to reproduce correctly the Gaussian distribution expected when P(S) = P₀ (S) (see Supporting Text). In practice, the denatured state structure is expected to be somewhat aspherical, as found experimentally ⁴⁰ and theoretically ^41,42. However, the quality of current experiments does not merit such detailed modeling of the denatured-state structure. Further, the effect of anisotropy on P(R_ee|S) is not expected to significantly affect the results of our analysis because of the FRET kernel in equation 5.

We are now in the position where we can evaluate ε from experimental data through Equations 3–5. We best fit ε for each protein and for each denaturant concentration to match the measured Ē of the denatured state. One final point that requires attention is the calculation in the case that labeling in was not done close to the termini. In this case we replace R_ee in the FRET efficiency kernel of Equation 5 by $R_{ee}\sqrt{l/n}$, where l is the actual number of residues separating the donor and acceptor.

Once ε is obtained for a protein at each denaturant concentration we can readily calculate different properties of the denatured state of the protein, such as its root mean-squared radius of gyration, 〈S²〉^1/2, which is convenient to present in terms of the expansion factor α² = 〈S²〉/〈S²〉₀. The free energy can be either calculated by using G(ε) = −k_BT〈ln P(S)〉, where 〈 〉 stands for an average over the distribution at ε, or by using G(ε) = n · g(φ̄, ε), in which φ̄ is the mean volume fraction. The two calculations give essentially identical results.

All proteins exhibit a continuous expansion

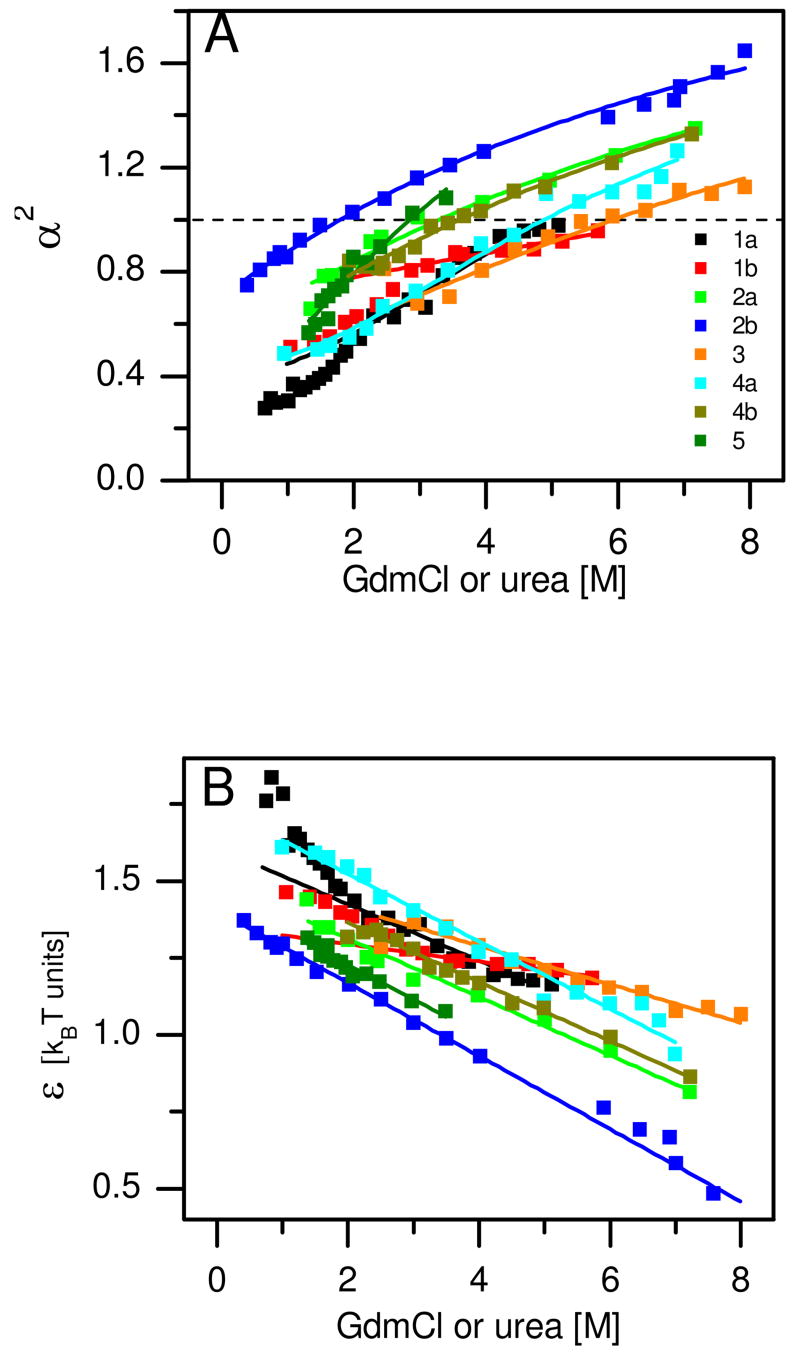
We analyzed twelve data sets measured on five different proteins (see Table 1 for details on the proteins) ^{25–27,29,30,32} using the method introduced above. Two of these proteins were measured in two different labs, namely protein L ^26,29 and CspTm ^29,30. Schuler and coworkers obtained FRET efficiency distributions for five different variants of CspTm, each labeled on a different pair of sites ³⁰; we analyzed all five variants (Table 1). Most data sets were measured using GdmCl as the denaturant; two of the data sets were measured with urea (Table 1). Figure 1A shows the expansion factor α², which describes the change in size as a function of solution conditions, calculated for all proteins (for clarity only one of the CspTm variants from reference ³⁰ is shown). There is a continuous expansion of the denatured state of these proteins over the whole range of D. Furthermore, most proteins span both sides of the α² = 1 line (the CG transition occurs formally at this point for very long polymers), while some remain below the transition point even at the highest D used, although they will likely cross this line at a slightly higher concentration. The D values matching the CG transition point (D_CG, see Table 1 and Supporting Text) are thus broadly distributed, but are always above that of the folding transition (D₅₀, Table 1).

Table 1.

Analysis of denaturant-induced CG transition from smFRET experiments

Number	Protein	n2	Labeling positions 3	Denaturant	D504[M]	DCG5[M]	SN6[Å]	SU,0M7[Å]	SU,D8[Å]	Ref.
1a–1b	Barstar	90	12, 89	GdmCl Urea	1.24 2.33	6.4 11.7	13.3	18.2 24.5	31.6 30.3	32
2a	CspTm	66	1, 66	GdmCl	2.0	5.3	12.7	20.4	30.2	29
2b–2f	CspTm	67	2, 67 10, 67 21, 67 22, 67 34, 67	GdmCl	2.0 1.7 2.3 1.9 2.4	3.4 5.1 3.8 4.4 3.4	12.7	22.5 18.2 20.8 19.8 23.0	32.4 30.7 32.1 31.5 32.3	30
3	Im9	86	23, 81	Urea	3.83	8.3	15.5	22.8	36.9	27
4a	Protein L	64	1, 64	GdmCl	1.64	6.8	13	17.1	28.9	26
4b	Protein L	65	1, 65	GdmCl	2.6	5.8	13	19.8	30.3	29
5	RNaseH	155	3, 135	GdmCl	1.37	3.7	17.1	24.8	50.4	25

Protein abbreviations: Barstar - Ribonuclease inhibitor protein from Bacillus Amyloliquefaciens (PDB: 1BTA), CspTm – Cold-shock protein from Thermotoga Maritima (1G6P), Im9 - immunity protein for colicin E9 (1IMP), Protein L – IgG binding domain B1 of protein L from Peptostreptococcus magnus (1HZ6), RNaseH - Ribonuclease Hi From Escherichia Coli (1RCH).

²Number of residues.

³As reported in original references.

⁴Denaturation midpoint, as reported in original references, or obtained from a fit of reported denaturation data to a two-state model.

⁵CG transition midpoint, defined as the point at which α=1+19/22·φ₀ (see Supporting Text).

⁶Radius of gyration of native state, calculated using HydroPro from published structures obtained from the Protein Data Bank.

⁷Radius of gyration of unfolded state at 0 M denaturant, calculated by extrapolation.

⁸Radius of gyration of unfolded state at 6 M GdmCl (8M urea), calculated by extrapolation.

Figure 1.

The CG transition in denatured proteins. Results of Sanchez theory analysis of smFRET experiments (see Table 1 for a full list of all proteins analyzed). A. The expansion factor α² ≡ 〈S²〉/〈S²〉₀ as a function of denaturant concentration. The dashed line marks the CG transition (α² = 1). Results calculated from the experimental data using the analysis outlined in the text are shown as squares. Expansion factor values were recalculated based on the linear fits of panel B, and are shown as solid lines. The numbers in the legend match the numbers in Table 1. B. the mean-field interaction energy ε as a function of denaturant concentration. Linear fits are shown as solid lines. In all proteins (apart from barstar) the fits encompass the whole range of denaturant concentrations. Color code as in A.

The mean-field interaction energy ε obtained from the analysis is shown in Figure 1B. It is positive (i.e. attractive), and decreases linearly in all proteins apart from barstar, for which it is linear only at high D. We therefore fitted ε to a linear model, taking only the high concentration points in the case of barstar (fits are shown in Figure 1B). We used the fitted lines to re-calculate the expansion factors, which are presented as solid lines in Figure 1A. The agreement of the solid lines with the experimental data shows that indeed the expansion is captured by the linear analysis of ε. We can use this analysis to extrapolate the experimental results and calculate the radii of gyration under native conditions (S_U,0M) and highly denaturing conditions (S_U,D). These values are given in Table 1. The extrapolated values indicate that under native conditions the size of the unfolded state of the proteins used for this calculation may be 30–50% larger than the size of their native state, correlating well with previous estimates ⁴³. Further, in all proteins studied there exists a remarkable expansion of the denatured state (50–100%) as solution conditions are changed from native to highly denaturing.

The free energy of collapse is linear with denaturant concentration

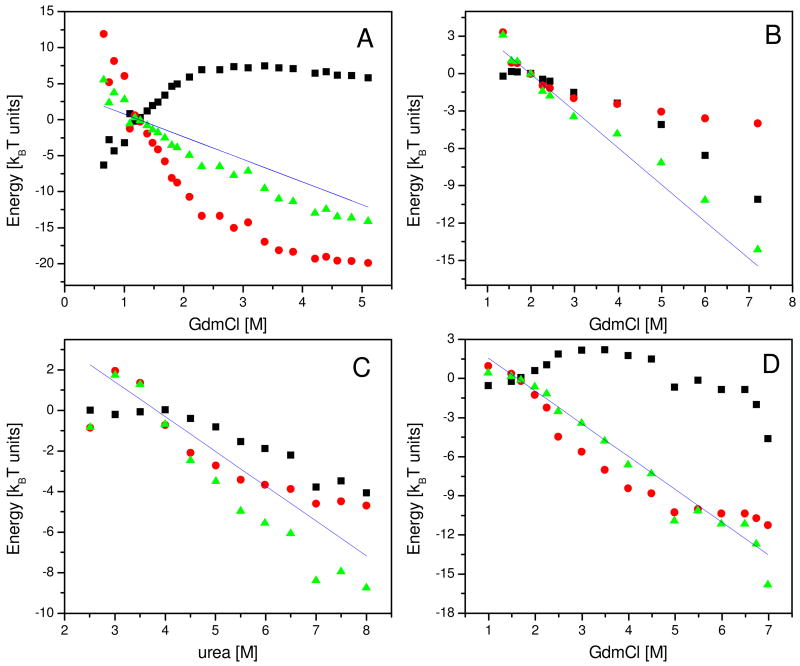
To calculate the free energy of collapse we define a new thermodynamic reference state which is the maximally collapsed denatured state (C). By definition, this state has volume fraction 1. This state may differ from U even under native conditions, as we have shown in the previous section. We calculate the free energy of collapse, ΔG_{U →C} as well as the enthalpy and entropy of collapse, ΔE_{U →C} and ΔS_{U →C} respectively, for each protein and D. Figure 2 shows the results for four proteins, while the rest are shown in Supporting Figure 1. Surprisingly, despite some differences between different proteins, in all cases neither ΔE_{U →C} nor ΔS_{U →C} show clear linear dependence on denaturant, but the sum of the two terms ΔG_{U →C} is clearly linear over a very broad range of denaturant concentrations, and over about 15k_BT (~25 kcal/mol) in energy. In most of the proteins, this linearity originates from compensating enthalpic and entropic contributions. The reason for the variation of the D-dependence of ΔE_{U →C} or ΔS_{U →C} between proteins is beyond the scope of this paper.

Figure 2.

Thermodynamic functions of collapse calculated from smFRET results for four different proteins. Values of the free energy of collapse, − ΔG_{U →C}, as a function of denaturant concentration, are shown as green triangles. The enthalpic contributions −ΔE_{U →C} and the entropic contributions k_BT · ΔS_{U →C} are shown as black squares and red circles, respectively. The interpolated value of each thermodynamic function at D₅₀ is subtracted from all points. Solid lines show the denaturant dependence of the free energy of folding, ΔG_{U →N}, as published in the literature. A. Results for protein L denatured in GdmCl (labeled 4a in Table 1). B. Im9 denatured in urea (3 in Table 1). C. CspTm denatured in GdmCl (2a in Table 1). D. Barstar denatured in GdmCl (1a in Table 1).

Denaturants affect protein stability by modulating denatured-state collapse

Comparing the slope of the free energy of collapse with the function −m · D for each protein (solid lines in Figure 2 and Supporting Figure 1), an excellent agreement is found essentially in all cases. Thus the change in the free energy of collapse with denaturant is described by the same m-value as the change in the free energy of folding. This surprising finding, which is the main result of this paper, is particularly intriguing in view of the fact that two very different experiments lead to the two curves. ΔG_{U →C} is obtained from smFRET experiments, which measure the change in the size of the denatured state. m · D, on the other hand, is obtained from standard denaturation experiments. Furthermore, these two measurements characterize two different phenomena, the second-order (continuous) coil-globule transition vs. the first-order folding transition, respectively.

Using the thermodynamic cycle depicted in Scheme 1B we can write

$$\mathrm{\Delta }{G}_{U\to N}-\mathrm{\Delta }{G}_{U^{\prime }\to N^{\prime }}=(\mathrm{\Delta }{G}_{C\to N}+\mathrm{\Delta }{G}_{U\to C})-(\mathrm{\Delta }{G}_{C^{\prime }\to N^{\prime }}+\mathrm{\Delta }{G}_{U^{\prime }\to C^{\prime }})$$ [6]

The remarkable result of our analysis of the experimental data implies that ΔG_{U →N} − ΔG_{U′ →N′} = ΔG_{U →C} − Δ_{U′ →C′.} Equation 6 is therefore valid only if ΔG_{C′ →N′} = ΔG_C→N, and observation of Scheme 1B shows that this immediately leads to $\mathrm{\Delta }{G}_N^{tr}=\mathrm{\Delta }{G}_C^{tr}$. Thus the maximally collapsed state (C), which was defined a-priori only by demanding that its volume fraction be set to 1, is found to have the same constant SASA and overall distribution of exposed amino acids as the native state (N). The important conclusion from this analysis is that all the effect of denaturants can be accounted for by that part of the cycle containing the U and C states. Thus the denaturant effect on folding is mediated through the collapse transition, i.e. through changes in the dimensions of the denatured state.

Expression for the m-value at high D

When both D and D ′ are high, typically (but not necessarily) above ~6 M, almost all proteins reach their maximum expansion, and φ becomes nearly constant (see Supporting Figure 2). Thus, the entropic terms in ΔG_U′→C′ and ΔG_U′→C′ become essentially identical, and only the enthalpic terms differ. Using φ̄_U, which is the average volume fraction at high D, and employing the substitution ε = ε⁰ − m̄D, which is based on the finding in Figure 1B that ε is linear with D, we get from Equations 4 and 6 that

$$\mathrm{\Delta }{G}_{U\to N}-\mathrm{\Delta }{G}_{U^{\prime }\to N^{\prime }}\approx \mathrm{\Delta }{E}_{U\to C}-\mathrm{\Delta }{E}_{U^{\prime }\to C^{\prime }}=-\frac{1}{2}n\stackrel{\sim }{m}(1-{\overline{\phi }}_U)(D^{\prime }-D)$$ [7]

Comparing Equations 1 and 7 we get the relation

$$m=\frac{1}{2}n\stackrel{\sim }{m}(1-{\overline{\phi }}_U).$$ [8]

Equation 8 suggests a physical interpretation for the m-value, which is alternative to the TM (Equation 2). It relates the linear dependence of ΔG_{U →N} with D to the change (slope) of the mean-field interaction energy (m̄) and the volume fraction of the denatured state in the highly expanded state (φ̄_U). We can validate this relation with the experimental data. As shown in Supporting Figure 2, φ̄_U is between 0.1 and 0.2. Taking an average value of 0.15 for this variable, the mean 1/2m̄(1−φ̄_U) for the set of proteins used in this study ⁴⁴ is (2.8±0.1)×10⁻² kcal/mol/M. For the same set of proteins we have m/n = (2.3 ± 0.3) × 10⁻² kcal/mol/M. It is important to note again that these very similar values on the right and left sides of Equation 8 come from two totally different types of measurements, namely the denaturation curve in the case of the m-value and the denatured-state size variation in the case of the m̄-value.

Discussion and Conclusion

In this work we used smFRET data of denatured-state expansion from a series of proteins to calculate the free energy of denatured-state collapse. It was found that ΔG_{U →C} is linear over the entire range of D used in these experiments, with essentially the same slope as ΔG_{U →N}. The similarity of the slopes suggests that changes in the free energy of folding with denaturant concentration are due to changes in the free energy of the denatured state. These changes, which are related to the CG transition of the denatured protein, have an enthalpic part, due to modulation of the solvation of amino-acid residues, but they also have a significant entropic part, due to an overall change in the size of the denatured protein. Interestingly, the analysis validates the linearity of ΔG_{U →N} (through the linearity of ΔG_{U →C}) over a much larger range of denaturant concentration then experimentally available in standard denaturation experiments, in which it can be measured only a few kcal/mol below and above D₅₀.

The expansion of the denatured state of proteins with increasing D poses a question on the validity of Tanford’s TM. We have shown that the TM is, in fact, not valid for low or moderate D, the range over which the conformational entropy changes continuously. Rather, we expect the TM to be strictly correct only for transfer of a protein between two denaturant concentrations at which the chain is already fully expanded and the change in conformational entropy is negligible. As was shown recently, however, by applying the TM separately to each individual member in the ensemble of denatured-state conformations, one can overcome the conformational entropy problem and reproduce many experimental results, including a protein’s denaturation curve and the measured m-value ⁴⁵.

The theory used in this paper to describe the CG transition assumes a non-specific collapse, so that a mean-field energy term can account for the interaction between monomers in the chain. It is possible that in some proteins the collapse transition is driven by specific interactions between protein residues. This is beyond the simple picture of the Sanchez theory, but may still be incorporated into it by parameterizing ε in terms of a more detailed model of the protein. Alonso and Dill employed this route ⁴⁶ and wrote an expression that allowed them to predict the value of ε from the ratio of hydrophobic to polar amino acids in a protein and their distribution within its folded structure. It will be interesting in the future to apply a similar calculation to the results presented in this work.

Our analysis pertains of course only to the thermodynamics of collapse and folding, and does not have immediate implications for the kinetics of folding. Kinetic experiments suggest that the free energy barriers for folding (ΔG_{U →TS}) and unfolding (ΔG_{N →TS}) are also linear with D. This can be explained by two alternative models. First, if the transition state (TS) has a fixed size, and therefore a constant SASA (which is larger than that of the native state, but smaller than that of the denatured state at all conditions), ΔG_{U →TS} and ΔG_{N →TS} will both be linear. On the other hand, if the transition state undergoes a continuous expansion with D similar to that of the denatured state, a sufficient condition for linearity of the folding barriers is that ΔG_{U →TS} is linearly-dependent on ΔG_{U →C}. Molecular dynamics simulations suggest the TS is, in fact, rather compact ^47,48. However, there is no evidence to support or dispel denaturant-induced changes in TS size.

There have been suggestions, based on time-resolved SAXS experiments, that in some proteins collapse may not temporally precede folding ^49,50. However, it is still possible that in equilibrium experiments, yet to be conducted, the denatured state of these particular proteins will show a collapse transition. Indeed, the collapse of protein L has been demonstrated independently by two labs in equilibrium experiments ^26,29, while not seen in a time-resolved SAXS study ⁵¹. For a fuller discussion of this issue see reference ²².

The analysis of smFRET data on denatured-state collapse of proteins in denaturant solutions has led here to a new paradigm for protein folding, in which the thermodynamics of the collapse transition is correlated with the thermodynamics of folding. As D is decreased, it is the change in conformation of the denatured state (from coil to globule) that modulates the energetic relation of this state to the folded state, driving the protein into a conformation more conducive to folding. The conformational entropy of the denatured protein becomes a key player in this process. Indeed, our analysis attributes a large fraction of the denaturant-related free energy of folding to conformational entropy changes. The current work emphasizes the essential role of the denatured state in protein folding. Further, it makes an important connection between the polymer physics of the denatured protein chain and the thermodynamics of folding. Our ability to reveal this connection and further verify the proposed physical interpretation for m-value in terms of denatured-state collapse (Equation 8), depended on the availability of new data on the CG transition from smFRET experiments. This is yet another example where single-molecule experiments and their analysis shed new (and unexpected) light on a familiar problem.

Supplementary Material

1_si_001. Supporting Information Available.

Details of computational methods, a table of m and m̄ values, a figure showing the thermodynamics of collapse for additional proteins and a figure showing the denaturant dependence of φ for all proteins. This material is available free of charge via the Internet at http://pubs.acs.org.

Abbreviations

CG

coil-to-globule

smFRET

single-molecule FRET