Shape separation of gold nanorods using centrifugation

Abstract

We demonstrate the use of centrifugation for efficient separation of colloidal gold nanorods from a mixture of nanorods and nanospheres. We elucidate the hydrodynamic behavior of nanoparticles of various shapes and illustrate that the shape-dependent drag causes particles to have shape-dependent sedimentation behavior. During centrifugation, nanoparticles undergo Brownian motion under an external field and move with different sedimentation velocities dictated by their Svedberg coefficients. This effects a separation of particles of different shape and size. Our theoretical analysis and experiments demonstrate the viability of using centrifugation to shape-separate a mixture of colloidal particles.

The physical and chemical properties as well as the applications of nanoparticles are critically controlled by their dimension and shape (1). Although significant research efforts are being directed to optimize the synthesis conditions, the typical, as-produced dispersions contain nanoparticles with polydispersity in shape and size (1–4). Postsynthesis purification and separation techniques that can maximize the yield of monodiperse samples have not received as much attention. Size-selective precipitation has been commonly used for nanospheres dispersed in organic solvents (4, 5). Capillary electrophoresis (6) and column chromatography (7) have been used in the separation of metal nanoparticles. Gold nanorod dispersions synthesized by wet chemical methods inevitably contain spherical particles as a by-product. Depending on the different methods, the fraction of by-product can be 10% to almost 90% (3, 8, 9). The use of separation methods mentioned above (4–7) is limited because either they are not applicable to shape separation or they result in partial separation (2). In this report, we provide a comprehensive set of theoretical arguments and experimental evidence showing how we used centrifugation to extract nanorods (NRs) from a mixture of rods and spheres.

Although centrifugation assisted sedimentation is routinely used to measure size and separate colloidal particles of different size (10, 11), successful separation based on shape (rods from spheres) is relatively less ubiquitous. By using the centrifugation parameters mentioned in the scattered reports in literature (9, 12–16) we failed to achieve efficient separation repeatedly and reproducibly. As in literature reports, depending on a case-to-case basis, seemingly small differences in concentrations, centrifugation parameters, and particle dimensions drove rods either to sediment out or remain in solution. Driven by the need and desire to understand these separation phenomena, we set out to identify the physics that drives shape separation in centrifugation.

We investigate the role of hydrodynamics in the centrifugation of Brownian rods and spheres, determine the size, shape, and concentration dependence of sedimentation coefficients and velocities, and establish conditions that affect shape separation. The arguments advanced here, with described caveats, are applicable to shape and size separation for organic, inorganic, and biological particles and molecules, and as an illustrative case we consider the separation of gold NRs. Further, the presented analysis successfully interprets and explains the experimental observations of centrifugation of other groups (9, 12–16). This is a unique systematic study of shape separation, where central role of hydrodynamics of these particles is elucidated to explain their separation procedure.

We use gold NRs synthesized by a seed-mediated method (3) for illustrating the use of centrifugation for shape separation. The size and shape of nanoparticles is gauged by using transmission electron microscopy (TEM) and UV-visible near-infrared (UV-vis-NIR) spectroscopy. In UV-vis spectrum, nanoparticles have size-dependent plasmon resonance peaks (1–3). Spheres have only one surface plasmon peak ≈520 nm, whereas the rods have both a transverse surface plasmon peak (TSP) (≈500–520 nm) and longitudinal surface plasmon peak (LSP) at higher wavelengths. The longitudinal peak position shifts to longer wavelength with increasing aspect ratio, and cumulative data from UV-vis-NIR and TEM is useful in characterizing both the size and shape separation (17). We demonstrate how our analysis is useful in obtaining high yield of nearly monodisperse dispersion of gold NRs.

Results

Theoretical Considerations and Results.

Sedimentation-diffusion equilibrium for rods and spheres.

Rigorously correct and general flow equations for centrifugation require nonequilibrium thermodynamics, and such analysis even for spherical particles is nontrivial, although it is required to make accurate predictions of centrifugation dynamics (18). First, we consider a simple phenomenological analysis of sedimentation-diffusion equilibrium. We compute the force balance on a particle, including centrifugal force, F_c = ω²rm, buoyant force, F_b = −ω²rm_o, Brownian fluctuating force, F_f, and viscous drag force, F_d = −ζv, where ω is the angular speed, m is mass of particle, m_o is mass displaced by the particle, r is the distance from the center to the location of particle, v is the sedimentation velocity, and ζ is the friction or drag coefficient. The balance of these forces leads to the Langevin equation of a particle undergoing Brownian motion under the influence of an external force. At equilibrium, F_total = F_d + F_b + F_c + F_f = 0 implies ω²r(m − m_o) − ζv = 0, which yields the Svedberg coefficient, S = v/ω²r = (m − m_o)/ζ, which expresses sedimentation velocity normalized by the applied angular acceleration. The Svedberg coefficient is a measure of sedimentation rate and depends on the ratio of effective mass and friction factor (10).

We next need a shape-dependent computation of the friction factor, ζ, so that a comparison of sedimentation rates of rods to that for spheres can be made. The relative importance of thermal diffusion and flow is judged by a dimensionless group called Peclet number, Pe, which for typical Brownian nanosphere is Pe = va/D = (m − m_o)ω²ra/k_BT > 1, where a is the radius of the sphere and D is the thermal diffusivity, implying that the thermal fluctuations are nonnegligible. This distinguishes nanoparticle sedimentation theories from the theories applied to macroscopic falling objects (19).

The expression for friction coefficient depends on the Reynolds number, Re and Re ≪ 1 for the typical sedimentation problems in nanoscale. Reynolds number, Re = ρUL/η, where η represents the viscosity, ρ represents density of the fluid, U represents characteristic speed, and L represents characteristic length, represents the ratio of characteristic magnitudes of inertial and viscous forces. Being in low Reynolds number regime implies that the inertial effects are negligible and the Stokes or creeping flow equations apply. Drag on a Stokesian sphere is 6πηaU, implying a friction coefficient, ζ = 6πηa, and S^sph = 2(ρ − ρ_o)a²/9η. In fact, the friction coefficients are similar for spherically isotropic objects, i.e., all regular polyhedra and bodies derived from them by symmetrically cutting or rounding off the corners, edges, and/or faces (20). Hence, the description of dynamics of spheres holds equally well for the cubic, icosahedral, and octahedral bodies encountered during synthesis of colloidal particles. Modified Stokes law gives v = K(ρ − ρ_o)a_eq²rω²/18η with K = 0.843 log₁₀(A_eq/A*0.065), where a_eq and A_eq correspond to diameter and area of the sphere with same volume as the particle. By using the equivalent sphere volume and including a correction factor, K ≈ 2–4 for difference in shape, the sedimentation of isotropic shapes is easily mapped from sphere case. However, for anisotropic bodies both force and torque balance is required, and coupling of translation and rotation needs to be considered.

Translational friction coefficient of a falling single rod depends of the orientation of rod, and friction felt parallel to the rod is ½ that of the transverse falling rods, i.e., ζ_⊥ = 2ζ_∥ (20–23). Unlike the spherical particles that settle in the direction of gravity, the nonspherical Brownian particle sediment an angle to the direction of effective gravity, which can be up to 19.5° for a thin rods (22). However, the Brownian rods, on an average, are guided in the direction of effective external field (22). In computing drag for the rods, orientation plays as big a role as the dimensions of the rod itself, one of the reasons that make both theoretical and experimental studies of dynamics of rods a lot more interesting and challenging. If 2 rods of equal dimensions make multiple rotations due to Brownian motion during the time they sediment a distance comparable to their length, then their velocity relative to each other is zero. In this case, the sedimentation velocity depends only on the average friction coefficient. Mathematically this requires L/v_st_{rot [infi]} ≈ 12k_BT/F[infi]cL ≪1 (21), where v_s is the sedimentation velocity and F_c is the centrifugal force, and this is satisfied for gold nanorods considered here. By using the expressions of average friction coefficient, and mass of the rods, we derive the Svedberg coefficient for rods to be S_o^rod = (ρ − ρ_o)D²[2 ln (L/D) − (υ_⊥ + υ_∥)]/24η_o, where υ_⊥ and υ_∥ are the correction factors of the rod perpendicular or parallel to the rods orientation, respectively.

Hydrodynamic interaction for spheres.

During the sedimentation of many bodies, the velocity of surrounding particles influences the velocity of a particle. This fluid-mediated particle interaction, called hydrodynamic interaction, makes the average sedimentation velocity different from that evaluated for a single sphere. In the presence of hydrodynamic interactions, the sedimentation velocity of sphere corrected up to first order in concentration is v^sph = v_o(1 − βφ) (11), and the value of β depends on the nature of the interaction, being 6.5 for hard spheres. Although the hydrodynamic interactions decrease the sedimentation velocity for hard spheres (repulsive interactions), the sedimentation velocity for associating or attracting spheres will be greater than that of a single sphere. It must be pointed out here that the sedimentation of colloids causes an inhomogeneous backflow of solvent, and the velocities we refer to in reality are ensemble averages that take into account the effect of walls, boundaries, and other divergences. Additionally, the particle undergoing sedimentation is kicked by diffusion or Brownian motion to make the boundaries between differently sized spheres diffuse, but a self-sharpening effect, which causes the particles that lag behind to have higher sedimentation speed, due to concentration dependence of the drag (for hard spheres) the overall effect is to provide well-defined regions of differently sized species.

Hydrodynamic interaction of rods.

Next, we examine the corresponding interaction in rods, where the computation is nontrivial because both hydrodynamic forces and torques need to be evaluated. Concentration dependence for sedimentation of hard rods was derived recently by Dogic et al. (21) and their theory agrees with the only other theoretical result of Peterson's theory (23) up to aspect ratio 30. In the calculations by Dogic et al. (14) hydrodynamic interaction is calculated by assuming that the timescale over which the rod travels distance of the order of L is much larger than the Brownian rotational relaxation time and the alignment of suspension and interactions are negligible. To the first order in concentration, i.e., for dilute solutions, the relationship is v^rod = v_o^rod (1 − αφ), where

[ref. 21]

[ref. 23]

Separation of shapes during centrifugation.

The essential step in determining the effectiveness of sedimentation, for a dilute dispersion of rods and spheres, turns out to be the calculation of the ratio of equilibrium sedimentation velocities or equivalently sedimentation coefficients of rods and spheres. The ratio s_o^rod/s_o^sph = v_o^rod/v_o^sph = λ_o = 6(D/2a)²[2 ln L/D − (υ_⊥ + υ_∥)] for single rod and single sphere allows us to see that, for this case, the central role in separation is played by the ratio of the squares of diameters of the rod and sphere. For a given L/D, whether the rods or spheres sediment faster is mainly controlled by the relative diameters of the particles, and because the aspect ratio dependence enters through the log term, the effect is much less dramatic than the effect of the diameters.

Including the hydrodynamic interaction terms, the ratio becomes λ = s_o^rod/s_o^sph = v_o^rod/v_o^sph = λ_o(1 − αφ)/(1 − βφ), where α ≥ β implies a stronger self-sharpening effect for the rods, allowing for better separation. For the typical concentrations encountered in as-made, colloidal gold dispersions, these interaction terms are negligible, but for separations from more concentrated samples, the rod–rod, sphere–sphere, and rod–sphere interactions become significant.

Concentration Profiles.

In nonequilibrium thermodynamics, the sedimentation during centrifugation can be described by using the Brownian motion under an external field using modified Smoluchowski equation (18, 24–26). In this version, the Brownian motion yields Fickian-type diffusion equation, called Lamm differential equation for centrifuge (18), with flux terms that account for the external field and the chemical potential gradients, i.e., ∂_tc(z, t) = ∂_z(D∂_zc(z, t) + κc(z, t)F^ext. The concentration profile, written by using nondimensionalized parameters [C(Z, T) = c(z, t)z_o/c_o, Z = z/z_o, T = D_ot/z_o², and ε = v_s^oz_o/D_o] is as follows (25, 26)

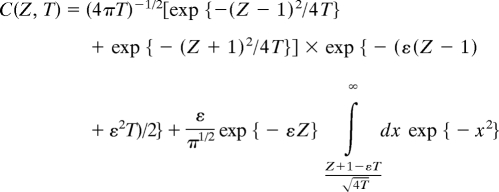The resulting concentration profile is Gaussian distribution (18, 24–26), such that the peak position of the Gaussian denotes corresponds to the position with the highest number of particles. As the centrifugation proceeds, the peak position shifts, reflecting that the whole distribution of particles is moving in the direction of centrifugal field. The shift in peak position as a function of time is dictated by the average sedimentation velocity of the particles. Different shapes and sizes result in differently peaked distributions leading to separation.

We note, however, that the long time solution yields barometric concentration profiles. This implies that if centrifugation is carried for a very long time, the distribution would be similar to that obtained once equilibrium is reached under gravity, which for 5,600 × g (the acceleration used in the experiments described) leads to nearly all particles going to the bottom. Another point to note is that the above consideration is equivalent to the probability distribution function of free particle in one dimension and provides only an expectation rather than an exact theory for multiparticle systems. Even for the non-Brownian particles, sedimentation phenomenon is a highly nonequilibrium process, and even though the behavior is described by deterministic equations, the dynamics is chaotic with high sensitivity to initial conditions and particles experience diffusive behavior induced by flows originating due to other particles, called hydrodynamic diffusion (19).

Experimental Results

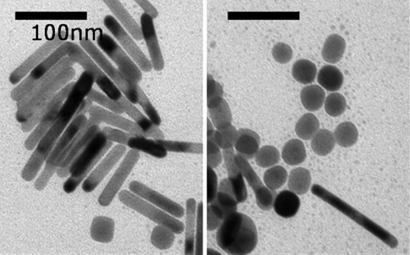
The gold NRs are synthesized by using an optimized seed-mediated method (27). We describe a representative example of shape separation accomplished by centrifugation. Fig. 1 shows the TEM images taken from the mother solution showing the mixture of rods and spherical particles. The average diameter of the spherical particles is 16 nm, whereas the average diameter of NRs is 8 nm. The average length of NR is 58 nm. Hence, the aspect ratio is 7.3. The number fraction of spherical particles is <10% (counting 700 particles), which is confirmed by the UV-vis-NIR spectroscopy where the intensity of the transverse surface plasmon peak (TSP) at ≈520 nm is low, as shown in Fig. 2.

Fig. 1.

TEM image of the nanoparticles in the mother (as-made) solution, showing coexistence of the nanorods and nanospheres. L/D of gold NRs is 7.3.

Fig. 2.

UV-vis-NIR spectrum of the mother solution. L/D of the gold NRs is 7.3.

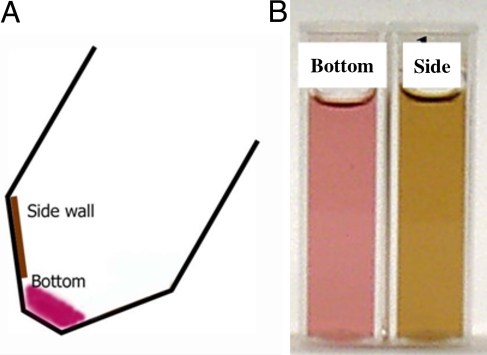
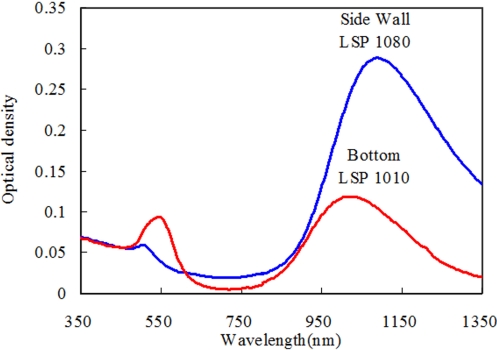
We observe that by centrifuging at 5,600 × g for 30 min, the spheres (and cubes) sediment at the bottom, segregating from rods that form a deposit with high purity on the side wall. Fig. 3A) schematically shows the centrifuge tube after the centrifugation. The color of the solutions taken from the bottom and the side wall of the centrifuge tube is distinctively different, as observed in Fig. 3B). The UV-vis-NIR spectrum of the solution of the NPs from the side wall, in Fig. 4, shows an intense longitudinal surface plasmon peak (LSP), red shifted from the mother solution (from 1074 nm to 1090 nm), and very weak TSP, indicating that it contains mostly NRs and the average aspect ratio is larger than that of the mother solution. The spectrum of the solution of the bottom shows broad TSP with higher intensity indicating that deposit comprises mainly the spherical particles, although the presence of LSP indicates that some nanorods are present as well. The LSP of this solution is blue shifted from the mother solution (from 1074 nm to 1022 nm), indicating that the aspect ratio of NRs is smaller than that of the mother solution.

Fig. 3.

Separated Au nanoparticles. (A) Schematic drawing of a centrifuge tube after the centrifugation and the color of resulting solutions. (B) The color of the solution taken from 2 different locations shown in A.

Fig. 4.

UV-vis-NIR spectra of the solutions of the deposits on the side wall of the tube and at the bottom.

The size of the particles in these two solutions was then characterized by TEM (counting 500 particles from each case). TEM images reveal that the separation of NRs was accomplished by centrifugation. The bottom solution predominantly contains spherical particles, whereas the solution from the side wall contains mostly NRs. We compared the dimension of NRs before separation and after separation. Separated NRs from the side wall on the average have longer length and smaller diameter, thus a higher aspect ratio, than those in the mother solution. Shorter and fatter NRs were found in the bottom deposit.

Discussion

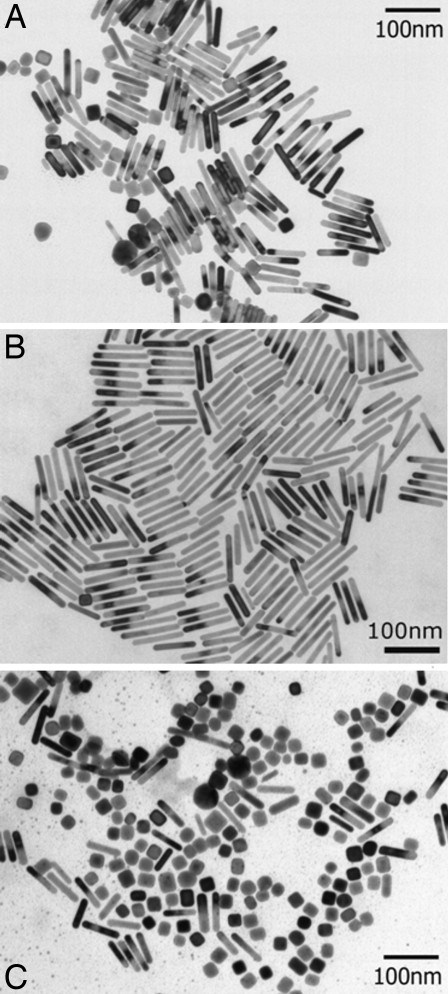
In the as-made or mother solution, TEM images in Fig. 1 show that the diameter of spherical particle is almost twice larger than that of NRs. After the centrifugation, when the nanoparticles are redissolved, the deposit from the bottom has a different color from the deposit at the side wall, as shown in Fig. 3B). The difference in absorption between the particles deposited due to the different size and shape causes this difference in color, and even the simple visual inspection reveals that the spherical particles sediment faster than the rods in this case. Further the UV-vis-NIR spectrum in Fig. 4 shows that thinner and longer nanorods form the deposit on the side wall, whereas fatter rods and spheres settle at the bottom. The longitudinal plasmon peak red shifts with an increase in aspect ratio, and a comparison with the spectrum of mother solution in Fig. 2 shows that the average aspect ratio of the rods from the side wall is longer. This is again confirmed by the TEM images as shown in Fig. 5.

Fig. 5.

TEM images of gold nanoparticles. (A) Mother solution; (B) after centrifugation, NRs deposited on the side wall of the tube; and (C) after centrifugation, nanocubes, spheres, and NRs with larger diameter, sedimented at the bottom of the tube.

In literature, it has been often stated that the long rods settle down preferentially at the bottom because they are heavier (9, 12) or because of so-called surfactant assisted self-assembly (13). In the present example, the weight of nanorods is greater than that of spheres and yet it is the spheres that settle to the bottom. Similarly, shorter and fatter rods segregated to the bottom, rather than the rods with longer length and comparable or higher effective weight. As explained in the theoretical considerations, one needs to remember that the dynamics of nanoparticles in this system is controlled by a ratio of their effective mass and friction coefficient. As the calculation of the ratio of velocities of rods and spheres illustrates, the relative ease of separation of these particles is mainly controlled by the relative diameters of the particles. This explains why spheres with larger diameter and fatter rods settle to the bottom in our case.

We claim that the separations reported in the literature (9, 12–16) conform to our analysis based on hydrodynamics, and like our case, Chang et al. (15) observed that spheres formed the bulk of sediments in their first centrifugation. The prediction that rods and spheres with similar diameters are hard to shape separate is also borne by reports in the literature (9, 13, 14). Repeated centrifugation followed by dissolution of sedimentation particles in a surfactant solution (9, 13, 14) is equivalent to selecting bigger particles in each run and, by dilution, rods tend to sediment faster than they can in a more concentrated solution as described above. We believe that the role of surfactant is mainly to keep the particles dispersed.

We add that our arguments are strictly applicable in dilute regime only; the thermodynamic considerations that come into play at higher concentrations may be part of the reason why rods assemble with a considerably higher purity on the side wall in described experiments. The concentration of the nanoparticles in the solutions used lies in the dilute range, as the average distance between particles, φ^−1/3 is much larger than L or φ ≪ L⁻³. Here, L is the size of the particles and φ denotes the number of particles per unit volume. The sedimentation cell used has these nanoparticles suspended uniformly to begin with, and because the standard cell for the centrifugation is used, the effects of heating, convection in fluid, etc., are minimized. The physics of centrifugation is modified both at higher concentrations of particles and in highly charged systems. Dogic et al. (21) reported that, in the highly concentrated solutions, nematic phase formation causes the faster sedimentation of rods in the denser LC phases, but since we observe rods assemble on the side wall, and concentration of as-made solution is very low, the formation of LC phase cannot occur in this case. We need to concentrate the solution by >1,000 times to reach the required concentration for phase transition from isotropic to nematic phase, and thus the probability of this happening in dispersed phase or particles aggregating is negligible.

Conclusions and Implications

In conclusion, by analyzing the hydrodynamics of rods and spheres we are able to elucidate the conditions under which centrifugation leads to the shape separation of nanoparticles. The understanding of the parameters and physics that drives separation is a necessary step in the widespread use of centrifugation to shape-separate particles. We believe our arguments will prove beneficial in approaching centrifugation for shape separation of all kinds of particles and provide impetus to research efforts directed toward study of separation techniques, that we believe is as necessary as efficient synthesis methodology to get nearly monodisperse, shape-segregated nanoparticle dispersions.

Materials and Methods

Synthesis of Nanorods.

The gold NRs are synthesized by using an optimized seed-mediated method (27). Seed solution was prepared by mixing hexadecyltrimethylammonium bromide (CTAB) solution (5.0 mL, 0.20 M) with 5.0 mL of 0.00050 M HAuCl₄. To the stirred solution, 0.60 mL of ice-cold 0.010 M NaBH₄ was added, which resulted in the formation of a brownish yellow solution. The solution was stirred for 2 min and was kept at 25 °C without further stirring.

The growth solution was prepared by mixing 5 mL of an aqueous solution of surfactant mixture [CTAB and benzyldimethylhexadecylammonium chloride (BDAC)] with 5 mL of 0.001 M HAuCl₄ solution; 200 μL of 0.0040 M AgNO₃ solution was added to the solution at 25 °C. After gentle mixing of the solution, 60 μL of 0.10 M ascorbic acid was added to the solution. The color of the growth solution changes from dark yellow to colorless. The final step was the addition of 10 μL of the seed solution to the growth solution. The color of the solution changes over the period depending on the final size of the NRs and the as-produced dispersions always contain spheres and cubes in addition to rods. The typical dimensions of the nanorods, expressed in terms of aspect ratio, i.e., length-to-diameter ratio, L/D, range from 3 to 10, with L from 30 to 150 nm and D from 8 to 20 nm. The size and aspect ratio of the rods are controlled by changing the concentration and mixing ratio of surfactants as described in detail in ref. 27.

Centrifugation.

As-made gold NR solution was centrifuged at 5,600 × g for 20–40 min by using the Jouan centrifuge MR23i. After the centrifugation, the tube was visibly inspected. The concentrated dark solution at the bottom (inside) of the tube was taken by using a syringe. The supernatant was carefully removed. The solid-like deposit on the side wall was dissolved in distilled water.

UV-vis-NIR Spectroscopy.

UV-vis-NIR spectra of resulting solutions were acquired with a Cary 5G UV-vis-NIR spectrophotometer.

Transmission Electron Microscopy.

The morphology and the mean size of NPs were examined by taking TEM images on JEOL100 at the accelerating voltage of 100 kV. For each sample, the size of >500 particles in the TEM images were measured to obtain the average size and the size distribution.