Beyond Poisson-Boltzmann: Modeling Biomolecule-Water and Water-Water Interactions

Abstract

We present an extension to the Poisson-Boltzmann model in which the solvent is modeled as an assembly of self-orienting dipoles of variable densities. Interactions between these dipoles are included implicitly using a Yukawa potential field. This model leads to a set of equations whose solutions give the dipole densities; we use the latter to study the organization of water around biomolecules. The computed water density profiles resemble those derived from molecular dynamics simulations. We also derive an excess free energy that discriminates correct from incorrect conformations of proteins.

Electrostatic interactions play a central role in physics, chemistry and biology as they directly relate to the stability of molecules as well as to the specificity of their interactions. Understanding electrostatics is especially important in biology: biomolecules can be considered as large polyelectrolytes, whose properties depend on their own charge distribution as well as on their interactions with surrounding charged molecules. Debye-Huckel theory was applied to proteins as early as in 1924 to predict the influence of ionic strength onto pH titrating curves [1]. Later, Kauzmann [2] foresaw the importance of electrostatics for protein stability, proposing that polar (charged) groups would either compensate for each other, or be solvated by water. Perutz [3] was able to confirm these qualitative predictions once the first high resolution protein structures were available, and further emphasized in considerable more detail the role of electrostatics in protein structure and function.

Many models for computing electrostatic interactions for bio-molecules account for the solvent implicitly. The most popular of these models derives the electrostatic potential by solving the Poisson-Boltzmann equation (PBE), where the solvent region is modeled as a homogeneous medium with a high dielectric constant (for recent reviews, see [4, 5]). PBE however is only a mean-field approximation to the multibody problem of electrostatic interactions. It is based on several approximations with proved limitations. Among those, the Poisson-Boltzmann (PB) model uses a constant and somewhat arbitrary value for the dielectric constant of the protein (usually set at 2–4 [6]), that abruptly jumps to 80 at the interface between the protein and the solvent. This assumption does not take into account the inhomogeneous dielectric response of water to the presence of a charged solute, that leads to non-uniform arrangement of water around the solute. This solvation phenomenon is however essential for understanding the stability and dynamics of biomolecules and therefore cannot be ignored. The standard PB model has been recently extended so that the solvent is described as an assembly of freely orienting dipoles placed on a lattice. This is a generalization of the Langevin Dipoles-Protein Dipoles (LDPD) model advocated by Warshel and collaborators [7, 8], with the key additional feature that the dipoles are now allowed to have a variable density at each lattice site. Such extensions, based on lattice field theory [9], have been implemented in the Dipolar Poisson-Boltzmann equation (DPBE) [10] or the Poisson-Bolzmann-Langevin equation (PBLE) [11, 12]. However, both DPBE and PBLE are also mean field approximations, and as such do not treat well dipolar-dipolar long-range correlations.

In this letter, we propose an extension to the Dipolar PB model, called the Yukawa Langevin Poisson-Boltzmann (YULP) model. Unlike in DPBE and PBLE where the dipoles interact only through electrostatics, we introduce an additional attractive field at each position in the lattice, that derives from a Yukawa potential. We show that inclusion of this attractive term is important in predicting the dielectric response in water induced by a biomolecule. The computed radial water density profiles show two layers of hydration around the solute. These water density profiles are then used to derive a simple excess free energy that can discriminate correct from incorrect protein models.

The dipolar Poisson-Boltzmann model is described in full details in Abreshkin et al [10] and Azuara et al [11, 12]. Briefly, we represent the water surrounding the solutes of interest as a set of orientable dipoles of constant module p₀ and bulk concentration $c_{\mathit{dip}}^b$. These water dipoles are distributed on a lattice to approximate the excluded-volume effects In the lattice gas formalism, the domain outside the boundary of the molecule is represented as a three dimensional lattice with N uniformly sized cuboids, of size a³, where a, the lattice spacing, is set to the geometrical dimension of the dipoles. As a first approximation, we assume that the dipoles are hard spheres of fixed sizes. The solute is described by a constant charge density ρ_f and a solvent accessibility function γ(r⃗) that is zero for points inside the envelope of the solute and one otherwise. This envelope can be taken as the molecular surface or the accessible surface of the solute.

Each site in the lattice can contain at most one dipole. If it is empty, its energy is 0. The energy of one dipole of constant magnitude p₀ at position r⃗ is obtained as the Boltzmann-weighted average of the interaction −p⃗₀ · E⃗ over all orientations of p⃗_0, where E⃗ is the local electric field. To mimic correlation effects between dipoles in a way compatible with a mean field approach, we add a Yukawa field Ψ (r⃗) to the energy of a dipole present at position r⃗ in the lattice. A similar approach was used by Coalson and colleagues to account for free ions steric repulsion in their lattice field theory of a Coulomb gas with finite size particles [13]. This Yukawa field is derived from a Yukawa potential $V_Y(r)=-v_0\frac{e^{-r/b}}{r}$ with two characteristic lengths b and l_Y=βv₀ where $\beta =\frac{1}{k_{B}T}$. This Yukawa potential is attractive to account for interactions between water molecules; we do not consider a repulsive term, as steric effects are accounted for by the lattice.

Following the formalism introduced by Borukhov et al [14], the grand canonical partition function Z_l (r⃗) for the lattice site at position r⃗ is then given by

$$Z_l(\overrightarrow{r})=1+{\lambda }_{\mathit{dip}}{e}^{-\beta \mathrm{\Psi }(\overrightarrow{r})}\text{sinhc}(u)$$ (1)

where λ_dip is the fugacity of the dipoles, u = βp₀|E⃗(r⃗)| and sinhc(u) = sinh(u)/u.

The free energy functional for the whole lattice includes the electrostatic energy, the functional form for the energy of the Yukawa field, the energy of the fixed charges and the logarithm of the partition function Z_l defined in equation 1:

$$\begin{array}{l}\beta \mathcal{F}=-\frac{\beta }{2}\int d\overrightarrow{r}{\epsilon }_0\mid \overrightarrow{\nabla }\mathrm{\Phi }(\overrightarrow{r}){\mid }^2\\ +\frac{\beta }{2v_0}\int d\overrightarrow{r}\left(\mid \overrightarrow{\nabla }\mathrm{\Psi }(\overrightarrow{r}){\mid }^2+\frac{\mathrm{\Psi }{(\overrightarrow{r})}^2}{b^2}\right)+\beta \int d\overrightarrow{r}{\rho }_f(\overrightarrow{r})\mathrm{\Phi }(\overrightarrow{r})\\ -\frac{1}{a^3}\int d\overrightarrow{r}ln(Z_l(\overrightarrow{r}))\end{array}$$ (2)

Writing $\frac{\delta \mathcal{F}}{\delta \mathrm{\Phi }}=0$ and $\frac{\delta \mathcal{F}}{\delta \mathrm{\Psi }}=0$, we get a system of two differential equations, which we refer to as the YUkawa Langevin Poisson-Boltzmann (YULP) equations:

1. A PBL equation [12] in Φ in which λ_dip is replaced by λ_dipe^{−βΨ(r⃗)}:

$$\overrightarrow{\nabla }·\left({\epsilon }_0\overrightarrow{\nabla }\mathrm{\Phi }(\overrightarrow{r})+\gamma (\overrightarrow{r})\beta p_0^2\frac{{\lambda }_{\mathit{dip}}{e}^{-\beta \mathrm{\Psi }(\overrightarrow{r})}{F}_1(u)}{a^3{Z}_l(\overrightarrow{r})}\overrightarrow{\nabla }\mathrm{\Phi }(\overrightarrow{r})\right)=-{\rho }_f(\overrightarrow{r})$$ (3)

where $F_1(u)=\frac{\text{sinhc}(u)}{u}\mathcal{L}(u)$; ℒ (u) = 1/tanh(u) − 1/u is the Langevin function.

1. A second order differential equation in Ψ (r⃗):

$$\frac{1}{v_0}\left(\mathrm{\Delta }\mathrm{\Psi }-\frac{\mathrm{\Psi }(\overrightarrow{r})}{b^2}\right)=\gamma (\overrightarrow{r})\frac{1}{a^3}\frac{{\lambda }_{\mathit{dip}}{e}^{-\beta \mathrm{\Psi }(\overrightarrow{r})}\text{sinhc}(u)}{Z_l(\overrightarrow{r})}$$ (4)

The bulk dipole concentration $c_{\mathit{dip}}^b$ verifies:

$${\mathcal{N}}_A{c}_{\mathit{dip}}^b={-\frac{\partial \mathcal{F}}{\partial {\mu }_{\mathit{dip}}}\mid }_{\phi =0,\mathrm{\Psi }={\mathrm{\Psi }}_{bulk}}$$ (5)

As λ_dip=e^βμ_dip, we get:

$${\lambda }_{\mathit{dip}}=e^{\beta {\mathrm{\Psi }}_{bulk}}\frac{{\mathcal{N}}_A{c}_{\mathit{dip}}^b{a}^3}{1-{\mathcal{N}}_A{c}_{\mathit{dip}}^b{a}^3}$$ (6)

The YULP equations include five parameters: the lattice size a, strength p₀, bulk concentration $c_{\mathit{dip}}^b$, and the parameters of the Yukawa field l_Y and b. We fix a = 2.4 Å. We set $c_{\mathit{dip}}^b$ to 55M, and p₀ to its value in solution, i.e. 2.35 D. b defines the range of the Yukawa potential; it is usually set to σ/1.8 Å, i.e. to a fraction of the diameter σ of the hard spheres representing the water [15]. Setting σ = 2.8 gives b = 1.55 Å. Note that full saturation of the lattice (i.e. with one dipole for each lattice site) leads to a maximum water density of 1/a³, i.e. approximately twice the density of bulk water for our choice of a. l_Y is a characteristic length that directly relates to the strength of the potential. We set l_Y = 7.0 Å(see below).

The two equations 3 and 4 are solved numerically on a finite domain Ω with boundaries δΩ. The domain Ω is set to be large enough so that Φ = 0, E⃗= 0→, and Ψ = Ψ_bulk at the boundary δΩ. The distance between the solute surface and the boundary is required to be at least 2l_B where l_B is the Bjerrum length (equal to 7 Å in water at T = 300K). From equations 4 and 6, we get $\beta {\mathrm{\Psi }}_{bulk}=-l_Y{b}^2{\mathcal{N}}_A{c}_{\mathit{dip}}^b$. With $c_{\mathit{dip}}^b=55M$ and b and l_Y set to the values given above, we get βΨ_bulk = −0.55.

We use a self-consistent iterative algorithm to solve for Φ(r⃗) and Ψ (r⃗). Full details on the algorithm will be published separately (see also [12]).

We define ${\rho }_b={\mathcal{N}}_A{c}_{\mathit{dip}}^b$. The density of dipoles is given by −∂ℱ/∂μ_dip:

$$\rho (\overrightarrow{r})={\rho }_b\frac{e^{-\beta (\mathrm{\Psi }(\overrightarrow{r})-{\mathrm{\Psi }}_{bulk})}\text{sinhc}(u)}{1-{\rho }_b{a}^3(1-e^{-\beta (\mathrm{\Psi }(\overrightarrow{r})-{\mathrm{\Psi }}_{bulk})}\text{sinhc}(u))}$$ (7)

for any position r⃗ inside the lattice gas. When u → 0 and Ψ (r⃗)→ Ψ_bulk, we get as expected ρ (r⃗) = ρ_b, i.e. the bulk density of water.

Equation 7 gives the density of water dipoles surrounding the biomolecules in the presence of a Yukawa field to model a short-range dipole-dipole attraction. We have computed the dipole densities around 12 proteins (PDB code 1ARB, 1CP4, 1EBD, 1PHP, 1SRP, 2ACS, 2APR, 2CTB, 2DRI, 2EXO, 2FCR, 5NLL). PDB files for each proteins are preprocessed with PDB2PQR [16] to assign charges and atomic radii according to the PARSE force-field [17]. The electrostatic potential and Yukawa field are computed on a uniform Cartesian numerical grid of 193³ points, with spacing h = 0.61 Å in all three directions. Global convergence takes 5 minutes CPU time on a 2.8 GHz Intel Core 2 processor. These dipole densities are used to compute water radial density profiles for each type of atoms defined in the PARSE parameter set [17]. The density profiles are computed numerically on line segments that are normal to the surface of an atom and that do not intersect other parts of the protein for at least 15 Å, with steps of size 0.1 Å

Results are shown in figure 1 for neutral oxygens, for different strengths of the Yukawa field and in figure 2 for all N, O and C species, with l_Y set to 7.0 Å.

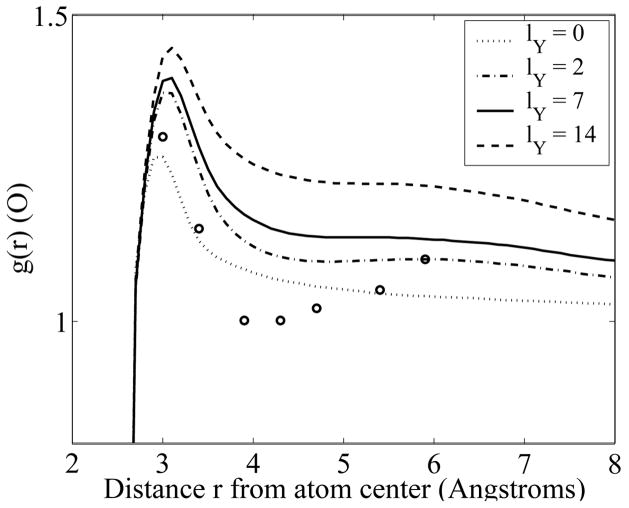
FIG. 1.

Water radial density profiles near neutral oxygens, as a function of the distance to the center of the atom, for different strengths of the Yukawa field. Experimental values derived from X-ray crystallographic data [18] are shown as open circles.

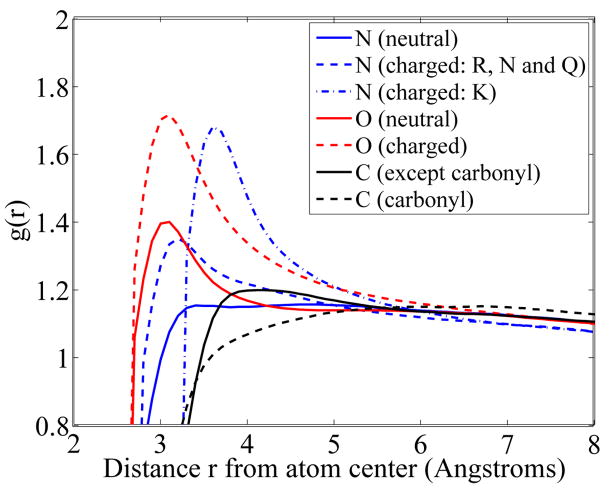
FIG. 2.

Water radial density profiles as a function of the distance to the center of the atom, for all N, O and C of the PARSE data set. The characteristic length defining the strength of the Yukawa field l_Y is set to 7.0 Å For clarity, the profiles are shown over one characteristic length. All curves converge to a value of one (i.e. bulk water) for large distances.

Figure 1 shows that increasing the strength of the Yukawa fields increases the dielectric response of the water to the fixed charges of the solute. Furthermore, in the presence of the Yukawa field, at least two water layers are perturbed by the protein surface, compared to a single layer when l_Y = 0. The two peaks in the radial density profiles are distant from each other by 2.4 Å, i.e. the size of the lattice that defines the minimal distance in our model between two water molecules. A comparison of water simulations in the presence of the Yukawa potential or the Lennard Jones potential yields l_Y ≈7 Å[15]. For l_Y = 7 Å, the first hydration layer corresponds to a 40% increase in water density next to oxygen atoms, while the second hydration layer corresponds to a 10% increase in density. This is consistent with the properties of water at protein surface reported from molecular dynamics calculations [19], as well as from analyzing crystallographic data [18]. Note however that compared to the experimental data, the profiles derived from YULP do not present a significant trough between the two water layers.

Figure 2 shows that the first hydration layer differs, depending on the proximity of polar or non polar solute atoms. Hydration (i.e. water density) is found to be strong next to net charged atoms, then weaker next to neutral polar atoms, and even weaker next to non polar atoms. This is in agreement with data obtained from molecular dynamics simulations with explicit water [19, 20].

To further quantify if YULP provides an accurate picture of the organisation of water around molecules, we define a posteriori a ”solvation” free energy from the dipole densities using the van der Waals theory of capillarity [21]. This excess free energy is linearly related to the integral of the square of the density gradients:

$${\mathcal{F}}_1=\frac{m}{2}\int {\mid \overrightarrow{\nabla }\rho (\overrightarrow{r})\mid }^{2}d\overrightarrow{r}$$ (8)

where m is the coefficient that relates to the surface tension [21]. This parameter m is assumed to be independent of the density ρ. We tested the power of the ℱ₁ energy to discriminate native from non native structural models of proteins. Two sets of misfolded structures were considered, i.e. the four pairs of correct and incorrect folds for haemerythrin and the Ig κ VL domain generated by Novotny and colleagues [22, 23], and a larger set of 26 native-misfolded pairs that was later created by Holm and Sander [24]. We compared the ℱ₁ energies of the misfolded models to those of the native structures for two values of l_Y, namely 0 (i.e. no Yukawa field), and 7 Å. Results are shown in figure 3.

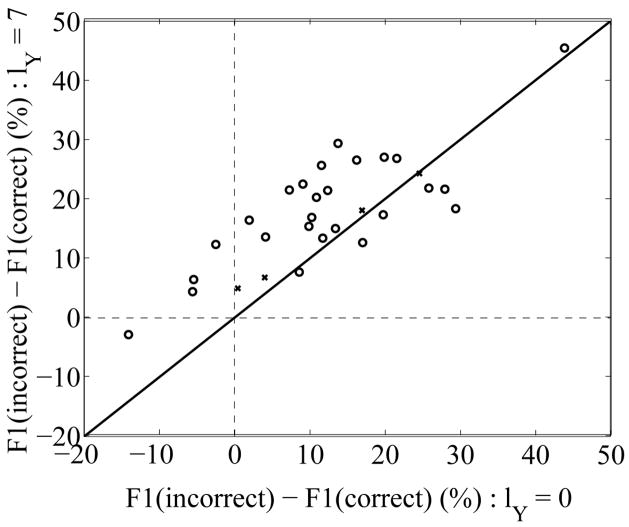
FIG. 3.

The excess free energies ℱ₁ of misfolded models compared to their native counterparts (in percent of the native free energies) are compared for two values of strength of the Yukawa field: l_Y = 0 (X-axis), and l_Y = 7 Å(Y-axis). The original native-misfolded pairs of Novotny [22, 23] are shown as +, while the set created by Holm and Sander [24] is shown as o. Positive values indicate that the native conformation has a lower energy than its misfolded counterpart. Values above the diagonal indicate that the Yukawa field improves discrimination of the native fold.

In the absence of Yukawa field, the ℱ₁ energy of the native model is better (lower) than the energy of its misfolded counterparts for 26 of the 30 native-misfolded pairs. Out of the four that are incorrectly predicted, only one remains marginally incorrect when the Yukawa field is added. The remaining error corresponds to the native-misfolded pair (1PPT,1PPT ON 1CBH). 1PPT is a small helical protein of 36 residues, while 1CBH is a small β-sheet proteins; both do not have well defined cores, and as such most charges remain exposed to the solvent; it is therefore not too surprising that ℱ₁ cannot distinguish the two models, as it only measures the water response to exposed charges of the solute protein.

Water plays a central role in biology as it defines the structures and properties of biomolecules. As such, it is the focus of many theoretical and computational modeling [25]. Recent models describe fine-scale properties with increased structural details, at heavy computational costs. The formalism presented here aims at characterizing the water surrounding macromolecules at an intermediate level of detail. It combines the standard PB model with a water model based on discrete non overlapping dipoles interacting through both electrostatics and an attractive Yukawa field. Our formalism is simple and its equations can be solved numerically with little computational cost; as such, it represents an attractive alternative to the computationally demanding explicit solvent models. It is general enough however to give a realistic picture of the dielectric response of water to the presence of a charged biomolecule. We have shown that this dielectric response leads to an organization of water into hydration layers that can be quantified into an excess free energy which proves useful to distinguish native from misfolded models of molecules. This formalism is not deprived of limitations. It is a mean-field treatment and as such lack long-range explicit correlations [26]. It does not account for the well-structured hydrogen bonds network between water molecules. Also, it is currently based on a symmetric model for water that cannot account for the specific packing observed in water. We are currently working on possible remediations of these issues.