Indirect genetic effects and the evolution of aggression in a vertebrate system

Abstract

Aggressive behaviours are necessarily expressed in a social context, such that individuals may be influenced by the phenotypes, and potentially the genotypes, of their social partners. Consequently, it has been hypothesized that indirect genetic effects (IGEs) arising from the social environment will provide a major source of heritable variation on which selection can act. However, there has been little empirical scrutiny of this to date. Here we test this hypothesis in an experimental population of deer mice (Peromyscus maniculatus). Using quantitative genetic models of five aggression traits, we find repeatable and heritable differences in agonistic behaviours of focal individuals when presented with an opponent mouse. For three of the traits, there is also support for the presence of IGEs, and estimated correlations between direct and indirect genetic (rA_O,F) effects were high. As a consequence, any selection for aggression in the focal individuals should cause evolution of the social environment as a correlated response. In two traits, strong positive rA_O,F will cause the rapid evolution of aggression, while in a third case changes in the phenotypic mean will be constrained by negative covariance between direct and IGEs. Our results illustrate how classical analyses may miss important components of heritable variation, and show that a full understanding of evolutionary dynamics requires explicit consideration of the genetic component of the social environment.

1. Introduction

Animals display aggression in a wide range of circumstances, from competition over mates or food resources, to the acquisition and defence of a territory, offspring protection against infanticide and the maintenance of dominance hierarchies within social groups (Verbeek et al. 1996; Koskela et al. 1997; Duckworth & Badyaev 2007; Ebenpserger & Blumstein 2007). There is an enormous interest in the circumstances under which selection may favour agonistic behaviours (Maynard-Smith & Price 1973; Parker 1974; Enquist & Leimar 1983; Dubois & Giraldeau 2005), and in the neurophysiological and genetic bases of aggression (De Boer et al. 2003; Nelson & Trainor 2007).

Despite the recommendations made over 30 years ago by Fuller & Hahn (1976) and Scott (1977), studies of the genetics of variation in aggressive behaviours have generally considered aggression as a characteristic of an individual, independent of the social context in which it is expressed (Hahn & Schanz 1996). However, with aggression defined as an individual's agonistic reaction towards a conspecific, assigning any given phenotypic observation to an individual is inherently problematic. This is because the behaviour expressed by an individual will usually depend on the behaviour of the conspecific with which it interacts. Although Fuller & Hahn (1976) proposed several experimental methods to cope with this difficulty, all of them show some limitations. For example, the methods proposed can hardly be applied to studies of wild animals, and are also unlikely to capture the full complexity of a social interaction. An alternative way to proceed is to treat social behaviours not as characters belonging to the single focal individual displaying them, but rather as the outcome of multiple interacting phenotypes (Moore et al. 1997). Here we take this approach to explore the genetic basis of variation for aggression in an experimental population of deer mice, Peromyscus maniculatus.

Quantitative genetic models normally partition an individual's phenotype into (additive) genetic and environmental components. Under classical models, it is the amount of additive genetic variance for a trait, commonly expressed as the heritability (h², the ratio of additive to total phenotypic variance), that determines the response to selection (Falconer & Mackay 1996). However, in the case of social behaviour, an individual's phenotype may well be determined (at least in part) by the genotypes of interacting conspecifics. In this way, the conventional separation of genetic and environmental effects on phenotype breaks down, or, put another way, the ‘environment’ is itself filled with genes and may be expected to evolve under appropriate selection (Griffing 1976; Moore et al. 1997; Wolf et al. 1998). This perspective can be accommodated using ‘indirect genetic effect’ (IGE) models, in which the trait of a focal individual is potentially influenced not only by its own genotype, but also by that of other individuals with which it interacts (Moore et al. 1997). Coupled with an appropriate model of multi-level selection, the characterization of IGEs allows the selection response of the social environment to be incorporated into predictions of phenotypic change (Cheverud 2003; Bijma & Wade 2008).

Broadly speaking, IGE models can be formulated in two ways. The first is a trait-based approach in which the expression of a measured trait in a focal individual is directly influenced by a second ‘interacting’ trait expressed by a conspecific (e.g. Moore et al. 1997; Agrawal et al. 2001). This allows direct scrutiny of the putative pathway by which one individual influences another individual's phenotype, but requires that both the trait of interest and the second ‘interacting trait’ be measured. An alternative approach is provided by ‘performance-based’ models in which indirect effects are tested for as the effect (or ‘performance’) of a particular individual on the phenotypic trait expressed in focal conspecifics (e.g. Willham 1972; Muir 2005; Bijma et al. 2007a). Since the interactor trait (or traits) is not actually measured, this approach cannot tell us about the specific mechanism by which one individual influences another. However, performance-based IGE models are empirically powerful since, provided the identities of interacting individuals are known, they allow detection and statistical estimation of IGEs without knowledge (or assumption) of which actual trait(s) influence the focal individual's phenotype.

While IGE models have particular applications in social evolution theory (Cheverud 1985; Queller 1992; Wolf et al. 1999), they actually provide a very general framework that is applicable to any type of trait likely to be influenced by social interactions (e.g. competition; Muir 2005). To date most empirical studies have focused on the particular case of maternal genetic effects, applying models developed for the situation in which the interacting individuals are a mother and her offspring (Willham 1972; Cheverud 1984; Kirkpatrick & Lande 1989). Here, an IGE occurs when an offspring trait is influenced by the maternal genotype (over and above the direct effect of genes inherited). Numerous studies have demonstrated the importance of maternal genetic effects in livestock, laboratory and wild populations (Mousseau & Fox 1998; McAdam et al. 2002; Wilson et al. 2005; Wilson & Réale 2006). Importantly, while maternal genetic variance can increase the ‘total heritability’ on which selection can act (Willham 1972), covariance between direct and maternal genetic effects is also common (Wilson & Réale 2006). Such covariance between direct and indirect genetic effects may arise through pleiotropy and will have a major impact on selection responses. Specifically, while positive covariance would facilitate very rapid responses to selection, negative covariance can act as an evolutionary constraint and can even result in counter-intuitive directions of phenotypic change (Wolf & Wade 2001).

In contrast to the work on maternal effects, other types of social environment (e.g. interactions among unrelated individuals) have received only limited empirical attention (but see Petfield et al. 2005; Mutic & Wolf 2007). Furthermore, while interest in the evolution of dominance and agonistic behaviour has provided particular impetus for the development of IGE models (e.g. Moore et al. 1997; Wolf et al. 1998), little is currently known about how widespread or large IGEs on aggression actually are (but see Moore et al. 2002 for an empirical example). Here we address this need for empirical study with an analysis of aggression in an experimental population of the deer mouse, P. maniculatus. Using observations made on pairs of mice, we first assess whether individual animals show consistent differences in aggressive behaviour. By modelling experimental observations as the outcome of interactions between phenotypes, we test not only the repeatability of aggression in focal individuals, but also the influence of the opponent mouse on the observed phenotype. Subsequently, we parametrize quantitative genetic models to assess the contributions of genetic effects to observed phenotypic variance. We consider the role of both direct and indirect genetic effects on aggression using performance-based IGE models and show that, by considering only the former, classical analyses of social behaviours are likely to miss much of the additive genetic variation available for selection to act on.

2. Material and methods

(a) Experimental population

Animals used in behavioural trials belonged to the third generation of a deer mouse (Peromyscus maniculatus sonoriensis) population maintained in our laboratory from 2005 to 2008. The population originated from a stock collected by Jack Hayes near the White Mountain Research Station, California, and subsequently maintained at the Peromyscus Genetic Stock Center (University of South Carolina; http://stkctr.biol.sc.edu). Animals were housed in either small (i.e. 30.5×15×18 cm) or large (i.e. 48×35×20 cm) rodent cages (Lab Products, Inc. Seaford, DE), under constant conditions (temperature of 24°C, humidity of 35% and a 16 L : 8 D inverse photoperiod). Mice were provided ad libitum food (rodent chow) and water. Each cage contained wood chips, cotton for the nest and a shelter. Large cages were enriched with a tubular structure and a wheel. As part of a research programme on inbreeding depression in behavioural traits, animals were bred with unrelated individuals or with full sibs in order to create individuals with inbreeding coefficients (F) varying between 0 and 0.3. Neither inbreeding nor cage enrichment showed any significant effects on the mean or variance of aggressive behaviours and these variables are not considered further. Females were placed in individual cages with a male for reproduction, and kept together until the first signs of pregnancy. Juveniles were separated from their mother at 31 days of age and maintained with sib groups until being used to produce the next generation. Each mouse was individually marked with a combination of ear punches.

(b) Aggression tests in a neutral arena

All the animals used in tests were virgin individuals aged 8–14 months. Mice were tested between 09.00 and 17.00 (i.e. in nocturnal phase) and we used same-sex dyadic encounter tests conducted in a neutral arena (see Fairbairn 1978; Bester-Meredith & Marler 2001). The arena consisted of a 50×26×30 cm aquarium separated into two areas of equal size by an opaque Plexiglas wall. The walls of the arena were covered by white plastic sheets in order to increase the contrast between the mice and the background.

Prior to testing, we created dyads at random within groups of 16 individuals of the same sex, so that each focal individual met four other non-sib ‘opponent’ individuals during the experiment. A maximum of two animals per cage were tested on the same day. Each animal was picked up from its own cage, marked with a non-toxic ink pencil and placed in one area of the arena. Animals were left for a minute in the arena in order to explore their new environment before the test. We randomly chose both the order of introduction and side of arena into which each animal was placed. The wall in the middle of the arena was then removed and interactions between the two mice were filmed under dim light with a video camera installed in front of the arena, at a distance of 50 cm. After the test, we cleaned the arena with 70 per cent ethanol before reusing it. In total, 490 dyadic tests were performed, involving 126 different individual mice. Mice were used as both focal and opponent individuals in multiple tests.

We analysed videos with the software ‘The Observer’ (Noldus Information Technology, Wageningen, The Netherlands). Following the ethogram proposed by Eisenberg (1962) and Fairbairn (1978), we noted the number of occurrences during the test of the following aggressive behaviours: approaches (the focal individual approaches the opponent in an elongated posture and sniffs in the direction of the opponent); naso-anal contacts (the focal individual initiates an inspection of the opponent ano-genital area in a head-to-tail position); mounting (the focal individual mounts its opponent); rearing (the focal individual exhibits an upright posture in response to the opponent approach); and the latency to fight by the focal individual. All these behaviour traits are expressed in an agonistic context: approach, naso-anal contacts and mounting are considered as signs of a dominant encountering a subordinate individual, while rearing and upright postures could be observed in a context of threat or avoidance of an approaching conspecific (Eisenberg 1962; Fairbairn 1978). A fight is generally preceded by naso-anal contact and is generally followed by a chase and biting by the winner (Eisenberg 1962). The test was ended either when a fight occurred or at 300 s. If no fight was observed, latency to fight was therefore recorded as 300 s.

(c) Data analysis

Univariate animal models were used to partition phenotypic variance into genetic (both direct and indirect) and environmental variance components. The animal model is a form of linear mixed model in which an individual's additive genetic effect is included as a random effect allowing the estimation of additive genetic variance in pedigreed populations (Henderson 1950; Kruuk 2004). Here the pedigree comprised 429 individuals: the 126 mice used in behavioural trials and an additional 303 known ancestors. Although phenotypically uninformative, the latter group contributes importantly to the analyses as they are informative for the expected additive genetic covariance between the behaviourally assayed animals.

Since phenotypic data distributions showed strong skew, all variables were transformed prior to analysis. Rates of approach, naso-anal contact, rearing and mounting were determined from the observed counts and trial durations, then log-transformed (after adding one) for analysis. The reciprocal of the trial duration (i.e. latency to fight) was similarly log-transformed. These transformations were not completely successful in normalizing the data, although visual inspection of residuals from subsequent model fits suggested a major improvement over untransformed data. Although an admittedly imperfect solution, the restricted maximum likelihood (REML) used is relatively robust to departure from normality (Lynch & Walsh 1998), and this strategy allowed model comparison using likelihood-ratio tests (avoiding the current difficulties of statistical inference associated with generalized mixed models). Note that henceforth all discussion of traits refers to these log-transformed variables unless explicitly stated otherwise.

For each of the transformed traits a set of four hierarchical models with a common fixed effect structure but increasingly complex random effect structure were fitted. For a focal individual i with opponent j, we modelled trait y as the following:

$$\begin{array}{ll}{y}_i=\mu \mu +\text{Order}+\text{Sex}+\text{Session}+e\hfill & (\text{null model})\hfill \\ y_i=\mu \mu +\text{Order}+\text{Sex}+\text{Session}+F_i+O_j+e\hfill & (\text{model}1)\hfill \\ y_i=\mu \mu +\text{Order}+\text{Sex}+\text{Session}+(a_{Fi}+{\text{pe}}_{Fi})+O_j+e\hfill & (\text{model}2)\hfill \\ y_i=\mu \mu +\text{Order}+\text{Sex}+\text{Session}+(a_{Fi}+{\text{pe}}_{Fi})+(a_{Oj}+{\text{pe}}_{Oj})+e\hfill & (\text{model}3),\hfill \end{array}$$

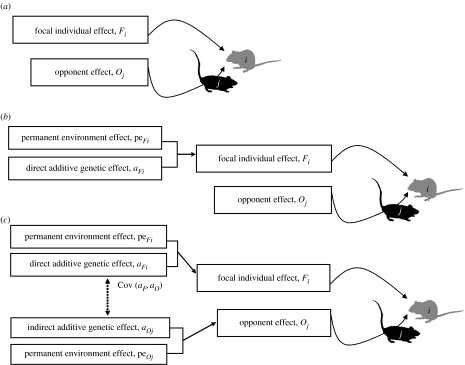
where μ is the mean phenotype, e is a residual error term and additional fixed effects of sex, order and session were all included as two-level factors. Order denotes which of the pair was placed in the arena first. All female trials were conducted over a single time period, but data on males were collected over two sessions, the second one being six months after the first. We therefore included session, which may be seen as a proxy for age, to account for this. Models 1–3 included varying random effects structures as specified above, where F_i and O_j are the effects on observation y_i that arise from the focal and opponent identities (i and j, respectively); a_Fi and a_Oi are the additive genetic contributions to these effects; and pe_Fi and pe_Oj are the corresponding permanent environment contributions (i.e. the environmental and non-additive genetic characteristics of the individual that are affecting its phenotype in a permanent way) (figure 1).

Figure 1.

Schematic of models tested. (a) Under model 1, the observed phenotype of the focal individual (y_i) is influenced by both the focal individual i and its opponent j. (b) Under model 2, the focal individual effect is decomposed into (direct) additive genetic and environmental components. (c) Under model 3, the opponent effect is similarly decomposed to test for an IGE of individual k on the phenotype of individual i and for covariance between the direct and indirect genetic effects.

We first fitted the null model containing only the fixed effects described above. This was compared with model 1, a repeatability model, in which the identities of focal and opponent individuals were fitted as random effects in a linear mixed model. Note that O_j is defined as the effect of the opponent individual j on the phenotype of the focal individual i. These effects were assumed to be normally distributed with means of zero and variance–covariance matrices among individuals of $\mathbf{I}{\sigma }_F^2$ and $\mathbf{I}{\sigma }_O^2$ where ${\sigma }_F^2$ and ${\sigma }_O^2$ are focal and opponent variance components, respectively, and I is an identity matrix with order equal to the number of individuals of each type. The residuals from the model (e) are assumed to be uncorrelated across records and to have a zero mean and variance ${\sigma }_E^2$ attributable to unmeasured environmental effects. For each trait we estimated the focal and opponent repeatabilities, defined as the ratios of ${\sigma }_F^2$ and ${\sigma }_O^2$ to total phenotypic variance $({\sigma }_P^2)$. ${\sigma }_P^2$ was determined as the sum of all variance components. The statistical significance of the focal and opponent repeatabilities was separately assessed by likelihood-ratio test in comparison with a reduced model in which the corresponding random effect was omitted. A series of bivariate models were then used to estimate covariances between individual effects among the five aggression traits for both focal and opponent individuals (i.e. Cov(F_ix, F_iy) and Cov(O_jx, O_jy) for all pairs of traits x,y). Covariances were rescaled to give the corresponding correlations, which we denote r_F and r_O, respectively. Note that although phenotypic covariances might also exist between an individual's focal effect and its performance as an opponent (either within or across traits), these cannot be estimated since the actual trait(s) influencing conspecific phenotypes are both unknown and unmeasured under the performance-based approach used herein. Model 2 is a standard repeated measures animal model, in which the random effect of the focal individual is decomposed into an additive genetic ‘breeding value’ (a_Fi) and a permanent environment (pe_Fi) effect. Breeding values are assumed to be normally distributed with zero mean and variance ${\sigma }_{\mathrm{AF}}^2$, the direct additive genetic variance among focal individuals. The variance–covariance matrix of additive effects among individuals is expected to equal $\mathbf{A}{\sigma }_{\text{AF}}^2$, where A is the additive numerator relationship matrix containing the individual elements A_ik=2Θ_ik; and Θ_ik is the coefficient of coancestry between any pair of individuals i and k in the pedigree. Θ_ik is obtained from the pedigree structure, allowing the model to be solved for ${\sigma }_{\text{AF}}^2$. Trait heritability (h²) was then determined as the ratio of ${\sigma }_{\text{AF}}^2$ to total phenotypic variance $({\sigma }_P^2)$. The permanent environment (assumed ${\text{pe}}_{Fi}\sim N\left(0,{\sigma }_{\text{PEF}}^2\right)$) accounts for fixed differences among individuals that are attributable to environmental (or potentially non-additive genetic) effects.

Model 3 similarly partitions the effect of the opponent on y_i into genetic and permanent environment contributions. Thus, a_O is the indirect (additive) genetic effect of the opponent on the focal individual's phenotype, with a population variance of ${\sigma }_{\text{AO}}^2$ estimated using the pedigree structure in a manner identical to that described above, and pe_O is the corresponding permanent environment effect of the opponent with a variance of ${\sigma }_{\text{PEO}}^2$. Direct and indirect genetic effects were free to covary, such that the direct–indirect genetic covariance (σ_{AF, AO}) was also estimated, and rescaled to a corresponding genetic correlation (rA_O,F). The traditional estimate of heritability was again calculated as described above. Finally, following Bijma et al. (2007a), and for a group size of two interacting individuals, we define the total breeding value (TBV_i) as the sum of direct and indirect breeding values (i.e. TBV_i=a_Fi+a_Oi), such that the total heritable variation for trait y is given as

$${\sigma }_{\text{TBV}}^2={\sigma }_{\text{AF}}^2+2{\sigma }_{\text{AF},\text{AO}}+{\sigma }_{\text{AO}}^2$$

(eqn. 6 of Bijma et al. 2007a with n=2). We therefore estimated ${\sigma }_{\text{TBV}}^2$ and calculated its ratio to ${\sigma }_P^2$.

All models were fitted using REML with the program ASReml 2.0 and statistically compared using likelihood-ratio tests (with the degrees of freedom equal to the number of additional parameters to be estimated in the more complex model). Thus model 2 was compared with model 1 as an explicit test of additive genetic variance for each behavioural trait, while the comparison of models 2 and 3 was used to test the hypothesis that IGEs play an important role in influencing phenotype.

3. Results

For each trait modelled, the estimated fixed effects were qualitatively and quantitatively similar across different random effect structures considered (results not shown). While the order of introduction to the test arena was not significant for any trait, effects of sex and session were common (electronic supplementary material, table 1). These fixed effects are not discussed further, but it should be noted that estimates of repeatability and heritability presented here are properly interpreted as proportions of phenotypic variance explained after conditioning on these terms (Wilson 2008).

Statistical comparison of model 1 with the null model (fixed effects only) provided evidence of individual-level effects on the (transformed) aggression traits. Thus there are consistent, repeatable differences among individual mice in the expression of behavioural traits (as focal individuals) and in their effects on the behaviour of others (as opponent individuals). This is supported by the finding that model 1, in which focal and opponent individuals were included as random effects, was a significantly better fit for all traits except naso-anal contact rate (table 1). With this exception, focal individual repeatabilities were statistically significant, with moderate effect sizes ranging from 0.134 to 0.205 (table 2). Repeatabilities for the opponent individual were non-significant for both naso-anal contact rate and mounting rate. (Note that the opponent repeatability for the latter trait can be interpreted as a measure of the tendency to be consistently mounted by focal individuals.) However, our results show that the opponent has a significant influence on phenotypic expression for the other traits (table 2). Although effects were generally smaller, opponent identity actually explains more variance than the focal individual in one case, although the difference is not significant (rearing rate; focal repeatability=0.177±0.043, opponent repeatability=0.232±0.046).

Table 1.

Model comparison for behavioural traits showing log-likelihoods (LnL) under the null model (i.e. no random effects) and under models 1–3. (In model 1, the identities of focal and opponent individuals were fitted as random effects in a linear mixed model. Model 2 is a standard repeated measures animal model, with additive genetic and permanent environment effects. Model 3 partitions direct and indirect genetic and permanent environmental effects, and allows direct and indirect genetic effects to covary. Statistical significance was assessed using likelihood-ratio tests, with the degrees of freedom equal to the number of additional parameters estimated under the more complex model.)

	null	model 1 (repeatability model)		model 2 (standard animal model)		model 3 (IGE model)
trait	LnL	LnL	p (versus null)	LnL	p (versus 1)	LnL	p (versus 1)	p (versus 2)
approach rate	379.04	389.59	<0.001	395.79	0.000	397.21	0.002	0.241
naso-anal contact rate	556.60	557.98	0.253	558.62	0.256	558.63	0.725	0.988
mounting rate	395.23	401.39	0.002	402.01	0.267	404.88	0.073	0.056
rearing rate	399.79	423.15	<0.001	425.49	0.030	428.69	0.011	0.041
reciprocal latency to fight	141.46	160.56	<0.001	161.57	0.156	167.46	0.003	0.003

Table 2.

Estimates of focal and opponent repeatabilities for each trait. (Parameters were estimated under model 1 and standard errors are shown in parentheses. p-values are based on likelihood-ratio tests against the reduced model).

trait	focal repeatabilitya	p	opponent repeatabilityb	p
approach rate	0.173 (0.046)	<0.001	0.074 (0.039)	0.035
naso-anal contact rate	0.042 (0.040)	0.283	0.038 (0.039)	0.305
mounting rate	0.134 (0.045)	0.001	0.032 (0.038)	0.385
rearing rate	0.177 (0.043)	<0.001	0.232 (0.046)	<0.001
reciprocal latency to fight	0.205 (0.047)	<0.001	0.130 (0.042)	<0.001

^aFocal repeatability corresponds to the tendency of the focal individual to express the specific aggressive behaviour.

^bOpponent repeatability corresponds the tendency of an individual to induce the specific aggressive behaviour in a focal individual.

Bivariate formulations of model 1 provided limited support for across-trait correlations of individual phenotypic effects (table 3). Large standard errors associated with estimated correlations suggest that power is limited, although significant correlations were found between traits in several cases. For focal individuals, r_F among traits was positive for eight out of nine pairwise comparisons (although significantly so for only two cases with a third marginally non-significant result; table 3). Thus, in general, more aggressive individuals tend to exhibit higher phenotypic values across the traits considered. For opponent individuals, r_O was positive in six of the comparisons (but significant only in one case). Furthermore, a strong and significant negative r_O between mounting rate and reciprocal latency to fight was found, although biological interpretation of this result is clearly problematic given that the opponent repeatability was not itself significant for the former (table 2).

Table 3.

Estimates within focal individual phenotypic correlation (r_F) (below the diagonal) and within opponent individual phenotypic correlation (r_O) (above the diagonal). (Correlations were estimated under bivariate formulations of model 1 with standard errors shown in parentheses.)

trait	approach rate	naso-anal contact rate	mounting rate	rearing rate	reciprocal latency to fight
approach rate		0.049 (0.533)	0.657 (0.525)	0.070 (0.247)	0.202 (0.285)
naso-anal contact rate	0.237 (0.346)		−0.751 (1.12)	0.019 (0.348)	−0.366 (0.510)
mounting rate	0.404 (0.200)**	0.278 (0.377)		−0.484 (0.461)	−1.082 (0.796)*
rearing rate	0.177 (0.193)	−0.133 (0.358)	0.462 (0.197)*		0.563 (0.156)*
reciprocal latency to fight	0.312 (0.175)	0.262 (0.336)	1.089 (0.156)*	0.341 (0.164)**

^*Denotes correlation significantly different from zero at p<0.05 using likelihood-ratio test.

^**Denotes a marginally non-significant result (p<0.1).

Inclusion of genetic effects (models 2 and 3) provided evidence for both direct and indirect additive genetic effects on the aggression traits analysed (table 1). Thus genetic effects contribute to the observed among-individual differences in aggression, and tendency to elicit aggression. IGEs are statistically supported for rearing rate and reciprocal latency to fight, and in both these cases a strong positive correlation was found between the direct and indirect genetic effects (rA_O,F) (table 4). Thus, in general, those genotypes that directly cause higher than average aggression in the focal individual also increase the aggressive response indirectly when expressed in the opponent. Primarily as a consequence of this, ${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$ was considerably greater than the traditional estimate of heritability considering direct genetic effects only. For rearing rate, ${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$ estimated from model 3 was 6.2 times greater than h² under model 2. For reciprocal latency to fight, the corresponding factor was even higher at 11.2. Comparison of models 3 and 1 was marginally non-significant for the third trait of mounting rate (Χ²₃=6.98, p=0.073). In this case, a strong negative correlation rA_O,F was estimated such that genes increasing the mounting rate of the focal individual decrease the propensity to be mounted in an opponent. Since the negative covariance term outweighs the contribution of the indirect additive variance $({\sigma }_{\text{AO}}^2)$, the ratio ${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$ under model 3 is lower than the traditional estimate of heritability (table 4). Model 3 was not supported for approach rate, although there was strong evidence of direct genetic effects on this trait (likelihood-ratio test of models 1 and 2, Χ²₁=21.1, p<0.001). Finally, model comparisons provide no support for either direct or IGEs on naso-anal contact rate, a result consistent with the absence of detectable repeatabilities (tables 1 and 2 ) and this trait is not discussed further.

Table 4.

Estimated genetic parameters for behavioural traits under model 2 (direct genetic effect only) and model 3 (IGE model).

	model 2		model 3
trait	${\sigma }_{\text{AF}}^2$	h2	${\sigma }_{\text{AF}}^2$	${\sigma }_{\text{AO}}^2$	rAO,F	${\sigma }_{\text{TBV}}^2$	${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$
approach rate	0.015 (0.005)	0.202 (0.057)	0.016 (0.005)	0.003 (0.003)	−0.300 (0.386)	0.015 (0.006)	0.190 (0.091)
naso-anal contact ratea	0.001 (0.001)	0.033 (0.039)	0.001 (0.001)	0.000 (–)	0.999 (–)	0.001 (–)	0.034 (–)
mounting rate	0.002 (0.003)	0.036 (0.045)	0.007 (0.005)	0.005 (0.003)	−0.853 (0.270)	0.002 (0.004)	0.025 (0.049)
rearing rate	0.007 (0.005)	0.098 (0.068)	0.018 (0.005)	0.009 (0.006)	0.789 (0.174)	0.047 (0.015)	0.607 (0.152)
reciprocal latency to fight	0.010 (0.011)	0.050 (0.054)	0.028 (0.015)	0.036 (0.012)	0.864 (0.158)	0.119 (0.039)	0.556 (0.147)

^aWith variance component estimates constrained to positive parameter space, no standard error could be estimated for ${\sigma }_{\text{AO}}^2$ or functions thereof.

4. Discussion

Our results confirm that consistent, repeatable differences in aggressive behaviour are present among individuals, and that these arise in part through genetic variance for the traits analysed. However, it is also clear that the social environment exerts a large influence, and that phenotypic expression can depend on the genotype of the opponent (as well as the focal) individuals. This conclusion is consistent with the assertion that social behaviours, including aggression, might best be understood as the consequence of interacting phenotypes, and hence genotypes (Moore et al. 1997, 2002; Wolf et al. 1999). Thus, while previous studies of rodent aggression have considered how genes and the environment contribute to phenotypic variation (e.g. Kessler et al. 1977; Brodkin et al. 2002; Nyberg et al. 2004), it is also necessary to consider the role of genes in the environment.

Indirect genetic effects arising from social interactions among individuals are expected to have major implications for evolutionary dynamics. This is highlighted in our results by the discrepancies between heritability estimates (h²) generated under the conventional (direct genetic effect) model, and estimates of ${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$ from the IGE model. The differences in these parameters arise from the inclusion in the latter of both the indirect (opponent) additive variance $\left({\sigma }_{\text{AO}}^2\right)$, and the genetic covariance term between direct and indirect effects. In particular, strong positive genetic covariance between direct and indirect effects was found for several traits. Most notably, estimates of ${\sigma }_{TBV}^2/{\sigma }_P^2$ are considerably larger than h² for rearing rate and reciprocal latency to fight (by factors of 6.2 and 11.2, respectively), a finding that reflects the strong positive covariance between genetic effects in focal and opponent individuals. Positive covariance of this sort is expected to facilitate rapid trait evolution by inducing positive feedback between genetic and ‘environmental’ effects, as dicussed by Moore et al. (1997) and Wolf et al. (1998). Thus, for rearing rate and reciprocal latency to fight, positive directional selection would not only increase the frequency of aggressive alleles in focal individuals of the next generation, but also lead to a social environment that is more likely to trigger high levels of agonistic behaviour. This scenario is consistent with prior theoretical treatments of the role of IGEs in the evolution of agonistic behaviours (e.g. Wolf et al. 1998), but has not, to our knowledge, been empirically demonstrated previously.

It is perhaps important to point out that the ratio ${\sigma }_{\text{TBV}}^2/{\sigma }_P^2$ is not a straightforward analogue or replacement for h² in the breeders equation used to predict a univariate response to selection (Falconer & Mackay 1996). This is because the magnitude of a phenotypic response will also depend on the relatedness among interacting individuals, and on the partitioning of selection into individual and higher-level (i.e. pair or group) components (Wolf et al. 1999; Bijma et al. 2007a; Bijma & Wade 2008). Nonetheless, even in the absence of multi-level selection, the genetic covariance between direct and indirect effects will be ‘visible’ to selection on focal individual traits such that positive covariance should result in accelerated selection responses.

Interestingly, mounting rate provides a counter-example for which the presence of IGEs should decrease the magnitude of any phenotypic response to directional selection. Specifically, the negative correlation rA_O,F indicates that genetic predisposition to mount opponents is associated with being less likely to be mounted as an opponent. This negative correlation is intuitive because, in contrast to fighting, which is usually expressed in symmetrical interactions between two aggressive mice (i.e. once one mouse starts a fight the other has no option but to engage; D. Réale 2007, personal observation), mounting rate is an asymmetric trait related to dominance (Eisenberg 1962; Fairbairn 1978). In a dyadic interaction, genes that predispose to dominance when expressed in the focal individual must necessarily predispose to subordination of the focal animal if expressed in an opponent instead (Moore et al. 2002). However, these inferences should be treated with caution here since the genetic effects for mounting rate (both direct and indirect) are admittedly small and marginally non-significant.

It is important to acknowledge that the present study is subject to a number of limitations that stem primarily from the available data. For example, having measured phenotype only in focal individuals, we cannot identify the actual traits by which opponents exert their influence. Although, given the required data, this is possible in trait-based studies of IGEs, we note that it should actually be feasible to parametrize models that include both trait- and performance-based sources of IGE effects simultaneously. This could be a fruitful strategy since, for example, after modelling the influence of a known opponent trait (e.g. following Moore et al. 1997), the presence of additional indirect genetic variance for performance would suggest an important role for further (unknown) traits.

We also encountered problems when attempting to fit multivariate formulations of the genetic models (i.e. models 2 and 3). Modelling the phenotypic effects alone (i.e. model 1) provided some evidence for among-trait positive correlations of focal individual effects. Thus, for example, those mice displaying higher rates of mounting also show increased rearing and lower latency to fight (i.e. higher reciprocal latency to fight), while correlations with approach rate were also positive (albeit not statistically significant). While this is consistent with some degree of phenotypic integration (i.e. such that some mice are consistently more aggressive than others based on all measures), we were not able to assess the genetic basis (or lack thereof) of these correlations. Similarly, our data were insufficient for meaningful comparison of (co)variance estimates between the sexes. Univariate sex-specific models provide little support for differences in variance components between males and females, but large standard errors associated with parameter estimates suggest that we have little power to test this (results not shown). Consequently, both male–male and female–female interactions were pooled for analysis. However, since sexual selection is commonly expected to shape agonistic behaviours (e.g. Kutsukake & Clutton-Brock 2006; Rosvall 2008), genetic architecture may differ substantially between males and females. Consequently, where possible, analyses of sex-specific traits may be useful for studies of aggression.

Despite these limitations, our results do clearly demonstrate the need to consider the genetic component of the social environment for a full understanding of the evolutionary dynamics of aggression. Furthermore, while our experimental design presents a very contrived and simplistic social environment, the IGE model used here is applicable to any complex pedigree structure, and can also be extended to include additional effects and complexity (e.g. larger or variable group sizes; Bijma et al. 2007a; Hadfield & Wilson 2007). This raises the possibility that such models could be applied to data from natural populations for which pedigree information is increasingly available (Pemberton 2008) and in which there is growing interest in understanding the quantitative genetics of social behaviours (Charmantier et al. 2007). Although an exciting prospect, there may well be some sources of real-world complexity that prove difficult to incorporate (e.g. dispersal of individuals between social groups).

Finally, we note that while we might certainly expect IGEs to assume particular importance for traits such as aggression (Moore et al. 1997) or mate choice (Petfield et al. 2005; Wolf et al. 2008), which are necessarily expressed in a social context, it is important to realize that their influence is not limited to those (primarily behavioural) traits that have been the focus of most studies in social evolution. For example, several recent empirical studies of livestock have shown that size and growth traits may equally be influenced by the social environment when individuals compete for limited resources (e.g. Bijma et al. 2007a; Ellen et al. 2007; Bergsma et al. 2008). Studies on IGEs may therefore have strong implications for many aspects of animal ecology. For instance, up to now empirical tests of the Chitty hypothesis (Chitty 1967) have only been able to find weak maternal effects and no heritability on behavioural and life-history traits in microtine populations, therefore rejecting the idea that population cycles could result from a delay between social conditions and density-dependent selection pressures on these traits (Boonstra & Boag 1987; Boonstra & Hochachka 1997). However, IGEs may increase the evolutionary potential of these traits, allowing them to evolve rapidly as a response to density-dependent selection pressures.

In conclusion, we have shown that IGEs play an important role in setting the evolutionary potential for aggression in this experimental system. As a consequence, classical analyses in which an individual's phenotype is assumed to be controlled by direct genetic effects alone have the potential to give very misleading expectations for evolutionary change.

Supplementary Material

Parameter estimates for fixed effects on expression of behavioural traits

Fixed effects on behavioural traits as estimated under Model 3 with significance testing using conditional Wald F-tests.