High temporal resolution and streak-free four-dimensional cone-beam computed tomography

Abstract

Cone-beam computed tomography (CBCT) has been clinically used to verify patient position and to localize the target of treatment in image-guided radiation therapy (IGRT). However, when the chest and the upper abdomen are scanned, respiratory-induced motion blurring limits the utility of CBCT. In order to mitigate this blurring, respiratory-gated CBCT, i.e. 4D CBCT, was introduced. In 4D CBCT, the cone-beam projection data sets acquired during a gantry rotation are sorted into several respiratory phases. In these gated reconstructions, the number of projections for each respiratory phase is significantly reduced. Consequently, undersampling streaking artifacts are present in the reconstructed images, and the image contrast resolution is also significantly compromised. In this paper, we present a new method to simultaneously achieve both high temporal resolution (~100 ms) and streaking artifact-free image volumes in 4D CBCT. The enabling technique is a newly proposed image reconstruction method, i.e. prior image constrained compressed sensing (PICCS), which enables accurate image reconstruction using vastly undersampled cone-beam projections and a fully sampled prior image. Using PICCS, a streak-free image can be reconstructed from 10–20 cone-beam projections while the signal-to-noise ratio is determined by a denoising feature of the selected objective function and by the prior image, which is reconstructed using all of the acquired cone-beam projections. This feature of PICCS breaks the connection between the temporal resolution and streaking artifacts’ level in 4D CBCT. Numerical simulations and experimental phantom studies have been conducted to validate the method.

Introduction

Modern three-dimensional radiotherapy and intensity-modulated radiation therapy enable precise dose painting in cancer treatment. The radiation dose delivery can be made conformal to the dimensions of the tumor while the sensitive structures around the tumor are spared. In order to achieve dose escalation, it is imperative to accurately position the patient and localize the target of the treatment, as high dose gradients may be utilized. To achieve this aim, x-ray CT scanning methods have been integrated with linear-accelerator-based treatment units. Different implementations have been developed using a kV source and a flat panel detector (Jaffray et al 2002, Jaffray and Siewerdsen 2000), a MV source and a flat panel detector (Ford et al 2002), and a MV source and a xenon CT detector inside a slip ring CT gantry (Mackie et al 1999).

The current kV CBCT data acquisition system in radiation therapy is comprised of a flat-panel imager and a kV source. The source–detector assembly is mounted on robotic arms so that as the linac rotates around the patient, cone-beam projection data sets can be acquired. Due to the limitation of the detector readout speed, about 600 cone-beam projections are acquired during a full gantry rotation for a 1 min scan. Although the acquired data are sufficient to reconstruct a streak-free three-dimensional volume for static image objects, motion artifacts impede the use of CBCT when the chest and the upper abdomen are scanned due to inevitable respiratory motion.

Recently, respiratory motion profiles extracted using either an external device or directly from projection data have been utilized to gate the acquired cone-beam projection data sets (Dietrich et al 2006, Kriminski et al 2005, Li et al 2006, Sonke et al 2005, Chang et al 2006). Namely, the cone-beam projection data are sorted into several respiratory phases. Image volumes for each respiratory phase are then reconstructed using the conventional FDK image reconstruction method (Feldkamp et al 1984). However, each phase has to be reconstructed using less than 100 cone-beam projections. As a result of the undersampling, streaking artifacts are rampant in reconstructed images. The cone-beam projections for each respiratory phase are bunched into several clusters. This non-uniform sampling pattern for each phase also significantly impedes an effective use of the undersampled projections. In order to balance the level of artifacts caused by undersampling and residual respiratory motion in each phase, for the state-of-the-art on-board CT imager, the cone-beam projections are often gated into only 4–10 respiratory phases. As a consequence, the temporal resolution of 4D CBCT is about 500–1000 ms, which is much worse than the temporal resolution of a 4D CT scan.

Recently, several interesting schemes have been proposed to mitigate streaking artifacts (Li et al 2007, Li and Xing 2006, Lu et al 2007). The first scheme is to use a multiple-gantry rotation scheme to acquire more projection data such that we may have more projections for each respiratory phase. The second scheme is to use a slow-gantry rotation. In this scheme, a reduction in the gantry rotation speed by factors of 2 and 4 were proposed to acquire cone-beam projection over more respiratory cycles. As a result, each respiratory phase may be reconstructed using more projections. These two schemes need longer scanning time in data acquisition. The third scheme is to take advantage of a high temporal resolution 4D CT image acquired in the treatment planning stage. Using a deformable image registration technique, the motion profile was extracted from the cone-beam projection data set. The motion profile was then utilized to warp the image volume to reconstruct an individual respiratory phase. This scheme has a nice feature of SNR enhancement. The SNR of the reconstructed image volume is dominated by the SNR of the prior image. The potential disadvantage of this scheme is the data inconsistency caused by different scanning parameters of planning CT data set and cone-beam CT data.

In this paper, we propose to break the connection between the level of streak artifacts and the temporal resolution using a newly developed image reconstruction method: prior image constrained compressed sensing (PICCS) (Chen et al 2008a, 2008b). The PICCS algorithm enables accurate reconstruction of an image object using a highly undersampled data set (about 10–20 projections) without streaking artifacts. In this paper, the prior image volume is the image volume reconstructed using all of the acquired cone-beam projections without gating. Using the PICCS algorithm, the width of the respiratory gating window can be significantly narrowed to improve the temporal resolution of 4D CBCT. We conducted numerical simulations and motion phantom experiments to demonstrate that PICCS enables reconstruction with ultra-high temporal resolution (~100 ms) and streak-free 4D CBCT images.

Methods and materials

The proposed image reconstruction algorithm

For CT imaging, it is well known that to avoid view aliasing artifacts, the view angle sampling rate needs to satisfy the Shannon/Nyquist sampling criteria (Kak and Slaney 1988, Natterer 1993). If the number of projections is fewer than that required by the sampling theory, which is usually the case for 4D CBCT, the undersampling streaking artifacts will contaminate the reconstructed images. However, a recently developed image reconstruction theory, compressed sensing (CS) (Candes et al 2006, Donoho 2006), demonstrates that the Shannon/Nyquist sampling theorymay be significantly violated if the target image is sparse. It has been proven that an N × N image can be accurately reconstructed from ~S ln(N) Fourier samples using a nonlinear optimization process provided that there are only S significant pixels in the image. This reconstruction framework can be described as solving a constrained minimization problem:

$$\text{min}(\parallel \mathrm{\Psi }I{\parallel }_{{\ell }_1}),\text{such that}AI=P,$$ (1)

where I is the image to be reconstructed and the ℓ₁ norm is utilized. For the constraint condition, A is the projection matrix and P is the measured projections. This constraint requires that the forward projections of the reconstructed images should agree with the measured projections at the same view angles. To take advantage of CS, the target image needs to be sparse. In medical imaging, target images are not always sparse. Thus, a sparsifying transform Ψ (e.g. a discrete gradient transform in this paper) can be applied to the target images so that the transformed images are sparse. Note that the ℓ₁ norm is utilized in CS theory, instead of the ℓ₂ norm that is used in most other iterative reconstruction algorithms. The reasons for this choice are twofold: first, using the ℓ₁ norm significantly promotes sparsity of an image (Candes et al 2006, Donoho 2006) while the ℓ₂ norm does not; second, the ℓ₁ norm maintains the convexity of the objective function, which is critical to ensure that the optimization process converges to a unique solution. In fact, mathematically speaking, one may think that ℓ_p (0 ≤ p < 1) would further promote sparsity and should be utilized in the design of the objective function. However, when 0 ≤ p < 1, the objective function is not convex and optimization is not numerically easily tractable. Fortunately, it has been mathematically proved (Donoho 2006) that the ℓ₁ norm minimization is nearly optimal and the solution is not different from the more complicated ℓ_p (0 ≤ p < 1) norm minimization. Thus, using the ℓ₁ norm minimization not only facilitates the implementation, but also enables us to obtain the nearly optimal sparse solution.

In CT imaging, a prior image is often available. For example, in 4D CBCT, the image reconstructed from all measured projections without gating can serve as a prior image. The difference images between phased images and the prior image are usually sparse. In this case, the newly developed generalization of the original CS algorithm, i.e. PICCS (Chen et al 2008a, 2008b), can be utilized to accurately reconstruct dynamic CT images from the vastly undersampled data sets.

Mathematically, the PICCS image reconstruction algorithm can be described as solving the following constrained minimization problem:

$$\text{min}(\alpha \parallel \mathrm{\Psi }(I-I_P){\parallel }_{{\ell }_1}+(1-\alpha )\parallel \mathrm{\Psi }I{\parallel }_{{\ell }_1}),\text{such that}AI=P.$$ (2)

The essential difference between CS and PICCS is that a prior image I_p is incorporated into the minimization procedure. The first term of the objective function aims to make the target images similar to the prior image. But the prior images are usually contaminated by motion and streaking artifacts caused by inconsistent projections. This effect is compensated by including the second term of the objective function. A free parameter, α, in the objective function is empirically selected. If α is selected to be 0, then equation (2) becomes degenerate with the conventional CS algorithm as equation (1).

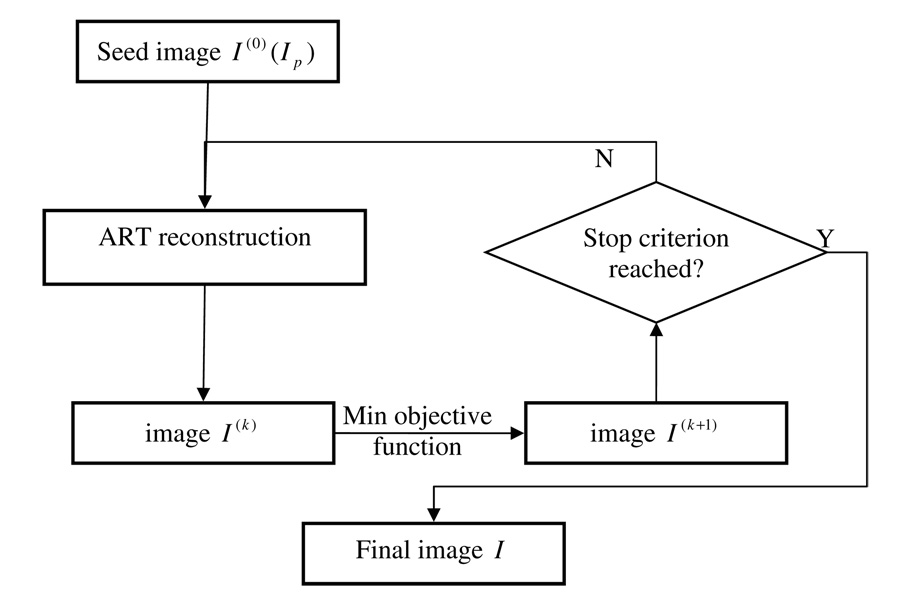
Several methods can be used to solve the constrained minimization problem in equation (2). In this study, itwas solved in two separate steps. In the first step, images were reconstructed using the algebraic reconstruction technique (ART) (Herman 1980) to meet the constraint AI = P. In the second step, the objective function α∥Ψ(I − I_P)∥_ℓ1 + (1 − α)∥ΨI∥_ℓ1 was minimized using the gradient descent method (Press 1997). The above two steps were implemented in an alternating manner. In our implementation, when the constraint, AI = P, is imposed in the ART step, due to the fact that the projection data set is highly undersampled, undersampling streaking artifacts will appear in the ART image which make it dissimilar with the prior image and increase the total variation of the image. When the objective function, α∥Ψ(I − I_P)∥_ℓ1 + (1 − α)∥ΨI∥_ℓ1, is minimized, streaking artifacts and dissimilarity relative to the prior image will be reduced in the reconstructed image. The iterative procedure was stopped when the squared difference of two successive images reached a predetermined threshold. For ART reconstruction, the major computation comes from the calculation of the system matrix, which contains intersection lengths between each ray with individual pixels. In our implementation, Siddon’s ray-driven forward projection method (Siddon 1985) was utilized due to its simplicity and efficiency. For clarity, a flow chart of the entire procedure is shown in figure 1.

Figure 1.

Flow chart of the implementation of the PICCS algorithm.

Dynamic phantoms used in numerical simulations

Numerical simulations were first conducted to demonstrate the advantage of using the PICCS algorithm in 4D CBCT. As demonstrated in figure 2(a), an analytical two-dimensional chest phantom was simulated and used in our numerical simulations. Two tumors were simulated inside the two lungs by two discs. Parameters of this phantom (at a 0% phase) are listed in the appendix. These two tumors were simulated to experience different motions during the respiratory cycle. The one inside the left lung undergoes a linear motion along the horizontal direction with the maximal displacement of 40 mm, which is equal to the diameter of the disc. The tumor inside the right lung deforms its vertical semi-axis length from 15 mm to 25 mm in one respiratory cycle. In these simulations, the breathing period was assumed to be 4 s. Six hundred projections were simulated in a full scan with a data acquisition time of 60 s. Images were reconstructed using both PICCS and a conventional filtered backprojection (FBP) algorithm (Kak and Slaney 1988). These images were compared to demonstrate the superiority of the PICCS algorithm.

Figure 2.

Phantom used in numerical simulations (a) and blurred image reconstructed from projections at all view angles.

Experimental motion phantom

Besides the numerical simulations, we also conducted physical motion phantom studies on a CBCT system integrated into the treatment gantry (Trilogy, Varian Medical Systems, Palo Alto, CA). To perform these studies, a motion platform was built in our laboratory. The platform consists of two sets of servo motors and linear stages, which enable simultaneous motion in two different directions. For 4D CBCT, a circular scanning trajectory is utilized. Since this scanning trajectory lies in a plane, motions will be categorized into in-plane motion and through-plane motion. In this study, the motion phantom was translated in both superior–inferior (SI) direction (through the plane motion) and anterior–posterior (AP) direction (in the plane motion).

Two physical phantoms were constructed and utilized in this study. In the first phantom, foam was inserted into a plastic cylinder to support two vertebra bones. Five ulna bones were attached outside of the cylinder to simulate sternum and ribs. A plastic ball was attached to the motion platform via a plastic rod so that the ball moves during the data acquisition to simulate a moving lung tumor. The maximal displacements for motion in these two directions are 20 mm (SI) and 10 mm (AP), respectively. The motion period was programmed to be 5.3 s. Note that there is an air cavity inside the plastic ball which can be observed in the reconstructed images.

During breathing, multiple organs may move in different directions with different velocities. In our first phantom, only a single object moves. To simulate simultaneous multi-organ motion, a second phantom was built. Three objects (one plastic ball and two plastic rods) were programmed to move simultaneously in the AP (10 mm) and SI (20 mm) directions. A picture of the three moving objects is shown in figure 3. The static portion is similar as the first phantom except that the vertebra bones were moved outside of the cylinder. The motion period for the moving objects was programmed to be 4.2 s.

Figure 3.

Three moving objects used in the second physical phantom.

Experimental data acquisition system

In this study, a Varian Trilogy treatment system was used to acquire cone-beam projections of the motion phantom. With the incorporated kV x-ray tube and flat panel detector, radiography or fluoroscopy can be performed to supply image guidance to the treatment procedure. Cone-beam CT is also available in this system by taking a series of 2D projections when the gantry rotates around the patient.

Compared with radiography, 3D CT images provide tomographic images without the superposition of anatomical structures. Hence, better low contrast detectability is obtained in CT images. This provides much more useful information than radiography. For example, the target tumor can be located in the CT images so that the patient positioning can be achieved based on the target tumor instead of the bony structures visible in the radiographs. In this study, typical scanning parameters, 125 kVp, 80 mA and the 12 ms pulse width, were selected. The detector dimension is 397 mm × 298 mm and it is separated into 1024 × 768 pixels. To reduce the computational load, a 2 × 2 binning mode was adapted so that the detector matrix is 512 × 384 with a pitch of 376 µm. In total, 640 projections were acquired over a 60 s rotation through 360°.

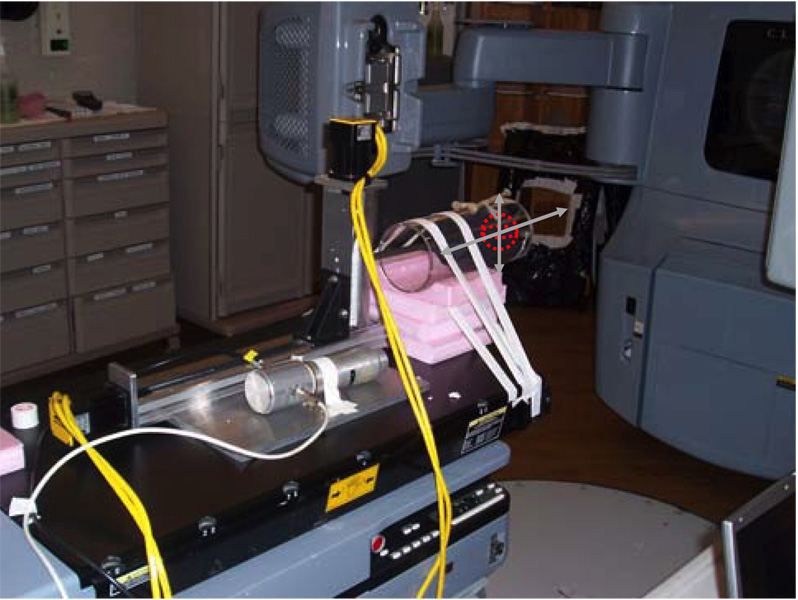
To perform gated reconstruction, the projections need to be gated into different groups based on the phase at which the projections are acquired. To achieve this, we placed a NaI(Tl) detector with a photomultiplier tube (PMT) close to but outside of the x-ray field of view to detect the x-ray scatter so that the ‘x-ray on’ signal can be passively obtained. A temporal stamp was thus achieved for each projection. This signal was sent to a personal computer so that it could be synchronized with the motion signal. The proper phase was then assigned for each projection based on these two synchronized signals. A picture of the system setup is presented in figure 4.

Figure 4.

System setup in phantom studies.

Results

Phantom experiments: numerical simulations

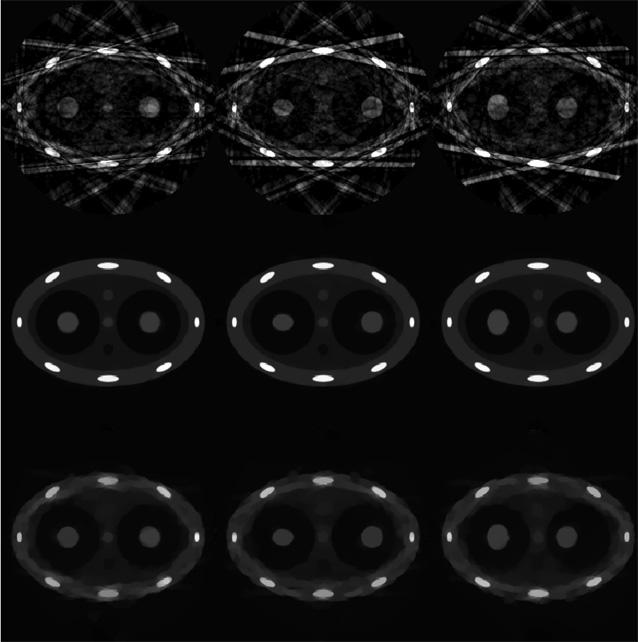
Numerical simulations were first conducted using the dynamic phantom presented in the previous section. A prior image was first reconstructed using all measured projections without gating. As shown in figure 2(b), the two simulated tumors are blurred due to the motion. Streaking artifacts outside of the moving objects are also observed due to the data inconsistency caused by the motions. These images, together with all other images in numerical simulations, are displayed inside a window of [−0.001 0.08] mm⁻¹ unless otherwise specified. Projections were then gated into 20 phases (the effective temporal gating window is 200 ms) and images were reconstructed using the gated projections at every phase. Images were first reconstructed using the conventional FBP algorithm, as shown in the upper row of figure 5. Due to the undersampling, severe streaking artifacts are observed in the entire image. These artifacts contaminate both the moving structures and the static structures in the image. The same projections were then used to reconstruct images using the newly proposed PICCS algorithm, and the results are presented in the middle row of figure 5. The image reconstructed from all projections (figure 2(b)) was used as a prior image in the PICCS algorithm. Compared with images reconstructed using the FBP algorithm, streaking artifacts are efficiently eliminated and the reconstructed images are almost free of artifacts. Also, by comparing the positions and shapes of the simulated tumors at different respiratory phases, the temporal information has been clearly restored. In these numerical simulations, the parameter α used in all these numerical simulations was chosen to be 0.28 and 12 iterations were conducted.

Figure 5.

Images reconstructed at phases of 0%, 30% and 70% are presented from left to right. Images reconstructed using FBP, PICCS and CS are from top to bottom. The gating window is 200 ms.

As shown in the previous section, PICCS becomes degenerate with standard CS if α is selected to be 0. To demonstrate the difference between PICCS and CS, images reconstructed using the standard CS method with the same reconstruction parameters as in PICCS were also given in the bottom row of figure 5. Blurred-patchy images, which are typical for the CS algorithm, are observed. By observing the images in figure 5, the superior image quality of PICCS reconstruction can be well appreciated.

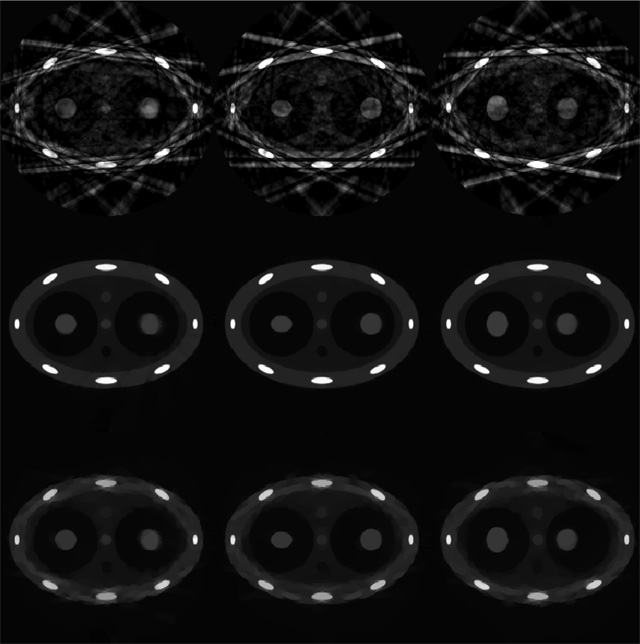
To study the effects of gating aperture on the image quality, the same projection data set was gated into ten phases which corresponds to a wider temporal window of 400 ms. Images reconstructed using the FBP, PICCS and CS algorithms at three different phases are shown in figure 6. Among these reconstruction algorithms, the PICCS algorithm outperforms both the FBP and CS algorithms. When a wider gating window is used, more projections are available for a given phase. For CS reconstruction, we can observe that the image quality is improved when compared with that using a 200 ms gating window. However, when a wider gating window is used, the projections inside the gating window are increasingly inconsistent. Therefore, motion blurring artifacts will present in the reconstructed images. This can be well appreciated by comparing the PICCS images at phase 0% with different gating window widths (figure 5).

Figure 6.

Images reconstructed at phases of 0%, 30% and 70% are presented from left to right. Images reconstructed using FBP, PICCS and CS are from top to bottom. The gating window is 400 ms.

A prior image is required in PICCS for the sparsifying transform. This image also serves as a seed image in this study. In previous simulations, the image reconstructed using all projections without gating has been used as the prior image. However, there is flexibility to choose different prior images. For example, it has been demonstrated that undersampling streaking artifacts can be mitigated using a correction algorithm previously proposed by our group (Leng et al 2008). In this correction algorithm, a time-averaged image over all the time bins is reconstructed using all available projections, i.e. no gating. In this case, static structures are well reconstructed while moving objects are blurred. The undersampling streaking artifacts from the static structures are estimated from this averaged image and utilized to mitigate streaking artifacts in the images for each phase. The corrected images obtained using the above correction algorithm can also be used as prior images in the PICCS algorithm. In figure 7, numerical simulation results are presented where the prior image is the corrected image obtained using our correction algorithm. The phase images given in figure 7 are reconstructed under the same parameters as those in figure 5 and figure 6. The results from figure 7 demonstrated that the aforementioned two different choices of prior image lead to nearly the same results which indicate that, in practice, the motion-blurred image reconstructed from all projections without gating is good enough for the PICCS algorithm to accurately reconstruct each individual phase image.

Figure 7.

PICCS reconstruction with a different choice of prior images. The correction algorithm in Leng et al (2008) was used to reconstruct prior images for each individual phase. Images reconstructed with gating windows of 200 ms (upper row) and 400 ms (lower row). Images reconstructed at phases of 0%, 30% and 70% are presented from left to right.

In summary, in these numerical simulations, we demonstrated that the PICCS algorithm can effectively reduce streaking artifacts due to the view angle undersampling while well maintaining the temporal information.

Phantom experiments: first motion phantom study

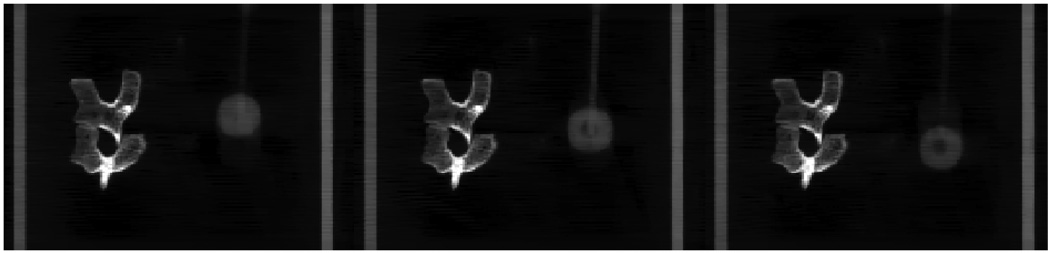
A home-made motion phantom was scanned using an on-board cone-beam CT imager. A 3D image volume was reconstructed using all of the acquired cone-beam projections without gating. Image slices from different directions (axial, sagittal and coronal) are presented in the top row of figure 8. Severe distortion of the moving ball is observed due to the motion blurring artifacts. Gated reconstruction was then performed to reduce the motion blurring. In this study, since the breathing period is 5.3 s, roughly 12 breathing cycles were measured during the 60 s data acquisition. The projection data were gated using a very narrow gating window (95 ms) such that only one projection was selected from each breathing cycle to reconstruct a given respiratory phase. Consequently, we only utilized 11 or 12 projections to reconstruct the image volume at a given phase. For comparison, images reconstructed using the standard FDK algorithm and the PICCS algorithm are presented in the second row and third row of figure 8. In PICCS reconstruction, the parameter α in equation (2) was selected to be 0.36 and eight iterations were utilized to generate the results. All images in the following sections are displayed inside the window [0 0.04] mm⁻¹ unless otherwise specified.

Figure 8.

4D CBCT images of a physical phantom. The top row shows images reconstructed from all views without gating, the second row shows images at 5% phase reconstructed using FDK with a 95 ms gating window, third row and bottom row show images reconstructed using PICCS (third row) and CS (bottom row) at the same phase as the second row. Images of axial, sagittal and coronal views are presented from left to right.

As shown in figure 8, severe streaking artifacts due to the view angle undersampling were observed in the images reconstructed using the conventional FDK algorithm. The streaking artifacts severely hinder the extraction of useful information from the reconstructed images. In contrast, images reconstructed using the PICCS algorithm are almost free of the streaking artifacts. In comparison with the prior images (top row in figure 8), the motion blurring artifacts observed in the prior images were clearly removed.

To demonstrate the performance difference between the PICCS algorithm and the original CS algorithm, the same respiratory phase is reconstructed using the CS algorithm under the condition of the same reconstruction parameters (note that we only need to set the parameter α to be zero in equation (2) to obtain the original CS reconstruction). The results are presented in the bottom row in figure 8. It is clear that the PICCS algorithm outperforms the CS algorithm.

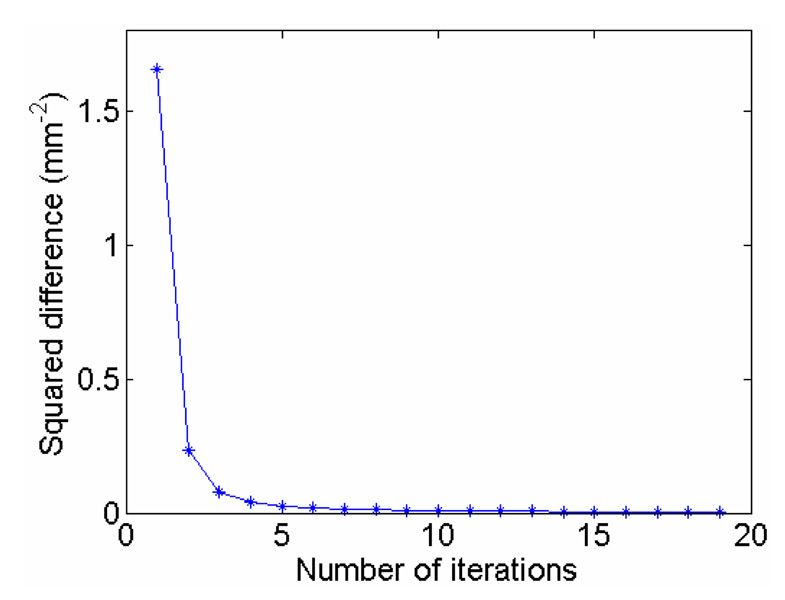
The convergence of the PICCS algorithm is guaranteed by the convexity of the objective function (by definition, the ℓ₁ norm is convex and the summation of two convex functions is still convex). In our study, the squared difference of two successive images is used as the stopping criteria. The iteration is stopped when the squared difference reaches a predetermined threshold, which is 0.01 mm⁻² in this study. The evolution of the squared difference versus the number of iterations is given in figure 9 using the 5% phase PICCS image in figure 8. The convergence is clearly demonstrated in figure 9.

Figure 9.

Convergence of the PICCS algorithm. The squared difference between two successive iterations is plotted against the number of iterations.

In order to demonstrate the preservation of the temporal dynamics in images reconstructed using the PICCS algorithm, three coronal image slices at different respiratory phases are presented in the middle row of figure 10. In comparison with the motion-blurred coronal image in the prior image (the top row in figure 8), temporal information has been well preserved using PICCS. This can be observed by the changes in the position and size of the moving ball. Note that the programmed motion was in both SI and AP directions. For comparison, images at the same phases reconstructed using the FDK and CS algorithms were also presented in the top row and bottom row in figure 10. Due to the poor image quality, it is difficult to extract temporal information from these images.

Figure 10.

Coronal images reconstructed at phases of 10%, 25% and 40% with FDK (top row), PICCS (middle row) and CS (bottom row).

In the numerical simulations, we have demonstrated that images reconstructed using our previous correction algorithm (Leng et al 2008) could be utilized as prior images. The same studies were conducted using the projection data of the physical phantom. As shown in figure 11 and figure 12, streak-free images are obtained when using prior images generated by the previous correction algorithm. Similar image quality is achieved compared with PICCS images in figure 8 and figure 10 where time-averaged prior images were utilized. In this case, the free parameter α in equation (2) was selected to be 0.3. When the quality of the prior image is relatively poor, a smaller value of the parameter α in equation (2) is needed in the PICCS algorithm.

Figure 11.

Images from axial (left), sagittal (middle) and coronal (right) views reconstructed using PICCS. Prior images were obtained from the correction algorithm in Leng et al (2008).

Figure 12.

Coronal images reconstructed at phases of 10%, 25% and 40% using PICCS. Prior images were obtained from the correction algorithm in Leng et al (2008).

Motion trajectories

In clinical practice, it is important to extract motion profiles of moving tumor or organs from the 4D CBCT images. This task strongly depends on the quality of the reconstructed images. As shown in figure 8 and figure 10, 4D CBCT images reconstructed using the conventional FDK algorithm were severely contaminated by streaking artifacts. Thus, the extraction of motion profiles from these images will be difficult and inaccurate. Since we have demonstrated that the PICCS algorithm can generate 4D CBCT images with superior quality, it is important to demonstrate the capability of extracting motion trajectories directly from the reconstructed 4D CBCT images.

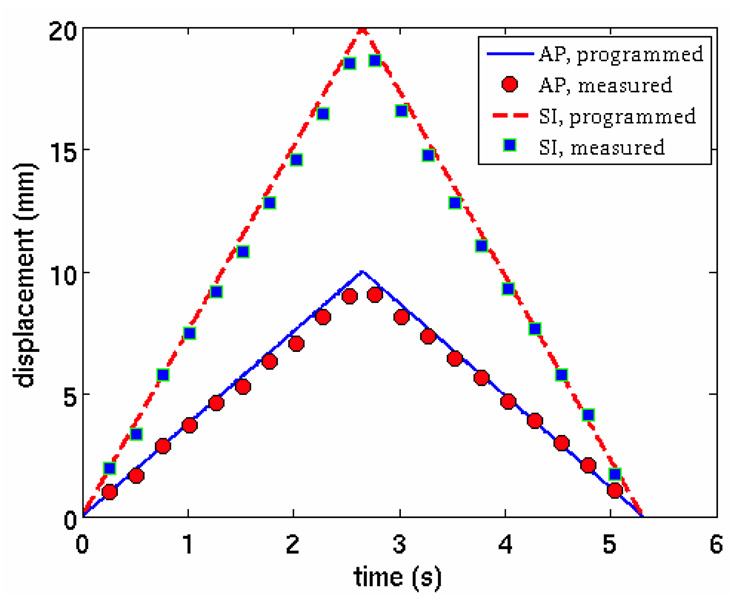
In practice, the motion trajectory should be derived in 3D space. In this study, the motions were programmed in both the AP and SI directions which can be utilized as the principal axes to study the motion profiles. Namely, the motion trajectory can be projected onto these two axes. Essentially, the motion is in a 2D plane. For each respiratory phase, the plastic ball was segmented out using a simple thresholding segmentation method. The center of mass of the segmented ball was calculated. The trajectory of the center of mass was plotted against the programmed motion profile (figure 13). Excellent agreement is observed between the measured profiles and the programmed profiles.

Figure 13.

Programmed and measured motion profiles. The measured motion profile was extracted from sagittal images reconstructed using PICCS.

Second phantom study

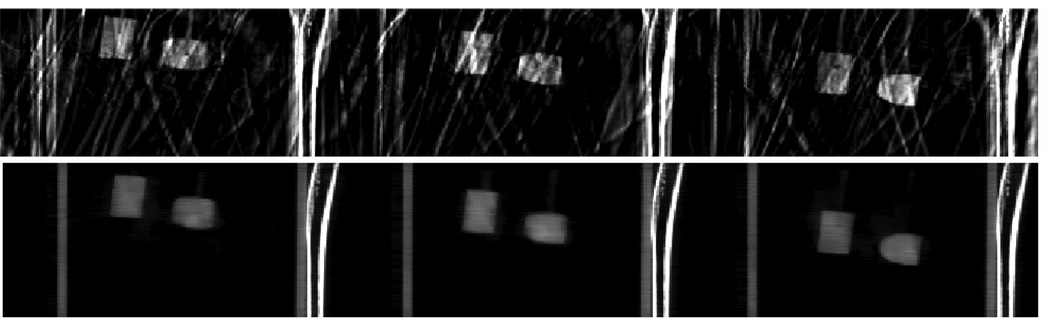
In the second phantom study, three different objects move simultaneously. The programmed breathing period was 4.2 s and the data acquisition time was 60 s. In this case, there were roughly 15 breathing cycles during the data acquisition. Once again, a 95 ms temporal gating window was utilized such that only one projection was selected in each breathing cycle. An axial slice and an oblique slice of the prior image are presented in figure 14. The oblique slice is parallel to the SI direction and is carefully selected to contain two moving objects. Motion blurring is observed in both slices, but is more pronounced in the oblique slice.

Figure 14.

Images reconstructed without gating. (a) Axial slice and (b) oblique slice.

The same oblique slice as in figure 14 was used to demonstrate the temporal information of the moving objects in the gated reconstructions. Images reconstructed using both the FDK and PICCS algorithms at the phases 0%, 25% and 60% are presented in figure 15. The undersampling streaking artifacts shown in the images reconstructed using the FDK algorithm were effectively removed in the images reconstructed using the PICCS algorithm. Also, note that temporal information is well preserved in the PICCS images and the motion blurring observed in the prior images was removed. This phantom study demonstrated that the PICCS algorithm works well with multiple moving objects.

Figure 15.

Images reconstructed by FDK (upper row) and PICCS (lower row) at 0%, 25% and 60% phases.

Discussion and conclusions

For lung cancer treatment, respiratory motion poses challenges for a cone-beam CT reconstruction to generate high temporal resolution images to guide the therapy. In order to mitigate the respiratory motion-induced motion blurring, 4D CBCT was introduced. However, poor image quality due to the streaking artifacts significantly limits the wide use of 4D CBCT in clinical practice.

In this work, a newly developed image reconstruction scheme, PICCS (Chen et al 2008a, 2008b), was proposed to reconstruct 4D CBCT images. Using the extensive numerical simulations and physical phantom studies, we have demonstrated that the PICCS algorithm enables accurate image reconstruction in 4D CBCT with a very narrow gating aperture (95 ms). The high temporal resolution and nearly artifact-free images also enable the accurate motion tracking in 4D CBCT.

Noise characteristics of the PICCS algorithm: a preliminary study

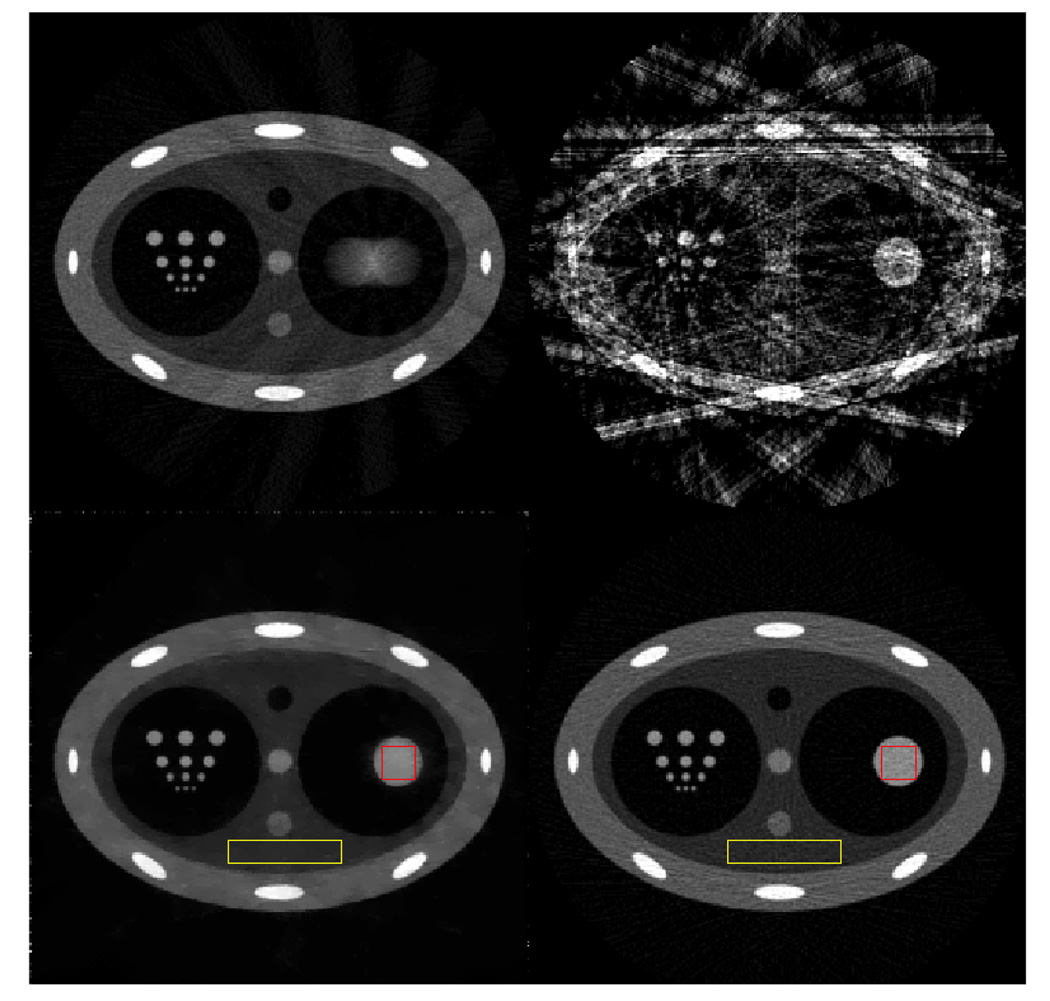
In 4D CBCT, the gating window critically impacts the final image quality. When a wider gating window is utilized, more projection data are available to reconstruct the given respiratory phase. Consequently, the reconstructed images contain less severe streaking artifacts and the contrast-to-noise ratio (CNR) is higher. However, when a wider gating window is utilized, the projection data within a given respiratory phase are more inconsistent due to residual respiratory motion. As a result, the motion blurring and motion-induced streaking artifacts are more severe. Therefore, the key issue in 4D CBCT is how to reconstruct artifact-free 4D CBCT images with simultaneously high temporal resolution and a high CNR. The CNR is determined by the available number of x-ray photons. When the same tube current and pulse width remain constant, the available number of photons is fundamentally determined by the number of cone-beam projections. Thus, when the conventional FDK image reconstruction algorithm is utilized, the requirements of a high CNR, streaking artifact-free and the high temporal resolution intrinsically contradict one another. The key contribution of the present paper is to demonstrate that the above three requirements can be met using the new PICCS image reconstruction algorithm. First, the new mathematical foundation of the compressed sensing enables accurate image reconstruction using highly undersampled data sets. The PICCS algorithm utilizes a subtraction operation in addition to other known sparsifying transforms in compressed sensing theory. This enables accurate image reconstruction using even fewer number of cone-beam projections. As a result, high temporal resolution image reconstruction is achieved. On the other hand, the prior image in the PICCS reconstruction was reconstructed using all of the acquired projection data. Images reconstructed with all of the projection data will be intrinsically high in the CNR. When the high CNR prior image is utilized in PICCS reconstruction, the target image inherits the high CNR feature from the prior image. Thus, the CNR of the reconstructed image is decoupled from the number of projections in each individual phase. In order to demonstrate this novel feature, numerical simulations were conducted to quantitatively study the intrinsic CNR in PICCS images. A simulated chest phantom was reconstructed using projections with simulated Poisson noise. In this study, 3000 photons per detector bin per view were simulated. A prior image, which was reconstructed from all 600 projections without gating, is shown in figure 16 (upper left image) and a representative phase image (30% phase) reconstructed using both the FBP (upper right in figure 16) and PICCS (lower left in figure 16) algorithms is also presented. Noise variances were measured in a region of interest (ROI) inside the moving disc (labeled with a red square) and in a static background region (labeled with a yellow rectangular) in the phase image. Please note that the moving object in the prior image was blurred. Thus, it is not suitable for noise variance measurements. For comparison, a static phantom in which the disc is at the same position as that in the PICCS phase image was also reconstructed using 600 projections with the same noise level (3000 photons for each detector bin). Noise variances were then measured inside the same ROIs as in the phase image. The noise measurements were conducted at equivalent spatial resolution, as is demonstrated by the resolution pattern in the right cavity. These results are presented in table 1.

Figure 16.

Prior image (upper left), 30% phase FBP image (upper right), 30% phase PICCS image (lower left) and image reconstructed using the FBP algorithm from a static phantom (lower right). All images are displayed inside the window [0 0.05].

Table 1.

Noise variance comparison.

	PICCS image	Static image
ROI inside moving object	2.13 × 10−6	2.14 × 10−6
ROI inside static background	3.52 × 10−7	1.92 × 10−6

The implication of the above numerical simulations can be summarized as follows: since the phase image was reconstructed using 30 total projections which are bunched into 15 subgroups, it is anticipated that the noise variance will drop by a factor of 600/30 = 20 in the reconstructed image. However, using the PICCS algorithm, the noise variance of the moving object is basically the same as that reconstructed from 600 projections. In the static background, the noise variance is also reduced roughly by a factor of 5. This portion of noise variance reduction can be attributed to the denoising feature of the total variation operation in image reconstruction (Velikina et al 2007). In summary, the results of this numerical simulation indicate that the noise variance in PICCS images for each phase is not worse than the FBP images reconstructed from a fully sampled data set.

Performance comparison between CS, PICCS and PWLS

Extensive investigations of iterative reconstruction algorithms have been conducted in x-ray CT and in nuclear medicine such as in positron emission tomography (PET) and single photon emission tomography (SPECT). These algorithms include algebraic reconstruction algorithms (Kak and Slaney 1988) and statistical image reconstruction algorithms such as maximum-likelihood expectation-maximization (ML-EM) (Dempster et al 1977, Lange and Fessler 1995), penalized weighted least square (PWLS) (Fessler 1994) and so on.

In this paper, we have demonstrated that the original CS method is not suitable for image reconstruction in 4D CBCT while the newly developed PICCS algorithm enables accurate image reconstruction in 4D CBCT with high temporal resolution. However, one may wonder whether other classical image reconstruction algorithms such as PWLS will work for 4D CBCT. In this work, we conducted both numerical simulations and physical phantom studies to compare the performance of the PWLS method with the CS method and the PICCS method.

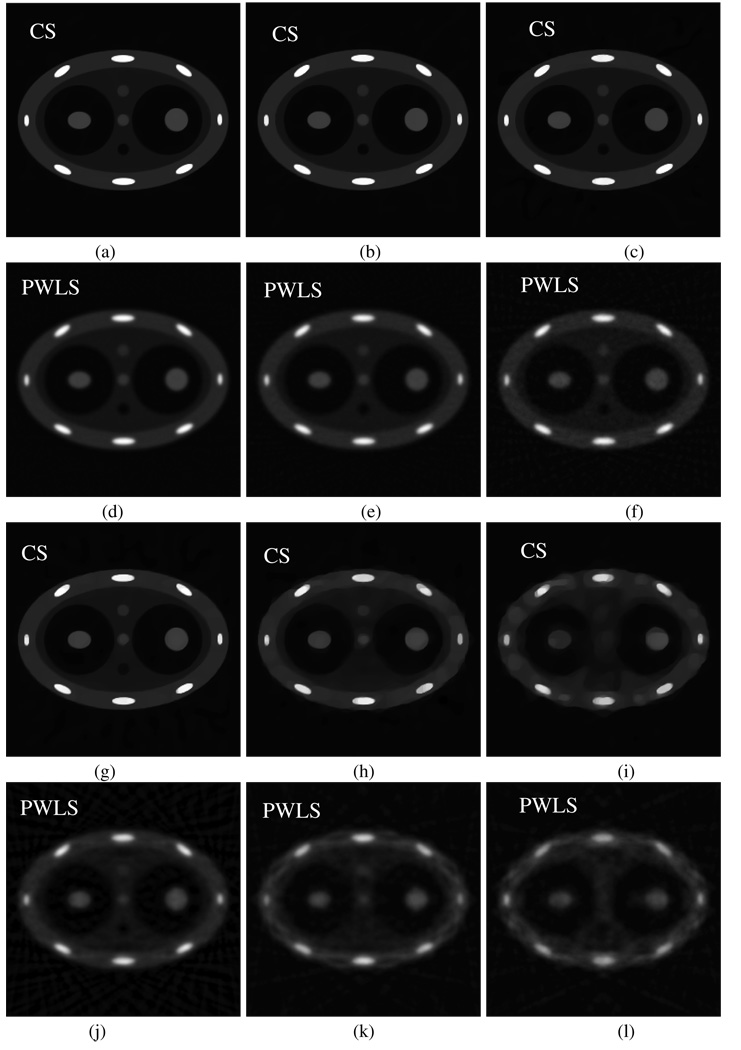
First, we studied how image performance changes with the number of available projections in the CS method and the PWLS method. The classic PWLS (Fessler 1994) algorithm was implemented in this study. As shown in figure 17, when the number of projections is high, there is a little difference in image quality for the two algorithms (figures 17(a) and (d)). However, with the decrease of the number of projections, the image quality of the PWLS algorithm is significantly degraded while the CS method still enables accurate image reconstruction until the number of projections drops down to about 20 projections (figure 17(h)). In contrast, more than 100 projections are required for PWLS to reconstruct acceptable images (figure 17(e)). Please note that uniform view angle sampling is utilized in the above numerical simulations while in 4D CBCT, the view angle sampling is not uniform. For a non-uniform sampling pattern, a significantly higher number of projections are required for an acceptable image reconstruction. In the PWLS algorithm, the weight of the nearest neighbor pixel is selected to be one and the next nearest neighbor pixel is $\sqrt{2}/2$. The weight of the penalty term used in our numerical simulations are 15 000, 5000, 4000, 3000, 2500 and 2000 for view angle numbers 300, 100, 60, 40, 20 and 12, respectively. In all numerical results in figure 17, 100 total iterations were utilized in reconstruction.

Figure 17.

Images reconstructed using CS (first and third rows) and PWLS (second and fourth rows) from uniformly sampled projections. The number of projections is 300 (a), (d); 100 (b), (e); 60 (c), (f); 40 (g), (j); 20 (h), (k) and 12 (i), (l). These images are displayed inside the window [−0.001 0.08].

Second, we directly compare the image performance of PICCS and PWLS using experimental phantom data. Note that it was shown in figure 8 and figure 10 that the PICCS algorithm is superior to the CS method. In figure 18, we compare PICCS with the PWLS method. From these results, it is clear that the PICCS algorithm outperforms the PWLS algorithm.

Figure 18.

Images reconstructed with PICCS (a) and PWLS (b). Only 11 projections were utilized in each image.

The above preliminary comparisons demonstrate the differences between the CS and PICCS methods and the classic PWLS method; CS and PICCS algorithms enable accurate image reconstruction from highly undersampled projection data. In contrast, the PWLS method does not perform very well when the number of projections drops.

In conclusion, the PICCS algorithm has been proposed to accurately reconstruct 4D CBCT images with high temporal resolution. The method has been validated in both numerical simulations and physical phantom experiments. The final clinical outcome of the PICCS algorithm in 4D CBCT must be validated in human subject studies. This step is ongoing at our institute and other collaborating institutes as well. We will share the results from a comprehensive clinical study in future publications.

Appendix

Table A1.

Parameters of the phantom used in numerical simulations.

Object index	x0 (mm)	y0 (mm)	Rotation angle (degree)	Semi-axis x (mm)	Semi-axis y (mm)	Density (mm−1)
1	0	0	0	180	120	0.02
2	0	0	0	150	90	−0.01
3	75	0	0	60	60	−0.01
4	−75	0	0	50	60	−0.01
5	0	105	0	20	6	0.06
6	0	−105	0	20	6	0.06
7	165	0	0	4	10	0.06
8	−165	0	0	4	10	0.06
9	104	84	65	6	16	0.06
10	104	−84	125	6	16	0.06
11	−104	84	−65	6	16	0.06
12	−104	−84	−125	6	16	0.06
13	0	0	0	10	10	0.015
14	0	50	0	10	10	−0.01
15	0	−50	0	10	10	0.01
16	75	0	0	20	20	0.03
17	−75	0	0	20	20	0.03