Automated Potentiometric Titrations in KCl/Water-Saturated Octanol: Method for Quantifying Factors Influencing Ion-Pair Partitioning

Abstract

The knowledge base of factors influencing ion pair partitioning is very sparse, primarily because of the difficulty in determining accurate log P^I values of desirable low molecular weight (MW) reference compounds. We have developed a potentiometric titration procedure in KCl/water-saturated octanol that provides a link to log P^I through the thermodynamic cycle of ionization and partitioning. These titrations have the advantage of being independent of the magnitude of log P, while maintaining a reproducibility of a few hundredths of a log P in the calculated difference between log P neutral and log P ion pair (diff (log P^N − I)). Simple model compounds can be used. The titration procedure is described in detail, along with a program for calculating pK_a′′ values incorporating the ionization of water in octanol. Hydrogen bonding and steric factors have a greater influence on ion pairs than they do on neutral species, yet these factors are missing from current programs used to calculate log P^I and log D. In contrast to the common assumption that diff (log P^N − I) is the same for all amines, they can actually vary more than 3 log units, as in our examples. A major factor affecting log P^I is the ability of water and the counterion to approach the charge center. Bulky substituents near the charge center have a negative influence on log P^I. On the other hand, hydrogen bonding groups near the charge center have the opposite effect by lowering the free energy of the ion pair. The use of this titration method to determine substituent ion pair stabilization values (IPS) should bring about more accurate log D calculations and encourage species-specific QSAR involving log D^N and log D^I. This work also brings attention to the fascinating world of nature’s highly stabilized ion pairs.

The lipophilicity of drugs has proven to be a valuable property in correlations of biological activity and associated ADMET properties. The log P or log D term in Hansch equations is almost always the most significant term.(1) In an article on ADMET studies, van de Waterbeemd depicts log D diagrammatically at the center of prediction paradise.(2) However, log D has a deficiency in one area. There is still a need for good measured data on the partition coefficients of ion pairs, log P^I.(3) Log P^I is a component of log D, as well as being capable of direct correlations in its own right. Our work suggests that dissatisfaction with the quality of calculated log D values^4,5 may well be due to the incorrect assumptions made in estimating log P^I. Our earlier titrations in water-saturated octanol⁶⁻⁸ proved so informative with respect to features that affect the lipophilicity of ion pairs that we undertook to simplify and fully automate the titration procedure.(9) In the process, valuable quantitative data was obtained and is presented here, along with details of the titration. A factor that makes this titration approach so useful is that, in contrast to other methods for determining partition coefficients, it is insensitive to the magnitude of P. It works as well for N-methyl-d-glucamine, log P −3.37, as for hexachlorophene, log P 6.91, with reproducibility of a few hundredths of a pK_a′′ unit.(3) This allows the use of simple model compounds to catalog the lipophilicity of ionizable groups and to analyze factors that influence log P^I.

In order to consider single phase titrations in octanol, one needs a definition of pH, or its equivalent, and pK_a in that system. We proposed such definitions for two-phase octanol/water systems, Figure 1, some years ago.(6) The protons are in equilibrium between the two phases so that the net free energy per unit volume in the octanol is equal to the free energy per unit volume in the aqueous phase. In other words, fewer protons in octanol, with higher free energy, balance a greater number of protons in water having a lower free energy. We define the pH of the octanol phase as being equivalent to the pH of the aqueous phase and call the values equal, even though the pH terminology in octanol has no meaning in solution theory. This definition puts all titrations in octanol on the same scale. It affects pK_a calculations, and by definition, all log P^I and log D calculations the same way, so there should be no relative error between compounds. The pK_a in octanol (pK_a oct), is equal to the pH at which the concentrations of the neutral and ionized species in the octanol phase are equal.(6) Both pK_a oct and log P^I are dependent on the counterion concentration, so that concentration must be stated, or it is otherwise assumed to be at physiological concentration, 0.15 M. The concept of a pK_a in octanol is not a familiar one, but its presence has been evident for many years in the lipophilic profiles of ionizable compounds (log D vs pH plots) covering a sufficient pH range.^6,10 The pK_a oct is at the lower inflection, complementing the aqueous pK_a at the upper inflection. The pK_a oct can be calculated from two-phase titrations, as described below. Two-phase titrations provide reference pK_a oct values for our single-phase titrations.

Figure 1.

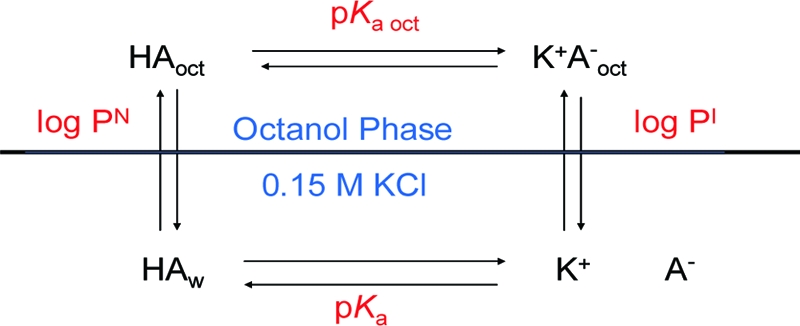
The thermodynamic cycle of the ionization and partitioning of an acid between octanol and water.

The four connected equilibria of ionization and partitioning in Figure 1 make up a thermodynamic cycle. Since every equilibrium has an associated Gibbs free energy (eq 1), the net free energy change around that cycle is zero. This provides the very useful relationships of eqs 2a and 2b, conveniently condensed to eq 2c, using the diff terminology of the Testa group.(11) Knowing any three of the equilibrium constants allows one to calculate the fourth. The value most often calculated is pK_a oct, using log P and log P^I obtained from two-phase titrations, and the aqueous pK_a. Since the diff terms of eq 2c represent differences in equilibria corresponding to differences in free energy, they are also free energy terms. One unit of difference in either diff pK_a oct or diff (log P^N − I) corresponds to 1.36 kcal/mol or 5.70 kJ/mol at 25 °C.

The Gibbs free energy equation is

Since the net free energy change around the cycle is zero, one can write the following relationships for the equilibria in Figure 1:

or, in combined form,

where diff pK_a oct is (pK_a oct − pK_a) for acids and (pK_a − pK_a oct) for bases.

If one could directly determine pK_a oct values by single-phase titrations in water-saturated octanol, it would offer a simple route to log P^I. That was the inspiration to try such titrations, which proved to be smooth and reproducible.(6) Their plots look like normal titration curves and provide useful information. The procedure has now been automated and further simplified to the form presented here. The BIOpKaCalc program used for calculating pK_a′′ values is detailed in the Supporting Information. Conveniently, pK_a′′ values appear to differ from pK_a oct values by a constant. This difference is discussed later under the .

Characteristics of Titrations in Octanol

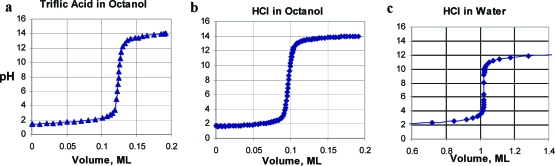
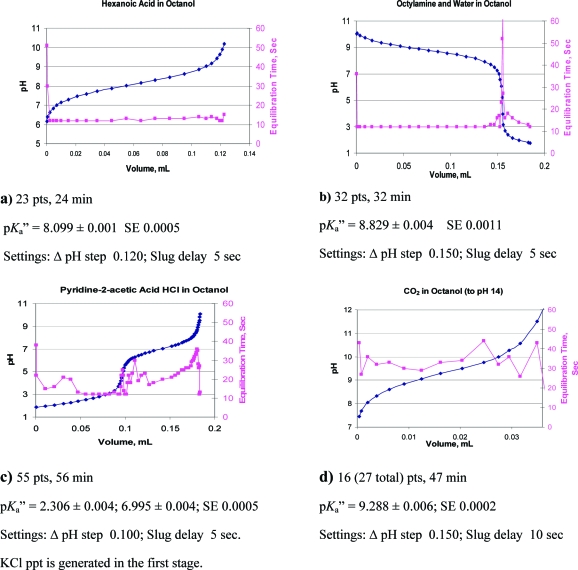
One can see from the comparisons in parts a−c of Figure 2 that titrations in octanol cover a greater pH range than in water. It is the two ionization constants of water in octanol that determine this range. Most of our initial concerns about such titrations dealt with the electrode, whether it would function properly, be stable, and give meaningful values. Representative titration curves are shown in parts a−d of Figure 3. The electrode equilibration time overlaid on these curves gives a sense of the quality of the titrations and relieves much of the concern about the electrode response. The slower response time in octanol requires loosening the equilibration requirement to 0.010 ΔpH units/min instead of 0.002 for aqueous systems. Electrode stress is evident with the initial few points and during periods of more rapid pH change. Parts a and b of Figure 3 show typical curves for a carboxylic acid and aliphatic amine. Titrations can be applied to more complex molecules, such as an internally compensated zwitterion, Figure 3c, which requires determining the pK_a′′ of water, as well as a carboxylic acid and an amine. Interestingly, the pK_a′′ results agree with observations made from the lipophilicity profile of charge-compensated zwitterions, that the amines are more basic and the acids more acidic, in octanol than in water.^8,12 Insoluble KCl is produced in Figure 3c, which may affect equilibration time. Figure 3d, for CO₂ (and/or H₂CO₃), illustrates a small sample size requiring only 0.03 mL of titrant in 15 mL of octanol. The second pK_a′′ of carbonate could not be determined due to insolubility of the double salt.

Figure 2.

Titration blanks of water in octanol and water in water, illustrating the greater dynamic pH range available in octanol. Insoluble KCl is produced in part b.

Figure 3.

Representative titration curves overlaid with plots of equilibration times. The pK_a′′ ± SE is shown for each titration. Equilibration times are indicative of the quality of a titration. Plots a and b represent near ideal parameter selections. Plot c has more points than needed. Equilibration times may be influenced by the production of insoluble KCl (c) or the concentration or nature of the ion pair produced (d).

Experimental Section

Equipment and Materials

The GLpKa-01 model titrator used was obtained from Sirius Analytical Instruments Ltd., East Sussex, U.K. (U.S. offices, Sirius Analytical Inc., Piscataway, NJ 08854). Its features include a provision for use with argon, an automated handling of octanol, a temperature-controlled 50-well sample tray, and a low minimum dispensing volume of 0.000 42 mL. A compact probe unit combines the electrode, stirrer, temperature probe, capillary dispenser tubes, and tubing for inert gas. The titrations take place in 25 mL flat-bottomed titration vials (“Sirius vials”). We used a Sirius electrode which is based on a Ag/AgCl reference half-cell and is made in the U.K.

Compounds 1−44 were obtained from commercial sources except for trifluoromethanesulfonamide (35) and its N-phenyl- (33) and N-methyl- (34) derivatives. These latter came from internal 3M sources but were prepared by published procedures.(13) The octanol is ACS spectrophotometric grade, ≥99%, from Aldrich.

Preparation of Titrants

The 0.5 N titrants were prepared using DILUT-IT analytical concentrates (J. T. Baker), designed for the preparation of 1.00 L solutions of 1.00 N KOH and HCl. By diluting each, instead, with USP absolute ethanol to 2.00 L, 0.5 N solutions were obtained. The water content was calculated by the difference in weight of the ampule contents and 1.00 mol of titrant. The concentration of water in the final solutions was 7.54% v/v for the KOH and 6.16% v/v for the HCl. This compares to 2.4 vol % water in KCl/water-saturated octanol. At the recommended sample size of 0.05 mmol, the titrant amounts to about 0.1 mL, less than 1% of the final volume. Standardizations were carried out in the usual manner in water. Potassium hydroxide was selected over sodium hydroxide to minimize the electrode sodium error following the example and guidance of Avdeef and the Sirius Company.(14)

Caution

The long-term stability of the glass components of the buret to 0.5 N KOH in ethanol is unknown. No problems or changes were observed with the Sirius buret, in which it was routine practice to use the ethanolic titrants for 1 week periods. In earlier work, a buret of different design and make was rendered useless by prolonged standing with 0.1 N NaOH in octanol/methanol (3:1) containing 4% water.

The Octanol Medium and KCl

The KCl/water-saturated octanol was prepared by equilibrating 25 mL of 0.15 M KCl per liter of octanol. It is the same preparation prescribed by Sirius for two-phase titrations. KCl eventually crystallizes from the small amount of remaining aqueous phase. The octanol contains 2.4 vol % water compared to 3.1 vol % water in saturated octanol when no salt is present.(14) The fact that the octanol is saturated with KCl has the positive benefit of providing a constant counterion background, even when KCl is produced during a titration. On the other hand, this higher concentration of KCl biases the results by favoring ion pair formation. The electrode correction factor (see below) automatically includes this influence.

Titration Procedure

(Complete details of the titration procedure are provided in the Supporting Information.) Publications by the Sirius Company directed toward two-phase titrations in octanol provide useful background information on the titrator performance and on ion pairs in octanol.^14,15 The titrator is converted for titrations in octanol by a simple process. It involves merely replacing the aqueous titrants in the burets and switching the electrode rinse baths to 50% ethanol. The automated titrator program for aqueous titrations is used with a few changes in parameters. The full list of optimum parameter settings is provided in Table S1 in the Supporting Information. Two important changes are (1) the stirring time after each pulse (slug) of titrant is set at 3−5 s, instead of 1 s, to avoid overshooting the desired pH interval between points. (2) The equilibration requirement is set at 0.010 ΔpH units/min instead of 0.002 for aqueous systems. The electrode is automatically calibrated in aqueous pH 7 buffer prior to each sample run. (A one-buffer calibration is built into the GLpKa titrator.) In contrast to aqueous procedures, we do not adjust the first point to a specific pH and only rarely will initially add a small volume of the opposite titrant. It is difficult to attain a specific pH as a first point, and the back-titration produces insoluble KCl. The sample to be titrated is predissolved in 15 mL of KCl/water-saturated octanol, usually with sonication, and often with slight warming.

Production of KCl in Titrations

Theoretically, there should be no change in the composition of the octanol solution with the formation of insoluble KCl, and the amount of precipitate should be irrelevant. Infrequently, whether due to a specific ion pair, a high equivalent of KCl precipitate, or other factors, the suspension of KCl will become slightly cloudy, possibly indicating some phase separation. No detectable curve shifts or deterioration of statistical terms were observed in these situations. This recalls a comment by Avdeef that single phase titrations in octanol can be viewed as extensions of two-phase titrations in which the octanol/water ratio approaches infinity.(16) Still, we prefer to avoid or minimize the production of KCl when possible. Comparison titrations of acids and bases and their corresponding salts are provided for compounds 2, 6, and 21, Table 2. A convenient sample size is 0.05 mmol in 15 mL of octanol, requiring 0.1 mL of titrant, and this can easily be reduced further. The titration of CO₂ in Figure 3g required only 0.033 mL of titrant.

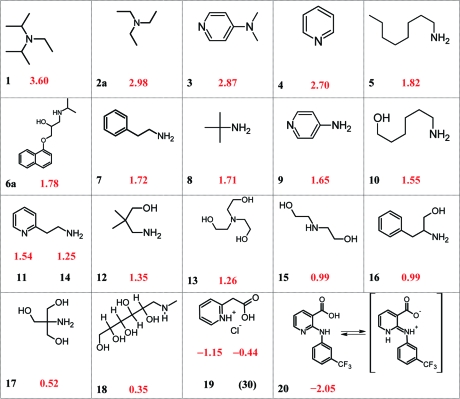
Table 2. Titration Results Sorted by Class and diff pK_a′′^a.

no.	compound	log PNb	pKab	pKa′′ ± SDc (n)	diff pKa′′ d
Bases
1	diisopropylethylamine	2.35e	11.44f	7.84 ± 0.00 (4)	3.60
2a	triethylamine	1.45	10.72	7.74 ± 0.03 (2)	2.98
2b	triethylamine HCl	1.45	10.72	7.65 ± 0.01 (2)g	3.07
3	4-(dimethylamino)pyridine	1.34	9.60	6.73 ± 0.02 (2)	2.87
4	pyridine	0.65	5.17	2.47 ± 0.02 (2)	2.70
5	n-octylamine	3.09	10.65	8.83 ± 0.01 (2)	1.82
6a	propranolol	3.48h	9.53h	7.75 ± 0.00 (2)	1.78
6b	propranolol HCl	3.48h	9.53h	7.79 ± 0.00 (2)g	1.74
7	phenethylamine	1.37i	9.96i	8.24 ± 0.00 (2)	1.72
8	tert-butylamine	0.40	10.68	8.97 ± 0.00 (2)	1.71
9	4-aminopyridine	0.32	9.11	7.46 ± 0.01 (2)	1.65
10	6-amino-1-hexanol	−0.01e	10.52j	8.97 ± 0.02 (2)	1.55
11	2-(2-pyridyl)ethylamine (pK1)k	0.08i	3.92i	2.38 ± 0.16 (2)	1.54
12	3-amino-2,2-dimethyl-1-propanol	−0.42e	9.84j	8.49 ± 0.02 (2)	1.35
13	triethanolamine	−1.00	7.76	6.50 ± 0.05 (4)	1.26
14	2-(2-pyridyl)ethylamine (pK2)k	0.08i	9.51i	8.26 ± 0.02 (3)	1.25
15	diethanolamine	−1.43	8.88	7.89 ± 0.03 (5)	0.99
16	2-amino-3-phenylpropanol	0.77e	8.74j	7.75 ± 0.00 (2)	0.99
17	tris(hydroxymethyl)aminomethane	−1.38e	8.08	7.56 ± 0.01 (4)	0.52
18	N-methyl-d-glucamine	−3.37e	9.62l	9.27 ± 0.03 (4)	0.35
19	pyridine-2-acetic acid HClk	−0.08	5.79	6.94 ± 0.05 (3)g	−1.15
20	niflumic acid (zwitterion, NH+)	3.88m	4.44m	6.49 ± 0.00 (2)	−2.05
Carboxylic Acids
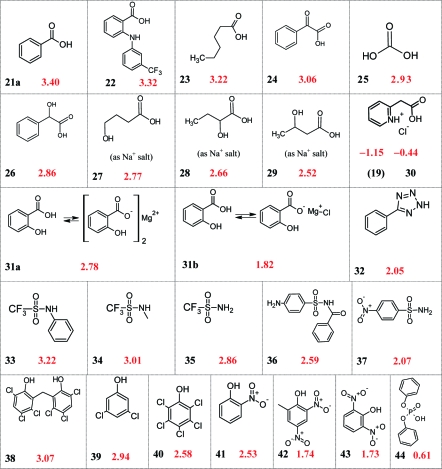
21a	benzoic acid	1.87	4.20	7.60 ± 0.04 (9)	3.40
21b	benzoic acid, K+	1.87	4.20	7.59 ± 0.04 (3)g	3.39
21c	benzoic acid, Na+	1.87	4.20	7.46 ± 0.07 (4)	3.26
22	flufenamic acid	5.93	3.85n	7.18 ± 0.02 (2)	3.32
23	hexanoic acid	1.92	4.88	8.10 ± 0.00 (2)	3.22
24	phenylglyoxalic acid	0.69e	1.21	4.27 ± 0.01 (2)	3.06
25	CO2/carbonic acid (pK1)	0.83o	6.35	9.28 ± 0.00 (3)	2.93
26	2′-hydroxyphenylacetic acid	0.62	3.39	6.25 ± 0.01 (2)	2.86
27	4-hydroxybutyric acid, Na+	−0.70e	4.60	7.37 ± 0.02 (2)	2.77
28	2-hydroxybutyric acid, Na+	−0.17e	3.68	6.34 ± 0.03 (3)	2.66
29	3-hydroxybutyric acid, Na+	−1.14e	4.39	6.91 ± 0.03 (3)	2.52
30	pyridine-2-acetic acid HClk	−0.08	2.73	2.29 ± 0.00 (3)g	−0.44
Carboxylic Acids, Mg2+ Salts
19d	(benzoic acid)2 Mg2+ (pK2)	1.87	4.20p	7.39 ± 0.06 (2)	3.19
19e	benzoic acid, Mg+Cl	1.87	4.20p	6.43 ± 0.02 (2)	2.23
31a	(salicylic acid)2 Mg2+ (pK2)	2.26	2.98p	5.76 ± 0.06 (2)	2.78
31b	salicylic acid, Mg+Cl	2.26	2.98p	4.80 ± 0.06 (2)	1.82
Other Acids
32	5-phenyltetrazole	1.65	4.38	6.43 ± 0.01 (2)	2.05
33	N-phenyltrifluoromethane-sulfonamide	3.05	4.45q	7.67 ± 0.01 (2)	3.22
34	N-methyltrifluoromethane-sulfonamide	1.28	7.56q	10.57 ± 0.05 (2)	3.01
35	trifluoromethanesulfonamide	0.24e	6.33q	9.19 ± 0.01 (2)	2.86
36	sulfabenzamide	1.19e	4.57	7.16 ± 0.02 (3)	2.59
37	4-nitrobenzenesulfonamide	0.64	9.48e	11.55 ± 0.00 (2)	2.07
38	hexachlorophene (pK1)	6.91r	3.60r	6.67 ± 0.01 (2)	3.07
39	3,5-dichlorophenol	3.52	8.22	11.16 ± 0.04 (4)	2.94
40	pentachlorophenol	5.12	4.83s	7.41 ± 0.00 (2)	2.58
41	2-nitrophenol	1.79	7.23	9.76 ± 0.02 (4)	2.53
42	2-methyl-4,6-dinitrophenol	2.13	4.46s	6.20 ± 0.00 (2)	1.74
43	2,6-dinitrophenol	1.37	3.56	5.29 ± 0.02 (5)	1.73
44	diphenylphosphate	1.34e	1.85t	2.46 ± 0.02 (2)	0.61

^aThe smaller the diff pK_a, the more lipophilic the ion pair is in relation to its neutral form.

^bPartition coefficients and pK_a values from the literature database of ACD/Laboratories Software version 10, unless otherwise indicated.

^cAt 25 ± 1 °C, by internal probe.

^dEqual to pK_a − pK_a′′ for bases and pK_a′′ − pK_a for acids.

^eCalculated by ACD10.

^fReference (26).

^gInsoluble KCl formed.

^hReference (15b), p 138.

ⁱReference (21).

^jThis work.

^kIonization data refer to the underlined group.

^lReference (15a), p 38.

^mReference (15a), p 11 and p 18.

ⁿReference (27).

^oFor CO₂.

^pThe pK_a is assumed to be unaffected by the presence of Mg²⁺.

^qReference (14).

^rReference (15a), p 4.

^sReference (28).

^tAlso reported as 1.36, ref (29).

Calculation of pK_a′′

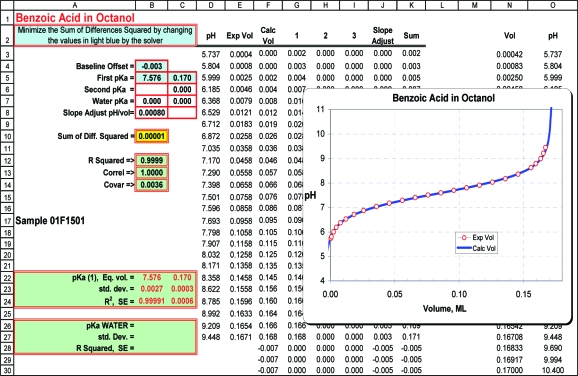
pK_a′′ values were determined using our BIOpKaCalc program in an Excel spreadsheet, along with the program, Solver (an add-in part of Excel), and a statistical program by Billo.(17) The BIOpKaCalc program provides for inclusion of the ionization of water in octanol for compounds with high or low pK_a′′. Explicit examples are provided in the Supporting Information. The data are fitted to eqs 3 and 4, which are based on the same Henderson−Hasselbalch relationships that apply in aqueous media for pK_a, pH, and the ratio of ionized to unionized compounds. V_e is the equivalent volume of titrant in milliliters, and V_x is the baseline offset for the initial point of the titration.

The Solver program iteratively varies the equivalent volume, the pK_a, and the baseline offset to obtain the best least-squares fit to the data. Equations 3 and 4 are used to set up a spreadsheet (Figure 4) with a column for each titratable group, whether part of the compound or an additional component. Additional columns and cells can be added to handle polyfunctional compounds, but as a practical matter, the limited solubility of the ionized species will be the determining factor. Water is included as a component when pH values extend below 3.5 or above 12.0. One spreadsheet column accounts for the Nernst slope of the titration curve, observable in plots, such as in parts a and b of Figure 2. The slope adjustment can be treated as a variable, but we prefer to set it at 0.0008 mL/pH. For uniformity in calculating pK_a′′, only points within ±2 pH units of the pK_a′′ are used. Typically, there are 17−22 points in this range. Full details for setting up the spreadsheet are provided in the Supporting Information.

Figure 4.

The worksheet layout for calculating pK_a′′ values illustrated for benzoic acid.

The pK_a′′ of water is calculated in the same way as any other pK_a′′, except that its equivalent volume is based on the molar content of water in the octanol. In KCl/water-saturated octanol, the 2.4% v/v water and 0.5 N titrant make the equivalent volume of water 40 mL for 15 mL of octanol. The pK_a′′ values of water, determined by a variety of titrations, are provided in Table S2 in the Supporting Information. They include titrations of HCl and KOH in octanol, of the octanol with no preadditions, as well as the extension of titrations of acids and bases to extreme pH values. The average pK_a′′ values of water in KCl/water-saturated octanol are −1.30 ± 0.06 (n = 6) and 17.00 ± 0.07 (n = 9).

Electrode Correction Factor (ECF)

It is evident from our results that one cannot simply substitute pK_a′′ for pK_a oct in eqs 2a−2c. The calculated diff (log P^N − I) values obtained (eq 3) are uniformly low by an average of 0.8 log units (Table 1). The consistently low values are reminiscent of the experience of Bates,(18) Ong,(19) and Newton(20) et al. who studied the function of electrodes over a range of methanol−water and ethanol−water mixtures. They determined that electrode responses in alcohol−water solutions are reliable and reproducible over a wide pH range, but they differ from reported (true) values by a constant. These can be corrected with eq 5 (for bases) as used by Newton et al.,(20)

in which p_sK_a and p_sK_a′ are the actual and glass-electrode-determined pK_a values, respectively, in a given aqueous alcoholic medium. The δ value depends on the solvent composition but is independent of the solute. In any given solvent mixture, the δ value is constant over normal titration ranges (“neither very high, nor very low”(20)). The δ value reflects the altered electrode response in a medium with reduced water content, compared to the aqueous buffers in which the electrode was calibrated. In our system we prefer to use the term electrode correction factor instead of δ. ECF are determined using eqs 6 and 7 with high quality pK_a oct values obtained independently, such as by two-phase titrations. A limitation is that ECF cannot be determined with more accuracy than associated with the other terms in eq 7, most notably, log P^I. The most useful application of pK_a′′ values, however, does not require knowing ECF. It is described under .

Table 1. Derivation of the ECF (Electrode Correction Factor) from Compounds with Measured log P^N and log P^I Values.

no.		diff (log PN − I)	diff pKa′′ a	calcd ECFb
Bases
6a	propranolol	2.70c	1.79	0.91
7	phenethylamine	2.96d	1.72	1.24
14	2-(2-pyridyl)ethylamine (pK2)	2.38d	1.25	1.13
			average	1.10 ± 0.17k
Acids
21a	benzoic acid	4.04e	3.40	0.64
23	hexanoic acid	4.08f	3.22	0.86
32	5-phenyltetrazole	2.90g	2.05	0.85
38	hexachlorophene (pK1)	3.89h	3.07	0.82
40	pentachlorophenol	3.56i	2.58	0.98
41	2-nitrophenol	3.36j	2.53	0.83
42	2,4-dinitro-6-methylphenol	2.54i	1.74	0.80
43	2,6-dinitrophenol	2.58j	1.73	0.85
			average	0.83 ± 0.09k

^aFrom Table 2.

^bThe difference between columns 3 and 4 (eq 3).

^cReference (15b), p 138.

^dReference (21).

^eFrom aromatic fragment values, ref (22).

^fFrom aliphatic fragment values, ref (22).

^gThis work.

^hReference (15a), p 4.

ⁱReference (9).

^jReference (23).

^kThe authors recommend using an interim value, ECF = 0.8, for both acids and bases; see text.

Once a good ECF value is available, log P^I can be determined for any compound from its pK_a′′ and the aqueous pK_a and log P of the neutral compound using eq 7. Equation 6 is analogous to eq 5:

in which the sign is + is for acids and − for bases. Equation 7 is obtained by substituting eq 6 into eq 2c:

where diff pK_a′′ is (pK_a′′ − pK_a) for acids and (pK_a − pK_a′′) for bases.

Direct Use of pK_a′′

A much better application is to use pK_a′′ values directly. The situation becomes simplified when one compares eq 7 for two similar compounds. The ECF terms drop out, and one is left with eq 8. The numerical value of Δdiff (log P^N − I) can be assigned to the structural feature(s) near the charge center that differentiates one compound from its reference. It is not a fragment value because, like π values, it ignores a hydrogen atom. We call it an ion pair stabilization value (IPS).

IPS values represent differences in free energy, but can be expressed in pK_a or log P units, the latter being the most practical. When Δdiff (log P^N − I) is negative, the difference between log P^N and log P^I is decreased, and the opposite when it is positive. Equation 8 allows one to take full advantage of the sensitivity of octanolic titrations. The influence of simple changes in structure on log P^I, such as adding a methyl or hydroxy group near the charge center, can be determined to within a few hundredths of a log P unit. We deliberately chose compounds for method development that could provide information on how H-bonding and steric factors influence log P^I values. These are discussed under . These mostly simple low-molecular weight compounds are not well suited for the best ECF values, which require more lipophilic compounds with more accurately determined log P^I.

Table 1 lists the titrated compounds for which diff (log P^N − I) have been independently determined. The number of phenols in the list was limited to maintain a balance with the other acidic groups. For acids, the differences between diff (log P^N − I) and diff pK_a′′ are fairly uniform, considering the variability found with log P^I determinations. This list provides an interim value of 0.8 for the ECF of acids, which should improve as more examples are added to the list. The 0.8 value compares well with the 0.76 difference we reported earlier comparing correlations of pK_a oct (23 phenols) and pK_a′′ in water-saturated octanol (13 phenols), with their corresponding aqueous pK_a values.(8)

Too few basic compounds are available to determine a separate value for ECF. Propranolol, 6a, has the best quality partition values, by far, having been measured many times during user-training courses. Alex Avdeef describes the current values as now being of “gold-standard” quality.(15b) Phenethylamine, 7, and 2-(2-pyridyl)ethylamine, 14, were part of a series studied by Mayer et al.(21) comparing the log P and log P^I of 20 homologous phenylalkyl- and pyridylalkylamines. Mayer’s ECF values using 0.10 M counterion are higher than they would be using 0.15 M counterion as Avdeef did. The averages in Table 1 suggest an ECF of 0.8 for acids and 1.1 for bases. With the limited data available, we prefer to use ECF = 0.8 for both acids and bases. As a reminder, an error of 0.2 units in ECF translates to an error in log P^I of only 0.2 log P units.

Results and Applications

The predominant form of an ionized compound in octanol is an ion pair in which the oppositely charged ions remain closely associated.(24) The free energy of such a pair is inversely related to the dielectric constant (permittivity) of the medium.(25) The high energy of the ion pair is the driving force that involves neighboring groups and draws in water to produce the lowest energy state. The free energy of ion pair formation is found in any of the “diff” terms mentioned earlier: diff (log P^N − I), diff pK_a oct, or (diff pK_a′′ + ECF). These terms are identical in value and represent the difference in free energy between the neutral species and its ion pair in octanol. The smaller the diff value, the more neutral-like, or lipophilic, the ion pair is in relation to its neutral form. Identifying and isolating the components of this energy term provides the IPS values needed to calculate log P^I from log P^N. The high energy of the ion pairs means that stabilizing factors, such as hydrogen bonding, and destabilizing factors, such as steric inhibition of solvation, have a much greater influence on free energy levels than the same factors have in the neutral state. Application of eq 8 can easily quantify these factors to within a few hundredths of a log P unit.

Structural Factors Influencing log P^I

A table of diff pK_a′′ values (Table 2) provides interesting insight into factors that influence the partitioning of ion pairs. The structures of the compounds in Table 2 are compiled in Charts 1 and 2 for ease in visualizing the many possible comparisons. To illustrate this approach, one can look at the influence of N-methyl groups on ion pair partitioning by subtracting the diff pK_a′′ for 4-aminopyridine (9), the reference compound, from the diff pK_a′′ for 4-dimethylaminopyridine (3). The difference (written in diff log P terms) is attributable to the two methyl groups of 3. From eq 8, we can write

Comparisons are sensitive to a few hundredths of a pK_a, corresponding to a few hundredths of a log P unit, or hundredths of a kilojoule per mole.

Chart 1. diff pK_a′′ Values for the Basic Compounds of Table 2.

^a Substituent values for calculating log P^I from log P^N are determined with high sensitivity by comparing diff pK_a′′ for similar structures (see text). In this chart, crowding around the ion pair, hydrogen-bonding effects, and internal compensation in zwitterions are dominant influences on diff pK_a′′ and diff (log P^N − I).

Chart 2. diff pK_a′′ Values for the Acids of Table 2.

^a The diff pK_a′′ of acids, like bases, is strongly influenced by steric effects, hydrogen bonding, pK_a, and chemical class, meaning these factors have the same influence on diff (log P^N − I).

Structure−log P^I Relationships

A few examples illustrate the value and convenience of this method and the range of log P values accommodated by the method. The fact that simple model compounds can be used is a major advantage in isolating substituent IPS values. To compare the physicochemical properties in octanol of a charged molecule with its neutral form, one need only focus on the features close enough to the charge to affect its free energy. After accounting for these influences, the rest of the molecule is considered to exhibit the same interactions and make the same free energy contributions as in the neutral form. This means that relatively few rules should be able to handle a broad range of compounds. The compounds in Table 2 illustrate four factors that account for the major differences between the log P of a compound and its ion pair.(8) To a large extent, these factors were observed or anticipated in the work of the Fujita(30) and Vittoria(31) groups. They are (1) steric hindrance around the charge centers, (2) hydrogen bond donors and acceptors near the charge center, (3) the pK_a of the compound, and (4) its chemical class.

Steric Factors

In an aqueous medium, an ionized compound and its counterion are independently solvated and require little additional stabilization from each other or neighboring groups. In the low-dielectric environment of octanol or a biolipid, on the other hand, there is a strong attraction between an ion and its counterion, which increases inversely with the dielectric constant.(25) The closer together the opposite charges can get, the lower the free energy of the ion pair. Steric factors also come into play by affecting access of water to the charge centers. Titrations in octanol clearly show the sensitivity of diff (log P^N − I) to steric effects. Steric factors in a series of protonated N-alkylbenzylamines were invoked by the Testa group to explain their partitioning behavior in octanol/saline and liposome/saline systems as determined by two-phase titrations.(32)

As noted earlier in the comparison of (3) and (9), their diff pK_a′′ values differ by 1.22 units. This difference is equivalent to 6.95 kJ/mol at 25 °C, or about 3.5 kJ per N-methyl (eq 1). More simply put, an N-methyl has an IPS of +0.61 and reduces log P^I by 0.61 log units. A consequence of this difference is that in water, 3 is more basic than 9 by 0.49 units, but in octanol, it is actually less basic by 0.73 units (Table 2, pK_a and pK_a′′ columns). This difference is enough to significantly affect log D and associated ADMET properties. It would have especially important consequences if the ionized species were the pharmacologically active form of a biologic agent or participated in the transition state of a biochemical reaction.

The hindered Koenig’s base, diisopropylethylamine (1), provides an example of extreme steric effects. It is used in chemistry when a base is needed that will resist quaternization. Its diff pK_a′′ is 0.62 units larger than for triethylamine (2), allowing one to attribute the influence of the α-methyl groups on the partition coefficient of the ion pair as −0.31 log P units per methyl group. With comparison of triethylamine to the simple primary amines, octylamine (5) and tert-butylamine (8), the latter have a smaller diff (log P^N − I) by over 1.15 units. All three compounds have about the same aqueous pK_a, but in octanol the lower free energy of protonation of the primary amines means their ion pairs form more easily and partition to a greater extent compared to their neutral form than does 2. In octanol, the primary amines are more basic than triethylamine by more than a log unit (Table 2). Note that in all of theses examples, lipophilic alkyl groups raise the log P of unionized amines but can strongly reduce the lipophilicity of the protonated species if they are close enough to the ionizing center. The use of diff (log P^N − I) terms focuses attention on the ion pair. It allows proposing an alternative to the CLOGP paradigm that the distribution of positive charge on the carbons of an alkylammonium group explains the lower lipophilicity of the alkyl fragments.^1,22 Steric hindrance to hydration and the close approach of the counterion is the alternative explanation.

The best evidence for the negative influence of steric factors on carboxylate ion pair partitioning comes from data obtained using an earlier version of this titration procedure.(7) Under these slightly different conditions, the Δdiff pK_a′′ for clofibric acid (2-(4-chlorophenoxy)-2-methylpropionic acid) and phenoxyacetic acid is 0.89. As a general approximation, each α-methyl group lowers log P^I of the sodium ion pair by about 0.44 log units.

The sulfonamides in Table 2 show that three kinds of N-substitution lower the lipophilicity of a sulfonamide ion pair relative to primary sulfonamides. Comparisons must go beyond steric factors, though, because of the range between their pK_a values and differences in chemical class, factors discussed below.

Influence of Hydrogen-Bond Donors and Acceptors on log P^I

Hydrogen bonding groups dramatically lower the free energy of ion pairs in a low dielectric environment, and the effects are cumulative. For a simple example, one can compare triethylamine (2) and triethanolamine (13). The diff (log P^N − I) of the latter is lower by 1.72 log units, or 0.57 units per β-hydroxy group. Of course, on a microscale, the three hydroxy groups are not identical. The influence of a single-hydroxy group is more focused, as seen in the comparison of phenethylamine (7), and its α-(hydroxymethyl) analogue 16. The difference between their diff pK_a′′ values is 0.73 units. With dependence on orientation and distance, a hydroxy group may hydrogen bond directly with an ion or serve as an anchor for a water bridge.

The three β-hydroxy groups of the common buffer Tris (17) reduce its diff (log P^N − I) by 1.19 units compared with the diff (log P^N − I) for tert-butylamine (8), or about 0.39 units per constrained β-hydroxy group. This is a desirable property for a biological buffer. Its pK_a is more nearly the same in all phases. β-Hydroxyalkylamines are more basic in biolipid environments, and their ion pairs more lipophilic than one would expect using current computational programs that do not consider this factor. An extreme example of ion pair stabilization by hydroxy groups is N-methyl-d-glucamine (meglumine, 18), for which the difference between its pK_a and pK_a′′ is only 0.35 units. A report from a workshop on two-phase titrations involving a large number of titrations of 18 concluded that the ion pair form does not partition into octanol.(15a) On the contrary, our results indicate that 18 partitions so well that it approaches undetectability by the algorithm used for two-phase titrations. Undetectability specifically occurs when log P^I equals log P^N.

Neighboring hydroxy groups also lower the free energy of carboxylate ion pairs. This can be seen for 4-, 2- and 3-hydroxybutyric acids, 27−29, where their diff (log P^N − I) are respectively, 0.45, 0.56, and 0.70 log units smaller than that for hexanoic acid.

Comparison of the difference between the diff pK_a′′ of phenethylamine (7) and 2-(2-pyridyl)ethylamine (14) allows one to quantify the influence of a neighboring (neutral) pyridine nitrogen on the free energy of a γ-primary-alkylammonium ion in octanol through a pseudo-five-membered ring arrangement. It lowers the free energy by 0.47 pK_a units, or 2.68 kJ/mol. There must be numerous low- and moderate-level H-bond donor and acceptor interactions with charge centers that would prove useful in modeling drug−receptor interactions, protein folding, or other interactions. Additional examples of steric and H-bonding influences on log P^I can be seen in Charts 1 and 2. Suggested comparisons include 5 and 7; 12 and 16; 13 and 15; 24 and 26; 19e and 31b; 21b and 21c; 34 and 35; 39 and 40; and 41 and 42. Structure−property relationships for phenols will be discussed in a separate paper.

It is evident that neglecting steric and hydrogen bonding factors in the vicinity of charge centers can drastically affect the accuracy of computer programs designed to calculate log D. This could be one of the reasons for the dissatisfaction with such calculations using commercially available software.^4,5 We suggest testing any program being considered for such use by comparing Δdiff (log P^N − I) values for pairs of compounds in Table 2.

Influence of pK_a on log P^I

A third factor contributing to the partition coefficient of an ion pair is its pK_a. Earlier titrations in octanol showed that the more acidic a phenol or benzoic acid, the more lipophilic its ion pair in relation to the neutral form.(8) The diff (log P^N − I) of phenols decreases by 0.19 log units per unit drop in pK_a, while for benzoic acids the drop is 0.25 units per unit drop in pK_a. This is rationalized as compounds are more acidic there is greater internal stabilization, or lower free energy, in the ionized form and therefore less stabilization is needed in a low dielectric environment. A corresponding relationship has not yet been demonstrated for basic compounds.

Influence of Chemical Class on log P^I

We do not know enough about unmeasured classes of compounds to predict their diff (log P^N − I). A representative of each class is a necessary starting point for the elaborations discussed above. Examples of variations in diff pK_a′′ with class are found in Table 2. Phenyltetrazole (32) has interesting properties. It has about the same pK_a in water as benzoic acid, but in octanol it is 15 times more acidic. Analysis of the sulfonamides in this table is complex because of the wide variation in pK_a. One of the more interesting compounds in Table 2 is diphenylphosphate, for which the diff pK_a′′ is only 0.61. The ubiquitous occurrence of phosphates in biology and biochemistry may relate to their ability to form relatively low free energy, lipid-compatible ion pairs.

Ion Pairs of Divalent Cations and Internally Compensated Zwitterions

Information about the behavior of divalent cations in biological media is hard to find, but titrations in octanol can be applied here also. Magnesium salts in octanol, Table 2, such as magnesium salicylate, 31, have two distinct pK_a′′ values. The latter has one for the disalicylate and another for chloromagnesium salicylate. The titration curve and alternative calculations are provided in the Supporting Information. Another category of compounds to which octanolic titrations can be usefully applied was referred to earlier. These are internally charge-compensated (type 4)(12) ampholytes. Examples are pyridine-2-acetic acid, 19 and 30, and niflumic acid, 20, which show the characteristic property(8) that the acids are more acidic and the bases more basic in octanol than in water, the opposite of the usual pattern. For 20 to be internally compensated, the cationic center must be on the central imino nitrogen, Chart 1. Further discussion on alternative strategies for calculating the pK_a′′ values of divalent compounds are found in the Supporting Information.

Conclusion and Future Applications

This work describes a convenient titration procedure in octanol that provides access to here-to-fore unavailable physicochemical properties of ion pairs. It also demonstrates that the ionization of compounds in biolipids and the use of pK_a and pH terms are as important and natural to use in these media as they are in water. The way is now open for future advances. The ability to generate ion pair stabilization values for substituents near an ionized center opens the possibility of someday being able to calculate diff (log P^N − I) values with confidence limits similar to measured log P^N. Quality log P^I values will enhance log D and even allow quantitative analysis using species-specific terms, such as log D^N and log D^I.(33)

Once one knows the features that characterize low free-energy ion pairs, it is fascinating and informative to see how common they are in nature. These include polyhydroxy compounds such as glucuronic acid derivatives, inositol phosphates, hexose phosphates, and glucosamines. The inositol phosphates, including tri- and tetraphosphates, play important rolls in signaling pathways and Ca²⁺regulation.^34,35

Titrations in KCl/water-saturated octanol provide essential information to advance our understanding of ion pair partioning in octanol, but the ultimate goal of lipophilicity studies is application of this knowledge to the anisotropic world of cells, membranes, proteins, and nucleic acids. In contrast to octanol, these biological systems contain charged groups which can have an especially strong influence on ionized drugs. One need only look at amines in liposomes to see this. As an example, the diff (log P^N − I) for 4-phenylbutylamine is 3.16 in octanol, vs 0.29 in liposomes.(36) Austin calls this an association with phospholipids,(37) but the magnitude of the free energy change indicates it might as well be called an ion pair. The basic drugs propranolol and desipramine actually form hydrophobic ion pairs (HIP^12,38) in membranes made from, or containing, negative phospholipids such as a phosphatidylinositol.^12,39,40 This is clearly seen in the published lipophilicity profiles from the Krämer group which show that the drugs are more basic in the membrane than they are in water.

We strongly encourage other laboratories to add the capability for titrations in KCl/water-saturated octanol. We offer our guidance and will gladly provide a working copy of the spread sheet to anyone wishing to explore this area.

Supporting Information Available

Additional information as noted in text. This material is available free of charge via the Internet at http://pubs.acs.org.