Abstract
Saccharopine dehydrogenase (N6-(glutaryl-2)-L-lysine: NAD oxidoreductase (L-lysine forming)) catalyzes the final step in the α-aminoadipate pathway for lysine biosynthesis. It catalyzes the reversible pyridine nucleotide-dependent oxidative deamination of saccharopine to generate α-Kg and lysine using NAD+ as an oxidizing agent. Proton shuttle chemical mechanism is proposed on the basis of the pH dependence of kinetic parameters, dissociation constants for competitive inhibitors, and isotope effects. In the direction of lysine formation, once NAD and saccharopine bind, a group with a pKa of 6.2 accepts a proton from the secondary amine of saccharopine as it is oxidized. This protonated general base then does not participate in the reaction again until lysine is formed at the completion of the reaction. A general base with a pKa of 7.2 accepts a proton from H2O as it attacks the Schiff base carbon of saccharopine to form the carbinolamine intermediate. The same residue then serves as a general acid and donates a proton to the carbinolamine nitrogen to give the protonated carbinolamine. Collapse of carbinolamine is then facilitated by the same group accepting a proton from the carbinolamine hydroxyl to generate α-Kg and lysine. The amine nitrogen is then protonated by the group that originally accepted a proton from the secondary amine of saccharopine, and products are released. In the reverse reaction direction, finite primary deuterium kinetic isotope effects were observed for all parameters with the exception of V2/KNADH, consistent with a steady state random mechanism, and indicative of a contribution from hydride transfer to rate limitation. The pH dependence, as determined from the primary isotope effect of DV2 and D(V2/KLys), suggests that a step other than hydride transfer becomes rate-limiting as the pH is increased. This step is likely protonation/deprotonation of the carbinolamine nitrogen formed as an intermediate in imine hydrolysis. The observed solvent isotope effect indicates proton transfer also contributes to rate limitation. A concerted proton and hydride transfer is suggested by multiple substrate/solvent isotope effect, as well as a proton transfer in another step, likely hydrolysis of the carbinolamine. In agreement, dome-shaped proton inventories are observed for V2 and V2/KLys suggesting proton transfer exists in at least two sequential transition states.
Saccharopine dehydrogenase (N6-(glutaryl-2)-L-lysine: NAD oxidoreductase (L-lysine forming); (EC 1.5.1.7)) (SDH1) catalyzes the final step in the α-aminoadipate pathway (AAA) for the de novo synthesis of L-lysine in fungi (1, 2). The enzyme catalyzes the reversible pyridine nucleotide-dependent oxidative deamination of saccharopine to generate α-Kg and lysine using NAD as an oxidant, eq. 1 (1).
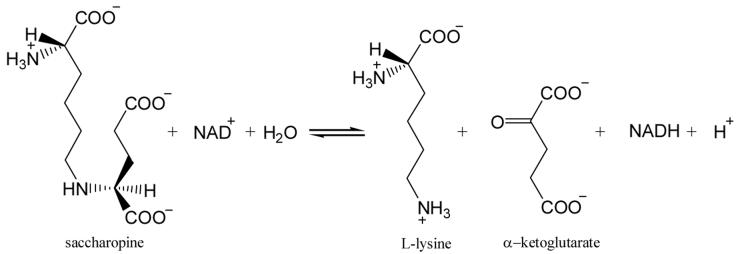 |
(1) |
The histidine-tagged SDH from S. cerevisiae has been overexpressed in Escherichia coli and purified to about 98% using a Ni-NTA resin (3). The kinetic mechanism of the SDH reaction has recently been determined from initial velocity studies in the absence and presence of product and dead-end inhibitors (3). The SDH catalyzes an ordered mechanism in which NAD is the first substrate bound followed by saccharopine in the physiologic reaction direction. In the reverse reaction direction, NADH adds to enzyme first, and there is no preference for binding of α-Kg and lysine at pH 7.0.
The presence of the AAA pathway for lysine biosynthesis has been demonstrated in several yeasts and molds including human pathogens such as Candida albicans, Cryptococcus neoformas, and Aspergillus fumigatus and plant pathogens such as Magnaporthe grisea (4, 5). The uniqueness of the AAA pathway makes it a target for the rapid detection, growth control of pathogenic yeasts and molds, and for antifungal drug design. Toward this end, it is important to determine the chemical mechanism of the enzyme. A first step in this process is the elucidation of the acid-base mechanism of SDH.
Preliminary information on the mechanism of the SDH has been obtained by other groups, and this will be summarized briefly. The S. cerevisiae enzyme has pH optima of 10.0 in the direction of lysine formation, and 7.0 in the direction of saccharopine formation (2). The pH dependence of V/KLys is bell shaped giving pKa values of 6.3 and 8.0, while the V/Kα-Kg profile exhibits a single pKa of 8.4 on the basic side (6). The V/KSacc pH-rate profile exhibits two pKa values of 6.0 and 7.1 on the acid side (6). A series of chemical modification experiments have also been carried out suggesting the presence of essential cysteine (7), histidine (8), lysine (9), and arginine residues (10) that may be involved in substrate-binding and/or catalysis. On the basis of the above, a chemical mechanism has been proposed for SDH in which saccharopine is first oxidized to ε-N-glutariminyl-L-lysine. A general base then activates water for attack to form a carbinolamine intermediate, which collapses to give the products, L-lysine and α-Kg via the participation of a general acid and a general base (6).
Previous studies of the chemical mechanism of SDH are incomplete and the identity of the groups involved is based on the observed pKa values, their temperature dependence, and chemical modification studies. In this paper, the pH dependence of the kinetic parameters, dissociation constants for competitive inhibitors, and isotope effects are used to probe the chemical mechanism of SDH. A proton shuttle mechanism is proposed and data are discussed in terms of potential rate limiting steps along the reaction pathway.
MATERIALS AND METHODS
Chemicals
L-Saccharopine, L-lysine, L-leucine, α-Kg, and Baker's yeast alcohol and aldehyde dehydrogenases were obtained from Sigma. β-NADH and β-NAD were purchased from USB. Oxalylglycine (OG) was from Frontier Scientific. Mes, Hepes, Ches, and Taps were from Research Organics, Inc. Deuterium oxide (D2O) (99 atom % D) and ethanol-d6 (99 atom % D) were purchased from Cambridge Isotope Laboratories, Inc. AG MP-1 resin and Bio-Gel P-2 resin were from Bio-Rad. All other chemicals and reagents were obtained from commercial sources, were reagent grade, and were used without further purification.
Cell growth, SDH expression and purification were carried out as reported previously (3). Glycerol (50%) was added to the stock enzyme solution to minimize any activity loss, and the diluted enzyme solution used for activity studies was prepared fresh daily.
Synthesis of A-side NADD
SDH is reported to be pro-R specific for hydride transfer (A-side) from C-2 of the saccharopine glutaryl moiety to the nicotinamide ring of NAD (6, 11). The A-side NADD was prepared according to (12, 13). The reaction mixture contained 2.8 mM ethanol-d6, 5.6 mM NAD, 50 units of yeast alcohol dehydrogenase, and 100 units of yeast aldehyde dehydrogenase in 10 ml of 6 mM Taps, at pH 9.0, 25 °C. The pH was adjusted to 9.0 with KOH throughout the reaction since protons are being produced and the reaction mixture is lightly buffered. The reaction was allowed to proceed overnight, several drops of CHCl3 were added to the mixture to quench the reaction, and the aqueous layer was adjusted to pH 10.0 with KOH and removed for ion exchange chromatography. The NADD eluted in a large single peak with baseline separation from NAD when eluted isocratically from an AG MP-1 column with 1 M LiCl, pH 10.0. The reported ratio of absorbance at 260 to 340 nm for A-side NADD was 2.15 ± 0.05 (12). The ratio obtained for the sample prepared above is 2.2 ± 0.05. The purified A-side NADD was concentrated by rotary evaporation at 25 °C to about 5 mL. The concentrated solution was then desalted via a 1.6 × 60-cm Bio-Gel P-2 column. The concentrations of NADH(D) stock solutions were adjusted spectrophotometrically, using an ε340 of 6.22 mM−1cm−1.
Enzyme Assays
SDH activity was measured by monitoring the increase or decrease in absorbance at 340 nm as NAD is reduced or NADH is oxidized. Reactions were carried out in semi-micro quartz cuvettes with a path length of 1 cm in a final volume of 1 or 0.5 ml containing 200 mM buffer and variable concentrations of substrates as indicated below. Initial velocities were measured with a Beckman DU640 UV/Vis spectrophotometer. All assays were performed at 25 °C and the temperature was maintained using a Beckman Temperature Controller. A unit of enzyme activity is defined as the amount of enzyme catalyzing the production or utilization of 1 μmole of NADH/min at 25 °C. Reactions were initiated by addition of 10 μL of an appropriately diluted enzyme solution (∼1.4 μM final concentration) to a mixture that contained all other reaction components, and the initial linear portion of the time course was used to calculate the initial velocity.
pH Studies
In order to determine whether the kinetic mechanism changes with pH, and to obtain estimates of the Km values of all of the substrates as a function of pH, initial velocity patterns were obtained at pH 5.5, 7.0, 8.0, 8.5, 9.5, by measuring the initial velocity as a function of NADH concentration, at different fixed levels of α-Kg and a fixed concentration of lysine. The experiment was then repeated at several different fixed concentrations of lysine. Initial velocity studies were also carried out in the direction of saccharopine oxidation at the pH extremes (6.0 and 9.6). In this case, the initial rate was measured as a function of NAD concentration at different fixed levels of saccharopine. The pH dependence of V and V/K for all substrates was then obtained under conditions in which one substrate concentration was varied with the others maintained at saturation (≥ 10 Km). Inhibition constants were obtained for inhibitors competitive with α-Kg and lysine at a fixed concentration of the other two substrates (10 Km) and different fixed levels of inhibitor including zero.
The pH was maintained using the following buffers at ≥ 100 mM concentration: Mes 5.5-6.8; Hepes, 6.8-8.2; Ches; 8.2-10.0. Sufficient overlap was obtained upon changing buffers to eliminate buffer effects (none were observed). The pH was recorded before and after initial velocity data were measured with changes limited to ≤ 0.1 pH unit. The enzyme is stable when incubated for 20 min over the pH range 5.5-9.8. pH profiles were then evaluated graphically for quality of data by plotting logV or log(V/K) against pH, while the inhibition profiles for oxalylglycine and leucine were evaluated by plotting log(1/Ki) against pH.
Primary Substrate Deuterium Kinetic Isotope Effects
Isotope effects were measured by direct comparison of initial velocities, with NADD used as the deuterated substrate. DV2 and D(V2/KLys) were obtained in triplicate by measuring the initial rate as a function of lysine concentration at saturating levels of either NADH(D) and α-Kg (10 Km)2. D(V2/KNADD) and D(V2/Kα-Kg) were obtained in the same manner, varying NADD or α-Kg, at saturating levels of the other two substrates, respectively. DV2 and D(V2/KLys) were also measured as a function of pH.
Solvent Deuterium Kinetic Isotope Effects and Proton Inventory Experiments
Initial velocities were measured in H2O and D2O. For rates measured in D2O, substrates (NADH, α-Kg and lysine) and buffers were first dissolved in a small amount D2O and lyophilized overnight to remove exchangeable protons. The lyophilized powders were then dissolved in D2O to give the desired concentrations and pD was adjusted using either DCl or NaOD. A value of 0.4 was added to pH meter readings to calculate pD (14). Data were obtained with lysine as the variable substrate at fixed concentrations (10 Km) of NADH and α-Kg. The isotope effects were obtained by direct comparison of initial rates in H2O and D2O over the pH(D) range 6.6-8.3, around the pH independent region of the V and V/K pH-rate profile. Reactions were initiated by adding 10 μL of enzyme solution in H2O, such that the final % D2O is ca. 99%.
In the direction of saccharopine formation, finite isotope effects were observed, and proton inventory experiments were carried out to measure the solvent deuterium kinetic isotope effects more accurately and estimate the number of proton(s) in flight in the rate-determining transition state(s) (15). V2 and V2/KLys were measured at pH(D) 7.1 in 100% H2O, 25% D2O, 50% D2O, 75% D2O, and ∼100% D2O with lysine as the variable substrate at a fixed concentration of NADH and α-Kg (10 Km).
Multiple Solvent Deuterium/Substrate Deuterium Kinetic Isotope Effects
The multiple isotope effect was obtained by direct comparison of initial rates in H2O and D2O with lysine varied and NADD and α-Kg fixed at 10 Km. It was also measured by comparison of initial rates using NADH and NADD in D2O with lysine as varied substrate. Rates were measured at pH(D) 7.1, the pH independent region of the V and V/K pH-rate profile.
Measurement of the Saccharopine Secondary Amine pKa by NMR
The pKa value of saccharopine was determined by measuring the 1H-NMR chemical shifts of protons β to the secondary amine nitrogen of saccharopine as a function of pH at 21 °C. Solutions in D2O of 20 mM saccharopine and 20 mM K2HPO4 buffer were prepared. The solution was adjusted to different pD values (5.0-11.9) using either DCl or NaOD. A value of 0.4 was added to pH meter readings (14). All 1D and 2D NMR experiments were performed on a Varian Mercury VX-300 MHz spectrometer with a Varian 4-nuclei auto-switchable PFG probe. 1H-NMR spectra were collected using the PRESAT pulse sequence supplied by Varian, Inc. The spectra were collected with a sweep width of 1510.1 Hz, 8 transients, and an acquisition time of 5.490 seconds and processed with 32K points resulting in a 0.09 Hz digital resolution. Assignment of chemical shifts was aided by gCOSY experiments. The gCOSY pulse sequence supplied by Varian, Inc. was used and data were collected with 1 transient and 128 increments.
Data Processing
Data were fitted to appropriate equations as discussed below, using the Marquardt-Levenberg algorithm (18) supplied with the EnzFitter program from BIOSOFT, Cambridge, U. K. and the Fortran programs of Cleland (19). Kinetic parameters and their corresponding standard errors were estimated using a simple weighting method. Data for initial velocity patterns obtained at pH 5.5, 7.0, 7.5, 8.5, and 9.5 in the direction of lysine formation were fitted using eq. 2, while in the direction of saccharopine formation, data were fitted using eq. 3. Competitive inhibition patterns were fitted using eq 4. Data for V and V/K deuterium isotope effects were fitted using eq 5.
| (2) |
| (3) |
| (4) |
| (5) |
In eqs 2-5, v and V are initial and maximum velocities, A, B, and C are substrate concentrations, I is inhibitor concentration, Ka, Kb, and Kc are Michaelis constants for substrates A, B, and C, respectively, while constant and coef terms are products of kinetic constants that depend on mechanism. In eq. 4, Kis represents the slope inhibition constant. In eq. 5, Fi is the fraction of D2O in the solvent or deuterium label in the substrate, and EV/K and EV are the isotope effects minus 1 on V/K and V, respectively.
Data for pH-rate profiles that decreased with a slope of 1 at low pH and a slope of −1 at high pH were fitted using eq. 6. Data for pH-rate profiles with a slope of 1 at low pH were fitted using eq. 7, while data for pH-rate profiles with a slope of −1 at high pH were fitted using eq. 8. Data for pH-rate profile that decreased with a slope of 2 at low pH were fitted using eq. 9. In the direction of saccharopine formation, data for logV pH-rate profile over the pH range 5.0-7.0 were fitted using eq, 7, while data for V for the pH range 6.5-10.0 and data for the leucine pKi profile were fitted using eq. 10.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
In eqs 6-10, y is the observed value of the parameter as a function of pH (V, V/K, or 1/Ki), C is the pH-independent value of y, H is the hydrogen ion concentration, K1 and K2 represent acid dissociation constants for enzyme or substrate functional groups important in a given protonation state for optimal binding and/or catalysis, and YL and YH are constant values of V or 1/Ki at low and high pH, respectively.
RESULTS
pKa of the Saccharopine Secondary Amine: Determination by NMR
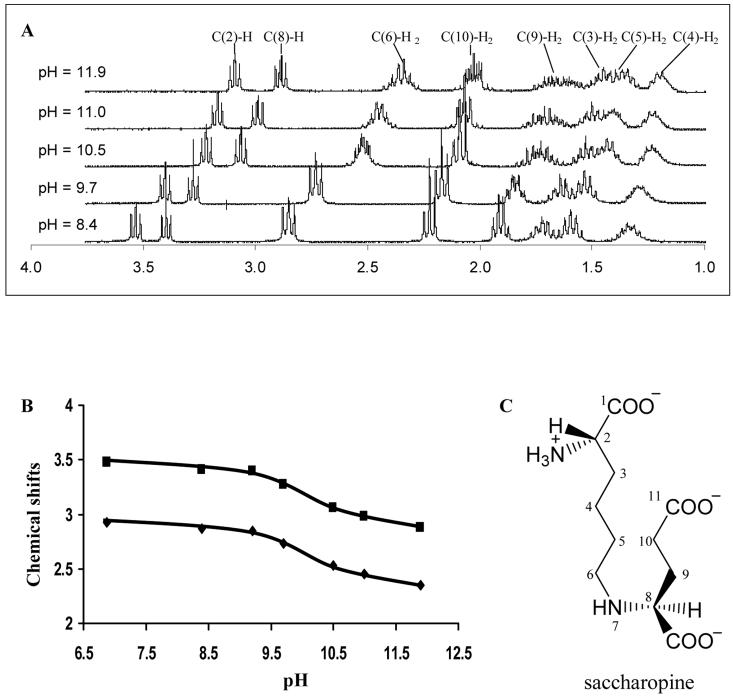
1H-NMR spectra of saccharopine were obtained at pH 6.86 and referenced to HDO (4.68 ppm). Chemical shifts are as follows: δ 3.6 (t, 1H, J = 6.7 Hz, C(2)-H), δ 3.5 (t, 1H, J = 5.8 Hz, C(8)-H), δ 2.9 (t, 2H, J = 7.9 Hz, C(6)-H2), δ 2.3 (t, 2H, J = 7.2 Hz, C(10)-H2), δ 1.95 (dd, 2H, J = 7.2 Hz, 5.8 Hz, C(9)-H2), δ 1.78 (m, 2H, C(3)-H2), δ 1.64 (p, 2H, J = 7.9 Hz, C(5)-H2), δ 1.38 (m, 2H, C(4)-H2). The 1H-NMR chemical shifts of saccharopine were assigned by gCOSY at pH 6.86 and 11.9. The correlations at pH 6.86 and 11.9 were identical. The correlations at pH 6.86 are listed in Table 1.
Table 1.
Results of Saccharopine gCOSY Experiments.
| Chemical Shift | Correlation |
|---|---|
| 3.62 C(2)-H | 1.78 C(3)-H2 |
| 3.48 C(8)-H | 1.95 C(9)-H2 |
| 2.93 C(6)-H2 | 1.64 C(5)-H2 |
| 2.26 C(10)-H2 | 1.95 C(9)-H2 |
| 1.95 C(9)-H2 | 3.48 C(8)-H, 2.26 C(10)-H2 |
| 1.78 C(3)-H2 | 3.62 C(2)-H, 1.38 C(4)-H2, |
| 1.64 C(5)-H2 | 2.93 C(6)-H2, 1.38 C(4)-H2 |
| 1.38 C(4)-H2 | 1.78 C(3)-H2, 1.64 C(5)-H2 |
The chemical shifts of peaks corresponding to C(2)-H, C(8)-H, and C(6)-H2 changed significantly as the pD was increased, Fig. 1A. The largest changes were seen in C(8)-H and C(6)-H2 (reflecting the protons β to the secondary amine) which moved 0.59 ppm and 0.58 ppm, respectively, upfield as the pH was increased from 6.86 to 11.90. A plot of the chemical shift vs. pH was used to estimate the pKa value of the secondary amine of saccharopine, Fig. 1B. Data were fitted by eq 10, which gave an estimated pKa of 10.5 ± 0.2. The pKa in H2O is 10.1 ± 0.2 (obtained by subtracting 0.4 (14)) in the range of 10-11 from model compounds (20).
Figure 1.
pH Dependence of the 1H-NMR Spectrum of Saccharopine. A. 1H-NMR spectra of saccharopine measured at the indicated pH values. Chemical shifts are referred to the carbons of saccharopine. B. pH dependence of the chemical shift of protons β to the secondary amine of saccharopine. Data are presented for the C(8)-H (■) and C(6)-H2 (▲) positions. C. Structure of saccharopine with main chain atoms labeled.
pH Dependence of Kinetic Parameters
The pH dependence of kinetic parameters potentially provides information on the optimum protonation state of enzyme and/or reactant functional groups required for enzyme conformation, binding, and catalysis. To be certain the kinetic mechanism of the enzyme does not change with pH and to obtain estimates of the Km values of all of the substrates as a function of pH, initial velocity patterns and diagnostic dead-end inhibition patterns were obtained at pH 5.0, 7.0, 8.0, 8.5, and 9.5. In the direction of saccharopine formation, initial velocity patterns and leucine dead-end inhibition patterns are consistent with the kinetic mechanism proposed previously (3); NADH binds first to free enzyme, and this is followed by random addition of α-Kg and lysine at pH 7.0, and the mechanism also applies at pH 8.0. However, the mechanism changes at the pH extremes (5.0, 8.5, and 9.5) to an ordered one with NADH binding first, followed by rapid equilibrium addition of α-Kg before lysine. In the direction of lysine formation, initial velocity and dead-end inhibition patterns obtained at the pH extremes (6.0 and 9.6) are consistent with a sequential ordered mechanism in which NAD is the first substrate bound and saccharopine binds second (data not shown).
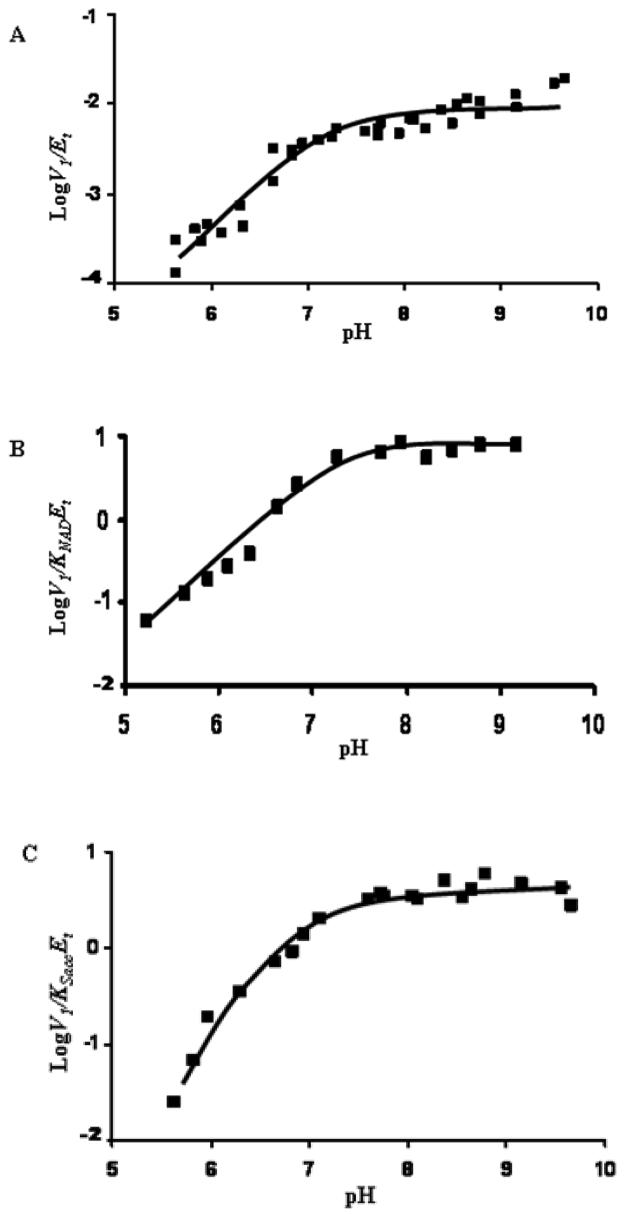
The pH dependence of the kinetic parameters for SDH was determined, and the results are shown in Figs. 2 and 3. In the direction of lysine formation, V1/Et and V1/KNADEt decrease at low pH with a limiting slope of +1, giving a pKa value of about 7.3 - 7.4 (Fig. 2A, B), while V1/KSaccEt decreases at low pH with a limiting slope of +2, giving pKa values of 6.2 and 7.2 (Fig. 2C). The pKa of the saccharopine secondary amine is 10.1, outside the pH range used for the V1/KSaccEt pH-rate profile. NAD is the first reactant bound, and the pH dependence of V1/KNADEt (the on-rate constant for binding NAD) reflects a group important for binding NAD. Since NAD and saccharopine have no pKa values over the pH range that was studied, the pKa of 7.2-7.4 exhibited in V1/Et, V1/KNADEt, and V1/KSaccEt may reflect the same enzyme side chain important in catalysis and binding (see Discussion below). The group on enzyme with the pKa of 6.2 in the V1/KSaccEt pH-rate profile likely contributes to the binding of saccharopine, since it is not observed in the V1/Et pH-rate profile. pKa values are summarized in Table 2. Estimates of the pH-independent values of the kinetic parameters are as follows: V1/Et, (9.5 ± 0.9) s−1, V1/KNADEt, (8.6 ± 1.6) × 103 M−1s−1, and V1/KSaccEt, (4.4 ± 0.4) × 103 M−1s−1.
Figure 2.
pH Dependence of Kinetic Parameters for the SDH Reaction from S. cerevisiae in the Direction of Saccharopine Formation. Data were obtained at 25 °C for V1/Et (A), V1/KNADEt (B), and V1/KSaccEt (C). The points shown are the experimentally determined values, while the curves are theoretical based on fits of the data using eq. 7 for V1/Et and V1/KNADEt, and eq. 8 for V1/KSaccEt.
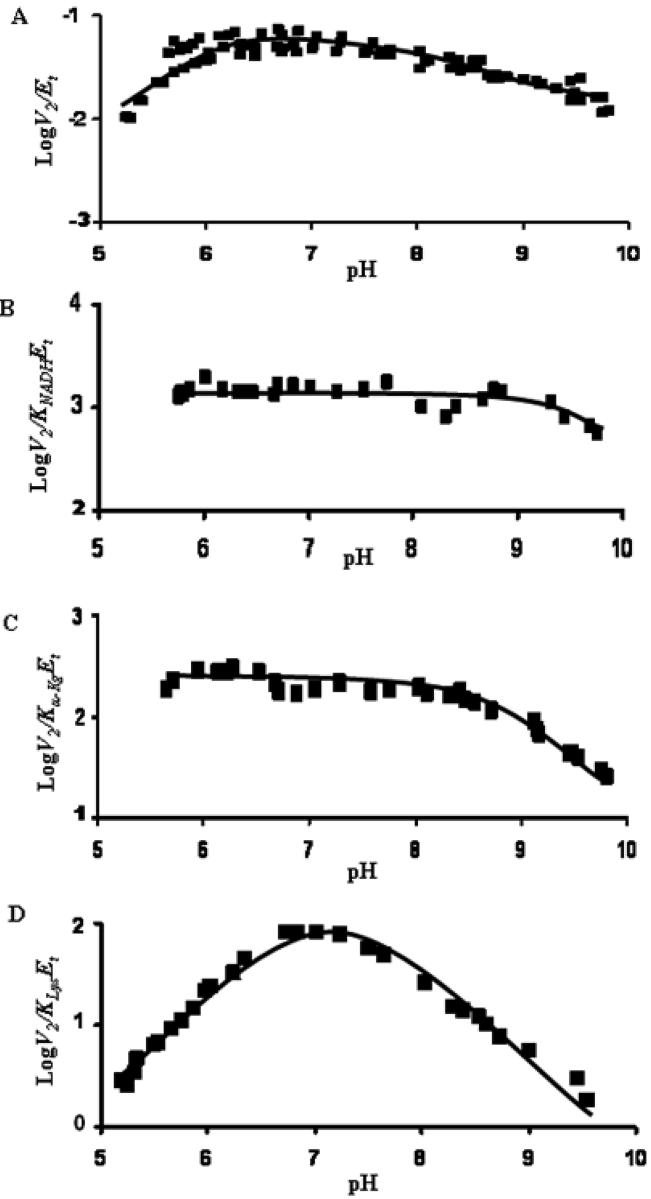
Figure 3.
pH Dependence of Kinetic Parameters for the SDH Reaction from S. cerevisiae in the Direction of Lysine Formation. Data were obtained at 25 °C for V2/Et (A), V2/KNADHEt (B), V2/Kα-KgEt (C), and V2/KLysEt (D). The points shown are the experimentally determined values, while the curves are theoretical based on fits of the data using eq. 9 for V2/KNADHEt and V2/Kα-KgEt, eq. 6 for V2/KLysEt, while the V2/Et profile were fitted as described in Methods.
Table 2.
pH Dependence of Kinetic Parameters for SDH from S. cerevisiae.
| Parameter | Acid side pKa ± SE |
Basic side pKa ± SE |
|---|---|---|
| V1 | 7.3 ± 0.2 | -- |
| V1/KNAD | 7.4 ± 0.2 | -- |
|
V1/KSacc |
6.2 ± 0.3 | -- |
| 7.2 ± 0.2 | ||
| V2 | 5.8 ± 0.2 | 8.4 ± 0.5 |
| V2/KNADH | -- | 9.6 ± 0.2 |
| V2/Kα-Kg | -- | 8.9 ± 0.1 |
| V2/KLys | 7.2 ± 0.5a | -- |
| pKiOG | -- | -- |
| pKiLeu | -- | 6.2 ± 0.7b |
| 9.2 ± 0.3c | ||
average value.
pKa for the EH complex.
pKa for the EH:leucine complex.
In the reverse reaction direction, V2/Et decreases at low pH with a limiting slope of +1 giving a pKa value of about 5.8, and decreases at high pH to a new constant value exhibiting a pKa of about 8.4, Fig. 3A. The pKa of 5.8 suggests an enzyme group important for catalysis, while the group with a pKa of about 8.4 suggests an enzyme group important, but not essential, for catalysis. The V2/KEt values for NADH and α-Kg both decrease at high pH with a slope of −1 giving pKa values of 9.6 and 8.9, respectively, Fig. 3B, C. V2/KNADH is the on-rate constant for NADH, and the pKa of about 9.6 reflects a group on enzyme important for binding the reduced cofactor. (Note that the group with a pKa of 7.2 important for NAD binding is not observed in the V2/KNADHEt profile.) The V2/KEt for lysine exhibits a bell-shaped pH-rate profile, which decreases at low pH with a slope of +1 and at high pH with a slope of −1, Fig. 3D. Because the difference in these two pKa values is less than 0.6, they were considered identical, and an average pKa of about 7.2 was estimated. pKa values are summarized in Table 2. The pH independent values of kinetic parameters are as follows: V2/Et, (58 ± 3) s−1, V2/KNADHEt, (1.41 ± 0.06) × 106 M−1s−1, V2/Kα-KgEt (2.16 ± 0.08) × 105 M−1s−1, and V2/KLysEt, (1.44 ± 0.07) × 105 M−1s−1.
pH Dependence of the Ki for Oxalylglycine and Leucine
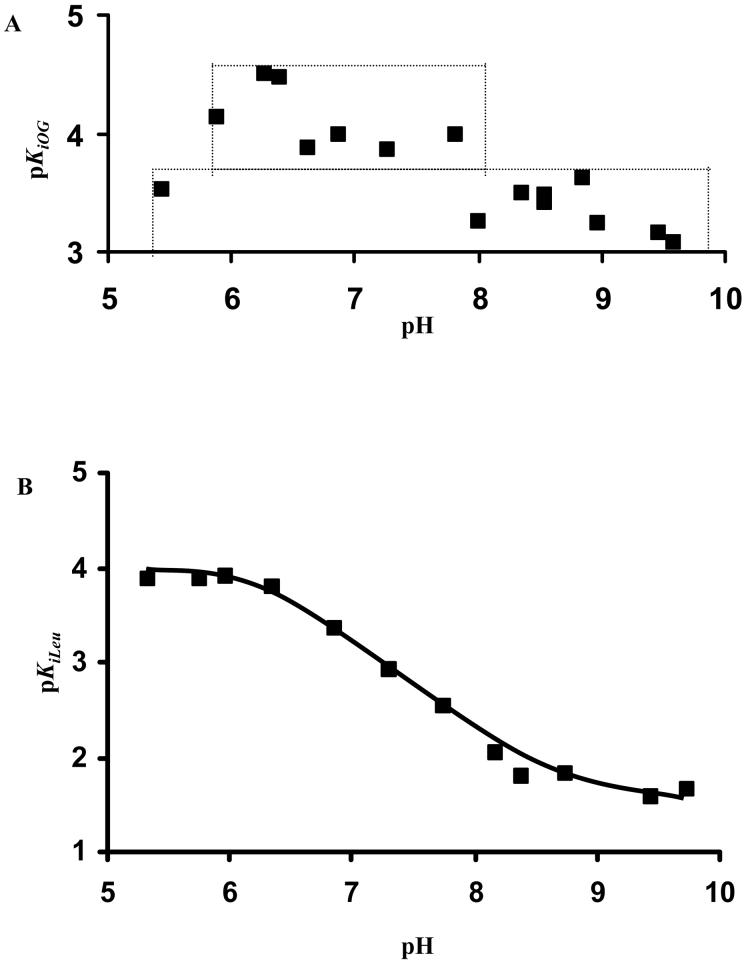
The pH dependence of the dissociation constant for competitive inhibitors vs. α-Kg and lysine were determined in order to obtain an estimate of intrinsic pK value(s) of group(s) required for optimum binding of reactants. Oxalylglycine was utilized as a dead-end analogue of α-Kg to measure its pKi profile. At pH 5.45 and 9.58, OG is competitive vs. α-Kg and its pKi profile is shown in Fig. 4A. It shows an increase in its Ki as the pH is decreased below 6, and increased above 8. Over the pH range studied, leucine is a competitive inhibitor against lysine. Its pKi decreases from a constant value below pH 6 to another constant value above pH 9.0, Fig. 4B. A pKa of about 6.2 is estimated for the enzyme complex EH:NADH:α-Kg and this pKa is perturbed to about 9.2 in the EH:NADH:α-Kg:leucine complex, Table 2. The pH independent dissociation constant for leucine is 0.09 ± 0.01 mM for EH:NADH:α-Kg, and increases to 30 ± 6 mM in the EH:NADH:α-Kg:leucine complex.
Figure 4.
pH Dependence of the Reciprocal of the Inhibition Constant for OG (A) and Leucine (B). The points shown are the experimentally determined values, while the curve in (B) is theoretical based on the fit of the data using eq. 10.
Primary Substrate Deuterium Kinetic Isotope Effects
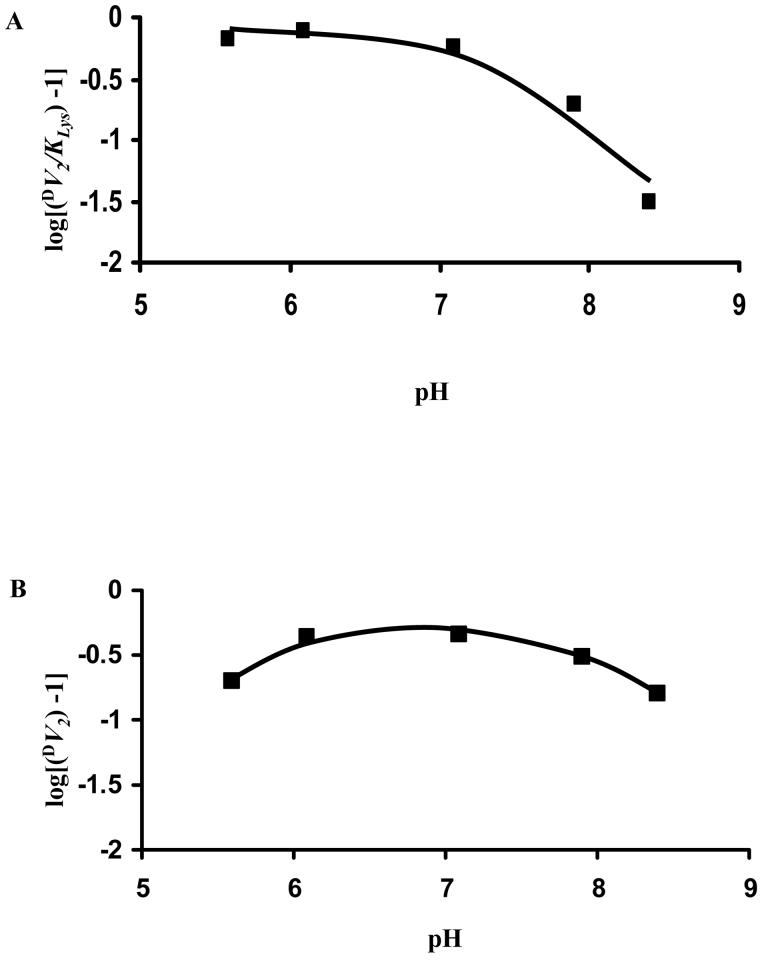
Primary deuterium kinetic isotope effects were measured by direct comparison of initial rates at pH 7.1 with A-side NADH(D) used as the labeled susbstrate. Finite effects were observed in all parameters, with the exception of V2/KNADH. DV2 = 1.45 ± 0.07, D(V2/KNADH) = 0.92 ± 0.08, D(V2/Kα-Kg) = 1.9 ± 0.1, and D(V2/KLys) = 1.56 ± 0.05. Isotope effects on V2 and V2/KLys were also obtained as a function of pH and are shown in Table 3. Since the isotope effects tend to unity as the pH increased, data are also plotted as the log(IE minus 1), Fig. 5, to better estimate the pKa for the process.
Table 3.
pH Dependence of Primary Deuterium Kinetic Isotope Effect for SDH.
| DV2 | D(V2/KLys) | |
|---|---|---|
| pH 5.6 | 1.20 ± 0.07 | 1.66 ± 0.12 |
| pH 6.1 | 1.44 ± 0.13 | 1.76 ± 0.10 |
| pH 7.1 | 1.45 ± 0.07 | 1.56 ± 0.05 |
| pH 7.9 | 1.3 ± 0.05 | 1.20 ± 0.08 |
| pH 8.4 | 1.16 ± 0.03 | 1.03 ± 0.04 |
Figure 5.
pH Dependence of Primary Substrate Deuterium Kinetic Isotope Effects of Saccharopine dehydrogenase. Data were plotted as the logarithm of the isotope effect minus 1. A. V2/KLys. B. V2. The points shown are the experimentally values, while the curves are theoretical based on fits of the data using eq. 8 for V2/KLys, and eq. 6 for V2.
Solvent Deuterium Kinetic Isotope Effects and Proton Inventory Studies
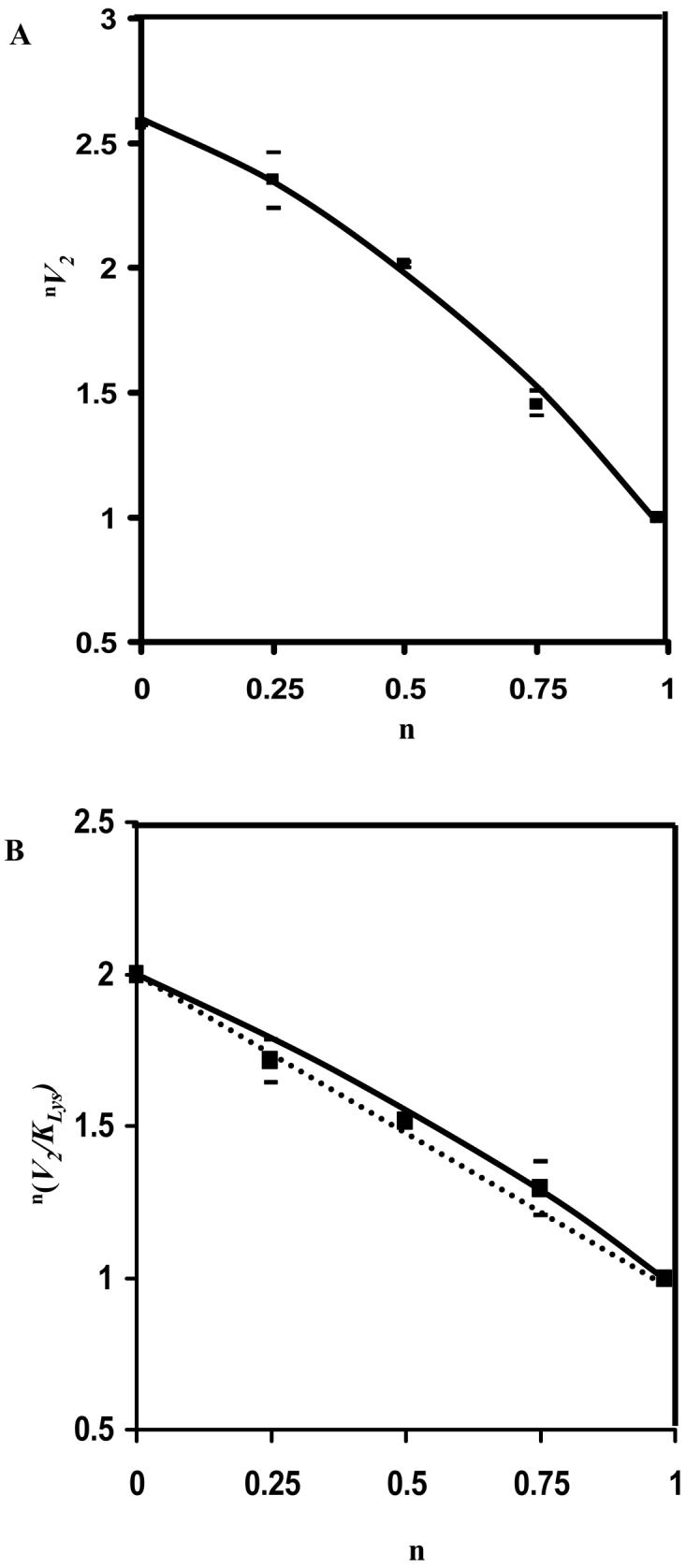
The pH(D) dependence of kinetic parameters was measured over the pH(D) range 6.5-8.5 to determine whether a solvent deuterium kinetic isotope effect is observed on V2 and V2/KLys. The pH(D) independent values of V2 and V2/KLys gave values of D2OV2 and D2OV2/KLys of 2.2 ± 0.1 and 1.9 ± 0.1, respectively.
Proton inventories (15) measured at pH(D) 7.1 is shown in Fig. 6. The proton inventories can be described as dome-shaped or bulging upward for V2 and V2/KLys, as shown in Fig. 6. The concavity is pronounced in the case of V2, and shallow in the case of V2/KLys.
Figure 6.
Proton Inventories for Saccharopine Dehydrogenase. Solvent deuterium dependence of n(V2) (A) and n(V2/KLys) (B) (ratio of V2 and V2/KLys at n fraction of D2O to that at 99.9% D2O) on the fraction of deuterium (n) in solvent. Velocities were measured at pH(D)-independent value of 7.1 in 100% H2O, 25% D2O, 50% D2O, 75% D2O, and ∼100% D2O. Points are experimental values, and curves are drawn by eye. The dotted line in B is theoretical for a linear proton inventory.
Multiple Solvent Deuterium/Substrate Deuterium Kinetic Isotope Effects
Multiple isotope effects allow one to determine whether two isotope effects reflect the same or different steps. A multiple kinetic deuterium isotope effect is obtained when A-side NADD is used in both H2O and D2O (80%) with D2O(V2)D = 1.76 ± 0.08 and D2O(V2/KLys)D = 1.86 ± 0.08. The multiple kinetic deuterium isotope effect obtained by using NADH(D) in D2O (90%) gives D(V2)D2O = 1.50 ± 0.15 and D(V2/KLys)D2O = 1.55 ± 0.14.
DISCUSSION
Isotope Effects
The study of deuterium isotope effects has enabled investigators to obtain information about the nature of the transition state in reactions catalyzed by specific dehydrogenases, e.g., formate dehydrogenase (21) and alanine dehydrogenase (22). In many cases, it has given an indication of the relative rates of the catalytic steps in the mechanism compared to the overall rate of the reaction.
Primary Substrate Deuterium Kinetic Isotope Effects
The kinetic mechanism of SDH in the direction of saccharopine formation at neutral pH can be written
 |
(11) |
where A, B, C, P, and Q represent NADH, α-Kg, lysine, saccharopine, and NAD, respectively. The rate constants k1 and k2 are for binding and dissociation of A; k3, k4, k7, and k8 are for binding and dissociation of α-Kg, and k5, k6, k9, and k10 are for binding and dissociation of lysine; k11 and k12 are the forward and reverse net rate constants for the catalytic pathway; while k13 and k15 are for release of saccharopine and NAD, respectively.
The substrate deuterium sensitive step, hydride transfer, contained in k11, the net rate constant for catalysis, may exhibit an isotope effect upon deuteration of NADH at the C-4 pro-R hydrogen of the dihydronicotinamide ring if it contributes to rate limitation. Conditions for measurement of V/K for a given reactant require all other reactants to be present at saturation. Thus, the expressions for V, V/Kb, and V/Kc are given by equations 12-14, while V/Ka is equal to k1.
| (12) |
| (13) |
| (14) |
In eqs. 12-14, cfb and cfc (forward commitments to catalysis for B and C) are , and , respectively, cr (reverse commitment to catalysis) is , and cvf (the catalytic ratio) is (16).
Substrate Dependence of Primary Deuterium Kinetic Isotope Effects
In an ordered kinetic mechanism, V/Ka, is the on-rate constant for binding of the first substrate, is not sensitive to substitution of deuterium for protium, and thus the isotope effect on V/Ka is unity. The magnitude of D(V/Kb) and D(V/Kc) provides information on the preference of the two pathways in eq. 11. The larger the value of D(V/K), the lower the value of the commitment factors, cf and cr. The lower commitment factor indicates the less favored pathway in a random mechanism (23). For example, if D(V/Kc) > D(V/Kb), cfc < cfb, B is stickier than C, and the pathway preference is E to EB to EBC. If D(V/Kb) = D(V/Kc), there are two possibilities. First, neither substrate B nor C is sticky, suggesting that the kinetic mechanism is rapid equilibrium random. Second, both substrates B and C are equally sticky, indicating a steady-state random addition of B and C, with k6 = k7 (24).
For the SDH reaction, D(V2/KNADH) is 0.92 ± 0.08 at pH 7.1, 25 °C, within error, identical to 1, consistent with the proposed ordered addition of NADH before α-Kg and lysine (3). Since D(V2/Kα-Kg) and D(V2/KLys) are both finite, their order of addition must be random, consistent with the proposed mechanism, and since D(V2/Kα-Kg) is greater than D(V2/KLys), the preferred pathway is E:NADH to E:NADH:Lys to E:NADH:Lys:α-Kg at pH 7.1. Since DV2 ≈ D(V2/KLys), the off-rate for lysine from E:NADH:Lys:α-Kg is likely about the same as that of NAD from E:NAD. That E:NAD exists in the steady state is known as a result of uncompetitive substrate inhibition by α-Kg (3). The off-rate for α-Kg from E:NADH:Lys:α-Kg is greater than that of lysine from the same complex.
pH Dependence of Primary Deuterium Kinetic Isotope Effects
Kinetic parameters depend on pH as a result of titration of groups responsible for reactant binding, catalysis, or maintaining the correct conformation of the enzyme. Information on kinetic and chemical mechanism can be obtained if the isotope effects are measured at the optimum pH and a pH where the kinetic parameter is decreasing by a factor of 10 per pH unit (24). In the case where the isotope-sensitive step is not solely rate-determining and substrate is sticky, the observed isotope effect can be enhanced by changing the pH, and eliminating substrate stickiness by making the catalytic pathway slow. For the SDH reaction, the maximum isotope effect is observed at low pH (1.7-1.8) and the effect decreases as the pH is increased above the pKa observed in the V2/KLys pH-rate profile.
At low pH, the isotope effect on V2/KLys increases compared to that measured at neutral pH and becomes equal to D(V2/Kα-Kg). It thus appears that lysine is sticky, while α-Kg is not. The stickiness factor, , can be estimated using the value of 1.8 for the maximum isotope effect and the following equation.
| (15) |
Substituting 1.56 and 1.8 for D(V/K) and D(V/K)max, a cf of about 0.4 is calculated suggesting that at neutral pH, once lysine is bound, it dissociates from enzyme 2.5-times faster than the rate of the catalytic pathway. The maximum value of 1.8 is not the intrinsic isotope effect, since the hydride transfer step is not completing limiting for the overall reaction (see below).
The value of D(V2/KLys) decreases to about unity as the pH increases over the pH range where V2/KLys is decreasing by a factor of 10 per pH unit. V2 does not vary significantly as the pH is decreased to 6.1, nor does DV2. However, the isotope effect does decrease toward unity as the pH is increased, as does D(V2/KLys), even though V2 decreases only slightly as the pH increases. In addition, DV2 decreases as the pH is decreased below 6.0. Data suggest the pH- and isotope-dependent steps are not the same in the direction of saccharopine formation (25) and that an isotope independent step contribute to V2 at low pH. Data will be discussed in the context of the mechanism below.
Solvent Deuterium Kinetic Isotope Effects and Proton Inventory Studies
The pH(D) dependence of kinetic parameters was measured for lysine with NADH and α-Kg maintained at saturation, over the pH(D) range 6.5 - 8.5 to determine whether a solvent deuterium kinetic isotope effect was observed. As predicted, the profile in D2O is shifted to higher pD as a result of the equilibrium solvent deuterium isotope effect on the pKa values (14). The solvent kinetic deuterium isotope effect, obtained as the ratio of the pH(D) independent values of the kinetic parameters, are significant, with estimated D2OV2 and D2OV2/KLys values of 2.2 ± 0.1 and 1.9 ± 0.1, respectively, suggesting a significant contribution from proton transfer step(s) to rate limitation of the overall reaction.
Multiple Solvent Deuterium/Substrate Deuterium Kinetic Isotope Effects
Multiple isotope effects potentially allow one to define the interrelationship between two isotope sensitive steps (26). Isotope effects that reflect the same transition state are independent of one another, since they reflect the same step. If the step is completely rate-limiting, the isotope effect will not change in the presence of the second isotope, while if it is not completely rate-limiting, the isotope effect will increase. If substrate and solvent deuterium isotope effects do not reflect the same step, deuteration of the substrate decreases the observed solvent isotope effect by making the deuterium-sensitive step more rate-limiting. Two kinds of multiple isotope effects are used in these studies, a solvent deuterium isotope effect measured with NADD and a primary substrate deuterium isotope effect measured in D2O. There is no significant decrease in the solvent deuterium isotope effect on V2 and V2/KLys when obtained using NADD compared to that using NADH. In addition, there is no change in the isotope effect upon measuring DV2 and D(V2/KLys) in 90% D2O compared to that in H2O. These data suggest a concerted proton and hydride transfer that is completely rate-limiting for the overall reaction. However, the isotope effect on V2/Kα-Kg is greater than that observed for V2/KLys at pH 7.1, D(V2/KLys) increases as the pH is decreased, and D2O(V2)D is decreased compared to D2O(V2)H. Thus, hydride transfer can not be the sole rate limiting step. The data can be reconciled by suggesting proton transfer in the hydride transfer step and in some other step. The one in the hydride transfer step results in an increase in the primary deuterium isotope effect, while the one in another step causes it to decrease, giving no net change in the isotope effect. In addition, the lack of change in the solvent deuterium isotope effect indicates that the effect is likely reflected differently by the two solvent sensitive steps with NADH and NADD, but the weighted average is the same in both cases. The origin of the proton transferred in the hydride transfer step is likely a proton transferred from the protonated secondary amine of saccharopine to an enzyme base as the hydride is transferred. There are several possibilities for the other proton transfer step(s), including hydrolysis of the imine that results from the oxidation of saccharopine.
Proton Inventory Studies
An estimate of the number of protons important to the overall reaction and the number of proton transfer steps that contribute to rate limitation can be obtained from the proton inventory method (15). If a single proton is transferred in the rate-limiting transition state, a plot of the rate constant versus atom fraction of deuterium (n) will be a linear. If more than one proton is transferred in a single transition state, the plot will be bowl-shaped (concave upward), while if protons are transferred in multiple transition states, the plot will be a dome-shaped plot (concave downward). Dome-shaped proton inventories require offsetting normal and inverse contributions to the solvent isotope effect, and can have several mechanistic origins (27). The replot of V2 versus the percent D2O at pH 7.1 gives a bulging dome-shaped plot, Fig. 7A, suggestive of contribution from proton transfer with a significant inverse contribution effect likely from a medium effect (15). However, the slight curvature observed in the case of V/K is more consistent with isotope effects in two or more sequential transition states, but with the absence of significant medium effect, Fig. 7B (27). Data are thus consistent with the multiple isotope effects and suggest that rate-limiting proton transfer exists in at least two sequential transition states, for example, substrate (de)protonation, hydride transfer, water elimination, or an enzyme conformational change. Of these, hydride transfer and formation of the imine from the carbinolamine are most likely. The medium effect seen in V2, but not V2/KLys, suggests that it is caused by a step(s) not included in V2/KLys under conditions of saturating substrate concentration, i.e., either product release, or a conformational change once substrates are bound, e.g., isomerization of E:NAD, E:NADH or E:NADH:α-Kg. This will be further discussed below.
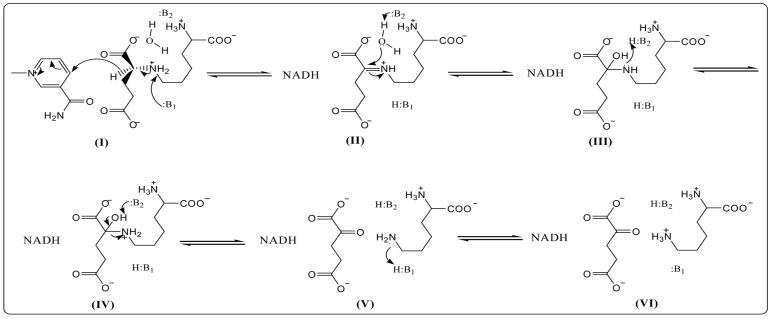
Scheme 1.
Proposed Chemical Mechanism for Saccharopine Dehydrogenase. I. the formed central complex E:NAD:saccharopine once NAD and saccharopine bind. II. Schiff base intermediate. III. carbinolamine intermediate. IV. protonated carbinolamine. V. the generated central complex E:NADH:α-Kg-Lys. VI. protonated lysine. With the exception of saccharopine, no stereochemistry is implied.
Interpretation of the pH Dependence of Kinetic Parameters
The pH dependence of logV/K versus pH is obtained at a limiting concentration of one of the reactants and saturating levels of all others, with free substrate and the enzyme form to which it binds predominant in the steady state. The logV versus pH profile is obtained at saturating concentrations of all substrates with the enzyme form(s) that build(s) up in the steady state predominant. The V profile will thus reflect groups on enzyme required for catalysis, while the V/K profile will reflect the protonation state of group(s) on enzyme and/or reactant responsible in a given protonation state for binding and/or catalysis (28). In the case of an ordered mechanism, the V/K for the first substrate is the rate constant for binding reactant to enzyme and will thus reflect groups important for binding, which may also contribute to catalysis, for example, if a catalytic group hydrogen-bonds to or is in the vicinity of the substrate.
The determination of a steady-state partial random mechanism at pH 7.0-8.0 and a rapid equilibrium ordered mechanism at low and high pH for SDH allows the pH profiles to be interpreted in terms of enzyme forms or species that predominate under any given conditions. In the direction of lysine formation, free enzyme and NAD predominate for the V1/KNAD profile, while the E:NAD enzyme form and saccharopine predominate for the V1/KSacc profile. Finite primary deuterium and solvent deuterium kinetic isotope effects, and proton inventory studies suggest central complexes (primarily E:NAD:Sacc and E:NADH:imine, where imine is the oxidized form of saccharopine) predominate for the V1 profile. In the reverse reaction direction, the free enzyme and NADH predominate for the V2/KNADH profile; while E:NADH:lysine and α-Kg predominate for the V2/Kα-Kg profile at 5.0 < pH < 8.5, and at pH values lower and higher, E:NADH and α-Kg predominate. In the case of the V2/KLys profile, E:NADH:α-Kg and lysine predominate, while central complexes and (E:NAD, or E:NADH, or E:NADH:α-Kg) predominate for the V2 pH profile (see discussion of isotope effects above).
The V1/KNAD is equal to the on-rate constant for NAD binding and the pKa of 7.4 reflects a group that must be deprotonated for optimum binding of NAD. The V1/KSacc pH-rate profile exhibits pKa values of 6.2 and 7.2, while the V1 pH-rate profile shows a pKa identical within error. The pKa of 7.2 likely reflects the same enzyme group in E:NAD and central complexes, which likely serves as a general base in the overall reaction needed to activate water in the hyfrolysis of the imine formed upon oxidation of saccharopine. The second group in V1/KSacc pH-rate profile with a pKa of 6.2 which needs to be deprotonated likely contributes to the binding of saccharopine only, since it is not observed in the V1 pH-rate profile. Since neither NAD nor saccharopine have pKa values in the pH range studied, the pKa must represent ionization of a group on the enzyme. Therefore, there are two groups on the enzyme with pKa values of 6.2 and 7.2 that must be deprotonated for binding of saccharopine, and catalysis, respectively. A group on enzyme with a pKa of about 7.2-7.4 is likely the same one that affects V1, V1/KNAD, and V1/KSacc, a catalytic group that also affects the binding of NAD. The protonation state of this group does not affect binding of NADH, and it is thus likely to be a cationic acid located in the vicinity of the positively charged nicotinamide ring of NAD.
In the direction of saccharopine formation, the SDH has a random kinetic mechanism with NADH bound to free enzyme first, followed by random addition of α-Kg and lysine at neutral pH. The V2/KNADH Et decreases at high pH with a slope of −1 giving pKa value of 9.6 ± 0.2. Since NADH is the first substrate bound, and considering the pKa of the pyrophosphate moiety of NADH is about 1-2, it is suggested that the group on enzyme with a pKa of 9.6 likely contributes to the binding of NADH, and must be protonated for optimal binding, likely interacting with the negatively charged phosphoryl oxygens of NADH via an ionic interaction. This group was not seen in the V1/KNAD pH-rate profile in the forward direction reaction, because the parameter was not measured above pH 9.0 in that reaction direction; the Km for saccharopine has become about 10 mM at pH values above 9.
The V2/Kα-Kg profile shows a single group with pKa 8.8 that must be protonated for optimum binding. In addition, V2 decreases to a new constant value at high pH exhibiting a pKa of about 8.4. These pKa values are identical, within error. The kinetic mechanism of SDH changes from random to rapid equilibrium ordered when the pH is above 8.0 or below 5.5. The V2/Kα-Kg pH-rate profile is independent of pH from 5.5 to about 8.0, but the rate constant decreases when the pH is increased above 8.0, at the point where the mechanism changes. Between pH 5.5 and 8.0, the predominant enzyme form is E:NADH:Lys, while above 8, the E:NAD form predominates. The decrease in V2/Kα-Kg likely reflects a kinetic pKa resulting from the change in kinetic mechanism due to a slower pathway with α-Kg binding before lysine. In agreement with the V2/Kα-Kg, V2 also decreases at high pH giving a partial change in activity, likely reflecting the same kinetic mechanism change. The group with a pKa of 7.2 in the V2/KLys profile is not observed in the V2/Kα-Kg pH-rate profile. Under these conditions lysine is bound, and the group with a pKa of 7.2 is likely locked in its correct protonation state. Since the group seen on the acid side functions to deprotonate the lysine є-amine, it is reasonable the group would not be observed with lysine bound. Overall, data are consistent with the steady state random nature of the mechanism with the E:NADH to E:NADH:Lys pathway preferred and faster than that with E:NADH:α-Kg.
The bell-shaped pH profile for V2/KLys observed in the reverse reaction direction shows that a group with a pKa of about 7.2 must be unprotonated and a group with a pKa of about 7.2 must be protonated for binding lysine to the E:NADH:α-Kg complex and catalysis. Since lysine has no ionizing groups corresponding to 7.2, they must reflect the ionization of groups on the enzyme. A group on enzyme with a pKa of 7.2 exhibited in V1, V1/KNAD, and V1/KSacc profiles must be deprotonated for catalysis in the direction of lysine formation. On the basis of the acid-base chemistry required in the oxidative deamination reaction, the group with a pKa of 7.2 is believed to represent a general base required to abstract a proton from H2O as it attacks the carbon of the imine formed upon oxidation of saccharopine. In the opposite direction reaction, the same group, seen in the V2/KLys pH-rate profile must be protonated to donate a proton to the hydroxyl of the carbinolamine intermediate to facilitate H2O elimination. The second group observed on the acid side of the V2/KLys profile with a pKa of 7.2 is responsible for deprotonating the є-amine of lysine, so that it can act as a nucleophile to form an imine with the α-oxo group of α-Kg. In the slow reaction direction (formation of lysine), the observed pKa in the V1/KSacc pH-rate profile is 6.2. This pKa is likely the intrinsic pKa for the binding group, while it is perturbed to higher pH in the opposite direction (V2/KLys pH-rate profile), suggesting lysine is sticky (see pKiLeu).
V2 also decreases at low pH with a limiting slope of +1 giving a pKa value of 5.8, indicating that another group on enzyme must be deprotonated for iptimum activity. It is possible that this pKa reflects a pH-dependent conformational change in enzyme once all substrates are bound; perhaps the same conformational change seen as a medium effect in the proton inventory of V2. In agreement with this suggestion, the primary deuterium isotope effect decreases from 1.6 at pH 6.1 to 1.2 at pH 5.6, suggestive of a step other the hydride transfer becoming rate-limiting at low pH.
Interpretation of pKi profiles
The pKi profile for leucine, a competitive inhibitor of lysine, indicates a group with a pKa of 6.2 must be protonated for optimal binding of leucine. This is the same pKa observed in the V1/KSacc pH-rate profile that must be unprotonated to bind saccharopine. The group must also be unprotonated to accept a proton from the є-amine of lysine. The difference between lysine and leucine is that one has a positive charge and the other is hydrophobic. Since the group must be protonated to allow binding of the hydrophobic side chain of leucine, it is likely that it is a neutral acid (Asp or Glu). The perturbation of the pKa observed in the V2/KLys pH-rate profile is in agreement with the stickiness of lysine, as discussed above under the pH dependence of primary deuterium isotope effect. Given the large standard error on the pKa values, the isotope effects provide a better quantitative estimate of stickiness. In addition, the pKa perturbation likely reflects an environmental change as lysine binds to enzyme. Consistent with this suggestion, when leucine is bound, the pKa of the binding group increases to about 9.2, consistent with a neutral acid in a more hydrophobic environment.
The pKiOG profile within the pH range 6.0-8.0 where the overall kinetic mechanism is random and OG binds to E:NADH:Lys is largely pH independent with an average Ki value of 100 μM. As the pH is increased above 8 and below 6 where the kinetic mechanism changes to equilibrium ordered, the pKi also becomes pH-independent with an average Ki value of about 500 μM. The approximately 5-fold change in the Ki value (see the boxes in Fig. 3A) over these two pH ranges likely reflects the change in mechanism itself and the difference in affinity of OG for E:NADH:Lys and E:NADH. There is a transition between the two pH independent regions, but the scatter in the data makes it difficult to see where the transition occurs. The boxes drawn in Fig. 4A are simply to highlight the two pH independent regions.
Proposed Chemical Mechanism
The pH-rate profiles and isotope effect experiments discussed above are consistent with a proton shuttle chemical mechanism as shown in Scheme 1. Two groups serve as acid-base catalysts in the reaction, but one of them catalyze most of the steps. In the direction of lysine formation, once NAD and saccharopine bind (I, in Scheme 1), the group with a pKa of 6.2, likely Asp or Glu as suggested on the basis of the difference in V2/KLys and pKiLeu pH-rate profiles, accepts a proton from the secondary amine of saccharopine as it is oxidized. This protonated general base then does not function until lysine is formed at the completion of the reaction. The concerted proton and hydride transfer is corroborated by the D/D2O multiple isotope effect. The general base with a pKa of 7.2, likely a cationic acid such as Lys or His (on the basis of the differences in V1/KNAD and V2/KNADH pH-rate profiles), accepts a proton from H2O as it attacks the Schiff base carbon (II) to form the carbinolamine intermediate (III). It is likely this step that reflects the solvent isotope effect on the step outside hydride transfer. The same residue then serves as a general acid and donates a proton to the carbinolamine nitrogen to give the protonated carbinolamine (IV). The carbinolamine collapses, facilitated by the proton shuttle accepting a proton from the carbinolamine hydroxyl to generate α-Kg and lysine (V). The amine nitrogen is then protonated by the group that originally accepted a proton from the secondary amine of saccharopine (VI).
Isotope effect data suggest a difference in the pH-dependent and isotope-dependent step (hydride transfer) at high pH. Data most likely reflect a pathway in which the general base with a pKa of 7.2 becomes deprotonated along the reaction pathway, committing reactants to go on to products. A protonated carbinolamine (IV) is formed from lysine and α-Kg (V). The base then accepts a proton from the carbinolamine nitrogen to generate the neutral carbinolamine (III). Deprotonation of the base at this point causes the reaction to be committed to forming saccharopine. This step precedes the hydride transfer step, and would still require protonation of the leaving hydroxide to generate the imine. This proton could be generated by the imine itself in II or from some other secondary proton donor. These details await additional experiments to sort out.
As we were completing this manuscript, the structure of apo-SDH was solved (Albert M. Berghuis, McGill University, Canada, personal communication). The active site could be located using a binary complex of AlaDH with pyruvate bound; AlaDH is the closest homolog of SDH (1). On the basis of a superposition of the binary complex structures of AlaDH (E:NAD and E:pyruvate) and the apo-structure of SDH, the active site of the two enzymes have significant similarity. There are several Arg residues that may be in proper position to ion pair the three carboxylates of saccharopine, in agreement with the role of arginine. The neutral acid we suggested that deprotonates saccharopine and lysine may be Asp 271, which located in the approximate vicinity predicted for the lysine side chain. In addition, the group with a pKa of about 7.2 in the proposed mechanism is likely Lys77, which is close to Lys 12, which may function as a Lys-Lys pair to serve as the general acid-base in the reaction. The Lys-Lys pair would account for the low pKa observed in the pH-rate profiles for V1, V1/KNAD, V1KSacc, and V2/KLys. If protonated, the binding of NAD would be hindered as a result of the positive charge in the vicinity of the nicotinamide ring.
A couple of additional points should be mentioned. The proton to be transferred to the group with a pKa of 6.2 requires that there be a better match the pKa values of the base and proton donor. The latter have solution values of 10-10.5 (saccharopine secondary amine and lysine є-amine), > 4 pH units higher than the base. As a result, there must be a shift in the pKa of the base to a higher value and the proton donor to a lower value, likely by about 2 pH units for each. The pKa perturbation likely results from neutralization of the charge of the binding groups in the active site (substrate carboxylates and Arg), which will make the site more hydrophobic, resulting in an increase in the putative enzymic carboxylate pKa and a decrease in the pKa of the proton donor (lysine є-amine or saccharopine secondary amine). The pKa of 9.2 observed in the pKiLeu profile once leucine is bound, is consistent with the pKa perturbation. Another important point is that although the group with a pKa of 6.2 is unprotonated at the beginning and end of the reaction, the group with a pKa of 7.2 is in opposite protonation states at the beginning and end of the reaction and must be deprotonated for a new round of catalysis, and the proton is most likely exchanged with bulk solvent after the active site is open and products are released.
Acknowledgements
We thank Dr. William E. Karsten for his technical assistance on experimental protocol and data analysis. We thank Rong Guan and Dr. Ying Lin for their insightful discussion of the results. We thank Dr. Albert M. Berghuis for atomic coordinates of SDH prior to publication, and we thank Dr. Babak Andi for help with the AlDH and SDH structures.
Footnotes
This work is supported by the Grayce B. Kerr Endowment to the University of Oklahoma (to P.F.C.), and a grant (GM 071417) from the National Institute of Health (to P.F.C. and A.H.W.).
Abbreviations: SDH, saccharopine dehydrogenase; AAA, α-aminoadipate pathway; α-Kg, α-ketoglutarate; Sacc, saccharopine; OG, oxalylglycine; NAD, nicotinamide adenine dinucleotide (the + charge is omitted for convenience); NADH, reduced nicotinamide adenine dinucleotide; NADD, reduced nicotinamide adenine dinucleotide with deuterium in the 4-A position; C, competitive; Hepes, N-(2-hydroxyethyl)piperazine-N′-(2-ethanesulfonic acid); Mes, 2-(N-morpholino)ethanesulfonic acid, monohydrate; Ches, 2-(N-cyclohexylamino)ethanesulfonic acid; Taps, N-[tris(hydroxymethyl)methyl]-3-aminopropanesulfonic acid; DCl, deuterium chloride; NaOD, sodium deuterioxide; D2O, deuterium oxide.
Nomenclature: Isotope effects are expressed using the nomenclature developed by Northrop (16) and Cook and Cleland (17). Primary and solvent deuterium kinetic isotope effects are written with a leading superscript D and D2O, e.g. a primary deuterium isotope effect on V/K is written D(V/K). Multiple isotope effects are written with a leading superscript to depict the isotope varied, and a following subscript to depict the fixed isotope, e.g. a solvent deuterium isotope effect measured with A-side NADD would be written D2O(V/K)D. A “sticky” substrate is one that reacts to give product as fast as or faster than it dissociates from the enzyme complex.
REFERENCES
- 1.Xu H, Andi B, Qian J, West AH, Cook PF. The α-aminoadipate pathway for lysine biosynthesis in fungi. Cell Biochem. Biophys. 2006;46:43–64. doi: 10.1385/CBB:46:1:43. [DOI] [PubMed] [Google Scholar]
- 2.Zabriskie TM, Jackson MD. Lysine biosynthesis and metabolism in fungi. Nat. Prod. Rep. 2000;17:85–97. doi: 10.1039/a801345d. [DOI] [PubMed] [Google Scholar]
- 3.Xu H, West AH, Cook PF. Overall kinetic mechanism of saccharopine dehydrogenase from Saccharomyces cerevisiae. Biochemistry. 2006;45:12156–12166. doi: 10.1021/bi0610808. [DOI] [PubMed] [Google Scholar]
- 4.Garrad RC, Bhattacharjee JK. Lysine biosynthesis in selected pathogenic fungi: characterization of lysine auxotrophs and the cloned LYS1 gene of Candida albicans. J. Bacteriol. 1992;174:7379–7384. doi: 10.1128/jb.174.22.7379-7384.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Johansson E, Steffens JJ, Lindqvist Y, Schneider G. Crystal structure of saccharopine reductase from Magnaporthe grisea, an enzyme of the α-aminoadipate pathway of lysine biosynthesis. Structure. 2000;8:1037–1047. doi: 10.1016/s0969-2126(00)00512-8. [DOI] [PubMed] [Google Scholar]
- 6.Sugimoto K, Fujioka M. Chemical mechanism of saccharopine dehydrogenase (NAD+, L-lysine-forming) as deduced from initial rate pH studies. Arch. Biochem. Biophys. 1984;230:553–559. doi: 10.1016/0003-9861(84)90436-3. [DOI] [PubMed] [Google Scholar]
- 7.Ogawa H, Okamoto M, Fujioka M. Chemical modification of the active site sulfhydryl group of saccharopine dehydrogenase (L-lysine-forming) J. Biol. Chem. 1979;254:7030–7035. [PubMed] [Google Scholar]
- 8.Fujioka M, Takata Y, Ogawa H, Okamoto M. The inactivation of saccharopine dehydrogenase (L-lysine-forming) by diethyl pyrocarbonate. J. Biol. Chem. 1979;255:937–942. [PubMed] [Google Scholar]
- 9.Ogawa H, Fujioka M. The reaction of pyridoxal-5′-phosphate with an essential lysine residue of saccharopine dehydrogenase (L-lysine-forming) J. Biol. Chem. 1980;255:7420–7425. [PubMed] [Google Scholar]
- 10.Fujioka M, Takata Y. Role of arginine residue in saccharopine dehydrogenase (L-lysine-forming) from baker's yeast. Biochemistry. 1981;20:468–472. doi: 10.1021/bi00506a004. [DOI] [PubMed] [Google Scholar]
- 11.Fujioka M, Takata Y. Stereospecificity of hydrogen transfer in the saccharopine dehydrogenase reaction. Biochim. Biophys. Acta. 1979;570:210–212. doi: 10.1016/0005-2744(79)90215-8. [DOI] [PubMed] [Google Scholar]
- 12.Viola RE, Cook PF, Cleland WW. Stereoselective preparation of deuterated reduced nicotinamide adenine nucleotides and substrates by enzymatic synthesis. Anal. Biochem. 1979;96:334–340. doi: 10.1016/0003-2697(79)90590-6. [DOI] [PubMed] [Google Scholar]
- 13.Northrop DB, Duggleby RG. Preparation and storage of isotopically labeled reduced nicotinamide adenine dinucleotide. Anal. Biochem. 1987;165:362–364. doi: 10.1016/0003-2697(87)90282-x. [DOI] [PubMed] [Google Scholar]
- 14.Schowen KB, Schowen RL. Solvent isotope effects on enzyme systems. Methods Enzymol. 1982;87:551. [PubMed] [Google Scholar]
- 15.Quinn DM, Sutton LD. In: Enzyme Mechanism for Isotope Effects. Cook PF, editor. CRC Press, Inc.; Boca Raton, FL: 1991. pp. 73–126. [Google Scholar]
- 16.Northrop DB. In: Isotope Effects on Enzyme-Catalyzed Reactions. Cleland WW, O'Leary MH, Northrop DB, editors. University Park Press; Baltimore, MD: 1977. p. 122. [Google Scholar]
- 17.Cook PF, Cleland WW. Mechanistic deductions from isotope effects in multireactant enzyme mechanisms. Biochemistry. 1981a;20:1790–1796. doi: 10.1021/bi00510a013. [DOI] [PubMed] [Google Scholar]
- 18.Marquardt DW. An algorithm for least square estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
- 19.Cleland WW. Statistical analysis of enzyme kinetic data. Methods Enzymol. 1979;63:103–108. doi: 10.1016/0076-6879(79)63008-2. [DOI] [PubMed] [Google Scholar]
- 20.Brown HC, McDaniel DH, Haflinger O. In: Determination of organic structures by physical methods. Braude EA, Nachod FC, editors. Vol. 1. Academic Press, Inc; NY: 1955. pp. 567–662. [Google Scholar]
- 21.Blanchard JS, Cleland WW. Kinetic and chemical mechanisms of yeast formate dehydrogenase. Biochemistry. 1980;19:3543–3550. doi: 10.1021/bi00556a020. [DOI] [PubMed] [Google Scholar]
- 22.Weiss PM, Chen CY, Cleland WW, Cook PF. Primary deuterium and 15N isotope effects as a mechanistic probe of alanine and glutamate dehydrogenases. Biochemistry. 1988;27:4814–4822. doi: 10.1021/bi00413a035. [DOI] [PubMed] [Google Scholar]
- 23.Cook PF, Cleland WW. pH variation of isotope effects in enzyme-catalyzed reactions. 1. Isotope- and pH-dependent steps the same. Kinetic mechanism of alcohol dehydrogenase. Biochemistry. 1981b;20:1797–1805. doi: 10.1021/bi00510a014. [DOI] [PubMed] [Google Scholar]
- 24.Karsten WE, Cook PF. In: Isotope effects in chemistry and biology. Kohen A, Limbach HH, editors. CRC Press, Inc.; Boca Raton, FL: 2006. pp. 793–809. [Google Scholar]
- 25.Cook PF, Cleland WW. pH variation of isotope effects in enzyme-catalyzed reactions. 2. Isotope-dependent step not pH-dependent. Kinetic mechanism of alcohol dehydrogenase. Biochemistry. 1981b;20:1805–1816. doi: 10.1021/bi00510a015. [DOI] [PubMed] [Google Scholar]
- 26.Hermes JD, Roeske CA, O'Leary MH, Cleland WW. Use of multiple isotope effects to determine enzyme mechanisms and intrinsic isotope effects. Malic enzyme and glucose-6-phosphate dehydrogenase. Biochemistry. 1982;21:5106–5114. doi: 10.1021/bi00263a040. [DOI] [PubMed] [Google Scholar]
- 27.Quinn DM, Sutton LD. Theoretical basis and mechanistic utility of solvent isotope effects. In: Cook Paul F., editor. Enzyme Mechanism from Isotope Effects. CRC Press, Inc; Boca Raton, FL: 1991. pp. 73–126. [Google Scholar]
- 28.Cleland WW. Determination the chemical mechanisms of enzyme-catalyzed reactions by kinetic studies. Adv. Enzymol. Relat. Areas Mol. Biol. 1977;45:273–387. doi: 10.1002/9780470122907.ch4. [DOI] [PubMed] [Google Scholar]