Model-Based Decision Making in Early Clinical Development: Minimizing the Impact of a Blood Pressure Adverse Event

Abstract

We describe how modeling and simulation guided program decisions following a randomized placebo-controlled single-rising oral dose first-in-man trial of compound A where an undesired transient blood pressure (BP) elevation occurred in fasted healthy young adult males. We proposed a lumped-parameter pharmacokinetic–pharmacodynamic (PK/PD) model that captured important aspects of the BP homeostasis mechanism. Four conceptual units characterized the feedback PD model: a sinusoidal BP set point, an effect compartment, a linear effect model, and a system response. To explore approaches for minimizing the BP increase, we coupled the PD model to a modified PK model to guide oral controlled-release (CR) development. The proposed PK/PD model captured the central tendency of the observed data. The simulated BP response obtained with theoretical release rate profiles suggested some amelioration of the peak BP response with CR. This triggered subsequent CR formulation development; we used actual dissolution data from these candidate CR formulations in the PK/PD model to confirm a potential benefit in the peak BP response. Though this paradigm has yet to be tested in the clinic, our model-based approach provided a common rational framework to more fully utilize the limited available information for advancing the program.

INTRODUCTION

The competitive environment for pharmaceutical development demands effective decision making in the face of considerable complexity and uncertainty. Pharmacokinetic/pharmacodynamic (PK/PD) modeling and simulation provide a means to extract and integrate information and therefore offer a rational basis for several stages of the drug development process (1–3). The motivation for this modeling effort with this compound was an undesired transient increase in blood pressure (BP) that became apparent during a single-rising dose first-in-man (FIM) study (given the early nature of this development program, this presentation is based upon a masked compound, “compound A”). Correspondingly, there was a twofold aim. First was the development of a PK/PD BP model that captured the transient effect of compound A upon BP following single-dose administration. Second was the use of this model in a rational decision-making process that contemplated approaches for minimizing the undesired BP elevation. To achieve our first aim, we proposed a lumped-parameter PK/PD model that captured both features of the BP response and several facets of the feedback mechanism responsible for BP homeostasis. Several PK/PD models, spanning empirical to physiological, have been proposed to capture the desired or anticipated effect of a drug upon BP (4–8). Our model development borrowed several features from the physiologically based PK/PD model of Francheteau et al. (5), which explicitly models key features of the baroreceptor reflex and the desired effects of intravenous dihydropyridines on lowering BP. However, in our case, the BP elevation was a safety side effect and not the intended therapeutic effect. As is generally the case early in clinical development, our study was not designed with the intent of developing a fully physiological PK/PD model to characterize a potential adverse event. The lumped-parameter approach therefore was a practical means to maximize the physiological information we could garner from a limited data set.

The limited data set available to us at this early stage of clinical development presented additional challenges as we strove to meet our second aim: the use of our PK/PD model to address this early obstacle to development. We considered if an oral controlled-release (CR) platform could provide an altered PK profile which would in turn minimize the peak BP effect. At this point in the program, the only clinical data available to us were obtained following administration of an immediate-release (IR) dosage form. As we discuss in greater detail below, we modified our PK model obtained from the IR data to allow for altered administration rates to the two-compartment plasma disposition model. By coupling the modified PK model to our PD model, we proposed a rational path forward for the compound involving CR.

MATERIALS AND METHODS

Clinical Protocol

The data were compiled from a randomized placebo-controlled rising single oral dose study in fasted healthy young adult male subjects. This study was conducted in conformance with applicable country or local requirements regarding ethical committee review, informed consent, and other statutes or regulations regarding the protection of the rights and welfare of human subjects participating in biomedical research. Both the protocol and informed consent form were approved by the Investigator's Ethical Review Committee and the study was conducted in accordance with the guidelines established by the Declaration of Helsinki. Subjects were assigned to one of three treatment panels in this single-rising dose study in which the same subjects within a given panel were to receive escalating doses or placebo across five treatment periods with a 7-day washout period in between doses. For panel A, data were obtained at the 0.1-, 0.2-, 0.5-, 1.0-, and 2.0-mg doses. For panel B, data were obtained at the 2.0-, 4.0-, 8.0-, and 15.0-mg levels. Due to tolerability, dose escalation was terminated in panel C (the third and final panel), where subjects received 15.0 and 20.0 mg doses only. For each panel of eight subjects, two subjects received placebo and six subjects were administered compound A. Within each panel, the same two subjects received placebo in each of the treatment periods. Except for the 2.0-, 15.0-, and 20.0-mg doses, there were six subjects per dose level. Since six subjects were dosed in both panels A and B at the 2.0-mg level, there were 12 subjects in total who received this dose. Though 12 subjects again received the 15-mg dose (given in panels B and C), one subject was repeat-dosed at the 15-mg level due to an elevated BP response (rather than escalated to the 20-mg dose); accordingly, there were only five subjects who received the 20-mg dose. The data collected from the repeated 15-mg dose were not included in the subsequent PD model fit. For panels A, B, and C, blood was collected for plasma samples in period 1 at predose (0) and at 1, 2, 6, 12, and 24 h postdose and in remaining periods at predose (0) and at 0.5, 1, 1.5, 2, 3, 4, 6, 9, 12, 18, 24, 30, 48, and 72 h postdose. Semirecumbent diastolic and systolic blood pressure (SBP) measurements were obtained at predose (0), 0.5, 1, 2, 3, 4, 6, 8, 12, 24, and up to 48 h postdose; the 18-h SBP was obtained at the discretion of the investigator. Orthostatic blood pressure data were collected much less extensively (at predose (0), 2, and 4 h postdose) and were not further considered in PK/PD model development.

Assay Methods

Human plasma samples were analyzed using reversed-phase high-performance liquid chromatography (HPLC) followed by tandem mass spectrometry (MS/MS) detection. Compound A along with its stable-isotope-labeled internal standard were extracted with Oasis HLB μElution 96-well solid phase extraction plate. The extract was separated on a Shimadzu HPLC system using Phenomenex Synergi Hydro RP column (75 × 2 mm, 4 μ) under a mobile phase of acetonitrile (ACN)/5 mM ammonium acetate pH 5.5 (60/40, v/v) at a flow rate of 0.3 mL/min. The MS/MS was performed on a Sciex API4000 using a Turbo Ionspray source under the positive ionization mode with multiple reaction monitoring to detect the analytes’ precursor → product ion transitions. The limit of quantification was 0.5 nM using 100 μL of plasma, and the linear range was 0.5–500 nM. The intraday precision and accuracy of the assay was determined by analyzing five replicate standard curves in five lots of control human plasma. The accuracy range was 95.0–104.8% of nominal with a precision (coefficient of variation of peak area ratios) of ≤3.09%. Replicate low (1.5 nM), medium (20 nM), and high (400 nM) QC samples were analyzed daily with clinical samples to assess interday precision and accuracy. The mean daily QC resulted a 102.6–104.0% accuracy and <5.13% precision across ten analytical runs. No interference was observed in the predose samples from all tested subjects.

Dog Regional Bioavailability

The dog regional relative bioavailability data were obtained using a modified model similar to the one previously published (9). In the modified dog model, in addition to the jejunal and colonic ports, an ileal port was placed. The jejunal, ileal, and colonic ports were located about 15 cm distal to the ligament of Treitz, 100 cm proximal to the ileocecal junction, and 15 cm distal to the ileocecal junction. A four-period crossover study with five dogs was conducted to compare the exposure after oral, jejunal, ileal, and colonic dosing, respectively.

Purpose-bred Beagle dogs from Marshall Farms (North Rose, NY, USA) were housed in a US Department of Agriculture-approved facility in accordance with Association for Assessment and Accreditation of Laboratory Animal Care guidelines. The dog weights ranged from 8.2 to 12.7 kg during this series of studies. The dogs were fasted overnight without access to food prior to each study day. Water was available ad libitum throughout the studies. For all routes, a solution of compound A in 10% Captisol at a concentration of 0.2 mg/mL was administered at a volume of 1.0 mL/kg followed by a water flush of 5 mL. Standard laboratory chow and water were offered ad libitum 4 h after dosing. One milliliter blood samples were withdrawn through a heparin lock on a 21G indwelling catheter in the cephalic vein at predose, 15 and 30 min, and 1, 2, 4, 6, and 8 h. The 12- and 24-h samples were obtained by venipuncture.

A validated method using LC/MS/MS for the determination of compound A in dog plasma was used for the analysis of the samples from the above study. Analytes in 0.1-mL dog plasma samples were extracted using a liquid–liquid extraction employing methyl-t-butyl ether. After vortexing, the organic layer was separated through a Bond Elute Matrix cartridge then dried with nitrogen at 25°C for 30 min. The dried extract was reconstituted with 0.2 mL 70/30 ACN/1 mM ammonia acetate (pH 4) for LC/MS/MS analysis. The HPLC employed a BetaBasic C18 (100 × 2.1 mm, 3 μm) with a premixed mobile phase solvent of 90/10 ACN/1 mM ammonia acetate (pH 4). The mass spectrometer coupled with an electrospray was operated in the positive ion mode. The linear dynamic range was from 1 to 7,500 ng/mL. The analysis time was 5 min per sample.

Formulation and Characterization of Controlled-Release Tablets

Formulation development of matrix tablets was conducted by screening a number of compositions containing different ratios of drug to hydrophilic swelling and nonswelling polymer. Total drug to polymer ratio ranged from 1 to 2 to 1 to 18 parts. The matrix tablets were prepared by direct blending of drug, polymer, and diluent components in a laboratory turbula mixer for about 15 min followed by final lubrication and compression on a Stokes F-press using 8/32″ and 10/32″ standard round concave tooling at compression forces of 7 and 12 kN with tablet weights of 100 and 200 mg, respectively. Tablet hardness values ranged from 12–15 kP. Both tablet weight and compression force were maintained at ±2%. Tablet content uniformity showed >97% of the label claim present. In vitro dissolution testing was conducted in water with both 0.02% sodium dodecyl sulfate (SDS) and 0.1% SDS to provide a three-time sink condition using US Pharmacopeia apparatus II at paddle speeds of 75 and 100 rpm.

PK/PD Model Development

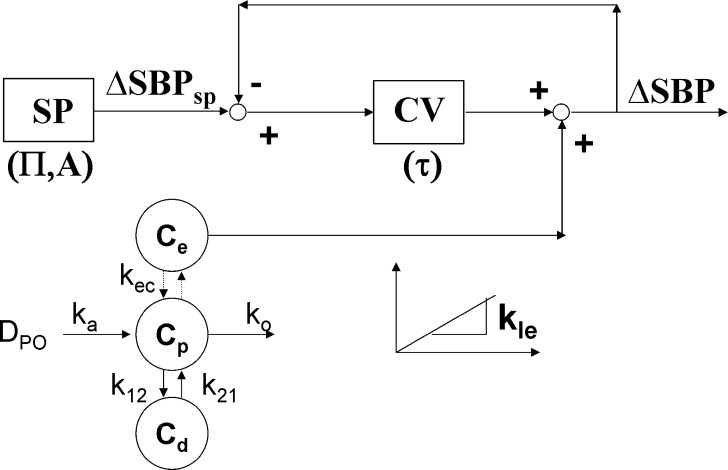
As described in greater detail in the “RESULTS AND DISCUSSION” section, from Fig. 1, three features were noted from inspection of the experimental data: (1) a delay between the plasma PK and the kinetics of the initial percent change of SBP relative to predose (ΔSBP, %), (2) a more rapid return to baseline BP relative to the terminal drug elimination phase, and (3) evidence of oscillatory behavior following the return to baseline. The feedback model depicted in Fig. 2 attempts to account for these features. Progressing first from left to right and then top to bottom, the first block depicted in this model represents a SBP set point (SP) relative to predose with circadian rhythm to provide ΔSBP_sp (%) as follows:

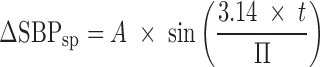1

where A (%) is the amplitude of the sine wave describing an underlying circadian rhythm of ΔSBP and Π (h) is the period of oscillation. Proceeding to the right, the actual ΔSBP was subtracted from ΔSBP_sp to provide an error signal sent to the cardiovascular system. The response of the cardiovascular system (CV) was described with a first-order transfer function as follows:

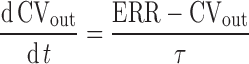2

where CV_out (%) represented the output from the CV block relative to predose, ERR (%) was the difference between ΔSBP_sp and ΔSBP, and τ (h) was the overall first-order time constant. Proceeding to the bottom left of Fig. 2, an effect compartment, characterized by k_ec (h⁻¹), captured the delay between plasma concentration, C_p (nM), and effect compartment concentration, C_e (nM). The C_p data were entered into the BP model via one of two PK models; a standard two-compartment PK model with both first-order absorption and elimination was used to calculate C_p for IR, while for CR scenarios, we used a modified PK model as described further below. A simple linear effect model characterized by k_le (%/nM) translated the effect compartment concentration C_e (nM) to a BP disturbance ΔSBP_dist (%).

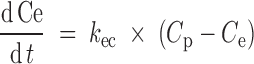3

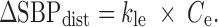4

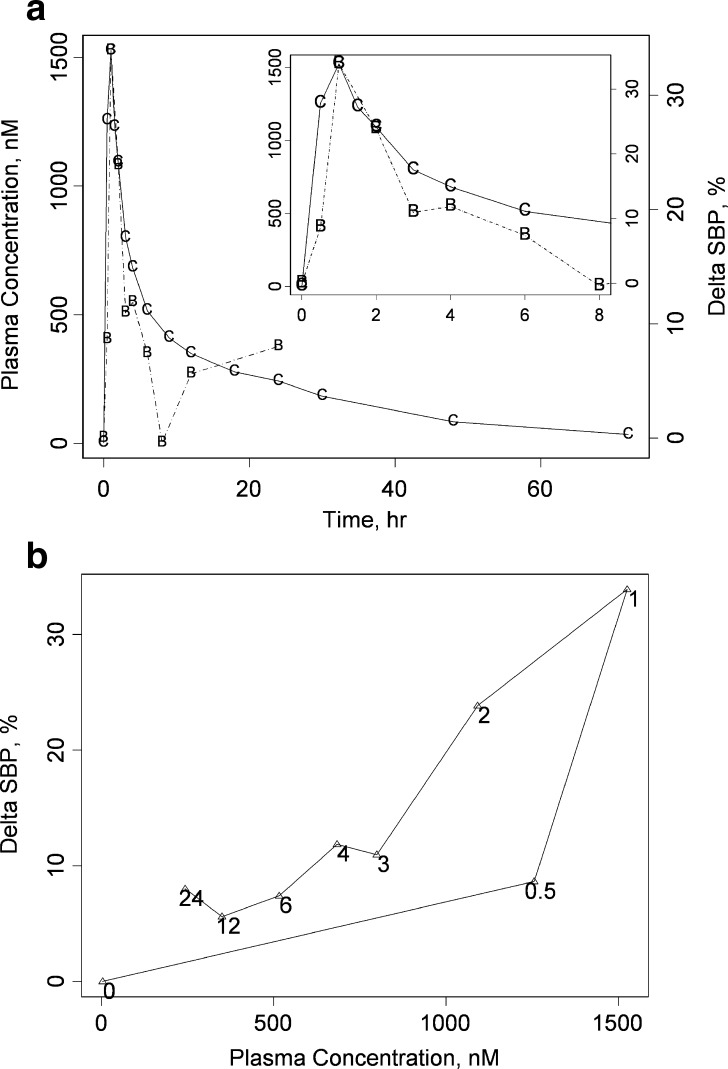
Fig. 1.

The representative PK/PD relationship at the 20-mg dose. Both a a double-y and b a hysteresis plot are provided to describe the arithmetic mean ΔSBP response following single-dose administration of 20 mg compound A at time = 0 (individual data are provided as ΔSBP versus time in Fig. 3). a The left y-axis corresponds to plasma concentration data of compound A; the arithmetic mean actual plasma concentration data are indicated by the letter C connected by solid lines. The right y-axis depicts the corresponding ΔSBP; observed ΔSBP are indicated with the letter B and a dashed line connects these points. An inset is provided to more clearly depict the early-time (t = 0 to 8 h postdose) behavior. b The hysteresis plot depicts ΔSBP as a function of plasma concentration of compound A. Only the data where both SBP and plasma concentration were measured contemporaneously are depicted. In b, the common observation times are depicted near their corresponding points. Collectively, a and b depict the early, intermediate, and late-time response of ΔSBP. From b, the early-time behavior is characterized by a counter-clockwise hysteresis loop, consistent with a delay between the plasma concentration and pharmacodynamic response. From a, the intermediate-time SBP response demonstrates a relatively rapid fall to ΔSBP = 0, and the late-time response indicates some degree of both rebound of ΔSBP and oscillatory behavior

Fig. 2.

A schematic of the proposed lumped-parameter PK/PD model for blood pressure homeostasis. Progressing from the top left, a sinusoidal SBP set point (ΔSBP_SP) of amplitude A and period П is compared to the measured ΔSBP to provide an error signal. The error signal is fed to the lumped cardiovascular process (CV), which is in turn characterized by a time constant τ. The output from CV is added to the disturbance due to compound A administration to provide the measured ΔSBP which loops back to be compared with ΔSBP_SP. The magnitude of the disturbance is related to the effect compartment concentration (C _e) by a linear effect (LE) model of slope k _le. The constant k _ec characterizes the delay between C _e and C _p

Finally, ΔSBP_dist was added to CV_out to provide ΔSBP.

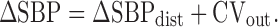5

Five model parameters were included in the model fit to actual ΔSBP data: k_ec, k_le, τ, Π, and A. Model fits were performed with the Advanced Continuous Simulation Language v. 2.5 (10; ACSL, Aegis Software; Huntsville, AL, USA). Model parameters and associated estimation precision (standard deviation, SD) were obtained by fitting to ΔSBP data as a naïve pooled data set; a generalized reduced gradient search algorithm was used to maximize the log-likelihood function (ACSL uses the log-likelihood function as the objective function). The heteroscedasticity parameter was optimized by the fitting algorithm. This weighting parameter approaches a value of 0 and 2 for absolute and relative error models, respectively.

Modified PK Model

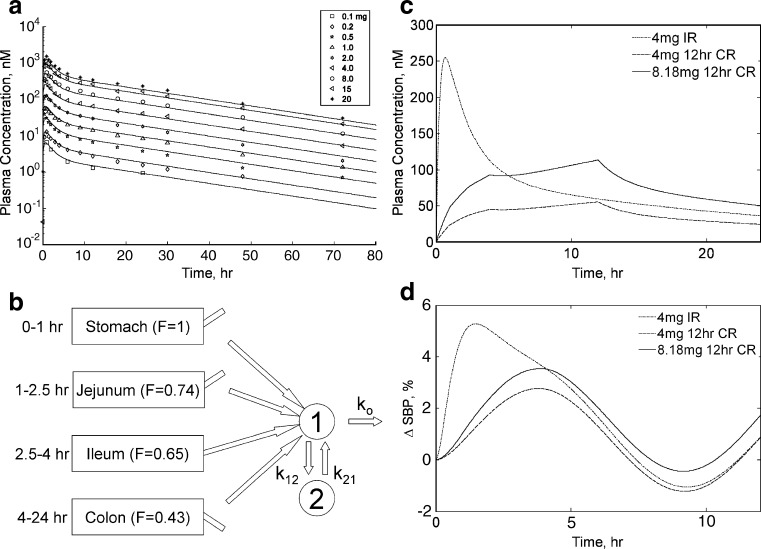
We previously obtained the relevant PK model parameters to the observed averaged C_p from the IR formulation. Since a previous noncompartmental analysis of pharmacokinetic data from this study indicated approximately linear dose-proportional pharmacokinetics, we modeled the pharmacokinetic profiles with a two compartment linear model with first-order absorption and elimination (Fig. 4a). We then altered the form of the PK model for the IR case (“modified PK model”; 11). We first replaced the first-order absorption process with a succession of steps as depicted in Fig. 4b. Each of the steps accounted for different regions of the gastrointestinal tract, progressing from stomach to colon. At this point in the program, human regional absorption data (F) were not available to parameterize the model. In lieu of human data, we used our available dog regional bioavailability data as surrogate values for human F. Dog F values for compound A are depicted in each of blocks, with F = 1, 0.74, 0.65, and 0.43 as we progress from stomach to jejunum, ileum, and finally, colon, respectively. These compartments were linked to the plasma disposition model obtained from the human FIM IR data. The rate of entry to the plasma disposition model was assumed to be governed by dissolution rate and is given by the product of F with the in vitro dissolution rate from a given formulation. Values of F were altered depending upon the time postdose relative to known transit times in the human (12,13).

Fig. 4.

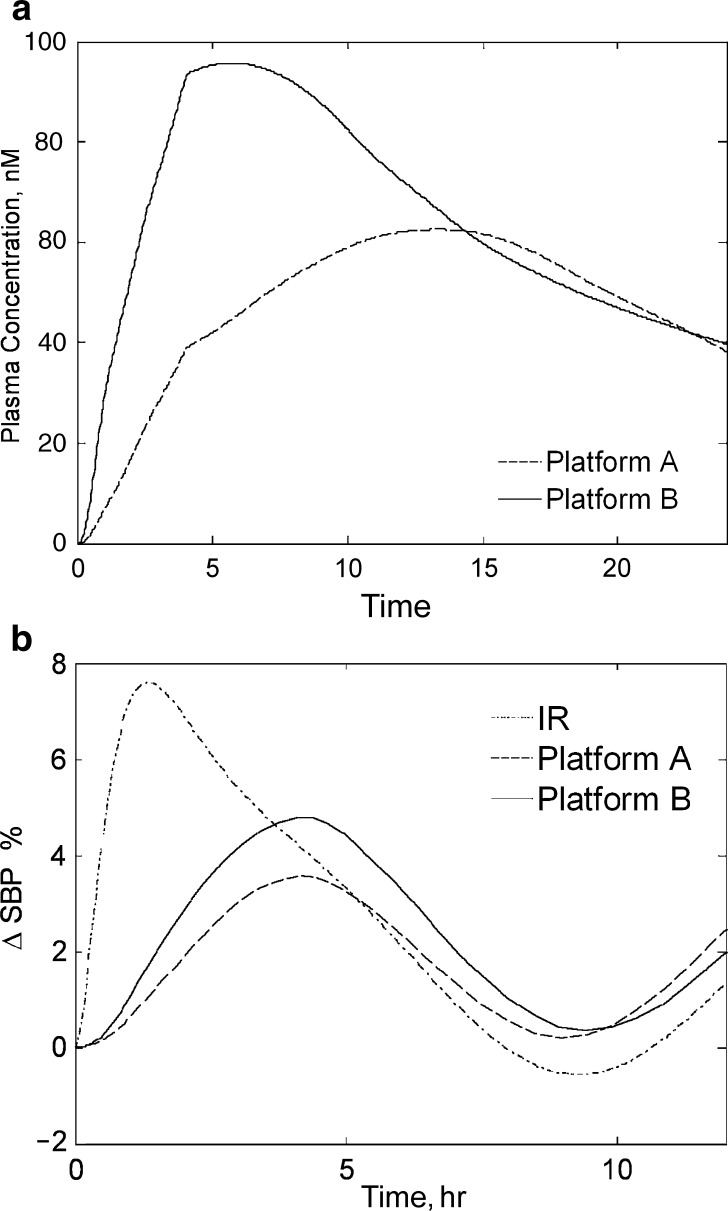
The ΔSBP projections for idealized zero-order controlled-release platforms. a Average plasma concentration data (symbols) in time with accompanying fit (solid lines) to a two-compartment PK model with first-order absorption and elimination for the doses studied in this investigation (doses are indicated in legend). b Illustration of the modified PK model used for simulating plasma PK profiles following administration of various controlled-release platforms. The modified PK model relied upon replacement of the first-order absorption process of the base PK model used to generate a with a succession of steps. Each of these steps was characterized with a duration that matched human transit times through the indicated segments of the gastrointestinal (GI) tract. Release from the controlled-release platform was assumed to govern entrance to the plasma disposition model. This release rate was adjusted by the corresponding regional bioavailability (F) determined previously in the dog and depicted upon the blocks corresponding to the specific region of the GI tract. c Projected plasma concentrations for idealized controlled-release systems of 12-h duration and fixed rate are superimposed over the simulated 4-mg immediate-release case and are depicted in the figure legend. Two hypothetical controlled-release platforms are depicted: one of equal initial loading to the 4-mg IR case and another that is dose-adjusted to provide an equivalent area under the plasma concentration–time curve. As anticipated, peak plasma concentrations were delayed and reduced relative to the immediate-release case. d The corresponding simulated ΔSBP behavior is depicted for each of the corresponding concentration profiles depicted in c. The corresponding simulated maximal ΔSBP was lessened for the hypothetical controlled-release cases, indicating some potential benefit to this approach

Simulated Plasma Concentration Profiles Following Controlled Release

We utilized the modified PK model to simulate C_p following administration of both idealized and actual controlled-release platforms. To explore the effect of delivery rate on simulated ΔSBP response, we first proposed an idealized time-invariant (“zero-order”) release rate delivery platform as an input to the system. The theoretical dissolution rate was set to 0.33 mg/h for the first 12 h, followed by 0 mg/h for the duration of the simulation (to allow delivery of 4 mg total drug). The procedure was repeated for a theoretical dose of 8.18 mg again over 12 h to correct for the calculated reduction in area under the concentration–time curve (AUC) for the 4-mg CR platform relative to the IR case. As discussed further in the “RESULTS AND DISCUSSION” section, these results suggested some benefit to controlled versus immediate release and were in turn used to provide a rational basis for controlled-release formulation development. To guide platform development, we considered the release rate characteristics from two candidate matrix formulations that were expected to deviate from zero-order behavior (14). Both a fast and a slow 6-mg formulation were considered for this exercise. Release rates were estimated from the cumulative dissolution profiles and were input to the modified PK model as described previously to provide the simulated plasma concentration profiles. These simulated profiles were generated using Matlab R14 with Simulink v. 6.2 (The Mathworks; Natick, MA, USA).

RESULTS AND DISCUSSION

Our goal was to provide a rational model-based guidance for bringing forward a lead compound given an early tolerability concern. We emphasized the physiology of the BP response through a semimechanistic model. Our selection of a semimechanistic model was driven by our desire to make the model more accessible to all members of the development team. In contrast, an empirical approach would not necessarily emphasize the relationship between the model and physiological processes; this would have potentially obscured the interpretation by members of the development team who were less familiar with the empirical approach. We divide our discussion into two sections: The first illustrates the proposed model fit, associated approximations, and physiological significance and the second describes how we used this model to provide guidance in the earliest phases of clinical drug development.

Model Fit, Approximations, and Physiological Significance

Measured BP Response and PK/PD Model Characteristics

The average PK and PD data from individuals receiving the 20-mg dose are depicted in both a double-y plot and hysteresis representation in Fig. 1a, b, respectively. At least three features of the PD response were evident from this representation as we progress from early to late times postdose: At early times, the counter-clockwise hysteresis is consistent with a delay between plasma concentration of compound A and ΔSBP; at intermediate times, the ΔSBP returned to baseline over a more rapid time course than the terminal elimination phase of the drug; at late times, there was evidence of oscillatory behavior in ΔSBP after the initial decent, followed by a return to baseline.

Table I gives both model parameters and diagnostics for successive simplifications of the full model given by Eqs. 1–5. The first entry of Table I corresponds to the linear effect model of Eq. 4 only; since the effect compartment is not incorporated for this model fit, C_p drives the BP response instead of C_e as indicated in Eq. 4. Replacement of Eq. 4 with a saturable Emax relationship gave rise to high parameter uncertainty and was not considered for further model development as mentioned in the discussion. From Table I, the objective function changes favorably from −3,054 for the linear model to −3,033 with the addition of an effect compartment. Addition of the cardiovascular process block and introduction of the feedback loop (Eq. 2) increases the objective function further to −3,022. A further modest improvement in model fit comes from the introduction of the sinusoidal set point block of Eq. 1 with a corresponding increase in the objective function to −3,010. The corresponding calculated Akaike Information Criterion was minimized for the final model. As we mention further in the discussion, both these model fit characteristics and physiological aspects were considered in support of this final model.

Table I.

Optimized Model Parameter Values for Both the Final Model and Successive Simplifications

Model	k le (%/nM−1)	k ec (h−1)	τ (h)	A (%)	Π (h)	LLFa	AICb
1	0.016 (0.0001)	–	–	–	–	−3,054	6,113
2	0.019 (0.001)	2.72 (0.42)	–	–	–	−3,033	6,072
3	0.029 (0.003)	1.51 (0.23)	4.30 (1.56)	–	–	−3,022	6,052
Final	0.029 (0.002)	1.60 (0.21)	2.45 (0.72)	4.73 (0.99)	5.43 (0.07)	−3,010	6,034

Precision standard deviation is indicated in parenthesis

LLF log-likelihood function, AIC Akaike Information Criteria

^aMaximum value of the log-likelihood function

^bCalculated Akaike Information Criteria

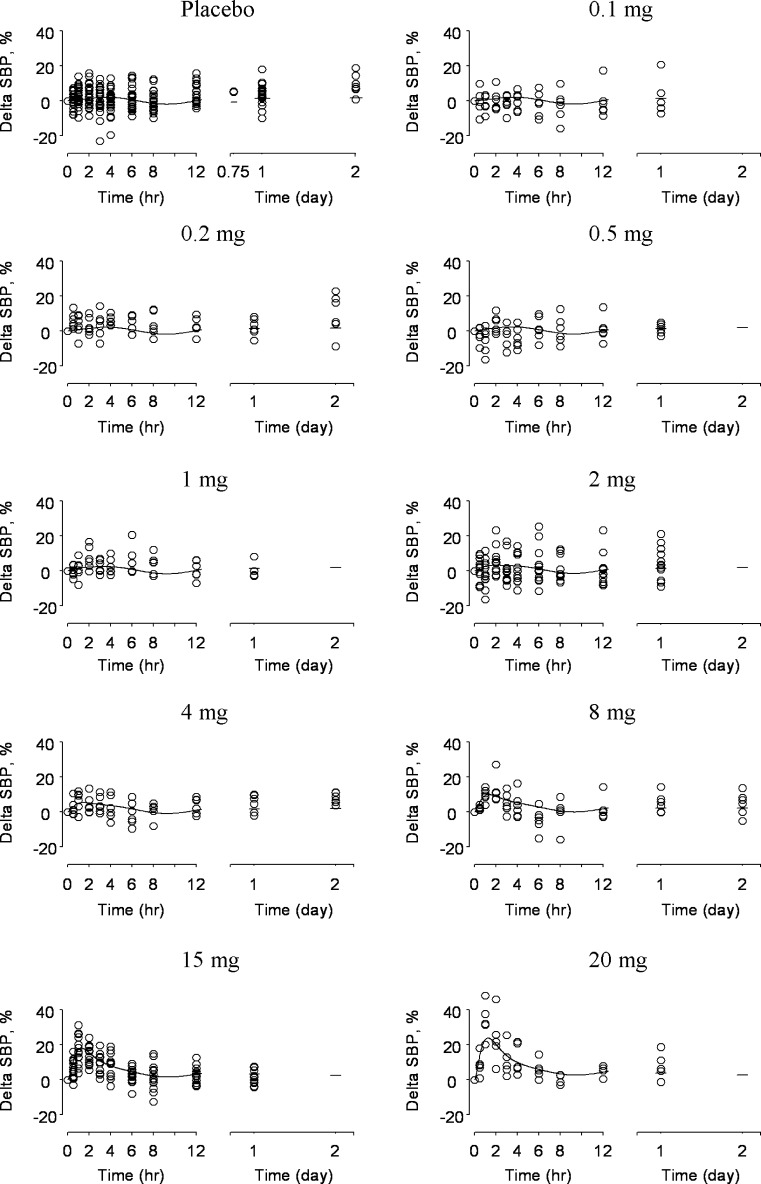
Figure 3 depicts both observed ΔSBP and associated fits of the final PK/PD model grouped by dose; the corresponding optimized parameter values for the final model are given in Table I. From Fig. 3, the model captured the central tendency of the data across the dose levels investigated in this study. The sinusoidal nature of the predicted response for placebo comes from the set point feature incorporated in the model, with optimized values (estimate (precision standard deviation)) of 5.43 (0.07) h for Π and 4.73 (0.99)% for A. Model predictions captured the transient peak response of observed ΔSBP that became more evident at higher doses. The interaction of the disturbance and feedback loop accounted for this behavior. Accordingly, the CV process is characterized by a τ of 2.45 (0.72) h, while k_ec and k_le are 1.60 (0.21) h⁻¹ and 0.029 (0.002)%/nM, respectively. As stated in the “MATERIALS AND METHODS” section, we did not include data corresponding to repeat administration of the 15-mg dose in the original evaluation. We included these repeat data in a subsequent sensitivity analysis and found that the effect of these repeat data on the final parameter estimates was minimal; model constants obtained with the 15-mg replicate data included are listed in where within ∼3.5% of the original estimates.

Fig. 3.

Model fits for the doses studied in this investigation. Equations 1–5 were fit to naïve pooled ΔSBP data and are separated by dose in this depiction (dose is indicated in mg at the top of each figure). The model fit is depicted as a solid line superimposed over individual ΔSBP data indicated as hollow circles. Model predictions captured the transient ΔSBP increase which became more apparent with increasing dose. Equations 3–5 accounted for the corresponding disturbance acting upon the feedback system which attempts to maintain ΔSBP homeostasis. At relatively low doses, this transient increase was minimal. Instead, the most prevalent feature of the model predictions was a circadian rhythm which was due to the sinusoidal set point of Eq. 1

Physiological Significance and Plausibility of the BP Model

The final proposed PK/PD model partitioned the BP response into three conceptual units: a sinusoidal BP set point, a transient disturbance, and a closed loop feedback system which attempted to maintain BP homeostasis. Each conceptual block was characterized by a governing rate; one can envision the overall BP homeostasis mechanism as a competition of processes characterized by these rates (though diastolic blood pressure was not included in this current analysis; a subsequent preliminary analysis including diastolic blood pressure gave consistent results with those discussed here). Here, we discuss the physiological plausibility and significance of the model and governing rates.

We commence with the set point block. The set point block forced the feedback system at a characteristic amplitude and period and approximately captured the well-known normal underlying circadian rhythm in BP (15). Introduction of this sinusoidal set point block is a convention which mimics approaches used to describe oscillations in both BP (6,8) and baseline body temperature (16). Other efforts describe nonlinear feedback systems to introduce oscillatory behavior in BP (17) and a set point model capable of damped oscillations for body temperature variation (18). We likewise attempted to introduce oscillatory behavior with a second-order system representing the cardiovascular system; however, we could not obtain robust parameter estimates, and sustainable oscillations were difficult to maintain. Using our approach, our estimate of the period for this oscillation (∏) from Eq. 1 is ∼5.4 h. The majority of the data were collected in the morning hours; this period coincides with the known early morning BP elevation that lasts 4–6 h (19). A more prolonged BP decrease during sleeping hours would result in BP fluctuations that would not oscillate in time with a fixed period and would consequently not be captured by our simple set point model. Previous studies that report 24-h ambulatory BP measurements have rich data sets for the entire 1-day period; these data sets were amenable to a more thorough analysis of circadian rhythms via cosine and sum of cosine terms (6,8). However, this study was not designed with BP effects as a primary endpoint since BP elevation with compound A was not the intended effect. Since we did not collect extensive SBP data in the sleeping hours, we could neither propose a more complicated model to capture this potential prolonged decrease nor could we estimate any model parameters relevant to this phenomenon. For this reason, we used the model to obtain insight relevant to the early, transient SBP elevation where data were intensively sampled rather than at times far later than this.

We characterized the closed loop BP homeostasis feedback system with a lumped time constant τ. The regulation of BP is comprised of a multiplicity of processes which take place over several time scales; these processes are concisely summarized by Guyton and Hall (20). Acute nervous responses comprise fast-acting systems, which act over characteristic time scales of seconds to minutes. Slower mechanisms which operate over several minutes to hours include the renin–angiotensin system and both pressure-driven expansion (and contraction) of the vasculature and extravasation of fluid to the extravascular space. The renal blood volume system provides long-term control. Our experimental data, which were compiled by sampling over the course of minutes to hours, would likely emphasize a subset of these processes. For example, very fast-acting systems such as baroreceptors (which fire at a rate on the order of 10–100 spikes/s in animal models; 21) operate over a characteristic time scale that is likely too fast to be captured with our experimental design. For this reason, we did not explicitly include a block corresponding to baroreceptor measurement of BP in our feedback model. Likewise, longer timescale mechanisms could potentially occur over a time span that is insufficiently captured by our relatively limited duration of BP monitoring. We believed the 2.45-h estimate of τ was consistent with the mechanisms that provide intermediate-term regulation of BP. To account for long-term multiple dose behavior, in addition to a more complicated expression for the circadian rhythm, it is likely that the present model would have to be modified to account for long-term BP homeostasis mechanisms and potentially a reset of the baroreceptor feedback mechanism (5).

Last, we consider the form of the disturbance block, which introduced the effect of compound A upon SBP homeostasis. The characteristic time for the disturbance to the BP feedback model was dictated by both by plasma and effect site kinetics of compound A. The value of k_ec, 1.60 h⁻¹ corresponds to a characteristic time of approximately 0.6 h. This time coincided with the noted time shift of approximately 0–1 h between the times of maximum BP and C_p, though this time shift was likely due to the kinetics of the entire BP homeostasis system and was not attributable to the effect compartment kinetics alone. While there was an active circulating metabolite for compound A, the exposure associated with this metabolite was 4–9% of parent; we did not attempt to include this minor circulating metabolite in the PK/PD model. Another consideration arose from the selection of the linear effect model of Eq. 4. Early attempts at model development explored more sophisticated forms of model of Eq. 4. Replacement of Eq. 4 with a saturable E_max relationship gave rise to high parameter uncertainty. This outcome was anticipated since the dose escalation was truncated due to safety concerns; it is likely that we did not generate maximal BP response data, but rather only in the rise to this maximal effect. Accordingly, selection of a linear effect model was justified in terms of model parsimony and the anticipated limited range of measured BP effect.

Model-Based Guidance in Drug Development

Simulated Plasma Concentration Profiles Following Controlled Release

Once we established our semimechanistic BP model, we could combine our relatively limited clinical data set with findings from a preclinical model to propose a potential path forward. The BP effects were noted as plasma concentrations approached target values thought to be necessary to achieve efficacy for the intended indication. At the time of this evaluation, we believed a 4-mg single dose would be the appropriate for a subsequent proof of pharmacology study, though this was not necessarily the intended dose and regimen for intended clinical use. Peak concentrations were not expected to be important for efficacy; rather, overall exposure (AUC) or trough concentrations were believed to likely drive clinical outcomes. While there may be some possibility to ameliorate C_max-driven BP effects by administering with food, if at all possible, we wanted to both have safety profile for the compound that was robust to food intake and no restrictions regarding food on the label. Accordingly, model-based simulations were used to explore whether CR might provide a means to minimize BP effects while maintaining overall drug exposure.

Using the modified PK model of Fig. 4b, we first simulated C_p following release from a hypothetical CR system with constant (zero-order) release. To parameterize the modified PK model, we obtained estimates of F from the preclinical dog experiments. From Table II, maximum plasma concentration values (C_max) were increasingly delayed and lessened following intrajejunal, intraileal, and intracolonic administration relative to oral; the arithmetic mean C_max values decreased from 0.31 μM following oral administration to 26% of this value following intracolonic administration. The time to maximum plasma concentration (T_max) increased from 0.5 to 2.25 h following oral to intracolonic administration. The corresponding arithmetic mean (standard deviation) AUC_0–24 values of 1.36 (0.49), 1.00 (0.50), 0.88 (0.39), and 0.58 (0.27) μM h were obtained following oral, intrajejunal, intraileal, and intracolonic administration; values of F (calculated as the ratio of arithmetic average AUC_0–24 for regional (i.e., intrajejunal, intraileal, etc.) administration to AUC_0–24 following oral) were 0.74, 0.65, and 0.43 for intrajejunal, intraileal, and intracolonic administration, respectively. As we describe below, the colonic F of 43% of oral was sufficiently high to support further development of a controlled-release platform since there was only a modest impact on overall simulated exposure relative to an equipotent immediate-release tablet. As discussed in the “MATERIALS AND METHODS” section, two idealized scenarios were then considered. The first scenario considered a theoretical dissolution rate of 0.33 mg/h for the first 12 h, followed by 0 mg/h for the duration of the simulation (to allow delivery of 4 mg total drug). The second considered a theoretical dose of 8.18 mg again over 12 h to correct for the calculated reduction in AUC for the 4-mg CR platform relative to the IR case. The simulated CR plasma concentration–time profiles obtained in this fashion are depicted in Fig. 4c. As anticipated, the simulated peak plasma concentration was delayed and blunted for both CR simulated profiles relative to the IR case. These profiles were input into the BP model to provide a corresponding family of simulated ΔSBP-time profiles as shown in Fig. 4d. The peak simulated ΔSBP was decreased for the idealized 4-mg CR case relative to the equipotent IR case. Likewise, the simulated profiles demonstrated a reduced maximum ΔSBP for the 8.18-mg (AUC-matched) platform.

Table II.

Mean (SD) Pharmacokinetic Parameters After Administration of Solution (0.2 mg/mL Compound A) in 10% Captisol via Oral, Intrajejunal, Intraileal, and Intracolonic Routes to Fasted Male Beagle Dogs (N = 5 or 4) at a Dose of 0.2 mg/kg

PK parameter	AUC0–24h (μM h)	C max (μM)	T max (h)
Oral	1.36 (0.49)	0.31 (0.06)	0.5 (0.31)
Intrajejunal	1.00 (0.50)	0.28 (0.06)	0.45 (0.11)
Ratio to oral	0.74	0.90
Intraileal	0.88 (0.39)	0.14 (0.06)	1.25 (0.5)
Ratio to oral	0.65	0.45
Intracolonic	0.58 (0.27)	0.08 (0.03)	2.25 (1.26)
Ratio to oral	0.43	0.26

AUC area under the concentration–time curve, PK pharmacokinetic

These results suggested some benefit to controlled versus immediate release and were in turn used to provide a rational basis for controlled-release formulation development. The PK/PD model in conjunction with the modified PK model provided a means to screen a variety of in vitro release rate profiles. As described in the “MATERIALS AND METHODS” section, slow and fast matrix CR tablets were prepared and the dissolution behavior for these systems was measured. These dissolution profiles were input to the modified PK model as described previously to provide the simulated plasma concentration profiles as depicted in Fig. 5a. Consistent with the findings from the idealized zero-order case, both platforms demonstrated some advantage in SBP reduction; the slower formulation (platform A) had a more blunted simulated C_max relative to the faster (platform B) formulation, resulting in a decreased simulated peak ΔSBP. From Fig. 5b, by matching the AUC of platforms A and B to the equipotent 6 mg IR case, both platforms again demonstrated amelioration of peak ΔSBP, with the slower Platform A still maintaining some advantage.

Fig. 5.

The simulated relative ΔSBP for the slow (platform A) and fast (platform B) candidate formulations. a The dissolution profiles were entered into the modified PK model of Fig. 4b to provide the corresponding simulated plasma concentration profiles. b The dissolution profiles of platforms A and B were dose-adjusted to provide an equivalent area under the plasma concentration–time curve to the IR case and entered as inputs to the ΔSBP PK/PD model; the resultant ΔSBP is depicted. As for the nonadjusted case (not shown), the peak ΔSBP remained slightly better for platform A relative to both platform B and the IR case, suggesting some benefit for this slower system

As described previously, a feedback model with circadian rhythm was selected to aid the development team in weighing the benefits of further CR optimization against the considerable resource obligation. By contrasting the result of the feedback model used in this analysis with the output using successively simpler models, we learn if the overall guidance provided by the simulation effort would be sensitive to the model used. We have conducted a subsequent analysis where we repeat the above procedure again with dissolution data from platforms A and B, except now with the successive simplifications of the full model (i.e., models 1–3 as depicted in Table I). Simulations using all three simplified models are consistent with the results of the full model; in all cases, CR holds advantages in BP amelioration, with platform A maintaining the greatest advantage overall.

Leveraging Our Model for Rational Drug Development

Our PK/PD model structure emphasized how the measured BP response was due to a collection of physiological processes governed by characteristic rates. The disturbance acting upon the BP feedback loop operated over a characteristic time of 0–1 h, while the homeostasis mechanism was characterized by a response time on the order of 2–3 h. This observation provided a motivation for simulating the response following a delayed and blunted administration of compound A relative to the IR case. Oral CR provided one possible avenue to modulate the release rate. However, extrapolation from in vitro release to the likely in vivo PK was not obvious at this early stage of development. Human regional bioavailability data were not available, and a validated in vitro–in vivo correlation was not established. Our modified PK model offered a practical, though approximate, solution. A similar dog model has been used successfully to predict both enhanced bioavailability and food effect for MK-0869 (aprepitant) in humans following administration of a nanoparticle formulation (9). However, the predictive capability of the dog model for celecoxib proved less accurate (22).

The accuracy of the modified PK model that forms the basis for extrapolation to the CR case has yet to be determined. However, initial efforts using a different set of assumed transit times for the modified PK model also indicated benefit to the slower platform (data not shown), suggesting that the outcome was not highly sensitive to model assumptions. Regardless, the lack of modified PK model validation in the clinic affected our ability to be certain of the precise magnitude of the BP amelioration, making this extrapolation to the controlled-release case only semiquantitative. Even with these caveats, our model-based approach allowed us to take full advantage of the limited data that were available even in an approximate fashion to guide decision making.

At the time of writing, the program has advanced to proof of pharmacology studies using an IR formulation. The development team has elected to use IR for the purposes of proof of pharmacology studies primarily for consistency with existing safety and tolerability using IR. In the meanwhile, the analysis we describe here has triggered manufacture of a CR formulation; further consideration of CR is contingent upon results of ongoing proof of pharmacology studies. We recall that our twofold objective at the time of this evaluation was to capture the transient effect of compound A upon BP following single-dose administration and to use the model as a common platform to contemplate approaches to ameliorate the undesired BP elevation. Our rationale for selection of a naïve-pooled approach with a semiphysiological model was matched to the modeling and simulation objectives outlined above, which were in turn reflective of the stage of development for this compound. With a positive readout from the proof of pharmacology studies, our modeling and simulation objective would evolve with the program and be tailored toward definition of therapeutic window and phase II dose selection. A limitation inherent to the current naïve-pooled approach is that we cannot distinguish between- from within-individual error. Our present simulations reveal information about the central tendency of the BP response rather than between-subject variability and would not be best suited to a subsequent objective aimed at learning how best to navigate a putative therapeutic window. Accordingly, we believe that developing a nonlinear mixed effect model based upon our current structural model would be appropriate upon proof of pharmacology.

CONCLUSION

As a drug candidate enters the earliest clinical stages, we enjoy a relative wealth of information from preclinical models and a paucity of data from humans; our model-based approach, though approximate, combined what information was known both from the clinical and preclinical case within a common physiologically based framework. This paradigm provided an estimate of improved tolerability to a BP safety concern that could be weighed against the considerable expenses associated with CR development. Moreover, this enabled us to best determine under what circumstances further development was warranted in general. In this fashion, our model-based approach could be used not only to characterize the observed response to our compound but also as a strategic tool to consider potential paths forward.