Modeling Subpopulations with the $MIXTURE Subroutine in NONMEM: Finding the Individual Probability of Belonging to a Subpopulation for the Use in Model Analysis and Improved Decision Making

Abstract

In nonlinear mixed effects modeling using NONMEM, mixture models can be used for multimodal distributions of parameters. The fraction of individuals belonging to each of the subpopulations can be estimated, and the most probable subpopulation for each patient is output (MIXEST_k). The objective function value (OFV) that is minimized is the sum of the OFVs for each patient (OFV_i), which in turn is the sum across the k subpopulations (OFV_i,k). The OFV_i,k values can be used together with the total probability in the population of belonging to subpopulation k to calculate the individual probability of belonging to the subpopulation (IP_k). Our objective was to explore the information gained by using IP_k instead of or in addition to MIXEST_k in the analysis of mixture models. Two real data sets described previously by mixture models as well as simulations were used to explore the use of IP_k and the precision of individual parameter values based on IP_k and MIXEST_k. For both real data-based mixture models, a substantial fraction (11% and 26%) of the patients had IP_k values not close to 0 or 1 (IP_k between 0.25 and 0.75). Simulations of eight different scenarios showed that individual parameter estimates based on MIXEST were less precise than those based on IP_k, as the root mean squared error was reduced for IP_k in all scenarios. A probability estimate such as IP_k provides more detailed information about each individual than the discrete MIXEST_k. Individual parameter estimates based on IP_k should be preferable whenever individual parameter estimates are to be used as study output or for simulations.

INTRODUCTION

Population pharmacokinetic and pharmacodynamic modeling has become increasingly important in drug development over the past decades and is also used to some extent in therapeutic drug monitoring and diagnostics. An advantage with the population approach is the possibility of studying the drug in the target population since this approach allows analysis of sparse data from many individuals. The nonlinear mixed-effect modeling program NONMEM (GloboMax/ICON, Ellicott City, MD) is the program most commonly used (1). NONMEM fits general statistical models to the data using an extended least-squares algorithm. During the fit, a minimum value is sought for the objective function value (OFV; −2 × log likelihood)). Typical population values for structural model parameters are obtained with estimates of the interindividual variability around these typical values, as well as the residual variability. It is assumed that the interindividual variability in the studied population around the model parameter is symmetrically distributed or that it can be transformed to a symmetric distribution. In cases where the data set includes subpopulations (e.g., due to genetic polymorphism affecting drug metabolism), this assumption about symmetry is very unlikely to hold. The subpopulations may have different typical model parameters and/or different variability around the parameters giving rise to multimodalities. To be able to describe populations with bi- or multimodal distributions, mixture models may be applied. Such models are implemented in NONMEM using the $MIXTURE subroutine where the individual patients will be assigned to the mixture (subpopulation) with the highest individual probability. This can be used to identify nonresponders, slow metabolizers, etc. The assigned subpopulation k (MIXEST_k) is provided in the NONMEM output but not the individual probability of belonging to that mixture (IP_k). This probability can be calculated from the individual objective function value (OFV_i) (2) and the total probability in the population of belonging to the mixture. Since IP_k is a probability, it provides more information about the parameter than the discrete MIXEST_k. Our objective was to explore the possible use of IP_k instead of or in addition to MIXEST_k in the analysis of mixture models. IP_k was also calculated for data sets where an increasing number of observations were included to investigate how IP_k may be useful in investigating the use of individual patient real-time monitoring. The analysis performed here can give an idea of how long a patient needs to be monitored before a relatively certain conclusion can be drawn regarding which subpopulation the patient belongs to. A literature search was performed to identify published models developed by using the $MIXTURE subroutine in NONMEM, where the calculation of IP_k could be of practical use. These are models where a decision (e.g., a diagnosis or treatment) is based on the specific assignment of individuals into subpopulations. For these models, decision making might improve by investigating the individual probability of belonging to a specific subpopulation. Finally, using a simple simulation example, individual parameter estimates based on IP_k and MIXEST_k were compared with respect to bias and precision.

MATERIALS AND METHODS

The likelihood that is minimized during a NONMEM run is composed of the individual likelihood for each patient in the data set. The likelihood is reported as the objective function value, being equal to −2 × log likelihood.

When the $MIXTURE subroutine is used, NONMEM will calculate an individual objective function value (OFV_i,k) for each alternative model (mixture 1, mixture 2, etc.).

From these values, together with the population probability for each subpopulation P_pop,k estimated in NONMEM, the individual probability of belonging to a specific subpopulation (mixture) IP_k can be calculated as follows:

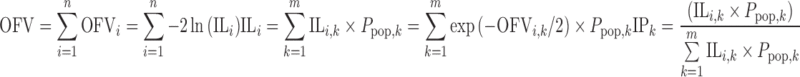1

where n is the number of individuals in a dataset, m is the number of mixtures, and IL_i,k is the individual likelihood for mixture k. The sum of IP_k for all mixtures is 1.

For NONMEM VI, only the categorical result MIXEST_k for each individual is provided (as a list of which mixture each patient has been assigned, based on the largest IP_k value). However, OFV_i can be obtained from NONMEM, and based on these values, IP_k can be calculated.

Two data sets described previously by NONMEM models that included the $MIXTURE subroutine were used in this study. The first data set, data set 1, is a six-category proportional odds model for clomethiazole sedation in stroke patients (n = 1,545, with 774 patients on active treatment) (3). A total dose of 68 mg/kg clomethiazole or placebo was given as a three-phase i.v. infusion over 24 h. Sedation was monitored throughout the entire treatment period, and the degree of sedation was measured on a discrete ordinal scale. In some cases, observations were also recorded even after 24 h. Stroke patients can be sedated both as a natural course of the stroke and as an adverse effect of the drug. The sedation scale used had the following categories: 1 (fully awake), 2 (drowsy but answers when spoken to), 3 (answers slowly when spoken to), 4 (reacts when spoken to but does not answer), 5 (reacts only to pain) and 6 (does not react to pain). The model included the natural course of sedation following placebo administration, a drug component (present or absent) and an interindividual variability component to describe the degree of sedation. Stroke severity and clomethiazole treatment were the most important covariates for sedation. It was not possible to determine a relationship between sedation and plasma concentration of the drug due to the study design. Stroke-induced sedation might be explained by the presence of edema. The model included a $MIXTURE subroutine separating and estimating the size of two subpopulations of patients, those without (mixture 1, P_pop,mix1 = 20%) or with (mixture 2, P_pop,mix2 = 80%) stroke-induced sedation.

Data set 2 contains monthly (28 days) seizure frequencies after pregabalin add-on treatment in epilepsy patients (n = 1042) where the response to treatment was modeled as a Poisson process (4). The study included 8 weeks of baseline observations and three periods of 28 days with active treatment. The mean number of seizures per 28 days was modeled as a function of drug effect, placebo effect, and subject-specific random effects. The $MIXTURE subroutine was used to estimate the sizes of two subpopulations containing responders (mixture 1, P_pop,mix1 = 75%) and nonresponders (mixture 2, P_pop,mix2 = 25%). E_max for the drug effect, the placebo effect, and the lognormal random effects was allowed to vary between the subpopulations.

IP_k was calculated for each patient in full and reduced data sets. The datasets were reduced so that observations were included only up to a certain time point or observation period. For example, for data set 2, all observations from baseline were first investigated. Then observations made during observation period 1 were included in the analysis, and so on. This was done to investigate when there was enough information in the data set to give a high probability for a specific subpopulation for each subject hence if there was a time point where the assigned subpopulation was less likely to change even if more observations were included.

All NONMEM runs, results, and postprocessing calculations were done using Perl scripts. Histograms showing how the different fractions of values for IP_k changes with an increasing number of observations and plots showing how the IP_k changes with an increasing number of observations for the individual patient was developed to investigate if IP_k can provide extra information compared with MIXEST_k. The numbers of patients having IP_k values close to 0.5 was investigated, as well as the numbers of patients changing between mixtures as more observations were added.

In a mixture model, individual parameter estimates will be estimated based on each of the existing mixture components. The individual (POSTHOC) estimates that are reported by default in NONMEM are calculated based on the MIXEST assignment and thus represent one mixture component only (denoted Φ_i,MIXEST). An alternative way to report individual parameter estimates is as the average of the estimates from each mixture, weighted by the IP_k (denoted Φ_i,IP). A small simulation study was performed to investigate the relative properties of two methods for calculating individual parameter values. A simple population pharmacokinetic model, which mimics a steady state infusion, was used:

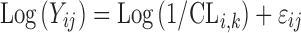2

Where i is an individual, j is a measurement, and clearance (CL) is described by two mixtures where inter-individual variability in each mixture was described by an exponential distribution:

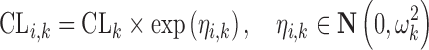3

In this example, we assumed parameter values of CL₁ = 1, CL₂ = 0.5 or 0.25 and ω₁ = ω₂ = 0.3. The residual error ɛ_ij was assumed to come from a normal distribution, centered around zero and with a standard deviation (σ) of 0.3 or 1. The probability of belonging to mixture 1 (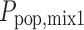) was 25% or 50%. Thus, three factors were varied: mixture component, residual error magnitude, and difference in mean CL values between the mixtures. All eight possible combinations were studied with simulations of 1,000 subjects for each condition. In each subject, only one observation was made. No estimation of population parameters took place as the study was intended to contrast the two methods for obtaining individual parameter estimates under a given population model. Therefore, the true population parameters were used in the estimation of each set of individual parameters. The root mean squared error (RMSE) was used as a measure of the precision of individual estimates for each condition.

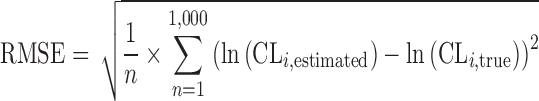4

The eight scenarios are tabulated in Table I.

Table I.

Scenarios for the Simulation Study

Scenario	P pop,mix1	σ	CL1	CL2
1	0.5	0.3	1	0.25
2	0.25	0.3	1	0.5
3	0.5	0.3	1	0.5
4	0.5	1	1	0.5
5	0.25	1	1	0.5
6	0.25	1	1	0.25
7	0.25	0.3	1	0.25
8	0.5	1	1	0.25

P _pop,mix1 is the probability of belonging to mixture 1. σ is the standard deviation of the random error. CL₁ and CL₂ are the clearances for the two simulated subpopulations (mixtures 1 and 2)

RESULTS

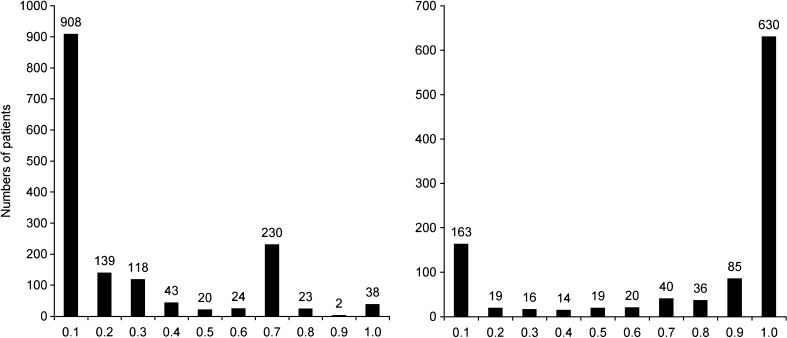
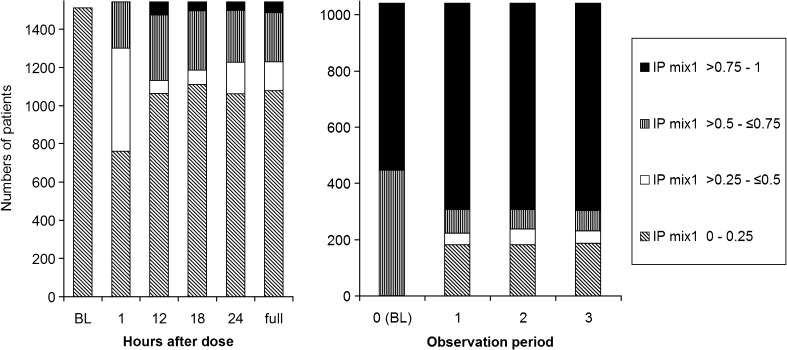
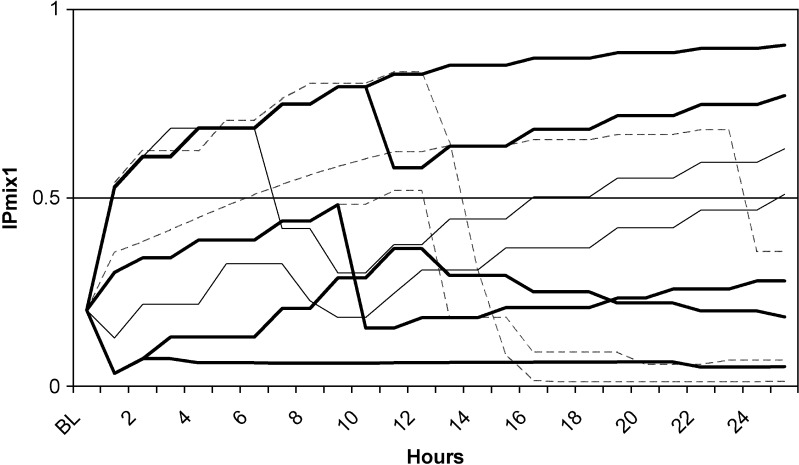
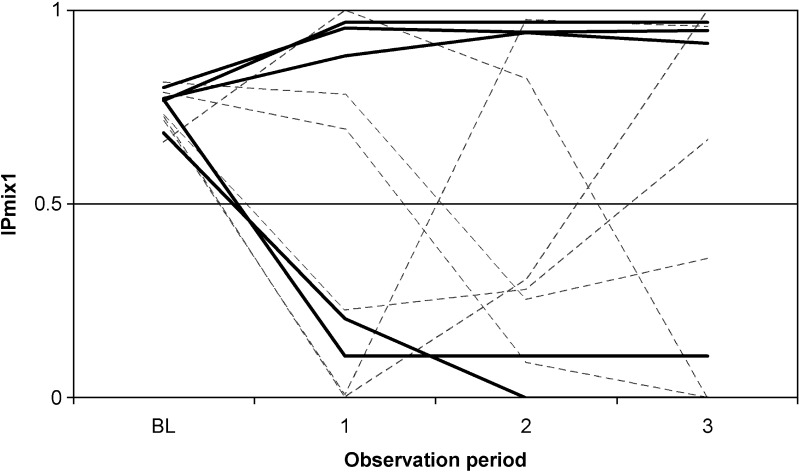
For the two real data sets, IP_k was calculated as described above. For the clomethiazole data (dataset 1), 4% of the patients had an IP_mix1 between 0.4 and 0.6, and 11% of the patients had an IP_mix1 between 0.25 and 0.75 (Fig. 1a). Seventeen percent of the patients had almost the same probability at baseline (IP_mix1 approximately 0.2) as at the completion of the study (IP_mix1 between 0.1 and 0.3). For the pregabalin data (dataset 2), 3% of the patients had an IP_mix1 between 0.4 and 0.6, and 26% of the patients had an IP_mix1 between 0.25 and 0.75 (Fig. 1b). Nine percent of the patients had similar probabilities at baseline (IP_mix1 0.75 on average) and at the end of the study (IP_mix1 between 0.6 and 0.8). IP_k was also calculated for reduced data sets, where only observations up to a certain time point or observation period were included. Figure 2 shows how the frequencies of the values of IP_k change from the reduced data sets with only baseline observations to the data sets with increasing number of observations. There is a clear shift from baseline, where little or no information is available, to the first observations after baseline. For the clomethiazole data (data set 1), the fraction of patients with an IP_mix1 above 0.5 seems to stabilize after approximately 12 h. After this, the larger mixture increases from 74% to 80% of the patients until all data are included. For pregabalin add-on treatment (data set 2), each observation contains information from 28 days, and the fraction of patients with IP_mix1 above 0.5 seems to stabilize as soon as the first observation of drug treatment is available. However, when the development of IP_k for individual patients is followed over time (hence with an increasing number of observations), it can be seen that a few patients change their MIXEST_k estimate even after the fraction of patients assigned to each subpopulation is more or less stable (Figs. 3 and 4). In data set 1, 119 patients (7.7%) change from MIXEST = 1 to MIXEST = 2 between 12 h and the last observation time (full data set), and 23 patients (1.5%) change MIXEST from 2 to 1. In data set 2, 58 patients (5.6%) change from MIXEST = 1 to MIXEST = 2 from observation 1 to observation 3. Fifty patients (4.8%) change MIXEST from 2 to 1.

Fig. 1.

Frequency distribution of IP_mix1 in the two test data sets. Column 1 includes patients with an IP_mix1 from 0 to ≤0.1, column 2 includes values >0.1 to ≤0.2, etc. The left panel shows results for probability of stroke-induced sedation following clomethiazole or placebo. Of the patients, 58.8% are found in column 1. In the next columns, 16.6%, 2.8%, 1.2%, 1.6%, 15.0%, 1.5%, and 2.5% of the patients can be found, respectively. The right panel shows responder probability following pregabalin treatment. Of the patients, 15.6% can be found in column 1. In the next columns, 1.8%, 1.5%, 1.3%, 1.8%, 1.9%, 3.8%, 8.2%, and 60.5% of the patients can be found, respectively

Fig. 2.

Frequency distribution of IP_mix1 when using reduced data sets with observations included up to x hours for data set 1 and up to (and including) observation period x for data set 2. The left panel shows results for probability of stroke-induced sedation following clomethiazole or placebo, and right panel shows the responder probability following pregabalin treatment. The y-axis shows the number of patients in each category of IP_mix1 values. BL = baseline

Fig. 3.

Probability of belonging to the subpopulation without stroke-induced sedation for patients treated with clomethiazole or placebo (data set 1). The changes in IP_mix1 after x hours after treatment start are shown for a selection of patients. Each line represents the IP_mix1 for an individual patient

Fig. 4.

The probability of being a responder to treatment for epilepsy in patients with pregabalin as add-on treatment (data set 2). The change in IP_mix1 after x observation periods are shown for a selection of patients. Each line represents the IP_mix1 for an individual patient

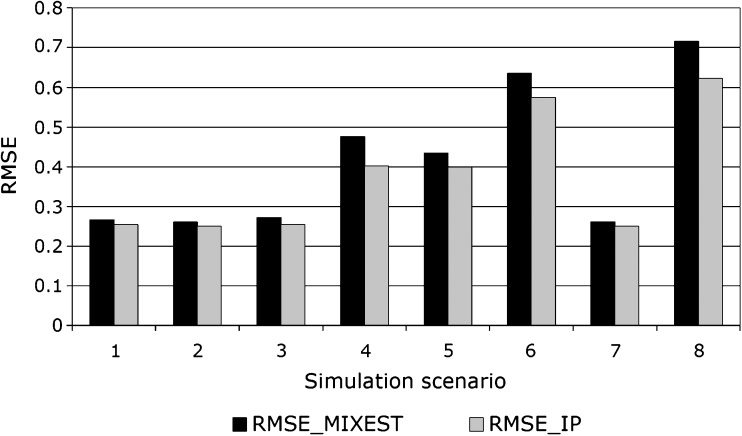
In the simulation study, precision as measured by RMSE was better (lower) for Φ_i,IP than Φ_i,MIXEST for all conditions studied (Fig. 5). The difference in performance between the methods was larger with a large residual error magnitude, with a large difference between the mean CL values for the two mixtures and when the two mixture components were of similar size. Thus, when CL₂ was 0.5, σ was 0.3, the mixture 1 proportion was 25%, and the RMSE was 0.25 and 0.26 for Φ_i,IP and Φ_i,MIXEST, respectively. When CL₂ was 0.25, σ was 1, and the mixture 1 proportion was 50%, the RMSE was 0.62 and 0.72 for Φ_i,IP and Φ_i,MIXEST, respectively.

Fig. 5.

Root mean squared error for the estimation of clearance in a simulation study with a mixture population consisting of two subpopulations with different CL (1 and 0.25 or 0.5). The standard deviation of the residual error was either 0.3 or 1, and the probability of belonging to mixture 1 was either 0.25 or 0.5, resulting in eight different simulation scenarios. RMSE was calculated for Φ _{i ,IP} and Φ _{i ,MIXEST}, respectively. The RMSE for Φ _{i ,IP} was lower than for Φ _{i ,MIXEST} in all scenarios

DISCUSSION

The individual probability of belonging to a specific subpopulation can be calculated from the individual objective function values in NONMEM. In this paper, the IP_k has been calculated for two real data sets, and wide range of IP_k values was found (Fig. 1). This is a result of the incomplete information available for classifying patients. For both test data sets, a fraction of the patients had an IP_k close to 0.5 (Fig. 1), indicating that the data from these patients are described almost equally well in both subpopulations.

In the reduced data sets, only data up until specific time points were included. The development of IP_k over time for each patient can then be studied, mimicking a situation where treatment is followed in real time for possible therapeutic intervention. Some patients have approximately the same probability at the end of the study as found at baseline. It can be argued that for these patients, the monitoring has not been able to give a better estimate of the IP_k than the baseline observation did.

When studying the value of IP_k, there is more information available than when just looking at the assignment of MIXEST_k, since IP_k is a continuous measure. Therapeutic decisions could then be more informatively based on IP_k rather than MIXEST_k. For example, the IP_k can be used as a more precise cut-off for a decision about whether a patient is a responder to treatment or not. If the IP_k for the responder mixture is low, then therapy can be stopped. If the IP_k is intermediate, monitoring should be continued. If IP_k is high, then maybe the monitoring can be stopped or be less frequent. The cut-off points would have to be chosen based on clinical judgment or based on prior risk-utility analysis. IP_k can be of use if the assignment into a subpopulation is to be used for making decisions, e.g., in diagnostics and in individualized therapy.

If calculated in real time, the IP_k for a patient will change as more data come in. Figure 2 shows the frequency distribution of values for IP_k for each time point. This kind of plot can give information about the necessary time to follow patients before making decisions that are based on the subpopulation assignment, for example decisions about changes in drug treatment, etc. The MIXEST_k estimates show shrinkage to the larger subpopulation when data are sparse, meaning that if no information is available for classification, then all individuals will be assigned to the subpopulation with the higher population probability. For IP_k, no shrinkage towards the dominant subpopulation will occur.

Even after the time point where the fraction of patients assigned to each subpopulation seems to stabilize, some patients still change from being assigned to one subpopulation to another (Figs. 3 and 4.) For clomethiazole, this can be explained by an increased sedation level at a late stage that is not necessarily induced by the drug. On the other hand, an improved sedation level after a dose reduction indicates that the sedation is drug induced. For the epilepsy patients, an increased level of seizures at a late stage can occur due to natural fluctuations in the disease, and then the patient should be classified as a nonresponder to treatment. An improvement in the number of seizures can be a part of natural fluctuations but can also be a treatment effect giving a change in classification from nonresponder to responder. It is likely that uncertainty in parameter estimates also can contribute, in the sense that with sparse data, changing classification will be more common than when data are plentiful.

The use of IP_k in covariate plots was tested (IP_k was plotted against various covariates such as age, body weight, gender, National Institutes of Health score in stroke patients, etc.) but did not seem to provide additional information compared to the use of MIXEST_k in these plots for the two models (results not shown). Still, this type of analysis might be useful for other data sets.

The results of the simulation study show that individual parameters are more precisely estimated by Φ_i,IP rather than the default Φ_i,MIXEST (Fig. 5). Imprecision in mixture assignment will increase the frequency of misclassification, and the consequence of misclassification will be larger the more different the two populations are. Thus, the difference between the methods increase the more imprecise the default assignment is and the larger the difference between mean values for the mixtures is. Also, in the particular case of two mixtures, the more similar in frequency the two mixtures are, the more likely are misclassifications. It should be noted that even if only some ηs in a model are directly affected by the mixture, all ηs will have different values dependent on mixture assignment. Thus, the choice between the methods Φ_i,IP and Φ_i,MIXEST concern all individual parameter calculations.

A literature search performed in MEDLINE and SCOPUS in October 2006 and in MEDLINE May 2008 identified several population studies performed in NONMEM where the $MIXTURE subroutine had been included in the model. Three of these papers presented models with two subpopulations describing a bi-modality in clearance. One of these three models (5) described the pharmacokinetics of repinotan, a full serotonin receptor antagonist that is metabolized by CYP2D6. Data from 500 healthy Japanese and Caucasian subjects and stroke patients participating in phase I and II were included. Since the data only supported the inclusion of two mixtures, the subpopulations were classified as having high and low CL even if there are four known subpopulations of CYP2D6 metabolizers. Since repinotan is used in the acute treatment of stroke, the authors recommend bedside monitoring of the drug concentration to be able to find the optimal dose for each patient. The dose should be adjusted to match the metabolizing status of the patient. A dosing tool that also takes into account the probability of belonging to one of the two respective phenotype subpopulations could then be of use. The second paper described multimodality in CL of perhexiline used in refractory angina. Perhexeline is also metabolized by CYP2D6 and is a candidate for therapeutic drug monitoring as well (6). The third paper described a model for the pharmacokinetics of ceftizoxime, a beta-lactam antimicrobial agent given to patients with proven or suspected bacterial infections (7). The authors included a mixture with two subpopulations describing an observed bimodality on CL, but no explanation was found for the bimodality. Another study found in the literature search described a model with two subpopulations, patients with or without lag time for absorption (8). Frey et al. developed a PKPD model for gliclazide in type 2 diabetes patients with a mixture separating responders and nonresponders (9). The percentage of nonresponders was 12% in patients previously treated with diet alone, 24% in patients previously treated by a single class of oral hypoglycemic agents, and 50% in patients previously treated by two classes of oral hypoglycemic agents. In both of these studies, the calculation of the IP_k could provide more detailed information about the classification into the two subpopulations. This could be of particular value if the model is to be used as a monitoring tool when making decisions regarding stopping or continuing the medication. Kowalski et al. developed a model for longitudinal adverse event severity data for an investigational drug (10). A $MIXTURE subroutine was included to separate individuals with and without adverse effects, similar to the model for data set 1 in this study. Spilker et al. used the $MIXTURE subroutine in NONMEM to classify mammary tumors in rats as benign or malign (11). It was assumed that the endothelial integrity in the tissue is disrupted in a manner proportional to the degree of malignancy and that the benign tumors show no disruption. The model developed in NONMEM described the microvascular blood-tissue exchange. The separation of individuals into two subpopulations with benign and malign tumors, respectively, was compared to a microscopic method investigating tumor histology. The model-based classification had 91% sensitivity, 93% specificity, and 92% accuracy. Even if the performance of this method is already impressive, there could be possible improvements if information about the IP_k were included in the analysis. Then, also the probability of a correct classification would be known, and possibly misclassifications could be explained by IP_k values being close to 0.5.

There are more examples of bi- and multimodalities described in the literature, which has been studied by using other methods and software. These have not been mentioned here. There are other software packages available, which also can be suitable when studying bi- and multimodalities. As an example, the nonparametric modeling software USC*PACK (Laboratory of Applied Pharmacokinetics, USC, Los Angeles, USA), can be used to detect bi- and multimodalities in a population, without prespecifying these modalities in the model. The MM-USC*PACK (Laboratory of Applied Pharmacokinetics, USC, Los Angeles, USA) has been developed as a nonparametric population PK/PD package with a built-in clinical monitoring tool. The patients can then be monitored by using models developed in NPAG (one of the programs in the USC*PACK).

In conclusion, the individual probability for belonging to a subpopulation, IP_k, can be useful for further analysis of a mixture model, especially if the classifications into subpopulations or individual parameter estimates are to be used for diagnostics or as basis for treatment decisions. Automation of IP_k calculation is available in the freeware program PsN available at psn.sf.net.