Amplification efficiency: linking baseline and bias in the analysis of quantitative PCR data

Abstract

Despite the central role of quantitative PCR (qPCR) in the quantification of mRNA transcripts, most analyses of qPCR data are still delegated to the software that comes with the qPCR apparatus. This is especially true for the handling of the fluorescence baseline. This article shows that baseline estimation errors are directly reflected in the observed PCR efficiency values and are thus propagated exponentially in the estimated starting concentrations as well as ‘fold-difference’ results. Because of the unknown origin and kinetics of the baseline fluorescence, the fluorescence values monitored in the initial cycles of the PCR reaction cannot be used to estimate a useful baseline value. An algorithm that estimates the baseline by reconstructing the log-linear phase downward from the early plateau phase of the PCR reaction was developed and shown to lead to very reproducible PCR efficiency values. PCR efficiency values were determined per sample by fitting a regression line to a subset of data points in the log-linear phase. The variability, as well as the bias, in qPCR results was significantly reduced when the mean of these PCR efficiencies per amplicon was used in the calculation of an estimate of the starting concentration per sample.

INTRODUCTION

During the last decade, quantitative real-time reverse transcriptase PCR, or qPCR for short, has become the method of choice for the quantification of mRNA transcripts (1,2). Despite the large number of papers on qPCR data analysis, most researchers still delegate this analysis to the software that comes with their PCR system (3). The mainstream of qPCR data analysis is based on the direct application of the basic equation for PCR amplification (Box 1; Equation 1), which describes the exponential increase in observed fluorescence when the PCR reaction is monitored using a fluorescent DNA-binding dye (e.g. SYBR Green I) (4). Alternative qPCR data analysis methods, such as those based on nonlinear curve fitting (5–7) will be considered in a separate section of this article.

Box 1. Equations used in the analysis of quantitative PCR data. The equations are numbered according to their appearance in the text. The basic equation for PCR kinetics (Equation 1) states that the amount of amplicon after c cycles (N_c) is the starting concentration of the amplicon (N₀) times the amplification efficiency (E) to the power c. The PCR efficiency in this equation is a number between 1 and 2 (2 indicates 100% efficiency). The PCR efficiency can be defined as the increase in amplicon per cycle (Equation 5). During the exponential phase of the PCR reaction this efficiency is constant. When a fluorescence baseline is included in the PCR model (parameter BL in Equation 4), and the estimation of the baseline is incorrect, the cycle-to-cycle efficiency contains a constant (B*) in both the denominator and the numerator (Equation 6), which leads to the observation of a biased efficiency. Equation 1 can be inverted (Equation 2) to calculate the starting concentration (N₀) from the user-defined fluorescence threshold (N_t), the efficiency and the fractional number of cycles needed to reach the threshold (C_t). This N₀ is expressed in arbitrary fluorescence units. The starting concentration of amplicon A (N_0,A) can be expressed relative to that of amplicon B (N_0,B) by direct division of these starting concentrations (Equations 3A and 3B). When the fluorescence thresholds for both amplicons are equal, the expression ratio in Equation 3B can be ‘simplified’ to Equation 3C. However, further reduction of the number of parameters leading to Equation 3D, requires that the efficiencies of both amplicons (E_A and E_B) are equal. If this requirement is not met, a bias is introduced in the expression ratio (Equation 7A). This bias is defined as the real ratio (Equation 3C) divided by the biased ratio (Equation 3D). Rearrangement (Equation 7B) and the assumption that E_common is the geometric mean of the amplicon efficiencies E_A and E_B then leads to Equation 7C. From this equation, it follows that the bias introduced by ignoring the difference between amplicon efficiencies is an exponential function of the relative error of E_common and the sum of the C_t values. Note that the application of Equations 2, 3B or 3C is mathematically equivalent to extrapolation of the regression line(s) through the log-linear phase to cycle 0 (Figure 1A).

The calculation of starting concentrations in qPCR analysis requires an estimate of the PCR efficiency, the setting of a fluorescence threshold and the determination of the C_t value, which is the fractional cycle number that is required to reach this threshold (8). Originally, qPCR analysis used a PCR efficiency value that was assumed to be constant (8) but currently the efficiency is derived from a standard curve (2,9) or calculated as the mean efficiency per amplicon (10–12). Analysis methods that are based on the PCR efficiency per sample (13–15) were shown to give highly variable results (10–12,16,17). This high variability remained a conundrum until it became clear that the observed PCR efficiency is strongly affected by the applied baseline estimate (Figure 1A). In the real-time PCR chemistry considered in this article, the baseline fluorescence is due to the fluorescence of unbound fluorochrome (e.g. SYBR Green I), and to fluorochrome bound to, among others, double strand cDNA and primers annealing to nontarget DNA sequences (Figure 1B). Other fluorescence sources also contribute to the baseline fluorescence. Although it was reported that a baseline has to be subtracted before a valid PCR efficiency value can be determined (18) and shortcomings in the baseline subtraction methods in system software have been recognized (19,20), the need to determine the correct baseline value has mainly been ignored in the literature. It has been addressed in some papers (7,21) and then it is mainly discussed in the context of the fit of the employed analysis model (5,7). Validation of the baseline estimation relies on visual inspection of the shape of the resulting dataset (2,20,21).

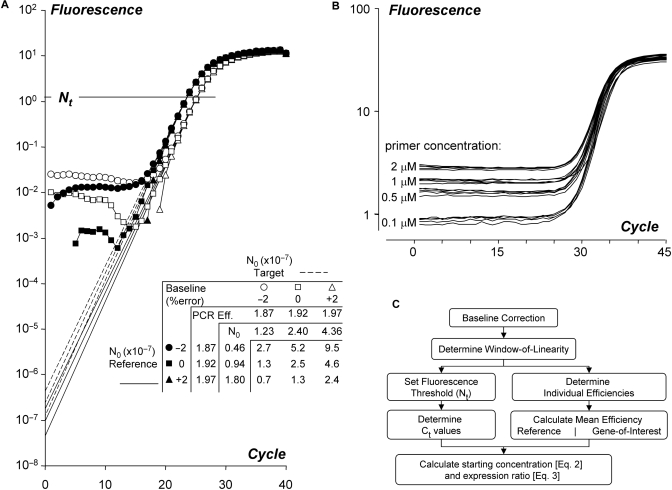
Figure 1.

Effect of baseline estimation errors in quantitative PCR data analysis. (A) The graph shows amplification curves of a reference (closed symbols, dashed lines) and a target gene (open symbols, solid lines) after subtraction of the correct and erroneous baselines. The different intercepts of the lines with the Y-axis illustrate the calculation of the starting concentration (N₀) based on the observed PCR efficiency values (Box 1; Equation 2). The table shows that with an independent and random baseline estimation error of up to 2%, in both the reference gene and the target gene, the observed expression ratio varies from 0.7 to 9.5. Note that the extrapolation of the regression line(s) through the log-linear phase to cycle 0 is mathematically equivalent to the application of Equations 2, 3B or 3C (Box 1). (B) Raw fluorescence data of a PCR reaction with different primer concentrations. The curves show the amplification of NppB in chicken heart tissue. The fluorescence baseline increases with increasing primer concentration. (C) Flowchart of the analysis of quantitative PCR data described in this article.

The current study shows how an improper baseline setting severely affects the estimated PCR efficiencies and will thus increase the variability as well as the bias in the reported absolute and relative levels of gene expression. To solve these issues, an algorithm to estimate the optimal baseline for each individual sample was developed. The body of this article deals chronologically with each of the issues required for qPCR data analysis, thus aiming at presenting a comprehensive qPCR data analysis protocol (Figure 1C). The described methods have been incorporated into the LinRegPCR quantitative PCR data analysis program (version 11.0, download: http://LinRegPCR.HFRC.nl).

MATERIALS AND METHODS

Tissue samples

Thirty hearts of chicken embryos of 3 days of development were isolated and separated into the five different compartments, i.e. sinus venosus (SV), atrium (A), atrioventricular canal (AVC), ventricle (V) and outflow tract (OFT). Post-mortem cortical brain tissue of eight control persons and 10 Huntington disease patients was obtained from Prof Dr R.A.C. Roos (Leiden University, the Netherlands). Total RNA was isolated using RNAeasy columns (Qiagen) according to the manufacturer's instructions. The total RNA was treated with DNase RQ1 (Promega) and the integrity of the RNA was checked using the BioAnalyzer and the Agilent RNA 6000 Nano kit (II). A 1–0.5 µg total RNA was converted into cDNA using an anchored poly-dT primer and the Superscript II (human samples) or III (chicken samples) Reverse transcription kit (Invitrogen).

PCR reactions

The samples of the ‘Huntington Disease’ and the ‘serial dilution’ data series were amplified in 96-well plates in an Applied BioSystems ABI7300. The qPCR reaction was done in 20 µl with primers for ATG5 (Forward: GGCCATCAATCGGAAACTCAT; Reverse: AGCCACAGGACGAAACAGCTT; product: 123bp), PSMB5 (Forward TGTCCCAGAAGAGCCAGGAAT; Reverse: GCAATGTAAGCACCCGCTGTA; product 116 bp) or EEF1A1 (Forward: AAGCTGGAAGATGGCCCTAAA; Reverse: AAGCGACCCAAAGGTGGAT; product: 54 bp), Q-PCR SYBR Green Mastermix (Applied Biosystems) in a concentration of 0.3 µM. The used protocol was identical for all primer sets: 10 min 95°C, 40× (15 s 95°C, 30 s 60°C, 30 s 72°C).

The samples of the ‘developing chicken heart’ dataset were amplified in 384-well plates in a Roche LightCycler480. The qPCR reaction was done in 10 µl with a primer concentration of 1 µM and SYBR Green qPCR Master Mix (Roche). The primers used were NppB (Forward: GATGCCCAGGATGATGAGAG; Reverse: CCTTGGGAGGATCAGGTTCT; product 157 bp), NDUFB3 (Forward: CTCGAGGAGGTCCAAAGAAGGT; Reverse: GTGGCAGGTTTTGCATAGCC; product 101 bp). These samples were measured in three separated runs using the following protocol 5 min 96°C, 45× (10 s 95°C, 20 s 58°C, 20 s 72°C).

PCR efficiency determination

The raw (i.e. not baseline-corrected) PCR data were used in the analysis. Baseline correction was carried out with a baseline trend based on a selection of early cycles or with the algorithm developed in this study. The PCR efficiency for each individual sample was derived from the slope of the regression line fitted to a subset of baseline-corrected data points in the log-linear phase using LinRegPCR (15).

Algorithm development

Next to the three datasets mentioned above, 19 raw datasets of four different qPCR platforms (2–10 datasets per platform) were used in the development of a baseline estimation algorithm. These datasets were selected because of the presence of ‘difficult’ samples. In these datasets, 56 different targets were amplified (3–30 tissue samples per amplicon per PCR run, 1–13 different amplicons per run). C_t values ranged from 4.5 up to 47. Several alternatives for the developed method to estimate the baseline fluorescence were applied to each of the datasets to determine their robustness. Similarly, the algorithm to set the Window-of-Linearity (W-o-L) was tested on all datasets.

RESULTS

Baseline estimation

Baseline is defined in this article as the level of fluorescence measured before any specific amplification can be detected. The raw qPCR data, i.e. the fluorescence intensities measured after each amplification cycle, follow the exponential model given by Equation 4 in which the baseline is assumed to be constant for all cycles.

In the exponential phase of the PCR reaction, the amplification efficiency can theoretically be estimated from cycle to cycle as E = N_c+1/N_c, which is the fold increase in PCR product per cycle (Equation 5) (10,22,23). When this cycle-to-cycle efficiency represents the real efficiency in the current PCR run, an underestimation of the baseline value will lead to the addition of a positive constant in both the numerator and the denominator of the cycle-to-cycle efficiency (Equation 6), which leads to an underestimation of the efficiency. In the same way, an overestimation of the baseline leads to an overestimation of the PCR efficiency. A simple exercise (Figure 1A and Supplementary Figure S1) shows that an error in the baseline leads to a similar error in the observed efficiency, whereas the resulting error in the N₀ estimation is about an order of magnitude larger.

Most PCR systems currently use a linear baseline trend derived from a user-defined set of early amplification cycles. Application of three baseline choices (‘baseline’ cycles 3–5, 3–10 and 3–15) to the three datasets results in highly variable PCR efficiencies per amplicon (Figure 2B, Supplementary Figures S2B, S3B and S4B). The log-linear plots of the baseline-corrected datasets show the characteristic convex and concave amplification curves that result from over- or underestimation of the fluorescence baseline (21) (Figure 2A; upper panel, Supplementary Figures S2A, S3A and S4A). A baseline based on a fixed number of early observations always runs the risk of being overestimated due to inclusion of amplification product.

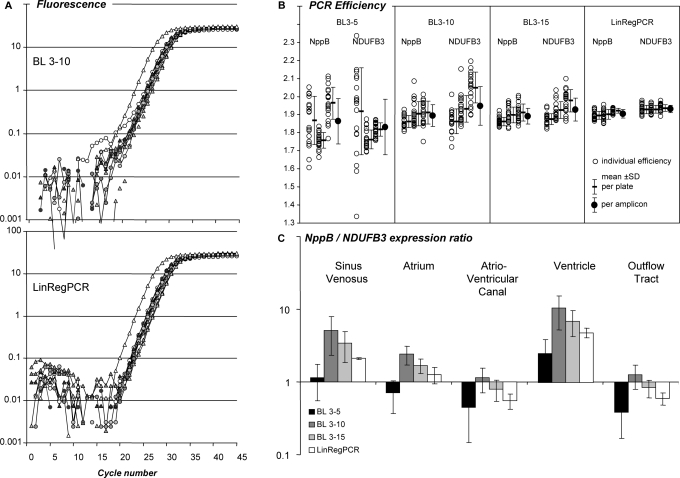
Figure 2.

Effect of the baseline estimation method on qPCR data analysis. (A) PCR amplification curves of NppB and NDUFB3 in samples of five different parts of the developing chicken heart. Baseline fluorescence was estimated by the system software as a linear trend through the observations of cycles 3 through 10 (BL 3–10, top panel) or with the baseline estimation method described in this article (LinRegPCR, bottom panel). See Supplementary Figure S2A for additional system baseline settings.(B) PCR efficiency values of NppB and NDUFB3 from each individual sample (open circles) in three independent PCR runs. An optimal W-o-L was applied per amplicon per plate. Mean efficiencies per plate and per amplicon were calculated. PCR efficiencies were determined after application of three baseline trends, as well as after the LinRegPCR baseline subtraction. The variation was lowest in LinRegPCR-derived PCR efficiency values (see Supplementary Figure S2B). (C) NppB/NDUFB3 gene expression ratio in different parts of the developing chicken heart for each of the baseline correction methods. Note that the pattern of observed expression ratios depends on the applied baseline correction method. Variation in expression ratios per tissue is lowest in data derived from LinRegPCR-corrected data.

Attempts to implement published algorithms, e.g. ref. (5) to determine the baseline value from the ground cycles prior to observable amplification proved to be pointless because of the noise and the behavior of the signal at the start of the PCR (7). The very nature of the data in the first cycles, as well as the unknown chemistry and physics underlying those data values, which display no reproducible trends from amplicon to amplicon, run to run and platform to platform, effectively prohibited the attempts to develop a robust baseline estimation algorithm based on the ground phase data (results not shown). The baseline estimation algorithm we propose is based on the assumption that amplification efficiency is constant from the very first cycle onward. The cycle-dependent change in efficiency that is predicted by some alternative analysis models, e.g. refs (19,20,24), will be considered in the discussion. A constant PCR efficiency would, on a semi-logarithmic plot, lead to a straight line of data points in the whole log-linear phase. A proper baseline estimate will therefore result in a dataset in which these points are on a straight line (Figure 3B). Details on the baseline estimation algorithm are given in Figure 3A. The algorithm is applied to each sample separately and does not include a criterion on the value of the slope of the resulting log-linear data points. However, when this baseline estimation algorithm is applied to the three datasets, all datasets show corrected data with amplification curves that are closely parallel per amplicon (Figure 2A, Supplementary Figures S2A; lower panel, S3A and S4A).

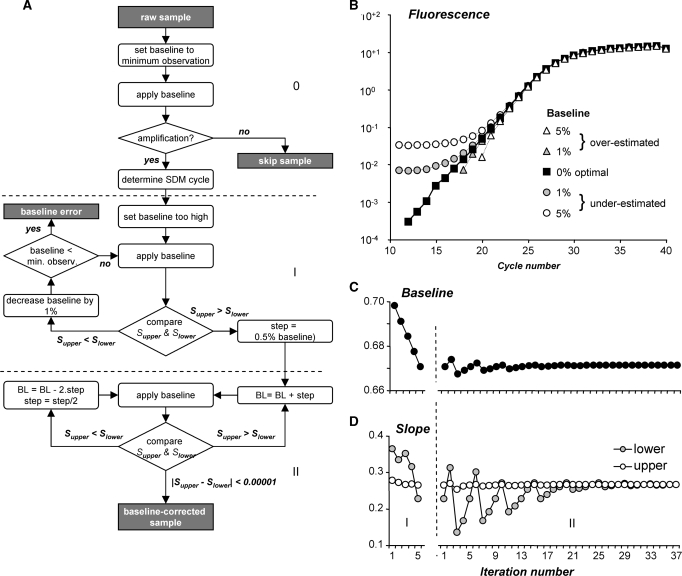
Figure 3.

Fluorescence baseline estimation. (A) Flowchart of the baseline estimation algorithm. For each sample, an initial baseline is set to the minimum observed fluorescence. Samples are skipped when less than seven times increase in fluorescence values is observed. For each sample that shows amplification, an iterative algorithm than repeatedly adjusts the baseline value until the slope of the regression line through the data points in the upper half of the exponential phase differs less than 0.0001 from the slope of the line through the data points in the lower half. At a PCR efficiency of 1.8, this criterion translates into an efficiency difference of 0.0004. The algorithm results in a set of data points on a straight line and effectively reconstructs the exponential phase. (B) Comparison of amplification curves resulting from an optimal baseline (filled squares) with the curves resulting from 1% to 5% over-estimated (gray and open triangles) and 1% to 5% under-estimated baselines (gray and open circles) showing that the shape of the curves is dependent on the baseline estimate (21). This change in shape of the curve is used to estimate the optimal baseline (A). (C) The graph shows the baseline values in both phases of the baseline estimation. (D) The graph shows the slopes of the regression lines through the upper (S_upper) and lower (S_lower) halves of the continuous set of data points in the exponential phase when the baselines in (C) are applied.

Window-of-Linearity and fluorescence threshold

The residual measurement noise, even after optimal baseline subtraction, still strongly affects the fluorescence values at the lower end of the log-linear phase. Therefore, a decision has to be made which data points in the log-linear phase will be used for the estimation of the PCR efficiency of each sample. In this article, these data points will be referred to as the data points in the W-o-L (15). Most PCR data analysis methods assume the PCR efficiency to be the same for all samples per amplicon and PCR run. Indeed, the variability in observed efficiency values seems to reflect primarily a random error, and not a real variation (16). Or, to quote Peirson and co-workers (10), ‘one must assume that the amplification efficiency is comparable unless there is sufficient evidence to suggest otherwise’.

Based on this consideration, the algorithm to set the W-o-L searches for the window with the least variation between efficiencies. This algorithm is illustrated in Figure 4A. The procedure has to be carried out per amplicon, because the PCR efficiency can differ per primer pair and amplicon sequence. The window with the minimum coefficient of variation of efficiency values is chosen as the optimal W-o-L. No criterion is set on the absolute value of the efficiencies. However, in all datasets, the minimum variance coincides closely with a maximum mean efficiency (Figure 4B, right). When the experimental condition is suspected to influence the PCR efficiency, a W-o-L has to be set per condition and the resulting PCR efficiencies should be compared.

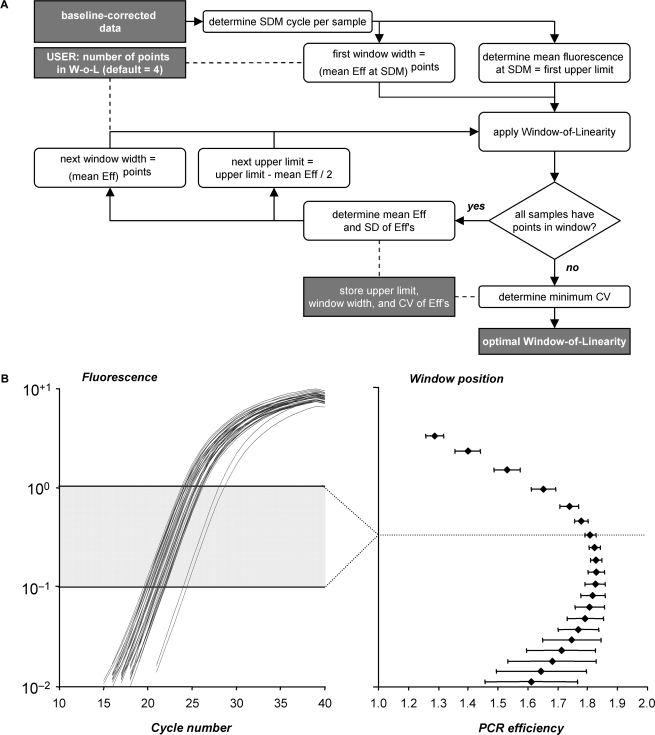
Figure 4.

Setting the W-o-L. (A) Flowchart of the algorithm to determine the position of the W-o-L. The search for the optimal W-o-L starts with the upper limit of this window set at the mean fluorescence level found at the maximum of the second derivative (SDM) of the baseline-corrected fluorescence data. After application of this initial window, a loop is started in which the window is systematically lowered by half of the fluorescence increase per cycle. For each window, the coefficient of variation (CV) is calculated from the mean and the standard deviation of the PCR efficiencies. The minimum CV marks the W-o-L in which the PCR efficiencies of the samples show the least variation relative to the mean efficiency. (B) Intermediate results of the W-o-L setting algorithm. The left panel shows the baseline-corrected amplification curves of an example data set and the optimal W-o-L. The mean PCR efficiency and its standard deviation are plotted for each W-o-L (right panel). The smallest CV, and thus the smallest between-sample PCR efficiency variation, marks the optimal W-o-L. Data points at the beginning of the log-linear phase are preferentially present when a positive statistical noise carries them just above baseline. Consequently, in a very low W-o-L those samples behave as if their baseline was under-estimated and they contribute a low efficiency to the mean. This leads to the decrease of the mean efficiency in the lower-than-optimal windows.

The threshold cycle C_t, which is defined as the fractional PCR cycle at which a preset threshold of PCR product is observed, has been the mainstay of qPCR data analysis since the introduction of fluorescence monitoring of the PCR reaction (8). This C_t value is proportional to the logarithm of the initial target concentration at constant amplification efficiency (Figure 1A, Equation 2). The best reproducibility of the C_t value is achieved when the fluorescence threshold is placed in the upper part of the log-linear phase (Supplementary Figure S3D). The effect of the baseline estimation on the observed C_t value is small; even with a 30% baseline error, the observed C_t values fall within a range of 0.3 cycles on either side of the ‘true’ C_t value (Supplementary Figure S1F).

The W-o-L algorithm was applied to all baseline-corrected datasets and the resulting PCR efficiencies per sample were plotted (Figure 2B). When the baseline was corrected with the above described baseline estimation algorithm, the variance among individual PCR efficiency values was significantly reduced compared to the variance after baseline correction with a baseline trend based on early cycles (Supplementary Figures S2B, S3B and S4B). C_t values were only marginally affected by different baselines (Supplementary Figure S4D).

Amplification efficiency

The choice of the efficiency value to be used in qPCR data analysis is a recurring theme in qPCR papers. In an extensive hierarchical design, Karlen and co-workers (11) showed that bias was removed and that high resolution, precision and robustness were reached when PCR efficiencies of different samples per amplicon were averaged over all measurements done on one cDNA. Similarly, Cikos and co-workers (12) showed that intra- and inter-assay variability decreased when the individual efficiencies were replaced by the mean efficiency per amplicon. These recommendations were based on the estimation of PCR efficiencies per sample in which each sample was fitted to its own W-o-L (15). However, setting the W-o-L per amplicon already reduces the variation between samples significantly (Supplementary Figure S3B). Different W-o-L settings were compared to determine which W-o-L to use, and which efficiencies to average.

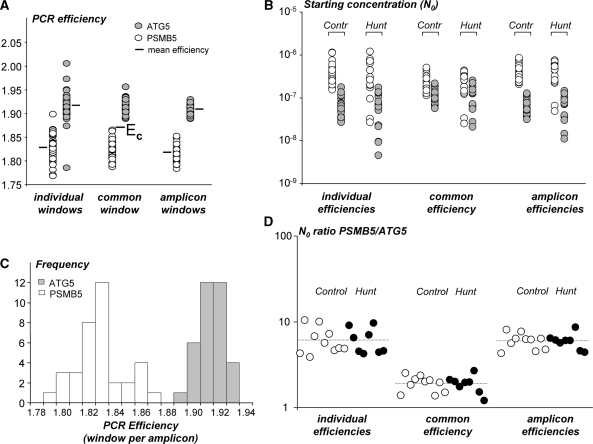
A dataset of qPCR samples of brain tissue containing Huntington patients and control samples served to study the effect of averaging efficiencies on the variation and the bias of the reported concentrations for two amplicons. Three different window settings were used. We previously proposed to base the W-o-L on the best-fitting straight line though 4–6 data points (15). This setting resulted in highly variable PCR efficiencies (Figure 5A, left). When the W-o-L is set per amplicon, the variability between individual PCR efficiencies is significantly reduced (Figure 5A, right) and neither amplicon showed a difference in PCR efficiencies between Control and Huntington patients (Supplementary Figure S4B). For both amplicons, the frequency distribution of the observed PCR efficiencies is normal and symmetrical around the mean PCR efficiency (Figure 5C). This justifies the use of the mean of these efficiencies as an estimate for the true PCR efficiency per amplicon. For further discussion, the efficiency values were also determined by setting a common window for both amplicons (Figure 5A, middle) and a common (mean) PCR efficiency (E_C) was calculated, thus ignoring the amplification difference between amplicons.

Figure 5.

Comparison of the use of individual, common or amplicon-specific PCR efficiencies. (A) PCR efficiency values for ATG5 (gray) and PSMB5 (white) in controls and Huntington patients were based on the individual sample (individual window), a W-o-L for all samples from both amplicons (common window) and a W-o-L set for each of the two amplicons (amplicon window). For each amplicon, the variation in PCR values was highest in individual windows and lowest when a W-o-L per amplicon (F-test, P < 0.001 for both amplicons) was used. The mean efficiency per amplicon did not differ between the three W-o-L settings (one-way ANOVA; P = 0.183 and P = 0.101, respectively) but for all windows the efficiencies of the two amplicons differed significantly (t-test: all P < 0.0001). E_C indicates the common PCR efficiency that results when the difference between amplicons is ignored. (B) Starting concentrations (N₀ expressed in arbitrary fluorescence units) in brain tissue for both amplicons in Controls and Huntington patients calculated with the individual, common, and amplicon efficiency. There is no significant difference between the variation in N₀ values per amplicon and experimental group although the variation is lowest when the common PCR efficiency was used. For both amplicons, the starting concentrations are significantly lower when the results were obtained with a common efficiency (t-test, P ≤ 0.001 for both amplicons and comparisons). The N₀ values do not differ when they were obtained with individual or amplicon efficiencies (t-test, P = 0.916 and P = 0.994 for ATG5 and PSMB5, respectively). (C) Frequency distributions of the individual PCR efficiency values determined with a W-o-L per amplicon. The distribution of efficiency values is symmetrical and normally distributed (Shapiro–Wilk test; P = 0.933 and P = 0.478 for ATG5 and PSMB5, respectively). (D) When the gene expression ratio (PSMB5/ATG5) in Controls and Huntington patients is based on the N₀ values calculated with the individual or the amplicon efficiency, the average ratios are similar (dotted lines), but the variation in the ratios is significantly reduced when the amplicon efficiencies are used [F-test on log(ratio); P = 0.009]. When the expression ratio is calculated with the common efficiency the average ratio is significantly biased (t-test; P < 0.0001 compared to both the individual and the amplicon efficiency results). This bias results from ignoring the difference between the amplicon efficiencies (Box 1; Equation 7).

The variability in estimated starting concentrations (Figure 5B) is not statistically different between the different W-o-L settings but there appears to be slightly less variation in the analysis in which a common efficiency is used (Figure 5B, middle). However, when for each sample the ratio of the two starting concentrations is calculated, the individual and the amplicon efficiencies result in similar ratios, with a larger variability for the individual efficiencies (Figure 5D, left and right). The ratios resulting from the common efficiency are significantly lower (Figure 5D, middle), which illustrates that ignoring the difference in PCR efficiency gives rise to biased ratio results. The magnitude of this bias depends on the relative difference between the amplicon efficiencies and the common efficiency, as well as on the C_t values of the two amplicons in the ratio (Equation 7).

Alternative data analysis approaches

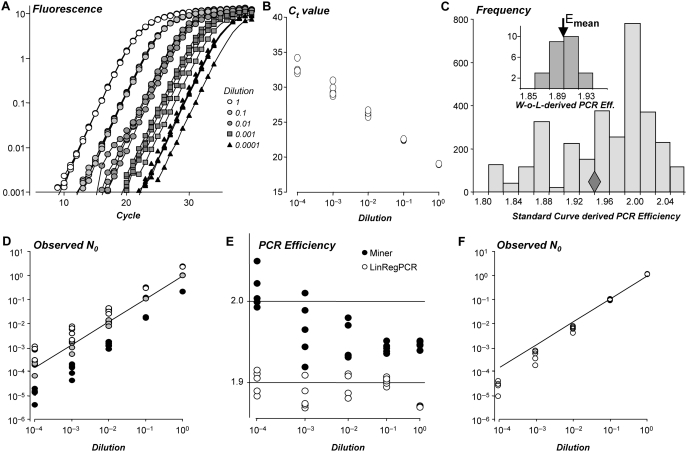
The efficiency value used in the qPCR data analysis has to be derived from the observed amplification data. Some papers report that a ‘mean’ efficiency can be calculated from the slope of a standard curve, which is a plot of observed C_t values versus the log-concentration of a serial dilution of a standard sample (Figure 6A and 6B) (2,8,25). The regression line fitted to these data points is then described by the equation C_t = log(N_c)/log(E) − 1/log(E) × log(N₀) which is Equation 2, log-transformed and rearranged to show the linear dependence of C_t on log(N₀). However, this equation does not describe a straight line with a fixed slope when the amplification efficiencies of the samples are not all equal (18). In that case, the presence of the log(E) variable in both the slope and intercept term of the above equation will result in a standard curve-derived efficiency that does not represent the true mean PCR efficiency of the samples (Figure 6C) (15,26). Accordingly, several authors reported that the mean of the individual PCR efficiencies gave less biased results than a standard curve-derived efficiency (10,11,26). A similar result was observed for the serial dilution dataset in this study (Figure 6D).

Figure 6.

Bias in starting concentrations introduced by standard curve-derived PCR efficiency values or nonlinear analysis procedures. (A) PCR amplification curves of a serially diluted brain tissue sample (4 steps of 10 times dilution; 5 replicates per dilution) after baseline correction (see also Supplementary Figure S3). (B) The standard curve scatter plot shows the C_t values plotted versus the known log-concentration of each serial dilution. This series of five dilutions, measured in five replicates per dilution, was used to construct 3125 (=5⁵) standard curves with one measurement per dilution. (C) Frequency distribution of the efficiency values derived from the slopes of the 3125 standard curves. The diamond indicates the efficiency value derived from the slope of the regression line fitted to all 25 observations. Inset: The individual efficiencies of the 25 amplification curves, calculated from the data points in a common W-o-L. The arrow marks the mean of these individual PCR efficiencies. (D) Starting concentrations (N₀) calculated with the mean of the individual efficiency values (C; arrow in inset). Results were expressed relative to the mean N₀ value of the undiluted samples. The graph shows that these N₀ values (grey circles) show a good correlation with the input values (observed = 0.962 × input; R² > 0.999). The N₀ values calculated with the minimum (white circles) or maximum (black circles) efficiency derived from the standard curves show a positive or negative bias, respectively. (E) The dilution series was analyzed with LinRegPCR (15) and with the Real-time PCR Miner application (7). Miner performs a nonlinear fit of Equation 4 (Box 1) to a subset of raw data points in the exponential phase. The PCR efficiency values resulting from Miner and LinRegPCR are plotted (filled and open circles, respectively). The Miner results show an increasing PCR efficiency with lower input concentrations (P < 0.001), LinRegPCR results do not (P = 0.06). (F) Starting concentrations (N₀) for the serial dilution dataset calculated by Miner (open circles). The solid line is the regression through the starting concentrations observed with LinRegPCR (D; gray circles). The Miner results show an increasing negative bias with lower input concentrations.

Data analysis methods that are based on the application of linear regression algorithms (10,15) require baseline subtraction before the logarithmic transformation because of the fit of the logarithm of Equation 1 to a subset of data in the exponential phase. In contrast, analysis methods based on nonlinear curve fitting do not require such an a priori baseline subtraction because the fitted mathematical models contain an additive term (i.e. y₀ or F_b) that represents a constant (6,27,28) or cycle-dependent baseline (5,19). These algorithms were applied to raw data (5) as well as data that were baseline corrected by the system software (6,20,28,29). In the latter papers the baseline term is, therefore, ignored (or set to zero) in the derivation of additional equations. This practice might lead to the erroneous opinion that these analysis approaches are independent of the proper handling of the fluorescence baseline.

Several authors use a sigmoid or logistic curve fit to select the data points in the exponential phase and then use nonlinear curve fitting to fit the exponential equation [F_C = F_b + F₀ × E^C (Equation 4)] to determine the PCR efficiency E (5,7). The start of the dataset used for this fit is defined as the first point above the ground phase noise which leads to an overestimation of the baseline parameter (F_b). The risk implied in the direct fitting of Equation 4 is that the balance between the two additive parts of this equation is determined by the input concentration of the amplicon (F₀); when the baseline is overestimated, the second term in the equation has to compensate. Especially, for low starting concentrations this compensation has to be found in a high efficiency value. Examples of the resulting upward trend of efficiency values with decreasing starting concentration can be found in literature, e.g. (19,24). The application of this nonlinear fit [i.e. Miner (7)] to the serial dilutions dataset also shows such a relation between input concentration and PCR efficiency (Figure 6E). Starting concentrations, calculated with these efficiency values, show an increasingly strong negative bias with lower input concentrations (Figure 6F). The same data were analyzed with the method described in this article and show a constant PCR efficiency, irrespective of the input concentration (Figure 6E).

The nonlinear fit of the exponential equation (Equation 4) (5,7,24) differs from the method described in the current article only because we propose a two step approach: first find an estimate for the baseline value and then fit the PCR amplification equation (Equation 1) to the baseline-subtracted data. The logarithmic approach used in our baseline estimation method gives more weight to the low, close to baseline, observations; constructing a straight line down from the start of the plateau phase thus leads to a more precise estimate of the baseline.

DISCUSSION

Currently, the mainstream of analysis of qPCR data is based on the C_t value of each sample and a PCR efficiency value per amplicon. Application of a calculation equation derived from Equation 1 then leads to an estimate of the starting concentration expressed in arbitrary fluorescence units or an estimate of the ratio between two starting concentrations of the transcript-of-interest (Equation 2 and Equations 3B or 3C, respectively). This article deals with the analysis of qPCR data resulting from the monitoring of DNA binding dyes like SYBR Green I, but most of the principles discussed in this article also apply to data collected with other fluorescent chemistries (e.g. hydrolysis probes). However, analysis of such data sets requires extra data processing steps that are not discussed in this text.

Analysis of qPCR data requires the derivation of a PCR efficiency value from the observed data. This article shows that the observed PCR efficiency is strongly influenced by small errors in the applied baseline correction. As described, it proves impossible to estimate a baseline value from the so-called ground phase data because the source of this fluorescence is not clear. The main source of baseline fluorescence is unbound fluorochrome (e.g. SYBR Green), which is not fully nonfluorescent (4). However, baseline fluorescence also depends on sample dilution, and thus on total cDNA concentration, and on primer concentration (Figure 1B). Together with the unidentified interactions between those fluorescence sources, the prediction and modeling of baseline behavior is currently unfeasible. Our conclusion that there is not enough ground for the development of an algorithm to determine the baseline from the ground phase data is in line with the findings of others (7).

The baseline estimation algorithm described in the current article is based on the kinetic model of PCR amplification (Equation 1) and a constant PCR efficiency. Cycle-dependent changes in PCR efficiency are predicted by sigmoid models used in qPCR analysis (20,28,29). The use of such sigmoid models is not based on biophysical/biochemical considerations of PCR kinetics, but mainly on their good fit to raw qPCR data. Recent papers show that despite their overall good fit, these models do not fit well to the exponential phase data (7,29). Therefore, these ‘empirical’ models do not provide a solid basis for modeling of the behavior of the PCR efficiency during the PCR reaction. On the other hand, it was established that, when modeling PCR as a statistical branching process, PCR efficiency is constant from the first cycle until the beginning of the plateau phase (30). A modeling study based on kinetic annealing confirmed this notion (23). Moreover, the N₀ value estimated with Equation 2, at large enough C_t, has been shown to be an unbiased estimate of the real starting amount (22).

With a constant PCR efficiency the value of each data point up till the start of the plateau phase is the sum of the baseline fluorescence and an exponentially increasing amplicon-dependent fluorescence (Equation 4). An algorithm that searches for a baseline value that results in the longest straight line of data points when plotted on a semi-logarithmic scale, isolates the exponentially increasing part of the observed fluorescence values. This algorithm requires a sufficiently large baseline-to-plateau ratio as well as a low observation noise. In datasets that do not fulfill these requirements a reliable straight line in the log-linear phase will not be found. The baseline value can be lowered by lowering the primer concentration (Figure 1B); observation noise can be reduced by setting a fixed, instead of an adaptive, exposure time in the qPCR apparatus. Note that the baseline estimation algorithm does not include a ‘goodness-of-fit’ criterion. The chosen algorithm ensures that points at lower cycle numbers are only included as long as they randomly deviate from the straight line defined by the points in the upper part of the exponential phase. Such a provision would not be possible when the algorithm includes a ‘goodness-of-fit’ criterion for the whole log-linear phase.

Even after minimizing PCR efficiency variability and setting of a W-o-L per amplicon, similar samples show slightly different observed PCR efficiencies. To the best of our knowledge, no sample-dependent PCR efficiency differences have ever been reported (10,31). Variability of the PCR efficiency values has been attributed to a limited precision of individual data (12) and thus reflects mainly a statistical error and not a real difference (16). Accordingly, most researchers choose to use a fixed or the mean efficiency per amplicon in their analysis of qPCR data. The symmetric distribution of the individual efficiency values (e.g. Figure 5B and inset of Figure 6C) justifies using the arithmetic mean efficiency. Although the use of a fixed PCR efficiency for all samples per amplicon is well supported, it is still important to use an efficiency value that represents the true efficiency. Equation 7 shows that the bias in the expression ratio resulting from using a common efficiency value for two amplicons, instead of the amplicon-specific efficiencies, depends on the relative difference in efficiencies as well as the C_t values of both samples. An example of such a bias is illustrated in Figure 5D.

Based on the results and considerations in the current paper, the LinRegPCR analysis program (15) has been updated. Although this updated version of the program can be used in a ‘load-and-click’ mode, the different variation sources in qPCR analysis make that no analysis system can be used as a black box. Every user of qPCR should stay aware of hitherto unknown variables affecting the analysis. The experimental set-up should be aimed at recognizing the variables of interest and should enable the analysis of the significance of such variables. Analysis systems cannot relief the researcher of this task.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

The Netherlands Heart Foundation (1996M002); European Union FP6 program HeartRepair (LSHM-CT-2205-018630). Funding for open access charge: same as above

Conflict of interest statement. None declared.