Abstract
Variance estimates can be used in conjunction with scientifically meaningful effect sizes to design experiments with type II error control. Here we present estimates of intra- and inter-subject variances for region of interest (ROI) from resting cerebral blood flow (CBF) maps obtained using whole brain, spin echo echoplanar (SE-EPI) continuous arterial spin labeling (CASL) imaging on 52 elderly subjects (age = 70.5 ± 7.9 years, 29 males). There was substantial intrasubject systematic variability in CBF of gray matter ROIs corresponding to a range of standard deviations = [39 – 168] (mL/(100g·min)). This variability was mainly due to two factors: 1) an expected inverse relationship between ROI volume and intrasubject variance, and 2) an increased effective post-labeling delay for more superior slices acquired later in the sequence. For example, intrasubject variance in Brodmann Area 4 (BA 4) was ∼ 8 times larger than in hippocampus, despite their similar gray matter volumes. Estimated ROI-wise power was computed for various numbers of acquired CBF images, numbers of subjects, and CBF effect sizes for two experimental designs: independent samples t-test and paired t-test. The theoretical effects of pulse sequence and field strength on general applicability of these results are discussed.
Keywords: ASL, CBF, fMRI, statistical power, intersubject variance, intrasubject variance
Introduction
Cerebral blood flow (CBF) is widely accepted as a physiological correlate of brain metabolic activity. Therefore, methods of measuring regional CBF, such as H2O15 positron emission tomography (PET), dynamic contrast enhanced (DCE) MRI and arterial spin labeling (ASL) MRI are important tools in studying brain pathology (Alsop et al., 2000; Brunet et al., 2003; Dieterich et al., 2005; Golay et al., 2004) as well as normal brain function (Kim and Ugurbil, 1997; Wang et al., 2003a). Measurement of CBF with ASL offers several practical and scientific advantages over PET and DCE methods (Alsop et al., 2000). Although different implementations of ASL have been developed, they are all based on the principle of the indicator dilution theory of Kety & Schmidt (Kety and Schmidt, 1948) with the modification that an endogenous tracer (arterial water) is used instead of an exogenous one. Differences between ASL methods consist of the way the water is labeled and as such they are generally classified as continuous ASL (CASL) or pulsed ASL (PASL) (Golay et al., 2004). Here we present data from CASL. In CASL, CBF is calculated from the difference between a labeled and control image. The labeled image is acquired with arterial water spins adiabatically inverted at a plane inferior to the imaging volume using a relatively long off-resonance RF pulse in the presence of a constant gradient in the direction of the flow. The control image is acquired using the same gradient but with a sine-modulated RF pulse to ideally produce no net magnetic inversion of the spins (Alsop and Detre, 1998). Each labeled and control pair is transformed to a single CBF map using a physical model and a set of measured or assumed MR parameters such as tissue and arterial T1 (Alsop and Detre, 1996; Golay et al., 2004). In general, CASL has been shown to have a higher inherent signal to noise ratio (SNR) and lower sensitivity to vascular transit time errors in multi-slice acquisition compared to PASL (Wang et al., 2002). However, CASL is technically more challenging to implement mainly due to its hardware requirement for long RF pulses.
Several reports of error analysis in CASL have shown it has very attractive statistical prospects relative to BOLD fMRI for experiments involving comparison of conditions over long time-scales (Floyd et al., 2003; Wang et al., 2003a). However, little quantitative work has been reported with regard to statistical power (1 – type II error rate). This is a concern because failure to control power leads to uninterpretable negative results. While in BOLD fMRI power is often neglected due to the lack of well-defined physiological units in which to express scientifically meaningful effect sizes (Zarahn and Slifstein, 2001), CASL yields CBF measurement in physiological units. In addition to meaningful CBF effect sizes, power calculations would also require specification of intra- and intersubject CASL CBF variances. Here, intrasubject variance is defined (see Appendix) as the variation over repeated measures within the same subject over several minutes, and reflects measurement noise from the subject and MR scanner as well as physiological nuisance sources such as cardiac pulsatility and motion. Intersubject variance is defined (see Appendix) to include the variation in true CBF among subjects combined with any subject-specificity in the systematic error of CASL CBF modeling such as misspecification of relaxation times. As such, intra- and intersubject variances reflect different sources of variation. Floyd et al. have reported CASL intrasubject variance estimates in ROIs from a young population (Floyd et al., 2003). However, statistical power itself was not explicitly considered, intersubject variance (required for power analysis when comparing resting flow between different populations) was not estimated, and the ROIs were defined by vascular territory and not by neuroanatomical or functional significance.
The main purpose of this study was to estimate intrasubject and intersubject variances of CASL CBF in a normal elderly population in ROIs defined by neuroanatomical criteria in a standard brain space. These estimates were then used to generate example power curves for select ROIs. The independent variables of the power curves were CBF effect size, number of acquired CBF images per subject, and number of subjects. The two fundamental ANOVA designs for which ROI-wise power was investigated were independent samples t-test (which allows comparison of CBF for a given state between two populations) and paired t-test (which allows comparison of CBF between two conditions within a population).
Controlling type II error leads to a great savings of financial, researcher and patient resources by ensuring that CASL CBF experiments will provide meaningful results. Our population of interest was elderly subjects, making the results highly relevant for studies of Alzheimer's Disease (AD) and other age-related diseases.
Materials and Methods
Subjects Demographics
Resting CBF values were obtained from CASL images from subjects (N′ = 52 years of age: 70.5 ± 7.9 (mean ± s.d.), 29 males) that were randomly sampled from the MRI sub-study cohort of the Northern Manhattan Study (NOMAS), a prospective community-based sample of a stroke-free population. Details of subject recruitment methods, demographics, and inclusion/exclusion criteria have been previously described (Sacco et al., 2004). Briefly, subjects were enrolled into the MRI sub-study using the following criteria: (1) age older than 55, (2) no contraindications to MRI, (3) provided written consent as approved by the Columbia University Institutional Review Board. Because this study was part of a larger study, the total scanning time was 45 minutes, 5 of which were spent on acquisition of CASL and 10 on acquiring the high-resolution T1-weighted structural image.
MRI acquisition parameters
SE-EPI CASL images were acquired on a 1.5 T Philips Intera scanner with: labeling duration = 2000 ms, post-labeling delay (PLD) = 800 ms, TE/TR = 35 ms/5000 ms, flip angle = 90°, acquisition matrix 64 × 58, in-plane resolution = 3.4 × 3.4 mm2; slice thickness/gap = 7.5 mm/1.5 mm gap, number of trans-axial slices = 15. Slices were acquired in ascending mode (i.e. inferior to superior) with slice acquisition time = 64 ms. Total number of CBF images (i.e. control/label pairs) per subject was 30.
To induce the flow-driven adiabatic inversion (labeling) of the water spins, a “block-shaped” RF pulse 2000 ms long and 3.5 μT amplitude in the presence of a z-gradient 2.5 mT/m was applied prior to acquisition of each labeled image (Alsop and Detre, 1998). To correct for off-resonance effects, an amplitude modulated (sinusoidal, 250 Hz) RF pulse of the same power and gradient was applied prior the acquisition of each control image (Alsop and Detre, 1998). The frequency offset of both RF pulses was set to position the labeling plane 40 mm inferior to the lower edge of the imaging volume.
To spatially normalize images into standard space, a high resolution, T1-weighted, 3D spoiled gradient image (SPGR) was acquired in each subject with: TE/TR = 3 ms/34 ms, flip angle = 45°, acquisition matrix = 256 × 256 × 124, voxel size = 0.94 mm × 0.94 mm × 1.29 mm.
MRI data processing
Preprocessing
Image pre-processing was implemented using SPM99 software (Wellcome Department of Cognitive Neurology) and other code written in MATLAB (Mathworks, Natick MA). For each subject, images were preprocessed as follows: (1) all control and labeled SE-EPI images were realigned to the first control image acquired. (2) The SPGR was co-registered with the first acquired SE-EPI image using the mutual information co-registration algorithm in SPM99. (3) The co-registered SPGR was then used to determine parameters (7 × 8 × 7 non-linear basis functions) for transformation into a Talairach standard space (Talairach, 1988) defined by the Montreal Neurologic Institute (MNI) template brain supplied with SPM99. (4) This transformation was then applied to the SE-EPI images, which were re-sliced using sinc-interpolation to 2 mm × 2 mm × 2 mm.
Segmentation of structural data
SPM99 was used to segment the structural image of each subject into gray matter (GM), white matter (WM), and CSF posterior probability images needed for masking and computation of CBF. These images were used in the subsequent computation of CBF and in obtaining subject-specific masks. For each subject, two types of masks were made: an EPI-mask which included only voxels with SE-EPI intensity > 0.80 of the image mean and therefore contained contributions from GM, WM, and CSF, and a GM-mask, which was based on each subject's GM posterior probability image including only voxels that satisfied P[GM] > 0.80. We are using the P[GM] as a probabilistic measure of relative GM volume; this is justified by the fact that the expected value of CBF for a voxel with a given P[GM], P[WM], and P[CSF] is the same as that for a single voxel with those relative tissue volumes.
CBF computation
The spatially normalized SE-EPI images were used to compute CBF at each voxel using the two-compartment formula derived by Alsop & Detre and later modified by Wang et al. (Alsop and Detre, 1996; Wang et al., 2002):
| Eq [1] |
The following parameter notation and values were used: (T1 of blood) T1a = 1400 ms; (blood/tissue water partition) λ = 0.9 mL/g; (tissue transit time) δ = 2000 ms; (labeling duration) τ = 2000 ms; (tissue T1 in the absence of RF) T1 = 1150 ms and 800 ms for GM and WM, respectively; (T1 in presence of RF) T1rf = 750 ms and 530 ms for GM and WM, respectively (Alsop and Detre, 1998); (labeling efficiency for CASL at 1.5 T Philips Intera) α = 0.70 (Werner et al., 2005). For each voxel, CBF was calculated as a sum of GM, WM, and CSF contributions weighted by the voxel's posterior probability of each tissue type. For each slice, the effective PLD, w, was adjusted to account for the slice acquisition time: w = (acquisition slice # -1)·(64 ms) + 800 ms. An assumption of Eq. [1] is that τ + w > δ, which we assume is satisfied in our experiment given the range of δ reported in the literature (1.0 – 1.6 s) (Mildner et al., 2005; Wang et al., 2003b).
ROI selection
To maximize inter-laboratory generalizability of our findings, a publicly available ROI software library (wfu_pickatlas, (Maldjian et al., 2004; Maldjian et al., 2003; Tzourio-Mazoyer et al., 2002)) was used. Seven ROIs per hemisphere (14 total) were selected in MNI space in 3-dimensional mode: Hippocampus, Inferior Frontal Gyrus, Middle Frontal Gyrus, Occipital Lobe, Precentral Gyrus, Brodmann Area (BA) 4, Temporal Lobe. These ROIs were selected because they have been considered in studies of aging of the brain as well as age-related pathologies (Alsop et al., 2000; Scarmeas et al., 2004). Moreover, we chose ROIs with substantial variation in size and anatomical location to account for the effect on estimated variances of ROI volume, arterial transit time (δa), and effective PLD (w), which increases with slices acquired later in the acquisition.
PLD experiment
An underlying assumption of Eq. [1] is w > δa (Wang et al., 2002). To test this assumption, CASL images were acquired on a single random subject from the cohort (66 y.o. female) at multiple PLD values (100 to 1500 ms, step of 100 ms). Percent change maps [(Mc - Ml)/Mc] maps were computed for the intersection of this subject's GM mask and each acquisition slice. To minimize the effect of motion, only voxels belonging to the same acquisition slice for all images were analyzed; i.e., if, due to motion, a voxel that was at a given slice for a given PLD acquisition had shifted to an adjacent slice in another PLD acquisition, was not included. Due to the time constraint of this experiment, only 9 slices (approximately positioned as slices 7 - 15 in the imaging volume of the main experiment) and 20 CASL images were acquired for each PLD. Otherwise, all other acquisition parameters and processing procedures were identical to the main experiment. δa and CBF for each slice were estimated from the best fit of the theoretical one-compartment vascular model of Buxton et al. (Eq. [5] in (Buxton et al., 1998)) to the percent change values.
Slice acquisition ordering effect
To test the effect of acquisition order on the validity of CBF measurement, CASL images were acquired on a young volunteer (26 y.o., female) in both ascending and descending order. The w for the slice of interest (chosen near the top of the brain) was fixed at 1640 ms for both ascending and descending modes, thus obviating any effect of w in the error measurement. All other acquisition parameters and image processing were the same as in the main experiment. Slice-wise mean CBF and were estimated for both acquisition orders.
Power analysis
ROI-wise power analyses for independent samples and paired t-tests required estimation of and (see Appendix for computational details). The ROI-wise variances were estimated for both GM and EPI masks using conjunction of CASL CBF image, ROI, and the respective mask. Note that the ROI-wise variance calculations involved not the variation in CBF measurements among voxels within an ROI but rather the variation in the ROI CBF average over repeated measurements or subjects (see Appendix). Also, to keep > 0, any negative values originating from its computation (Eq. [A10]) were set to zero.
While we present estimates of and for all ROIs and for both masking procedures, in the interest of concision, we restricted presentation of estimated power results to only two GM ROIs, left hippocampus and left BA 4. (Results for the right hemisphere and/or SE-EPI masking were very similar). These ROIs were selected because they have similar size but substantially different z-coordinates, therefore providing variability in w which is expected to affect noise. Furthermore, each is of immediate interest to one of the two design types: hippocampus for an independent samples t-test in the context of AD (Scarmeas et al., 2004) and BA 4 for a paired t-test in the context of motor execution. For these two ROIs, power was computed for both experimental designs with two-tailed α = 0.05 for various values of N (# of subjects per group) and n (# of observations per subject). N and n are not to be confused with N′ and n′ (see Appendix). Effect sizes of μ = 10 and 20 mL/(100g·min) were assumed. These values of μ were selected to represent small and moderate CBF effect sizes (Kim and Ugurbil, 1997).
Results
CASL CBF measurements
To provide a qualitative sense of the images on which the analysis was based, group mean SPGR and CASL CBF images are shown in Fig.1A and 1B, respectively. Visual inspection shows a general lack of strong intravascular signal as well as good tissue contrast of the CBF signal (Fig. 1B). Fig. 2 provides a quantitative description of GM CBF group mean values versus acquisition slice. The range of slice-wise CBF values [49 – 77 mL/(100 g·min)] is in reasonable agreement with what has been reported for non-partial volume corrected GM CBF with PET (Kudo et al., 2003) and ASL (Golay et al., 2004)
Fig.1.
Images of SPGR (A), CASL CBF (B), estimated intrasubject variance, (C), and estimated voxelwise inter-subject variance, (D). A-C show images averaged across all subjects. Note good coregistration and spatial normalization. MNI z-coordinates of the slices shown are 19, 35, 53, and were chosen to represent lower, middle, and upper brain, containing portions of hippocampus, lateral ventricles, and BA 4, respectively. (Note that the negative values in D were zeroed to keep > 0.)
Fig. 2.
Plot of GM CBF vs. slice acquisition number. Only slices having usable data from all subjects (N′ = 52) are shown. Error bars represent ± 1 S.E.M. across subjects.
There is an evident pattern in the CBF vs. acquisition slice (Fig.2). This pattern could reflect a property of true CBF, GM density, or a bias inherent in the CASL model used. The variation of mean P[GM] > 0.8 and P[WM] > 0.8 across slices was 2% and 6%, respectively, and therefore cannot account for the ∼ 26% slice-wise variation seen in CBF (Fig.2).
Figs.1C and 1D are maps of (pooled over subjects) and , respectively. Note that there is no theoretical reason why high implies the presence of CBF; comparison of sagittal sinus signal between Fig. 1B and 1C shows a lack of CBF signal even in the presence of high (which we believe is due to variations in intensity in the SE-EPI images due to the slow flow sagittal sinus). Conversely, high (Fig. 1D) is expected to co-localize with CBF; comparison of Fig. 1B and 1D bears this out. Also note the general increase in as one moves superiorly.
Effect of PLD
An underlying assumption in Eq.[1] is that w > δa, (Alsop and Detre, 1996; Wang et al., 2002). To validate this assumption, δa was estimated by acquiring CASL images at varying PLD values as described in Methods. Fig. 3 shows the dependence of percent change signal on w for each acquisition slice with the solid line representing the best fit. The estimated δa ranged from 333 – 1068 ms, increasing linearly with ascending slice position (slope =122 ms/cm). For all slices, w - δa > 500 ms. Furthermore, since the first slice acquired in our main CBF dataset was approximately 5 cm inferior to the one in this experiment, this provides an estimated lower bound on the satisfaction of w > δa. However, careful inspection of Fig. 1B shows the presence of some high intravascular signal, which means that the above condition was most likely not fulfilled for all the subjects.
Fig. 3.
Plots of GM CASL percent change signal from each acquisition slice vs. w from a single elderly subject. Small circles indicate the actual data points whereas solid lines represent the best fit. Data from each acquisition slice is color-coded with the most inferior slice (blue, corresponding approximately to slice 7 of the main experiment), and the most superior slice (red, corresponding approximately to slice 13 of the main experiment.) Each plot is shifted by 64 ms (slice acquisition time) relative to the previous one with the most superior slice (red) having the longest w values. Only slices having usable data from all PLDs are shown.
Effect of slice acquisition order
Theoretically, for an ascending acquisition order, w > δa implies no saturation of labeled spins destined for the imaged slice, further implying that computed CBF is independent of acquisition order. To validate this reasoning, we acquired CBF images using both ascending and descending acquisition orders with w fixed at 1640 ms for a slice of interest near the top of the brain (where the saturation effect would be more prominent). The estimated CBF values in GM of that slice were 47.0 and 50.9 mL/(100 g·min), for ascending and descending acquisition order, respectively. This difference was not significant [t(56) = -0.60, p = 0.55].
Power Analysis
Normality of CASL CBF distribution
The power analysis in this study formally assumes that errors are normally distributed. In practice, except for highly non-normal errors, the theory is expected to hold well in approximation due to the central limit theorem. For qualitative inspection, sample histograms of the ROI means for left hippocampus (Fig. 4A) and left BA 4 (Fig. 4B) are provided as representative.
Fig. 4.
Histograms of GM ROI-wise CBF averages for A) left hippocampus and B) left BA 4. (One value per subject, each the temporal average of 30 CBF observations.)
To quantitatively test for any evidence of non-normality, we estimated the skewness (S) and kurtosis (K) (computed such that their expectation equals zero for a normal density) of the ROI-wise CBF distribution across subjects (N′ = 52). In all ROIs, the 95% confidence intervals for both S and K contained zero.
If the underlying voxelwise distributions deviate sufficiently from normal, |S| and/or |K| would be expected to increase as ROI volume decreases. However, if strong spatially coherent non-normal noise sources are present, |S| and/or |K| would be expected to increase as ROI volume increases. For all our ROIs, the estimated correlations between either |S| or |K| with ROI volume were not significant (two-tailed p > 0.10 for all). This result suggests that neither non-normal voxel-wise distributions or non-normal spatially coherent noise sources are appreciable in CASL CBF measurements for the ROIs examined.
ROI-wise variances
Table 1 shows and for all ROIs for both GM and SE-EPI masking procedures. CBF, , and were each highly correlated between the two masks employed (R = 0.74, 0.99 and 0.94, respectively). Within each masking procedure, and were also positively correlated (R = 0.61 and 0.72 for GM and SE-EPI masking, respectively), which was unexpected. A possible explanation for at least some component of this correlation is that only a single value of tissue transit time, δ, was used for CBF computation for all slices. However, δ would be expected to vary approximately linearly with δa if one thinks of it as simply the sum of arterial transit time, δa, plus the time it takes labeled water to diffuse into the tissue. Assuming a uniform δ could introduce a scaling error into CBF computation, which would contribute a positive covariance between and across space. As an aside, a correlation between and across space would be unrelated to (and does not in any way invalidate) the assumption that intra- and intersubject errors are independent at each location in space (see Appendix).
Table 1.
Estimated ROI-wise CASL CBF intra- and intersubject variances
| ROI | masking procedure | average size | average CBF | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Right Hippocampus | GM | 405 | 73.7 | 2968 | 153 | 19.4 | |||
| Right Inferior Frontal Gyrus | GM | 1973 | 74.3 | 5219 | 103 | 50.6 | |||
| Right Middle Frontal Gyrus | GM | 2695 | 69.4 | 10553 | 236 | 44.7 | |||
| Right Occipital Lobe | GM | 4213 | 76.7 | 1549 | 439 | 3.5 | |||
| Right Precentral Gyrus | GM | 1235 | 71.1 | 11566 | 306 | 37.8 | |||
| Right Brodman Area 4 | GM | 386 | 64.8 | 22365 | 570 | 39.2 | |||
| Right Temporal Lobe | GM | 7475 | 76.2 | 1699 | 272 | 6.2 | |||
| Left Hippocampus, | GM | 423 | 74.2 | 3417 | 137 | 24.9 | |||
| Left Inferior Frontal Gyrus | GM | 1794 | 74.2 | 5282 | 123 | 42.9 | |||
| Left Middle Frontal Gyrus | GM | 2428 | 69.9 | 10914 | 270 | 40.4 | |||
| Left Occipital Lobe | GM | 4447 | 77.1 | 1686 | 444 | 3.8 | |||
| Left Precentral Gyrus | GM | 1185 | 70.6 | 12777 | 340 | 37.5 | |||
| Left Brodman Area 4 | GM | 382 | 66.9 | 27415 | 540 | 50.7 | |||
| Left Temporal Lobe | GM | 6981 | 74.5 | 1526 | 239 | 6.3 | |||
| Right Hippocampus, | SE-EPI | 548 | 69.3 | 2730 | 182 | 15.0 | |||
| Right Inferior Frontal Gyrus | SE-EPI | 4731 | 62.6 | 4642 | 47 | 98.7 | |||
| Right Middle Frontal Gyrus | SE-EPI | 7297 | 57.8 | 9302 | 141 | 65.9 | |||
| Right Occipital Lobe | SE-EPI | 10419 | 61.8 | 1599 | 286 | 5.6 | |||
| Right Precentral Gyrus | SE-EPI | 4169 | 56.4 | 14322 | 261 | 54.9 | |||
| Right Brodman Area 4 | SE-EPI | 1354 | 53.5 | 26218 | 551 | 47.6 | |||
| Right Temporal Lobe | SE-EPI | 16453 | 64.2 | 1895 | 161 | 11.8 | |||
| Left Hippocampus, | SE-EPI | 577 | 71.5 | 3451 | 139 | 24.8 | |||
| Left Inferior Frontal Gyrus | SE-EPI | 4651 | 61.1 | 4448 | 67 | 66.4 | |||
| Left Middle Frontal Gyrus | SE-EPI | 7302 | 56.2 | 9172 | 162 | 56.6 | |||
| Left Occipital Lobe | SE-EPI | 10303 | 64.9 | 1652 | 344 | 4.8 | |||
| Left Precentral Gyrus | SE-EPI | 4164 | 56.0 | 15066 | 261 | 57.7 | |||
| Left Brodman Area 4 | SE-EPI | 1276 | 55.6 | 30193 | 427 | 70.7 | |||
| LeftTemporal Lobe | SE-EPI | 16414 | 62.4 | 1678 | 152 | 11.0 |
Units of ROI size are voxels (1 voxel = 8 mm3 = 8 × 10-3 cc). Units of CBF are mL/(100g•min). Units of and are CBF2.
As expected, GM masking led to smaller (∼ 40%) ROIs with higher (∼ 19%) mean CBF than SE-EPI masking. However, ROI-wise obtained from SE-EPI masking showed no tendency to be smaller than that from GM masking. These results suggest that compared to GM masking, SE-EPI masks are less sensitive for CASL activation experiments. On the other hand, ROI-wise from SE-EPI masking was on average 25 (± 8) % smaller than that from GM masking, which is consistent with the idea that most of the true intersubject variability in CBF comes from GM.
While power for a paired t-test (without Subject × Condition interactions, see Appendix) only depends on , power for an independent samples t-test depends on both and . To determine which of the two dominates var 〈μ̂〉 in an independent samples t-test we use the fact that when n = , the contributions of intra- and intersubject variances are equal; when n > , the intersubject variance is the dominating term (see Eq. [A6]). For GM masking, Table 1 shows a range of from 3 – 98. Thus, when using any of these ROIs, for an independent samples t-test with n > 98, var 〈μ̂〉 will be dominated by the intersubject variance.
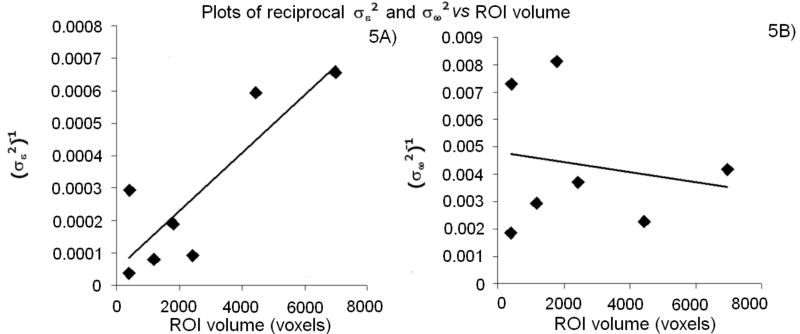
For independent and identically distributed errors at each voxel, should vary as the inverse of ROI size. However, does not theoretically depend on MRI noise or any error that varies randomly across voxels, and therefore should not depend on ROI size. These predictions were borne out in Fig. 5A and 5B, respectively. Fig. 5A suggests that other sources of variability in addition to size contribute to ROI-wise . In particular, left BA 4 and left hippocampus ROIs were very similar in size (382 and 423 voxels, respectively, with GM masking), but ROI-wise was 8.0 times larger for left BA 4 despite the mean CBF being similar [66.9 and 74.2 mL/(100 g·min), respectively]. This was also true for the right hemisphere where ROI-wise was 7.5 times larger for right BA 4 than for right hippocampus. As we discuss below, this difference can be explained by the increase of w with superior slices.
Fig.5.
A) Plot of reciprocal vs. GM ROI volume with best-fit line (R2 = 0.73). B) Plot of reciprocal vs. GM ROI volume with best-fit line (R2 = 0.03). Only data from left hemisphere GM ROIs are plotted. Results (not shown) are very similar for right hemisphere ROIs and ROIs using SE-EPI masking.
Power curves
Based on the variance values from GM masked ROIs (Table 1), estimated power curves for left hippocampus and left BA 4 are shown as a function of the number of subjects per group for an independent samples t-test (Fig. 6) and the total number of subjects for a paired t-test (Fig. 7). Each curve corresponds to a certain number of CBF images acquired per subject; μ was either 10 (Figs. 6A,C & 7A,C) or 20 mL/(100 g·min) (Figs. 6B,D & 7B,D). A consequence of both and being larger for BA 4 than hippocampus is that power is substantially lower for BA 4 in all designs.
Fig.6.
Independent samples t-test design power curves for selected effect sizes and GM ROIs. A) Left hippocampus, μ = 10 ml/(100 g·min). B) Left hippocampus, μ = 20 ml/(100g·min). C) Left BA 4, μ = 10 ml/(100g·min). D) Left BA 4, μ = 20 ml/(100g·min). Moving upward, each curve corresponds to an increasing number of CBF images per subject starting with 10 (thin gray line), 20 (thin black line), 50 (thick gray line), and 100 (thick black line).
Fig.7.
Paired t-test design power curves for selected effect sizes and GM ROIs. A) Left hippocampus, μ = 10 ml/(100g·min). B) Left hippocampus, μ = 20 ml/(100g·min). C) Left BA 4, μ = 10 ml/(100g·min). d) Left BA 4, μ = 20 ml/(100g·min). Moving upward, each plot corresponds to an increasing number of CBF images per subject starting with 10 (thin gray line), 20 (thin black line), 50 (thick gray line), and 100 (thick black line). The number of CBF images per condition equals half that per subject. α equals two-tailed 0.05 for all plots.
The hippocampus ROI exhibits acceptable power for an independent samples t-test at feasible clinical sample sizes and moderate effect sizes. For example, to obtain power = 0.90 when 100 CBF images are acquired per subject, an estimated < 10 subjects per group would be needed to detect μ = 20 mL/(100 g·min) difference between groups. All other parameters being equal, for a small effect size of μ = 10 mL/(100 g·min) (i.e., a deviation of ∼ 15% from normal hippocampal CBF), 36 subjects per group would be needed. This example provides a sense of the practical limits of sensitivity of CASL to detect group differences in resting CBF.
A concrete example of a paired t-test for neuroimaging would be an experiment in which a finger tapping condition is compared, within subject, to a resting condition. Fig. 7D indicates that in BA 4 for μ = 20 mL/(100 g·min), to obtain power = 0.80 with 50 CBF images acquired per condition (i.e., 100 images per subject), an estimated 22 subjects would be needed.
Discussion
We have estimated intra- and intersubject variances of CASL CBF measurements in GM from several neuroanatomically defined ROIs for an elderly population. SE-EPI acquisition was used, thus minimizing signal dropout due to susceptibility effects. We restricted our analysis to GM as this tissue is of greater interest in the context of brain metabolism. Our GM CBF estimates are biased downwards due to partial volume effects. However, we do not expect this bias to be large because our GM ROIs included only voxels that were expected to be 80% or more GM. Donahue et al. measured the error induced in GM CBF estimates by partial volume effects at 3T and found it to be 10-20% (Donahue et al., 2006).
Using these results and the relevant equations (see Appendix), power can be estimated for any of the ROIs with any desired μ, n, N, and α. We have also provided explicit power curves for BA 4 and hippocampus, which are especially relevant for studies of motor execution and AD, respectively.
While the emphasis of this study was the sensitivity of CASL CBF in general, the specific population studied was that of normal, elderly subjects. The results are therefore directly relevant for the design of CASL CBF experiments to study AD and other age-related diseases, as well as normal aging. However, if one surmises that and are similar between different populations, the results obtained here would be qualitatively germane for other populations. We conjecture that both and are larger in elderly than young because of potentially increased motion (which would impact ) and increased intersubject variability in sub-clinical aged-related pathology (which would impact ) in elderly.
reflects all sources of MR scanner noise, which would include Johnson noise (thermally mediated random variation in voltage across a resistor) from the subject load (and to some extent the RF coil), as well as head motion and physiological noise such as that due to cardiac pulsatility or even random neurogenic CBF fluctuations. For the designs to yield exact t-statistics, the need to be the same across subjects. Inspection of distributions of for BA 4 and hippocampus suggested that this was not the case, as they did not conform well to a χ2 density with N′ - 1 degrees of freedom (data not shown). Even in the extreme, non-identical across subjects would not bias the estimation of var 〈μ̂〉 (see Appendix), but instead would invalidate the use of the t-distribution and consequently invalidate the power analysis. However, the distribution of the ROI-wise averages for BA 4 and hippocampus were approximated well as normal, therefore concern about validity of t-tests and corresponding power analyses is mitigated. The apparent heterogeneity of does, however, suggest the use of weighted least squares estimation on CASL CBF to improve sensitivity.
There was a substantial variation in between ROIs that could not be explained simply by ROI volume. For example, BA 4 ROI-wise was ∼8 times larger than that of hippocampus, despite the ROIs being very similar in size. One mechanism theoretically expected to affect through the acquisition slice is the effective post-labeling delay, w. The amount of label diminishes during w through T1 relaxation, which, for a given CBF and for an ascending acquisition, should lead to a smaller percent change signal in more superior slices. This decrease should not lead to a smaller estimated CBF as w is explicitly accounted for in the physical model (Eq. [1]). It also should not affect the intrasubject variance of percent change signal assuming noise is additive and not multiplicative to MR signal. However, this decrease should result in an increased because, for a given CBF, the smaller the CASL percent change signal, the larger the multiplicative factor used to transform this signal to flow, and therefore the larger the inflation. Indeed, ancillary analyses confirmed that w explains most of the difference in between BA 4 and hippocampus (data not shown). Furthermore, the maps of showed greater values as one moved superiorly, as would be expected under this PLD effect.
One might conjecture that in studies where superior slices are of interest, the aforementioned w effect could be obviated by acquiring them with shorter w. However, as the validity of the CBF model used assumes w > δa, the minimum required w increases as slice position moves superiorly. Therefore, to fully eliminate relaxation related sensitivity loss at superior slices, one would have to reduce δa by placing the labeling plane as close to the slice as saturation effects and adiabatic conditions permit. However, the positioning of labeling plane is restricted in applications where whole brain coverage is needed.
In a single elderly subject, for each slice, we estimated arterial transit time, δa, ranging from 0.33 – 1.07 s, corresponding to an average 122ms/cm or a z-velocity an average z-velocity of spins of ∼ 8 cm/s. These estimates are in good agreement with literature values for arterial transit time in GM in various regions of the brain: 0.6 – 1.2 s by Gonzales et al., 0.73 – 0.97 s by Yang et al. (Gonzalez-At et al., 2000; Yang et al., 2000). In our sequence, w was at least 0.5 s longer than δa for each slice. Although there is conceivably a distribution of δa amongst the elderly population, we conjecture that w > δa in a large proportion of the non-diseased elderly population. Further work is needed to establish the effect of age in arterial transit times. Furthermore, by comparing CBF in the same slice at a given w for both acquisition orders, we showed that our implementation of CASL CBF was independent of the acquisition order. Together, these results suggest that saturation of labeled spins (which would be expected if w < δa) was not appreciable. However, the presence of some intravascular signal (Fig. 1B) indicates that the assumption w > δa was most likely not met by all the subjects.
Floyd et al. measured intrasubject variance of CASL CBF at 1.5 T using ascending acquisition in ROIs defined by vascular territories (Floyd et al., 2003). Instead of using time series variance to define intrasubject variance, they used the variation in ROI means between runs (n′ = 45 CBF images/run) separated by either one hour or one week. Therefore, if resting CBF varies substantially over time within subjects, Floyd et al.'s estimates would include sources of variation that in our analysis were absorbed implicitly by . However, in the approximation of stable CBF over time, their measure of intrasubject variance, “wSD”, should equal . Their reported range (over ROIs) for wSD for the one hour data was 3.0 – 9.1 mL/(100g·min) and for the one week data was 6.8 – 8.7 mL/(100g·min) with a median of 7.4 in both cases. These ranges of ROI-wise wSD overlap with those of the current study [GM masked ROIs wSD range: 5.8 – 24.7 mL/(100g·min), median = 10.8; SE-EPI masked ROIs wSD range: 6.0 – 25.9 mL/(100g·min), median = 10.0]. As Floyd et al. did not report ROI volumes, a more direct comparison to our values is not possible. However, considering that the ROIs used in Floyd et al. covered entire perfusion territories, it is likely that they were larger than the neuroanatomical ROIs used in our study.
Yen et al. reported variance of PASL CBF at 1.5 T from GM ROI in a single slice (Yen et al., 2002). ROI size across subjects varied from 50 – 80 cc, similar in size to our hippocampal and BA 4 ROIs. We calculated wSD from the results of Yen et al. and it was 4.1, which is ∼ 2 and 6 times smaller than that of our hippocampal and BA 4 ROIs, respectively. In contrast, from Yen et al. was 114 [mL/(100 g·min)]2, which lies within the range of our ROI-wise results.
reflects the variation between subjects in the CASL CBF in the absence of intrasubject error. Contributions to theoretically include variation in neuronal/neuropil/glial density, baseline neuronal metabolism, blood T1 due to differences in hematocrit content, hormonal levels, and metabolic-vascular coupling which in turn could be affected by within-population pathological variation, developmental differences, and other aspects of genotypic variation. Other, non-physiological sources of variation such as subject-specific misspecification of transit time and/or other MR/physiologic parameters would also contribute to . Furthermore, any within-subjects variation in CBF over long time scales would also implicitly contribute to our ; however, this type of variation over one week has been shown to be insubstantial (Floyd et al., 2003). Though we did not rigorously quantitate differences in between GM and WM, the estimated map of (Fig.1D) suggests that it is larger in GM than in WM, which, if true, would imply that physiological CBF variation is greater in GM.
Recently, implementations of CASL at higher fields have been reported (Wang et al., 2002; Wang et al., 2005a; Wang et al., 2005b). Presently, there have been no empirical studies that explicitly address the effect of Bo on sensitivity for CASL. Theoretically, however, ASL signal is expected to increase with Bo due to two main factors: an inherent increase in MR SNR with Bo, and a longer longitudinal relaxation time of labeled arterial water (Golay and Petersen, 2006). Wang et al. have provided a theoretical framework for the dependence of ASL signal with Bo (Wang et al., 2002). They found that in the absence of T2* effect (appropriate for SE-EPI), CASL SNR is expected to an ∼ 3 × increase at 3 T compared to 1.5 T, which should correspond to an ∼ 9 × decrease in if thermal noise dominates physiological noise in CBF time series.
Using gradient echo EPI, Wang et al. have reported that compared to a standard volume coil, an 8-channel array coil with (2-fold) and without acceleration provided a 45% and 56% decrease in intrasubject standard deviation, respectively (Wang et al., 2005b). These effects could conceivably be different for a SE acquisition where susceptibility effects are less.
Although, depends on pulse sequence and hardware characteristics, the CASL implementation used in this study is the most commonly used (Golay et al., 2004) and as such the results presented here should be quite useful in a variety of applications for CASL in the elderly population. Furthermore, the data presented here can still be useful for other CASL implementations assuming theoretical predictions about changes in SNR can be made. For example, if SNR at 3 T is 3 times of that at 1.5 T (Wang et al., 2002) then, all other parameters being equal, the estimates reported here could be reduced 9-fold for power calculations for the desired design. The same logic holds for post-processing techniques that aim at reducing (Restom et al., 2006). In contrast, should not be affected appreciably by Bo, coil implementation, pulse sequence, or post-processing strategy. Even more fundamentally, is, theoretically, method-independent and should therefore be the same for CASL, PASL, and even other non-MRI imaging techniques such as PET.
We presented estimates of and using a particular CASL physiological model (Wang et al., 2002). The use of other CBF models would, to a first approximation, preserve the ratio of mean to standard deviation. Therefore, the current results could be used to perform power analyses for effect sizes expressed as percentages of the resting ROI CBF means (instead of CBF units) in an approximately model-free manner.
Because our study involved the measurement of only one condition, rest, a Subject × Condition variance term (see Appendix) could not be estimated. Therefore the paired t-test model we used was based on the assumption that the variance of μ̂ depends only on and not on an additional variance term associated with a Subject × Condition interaction. If incorrect, this assumption would introduce an additional source of physiological variability into the estimation for this design, and effectively make the power analysis presented for paired t-test relevant only for “fixed effects” inference. That is, inference valid only for the particular set of subjects sampled, and not the population from which they were sampled (Friston et al., 2005). The quantitative effect of ignoring this term in the context of paired t-test depends on its actual magnitude relative to . For now, one can consider the paired t-test power analysis we present here to be correct for fixed effects inference, and potentially too lenient (i.e., leading to an overestimation of power) for population-level (or “random effects”) inference.
The elderly population under study was screened to exclude stroke (Sacco et al., 2004), but includes individuals with diabetes, heart disease, and other diseases at standard prevalence rates (DeCarli et al., 2005). Although the definition of what is considered “healthy” for the elderly population is under clinical debate (DeCarli et al., 2005), possibly a more homogenously healthy population would exhibit smaller . The CASL power estimates presented here should nevertheless prove useful and relevant in designing experiments in elderly subjects.
Acknowledgments
This work was supported by grants from National Institute of Neurological Disorders and Stroke R01 NS 29993 and K12 RR 176548. Eric Zarahn was supported by a NARSAD Young Investigator Award.
Appendix
Power analysis
Power is equal to the integral of the probability density function (pdf) of the test statistic under a given alternative hypothesis with the lower limit of integration L being determined at least in part by the statistical threshold chosen to control type I error. For both independent samples and paired t-tests, assuming normal errors, the correct pdf to integrate is the non-central t. However, for simplicity the standard normal pdf was used:
| [A1] |
where d is an abstract vector parameter representing experimental design [number of subjects, nature of effects (within or between subjects), pulse sequence parameters, etc.], and L is
| [A2] |
where zα/2 is the upper threshold corresponding to a two-tailed type I error rate of α, and var〈μ̂〉 is the variance of μ̂ (the ordinary least squares estimator of the effect size, μ, which is the CBF value being tested against 0 in either experimental design.)
Let yhijk be the CASL CBF observation at a given voxel or ROI from group h, condition i, subject j, and replication k. A univariate statistical model for yhijk is
| [A3] |
where μhi is the true CBF for condition i in group h. The normally distributed inter-subject errors ωj have variance . The normally distributed time-series errors εhijk are assumed to be independent with identical variance , which does not depend on j. ωj and εhijk are assumed to be independent (if they were not, then time-series error would somehow “know” to be correlated with subject-wise variation in CBF). For completeness, [A3] includes the Subject × Condition interaction term ηij. If data were acquired over both conditions of a paired t-test, then a could be estimated, which would contribute to var〈μ̂〉. However, we only acquired data for one condition, and so we cannot estimate a , therefore our paired t-test inference is formally valid only for fixed effects inference.
For an independent samples t-test, let μ = μ1i − μ2i. Then, μ̂ = y1i.. - y2i.., where:
| [A4] |
| [A5] |
with N and n denoting the number of subjects per group and the number of observations per subject, respectively. The variance of μ̂ is:
| [A6] |
For a paired t-test, let μ = μh1 − μh2 and μ̂ = yh1.. - yh2… The fixed effects variance of μ̂ is:
| [A7] |
where N is the number of subjects and n is the total number of observations per subject (i.e., the number of observations per subject per condition is n/2).
and can be estimated from a random sample of N′ subjects with n′ observations per subject from condition i. The estimate of in the jth subject is
| [A8] |
Since we assume does not depend on j, can be pooled over the N′ subjects to provide a better estimate:
| [A9] |
can be estimated as a weighted difference between the sample variance of {yhi1., yhi2.,…yhinN′ and :
| [A10] |
and can be substituted into Eq. [A6] and [A7] to provide an unbiased estimator of var〈μ̂〉.
References
- Alsop DC, Detre JA. Reduced transit-time sensitivity in noninvasive magnetic resonance imaging of human cerebral blood flow. J Cereb Blood Flow Metab. 1996;16:1236–1249. doi: 10.1097/00004647-199611000-00019. [DOI] [PubMed] [Google Scholar]
- Alsop DC, Detre JA. Multisection cerebral blood flow MR imaging with continuous arterial spin labeling. Radiology. 1998;208:410–416. doi: 10.1148/radiology.208.2.9680569. [DOI] [PubMed] [Google Scholar]
- Alsop DC, Detre JA, Grossman M. Assessment of cerebral blood flow in Alzheimer's disease by spin-labeled magnetic resonance imaging. Ann Neurol. 2000;47:93–100. [PubMed] [Google Scholar]
- Brunet E, Sarfati Y, Hardy-Bayle MC, Decety J. Abnormalities of brain function during a nonverbal theory of mind task in schizophrenia. Neuropsychologia. 2003;41:1574–1582. doi: 10.1016/s0028-3932(03)00119-2. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Frank LR, Wong EC, Siewert B, Warach S, Edelman RR. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med. 1998;40:383–396. doi: 10.1002/mrm.1910400308. [DOI] [PubMed] [Google Scholar]
- DeCarli C, Massaro J, Harvey D, Hald J, Tullberg M, Au R, Beiser A, D'Agostino R, Wolf PA. Measures of brain morphology and infarction in the framingham heart study: establishing what is normal. Neurobiol Aging. 2005;26:491–510. doi: 10.1016/j.neurobiolaging.2004.05.004. [DOI] [PubMed] [Google Scholar]
- Dieterich M, Bartenstein P, Spiegel S, Bense S, Schwaiger M, Brandt T. Thalamic infarctions cause side-specific suppression of vestibular cortex activations. Brain. 2005;128:2052–2067. doi: 10.1093/brain/awh551. [DOI] [PubMed] [Google Scholar]
- Donahue MJ, Lu H, Jones CK, Pekar JJ, van Zijl PC. An account of the discrepancy between MRI and PET cerebral blood flow measures. A high-field MRI investigation. NMR Biomed. 2006;19:1043–1054. doi: 10.1002/nbm.1075. [DOI] [PubMed] [Google Scholar]
- Floyd TF, Ratcliffe SJ, Wang J, Resch B, Detre JA. Precision of the CASL-perfusion MRI technique for the measurement of cerebral blood flow in whole brain and vascular territories. J Magn Reson Imaging. 2003;18:649–655. doi: 10.1002/jmri.10416. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Stephan KE, Lund TE, Morcom A, Kiebel S. Mixed-effects and fMRI studies. Neuroimage. 2005;24:244–252. doi: 10.1016/j.neuroimage.2004.08.055. [DOI] [PubMed] [Google Scholar]
- Golay X, Hendrikse J, Lim TC. Perfusion imaging using arterial spin labeling. Top Magn Reson Imaging. 2004;15:10–27. doi: 10.1097/00002142-200402000-00003. [DOI] [PubMed] [Google Scholar]
- Golay X, Petersen ET. Arterial spin labeling: benefits and pitfalls of high magnetic field. Neuroimaging Clin N Am. 2006;16:259–268. doi: 10.1016/j.nic.2006.02.003. x. [DOI] [PubMed] [Google Scholar]
- Gonzalez-At JB, Alsop DC, Detre JA. Cerebral perfusion and arterial transit time changes during task activation determined with continuous arterial spin labeling. Magn Reson Med. 2000;43:739–746. doi: 10.1002/(sici)1522-2594(200005)43:5<739::aid-mrm17>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Kety SS, Schmidt CF. The Nitrous Oxide Method for the Quantitative Determination of Cerebral Blood Flow in Man: Theory, Procedure and Normal Values. J Clin Invest. 1948;27:476–483. doi: 10.1172/JCI101994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SG, Ugurbil K. Comparison of blood oxygenation and cerebral blood flow effects in fMRI: estimation of relative oxygen consumption change. Magn Reson Med. 1997;38:59–65. doi: 10.1002/mrm.1910380110. [DOI] [PubMed] [Google Scholar]
- Kudo K, Terae S, Katoh C, Oka M, Shiga T, Tamaki N, Miyasaka K. Quantitative cerebral blood flow measurement with dynamic perfusion CT using the vascular-pixel elimination method: comparison with H2(15)O positron emission tomography. AJNR Am J Neuroradiol. 2003;24:419–426. [PMC free article] [PubMed] [Google Scholar]
- Maldjian JA, Laurienti PJ, Burdette JH. Precentral gyrus discrepancy in electronic versions of the Talairach atlas. Neuroimage. 2004;21:450–455. doi: 10.1016/j.neuroimage.2003.09.032. [DOI] [PubMed] [Google Scholar]
- Maldjian JA, Laurienti PJ, Kraft RA, Burdette JH. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage. 2003;19:1233–1239. doi: 10.1016/s1053-8119(03)00169-1. [DOI] [PubMed] [Google Scholar]
- Mildner T, Moller HE, Driesel W, Norris DG, Trampel R. Continuous arterial spin labeling at the human common carotid artery: the influence of transit times. NMR Biomed. 2005;18:19–23. doi: 10.1002/nbm.917. [DOI] [PubMed] [Google Scholar]
- Restom K, Behzadi Y, Liu TT. Physiological noise reduction for arterial spin labeling functional MRI. Neuroimage. 2006;31:1104–1115. doi: 10.1016/j.neuroimage.2006.01.026. [DOI] [PubMed] [Google Scholar]
- Sacco RL, Anand K, Lee HS, Boden-Albala B, Stabler S, Allen R, Paik MC. Homocysteine and the risk of ischemic stroke in a triethnic cohort: the NOrthern MAnhattan Study. Stroke. 2004;35:2263–2269. doi: 10.1161/01.STR.0000142374.33919.92. [DOI] [PubMed] [Google Scholar]
- Scarmeas N, Habeck CG, Zarahn E, Anderson KE, Park A, Hilton J, Pelton GH, Tabert MH, Honig LS, Moeller JR, Devanand DP, Stern Y. Covariance PET patterns in early Alzheimer's disease and subjects with cognitive impairment but no dementia: utility in group discrimination and correlations with functional performance. Neuroimage. 2004;23:35–45. doi: 10.1016/j.neuroimage.2004.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J, T P. Co-Planar Stereotaxic Atlas of the Human Brain. Thieme, Stuttgart, Germany: 1988. [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Wang J, Aguirre GK, Kimberg DY, Roc AC, Li L, Detre JA. Arterial spin labeling perfusion fMRI with very low task frequency. Magn Reson Med. 2003a;49:796–802. doi: 10.1002/mrm.10437. [DOI] [PubMed] [Google Scholar]
- Wang J, Alsop DC, Li L, Listerud J, Gonzalez-At JB, Schnall MD, Detre JA. Comparison of quantitative perfusion imaging using arterial spin labeling at 1.5 and 4.0 Tesla. Magn Reson Med. 2002;48:242–254. doi: 10.1002/mrm.10211. [DOI] [PubMed] [Google Scholar]
- Wang J, Alsop DC, Song HK, Maldjian JA, Tang K, Salvucci AE, Detre JA. Arterial transit time imaging with flow encoding arterial spin tagging (FEAST) Magn Reson Med. 2003b;50:599–607. doi: 10.1002/mrm.10559. [DOI] [PubMed] [Google Scholar]
- Wang J, Zhang Y, Wolf RL, Roc AC, Alsop DC, Detre JA. Amplitude-modulated continuous arterial spin-labeling 3.0-T perfusion MR imaging with a single coil: feasibility study. Radiology. 2005a;235:218–228. doi: 10.1148/radiol.2351031663. [DOI] [PubMed] [Google Scholar]
- Wang Z, Wang J, Connick TJ, Wetmore GS, Detre JA. Continuous ASL (CASL) perfusion MRI with an array coil and parallel imaging at 3T. Magn Reson Med. 2005b;54:732–737. doi: 10.1002/mrm.20574. [DOI] [PubMed] [Google Scholar]
- Werner R, Norris DG, Alfke K, Mehdorn HM, Jansen O. Improving the amplitude-modulated control experiment for multislice continuous arterial spin labeling. Magn Reson Med. 2005;53:1096–1102. doi: 10.1002/mrm.20443. [DOI] [PubMed] [Google Scholar]
- Yang Y, Engelien W, Xu S, Gu H, Silbersweig DA, Stern E. Transit time, trailing time, and cerebral blood flow during brain activation: measurement using multislice, pulsed spin-labeling perfusion imaging. Magn Reson Med. 2000;44:680–685. doi: 10.1002/1522-2594(200011)44:5<680::aid-mrm4>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Yen YF, Field AS, Martin EM, Ari N, Burdette JH, Moody DM, Takahashi AM. Test-retest reproducibility of quantitative CBF measurements using FAIR perfusion MRI and acetazolamide challenge. Magn Reson Med. 2002;47:921–928. doi: 10.1002/mrm.10140. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Slifstein M. A reference effect approach for power analysis in fMRI. Neuroimage. 2001;14:768–779. doi: 10.1006/nimg.2001.0852. [DOI] [PubMed] [Google Scholar]