Rician noise removal by non-Local Means filtering for low signal-to-noise ratio MRI: applications to DT-MRI

Abstract

Diffusion-Weighted MRI (DW-MRI) is subject to random noise yielding measures that are different from their real values, and thus biasing the subsequently estimated tensors. The Non-Local Means (NLMeans) filter has recently been proposed to denoise MRI with high signal-to-noise ratio (SNR). This filter has been shown to allow the best restoration of image intensities for the estimation of diffusion tensors (DT) compared to state-of-the-art methods. However, for DW-MR images with high b-values (and thus low SNR), the noise, which is strictly Rician-distributed, can no longer be approximated as additive white Gaussian, as implicitly assumed in the classical formulation of the NLMeans. High b-values are typically used in high angular resolution diffusion imaging (HARDI) or q-space imaging (QSI), for which an optimal restoration is critical. In this paper, we propose to adapt the NLMeans filter to Rician noise corrupted data. Validation is performed on synthetic data and on real data for both conventional MR images and DT images. Our adaptation outperforms the original NLMeans filter in terms of peak-signal-to-noise ratio (PSNR) for DW-MRI.

1. Introduction

In MRI the data are acquired as complex values which are corrupted by Johnson noise. This noise is well modeled by a Gaussian probability density function in the real and imaginary parts of the complex data. The scanner usually only provides the magnitude of the complex data. In this magnitude image, the initial Gaussian noise in complex space is nonlinearly transformed and the resulting noise is Rician-distributed. This noise induces a bias in the MR intensities, which on average are overestimated compared to their true, unknown value. However, when the SNR is high, the Rician distribution can be conveniently approximated by a Gaussian distribution.

In previous works [1, 2], the non-local means (NLMeans) filter has been applied to conventional MRI and DW-MRI with high SNR and allows the best restoration of image intensities for DT images compared to state-of-the-art methods. The quality of image restoration was compared for three variants of the NLMeans filter and with the anisotropic diffusion (AD) and total variation (TV) method.

However, for DW-MR images with high b-values, the signal is very much attenuated, which yields low SNR values. The noise can no longer be approximated as additive white Gaussian, as implicitly assumed in the classical formulation of the NLMeans. High b-values are typically used in high angular resolution diffusion imaging (HARDI) or q-space imaging (QSI), for which an optimal restoration is critical.

In this paper, we adapt the NLMeans filter to Rician noise corrupted data and we show that our new version outperforms the previously proposed NLMeans filter. In Section 3, we give an overview of the NLMeans filter and the adaptation to Rician distributed noise, and in Section 4, we describe the experiments for the validation of the method on synthetic and real data.

2. Related work

Some methods have been proposed to correct the Rician bias, but most often assume either that 1) the complex data is available (which is not common on clinical scanners, and most importantly useless in case of DW data, due to the motion-induced phase shifts) or that 2) several measures of diffusion induced attenuation are performed at each voxel (which is not realistic in clinical settings) (see Sijbers et al. [3] and references therein). These techniques are thus not applicable at hand, but two remarks can be made. First, there are usually much more DW images to be acquired than what is required to estimate a 6-parameter tensor, or even higher-order representations of diffusion (multiple tensors, spherical harmonics, etc.). Second, most voxels in the image are very likely to exhibit the same diffusion properties as many others in the image (for instance, but not exclusively, voxels in a spatial neighbourhood of the voxel under study). In a word, there is always some (often hidden) redundancy of information in the DW data that could/should be used to explicitly tackle the Rician noise in both estimation and regularisation steps.

In fact, little has been proposed to do so. In DTI, most estimation schemes are based on least squares (LS) regression and variants (linear, non-linear, robust, etc.) on the intensities (or their logarithm), which implicitly considers the underlying noise as Gaussian [4, 5]. In parallel, techniques have been developed to regularize such LS-estimated tensor images [6–11]. It is noteworthy that some of these methods tried to couple estimation and regularisation, but still with an implicit Gaussian assumption on the noise [6], until a recent paper showed how to combine the two tasks with a Rician assumption [11]. Two other attempts have been made to account for the Rician noise to estimate the DT image [12] or to regularize the DW data [13]. The last work experimentally found the regularisation to be more efficient on DWI before tensor estimation compared to the opposite. This is the approach we follow in this paper.

3. Method

3.1. The non-local means filter

The NLMeans filter [1, 14] relies on the redundancy of information contained in the images to remove noise. The filter restores the intensity of the voxel x_i by computing a weighted average of all voxels intensities in the image I.

In the following, we make a few heuristic, intuitive remarks and show how they underlie the original NLMeans algorithm. Then we show how to adapt the NLMeans to Rician-corrupted data.

Gaussian NLMeans

Let us suppose that we have an MR image corrupted by i.i.d. Gaussian noise (0, σ²). If we are given a homogeneous region with n voxels v₁, …, v_n (or equivalently, n measures of the same voxel value), a probabilistic interpretation is to see the voxel values x₁, …, x_n as the realisations of n independent random variables X_i following the same Gaussian law (μ, σ²). A natural way to restore the value x of voxel v in this region is then to replace it by the average $\widehat{x}={\sum }_i\frac{1}{n}{x}_i$. This estimate is very satisfying as it is the maximum likelihood (ML) estimate of x. It can then be noted that, given some weights w_i, E(Σ_i w_iX_i) = μ, even if $w_i\ne \frac{1}{n}$, provided Σ_i w_i = 1.

In practice, no such homogeneous region is available at hand, and several measures of the same voxel value are rarely acquired. However, if one has a way to evaluate the likelihood of each voxel value in the overall image (or in a search volume V) to have been drawn from the same distribution as the current voxel v, and to reflect this likelihood in a weight w_i, then the voxel value x can be restored, using the abovementioned remark, as:

$$NL{M}_G(x)=\sum _{x_i\in V}{w}_i{x}_i.$$ (1)

The idea of the NLMeans filter is to weigh each voxel value x_i in V in the restoration of x using the similarity (in terms of intensity) between their spatial neighbourhoods N and N_i of size S as follows:

$$w_i=\frac{1}{Z(i)}{e}^{-\frac{\sqrt{\frac{1}{S}{\sum }_{k=1}^S\parallel y_k-z_k\mid {\mid }^2}}{h}}$$ (2)

where Z(i) is a normalization constant with Z(i) = Σ_i w_i, y_k and z_k are the values of the k-th voxels in the neighbourhoods N and N_i, and h acts as a filtering parameter (for more details see [1] and Fig. 1). The filtering parameter h is related to the noise variance σ² [15], and is estimated using the pseudo-residual technique proposed by Gasser et al. [16].

Fig. 1. NLMeans principle: A two-dimensional illustration.

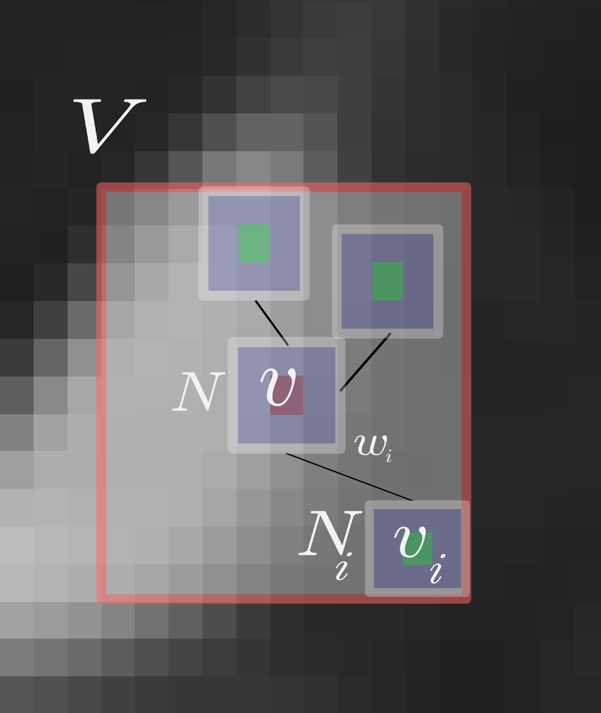
The restored value of voxel v with value x is a weighted average of all intensities x_i of voxels v_i in the search volume V. The weight w_i is based on the similarity of the intensities in cubic neighbourhoods N and N_i around v and v_i.

Rician NLMeans

In case of Rician noise, there is no closed-form for the ML estimate of the true signal μ given n such measures x_i [3]. However, the even order moments of the Rician law have very simple expressions. In particular, the second-order moment is: $E(X_i^2)={\mu }^2+2{\sigma }^2$ where σ² is the variance of the Gaussian noise of complex MRI data. The measured value of $x_i^2$ (and that of x_i) is thus usually overestimated compared to its true, unknown value, which is termed the Rician bias in the following. Using the same remark as in the Gaussian case, that is $E({\sum }_i{w}_i{X}_i^2)={\mu }^2+2{\sigma }^2$ it then seems natural to restore x as $\sqrt{{\sum }_i{w}_i{x}_i^2-2{\sigma }^2}$, the weights w_i being carefully chosen and summing to 1. The voxel value x can be restored as:

$$NL{M}_R(x)=\sqrt{\left(\sum _{x_i\in V}{w}_i{x}_i^2\right)-2{\sigma }^2},$$ (3)

where σ²is the noise variance. As noted by others in case of i.i.d. random variables X_i and with $w_i=\frac{1}{n}$, the term under the square root has a non-null probability to be negative, which decreases when n is large [3]. In such cases the restored value is set to zero. In practice, on real data, negative values are mainly found in the background of the images.

Multiple techniques can be used to estimate the variance of the noise. Fillard et al. [11] estimate the variance by the computation of the average of the squared signal in the background, assuming the true signal to be null in that area and reusing the second-order moment of the Rician p.d.f. According to Landman et al. [12] this approach is not correct due to zero padding in the Fourier transform performed in the scanner. They propose another method requiring multiple acquisitions, which is not desired in clinical settings. Thus we simply estimated the noise variance using the pseudo-residual technique [16]. An online version of both filters (NLM_G and NLM_R) is available for testing on our website: http://www.irisa.fr/visages/benchmarks/.

4. Validation and results

In this section, we propose a validation of the NLM_R filter in comparison with the previously proposed NLMeans [1] called NLM_G in the following. In a first part we compare the quality of both filters in terms of PSNR, on synthetic data corrupted by Rician noise. In a second part, a visual assessment of the filters applied on real images is performed.

4.1. Generation of Rician noise

Given a noise-free image, we generated Rician-corrupted data as follows. For each voxel x of the image, we computed s as:

$$s=\sqrt{{\left(\frac{x}{\sqrt{2}}+n_r\right)}^2+{\left(\frac{x}{\sqrt{2}}+n_i\right)}^2}$$ (4)

where n_r and n_i ~ (0, σ²). The value s is the realisation of a random variable with a Rician p.d.f. with parameters x and σ.

4.2. Validation on synthetic data

A ground truth image was selected and corrupted with Rician noise of known variance, and the PSNR between the reference and denoised image was computed. In these experiments the filtering parameter h (Eq. 2) was set to the noise variance, i.e. h = σ.

Synthetic MRI

The comparison was performed on the total head area and on specific brain tissues for both BrainWeb’s T1w and T2w MR images. Figure 2 displays the PSNR curves on the BrainWeb T1w (resp. T2w) MRI for the different tissues classes. The graph on the left displays the PSNR of the complete head and the graph on the right displays the graph of PSNR for the Gray Matter (GM), White Matter (WM) and Cerebro-Spinal Fluid (CSF) versus the standard deviation σ of the noise, for both filters.

Fig. 2.

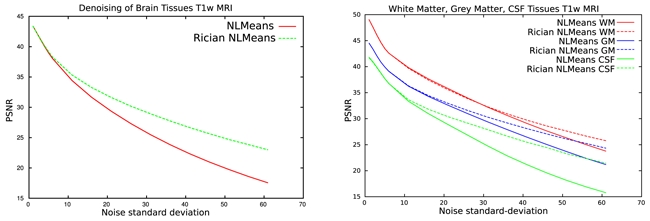
PSNR of synthetic T1w images at different Rician noise levels. Left: PSNR in the head. Right: PSNR in WM, GM and CSF.

These graphs clearly indicate that the NLM_R filter outperforms the NLM_G filter in terms of PSNR values for both tested MR images. For low noise variance the performance of the NLM_R is very close to that of the NLM_G which was expected because for high SNR the Rician noise is almost Gaussian distributed.

Synthetic Diffusion tensors

The application of our filter can remove the need for averaging in HARDI acquisitions and thus allows faster acquisition which will make the HARDI acquisition clinically more feasible. A synthetic DT field was created [6] using anisotropic tensor with different orientations. The DW images were reconstructed using the Stejskal-Tanner [17] equation: $S_i=S_0{e}^{-b{g}_i^{T}D{g}_i}$.

In order to simulate DW-MRI with low SNR values, Rician noise was added to the synthetic DWI and a high b-value (3000 s.mm⁻²) was selected. The gradient directions g_i were taken from a real MR acquisition with 80 directions. In order to compare the ground truth with the resulting denoised tensor fields at different SNR, a Log-Euclidean RMS was used [18]. The NLM_R is closer to the reference tensor image than the NLM_G for the different noise levels (Figure 4).

Fig. 4.

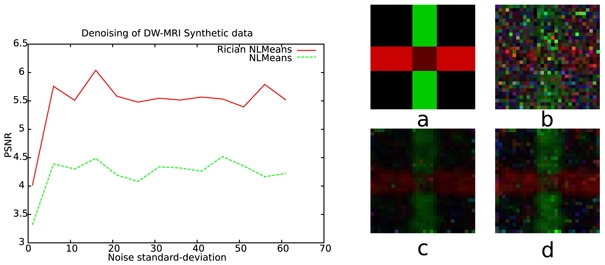
Left: Diffusion tensor RMS comparison of the NLM_G and NLM_R on synthetic data. Right: a) Synthetic tensor field, b) noisy tensor field, c) NLM_G, d) NLM_R.

4.3. Results on real data

In this section, we applied the NLM_R filter on real data for both conventional (T1w and T2w) and DW-MRI data.

T1w and T2w MRI

In the experiments with real conventional MRI data, the behaviour of both filters are quite similar due to the high SNR values of the images acquired in a clinical context. Figure 5 displays a close-up of an acquisition, and the NLM_G and NLM_R filtered version of a T2w MRI. A visual inspection shows a difference between the original version and the two filtered versions. However the two filtered images are visually quite similar.

Fig. 5.

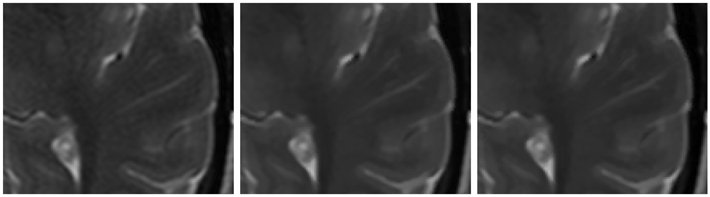
Close-up of a T2w MR image. Left: Acquired Data, Middle: NLM_G, Right: NLM_R

Diffusion-Weighted MRI

In this section, we focus on DW-MRI at high b-value (3000 s.mm²) and with 200 different directions. The experiments on 10 subjects display a higher FA for NLM_R in highly anisotropic regions of the brain compared to the estimation of the tensors on both native data and NLM_G filtered data (Fig. 6).

Fig. 6.

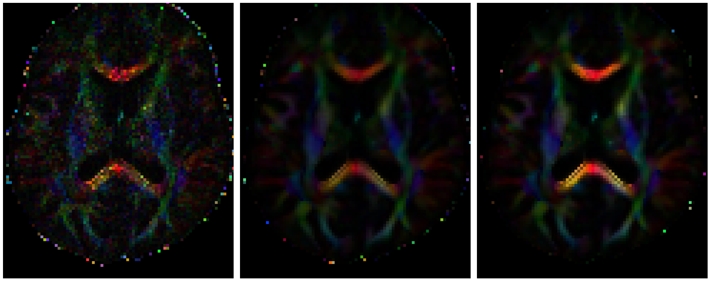
Color Map of diffusion tensor main orientation weighted by the fractional anisotropy. Left: Acquired data, Middle: NLM_G, Right: NLM_R. The Fractional anisotropy of the data is higher in the Rician NLMeans version. The orientations seem in agreement with the known brain anatomy.

5. Discussion and Conclusion

For conventional MRI the Rician NLMeans filter outperforms the previous version of the NLMeans filter. A comparison between the two approaches will be performed in a near future. Previous work showed that this filter is the best one for denoising MRI when compared with state-of-the-art filters [1, 2]. Both NLMeans filters preserve the edges and small structures of the brain such as vessels or multiple sclerosis lesions. Using other arguments, Manjón et al. [19] have recently derived another formula to denoise Rician-corrupted data while removing the bias. Essentially, they proposed to remove 2σ² to the squared restored value (using the Gaussian NLMeans) while we remove it from the restored squared value (using the Gaussian NLMeans). These results on DW-MRI are very important as there is increasing research interest for higher b-values since they have clear advantages compared to lower b-values for angular discrimination (QBalls, ODF) especially in clinical settings for strokes [20] or Alzheimer’s disease [21]. These clinical results could be even further improved with the restoration of the data. The impact of the NLM_R version for HARDI data is evaluated in Descoteaux et al. [22].

Fig. 3.

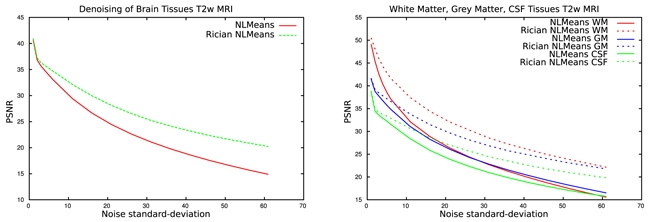
PSNR of synthetic T2w images at different Rician noise levels. Left: PSNR in the head. Right: PSNR in the WM, GM and CSF.