Abstract
Multiple sequence alignments have become one of the most commonly used resources in genomics research. Most algorithms for multiple alignment of whole genomes rely either on a reference genome, against which all of the other sequences are laid out, or require a one-to-one mapping between the nucleotides of the genomes, preventing the alignment of recently duplicated regions. Both approaches have drawbacks for whole-genome comparisons. In this paper we present a novel symmetric alignment algorithm. The resulting alignments not only represent all of the genomes equally well, but also include all relevant duplications that occurred since the divergence from the last common ancestor. Our algorithm, implemented as a part of the VISTA Genome Pipeline (VGP), was used to align seven vertebrate and six Drosophila genomes. The resulting whole-genome alignments demonstrate a higher sensitivity and specificity than the pairwise alignments previously available through the VGP and have higher exon alignment accuracy than comparable public whole-genome alignments. Of the multiple alignment methods tested, ours performed the best at aligning genes from multigene families—perhaps the most challenging test for whole-genome alignments. Our whole-genome multiple alignments are available through the VISTA Browser at http://genome.lbl.gov/vista/index.shtml.
Genome conservation is an essential guide for biologists and bioinformaticians attempting to locate functional elements and formulate biological hypotheses for testing in the laboratory. By searching for highly conserved sequences across multiple species, scientists have identified critical functional elements (Bejerano et al. 2004; Pennacchio et al. 2006; Prabhakar et al. 2006). Sequence conservation is commonly used as input to programs that predict genes (Dewey et al. 2004; Majoros et al. 2005; Gross and Brent 2006), find transcription factor binding sites (Lenhard et al. 2003; Moses et al. 2004), and find other regulatory elements (de la Calle-Mustienes et al. 2005; Abbasi et al. 2007). The conservation signal used by all of these applications is based on alignments between the input genomic sequences.
The first tools developed for alignment of longer genomic regions, such as GLASS (Batzoglou et al. 2000), AVID (Bray et al. 2003), and BLASTZ (Schwartz et al. 2003), could not align more than two DNA sequences. At the same time multiple alignment tools, such as ClustalW (Thompson et al. 1994) and DIALIGN (Morgenstern et al. 1998; Morgenstern 2000), could not handle more than a few kilobases of sequence. To address the need for multiple (three or more sequences) alignment of long genomic regions, several tools have been developed, including LAGAN (Brudno et al. 2003a), MAVID (Bray and Pachter 2004), and TBA (Blanchette et al. 2004). Most recently several methods have been developed for probabilistic alignment of DNA sequences (Lunter et al. 2008; Paten et al. 2008). These tools differ from previous approaches in that they can learn correct alignment parameters directly from the data, and use a probability-based score, instead of the heuristic Needleman–Wunsch penalties used by previous methods. All of these tools use a progressive alignment technique, which is based on the phylogenetic relationship between the sequences being aligned. First, the closest sequences are aligned to each other, and then the resulting alignment is aligned to the more distant sequences, following a phylogenetic tree. The progressive heuristic, because it closely mirrors the evolution of the organisms, has been found to be highly effective for alignment of both DNA (Brudno et al. 2003a; Blanchette et al. 2004; Bray and Pachter 2004; Paten et al. 2008) and protein (Thompson et al. 1994; Do et al. 2005) sequences. In fact, it was shown that multiple DNA sequence alignment methods (as opposed to pairwise) are better at capturing functional signals from phylogenetically diverse vertebrates because of the use of intermediate sequences in multiple alignments (Margulies et al. 2006).
The problem of aligning whole genomes is more difficult than that of aligning individual, shorter DNA segments because it is necessary to find the corresponding (orthologous) blocks in the genomes prior to the actual alignment. Perhaps the most straightforward approach to aligning two whole genomes is to perform local alignment between all of the chromosomes of both of the genomes. However, classical local alignment methods do not consider whether a particular local alignment falls into a larger syntenic block (region without rearrangements). This leads to difficulties with unmasked repeats, and with paralogous copies of various genomic features: For example, when both sequences have n paralogous genes, the classic local alignment methods would yield n 2 alignments between all pairs of these. Despite some of the disadvantages, local alignments were used for comparison of the human and mouse genomes (Ma et al. 2002; Schwartz et al. 2003) and for the human/mouse/rat three-way alignments (Blanchette et al. 2004), because of their high sensitivity when aligning large mammalian genomes with complex rearrangements.
An alternate approach proposed for human/mouse comparison was the tandem local–global approach (Couronne et al. 2003). In this technique, one genome is split up into arbitrary-sized pieces (the authors used 250 kb), and the potential orthologs for each piece is found in the second genome using a rapid, though less sensitive, alignment program, e.g., BLAT (Kent 2002). The sequence was extended around the BLAT anchors and aligned using a global alignment program. This procedure was later expanded to three-way alignment of the human, mouse, and rat genomes (Brudno et al. 2004). Although the tandem approach produces a map that is accurate within large syntenic blocks (regions of genomes without rearrangements), it has two main weaknesses: Small syntenic blocks, resulting from rearrangements within a larger region, may be missed, and the initial arbitrary division of one genome into segments can split a syntenic region, making it difficult to map the region to its true ortholog.
Because of the shortcomings of these methods, there has been increased effort in developing hybrid, “glocal” alignment methods. These methods attempt to combine the advantages of the local and global approaches by modeling the rearrangements (shuffling) that a genome undergoes during evolution. Some of the most common rearrangement events are inversions (a block of DNA changes direction, but not location in the genome), translocations (a piece of DNA moves to a new location in the genome), and duplications (two copies of a block of DNA appear where there was one previously). The more recent algorithms for whole-genome alignments attempt to incorporate the likely evolutionary events as “operations” into their scoring schemes, including several tools that decide whether to accept or reject a local alignment based on other alignments near it. These include Shuffle-LAGAN (Brudno et al. 2003b), Chains and Nets on the UCSC Browser (Kent et al. 2003), Mercator (Dewey 2007), A-Bruijn Block Aligner (Raphael et al. 2004), and Mauve (Darling et al. 2004).
While most of the pairwise whole-genome alignment algorithms described above have been generalized to multiple alignment, these approaches rely on a reference genome, against which all of the other sequences are laid out, or require a one-to-one mapping, where each nucleotide of one genome is constrained to align to, at most, one place in the other genome. Both of these approaches have drawbacks for whole-genome comparisons: The first will not align segments conserved among some genomes, but missing in the reference, while the second will fail to align any element that has undergone a duplication. Most recently, nonreferenced genome alignment implementations have appeared, for example, the Enredo package (Paten et al. 2008), used by the Ensembl genome browser. Enredo builds a genome alignment graph, akin to the A-Bruijn graph alignment of Raphael et al. (2004), and all of the genomes are aligned simultaneously. This approach has the disadvantage of not taking into account the phylogenetic information about the species, making it more difficult to align distant genomes.
In this work, we present a novel, nonreferenced, multiple alignment algorithm. Our approach is based on the progressive technique for multiple alignment and has several advantages over previous algorithms: (1) It does not utilize a reference genome but creates a symmetric alignment equally valid for all genomes; (2) it allows for arbitrary duplications in all genomes and does not require the nucleotides to have a one-to-one mapping; and (3) it is able to align short syntenic blocks based on their adjacency to high-similarity areas, even in the presence of rearrangements. Our results demonstrate that our alignments have high exon alignment accuracy and outperform other approaches, especially for alignment of genes from multigene families and distant species.
Results
Algorithms
Our algorithm is based on progressive alignment, with genomes aligned up the phylogenetic tree. After aligning two genomes, our algorithm joins together syntenic blocks based on the outgroups (those sequences that will be aligned at a later stage: For example, if we have aligned mouse with rat, then human, dog, and chicken are all outgroups). By picking an order of the syntenic blocks that is closest to the outgroups, we facilitate alignment of the more distant genomes.
In the sections below we start by describing SuperMap—a symmetric extension of the pairwise Shuffle-LAGAN algorithm capable of alignment of whole genomes. Secondly, we describe a novel multiple whole-genome alignment algorithm that uses SuperMap for pairwise genome alignment and uses an algorithm based on the Maximum Weight Perfect Matching (MWPM) problem to order the aligned areas of the two genomes to simplify the mapping in the next stages of the progressive algorithm.
SuperMap: Pairwise alignment of genomes
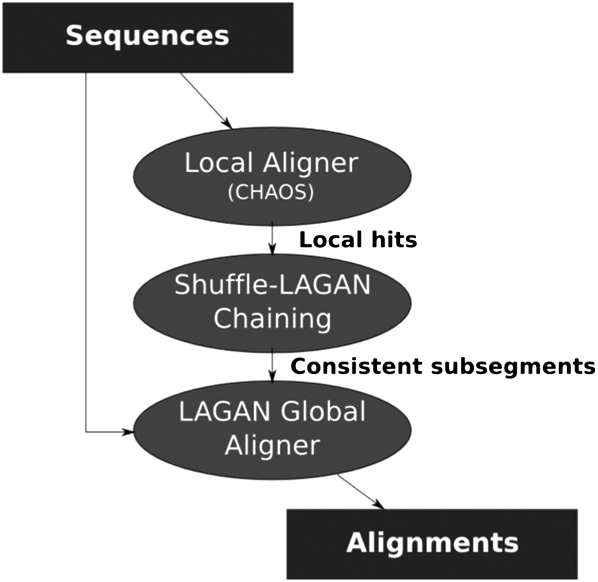
The SuperMap algorithm is based on the original Shuffle-LAGAN (S-LAGAN) chaining algorithm (Brudno et al. 2003b). The S-LAGAN alignment algorithm runs in three stages (Fig. 1). During the first, all local alignments between the two input sequences are located. In the second stage, we select a subset of these alignments to represent a rearrangement map between the two sequences. Finally, regions of conserved synteny (those without rearrangements) are realigned using the LAGAN global alignment algorithm.
Figure 1.
Overview of the Shuffle-LAGAN algorithm. S-LAGAN first locates all local areas of similarity between the two sequences using a local alignment algorithm. A subset of these is selected using the 1-monotonic chaining algorithm (Fig. 2). Finally, global alignments are built (using LAGAN) for consistent subsegments of the 1-monotonic chain (areas without rearrangements). The S-LAGAN algorithm is not symmetric, requiring two alignments to identify all duplications.
The S-LAGAN chaining program takes as input a set of local alignments between the two sequences and returns the maximal scoring subset of these under certain gap criteria. To allow S-LAGAN to catch rearrangements, the collinearity assumption of global algorithms was relaxed to allow the map to be nondecreasing (monotonic) in only one sequence (the “base”), without putting any restrictions on the second sequence. This is called a 1-monotonic conservation map. Perhaps the main weakness of the Shuffle-LAGAN chaining algorithm is its asymmetry, since it depends on one genome being labeled as the “base,” and duplications only in the base genome are aligned.
To address this issue we have built the SuperMap algorithm that solves the symmetry problem by adding a post-processing step. We run S-LAGAN twice, using each sequence as the base (see Fig. 2). This gives us three pieces of data: the original local alignments, which were common to the two runs of S-LAGAN, and two chains of these alignments, each corresponding to the S-LAGAN 1-monotonic maps. We then classify all local alignments as belonging to both chains, and consequently orthologous (best bidirectional hits), or being in only one chain, and hence belonging to a duplication. Local alignments that do not fall into either chain are considered to be false positives and are removed from consideration. We transform the two S-LAGAN chains into a graph as follows: Every alignment becomes a node. If the alignment A2 follows A1 on an S-LAGAN chain, we add an edge going from A1 to A2. Every node that has incoming edges from two different nodes is the beginning of a syntenic block, and every node with two outgoing edges to two different nodes is the end of such a region. Identifying all regions can easily be accomplished in linear time once the S-LAGAN chains are built.
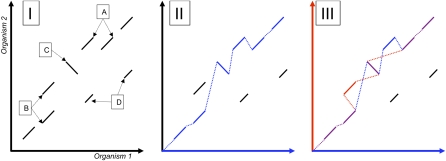
Figure 2.
SuperMap Algorithm. The left side (I) is a dotplot demonstrating the local alignments between two hypothetical genomes. Local alignments A and B correspond to duplications in Organism 1 and Organism 2, respectively. Local alignment C corresponds to an inversion, and local alignments D are spurious false positives. The middle panel (II) shows (in blue) the result of running the regular S-LAGAN 1-monotonic chaining algorithm using Organism 1 as the base. On the right (III) we have built the 1-monotonic maps for Organism 1 (blue) and 2 (red). Whenever these chains merge, they are shown as purple. Similarly, local alignments are colored based on which chains they belong to blue (M1), red (M2), or purple (both, DM). All points where the two chains split or join are borders of a region of conserved synteny.
This SuperMap algorithm has several advantages over regular S-LAGAN: (1) It is able to locate duplications in both sequences, overcoming a major weakness of the original algorithm; (2) in case of transpositions, two of the pieces are no longer arbitrarily joined together; (3) this approach locates both regions of one-to-one similarity (those that were in both 1-monotonic chains) and likely duplications.
Multiple alignment
We have generalized the SuperMap algorithm to alignment of more than two genomes through a progressive alignment framework. Our algorithm reorders, at each internal node of the phylogenetic tree, the alignments between its children genomes to simplify the alignment of these alignments to the next outgroup. We refer to this ordering as the “ancestral” ordering, as it most closely resembles the order of the same regions in the genomes of other, close genomes.
For every node of the tree, our algorithm starts by generating a set of local alignments between the two children genomes. SuperMap chaining is used to identify all rearrangements and define consistent subsegments among the local alignments. The resulting regions are aligned with LAGAN. Given the output of the SuperMap algorithm, for every syntenic block, we consider the two children genomes as the two possible next blocks in the best ordering of the alignments. To decide on the better ordering we use the most proximal outgroups to compute the support for each edge, and then select a subset of these edges such that each syntenic region is preceded by, at most. one region, and followed by, at most, one region.
To build this ancestral ordering, we first use Fitch's algorithm to build a consensus representation of all alignments. Fitch's algorithm recreates the character that should be used in the ancestral genome so as to minimize the number of mutations that take place in the alignment. We align these ancestral contigs to the most proximal outgroups (since we assume that the tree is binary, we follow one edge up the tree, and locate those genomes that are present in the other child of this node). For every breakpoint between syntenic blocks, we determine which of the two children is most likely to be the ancestral order by letting the outgroups “vote” on the proper ordering. Each outgroup is assigned a weight based on its proximity to the ancestral node. The outgroup's vote is distributed between the two children, with the child whose order of conserved elements is closest to the outgroup receiving the bigger fraction.
This problem can be formally written as the Maximum Weight Path Cover problem, in a similar manner to the reduction of the breakpoint median problem to the Traveling Salesman Problem (Sankoff and Blanchette 1998). Each path corresponds to an ordered segment of the ancestral genome. However, this problem is known to be computationally intractable (NP-hard). Consequently, we solve the MWPM problem instead. We reduce the alignment problem to a graph in the same way as in the SuperMap algorithm (see Fig. 3), though the new graph is built based on the syntenic regions that are produced by SuperMap. We define the weights for each edge in the graph based on how much it is supported by outlying genomic sequences. This procedure is explained in detail in the Methods section. The MWPM solution is a set of paths and cycles. We remove the smallest weight edge in each such cycle to break the circular path, and create a (possibly nonoptimal) path cover. For each path we build an ancestral “contig” by filling the gaps between alignments with the genomic sequence that was closer to the ancestor. We use these ancestral contigs in higher levels of the tree.
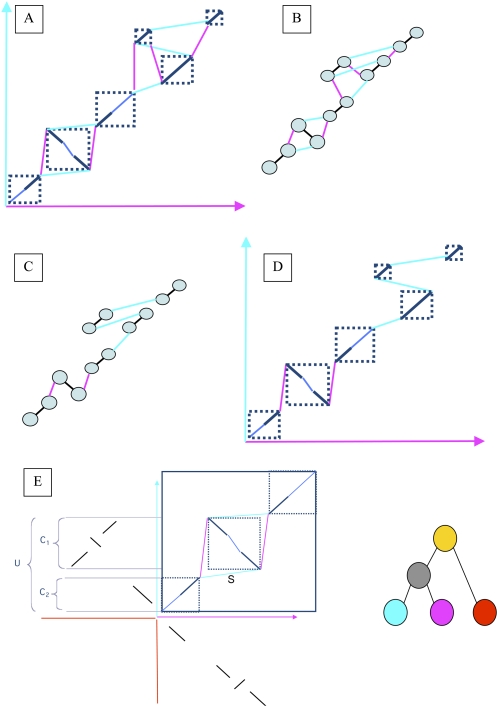
Figure 3.
A schematic representation of the reconstruction of ancestral orderings. (A) The result of running SuperMap on a set of local alignments. (B) The corresponding graph representation, with alignment edges colored black, and connection edges colored by the color of the genome in which these syntenic blocks are adjacent. The weight of all of the edges is computed as shown in E. (C) The output of running the maximum matching algorithm: Each node is connected to only one connection edge, as well as the alignment edge. Note that by removing the alignment edges this graph is decomposed into two connected components, which can be solved separately. (D) The translation of the maximum matching output back to the alignments: The result of the algorithm is a chain of alignments, where the letters of the appropriate genome can be inserted between the sequences. These chains can then be used for alignment in higher nodes of the tree. (E) In this example we are recreating the ancestral order of the gray node in the phylogeny on the right. The top right quadrant shows the output of the SuperMap algorithm applied to the blue and purple genomes. The top left and bottom right quadrants show the local hits of the two genomes on the red outgroup. The selected regions on the left are used to compute the score for the blue edge marked S (S = (U − MIN(C 1 ,C 2))/MAX(C 1 ,C 2)). All of the other edges will be scored the same way, and the MWPM problem is solved in the resulting graph. In this particular case the purple genome will have more support for being the ancestral order than the blue genome.
It is important to note that our “ancestral genome order” and “ancestral contigs” should not be thought of as representing the genome of the ancestor of the organisms being aligned—in fact, it is an ordering of the pieces that will make it easiest to align them to the next outgroup. This idea also appears in the context of progressive alignments of protein sequences, where alignment programs use the UPGMA guide tree to align the sequences, rather than the neighbor-joining tree, even though the neighbor-joining tree is a better approximation of the true phylogeny (Edgar 2004; Nelesen et al. 2008).
Evaluation
Our multiple genome alignment algorithm has been implemented as part of the VISTA Genome Pipeline (VGP) and has been used to align seven vertebrate genomes (human, rhesus, dog, horse, mouse, rat, chicken) and six Drosophila genomes (D. melanogaster, D. ananassae, D. erecta, D. pseudoobscura, D. simulans, and D. yakuba). To evaluate the quality of our alignments we considered two metrics commonly used in alignment literature: the overall coverage of the genome and of important genomic features by high scoring alignments (Schwartz et al. 2003), and the accuracy of alignment of annotated exons (Brudno et al. 2003a; Bray and Pachter 2004). Another metric commonly used to evaluate alignments is the comparison of sequences that have undergone simulated evolution, and for which the true alignment is known. While this approach is useful for comparison of the alignments of regions without rearrangements (Blanchette et al. 2004), where the only allowed evolutionary events are substitutions and insertions/deletions, it is not currently practical for whole-genome alignment, as currently there are no tools for realistic simulation of evolution of a complete genome.
Genome coverage
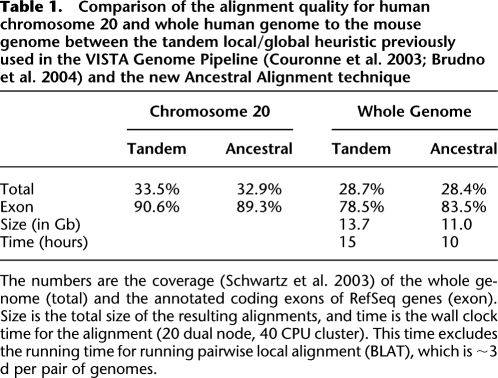
The first analysis we conducted was the comparison of the three-way human–mouse–rat alignment obtained using our progressive whole-genome algorithm with the tandem local/global heuristic previously used by the VISTA Genome Pipeline (Couronne et al. 2003; Brudno et al. 2004). We evaluated the alignments based on the fraction of the gene coding regions and of the whole genome that are aligned above a certain threshold (coverage), and based on the total size of the alignments (specificity). The results (summarized in Table 1) show higher sensitivity and accuracy of the new method in aligning coding regions, while the overall length of the alignment was lower, indicating higher specificity. The increase in exon coverage is due to the fact that the new method is better able to align genes in regions with rearrangements. To illustrate this we demonstrate coverage statistics for chromosome 20, which has almost no rearrangements between the species, and the results of the two methods are very similar.
Table 1.
Comparison of the alignment quality for human chromosome 20 and whole human genome to the mouse genome between the tandem local/global heuristic previously used in the VISTA Genome Pipeline (Couronne et al. 2003; Brudno et al. 2004) and the new Ancestral Alignment technique
The numbers are the coverage (Schwartz et al. 2003) of the whole genome (total) and the annotated coding exons of RefSeq genes (exon). Size is the total size of the resulting alignments, and time is the wall clock time for the alignment (20 dual node, 40 CPU cluster). This time excludes the running time for running pairwise local alignment (BLAT), which is ∼3 d per pair of genomes.
Exon alignment accuracy
Secondly, we compared the overall alignment accuracy of our progressive technique with the alignments produced by the Penn State/UCSC Alignment Pipeline and displayed by the UCSC Genome Browser for two clades: vertebrates and Drosophila. We also compared our vertebrate alignments to the Enredo/Pecan alignments displayed at the Ensembl Genome Browser. To measure the alignment quality we use the method that evaluates exon alignment (Brudno et al. 2003a; Bray and Pachter 2004). For both clades we have designated a reference organism (human and D. melanogaster, respectively). We decomposed the multiple alignments into pairwise alignments between the reference and all other species, and rank each exon of the nonreference genomes based on what percentage of its nucleotides are aligned within an exon in the reference genome. The results are summarized in Figure 4. For the mammalian genomes (Fig. 4A,C) our alignment method consistently achieved exon alignment accuracies of >90%, with the highest accuracy being for dog (94%). The difference between our alignments and those of the UCSC browser were small—we aligned anywhere between 1.6% (rhesus) and 4.8% (horse) more exons completely within a human exon than the UCSC pipeline, with a similar decrease in the number of exons not aligned at all (first column). However, the differences grew when we considered more distant genomes: We were able to align 85% of the annotated chicken exons over their full length to human exons, while the UCSC pipeline aligned 15% less. We found the differences in exon alignment accuracy between the Ensembl and our alignments even greater (Fig. 4D). As became evident from our analysis of multigene families (see below), these differences were mainly due to the inability of the Ensembl pipeline to properly deal with some duplication events.
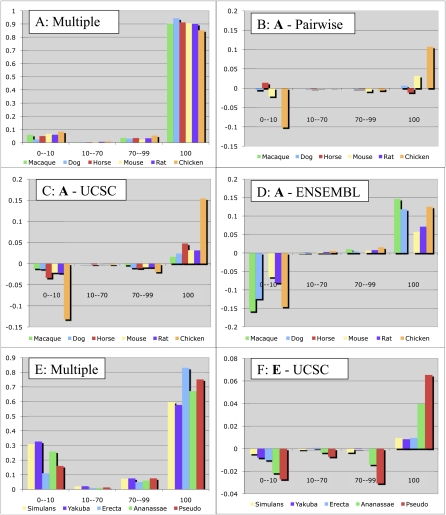
Figure 4.
Exon alignment accuracy for vertebrate (A–D) and Drosophila (E,F) genomes. Each category on the X-axis shows the exons for a particular species that are aligned to a reference genome exon over the given fraction of their length. The Y-axis for A and E shows the overall fraction of exons in each category for our alignments, while the other plots show the difference of these fractions between our multiple alignments and those from the UCSC Genome Browser (ours minus UCSC, C and F), those from the Ensembl browser (D), and our pairwise alignments (B). Our algorithms align more exons perfectly (100% category) and fewer exons are not aligned at all (0–10 category) for all species. In the comparison between our multiple and our pairwise alignments, while the macaque alignments are identical, and the dog alignments are nearly identical (the two species are close), the human/mouse alignment is slightly improved, and nearly 10% of chicken exons were aligned in the multiple but not pairwise alignment. The 23-way Ensembl alignments that we used had a different version of the horse genome, preventing a direct comparison, and we did not generate a pairwise human/rat alignment (rat would be very similar to mouse), hence the missing columns in B and D.
While the overall level of alignment accuracy in the Drosophila genomes was much lower (Fig. 4E, from 83% to 60% of the exons aligned), the overall tendency of our alignment pipeline to perform better than the UCSC browser for alignment of more distant sequences is still evident (Fig. 4F).
Pairwise versus multiple alignment
We wanted to test whether the ancestral multiple alignment method improves results compared with the pairwise one (using the SuperMap anchoring algorithm). Although the algorithm is generally the same, the use of intermediate sequences has been previously shown to improve the alignment of distant orthologs. For example, Margulies et al. (2006) showed that multiple DNA sequence alignment methods (as opposed to pairwise) are substantially better at aligning (or ”capturing”) functional signals from phylogenetically diverse vertebrates. To test this hypothesis we compared the exon accuracy of pairwise alignments between the genomes present in our whole-genome alignment set with the multiple alignment results. The results, summarized in Figure 4B, confirm that using intermediate sequences improves alignment quality, especially when aligning more distant sequences, such as chicken.
Alignment of Inparanoid gene families
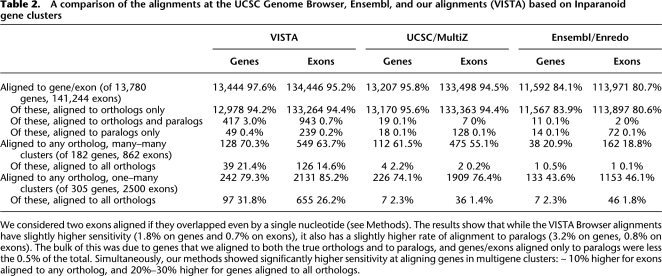
To test not only the sensitivity, but also the specificity of our method, we have compared the multiple alignments to the Inparanoid gene clusters for human and mouse genomes (O'Brien et al. 2005). Inparanoid organizes human and mouse genes into groups, each containing one or more genes from each genome. All of the human and mouse genes within a group (cluster) are orthologs of each other and putatively evolve from a single gene in the genome of the human/mouse ancestor. The Inparanoid clusters are based on pairwise protein BLAST alignments between all of the genes; since this method is significantly different from whole-genome multiple alignments, it provides an independent method for evaluating the accuracy of the alignments. Good genomic multiple alignments should align truly orthologous, rather than paralogous, genes. We considered all of the mouse exons and evaluated their alignments to human exons, labeling every alignment orthologous (aligned within a gene that is an Inparanoid ortholog) or paralogous (to an exon that is not an ortholog). For genes, we considered them orthologous/paralogous if any exon in them was orthologous/paralogous. As is illustrated in Table 2, the alignments generated by our method were the most sensitive (highest fraction of orthologous genes/exons aligned), while the UCSC-based alignments and those from Ensembl were more specific (fewer nonorthologous genes/exons).
Table 2.
A comparison of the alignments at the UCSC Genome Browser, Ensembl, and our alignments (VISTA) based on Inparanoid gene clusters
We considered two exons aligned if they overlapped even by a single nucleotide (see Methods). The results show that while the VISTA Browser alignments have slightly higher sensitivity (1.8% on genes and 0.7% on exons), it also has a slightly higher rate of alignment to paralogs (3.2% on genes, 0.8% on exons). The bulk of this was due to genes that we aligned to both the true orthologs and to paralogs, and genes/exons aligned only to paralogs were less the 0.5% of the total. Simultaneously, our methods showed significantly higher sensitivity at aligning genes in multigene clusters: ∼ 10% higher for exons aligned to any ortholog, and 20%–30% higher for genes aligned to all orthologs.
Secondly, we evaluated the three methods on how well they can align genes that have undergone recent (since the divergence of human and mouse) duplications. To test this we considered only those genes and exons that were in clusters with multiple human and multiple mouse genes (many–many) and those with multiple human genes and a single mouse gene (one–many). For both of these groups, all of the alignment methods were able to align (even to a single ortholog) significantly fewer genes than in the genome as a whole. This trend was especially pronounced for Ensembl, which aligned only 20% of the many–many genes and 44% of the one–many genes to even a single ortholog. Our alignments were the most sensitive for these clusters, aligning 70% and 79% of the genes, respectively. Furthermore, our alignments were the only ones that were able to align more then 3% of either the genes or the exons to all of the orthologs: Only 46 of the 2500 exons in multigene clusters were aligned to all of the orthologs in Ensembl alignments (36 in the UCSC alignments), while 655 were in our alignments.
Discussion
In this paper we describe the design and implementation of a progressive alignment algorithm for whole genomes. Our method differs from other multiple alignment algorithms for whole genomes in that it does not assume a reference genome against which all of the other genomes are laid out. Instead, we combine the “glocal” alignment framework that is widely used in whole-genome alignment with a progressive approach, where at every progressive step we attempt to order the obtained alignments in such a way as to ease the comparison to the next outgroup. Thus, our approach takes advantage of highly conserved segments to align nearby less conserved ones, even in the cases where there has been a rearrangement at the locus in one of the species. We have implemented our method as part of the VISTA Genome Pipeline and applied it to the alignment of seven vertebrate and six fly genomes. We compared the resulting alignments to those available through the UCSC Genome Browser and Ensembl, and show that our approach is more accurate at aligning exons between the species, especially as the evolutionary distance between the organisms grows. All multiple alignments generated by our algorithm are available for browsing and analysis through the VISTA Browser at http://genome.lbl.gov/vista/index.shtml.
At the same time our approach to whole-genome alignment has several weaknesses, which may prove to be fruitful grounds for future work. Our approach toward the reconstruction of “ancestral” sequences for further alignment in the progressive framework does not attempt to reconstruct the true genome of the ancestor species but rather to construct the sequence that is easiest to align to the outgroup. A method that will attempt to reconstruct the true ancestor may be preferable for a wide range of evolutionary studies (Ma et al. 2006). Another potential area of improvement is our treatment of poorly assembled, draft genomes. For such genomes, our algorithm currently resorts to using the reference-based alignment approach, as using a draft genome in our ancestor reconstruction stage has lead to decreased alignment accuracy. Designing a progressive nonreferenced framework for aligning both finished and draft genomes is an important future goal, as many genomes sequenced today are left in draft form.
Perhaps the most evident weakness of ours (and all of the other existing whole-genome alignment algorithms) is the inability to deal with multigene families. While our alignment method was the most sensitive in capturing multigene Inparanoid gene clusters (O'Brien et al. 2005), aligning 70% of the genes and 64% of the exons in Inparanoid clusters with multiple genes from both humans and mice to an ortholog, only 21% and 15% of these were aligned to all of the orthologs (see Table 2). This shows that there is still significant room to improve upon our methods for whole-genome alignments.
Methods
The sections below provide a more thorough description of the various components of our alignment pipeline. The Shuffle-LAGAN chaining algorithm and the original Multi-LAGAN alignment algorithms have been described earlier (Brudno et al. 2003a,b).
Implementation and availability
The whole-genome pipeline algorithm has been implemented in a combination of Perl and C programs, using a MySQL relational database to store both input genomic sequences and generated alignments. All major stages of the pipeline—obtaining local hits with BLAT, SuperMap chaining, aligning syntenic regions with LAGAN, and computing ancestral contigs—make use of a Linux cluster. The pipeline software is publicly available at http://genome.lbl.gov/vista/downloads.shtml.
Local alignments
The local alignments between all sequences can be computed using any alignment algorithm. We typically use BLAT, as it allows for rapid alignment. We run it in a translated DNA mode, indexing nonoverlapping 5-amino acid words, and requiring one word to trigger an alignment.
Global alignments
Global alignments are done with PROLAGAN, which is a variation of the original Multi-LAGAN program that allows for the alignment of two alignments (profiles). The alignment of two profiles is a basic step in the Multi-LAGAN algorithm, and the PROLAGAN executable separates this functionality into a stand-alone program. The algorithm used is identical to the progressive step of the original LAGAN algorithm (Brudno et al. 2003a) and is available as part of the LAGAN toolkit starting with version 2.0.
SuperMap
The SuperMap algorithm is implemented as a stand-alone Perl application and is available as part of the LAGAN Toolkit. After running the S-LAGAN algorithm with both genomes as bases, the local hits that form both of the chains are sorted by their positions in the first genome. The two lists are traversed to identify local alignments that are in both chains, which are referred to as dual monotonic (DM), and those that are in only one of the chains (labeled M1 and M2, depending on the chain). In this first pass we also group alignments that are labeled DM and M1 into segments of conserved synteny by unifying any alignment with the previous one if they are consistent (can be a part of the same global alignment) and have the same type (both M1 or both DM). The local alignments are then re-sorted based on the second genome, and the segments of the type M2 are formed.
This algorithm keeps all of the local alignments on disk, sorted using the Unix sort command. We use only a constant amount of memory, thus allowing for processing of extremely large sets of local alignments efficiently.
Extending the alignments
One of the major weaknesses of fast, heuristic local alignment algorithms is that they often fail to discover weaker areas of similarity, and the borders of syntenic blocks based on these alignments may fail to include important conserved regions nearby because they failed to meet the local alignment criteria. Consequently, the Shuffle-LAGAN algorithm expanded the borders of every syntenic block to the subsequent syntenic block in the base sequence, or up to a constant, whichever was smaller. Expansion in the second sequence was based on a fixed multiplicative factor of the expansion in the first sequence. In SuperMap, we augment this approach by expanding each alignment to the nearest M1 or DM alignment in sequence 1, and either M2 or DM alignment in sequence 2. This approach limits the expansion of alignments to a minimum, while allowing for the addition of the border regions not included in the original set of local alignments.
Computing ancestral contigs
After an alignment between two segments is built, we compute the ancestral contigs as follows:
Infer an ancestral sequence for all of the alignments using Fitch's algorithm (Fitch 1971). Gaps are treated as a fifth character.
Build local alignment between the ancestral sequence and the genomes in the nearest outgroup (the nearest outgroup can have either one or two genomes).
Convert every alignment to an edge that connects the two nodes corresponding to its two endpoints. We will refer to such edges as “alignment edges.” Connect two endpoints if there is no third alignment that falls between them in the genome. This type of edge is referred to as a “connection edge.” See Figure 3, A and B, for an illustration.
Compute the weight for every connection edge by running the S-LAGAN chaining algorithm on all of the local alignments built from every alignment edge, and also on pairs of alignments connected by a connection edge. Let a and b be two syntenic blocks joined by a connection edge. The weight for this edge is computed as follows: For both of the outgroup genomes X1, X2 we find all of the alignments between Xi and both a and b. We find the highest scoring consistent chain of local alignments between Xi and a, Xi and bI, and between Xi and (a ∪ b). Let the cumulative scores of these three chains be called C 1, C 2, and U, respectively. Then we set Wi ab = (U − MIN(C 1,C 2))/MAX(C 1,C 2). Note that Wi ab ranges between 1 and 0, and is the support for the edge EL(a,b) from sequence Xi. We combine the supports to get the weight for the edge between a and b to be Wab = ∑Wi ab/n. This is illustrated in Figure 3E.
Remove the alignment edges from the graph and compute the maximum weight matching on the resulting graph. Remove the smallest edge from every cycle. For efficiency we split the graph into the connected components and perform the procedure on all connected components separately. The result of the maximum weight matching algorithm is shown in Figure 3C.
Any edge in the matching joins together two alignments through a particular genome. Build an ancestral contig by resolving any overlap between the alignment if they overlap in the genome through which they were joined, or by inserting any in-between piece in the joining genome if they do not overlap. This is illustrated in Figure 3D.
Handling low-quality assemblies
When aligning a genome consisting of many short contigs to a high-quality assembly, which usually consists of chromosomes, we modify our algorithm by replacing the ancestral genome ordering stage with one that orders all of the alignments based on their order in the better genome. This is done because a low-quality genome assembly is likely to have regions that appear as duplications but are in reality undercollapsed copies of the same genomic region. The copies are handled as duplications and lead to inaccuracies in the ancestral reconstruction step. Instead, in such cases we create a “faux ancestor” by ordering all of the M1 and DM alignments based on their order in the high-quality genome.
Evaluation based on Inparanoid clusters
We have downloaded the database of human/mouse Inparanoid orthologous gene clusters (O'Brien et al. 2005) from http://inparanoid.sbc.su.se and found the location of the orthologs in our genome assemblies using the tables at the UCSC Genome Browser. Inparanoid builds clusters of orthologous genes based on their pairwise BLASTP scores. We removed from consideration all overlapping genes, as well as clusters where any of the genes had missing locations. The remaining set consisted of 13,780 genes with 141,244 exons. We counted two exons aligned if they overlapped by a single nucleotide in the multiple alignment. Two exons were considered orthologous if they were located on two genes that were members of a single Inparanoid cluster. The one–many and many–many clusters were those that had multiple genes from human and both human and mouse genomes, respectively.
Acknowledgments
We thank Rotem Sorek, Adrian Dalca, and Nilgun Donmez for critical readings of this manuscript. We are also grateful to the anonymous reviewers for their feedback. Funding was provided by the US NIH grant R01-GM81080 and NSERC Discovery Grant 327669. This work was also supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Footnotes
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.081778.108.
References
- Abbasi A.A., Paparidis Z., Malik S., Goode D.K., Callaway H., Elgar G., Grzeschik K.H. Human GLI3 intragenic conserved non-coding sequences are tissue-specific enhancers. PLoS One. 2007;2:e366. doi: 10.1371/journal.pone.0000366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batzoglou S., Pachter L., Mesirov J.P., Berger B., Lander E.S. Human and mouse gene structure: Comparative analysis and application to exon prediction. Genome Res. 2000;10:950–958. doi: 10.1101/gr.10.7.950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bejerano G., Pheasant M., Makunin I., Stephen S., Kent W.J., Mattick J.S., Haussler D. Ultraconserved elements in the human genome. Science. 2004;304:1321–1325. doi: 10.1126/science.1098119. [DOI] [PubMed] [Google Scholar]
- Blanchette M., Kent W.J., Riemer C., Elnitski L., Smit A.F., Roskin K.M., Baertsch R., Rosenbloom K., Clawson H., Green E.D., et al. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 2004;14:708–715. doi: 10.1101/gr.1933104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray N., Pachter L. MAVID: Constrained ancestral alignment of multiple sequences. Genome Res. 2004;14:693–699. doi: 10.1101/gr.1960404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray N., Dubchak I., Pachter L. AVID: A global alignment program. Genome Res. 2003;13:97–102. doi: 10.1101/gr.789803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno M., Do C.B., Cooper G.M., Kim M.F., Davydov E., Green E.D., Sidow A., Batzoglou S. LAGAN and Multi-LAGAN: Efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 2003a;13:721–731. doi: 10.1101/gr.926603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno M., Malde S., Poliakov A., Do C.B., Couronne O., Dubchak I., Batzoglou S. Glocal alignment: Finding rearrangements during alignment. Bioinformatics. 2003b;19:i54–i62. doi: 10.1093/bioinformatics/btg1005. [DOI] [PubMed] [Google Scholar]
- Brudno M., Poliakov A., Salamov A., Cooper G.M., Sidow A., Rubin E.M., Solovyev V., Batzoglou S., Dubchak I. Automated whole-genome multiple alignment of rat, mouse, and human. Genome Res. 2004;14:685–692. doi: 10.1101/gr.2067704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couronne O., Poliakov A., Bray N., Ishkhanov T., Ryaboy D., Rubin E., Pachter L., Dubchak I. Strategies and tools for whole-genome alignments. Genome Res. 2003;13:73–80. doi: 10.1101/gr.762503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darling A.C., Mau B., Blattner F.R., Perna N.T. Mauve: Multiple alignment of conserved genomic sequence with rearrangements. Genome Res. 2004;14:1394–1403. doi: 10.1101/gr.2289704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Calle-Mustienes E., Feijoo C.G., Manzanares M., Tena J.J., Rodriguez-Seguel E., Letizia A., Allende M.L., Gomez-Skarmeta J.L. A functional survey of the enhancer activity of conserved non-coding sequences from vertebrate Iroquois cluster gene deserts. Genome Res. 2005;15:1061–1072. doi: 10.1101/gr.4004805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewey C.N. Aligning multiple whole genomes with Mercator and MAVID. Methods Mol. Biol. 2007;395:221–236. doi: 10.1007/978-1-59745-514-5_14. [DOI] [PubMed] [Google Scholar]
- Dewey C., Wu J.Q., Cawley S., Alexandersson M., Gibbs R., Pachter L. Accurate identification of novel human genes through simultaneous gene prediction in human, mouse, and rat. Genome Res. 2004;14:661–664. doi: 10.1101/gr.1939804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do C.B., Mahabhashyam M.S., Brudno M., Batzoglou S. ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome Res. 2005;15:330–340. doi: 10.1101/gr.2821705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. MUSCLE: A multiple sequence alignment method with reduced time and space complexity. BMC Bioinformatics. 2004;5:113. doi: 10.1186/1471-2105-5-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitch W.M. Toward defining the course of evolution: Minimum change for a specific tree topology. Syst. Zool. 1971;20:406–416. [Google Scholar]
- Gross S.S., Brent M.R. Using multiple alignments to improve gene prediction. J. Comput. Biol. 2006;13:379–393. doi: 10.1089/cmb.2006.13.379. [DOI] [PubMed] [Google Scholar]
- Kent W.J. BLAT—the BLAST-like alignment tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent W.J., Baertsch R., Hinrichs A., Miller W., Haussler D. Evolution's cauldron: Duplication, deletion, and rearrangement in the mouse and human genomes. Proc. Natl. Acad. Sci. 2003;100:11484–11489. doi: 10.1073/pnas.1932072100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenhard B., Sandelin A., Mendoza L., Engstrom P., Jareborg N., Wasserman W.W. Identification of conserved regulatory elements by comparative genome analysis. J. Biol. 2003;2:13. doi: 10.1186/1475-4924-2-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunter G., Rocco A., Mimouni N., Heger A., Caldeira A., Hein J. Uncertainty in homology inferences: Assessing and improving genomic sequence alignment. Genome Res. 2008;18:298–309. doi: 10.1101/gr.6725608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma B., Tromp J., Li M. PatternHunter: Faster and more sensitive homology search. Bioinformatics. 2002;18:440–445. doi: 10.1093/bioinformatics/18.3.440. [DOI] [PubMed] [Google Scholar]
- Ma J., Zhang L., Suh B.B., Raney B.J., Burhans R.C., Kent W.J., Blanchette M., Haussler D., Miller W. Reconstructing contiguous regions of an ancestral genome. Genome Res. 2006;16:1557–1565. doi: 10.1101/gr.5383506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majoros W.H., Pertea M., Salzberg S.L. Efficient implementation of a generalized pair hidden Markov model for comparative gene finding. Bioinformatics. 2005;21:1782–1788. doi: 10.1093/bioinformatics/bti297. [DOI] [PubMed] [Google Scholar]
- Margulies E.H., Chen C.W., Green E.D. Differences between pair-wise and multi-sequence alignment methods affect vertebrate genome comparisons. Trends Genet. 2006;22:187–193. doi: 10.1016/j.tig.2006.02.005. [DOI] [PubMed] [Google Scholar]
- Morgenstern B. A space-efficient algorithm for aligning large genomic sequences. Bioinformatics. 2000;16:948–949. doi: 10.1093/bioinformatics/16.10.948. [DOI] [PubMed] [Google Scholar]
- Morgenstern B., Frech K., Dress A., Werner T. DIALIGN: Finding local similarities by multiple sequence alignment. Bioinformatics. 1998;14:290–294. doi: 10.1093/bioinformatics/14.3.290. [DOI] [PubMed] [Google Scholar]
- Moses A.M., Chiang D.Y., Pollard D.A., Iyer V.N., Eisen M.B. MONKEY: Identifying conserved transcription-factor binding sites in multiple alignments using a binding site-specific evolutionary model. Genome Biol. 2004;5:R98. doi: 10.1186/gb-2004-5-12-r98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelesen S., Liu K., Zhao D., Linder C.R., Warnow T. The effect of the guide tree on multiple sequence alignments and subsequent phylogenetic analyses. Pac. Symp. Biocomput. 2008;13:25–36. doi: 10.1142/9789812776136_0004. [DOI] [PubMed] [Google Scholar]
- O'Brien K.P., Remm M., Sonnhammer E.L.L. Inparanoid: A comprehensive database of eukaryotic orthologs. Nucleic Acids Res. 2005;33:D476. doi: 10.1093/nar/gki107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paten B., Herrero J., Beal K., Fitzgerald S., Birney E. Enredo and Pecan: Genome-wide mammalian consistency-based multiple alignment with paralogs. Genome Res. 2008;18:1814–1828. doi: 10.1101/gr.076554.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennacchio L.A., Ahituv N., Moses A.M., Prabhakar S., Nobrega M.A., Shoukry M., Minovitsky S., Dubchak I., Holt A., Lewis K.D., et al. In vivo enhancer analysis of human conserved non-coding sequences. Nature. 2006;444:499–502. doi: 10.1038/nature05295. [DOI] [PubMed] [Google Scholar]
- Prabhakar S., Poulin F., Shoukry M., Afzal V., Rubin E.M., Couronne O., Pennacchio L.A. Close sequence comparisons are sufficient to identify human cis-regulatory elements. Genome Res. 2006;16:855–863. doi: 10.1101/gr.4717506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raphael B., Zhi D., Tang H., Pevzner P. A novel method for multiple alignment of sequences with repeated and shuffled elements. Genome Res. 2004;14:2336–2346. doi: 10.1101/gr.2657504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankoff D., Blanchette M. Multiple genome rearrangement and breakpoint phylogeny. J. Comput. Biol. 1998;5:555–570. doi: 10.1089/cmb.1998.5.555. [DOI] [PubMed] [Google Scholar]
- Schwartz S., Kent W.J., Smit A., Zhang Z., Baertsch R., Hardison R.C., Haussler D., Miller W. Human–mouse alignments with BLASTZ. Genome Res. 2003;13:103–107. doi: 10.1101/gr.809403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson J.D., Higgins D.G., Gibson T.J. ClustalW: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]